Как найти ток до разветвления цепи

Последовательное и
параллельное соединение сопротивлений

Последовательное соединение сопротивлений

Возьмем три постоянных сопротивления R1, R2
и R3 и включим их в цепь
так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R2, конец второго — с началом третьего R3, а к началу первого сопротивления и к концу
третьего подведем проводники от источника тока (рис. 1).

Такое соединение сопротивлений называется
последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и
тот же. 

 

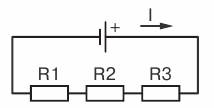
Рис 1. Последовательное
соединение сопротивлений

Как определить общее сопротивление цепи, если все
включенные в нее последовательно сопротивления мы уже знаем? Используя
положение, что напряжение U на зажимах источника тока равно сумме падений
напряжений на участках цепи, мы можем написать:

U = U1 + U2 + U3

где

U1 = IR1 U2 = IR2 и U3 = IR3

или

IR = IR1 + IR2 + IR3

Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3).

Поделив теперь обе части равенства на I, будем окончательно иметь R = R1 + R2 + R3

Таким образом, мы пришли к выводу, что при
последовательном соединении сопротивлений общее сопротивление всей цепи равно
сумме сопротивлений отдельных участков.

Проверим этот вывод на следующем примере. Возьмем
три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R2 = 20 Ом и R3 = 50 Ом). Соединим их последовательно
(рис. 2) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).

 

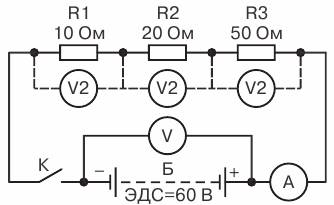
Рис. 2. Пример
последовательного соединения трех сопротивлений

Подсчитаем, какие показания должны дать приборы,
включенные, как показано на схеме, если замкнуть цепь. Определим внешнее
сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.

Найдем ток в цепи по закону Ома: 60 / 80=
0,75 А

Зная ток в цепи и сопротивления ее участков,
определим падение напряжения на каждое участке цепи U1 = 0,75х 10 = 7,5 В, U2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.

Зная падение напряжений на участках, определим
общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника
тока U = 7,5+15 + 37,5 = 60 В.

Мы получили таким образом, что U = 60 В, т. е.
несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это
тем, что мы пренебрегли внутренним сопротивлением источника тока.

Замкнув теперь ключ выключатель К, можно
убедиться по приборам, что наши подсчеты примерно верны. 

Параллельное соединение сопротивлений

Возьмем два постоянных сопротивления R1 и R2 и
соединим их так, чтобы начала этих сопротивлений были включены в одну общую
точку а, а концы — в другую общую точку б. Соединив затем точки а и б с
источником тока, получим замкнутую электрическую цепь. Такое соединение
сопротивлений называется параллельным соединением. 

 

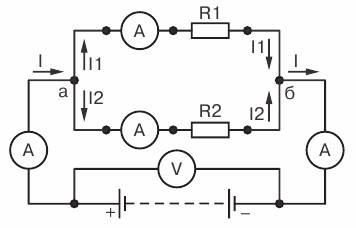
Рис 3. Параллельное соединение
сопротивлений

Проследим течение тока в этой цепи. От
положительного полюса источника тока по соединительному проводнику ток дойдет
до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на
две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с
сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I2. Каждый из этих токов пойдет по своей ветви до
точки б. В этой точке произойдет слияние токов в один общий ток, который и
придет к отрицательному полюсу источника тока.

Таким образом, при параллельном соединении
сопротивлений получается разветвленная цепь. Посмотрим, какое же будет
соотношение между токами в составленной нами цепи.

Включим амперметр между положительным полюсом
источника тока (+) и точкой а и заметим его показания. Включив затем амперметр
(показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным
полюсом источника тока (—), заметим, что прибор покажет ту же величину силы
тока.

Значит, сила тока в цепи до ее
разветвления (до точки а) равна силе тока после разветвления цепи (после точки
б).

Будем теперь включать амперметр поочередно в
каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр
покажет силу тока I1, а во второй — I2. Сложив эти два показания амперметра, мы получим суммарный ток, по
величине равный току I до разветвления (до точки а).

Следовательно, сила тока, протекающего до
точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой,
получим

Это соотношение, имеющее большое практическое
значение, носит название закона разветвленной цепи.

Рассмотрим теперь, каково будет соотношение между
токами в ветвях.

Включим между точками а и б вольтметр и
посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение
источника тока, так как он подключен, как это видно из рис. 3, непосредственно
к зажимам источника тока. Во-вторых, вольтметр покажет падения напряженийU1 и U2 на сопротивлениях R1 и R2, так как он соединен с началом и концом
каждого сопротивления.

Следовательно, при параллельном соединении
сопротивлений напряжение на зажимах источника тока равно падению напряжения на
каждом сопротивлении.

Это дает нам право написать, что U = U1 = U2,

где U — напряжение на зажимах источника тока;
U1 — падение напряжения на сопротивлении R1, U2 — падение напряжения на
сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно
равно произведению силы тока, протекающего через этот участок, на сопротивление
участка U = IR.

Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2, но так как U1 = U2, то и I1R1 = I2R2.

Применяя к этому выражению правило пропорции,
получим I1/ I2 = U2 / U1 т. е. ток в первой ветви будет во столько раз
больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой
ветви меньше (или больше) сопротивления второй ветви. 

Итак, мы пришли к важному выводу, заключающемуся
в том, что при параллельном соединении сопротивлений общий ток цепи
разветвляется на токи, обратно пропорциональные величинам сопротивлении
параллельных ветвей. Иначе говоря, чем больше сопротивление
ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление
ветви, тем больший ток потечет через эту ветвь. 

Убедимся в правильности этой зависимости на
следующем примере. Соберем схему, состоящую из двух параллельно соединенных
сопротивлений R1 и R2, подключенных к источнику тока. Пусть R1= 10 Ом, R2 = 20 Ом и U = 3 В.

Подсчитаем сначала, что покажет нам амперметр,
включенный в каждую ветвь:

I1 = U / R1 = 3 / 10 = 0,3 А = 300 мА

I2 = U / R2 = 3 / 20 = 0,15 А = 150 мА

Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА

Проделанный нами расчет подтверждает, что при
параллельном соединении сопротивлений ток в цепи разветвляется обратно
пропорционально сопротивлениям.

Действительно, R1 == 10 Ом вдвое меньше R2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что
большая его часть (I1 = 300 мА) пошла через меньшее сопротивление (R1 = 10 Ом), а меньшая часть (R2 = 150 мА) —через большее сопротивление (R2 = 20 Ом).

Такое разветвление тока в параллельных ветвях
сходно с течением жидкости по трубам. Представьте себе трубу А, которая в
каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4).
Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то
же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды
большее сопротивление. 

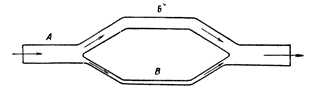
Рис. 4. Через тонкую
трубу в один и тот же промежуток времени пройдет воды меньше, чем через толстую

Рассмотрим теперь, чему будет равно общее
сопротивление внешней цепи, состоящей из двух параллельно соединенных
сопротивлений.

Под этим общим сопротивлением внешней
цепи надо понимать такое сопротивление, которым можно было бы заменить при
данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при
этом тока до разветвления. Такое сопротивление называется эквивалентным
сопротивлением.

Вернемся к цепи, показанной на рис. 3, и
посмотрим, чему будет равно эквивалентное сопротивление двух параллельно
соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем
написать: I = U/R, где I — ток во внешней цепи (до точки
разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т.
е. эквивалентное сопротивление.

Точно так же для каждой ветви I1 = U1 / R1, I2 = U2 / R2, где I1 и I2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей. 

По закону разветвленной цепи: I = I1 + I2

Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2

Так как при параллельном соединении U = U1 = U2, то можем написать U / R = U / R1 + U / R2

Вынеся U в правой части равенства за скобки,
получим U / R = U (1 / R1 + 1 / R2)

Разделив теперь обе части равенства на U, будем окончательно иметь 1 / R= 1 / R1 + 1 / R2

Помня, что проводимостью называется
величина, обратная сопротивлению, мы можем сказать, что в полученной
формуле 1 / R – проводимость
внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость
второй ветви.

На основании этой формулы делаем вывод: при
параллельном соединении проводимость внешней цепи равна сумме проводимостей
отдельных ветвей.

Следовательно, чтобы определить
эквивалентное сопротивление включенных параллельно сопротивлений, надо
определить проводимость цепи и взять величину, ей обратную.

Из формулы также следует, что проводимость цепи больше
проводимости каждой ветви, а это значит, что эквивалентное
сопротивление внешней цепи меньше наименьшего из включенных параллельно
сопротивлений. 

Рассматривая случай параллельного соединения
сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако
на практике могут встретиться случаи, когда цепь состоит из трех и более
параллельных ветвей. Как же поступать в этих случаях?

Оказывается, все полученные нами соотношения
остаются справедливыми и для цепи, состоящей из любого числа параллельно
соединенных сопротивлений.

Чтобы убедиться в этом, рассмотрим следующий
пример.

Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно.
Определим эквивалентное сопротивление цепи (рис. 5). 

 

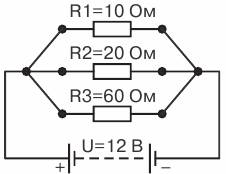
Рис. 5. Цепь с тремя
параллельно соединенными сопротивлениями

Применяя для этой цепи формулу 1 / R= 1 / R1 + 1 / R2, можем написать 1 / R= 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R= 1 / 10 + 1 / 20 + 1 / 60

Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е..
проводимость цепи 1 / R = 1 / 6 Следовательно,эквивалентное сопротивление R =
6 Ом.

Таким образом, эквивалентное
сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений,
т. е. меньше сопротивления R1.

Посмотрим теперь, действительно ли это
сопротивление является эквивалентным, т. е. таким, которое могло бы заменить
включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы
тока до разветвления цепи.

Допустим, что напряжение внешней цепи, а следовательно,
и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1,2 А I2 = U/R2 = 12 / 20 = 1,6 А I3 = U/R1 = 12 / 60 = 0,2 А

Общий ток в цепи получим, пользуясь
формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.

Проверим по формуле закона Ома, получится ли в
цепи ток силой 2 А, если вместо трех параллельно включенных известных нам
сопротивлений включено одно эквивалентное им сопротивление 6 Ом.

I = U/R= 12 / 6 = 2 А

Как видим, найденное нами сопротивление R = 6 Ом
действительно является для данной цепи эквивалентным.

В этом можно убедиться и на измерительных
приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во
внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления
одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и
в другом случае будут примерно одинаковыми.

На практике могут встретиться также параллельные
соединения, для которых рассчитать эквивалентное сопротивление можно проще, т.
е. не определяя предварительно проводимостей, сразу найти сопротивление.

Например, если соединены параллельно два
сопротивления R1 и R2, то формулу 1 / R= 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство
относительно R, получитьR = R1 х R2 / (R1 + R2), т. е. при
параллельном соединении двух сопротивлений эквивалентное сопротивление цепи
равно произведению включенных параллельно сопротивлений, деленному на их сумму.

Электрическая цепь и ее
элементы

В электрической
цепи должен быть источник движения электрически заряженных частиц, которое и
называется электрическим током. Иными словами, электрический ток должен иметь
своего возбудителя. Такой возбудитель тока, именуемый источником (генератором),
является составным элементом электрической цепи.

Электрический ток может вызывать различные по
характеру эффекты — так, он заставляет светиться лампочки накаливания, приводит
в действие нагревательные приборы и электродвигатели. Все эти приборы и
устройства принято называть приемниками электрического тока. Так как через них
протекает ток, т. е. они включены в электрическую цепь, то приемники также
являются элементами цепи.

Протекание тока требует, чтобы между источником и
приемником существовала связь, которая и реализуется при помощи электрических
проводов, представляющих со­ бой третий важный составной элемент электрической
цепи. 

Электрическая цепь – совокупность устройств, предназначенных для прохождения
электрического тока. Цепь образуется источниками энергии (генераторами),
потребителями энергии (нагрузками), системами передачи энергии (проводами).

Электрическая цепь – совокупность устройств и
объектов, образующих путь для электрического тока,
электромагнитные процессы в которых могут быть описаны с помощью понятии об
электродвижущей силе, токе и напряжении.

Простейшая электрическая установка состоит из
источника (гальванического элемента, аккумулятора, генератора и т. п.),
потребителей или приемников электрической энергии (ламп накаливания, электронагревательных приборов,
электродвигателей и т. п.) и соединительных проводов, соединяющих зажимы
источника напряжения с зажимами потребителя. Т.е.электрическая цепь –
совокупность соединенных между собой источников электрической энергии,
приемников и соединяющих их проводов (линия передачи).

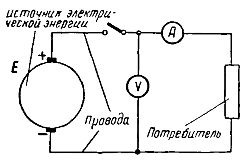
Рис.1. Схема электрической
цепи

Электрическая цепь делится на внутреннюю и
внешнюю части. К внутренней части электрической цепи относится сам источник
электрической энергии. Во внешнюю часть цепи входят соединительные провода,
потребители, рубильники, выключатели, электроизмерительные приборы, т. е. все то,
что присоединено к зажимам источника электрической энергии. 

Электрический ток может протекать только по
замкнутой электрической цепи. Разрыв цепи
в любом месте вызывает прекращение электрического тока. 

Под электрическими цепями постоянного тока в электротехнике подразумевают цепи, в которых ток не меняет
своего направления, т. е. полярность источников ЭДС в которых постоянна. 

Под электрическими цепями переменного
тока имеют ввиду цепи, в которых протекает ток, который изменяется во
времени (смотрите, переменный ток). 

Источники питания цепи – это гальванические
элементы, электрические аккумуляторы, электромеханические генераторы,
термоэлектрические генераторы, фотоэлементы и др. В современной технике в
качестве источников энергии применяют главным образом электрические генераторы.
Все источники питания имеют внутреннее сопротивление значение которого невелико по сравнению с сопротивлением других
элементов электрической цепи. 

Электроприемниками постоянного тока являются
электродвигатели, преобразующие электрическую энергию в механическую,
нагревательные и осветительные приборы, электролизные установки и др. 

В качестве вспомогательного оборудования в
электрическую цепь входят аппараты для включения и отключения (например,
рубильники), приборы для измерения электрических величин (например, амперметры
и вольтметры), аппараты защиты (например, плавкие предохранители).

Все электроприемники характеризуются
электрическими параметрами, среди которых основные – напряжение и мощность. Для
нормальной работы электроприемника на его зажимах необходимо поддерживать номинальное напряжение. 

Элементы электрической цепи делятся на активные и
пассивные. К активным элементам электрической цепи относятся
те, в которых индуцируется ЭДС (источники ЭДС, электродвигатели, аккумуляторы в
процессе зарядки и т. п.). К пассивным элементам относятся
электроприемники и соединительные провода. 

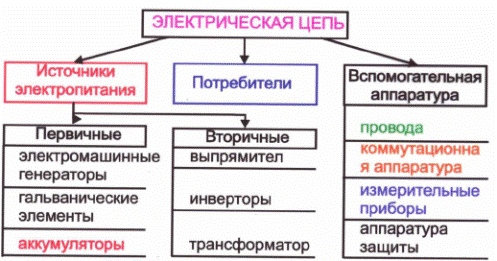
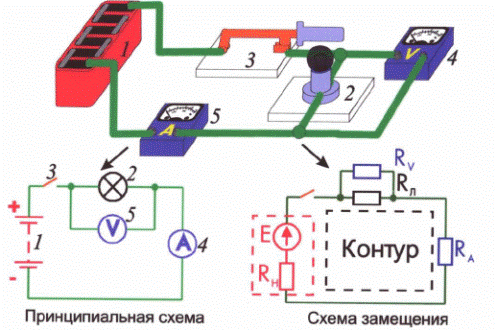
Для условного изображения электрических цепей
служат электрические схемы. На этих схемах источники, приемники, провода и все
другие приборы и элементы электрической цепи обозначаются при помощи
выполненных определенным образом условных знаков (графических обозначений).

Согласно ГОСТ 18311-80:

Силовая электрическая цепь – электрическая цепь, содержащая элементы, функциональное
назначение которых состоит в производстве или передаче основной части
электрической энергии, ее распределении, преобразовании в другой вид энергии
или в электрическую энергию с другими значениями параметров.

Вспомогательная цепь электротехнического изделия
(устройства) – электрическая цепь различного
функционального назначения, не являющаяся силовой электрической цепью
электротехнического изделия (устройства).

Электрическая цепь управления – вспомогательная цепь электротехнического изделия (устройства),
функциональное назначение которой состоит в приведении в действие
электрооборудования и (или) отдельных электротехнических изделий или устройств
или в изменении значений их параметров.

Электрическая цепь сигнализации – вспомогательная цепь электротехнического изделия (устройства),
функциональное назначение которой состоит в приведении в действие сигнальных
устройств.

Электрическая цепь измерения – вспомогательная цепь электротехнического изделия (устройства),
функциональное назначение которой состоит в измерении и (или) регистрации
значений параметров и (или) получении информации измерений электротехнического
изделия (устройства) или электрооборудования.

По топологическим особенностям электрические цепи подразделяют: 

·        
на простые (одноконтурные), двухузловые и сложные
(многоконтурные, многоузловые, планарные (плоскостные) и объемные); 

·        
двухполюсные, имеющие два внешних вывода
(двухполюсники и многополюсные, содержащие более двух внешних выводов (четырехполюсники,
многополюсники).

Источники и приемники (потребители) энергии с
точки зрения теории цепей являются двухполюсниками, так как для их работы
необходимо и достаточно двух полюсов, через которые они передают либо принимают
энергию. Тот или иной двухполюсник называют активным, если он содержит
источник, или пассивным – если он не содержит источник (соответственно, левая и
правая части схемы). 

Устройства, передающие энергию от источников к
приемникам, являются четырехполюсниками, так как они должны обладать, по
меньшей мере, четырьмя зажимами для передачи энергии от генератора к нагрузке.
Простейшим устройством передачи энергии являются провода. 

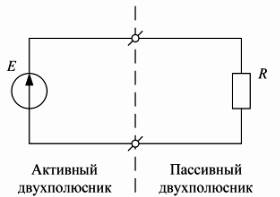
Активный и пассивный
двухполюсники в электрической цепи

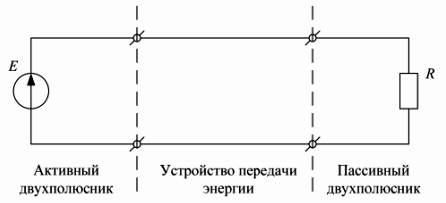
Обобщенная эквивалентная схема
электрической цепи

Элементы электрической цепи, обладающие
электрическим сопротивлением и называемые резисторами, характеризуются так
называемой вольт-амперной характеристикой –зависимостью
напряжения на зажимах элемента от тока в нем или зависимостью тока в элементе
от напряжения на его зажимах.

Если сопротивление элемента постоянно при любом
значении тока в нем и любом значении приложенного к нему напряжения, то
вольт-амперная характеристика прямая линия и такой элемент называется линейным
элементом. 

В общем случае сопротивление зависит как
от тока, так и от напряжения. Одна из причин этого состоит в изменении
сопротивления проводника при протекании по нему тока из-за его нагрева. При
повышении температуры сопротивление проводника увеличивается. Но так как во
многих случаях эта зависимость незначительна, элемент считают линейным. 

Электрическая цепь, электрическое сопротивление
участков которой не зависит от значений инаправлений токов и напряжений
в цепи, называется линейной электрической цепью. Такая цепь состоит
только из линейных элементов, а ее состояние описывается линейными
алгебраическими уравнениями. 

Если сопротивление элемента цепи существенно
зависит от тока или напряжения, то вольт-амперная характеристика носит
нелинейный характер, а такой элемент называется нелинейным элементом. 

Электрическая цепь, электрическое сопротивление
хотя бы одного из участков которой зависит от значений или от направлений токов
и напряжений в этом участке цепи, называется нелинейной электрической цепью. Такая цепь содержит хотя бы один нелинейный элемент. 

При описании свойств электрических цепей
устанавливается связь между величинами электродвижущей силы (ЭДС), напряжений и
токов в цепи с величинами сопротивлений, индуктивностей, емкостей и способом
построения цепи. 

При анализе электрических схем пользуются
следующими топологическими параметрами схем: 

·        
ветвь — участок
электрической цепи, вдоль которого протекает один и тот же электрический
ток; 

·        
узел — место соединения
ветвей электрической цепи. Обычно место, где соединены две ветви, называют не
узлом, а соединением (или устранимым узлом), а узел соединяет не менее трех
ветвей; 

·        
контур —
последовательность ветвей электрической цепи, образующая замкнутый путь, в
которой один из узлов одновременно является началом и концом пути, а остальные
встречаются только один раз.

Скачано с www.znanio.ru

На прошлом уроке мы рассмотрели последовательное соединение проводников. При нем сила тока на всех участках цепи одинакова ($I = I_1 = I_2 = … = I_n$), а сопротивление всей цепи складывается из сопротивлений всех проводников, составляющих ее ($R = R_1 + R_2 + … + R_n$). Напряжение (подобно сопротивлению) всей цепи рассчитывается сложением напряжений на концах всех элементов, составляющих такую электрическую цепь ($U = U_1 + U_2 + … + U_n$).

На данном уроке мы рассмотрим другой вид соединения проводников — параллельный. Так мы подсоединяли вольтметр, когда измеряли напряжение на каком-либо участке цепи. Сейчас же мы рассмотрим закономерности для силы тока, сопротивления и напряжения в цепи для такого типа соединения.

Параллельное включение элементов в электрическую цепь

Какое соединение проводников называют параллельным?

Соберем электрическую цепь с таким соединением. Цепь будет состоять из источника тока, ключа и двух электроламп. Электролампы включены в цепь параллельно (рисунок 1).

Схема этой электрической цепи изображена на рисунке 2.

На схеме обозначены две точки A и B. Важный момент:

При параллельном соединении все входящие в него проводники одним своим концом присоединяются к точке A, а вторым концом — к другой точке B.

Так мы можем подключить еще несколько ламп или некоторое количество других потребителей электроэнергии. Поэтому все закономерности, которые мы рассмотрим далее, будут справедливы для любого количества параллельно подключенных в цепь проводников между точками A и B.

Напряжение в цепи при параллельном соединении проводников

Вольтметр подсоединяется в цепь параллельно. Взгляните на рисунок 3.

Можно ли сказать, что мы измеряем напряжение только на одной из ламп? Нет. Получается, что одновременно мы измеряем напряжения и на одной, и на другой лампе. Мы приходим к следующему заключению.

Напряжение на участке цепи AB и на концах всех параллельно соединенных проводников одно и то же:
$U = U_1 = U_2 = … = U_n$.

Значит, напряжение — это электрическая величина, которая одинакова для всех проводников, соединенных параллельно.

По этой причине в быту и технике очень удобно применять параллельный тип соединения проводников. Почему?

Во-первых, в таком случае все потребители электроэнергии изготавливаются в расчете на одну и ту же величину напряжения. Во-вторых, если исключить из цепи один потребитель, то другие продолжат работать. Цепь останется замкнутой.

Сила тока в цепи при параллельном соединении проводников

Теперь рассмотрим, что происходит с силой тока при параллельном подключении.

Взгляните на рисунок 4, а. В точке B ток разветвляется на два тока: $I_1$ и $I_2$.

Эти два тока сходятся снова в точке A. По смыслу этот момент очень похож на разветвление реки (рисунок 4, б) на два потока воды, которые через какое-то расстояние вновь сходятся в одно русло.

Как выражается сила тока в цепи до ее разветвления через силы токов в отдельных ветвях разветвления?

Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединенных проводниках:
$I = I_1 + I_2 + … + I_n$.

Сопротивление в цепи при параллельном соединении проводников

Перейдем к сопротивлению. При параллельном соединении можно представить все проводники как один. Этот один проводник будет явно больше в диаметре, чем каждый из них по отдельности. Получается, что площадь поперечного сечения проводника как бы увеличивается при таком соединении.

Сопротивление рассчитывается по формуле $R = frac{rho l}{S}$. Чем больше поперечное сечение, тем меньше сопротивление.

Значит, общее сопротивление цепи уменьшается. Оно становится меньше сопротивления каждого из проводников, которые входят в такую электрическую цепь.

В цепи на рисунке 1 у нас две одинаковые лампы с сопротивлениями $R_1$. Общее сопротивление цепи $R$  будет в два раза меньше сопротивления каждой лампы: $R = frac{R_1}{2}$.

Общее сопротивление цепи при параллельном соединении проводников рассчитывается по формуле:
$frac{1}{R} = frac{1}{R_1} + frac{1}{R_2} + … + frac{1}{R_n}$.

Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?

Очевидно, что чем больше проводников будет в разветвлении, тем меньше будет общее сопротивление цепи.

Пример параллельного соединения проводников

Взгляните на рисунок 5. Здесь изображена часть схемы электрической цепи. Здесь параллельно включены электрические лампы, нагревательные приборы и электродвигатель.

Где может использоваться такая схема соединения?
Например, в жилых помещениях. В точках A и B провода вводятся в квартиру.

Также в наших квартирах все стандартные розетки находятся под одинаковым напряжением в $220 space В$. Большинство производителей техники изготавливают приборы как раз под это напряжение.

Использовать параллельное подключение к одной и той же цепи очень удобно, поскольку в нее могут быть включены самые разные потребители энергии (рисунок 6).

Благодаря такому способу подключения, выключая свет в своей квартире, мы не выключаем его и у наших соседей. Любые электроприборы могут работать независимо от подключения или отключения в сеть других.

На практике также часто можно увидеть смешанное соединение проводников. В таких цепях присутствует и последовательный тип соединении, и параллельный.

Пример задачи

В осветительную сеть комнаты включены две электрические лампы, сопротивления которых равны $200 space Ом$ и $300 space Ом$. Напряжение в сети составляет $120 space В$. Определите силу тока в каждой лампе, силу тока в проводящих проводах (то есть силу тока до разветвления), общее сопротивление участка, состоящего из двух ламп.

Подразумевается, что лампы подключены в сеть параллельно. Запишем условие задачи и решим ее.

Дано:
$R_1 = 200 space Ом$
$R_2 = 300 space Ом$
$U = 120 space В$

$I_1 — ?$
$I_2 — ?$
$I — ?$
$R — ?$

Решение:

Запишем закон Ома для участка цепи с первой лампой:
$I_1 = frac{U_1}{R_1}$.

Значение сопротивления нам известно. Что с напряжением на этом участке?
Так как лампы подсоединены параллельно, то напряжение на каждой будет равно напряжению во всей цепи:
$U_1 = U_2 = U = 120 space В$
Тогда мы можем рассчитать силу тока в каждой лампе.

Сила тока в первой лампе:
$I_1 = frac{U}{R_1}$,
$I_1 = frac{120 space В}{200 space Ом} = 0.6 space А$.

Сила тока во второй лампе:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{120 space В}{300 space Ом} = 0.4 space А$.

Сила тока до разветвления будет равна сумме сил этих двух токов в лампах:
$I = I_1 + I_2$,
$I = 0.6 space А + 0.4 space А = 1 space А$.

Общее сопротивление цепи мы можем определить двумя способами.

Способ №1
Используя закон Ома для участка цепи, состоящего из двух параллельно соединенных ламп:
$I = frac{U}{R}$,
$R = frac{U}{I}$,
$R = frac{120 space В}{1 space А} = 120 space Ом$.

Способ №2
Используя формулу для расчета сопротивления при параллельном соединении проводников:
$frac{1}{R} = frac{1}{R_1} + frac{1}{R_2}$,
$frac{1}{R} = frac{1}{200 space Ом} + frac{1}{300 space Ом} = frac{5}{600 space Ом} = frac{1}{120 space Ом}$.

Отсюда, $R = frac{1}{frac{1}{120 space Ом}} = 120 space Ом$.

При решении этой задачи мы убедились, что общее сопротивление цепи меньше сопротивления каждого из параллельно подключенных проводников: $R < R_1 < R_2$.

Ответ: $I_1 = 0.6 space А$, $I_2 = 0.4 space А$, $I = 1 space А$, $R = 120 space Ом$.

Упражнения

Дано:
$R_1 = 10 space Ом$
$R_2 = 15 space Ом$
$U = 12 space В$

$I_1 — ?$
$I_2 — ?$
$I — ?$

Показать решение и ответ

Скрыть

Потому что бытовые приборы рассчитаны на то же напряжение, которое подается от городской сети — $220 space В$. При параллельном соединении это напряжение будет одинаковым на всех участках цепи.

Также параллельное соединение позволяет включать и выключать приборы независимо друг от друга, что невозможно при последовательном соединении.

Дано:
$R_1 = 20 space Ом$
$R_2 = 40 space Ом$
$R_3 = 24 space Ом$
$U = 24 space В$

$I_1 — ?$
$I_2 — ?$
$I_3 — ?$
$I — ?$
$R — ?$

Показать решение и ответ

Скрыть

При последовательном соединении проводников общее сопротивление цепи будет равно сумме сопротивлений составляющих ее проводников.
Общее сопротивление при последовательном соединении:
$R = R_1 + R_2 = 5 space Ом + 500 space Ом = 505 space Ом$.

Это значение действительно больше, чем $500 space Ом$.

При параллельном соединении общее сопротивление мы рассчитываем следующим образом:
$frac{1}{R} = frac{1}{R_1} + frac{1}{R_2}$,
$frac{1}{R} = frac{1}{5 space Ом} + frac{1}{500 space Ом} = frac{101}{500 space Ом}$,
$R = frac{1}{frac{101}{500 space Ом}} = frac{500 space Ом}{101} approx 5 space Ом$.

Согласитесь, что $5 space Ом$ намного меньше, чем $500 space Ом$.

Можно посмотреть на этот вопрос и с другой стороны. Сопротивление рассчитывается по формуле $R = frac{rho l}{S}$. Оно прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения.

При последовательном соединении проводников мы можем сказать, что длина проводника увеличивается. Значит, увеличивается и сопротивление. Общее сопротивление будет больше, чем сопротивление каждого отдельного проводника.

А при параллельном соединении увеличивается площадь поперечного сечения. Значит,  сопротивление будет уменьшаться. Получается, что общее сопротивление такой цепи будет меньше сопротивления каждого из проводников.

Дано:
$R_1 = 4 space Ом$
$R_2 = 6 space Ом$
$R_3 = 12 space Ом$
$R_4 = 2 space Ом$
$I_3 = 1 space А$

$U — ?$
$I_1 — ?$
$I_2 — ?$
$I_4 — ?$

Показать решение и ответ

Скрыть

От источника тока энергия может быть передана по проводам к
устройствам, потребляющим энергию: электрической лампе, радиоприёмнику и так
далее.

Совокупность устройств и элементов, предназначенных для
протекания электрического тока, называют электрической цепью.

Любая электрическая цепь содержит, во-первых, источник тока,
создающий необходимое напряжение, а во-вторых, нагрузку, то есть то устройство,
в котором нужно создать ток и использовать одно из его действий. Нагрузкой
может быть нагреватель или лампа накаливания (здесь используют тепловое
действие тока), электродвигатель или звонок (используется магнитное действие
тока), аккумулятор (это проявление химического действия тока). Звеньями же цепи
являются соединительные провода и ключ, служащий для удобства и безопасности работы.

Рисунки, на которых изображены способы соединения
электрических приборов в цепь, называются электрическими схемами.

Приборы на схемах принято обозначать условными знаками, часть
из которых представлена на экране в виде таблицы.

Электрические цепи, с которыми приходится иметь дело на
практике, обычно состоят не из одного проводника, а из системы различных
проводников, которые могут быть соединены между собой по-разному.

Рассмотрим простую цепь, составленную из источника ток, ключа
и двух проводников. Обратите внимание на то, что в представленной цепи конец
одного проводника соединяется с началом другого, его конец — с началом третьего
и так далее. Проще говоря, проводники имеют по одной общей точке. Такое
соединение проводников принято называть последовательным соединением.

Как вы уже знаете, в проводниках, по которым течёт постоянный
ток, электрический заряд не накапливается, и через любое поперечное сечение
проводника за определённое время протекает один и тот же заряд. Следовательно, ток
во всех частях последовательно соединённой цепи в каждый данный момент времени
одинаков:

Напряжение же на концах каждого из проводников будет
различно. Покажем это. Пусть I — это сила тока в
цепи, R₁ и R₂
— сопротивления проводников, a U₁ и U₂ — напряжения на концах этих проводников.

На основании закона Ома мы с вами можем записать, что напряжения
на концах проводников пропорциональны силе тока в цепи и их сопротивлениям:

Разделив первое равенство на второе, получим, что при
последовательном соединении напряжения на проводниках пропорциональны их
сопротивлениям:

Только при таком распределении напряжений и становится
возможным один и тот же ток во всех участках цепи.

А полное напряжение на обоих проводниках (или напряжение
на полюсах источника тока) равно сумме напряжений на отдельных проводниках:

Это легко проверить, если измерить напряжение на концах обоих
проводников и на двух проводниках одновременно.

Также записанное нами равенство вытекает из того, что
напряжение есть величина, измеряемая работой, совершаемой при перемещении
единицы заряда на данном участке цепи:

Работа же по перемещению заряда во всех последовательно
соединённых проводниках равна сумме работ на отдельных проводниках.

Применяя закон Ома для всего участка цепи с последовательным
соединением и для каждого проводника в отдельности, нетрудно показать, что
полное сопротивление участка цепи равно сумме сопротивлений отдельных проводников:

Совершенно аналогично можно показать, что в случае п
последовательно соединённых проводников общее сопротивление участка цепи,
состоящей из нескольких последовательно соединённых проводников, равно сумме
сопротивлений отдельных проводников:

Рост сопротивления цепи при добавлении в неё новых
проводников объясняется увеличением длины проводящей части. Поэтому
сопротивление цепи становится больше сопротивления одного проводника.

На практике последовательное соединение нескольких
проводников используется очень редко, например, в ёлочной гирлянде. Дело в том,
что недостатком такого соединения является то, что в такую цепь можно
подключать только тех потребителей, которые рассчитаны на одинаковую силу тока.
Кроме того, если в такой цепи выключить ток в одном звене (например, перегорит
одна из лампочек в гирлянде), то разрывается вся цепь.

Этих недостатков лишена цепь, в которой потребители соединены
параллельно.

Параллельное соединение — это такое соединение
проводников, при котором одни их концы соединены в один узел, другие концы — в
другой узел.

Узлом принято называть точку разветвлённой цепи, в которой
сходятся более двух проводников.

Следствием этого является то, что напряжение на каждом
параллельно соединённом проводнике одинаково и равно напряжению на всём участке
параллельно соединённых проводников:

При параллельном соединении ток распределяется по проводникам
так же, как поток воды, разветвляющийся на два параллельных канала. Количество
воды, протекающее ежесекундно через неразвтвлённую часть потока воды, равно
сумме количеств воды, протекающих ежесекундно через каждый из каналов.

Аналогично обстоит дело и с прохождением электрических
зарядов через параллельно соединённые проводники. Включив амперметры в цепь до
разветвления и в каждую ветвь разветвления, можно убедиться, что ток в
неразветвлённой части цепи равен сумме токов, текущих в отдельных параллельно
соединённых проводниках:

Этот опыт служит лишь подтверждением того, что в случае
установившегося тока электрические заряды не скопляются в точках разветвления, а
сколько их подходит к точкам разветвления, столько же и уходит.

Обозначим сопротивление каждого из разветвлённых участков
цепи через R₁ и R₂,
a напряжение во всей цепи через U. Теперь применим
к каждой ветви закона Ома для участка цепи:

И выразим из этих формул напряжение.

Так как напряжение на каждом параллельно соединённом
проводнике одинаково, то давайте приравняем правые части последних двух
равенств:

Отсюда находим, что токи в отдельных ветвях разветвлённой
части цепи обратно пропорциональны их сопротивлениям:

Третья закономерность параллельного соединения определяет
общее сопротивление разветвлённого участка. Учтём, что сила тока в цепи равна
сумме сил токов в ветвях, а напряжение везде одинаково. Тогда, на основании
закона Ома, получим, что величина, обратная сопротивлению участка
параллельно соединённых проводников, равна сумме величин, обратных
сопротивлению отдельных проводников:

При этом общее сопротивление разветвлённой части цепи меньше
наименьшего из сопротивлений её ветвей.

Нетрудно показать, что если в разветвление будет включено не
два, а несколько проводников, то данная закономерность также будет выполняться:

Из этого равенства следует, что общее сопротивление
участка цепи, состоящего из п параллельно соединённых проводников с
одинаковым сопротивлением, в п раз меньше сопротивления одного из них:

Параллельное соединение — это основной способ включения в
электрическую цепь различных потребителей, так как в одну и ту же электрическую
цепь могут быть включены самые различные потребители. Однако следует иметь в
виду, что параллельно включаемые в данную цепь потребители должны быть рассчитаны
на одно и то же напряжение, соответствующее напряжению в цепи.

Большинство задач на расчёт цепи сводится к определению
токов, текущих в отдельных её участках, по заданному напряжению и по
сопротивлениям отдельных проводников.

Для примера рассмотрим цепь, представленную на рисунке.

Пусть нам известно общее напряжение, питающее цепь, и
сопротивления включённых в цепь резисторов (сопротивлением амперметра мы пренебрегаем,
так как оно очень мало). Пусть нам надо найти силу тока, протекающего по
каждому из резисторов.

Прежде всего мы должны установить, из скольких
последовательных участков состоит наша цепь. Легко видеть, что таких участков
три, причём второй и третий участки представляют собой разветвления. Обозначим
сопротивления трёх последовательных участков нашей цепи через R_I, R_II,
R_III.

Тогда всё сопротивление цепи выразится как сумма
сопротивлений этих участков:

Общее сопротивление цепи необходимо знать, так как заданное
общее напряжение можно отнести только к полному общему сопротивлению цепи.
Применяя закон Ома, мы найдём полный ток, текущий в нашей цепи:

Нетрудно увидеть, что сила тока на первом резисторе равна
силе тока во всей цепи:

Для того чтобы найти токи в отдельных ветвях, надо
предварительно найти напряжение на отдельных участках последовательных цепей. А
поможет нам это сделать закон Ома:

Незабываем о том, что R_II и R_III — это эквивалентные сопротивления разветвлённых
участков. Эти сопротивления мы с вами можем легко найти по закону параллельного
соединения

Ну а дальше, зная напряжения на отдельных разветвлениях,
найдём и токи в отдельных ветвях используя всё тот же закон Ома (при этом не
забываем, что напряжение на концах всех параллельно соединённых проводников
одно и то же):

Таким образом, задача, поставленная перед нами, полностью
решена.