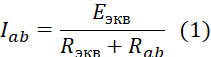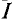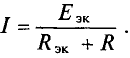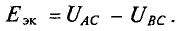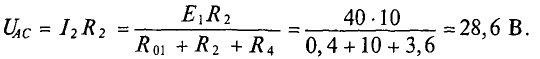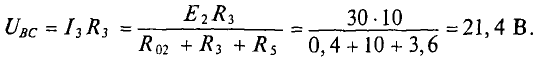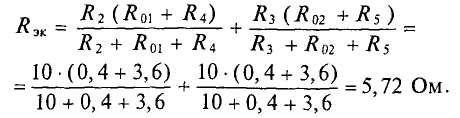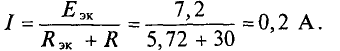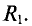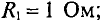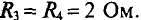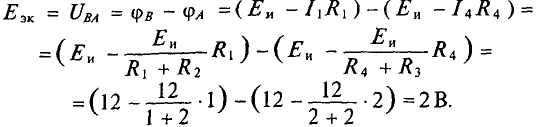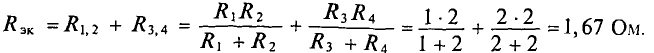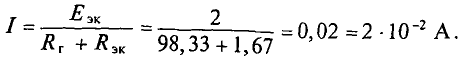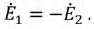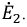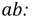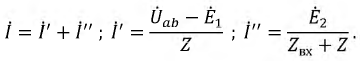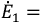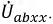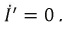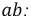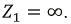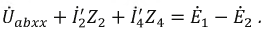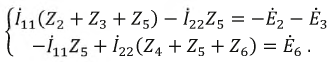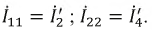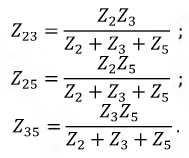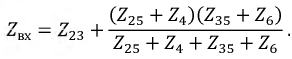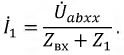Метод эквивалентного генератора применяется для определения тока одной из ветвей электрической цепи в том случае, когда расчет всей схемы не требуется. В основу метода положена теорема об активном двухполюснике (теорема Гельмгольца-Тевенена). Основная идея метода заключается в том, что часть цепи, параметры которой определять нет необходимости, заменяется эквивалентным генератором с известной эдс и сопротивлением. Метод часто применяется для расчета режима электрической цепи.
Алгоритм состоит из следующих шагов:
- Выбранная для расчета ветвь удаляется из схемы, а места образовавшегося разрыва обозначаются буквами. Оставшаяся часть схемы будет представлять собой эквивалентный генератор.
- Рассчитывается эквивалентная эдс генератора.
- Определяется эквивалентное сопротивление генератора.
- По найденным в пунктах 2 и 3 параметрам генератора определяется ток через исключенную в пункте 1 ветвь.
Метод эквивалентного генератора: примеры решения
Рассмотрим пример расчета электрической схемы методом эквивалентного генератора (рисунок 1).
Допустим, что необходимо рассчитать ток Iab через резистор R4. Тогда преобразования схема будет иметь вид, представленный на рисунке 2.
После преобразования ток через резистор Rab (R4) определяется по формуле
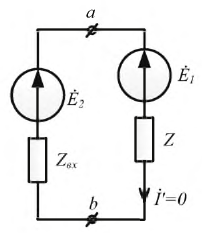
Для того, чтобы рассчитать значения Еэкв и Rэкв необходимо рассмотреть режим холостого хода генератора. Для этого необходимо обеспечить его работу без нагрузки, то есть условно отсоединить от цепи исследуемую ветвь ab (рисунок 3).
Для представленной схемы напряжение Еэкв будет равно
Далее требуется определить эквивалентное сопротивление. Для этого воспользуемся методом пассивного двухполюсника. В этом случае необходимо исключить из схемы источник эдс и найти общее сопротивление цепи (рисунок 4).
Эквивалентное сопротивление полученной схемы определяется по формуле
Теперь можно определить ток, проходящий через резистор ab согласно выражению (1).
Поставленная задача решена.
Продолжаем решать задачи по основам электротехники(ТОЭ). В сегодняшней статье будет метод, по которому задают больше всего вопросов. Это понятно, поскольку этот метод является, на мой взгляд, самым сложным методом расчета сложных электрических цепей постоянного тока.
В свое время и я его понял далеко не сразу. Поэтому рассмотрим каждый пункт подробно. Начнём с того, что необходимо знать и понимать для успешного решения этим методом.
1) Закон Ома. Без него не только этот метод, но и многие другие задачи не решаются.
2) Правила последовательного и параллельного соединения резисторов.
3) Хотя бы один любой метод расчета сложных цепей, то есть по Кирхгофу, контурными токами, узловыми потенциалами и так далее.
4) И, самое важное, для этого метода – это умение строить потенциальную диаграмму. Именно потенциальную, а не векторную. Потому что векторная диаграмма строится для цепей переменного тока, а мы рассматриваем цепь постоянного тока. Строить мы конечно потенциальную диаграмму тут не будем. Но чтобы её построить, необходимо знать два основных правила, которые нужны и в методе эквивалентного генератора.
Первое правило: ток течет через резистор всегда от большего потенциала к меньшему.
Второе правило: у ЭДС “+” всегда больше “-“.
Давайте перейдем к решению задачи. На конкретном примере всегда понятнее.
Имеется данная схема цепи. Даны ЭДС и сопротивления резисторов. Требуется найти ток I3 методом эквивалентного генератора.
Поскольку нужно найти ток I3, который протекает по третьей ветви, нам нужно обеспечить холостой ход, сделав обрыв той части цепи, по которой протекает интересующий нас ток. То есть делаем обрыв третьей ветви. Это ветвь подключена между точками “c” и “d”. Сами точки мы не трогаем, а лишь убираем только ветвь.
В точках “c” и “d” узлов нет, поскольку там сходятся только по две ветви. А узел – это место соединения трех и более ветвей.
Наша цель – определить две величины:
1) Напряжение Ucd между точками “c” и “d”, оно же ЭДС эквивалентного генератора(Еэг). И, поскольку, мы обеспечили холостой ход, оборвав третью ветвь, все токи и напряжения будем указываем на схеме с индексом “х”, при коротком замыкании указывают кз.
2) Сопротивление эквивалентного генератора rэг, оно же сопротивление между точками “c” и “d”. А определить это сопротивление нам поможет правило последовательного и параллельного соединения резисторов.
В первом случае, когда мы ищем напряжение Ucd(оно же Еэг), применим один любой метод расчета сложных электрических цепей.
Сложной считается цепь, если в ней два и более источников энергии.
В данном случае два источника. Давайте для начала найдём, каким будет напряжение между точками “c” и “d”. Воспользуемся методом контурных токов.
Получили два неизвестных контурных тока. В цепи, в общем случае, три ветви и два узла. Поскольку две неизвестные, значит составим два уравнения и из этих уравнений найдём контурные токи I11 и I22.
Напряжение Ucd снимается с точек “c” и “d”, а между ними включены резисторы r2 и r4. Нам остается найти напряжение на этих элементах. Их сопротивления известны. Найдем токи I4 и I2, умножим эти токи на сопротивления, получим напряжения.
Контурные токи мы уже нашли. Тогда токи ветвей:
I2x=-I22=0.3333 A; I4x=-I11=0.2222 A;
Напряжения на резисторах r4 и r2:
U4x=I4x*r4=0.2222*4=0.8888 B; U2x=I2x*r2=0.3333*2=0.6666 B;
Так как оба тока направлены в одну и ту же сторону, тогда
Ucdx=U2x+U4x=0.6666+0.8888=1.5554 B;
А теперь самое главное в этом методе. Почему именно взяли U2 + U4? Почему не -U2-U4? А здесь нужно воспользоваться правилом, что ток течет от большего потенциала к меньшему и стрелкой под напряжением Ucdx мы указали, что φс больше чем φd. А так как нам нужно найти ЭДС эквивалентного генератора, давайте представим именно эту часть схемы отдельно.
Предположим, что φc больше чем φd и стрелкой под напряжением укажем направление от большего потенциала к меньшему.
Заменим напряжение Ucd на Eэг. Еэг будет направлен от “d” к “c”(минусом на “d”, а плюсом на “c”, потому что “плюс” у ЭДС всегда больше чем “минус”).
Запишем второй закон Кирхгофа:
I4x*r4+I2x*r2=-Еэг
В данном случае ЭДС эквивалентного генератора Еэг получится отрицательным. Можно в принципе оставить как есть, это ошибкой не будет. Но если мы на данном этапе поменяем направление ЭДС эквивалентного генератора на этой схеме, тогда мы получим положительное значение ЭДС эквивалентного генератора. Или оставляем как есть. Как поступить – без разницы. Давай поменяем направление.
Тогда I4x*r4+I2x*r2=Еэг; Еэг=U4x+U2x=0.8888+0.6666=1.5554 B;
Это говорит о том, что потенциал в точке “d” большие чем в точке “с”. Это и так изначально было понятно cудя по тому, как мы направили токи. А ток течет от большего потенциала к меньшему, т. е. мы изначально указали точки от “d” к “e” и от “e” к “c” и эти токи получились положительными. Значит мы их верно расставили.
С ЭДС эквивалентного генератора мы разобрались, осталось посчитать сопротивление эквивалентного генератора (сопротивление между точками “c” и “d”). Для этого мы должны исключить все источники энергии и оставить только резисторы.
Когда исключаем ЭДС, на его месте остается короткое замыкание (это в случае если источник напряжения идеальный и его внутреннее сопротивление равно нулю). Если имеется какое-то внутреннее сопротивление, то оно остается в ветви, это нужно учитывать. Если в схеме цепи есть источник тока, то после его исключения на его месте остается обрыв, поскольку его внутреннее сопротивление бесконечно большое. А после исключения источника тока, его внутреннее сопротивление остается в схеме, и так как оно бесконечно большое, это равносильно обрыву.
В схеме, изображенной на рисунке 9, применяя правила последовательного и параллельного соединения резисторов:
r4 и r5 включены параллельно;
r1 и r2 включены параллельно;
r45 и r12 включены последовательно;
Численные значения r45, r12 и rэг рассчитаны на рисунке 9.
Осталось изобразить последнюю схему, в которой будет протекать ток I3.
Ток получился отрицательным, значит на самом деле он течет не вправо, а влево от “d” к “c”. Это и понятно, поскольку, как мы ранее выяснили, φd больше чем φc, и, повторюсь, ток течет от большего потенциала к меньшему.
Таким образом решаются задачи методом эквивалентного генератора.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток – простыми словами;
Метод эквивалентного генератора:
Метод эквивалентного генератора рационально применять в случае необходимости определения тока (напряжения, мощностн и др.) только одной ветви сложной электрической цепи.
Для этой цели разбивают сложную электрическую цепь на две части — на сопротивление R, ток которого
Активным этот двухполюсник называют потому, что в нем имеется источник ЭДС. Этот активный двухполюсник обладает определенной ЭДС
Ток в резисторе с сопротивлением R определяют по закону Ома
Таким образом, определение тока 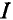
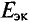
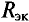
Величина ЭДС 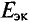
Внутреннее сопротивление эквивалентного генератора 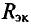
Практически для определения внутреннего сопротивления эквивалентного генератора измеряют амперметром ток между точки А и В работающего двухполюсника при коротком замыкании так как сопротивление амперметра настолько мало, что им можно пренебречь. Тогда
где 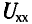
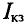
Такой метод практического определения внутреннего сопротивления эквивалентного генератора 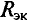
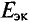
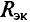
Пример 4.12
Определить ток в сопротивлении 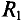
Решение
Для определения тока 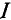
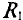
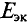
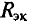
Знак «минус» обусловлен тем, что источники в схеме включены встречно и потенциал в точке А больше потенциала в точке В, так как 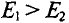
Напряжение
Напряжение
Следовательно, 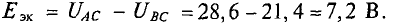
Искомый ток
Такой же ток получен в примере 4.6 на сопротивлении
Пример 4.13
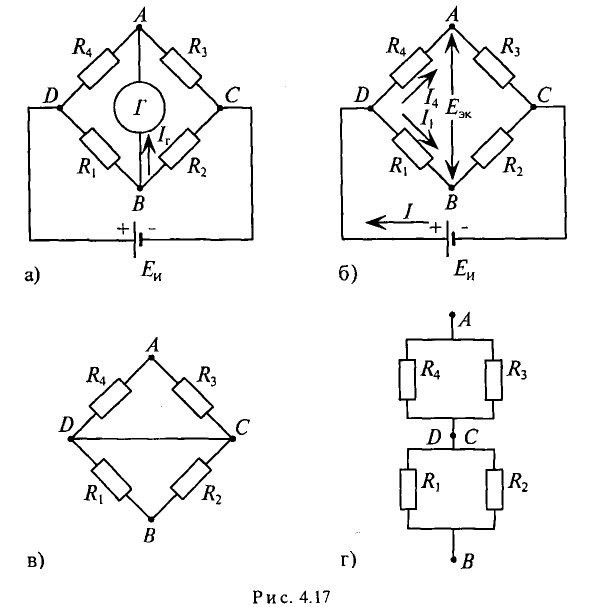
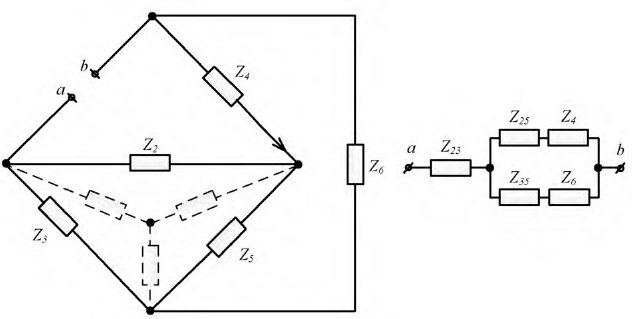
В схеме рис. 4.17а сопротивления плеч моста равны
Сопротивление гальванометра Rr = 98,33 Ом, ЭДС источника 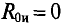
Решение
Для определения тока в цепи гальванометра 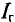
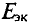
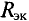
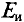
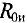
Для определения ЭДС эквивалентного генератора 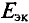
Тогда
При замене источника ЭДС 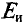
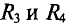
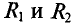
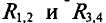
Тогда ток в ветви с гальванометром, который направлен из точки В в точку А, т. е. из точки с большим потенциалом в точку с наименьшим потенциалом (рис. 4.17а), будет равен
Метод эквивалентного генератора (активного двухполюсника)
Все методы, рассмотренные ранее, предполагали расчет токов одновременно во всех ветвях цепи. Однако в ряде случаев бывает необходимым контролировать ток в одной отдельно взятой ветви. В этом случае применяют для расчета метод эквивалентного генератора.
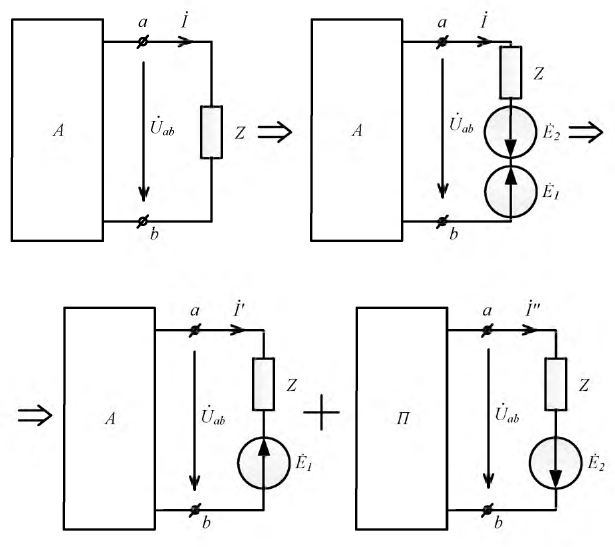
Пусть дана некоторая электрическая цепь, которую заменим активным двухполюсником (рис. 3.10), оставив только ветвь 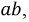
Сначала, введем в ветвь 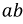
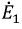
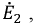
Затем, используя принцип наложения, данную цепь представим суммой двух цепей. В первой оставим все источники активного двухполюсника и источник ЭДС 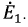
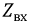
Рис. 3.10. Преобразование исходного двухполюсника в сумму двух цепей
На основании принципа наложения ток ветви
Поскольку 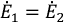
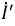
Напряжение на зажимах источника в режиме холостого хода численно равно его ЭДС. Тогда активный двухполюсник с источником 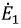
Рис. 3.11. Схема замещения активного двухполюсника
В этой схеме ЭДС 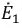
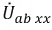
Таким образом, ток в ветви
Пусть дана цепь (рис. 3.12), в которой необходимо рассчитать ток 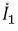
Рис. 3.12. Исходная цепь
Последовательность расчета:
1. Разомкнем ветвь с сопротивлением 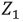
2. Зададим положительное направление 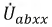
3. Токи 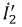
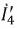
Тогда
4. Определим эквивалентное сопротивление пассивного двухполюсника. Для этого мысленно закоротим все источники ЭДС исходной цепи, оставляя в схеме для реальных источников их внутренние сопротивления.
В образовавшейся схеме пассивного двухполюсника невозможно определить эквивалентное сопротивление относительно зажимов 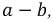
Преобразуем, например, «треугольник» сопротивлений 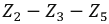
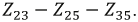
Рис. 3.14. Схема пассивного двухполюсника
Сопротивления этой схемы будут:
Входное сопротивление цепи 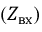
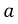
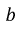
Окончательно имеем:
- Теоремы теории цепей
- Теорема обратимости (или взаимности)
- Теорема компенсации
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
- Метод свертывания электрической цепи
- Метод преобразования схем электрических цепей
- Параллельное соединение генераторов
- Метод узловых и контурных уравнений
Метод эквивалентного генератора
Для
определения тока в одной (или нескольких)
из ветвей сложной электрической
цепи целесообразно использовать метод
эквивалентного генератора. Этот
метод основан на теореме об активном
двухполюснике: ток в
некоторой заданной ветви не изменится,
если активную цепь, к которой подключена
эта ветвь, заменить источником энергии,
ЭДС которого равна напряжению
холостого хода на зажимах разомкнутой
ветви, а его (источника)
внутреннее сопротивление равно
сопротивлению пассивной цепи относительно
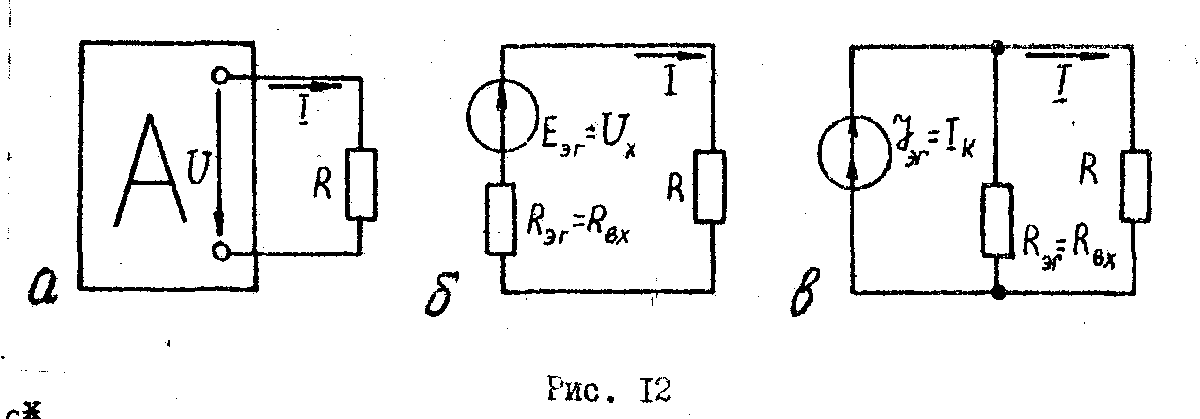
зажимов искомой ветви (рис. 12).
34
Если
эквивалентный генератор представляется
источником ЭДС, ток в заданной ветви
определяется по закону Ома (рис. 12,6):
.
Если
эквивалентный генератор представляется
источником тока, ток в
заданной ветви находится по правилу
“чужого сопротивления” (рис.
12,в):
.
В
формулах Uх
– напряжение
холостого хода активного двухполюсника
на зажимах ветви, в которой определяется
ток; Iк
– ток
короткого
замыкания активного двухполюсника при
закороченной заданной ветви; Rвх
– входное
сопротивление пассивного двухполюсника,
найденное относительно
зажимов заданной ветви; R
– сопротивление заданной ветви.
Выбор
схемы замещения эквивалентного генератора
определяется схемой цепи, в которой
рассчитывается ток.
Если
в заданной ветви, кроме резистора, есть
источник ЭДС и для расчета
используется последовательная схема
замещения эквивалентного генератора
(рис. 12,6), ток можно определить из выражения
.
35
ЭДС
Е
учитывается
с положительным (отрицательным) знаком,
если напряжение
Uх
и ЭДС Е
совпадают
(противоположны) по направлению.
Определение
тока в заданной ветви электрической
цепи методом эквивалентного генератора
удобно производить в следующей
последовательности.
1.
Разомкнуть (закоротить) заданную ветвь
с искомым током.
2.
Определить напряжение холостого хода
/ток короткого замыкания/активного
двухполюсника относительно заданной
ветви.
3.
Исключая из активного двухполюсника
все источники энергии, определить
входное сопротивление двухполюсника
относительно зажимов заданной
ветви. При исключении источников в схеме
должны быть сохранены их внутренние
сопротивления.
4.
Используя закон Ома (правило “чужого
сопротивления”), найти ток
в заданной ветви. Направление тока
определяется направлением напряжения
холостого хода /тока короткого замыкания”/.
Пример
8.
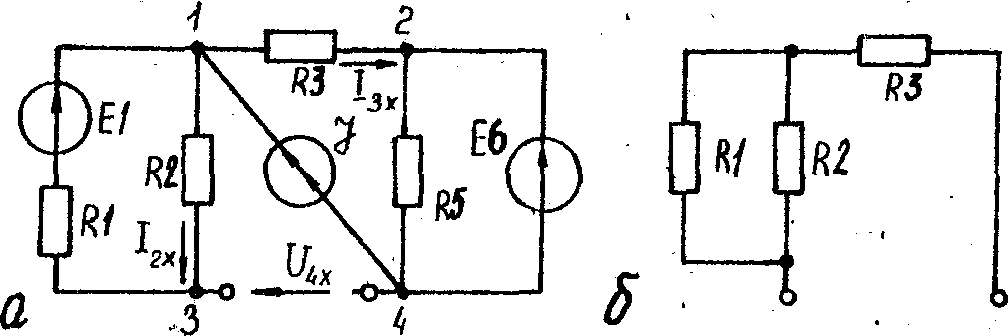
В цепи, схема которой изображена на рис.
2, определить ток
I1
методом эквивалентного генератора ЭДС
(напряжения).
После
исключения ветви с ЭДС Е1
и
резистором R1
получаем схему, изображенную
на (рис.
13,а).
В исходной цепи ток I1
направлен от узла 3 к
узлу 1, такое же направление выбрано и
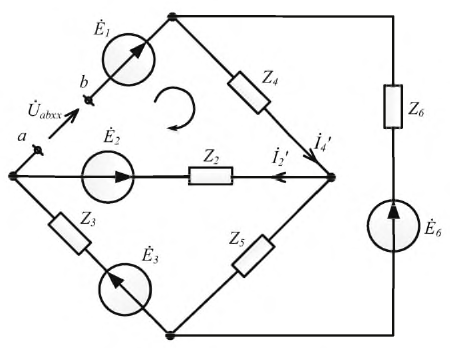
для напряжения холостого хода U1x.
36
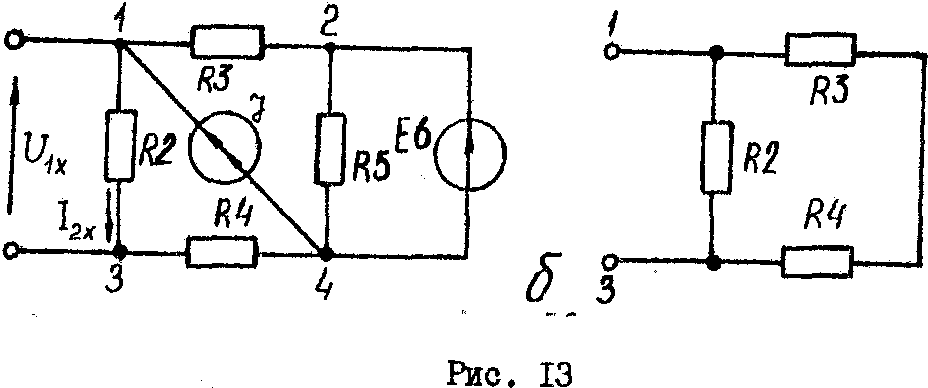
Для
расчета напряжения холостого хода U1x
сначала
нужно найти ток
I2х
в ветви с резисторами R2
и
R4;
удобнее всего это сделать методом
узловых потенциалов.
Положим
потенциал узла 4 равным нулю, тогда
потенциал узла 2
,
.
Для
узла 1 составим уравнение методом узловых
потенциалов:
,
где
,
.
Подставляя
подученные значения в расчётное
уравнение, имеем
0,0567φ1-200*0,04
= 5
откуда
φ1=229
В.
37
Ток
в ветви о резисторами R2
и R4
.
Напряжение
холостого хода находится по второму
закону Кирхгофа:
Схема
для определения входного сопротивления
пассивного двухполюсника
изображена на рис. 13,6. В месте включения
идеального источника ЗДС Е6
поставлена
закоротка, в месте включения идеального
источника тока J
цепь
разомкнута. Резистор R5
из
схемы
исключен, так как он
закорочен шестой ветвью. Входное
сопротивление относительно заданной
ветви
.
Искомый
ток I1
определяется
по схеме с эквивалентным генератором
напряжения
(рис. 12,6). ЭДС E1
учитывается
со знаком “+”, так как ее направление
совпадает с направлением тока I1
, а
значит и с направлением напряжения
холостого хода:
.
Пример
9.
В цепи, схема которой изображена на рис.
2, определить ток I2
методом
эквивалентного генератора тока.
38
Закорачиваем
в исходной схеме ветвь с резистором;
получаем схему,
изображенную на (рис. 14,а). В исходной
цепи ток I2
направлен от узла
1 к узлу 3, такое же направление выбрано
и для тока короткого замыкания
I2k.
Этот ток в схеме (рис. 13,6) можно найти,
например, методом наложения:
.
Схема
для определения входного сопротивления
пассивного двухполюсника,
изображена на (рис. 14,6). В месте включения
идеальных источников
ЭДС Е1 и Е6
поставлены
закоротки, в месте включения идеального
источника тока J
цепь
разомкнута. Резистор R5
из
схемы исключен, так как
он закорочен шестой ветвью. Входное
сопротивление относительно заданной
ветви
Искомый
ток I2
определяется
по схеме с эквивалентным генератором
тока
(рис. 12,в):
.
39
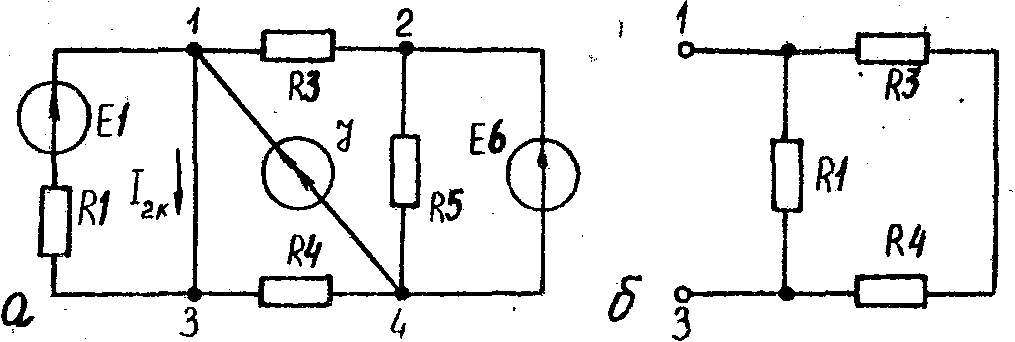
Рис.
14
Пример
10.
В цепи, схема которой изображена на
(рис. 2), определить ток I4
методом
эквивалентного генератора напряжения.
Размыкаем
в исходной схеме ветвь с резистором R4;
получаем
схему, изображенную
на (рис. 15,а). В исходной цепи ток I4
направлен
от узла 4 к
узлу 3, такое же направление выбрано и
для напряжения холостого хода
U4x
Рис.
15
Размыкание
заданной ветви существенно упрощает
схему: ток I2x
определяется
только источником ЭДС E4
и
не зависит от других источников
энергии, ток I3x
равен
току источника тока J
в
силу принципа не прерывности
электрического тока:
,
.
40
Напряжение
холостого хода находится по второму
закону Кирхгофа:
.
Схема
для определения входного сопротивления
пассивного двухполюсника
изображена на (рис. 15,6). В месте включения
идеальных источников ЭДС E1
и
E6
поставлены
закоротки, а в месте включения идеального
источника
тока J
цепь
разомкнута. Резистор R5
из
схемы исключен, так
как он закорочен шестой ветвью. Входное
сопротивление относительно
заданной ветви
Искомый
ток I4
определяется по схеме с эквивалентным
генератором напряжения
(рис. 12,6):
МЕТОД
НЕНАПРАВЛЕННЫХ ГРАФОВ
В
методе ненаправленных графов за основу
принимается информация о так называемом
графе цепи, выраженная в виде остова
заданной цепи, на
котором показаны только узлы и ветви
цепи. Определяется передаточный
коэффициент (передача) между входным
воздействием (источником энергии) и
искомой реакцией (током или напряжением).
Передача
определяется по топологической формуле
41
где
Т
– передача
цепи, т.е.
любая передаточная функция цепи (входные
и взаимные сопротивления и проводимости,
коэффициент передачи по току
и напряжению); ∆
–
узловой определитель графа цепи,
найденный с
помощью разлояения по путям между двумя
произвольно выбранными узлами;
П’к
– к-ый путь
передачи, равный произведению проводимое
тек ветвей, входящих в данный путь;
всегда начинается на положительном
зажиме
источника и заканчивается на отрицательном
его зажиме, должен включать
в себя ветвь с искомой реакцией и не
проходить по ветви с источником; ∆’к
–
определитель
к-го
пути передачи графа; определяется из
графа,
полученного при закорачивании этого
пути передачи в исходном графе;
Пк,∆к
– соответственно к–ый
путь
и его определитель, полученный
на основании исходного графа с закороченным
к-ым путем.
Если
искомой реакцией является ток, в ветвь
этого тока включают амперметр
с единичной проводимостью; если искомой
реакцией является напряжение ветви,
параллельно этой ветви включают вольтметр
с единичной
проводимостью. При наличии в схеме
идеального источника ЭДС закорачивают
узлы, к которым подключен этот источник;
ветвь с идеальным источником тока в
граф цепи не входит.
Топологический
метод применим только для цепей с одним
источником
энергии. Если цепь содержит несколько
источников, для расчета используется
принцип наложения.
Пример
11.
Определить передачу в мостовой цепи
(рис. 16,а) от источника
напряжения, подключенного к
42
узлам
1 и 3, к току I4
в
ветви с проводимостью G4
.
Положительное направление этого тока
(и положительное
направление вдоль этой ветви) совпадает
с заданным направлением напряжения
источника.
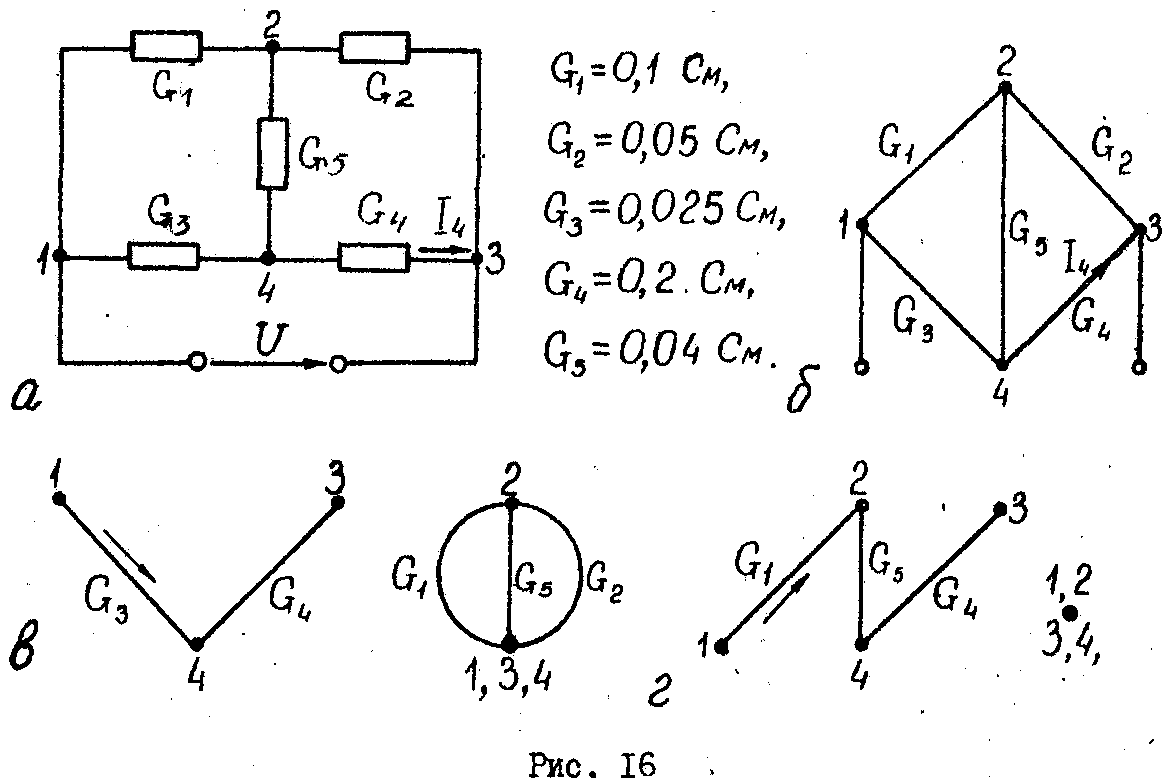
Граф
цепи показан на (рис. 16,6). В цепи два пути
передачи от узлов
1 и 3 источника к ветви G4
Первый
путь передачи проходит по ветви G3
. При
закорачивании этого пути передачи узлы
1, 3 и 4 соединяются
вместе, образуя с узлом 2 одну ветвь,
состоящую из параллельно соединенных
проводимостей G1
, G2
и
Gs
(рис.
16,в). Следовательно,
,
.
Второй
путь передачи проходит по ветвям G1
и
Gs.
При
закорачивании
этого пути передачи все четыре узла
объединяются (рис. 16,г). Следовательно,
,
.
43
Пути
П1
и
П2
,
а также их определители ∆1
и
∆2
находятся
для
пары узлов 2 и 4, узлы 1 и 3 источника должны
быть закорочены. Тогда
соединяются параллельно ветви G1
и
G2
, а
также G3
и
G4
(рис.
17,а).
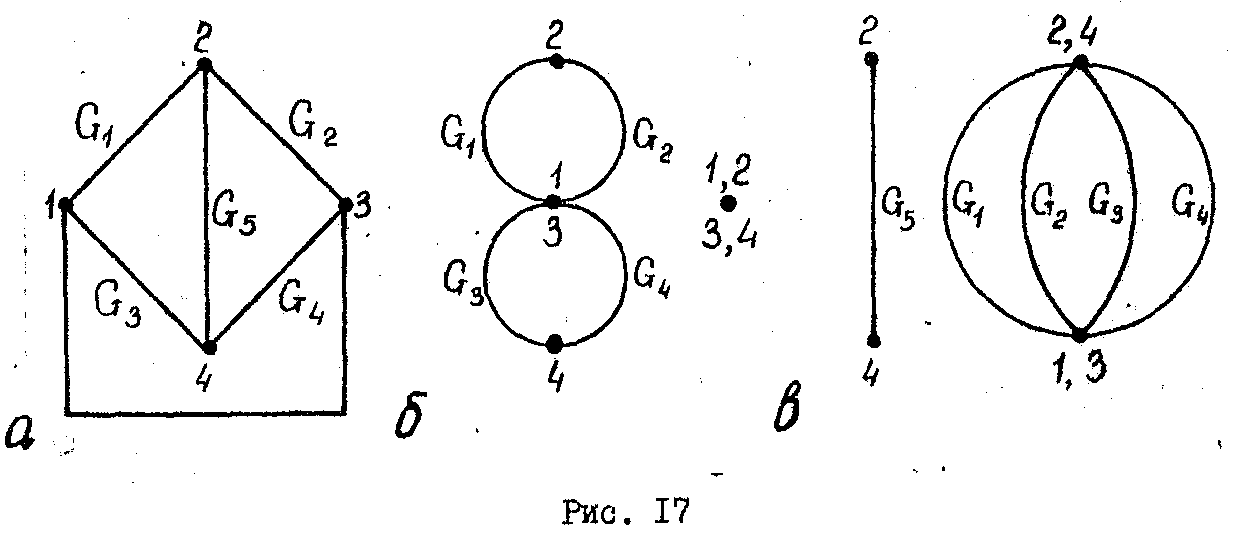
Первый
путь от узла 2 к узлу 4 проходит
последовательно по этим двум
параллельным разветвлениям; при
закорачивании этого пути все четыре
узла объединяются (рис. 17,6). Следовательно,
;
.
Второй
путь от узла 2 к узлу 4 проходит по ветви
G5
при
закорачивании
этого пути все остальные ветви оказываются
соединенными параллельно
(рис. 17,в). Следовательно,
,
В
результате передача (взаимная проводимость)
44
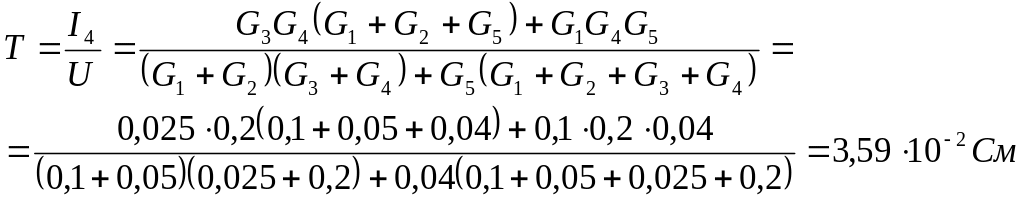
Если,
например, напряжение источника U
=
100 В, ток в четвертой ветви
Пример
12.
Определить топологическим методом ток
I6
в
цепи, изображенной
на (рис. 18,а). Положительное направление
тока показано на рисунке.
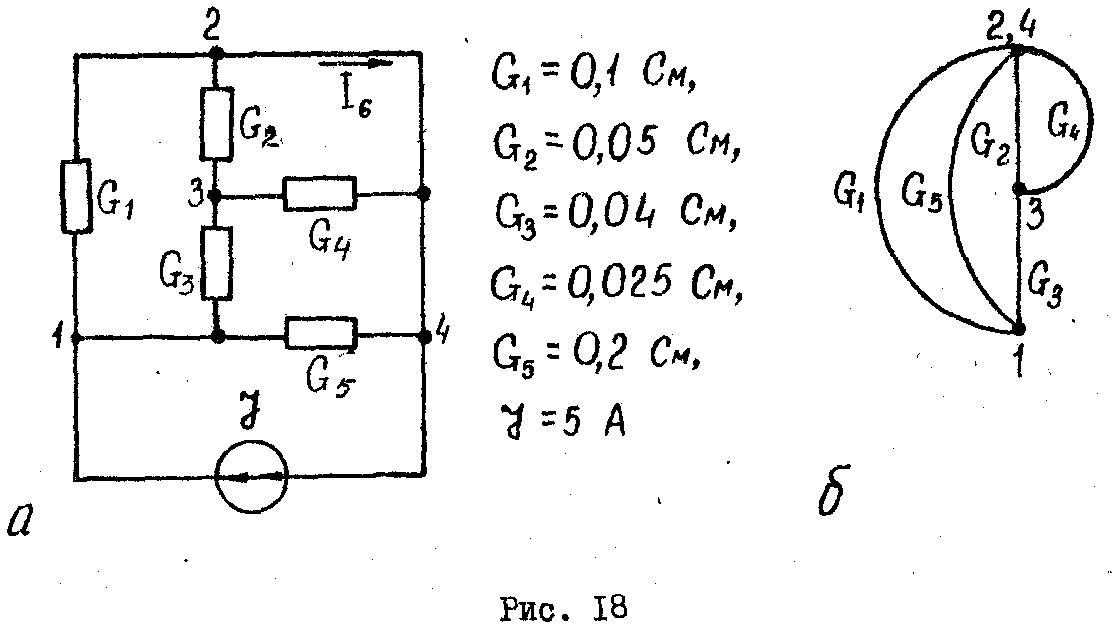
Граф
цепи изображен на (рис. 18,6). Ветвь с
идеальным источником тока
в граф цепи не входит (G3
=
0),
искомая ветвь стянута в точку (узлы
2 и 4 слиты в один).
45
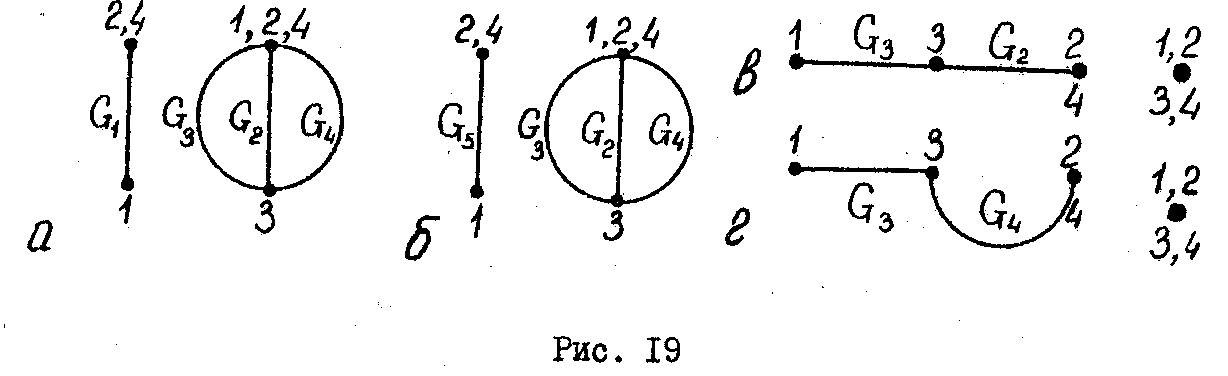
Главный
определитель графа определяют по путям
между двумя произвольно
выбранными узлами 1 и 2. Определители
путей находят для графов с
соответственно закороченными путями
(рис. 19):
,
,
(рис. 19, а);
,
,
(рис. 19, б);
,
,
(рис. 19, в);
,
(рис. 19, г).
(Определитель
пути равен единице, если этот путь
проходит по всем узлам графа.)
Главный
определитель графа
Для
определения путей передачи и их
определителей используют граф,
изображенный
на (рис. 20), а заданная ветвь учитывается
единичной проводимостью.
46
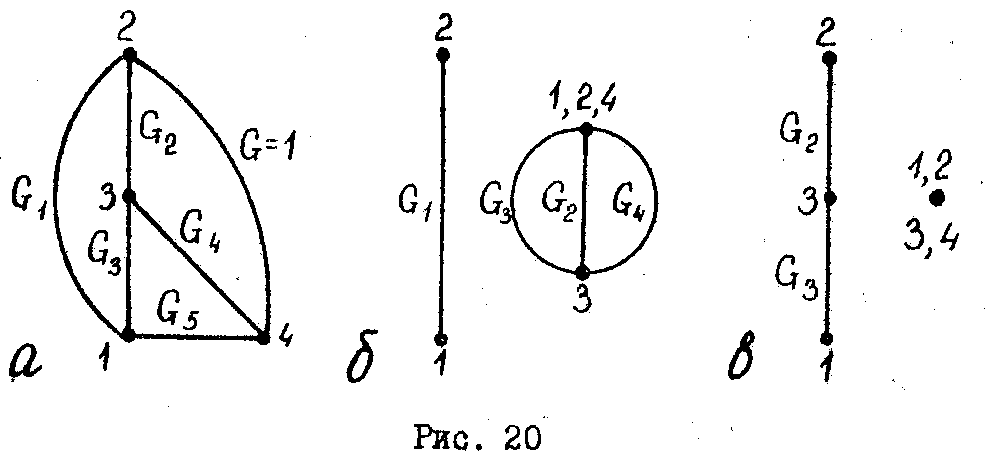
Первый
путь передачи проходит по ветви G1
;
при закорачивании этого
пути передачи узлы 1, 2 и 4 объединяются
вместе, образуя параллельное
соединение ветвей G2
, G4
и
G3
(рис. 20,6):
;
.
Второй
путь передачи проходит по ветвям Gs
и
G2;
при закорачивании
этого пути передачи все четыре узла
объединяются (рис. 20,в), следовательно,
;
.
Оба
пути передачи проходят через заданную
ветвь в том же направлении, что и ток
I6
, поэтому
произведения путей передачи на их
определители в формуле передачи
должны быть учтены с положительным
знаком:
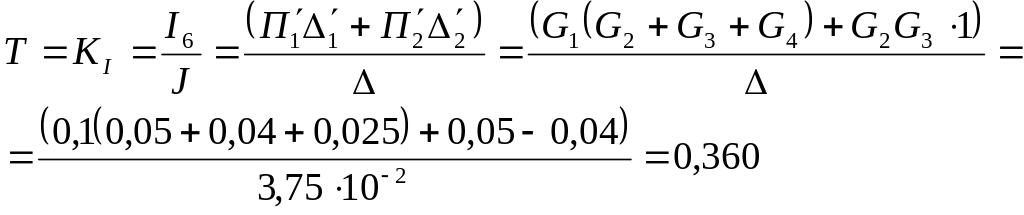
47
Искомый
ток I6
= TJ
=
0,36 • 5 = 1,8 А.
Аналогичным
образом могут быть найдены и напряжения
в заданных ветвях; передача при этом
имеет размерность сопротивления.
МЕТОД
СИГНАЛЬНЫХ (НАПРАВЛЕННЫХ) ГРАФОВ
Сигнальным
графом (направленным графом, графом
уравнения) называется
совокупность узлов и соединяющих их
ветвей, имеющих направление, указываемое
стрелкой. В отличие от ненаправленного
графа, сигнальный граф
представляет собой геометрический
образ системы линейных алгебраических
уравнений, описывающих электрическое
состояние цепи, иными словами,
сигнальный граф не повторяет электрическую
цепь, а представляет собой графическое
изображение уравнений, связывающих
величины, характеризующие эту цепь.
Узел
графа, к которому подключена одна
уходящая ветвь, характеризуется
входным сигналом – свободным членом
системы уравнений (заданным напряжением
или током), узел с одной входящей ветвью
– выходным сигналом, т.е. искомой
величиной, остальные узлы – другими
неизвестными величинами, которые
должны быть исключены в процессе решения
задачи.
Каждая
ветвь характеризуется передачей,
являющейся функцией коэффициентов
уравнений и равной отношению сигналов
выходного (по направлению ветви) узла
к входному. К узлам графа может подходить
и уходить по нескольку ветвей; сигнал
узла равен сумме сигналов, приходящих
к этому
узлу (уходящие сигналы не учитываются).
Граф
цепи позволяет по заданному входному
сигналу (напряжению или току источника
энергии) найти выходной сигнал (ток или
напряжение приемника).
Эта задача может быть решена или
последовательным упрощением графа, или
48
применением
общего выражения для передачи сигнала
(формула Мезона). При упрощении исходный
граф преобразуется в эквивалентный с
одной
ветвью, непосредственно связывающей
входной и выходной узлы. Сигнальный
граф цепи может быть построен по системе
расчетных уравнений,
составленных для заданной цепи методом
контурных токов или узловых потенциалов.
Однако
преимущества использования сигнальных
графов для
расчета электрических цепей сказываются
в полной мере лишь тогда, когда
граф строится сразу по схеме цепи без
составления и преобразования
уравнений.
В
случае построения графа контурных
уравнений необходимо задаться
положительными
направлениями контурных токов, выбирая
в качестве контуров ячейки, на которые
разбита цепь; положительные направления
контурных
токов цепи принимаются одинаковыми
(например, по часовой стрелке).
Количество узлов будущего графа
определяется количеством неизвестных
контурных токов и количеством источников
энергии в исходной цепи.
Далее поступают следующим образом.
1.
На поле графа располагают узлы,
соответствующие искомым переменным и
источникам схемы.
2.
Узлы-переменные (контурные токи)
соединяются двумя параллельными
противоположно направленными ветвями,
причем, если ветвь направлена
от узла j
к узлу i
,
то передача этой ветви принимается
равной –Rij/Rii
3.
Источники ЭДС схемы соединяются с
узлами-переменными, направление
передачи всегда от источника к
соответствующему узлу – переменной,
т.е.
к тому току, в контуре которого находится
данная ЭДС. Передача ветви,
соединяющая источник ЭДС, с i-м
контурным
током численно равна
+(-)1/Rii.
Знак
“+” берется в случае, если i-й
контурный
ток совпадает
по направлению с данной ЭДС.
49
4.
Источники тока схемы соединяются с теми
узлами-переменными, в контуре которых
находятся сопротивления, включенные
параллельно самим
источникам тока; передачи этих ветвей
численно равны +(-)Rk/Rii
(здесь
под Rk
понимается
сопротивление резистора, включенного
параллельно
данному к-му
источнику
тока и входящего в i-й
контур). Знаменатель
Rii
означает,
что данный источник тока соединен с i-м
узлом,
т.е. с i-м
контурным
током. Знак «+» отношения Rk/Rii
принимается
в случае, если эквивалентная ЭДС к
-го
источника тока направлена
согласно с i-м
контурным
током.
Пример
13.
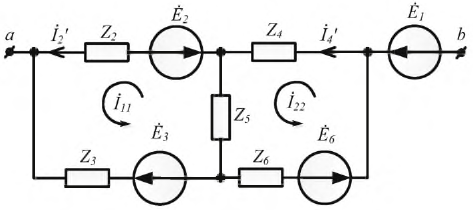
Построить граф контурных уравнений для
цепи, схема которой изображена на
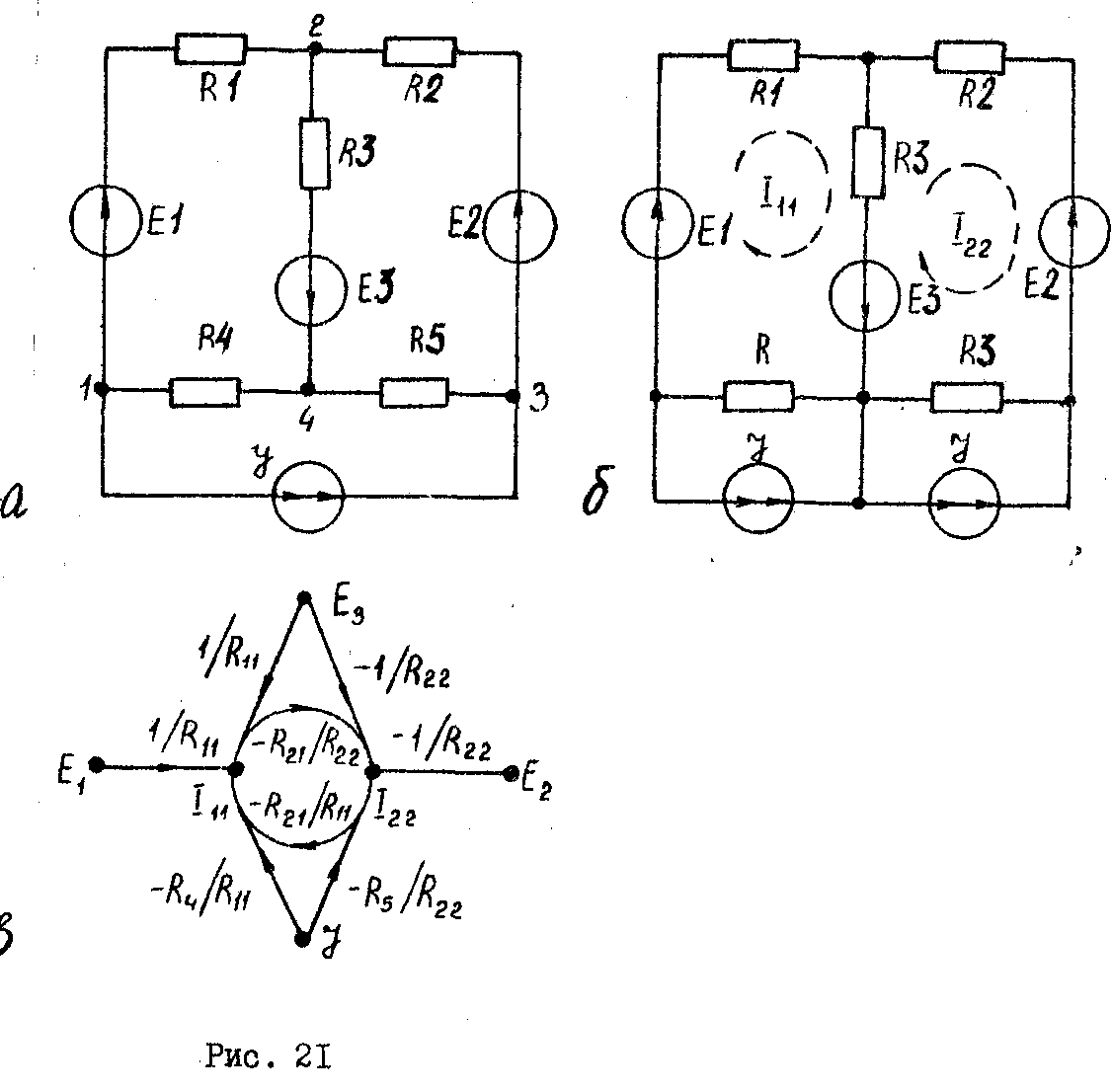
(рис. 21,а).
Для
большего удобства построения графа
необходимо видоизменить схему
так, чтобы каждому источнику тока
соответствовал параллельно включений
резистор /рис.21,б/.
Задаемся
положительными направлениями
контурных токов I11
и
I22
по
часовой стрелке. Граф будет содержать
шесть узлов, четыре из которых
принадлежат источникам энергии.
Контурные
сопротивления:
;
.
Взаимное
сопротивление контуров
.
Сигнальный
граф для цепи (рис. 21,а) изображен на
(рис. 21,в).
50
В
случае построения графа узловых уравнений
в качестве узлов-переменных
принимаются потенциалы узловых точек
цепи, причем их количество
на единицу меньше числа узлов цепи. Если
в схеме действует идеальный
источник ЭДС, необходимо предварительно
произвести преобразование
цепи, например перенести источник через
узел.
Общее
количество узлов графа равно количеству
узлов-источников и узлов-переменных.
Далее поступают следующим образом.
1.
Располагая узлы на поле графа, соединяют
их между собой, причем
узлы-переменные соединяются двумя
параллельными противоположно направленными
ветвями, а узлы-истоки соединяются
одиночными ветвями с теми
узлами-переменными, между которыми
включен данный источник в электрической
цепи. Если ветвь направлена от j-го
узла-переменной к i-му
узлу-переменной,
передача ветви равна –Gij/Gii/
51
2.
Передача ветви, соединяющей источник
ЭДС Ек
с
i-ом
узлом-переменной,
равна +(-)Gk/Gii
(
Gк–
проводимость
ветви с ЭДС Eк
). Знак
“+” принимается
в случае, когда ЭДС Eк
направлена
к i-му
узлу.
3.
При соединении источника тока JK
с
i-му
узлом-переменной
в граф
вводится ветвь с передачей +(-)1/Gii
,
причем знак “+” берется тогда,
когда ток JK
направлен
к i-му
узлу.
Пример
14.Построить
граф
узловых уравнений для цепи, схема
которой
изображена на рис. 22,а. Используя формулу
Мезона, определить ток
J5
в
ветви с резистором R5
ЭДС
E5.
Положительное
направление
тока
показано на рисунке.
52
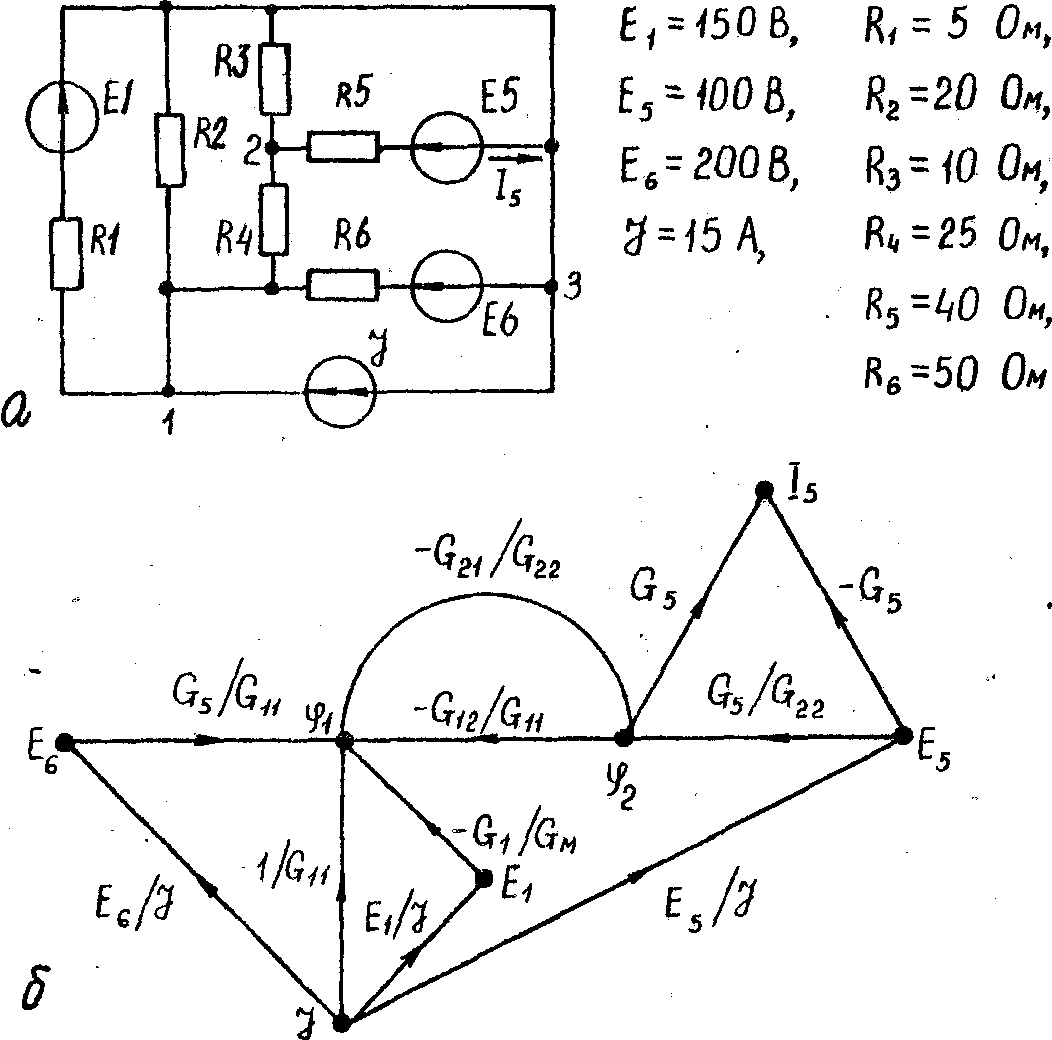
Рис.
22
Учитывая
приведенные рекомендации, строим
сигнальный граф цепи (рис.22,6).
Узловые и межузловые проводимости:
;
.
53
Поскольку
решение графа с помощью топологической
формулы Мезона предполагает наличие
только одного источника энергии,
преобразуем несколько
истоков в один эквивалентный; при этом
в графе появляются ветви
между Е6
и
J
, между
Е1
и
J
, а
также между Е5
и
J.
Передачи
этих
ветвей соответственно равны:
;
;
.
В
результате такого преобразования
истоком графа является только узел
J
, остальные
истоки графа превратились в зависимые
(смешанные) узлы.
Передачи остальных ветвей вычисляются
согласно известным правилам
и обозначаются на графе (см. рис. 22,6).
Нахождение
определителя графа топологическим
методом осуществляется по формуле
,
где
∑Li
–
сумма величин всех контуров графа без
исключения;
∑Li–Lj
— сумма
произведений величин контуров графа,
взятых попарно и не соприкасающихся
между собой;
∑LiLjLk.-
сумма
произведений величин контуров
графа, взятых по три и не соприкасающихся
между собой и т.д.
В
графе (рис. 22,6) есть только один контур,
величина которого
54
(Напомним,
что контур сигнального графа должен
замыкаться по ветвям одного направления.)
Таким образом, узловой определитель
сигнального
графа
.
Остальные
слагаемые топологической формулы
определителя равны нулю, так как
отсутствуют пары, тройки и другие
комбинации несоприкасающихся
контуров.
Формула
Мезона для передачи узлового графа
между истоком и стоком
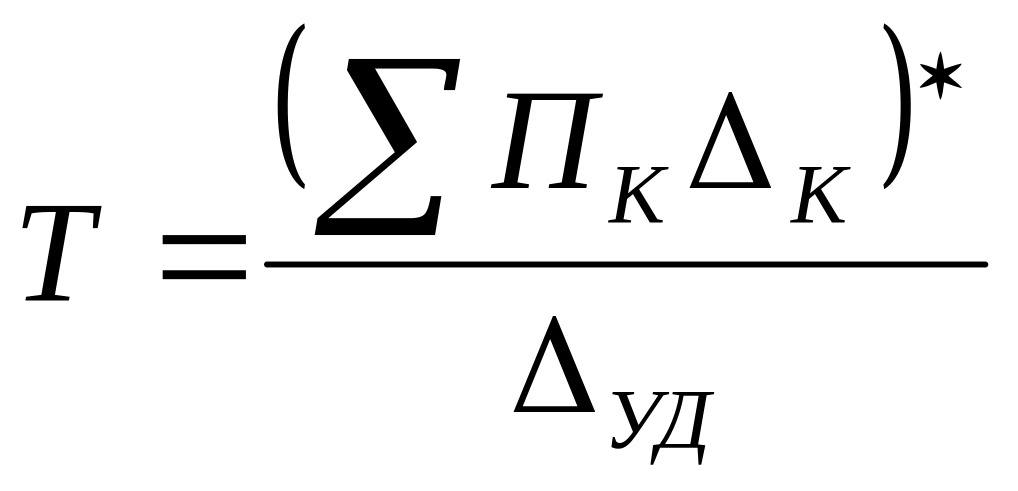
где
Пк
–
величина к-го
пути графа между заданным истоком и
искомой величиной
стока;
∆к
–
определитель
к-го
пути; вычисляется по топологической
формуле разложения определителя с
учетом дополнительного условия:
все контуры в выражениях
,
,
.
и
т.д. не должны
соприкасаться с данным к-м
путем (об этом напоминает “звездочка”
в числителе формулы передачи).
Искомой
величиной (стоком графа) является ток
I5
в
ветви
с резистором
R5
и ЭДС Е5.
Передачи
ветвей, подходящих к стоку, определяются
из уравнения:
.
55
Величины
путей графа и их определителей:
,
;
,
;
,
;
,
;
,
.
После
подстановки в топологическую формулу
передачи и необходимых алгебраических
преобразований имеем:
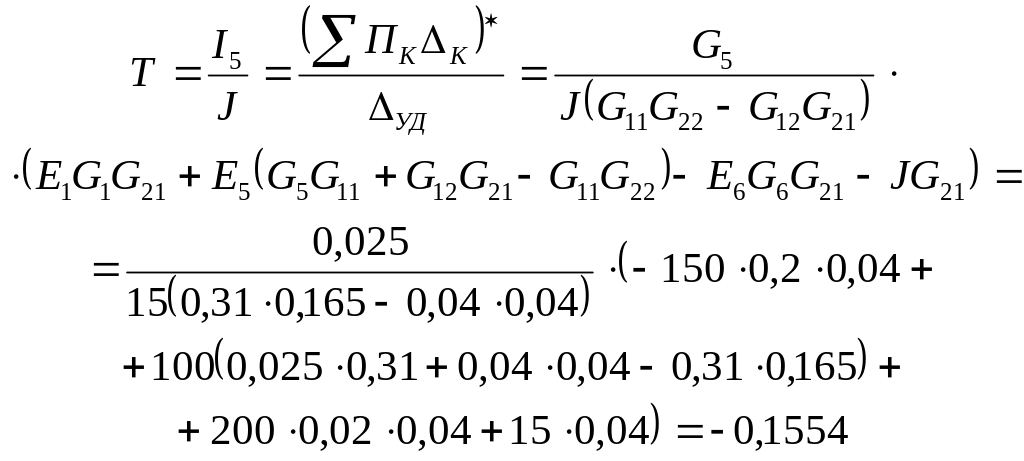
Ток
в заданной ветви
I5=TJ
= -0,1554*15
= -2,33 А.
Знак
“-” указывает, что истинное направление
тока противоположно выбранному на рис.
22,а.
56
Полученное
выражение для передачи можно использовать
для анализа влияния
параметров цепи на силу тока в заданной
ветви, для оптимизации режима работы
цепи по заданным условиям. Аналогично
могут быть найдены передачи (коэффициенты
по току и напряжению) для других ветвей
цепи.
Далее
приводятся условия задания на расчет
сложной линейной электрической
цепи постоянного тока и данные вариантов
этого задания.
Метод эквивалентного генератора
При решении задач по электротехнике, зачастую требуется знать режим работы не всей цепи, а только одной определённой ветви. Для определения параметров такой ветви существует метод эквивалентного генератора.
Суть метода эквивалентного генератора состоит в нахождении тока в одной выделенной ветви, при этом остальная часть сложной электрической цепи заменяется эквивалентным ЭДС Еэкв, с её внутренним сопротивлением rэкв. При этом часть цепи, в которую входит источник ЭДС называют эквивалентным генератором или активным двухполюсником, откуда и название метода.
Для наглядности рассмотрим схему представленную ниже. Допустим, что R1=5 Ом, R2=7 Ом, R3=10 Ом, Rab=3 Ом, E=10 В.

Согласно методу эквивалентного генератора получим схему

Искомый ток Iab находится по закону Ома для полной цепи
Для нахождения тока нужно узнать Еэкв и rэкв с помощью режимов эквивалентного генератора.
Для того чтобы найти эквивалентную ЭДС, нужно рассмотреть режим холостого хода генератора, другими словами нужно отсоединить исследуемую ветвь ab, тем самым избавив генератор от нагрузки, после чего он будет работать на так называемом холостом ходу.

Напряжение холостого хода Uх, будет равно эквивалентной ЭДС Eэкв. Таким образом мы можем найти Eэкв.
Следующим этапом решения задачи будет нахождение эквивалентного сопротивления rэкв. Можно воспользоваться режимом короткого замыкания генератора, при котором сопротивление Rab отсутствует, но в более сложных схемах это может привести к более громоздким расчётам, поэтому найдем rэкв как входное сопротивление пассивного двухполюсника. Пассивным называется двухполюсник у которого отсутствуют источники ЭДС. Простыми словами нужно убрать во внешней цепи источник ЭДС и найти сопротивление цепи, так и поступим.
Эквивалентное сопротивление rэкв равно ( тем, кто не умеет находить эквивалентное сопротивление, нужно прочитать статью виды соединения проводников )
Итак, найдя эквивалентные ЭДС и сопротивление, мы можем найти силу тока в ветви ab
На этом всё, ток в нужной ветви найден, а значит, задача решена методом эквивалентного генератора.
Читайте также – Метод двух узлов