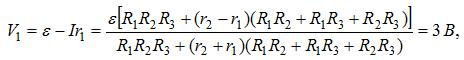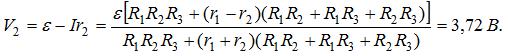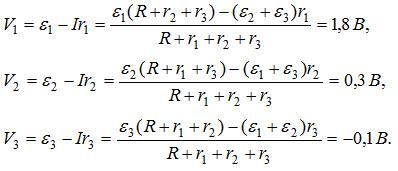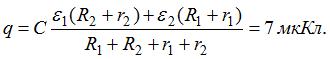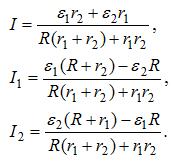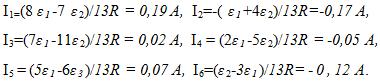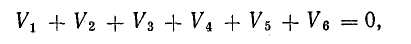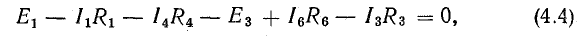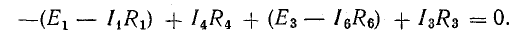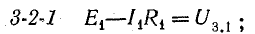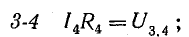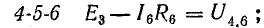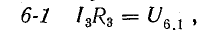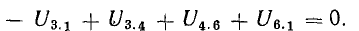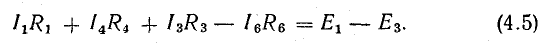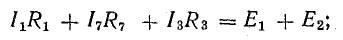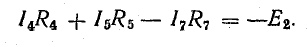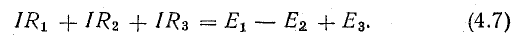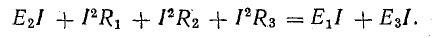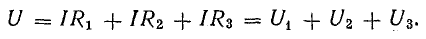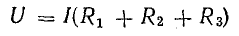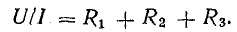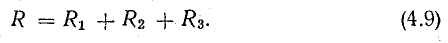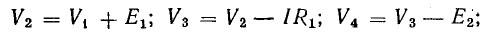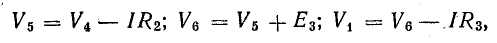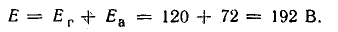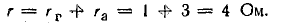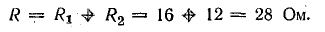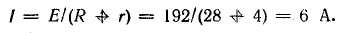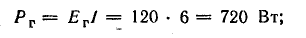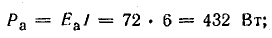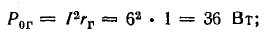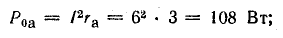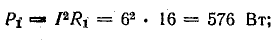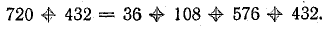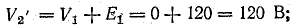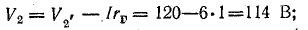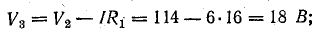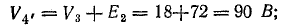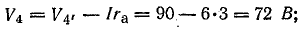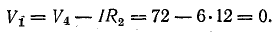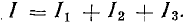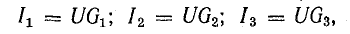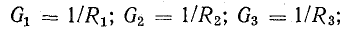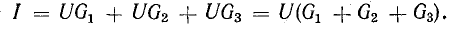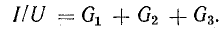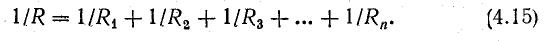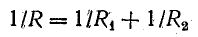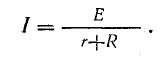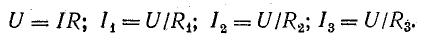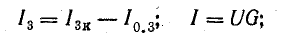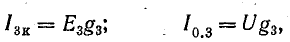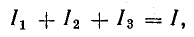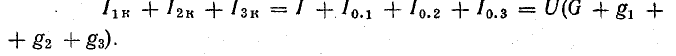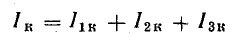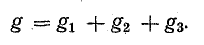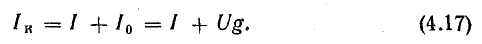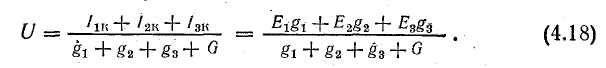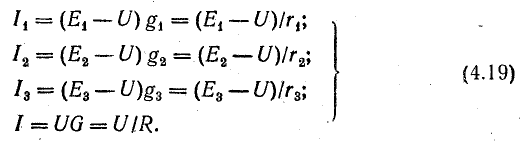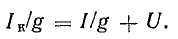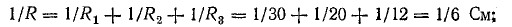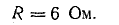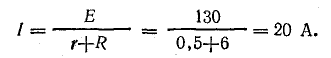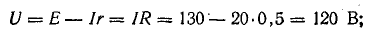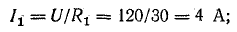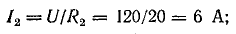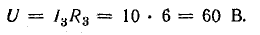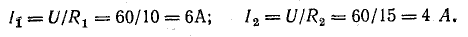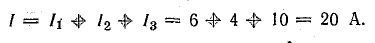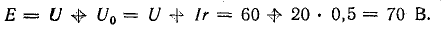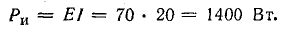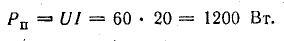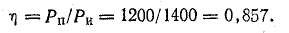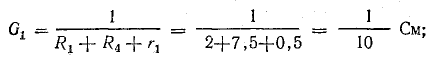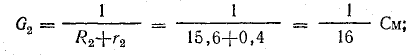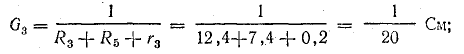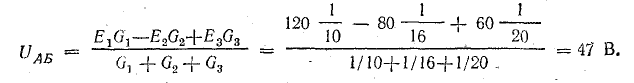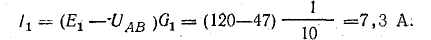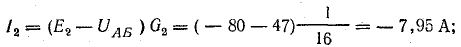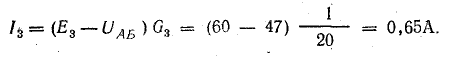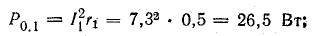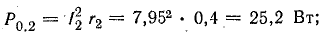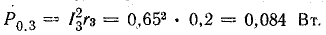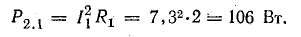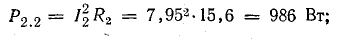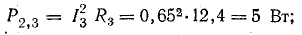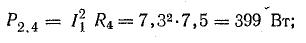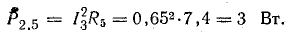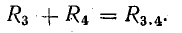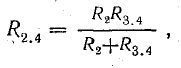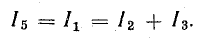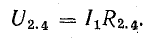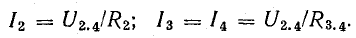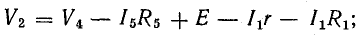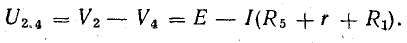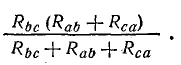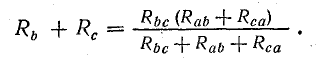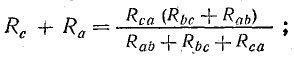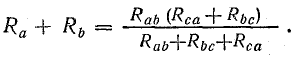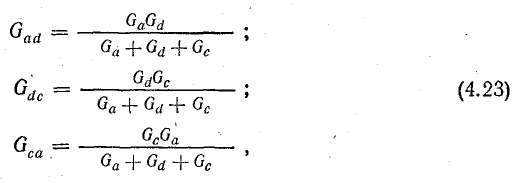Содержание
- ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ МЕЖДУ ДВУМЯ ТОЧКАМИ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
- Закон Ома
- Закон Ома для участка цепи
- Онлайн калькулятор
- Найти силу тока
- Формула
- Пример
- Найти напряжение
- Формула
- Пример
- Найти сопротивление
- Формула
- Пример
- Закон Ома для полной цепи
- Онлайн калькулятор
- Найти силу тока
- Формула
- Пример
- Найти ЭДС
- Формула
- Пример
- Найти внутреннее сопротивление источника напряжения
- Формула
- Пример
- Найти сопротивление всех внешних элементов цепи
- Формула
- Пример
- Сакович А.Л. Точки равного потенциала
- Символический (комплексный) метод расчета цепей переменного тока
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ МЕЖДУ ДВУМЯ ТОЧКАМИ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
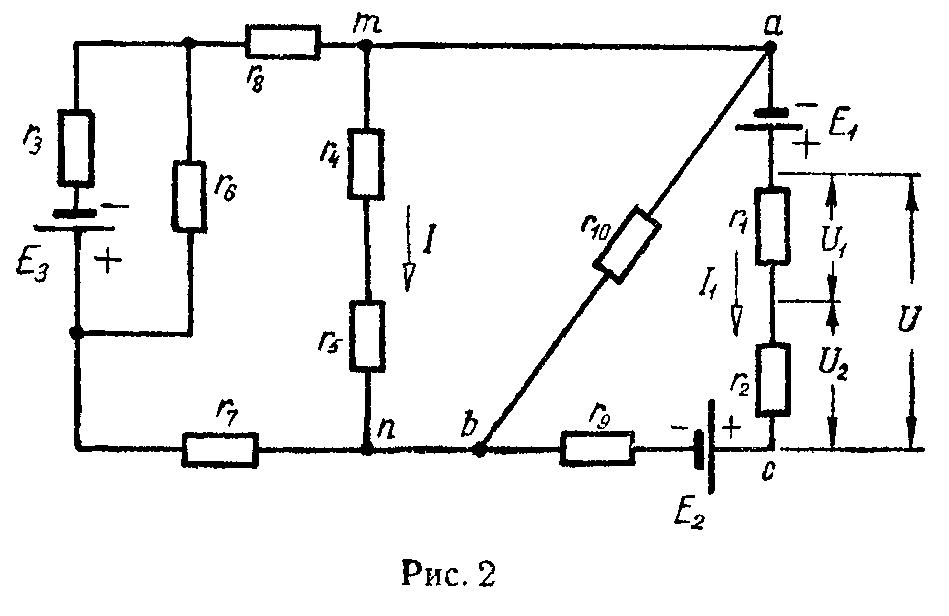
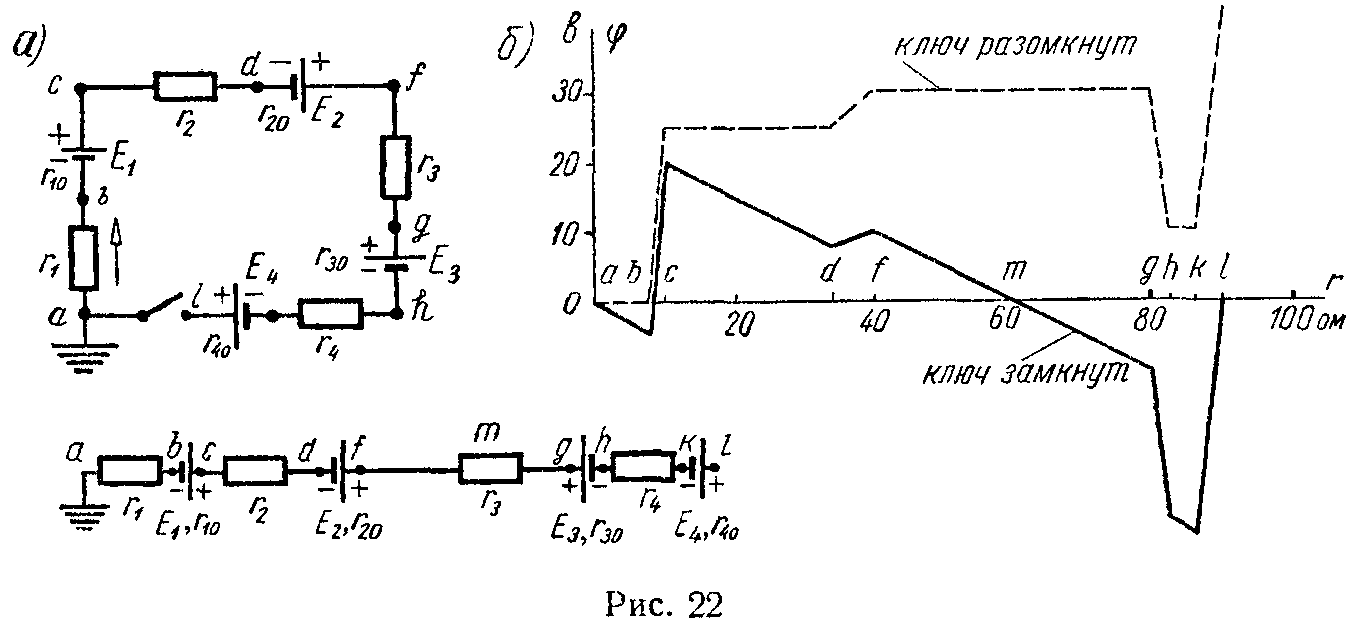
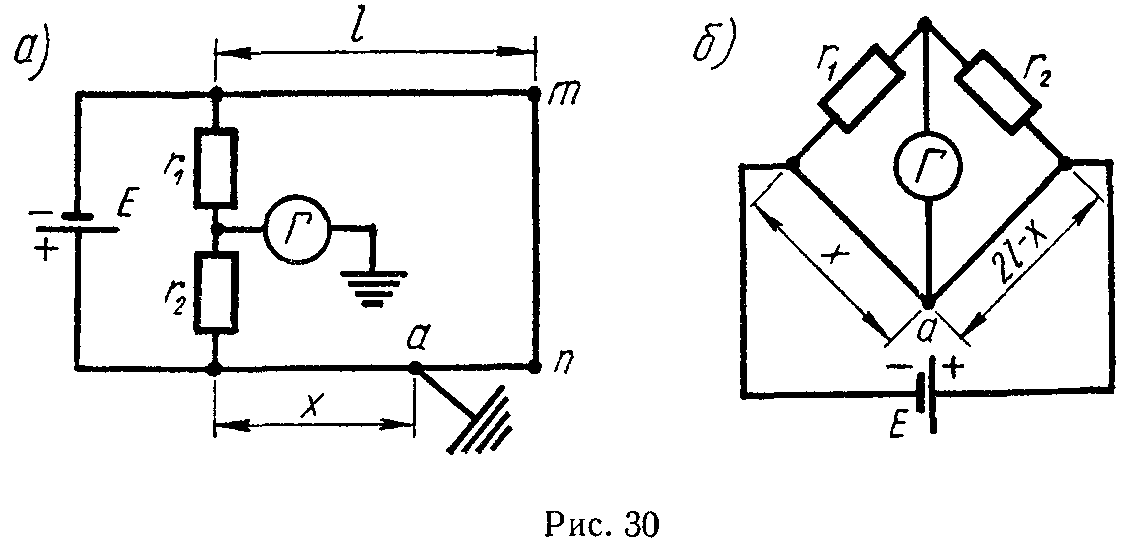
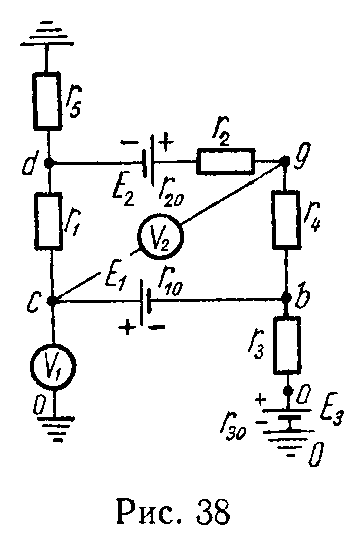
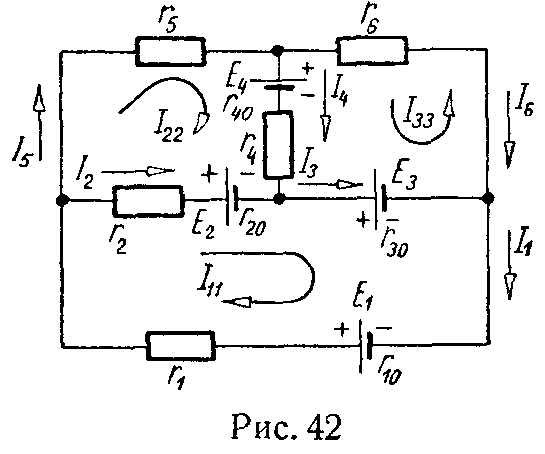
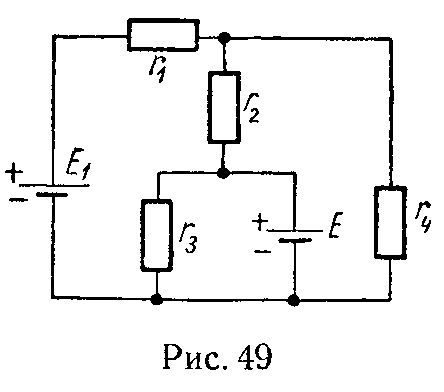
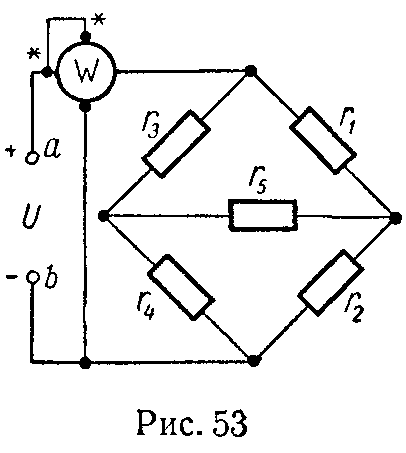
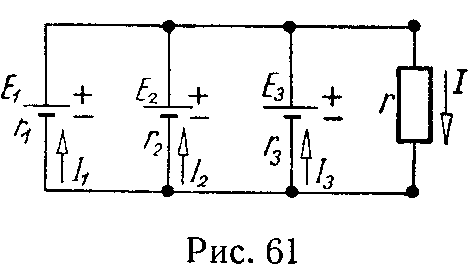
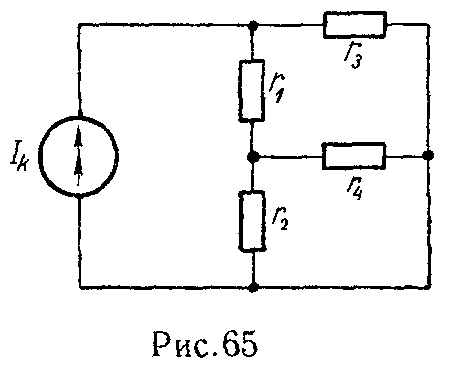
Эта задача при расчете электрических цепей встречается очень часто. Пусть, например, в цепи на рис. 2.1 требуется найти напряжение между точками m и n.
Прежде всего необходимо показать на схеме или мысленно представить стрелку этого напряжения. Её направление определяется порядком следования индексов у буквы . Для напряжения она направлена отточки m к точке n. Если мы меняем местами индексы у буквы , то следует изменить и направление стрелки на схеме. При этом при расчете меняется знак полученного напряжения, так как .
Дальше записываются уравнения по второму закону Кирхгофа для любого контура, включающего в себя эту стрелку, как было сделано при расчете напряжений и . Так, для контура m31nm при обходе его по часовой стрелке
При соответствующем навыке последняя формула может быть записана сразу, без составления уравнения второго закона Кирхгофа.
В указанном контуре напряжение складывается из трех напряжений:
Порядок индексов у букв U соответствует порядку, в котором мы проходим участок электрической цепи, идя от точки m к точке n по элементам , и .
Теперь находим значение каждого слагаемого в последнем уравнении.
Величина , определяющая напряжение между точками m и 3, представляет собой падение напряжения на сопротивлении , которое мы должны взять со знаком минус, так как от точки m к точке 3 мы идем против тока :
Здесь в правой части уравнения стоит плюс, так как мысленная стрелка напряжения и ток направлены в одну сторону.
Третье слагаемое представляет собой напряжение на зажимах источника. Если внутреннее сопротивление последнего равно нулю, то это напряжение по величине равно ЭДС, а знак его зависит от взаимного направления стрелок напряжения и ЭДС (рис. 7.1).
Рис. 7.1. Напряжение на зажимах источника
Рассмотрим рис. 7.1.
При указанной на схеме полярности зажимов источника потенциал точки b выше потенциала точки a на величину ЭДС:
Поэтому при одинаковых направлениях стрелок и (рис. 7.1, а)
Если направления стрелок и противоположны друг другу
(рис. 7.1, б), то
С учетом сказанного напряжение на участке 1n (см. рис. 2.1) равно
Подставляя найденные значения напряжений на участках в формулу (7.2), приходим к выражению (7.1).
То же самое напряжение, определяемое по участку m2n, будет равно
Разумеется, вычисление одного и того же напряжения по двум различным формулам должно привести к одинаковым результатам.
ПОСТРОЕНИЕ ГРАФИКОВ
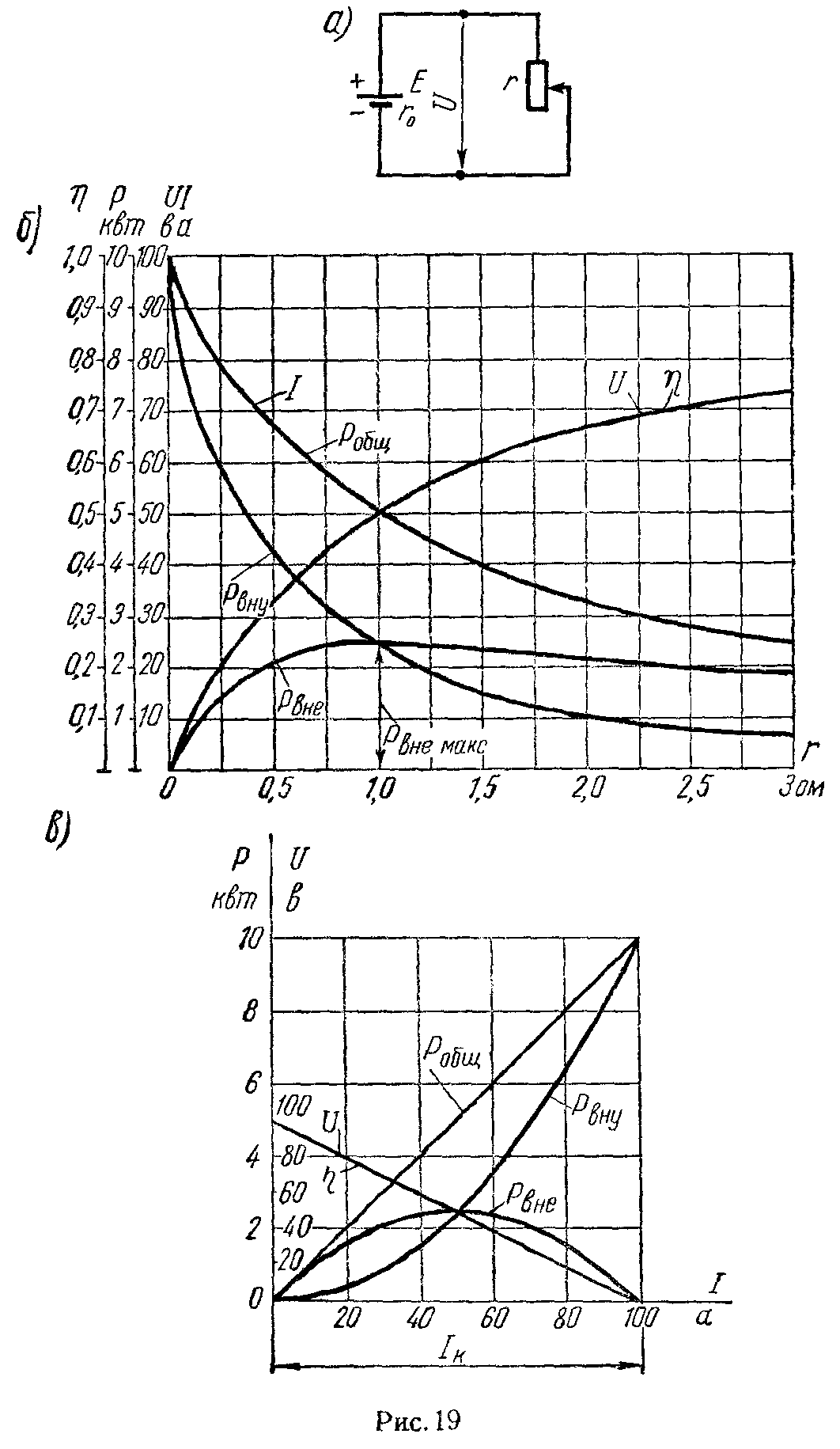
Общие требования к оформлению графиков. Зависимость мощности от тока
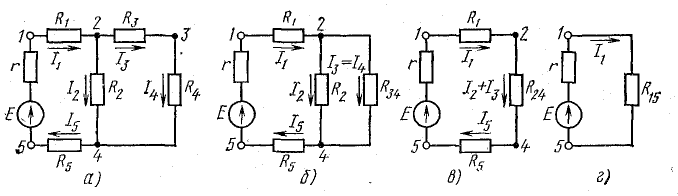
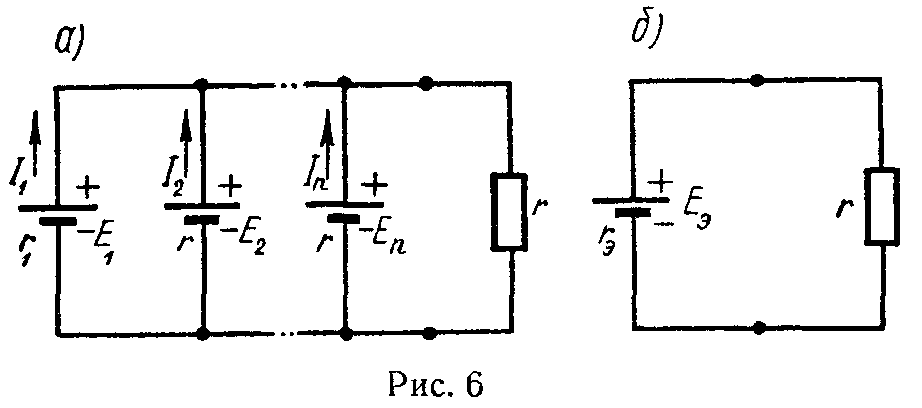
Правила построения графиков рассмотрим на примере зависимости мощности Р1,выделяющейся в сопротивлении первой ветви, от тока I1 в этой ветви. Эта зависимость определяется уравнением баланса мощностей в схеме рис. 6.1, в:
Это – уравнение параболы со смещенной вершиной и направленными вниз ветвями (рис. 8.1).
Значения тока, при которых парабола пересекает горизонтальную ось, находятся из уравнения
и соответственно равны
По смыслу – это ток, протекающий в схеме рис. 6.1, в при закороченном сопротивлении . При токе, равном половине этого значения, мощность максимальна:
Предположим, что параметры цепи на рис. 6.1, в имеют следующие численные значения:
= 72,4 В; = 130 В; = 43,6 Ом.
Прежде всего находим максимальные значения абсциссы и ординаты, которые будут определять размеры графика. В нашем примере – это значения и :
Исходя из этих величин и предполагаемых размеров графика, выбираем масштаб, который указываем на каждой оси графика в виде равномерной шкалы.
В одной единице длины (сантиметре, миллиметре) может содержаться m × 10 n именованных единиц. Здесь n – целое число, положительное или отрицательное, а для mрекомендуются числа 1, 2, 5.
Положительные значения величин откладываются вправо по оси абсцисс и вверх по оси ординат.
В конце каждой оси ставится буквенное обозначение откладываемой величины и через запятую – ее единица измерения.
Если график строится на белой (нелинованной) бумаге, то чертится масштабная сетка.
Данные для построения графика рассчитываем по формуле (8.1) и сводим их в таблицу (табл. 8.1).
Данные для построения графика
| , А | 0,2 | 0,4 | 0,5 | 0,6 | 0,66 | 0,8 | 0,9 | 1 | 1,2 | 1,32 | |
| , Вт | 9,78 | 16,1 | 17,9 | 18,9 | 19 | 18,2 | 16,5 | 14 | 6,34 |
Абсциссы точек, выбираемых для построения графика, желательно располагать по оси равномерно. Но вблизи характерных областей кривой (в нашем случае у вершины параболы) точки можно взять чаще. В таблицу внесены также значения максимальной мощности и тока, которому эта мощность соответствует. При построении графика числа из таблицы на осях не показываются (рис. 8.2).
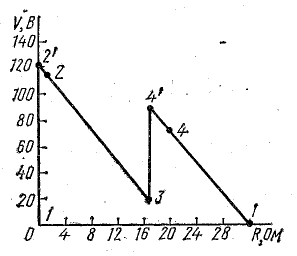
8.2. Зависимость тока от сопротивления
Зависимость тока в первой ветви от сопротивления этой ветви строим по уравнению (6.2), которое при выбранных значениях , и принимает вид:
Подставляя сюда различные значения сопротивления , приходим к результатам, представленным на рис. 8.3.
| , Ом | , А |
| 1,32 | |
| 10 | 1,07 |
| 20 | 0,91 |
| 30 | 0,78 |
| 40 | 0,69 |
| 50 | 0,62 |
| 60 | 0,56 |
| 70 | 0,51 |
| 80 | 0,47 |
Рис. 8.3. Зависимость тока от сопротивления
Дата добавления: 2019-07-17 ; просмотров: 1270 ; Мы поможем в написании вашей работы!
Источник
Закон Ома
Закон Ома для участка цепи
Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).
Онлайн калькулятор
Найти силу тока
Напряжение: U = В
Сопротивление: R = Ом
Формула
Пример
Если напряжение на концах участка цепи U = 12 В, а его электрическое сопротивление R = 2 Ом, то:
Сила тока на этом участке I = 12 /2= 6 А
Найти напряжение
Сила тока: I = A
Сопротивление: R = Ом
Формула
Пример
Если сила тока на участке цепи I = 6 А, а электрическое сопротивление этого участка R = 2 Ом, то:
Напряжение на этом участке U = 6⋅2 = 12 В
Найти сопротивление
Напряжение: U = В
Сила тока: I = A
Формула
Пример
Если напряжение на концах участка цепи U = 12 В, а сила тока на участке цепи I = 6 А, то:
Электрическое сопротивление на этом участке R = 12 /6 = 2 Ом
Закон Ома для полной цепи
Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.
Онлайн калькулятор
Найти силу тока
ЭДС: ε = В
Сопротивление всех внешних элементов цепи: R = Ом
Внутреннее сопротивление источника напряжения: r = Ом
Формула
Пример
Если ЭДС источника напряжения ε = 12 В, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
Сила тока I = 12 /4+2 = 2 А
Найти ЭДС
Сила тока: I = А
Сопротивление всех внешних элементов цепи: R = Ом
Внутреннее сопротивление источника напряжения: r = Ом
Формула
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
ЭДС ε = 2 ⋅ (4+2) = 12 В
Найти внутреннее сопротивление источника напряжения
Сила тока: I = А
ЭДС: ε = В
Сопротивление всех внешних элементов цепи: R = Ом
Внутреннее сопротивление источника напряжения: r =
Формула
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а ЭДС источника напряжения ε = 12 В, то:
Внутреннее сопротивление источника напряжения r = 12/2 — 4 = 2 Ом
Найти сопротивление всех внешних элементов цепи
Сила тока: I = А
ЭДС: ε = В
Внутреннее сопротивление источника напряжения: r = Ом
Сопротивление всех внешних элементов цепи: R =
Формула
Пример
Если сила тока в цепи I = 2A, внутреннее сопротивление источника напряжения r = 2 Ом, а ЭДС источника напряжения ε = 12 В, то:
Сопротивление всех внешних элементов цепи: R = 12/2 — 2 = 4 Ом
Источник
Сакович А.Л. Точки равного потенциала
Рассмотрим способы нахождения точек одинакового потенциала более подробно. Пусть нам дана электрическая цепь, состоящая из сопротивлений R1, R2, …, R8 (рис. 1 а). Проведем через точки подключения цепи прямую АВ (рис. 1 б).
1 способ. Если схема содержит проводники с одинаковым сопротивлением, расположенные симметрично относительно определенной оси или плоскости, то концы этих проводников имеют одинаковый потенциал. При этом точки будут симметричными относительно прямой АВ, если равны сопротивления участков цепи между данными точками и любыми точками этой прямой.
Используя этой признак, можно сделать вывод, что точки С1 и С2 (рис. 1 б) будут симметричны относительно прямой АВ, если R1 = R2 (сопротивления между точкой А и С1 и между точкой А и С2 равны) и R5 = R6 (сопротивления между точкой В и С1 и между точкой В и С2 равны). Аналогично, точки С3 и С4 будут симметричны относительно прямой АВ, если R3 = R4 и R7 = R8.
2 способ. Точки имеют одинаковый потенциал, если равны отношения сопротивлений между данными точками и точками подключения.
Например, точки С1 и С2 (рис. 1 а) имеют одинаковый потенциал, если . Аналогично, точки С3 и С4 имеют одинаковый потенциал, если .
Покажем на примерах, как можно использовать эти способы для преобразования электрических цепей.
Метод объединения равнопотенциальных узлов:точки с одинаковыми потенциалами можно соединять в узлы.
а) Если провести через точки подключения прямую АВ (рис. 3 а), то равны сопротивления участков АС1 и АС2 (R1 = R3), и равны сопротивления участков ВС1 и ВС2 (R2 = R4). Следовательно, точки С1 и С2 симметричны относительно прямой АВ и имеют равные потенциалы.
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 3, б). Резисторы R1 и R3 соединены параллельно, и резисторы R2 и R4 – параллельно, участки 1/3 и 2/4 последовательно. Следовательно,
б) Если провести прямую АВ (рис. 3 а), то сопротивления участков АС1 и АС2 не равны , следовательно, точки С1 и С2 не симметричны относительно прямой АВ. НО точки С1 и С2имеют равные потенциалы, т.к. .
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 3 б). Резисторы R1 и R3 соединены параллельно, и резисторы R2 и R4 – параллельно, участки 1/3 и 2/4 последовательно. Следовательно,
Пример 2. Найдите сопротивление проволочного куба между точками А1 и В3 (рис. 4). Сопротивление каждого ребра R.
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 6). Три резистора R соединены параллельно между точками А1 и А2 (В1, А4), шесть резисторов R – параллельно между точками А2 (В1, А4) и А3 (В2, В4), три резистора R – параллельно между точками А3 (В2, В4) и В3, участки между этими точками соединены последовательно. Следовательно,
Пример 3. Найдите сопротивление проволочного куба между точками А1 и В2 (рис. 4). Сопротивление каждого ребра R.
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 7 б). Используя рекуррентный метод, схему можно упростить (рис. 7 в или г).
Точки А2 и В4имеют равные потенциалы, т.к. . Точки с одинаковыми потенциалами можно соединять в узлы (рис. 7 д). Резисторы на участке А1А2 соединены параллельно, и резисторы на участке А2В2 – параллельно, а эти участки соединены последовательно. Следовательно,
Если возможно объединение двух равнопотенциальных узлов, то возможен и обратный переход.
Метод разделения узлов: узел схемы можно разделить на два или несколько узлов, если получившиеся при этом узлы имеют одинаковые потенциалы.
Обязательным условием при этом является проверка получившихся при разделении узлов на равенство потенциалов (симметричность или пропорциональность сопротивлений).
Пример 4. Найдите сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис. 8) сопротивлением R каждый.
Разделим узел в середине каркаса на два узла О1 и О2 так, как показано на рис. 9 а. Это можно сделать, так как точки О1 и О2 имеют равные потенциалы: равны сопротивления участков AO1, AO2, и равны сопротивления участков BO1, BO2. Перерисуем схему в стандартный вид (рис. 9 б). Используя рекуррентный метод, схему можно упростить (рис. 9 в), т.к. сопротивление участка C1F1 равно , аналогично . Тогда общее сопротивление цепи равно .
Обратите внимание. С точки зрения геометрии точки О3 и О4 симметричны относительно прямой а (рис. 9 г), но потенциалы этих точек не равны, т.к. сопротивления участков АО3 и АО4 не равны, а отношения сопротивлений участков АО3 и АО4 не равны отношению сопротивлений участков ВО3 и ВО4.
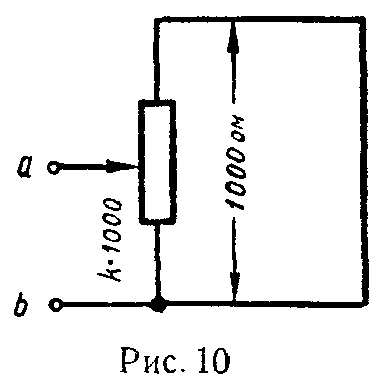
Пример 5. Найти сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис. 10) сопротивлением R каждый.
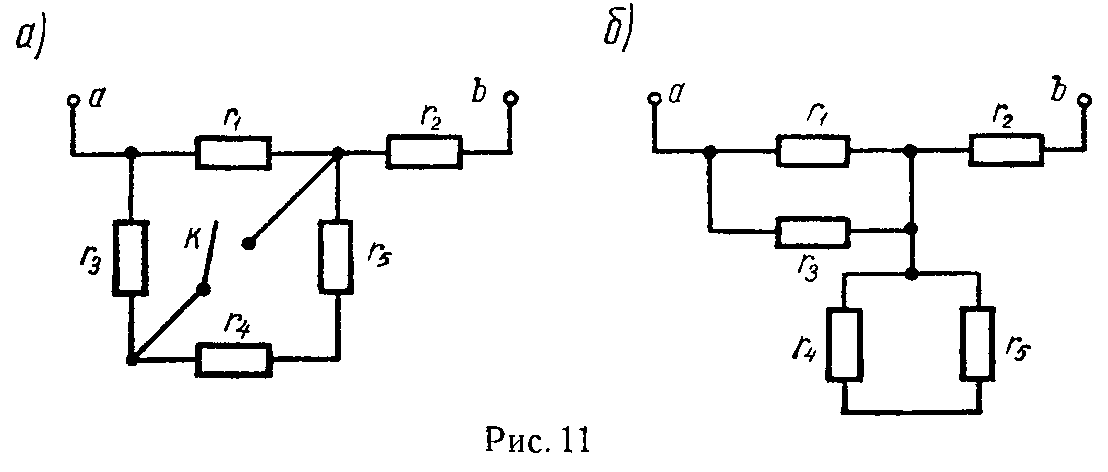
Разделим узел в середине каркаса на три узла О1, О2 и О3 так, как показано на рис. 11 а. Это можно сделать, так как точки О1, О2 и О3 имеют равные потенциалы: равны сопротивления участков AO1 и BO1, участков AO2 и BO2, и участков AO3 и BO3, следовательно, отношения сопротивления этих участков равны.
Перерисуем схему в стандартный вид (рис. 11, б). Используя рекуррентный метод, схему можно упростить (рис. 11 в), т.к. сопротивление участка C1F1 равно , аналогично , сопротивление . Тогда общее сопротивление цепи равно
Литература
- Зильберман А. Расчет электрических цепей // Квант. – 1988. – № 8. – С. 30-34.
- Петросян В.Г., Долгополова Л.В., Лихицкая И.В. Методы расчета резисторных схем постоянного тока // Физика. – 2002. – № 14, 18, 22.
- Хацет А. Методы расчета эквивалентных сопротивлений // Квант. – 1972. – № 2. – С. 54-59.
Источник
Символический (комплексный) метод расчета цепей переменного тока
Одним из способов расчета цепей переменного тока является комплексный, или еще как говорят, символический метод расчета. Этот метод применяется при анализе схем с гармоническими ЭДС, напряжениями и токами. В результате решения получают комплексное значение токов и напряжений, используя для решения любые методы (эквивалентных преобразований, контурных токов, узловых потенциалов и т.п.). Но для начала необходимо иметь понятие, в каких именно формах может представляться синусоидальная величина. 1. Одна из форм представления – это вращающийся вектор (см. рис.1):
Рис.1. Вращающийся вектор
С помощью рисунка ясно видно, как с течением времени меняется значение синусоидальной величины. В нашем случае – это величина а на графике, которая может быть, например, входным напряжением. Величина имеет некоторое начальное значение при t = 0 при начальной фазе φ
имеет положительное максимальное значение при угле ωt3, когда при времени t3 сумма ωt3 + φ = 90° и соответственно,
имеет отрицательное максимальное значение при угле ωt7, когда при времени t7 сумма углов ωt7 + φ = 270° и, соответственно,
и имеет два нулевых значения при ωtn + φ = 0, когда ωtn = —φ (на рис.1 эта область не показана и находится слева от начала координат)
и имеет нулевое значение при угле ωt11, когда при времени t11 сумма ωt11 + φ = 360° и соответственно,
Именно по такому закону и меняется привычное нам переменное напряжение 220 В, изменяясь по синусоидальному закону от значения 0 В до максимальных 311 В и обратно.
2. Другая форма представления – это комплексное число. Чтобы представить ранее рассмотренную форму представления синусоидальной величины, которая имеет некоторую начальную фазу φ, создают комплексную плоскость в виде графика зависимости двух величин (рис.2)
Рис.2. Комплексное число на комплексной плоскости
Длина вектора Am на такой комплексной плоскости равна амплитуде (максимальному значению) рассматриваемой величины. С учетом начальной фазы φ такое число записывают как 
На практике при использовании для расчетов символического (комплексного) метода расчета используют для некоторых удобств не амплитудное значение величины, а так называемое действующее значение. Его величина в корень из двух раз меньше амплитудного и обозначается без индекса m, т.е. равна
На рисунке выше этот вектор также показан.
Например, при том же нашем напряжении в сети, максимальное значение синусоидально изменяющегося напряжения равно 311 В, а действующее значение, к значению которого мы привыкли
При работе с комплексными числами и расчетов применяют различные формы записи комплексного числа. Например, при сложении комплексных чисел удобнее использовать алгебраическую форму записи таких чисел, а при умножении или делении – показательную форму записи. В некоторых случаях пишут тригонометрическую форму.
Итак, три формы записи комплексного числа:
1) показательная форма в виде
2) тригонометрическая форма в виде
3) алгебраическая форма
где ReA — это действительная составляющая комплексного числа, ImA — мнимая составляющая.
Например, имеем комплексное число в показательной форме вида
в тригонометрической форме записи это запишется как
при подсчете получим число, плавно переходящее в алгебраическую форму с учетом того, что
В итоге получим
При переходе от алгебраической формы к показательной комплексное число вида
переходит к показательному виду по следующим преобразованиям
Таким образом, и получим
Перейдем к рассмотрению несложных примеров использования символического, или по-другому, комплексного метода расчета электрических цепей. Составим небольшой алгоритм комплексного метода:
-
-
- Составить комплексную схему, заменяя мгновенные значения ЭДС, напряжений и токов их комплексным видом
- В полученной схеме произвольно выбирают направления токов в ветвях и обозначают их на схеме.
- При необходимости составляют комплексные уравнения по выбранному методу решения.
- Решают уравнения относительно комплексного значения искомой величины.
- Если требуется, записывают мгновенные значения найденных комплексных величин.
-
Пример 1. В схеме рис.3 закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи.
Рис.3. Схема с последовательным соединением элементов
Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.4):
Рис.4. Схема с комплексными обозначениями
По закону Ома ток в цепи равен
где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как
Пояснение: здесь начальная фаза φ = 0°, так как общее выражение для мгновенного значения напряжение вида 
Соответственно, комплекс входного напряжения в показательной форме запишется как
Полное комплексное сопротивление цепи в общем виде
Находим комплексное сопротивление индуктивности
Находим комплексное сопротивление емкости
Соответственно, общее комплексное сопротивление цепи
Комплексные напряжения на элементах
Проверяем второй закон Кирхгофа для замкнутого контура, т.е. должно выполняться равенство
С небольшим расхождением из-за округлений промежуточных вычислений всё верно.
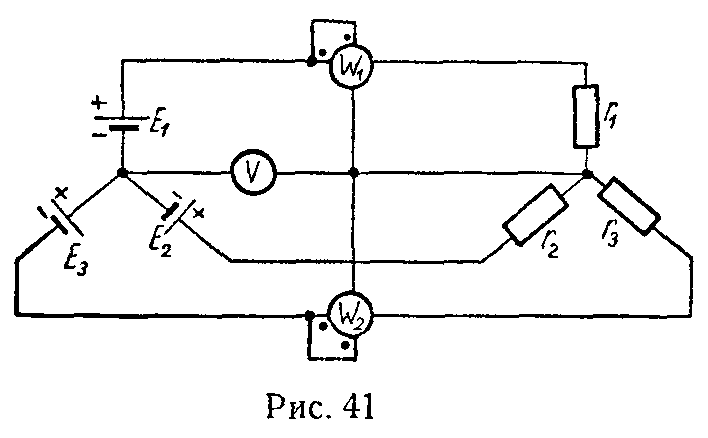
Пример 2. В электрической цепи (рис.5) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1) полное сопротивление электрической цепи и его характер;
2) действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;
- Исходные данные: Е = 220 В, f = 50 Гц, L1 = 38,2 мГн, R2 = 6 Ом, С2 = 318 мкФ, L2 = 47,7 мГн, R3 = 10 Ом, С3 = 300 мкФ.
Рис.5.Цепь однофвзного синусоидального тока
Решение:
1. Находим комплексные сопротивления ветвей и всей цепи:
Учитываем, что
Комплексное сопротивление первой ветви:
Комплексное сопротивление второй ветви:
Комплексное сопротивление третьей ветви:
Общее сопротивление цепи

2. Находим действующие значения токов в ветвях:
Рис.6. Схема с обозначенными комплексными токами
Действующие значения, соответственно,
3. Определим показания приборов:
Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:
U=220 В
Ваттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом, активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания:
Источник
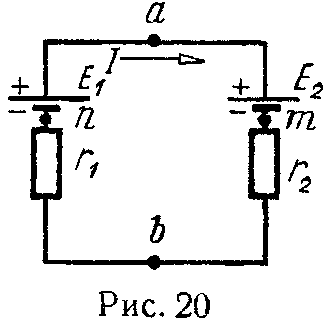
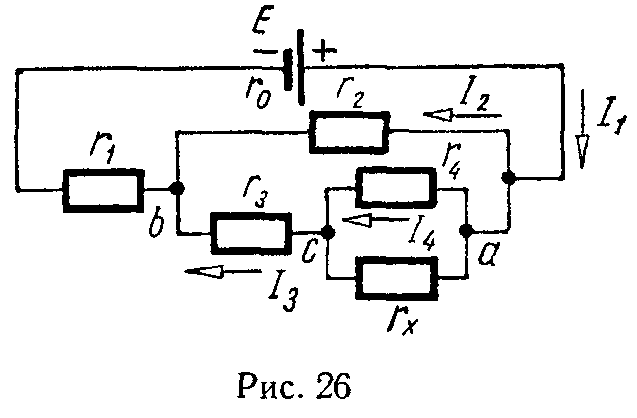
Правило Кирхгофа
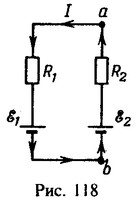
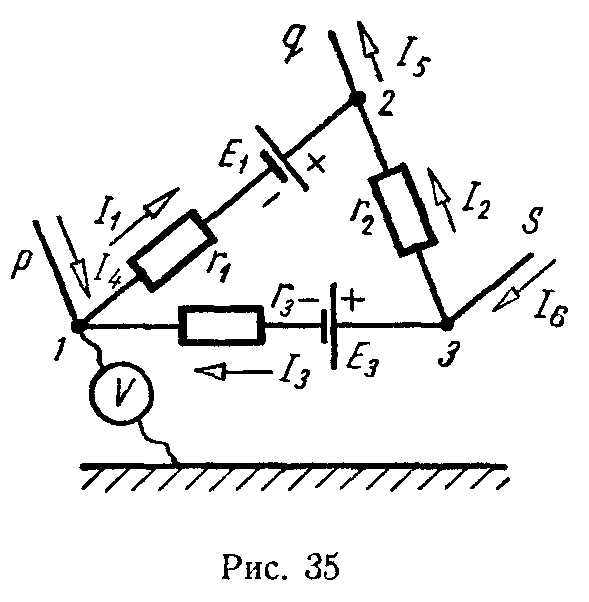
1 Найти разность потенциалов между точками а и b в схеме, изображенной на рис. 118. Э. д. с. источников тока ε1= 1 В и ε1 =1,3 В, сопротивления резисторов R1 = 10 Ом и R2 = 5 Ом.
Решение:
Поскольку ε2>ε1 то ток I будет идти в направлении, указанном на рис. 118, при этом разность потенциалов между точками а и b
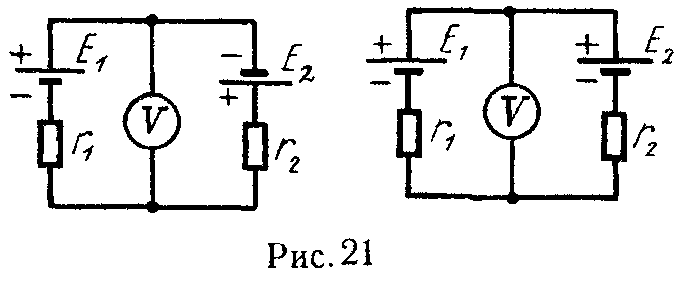
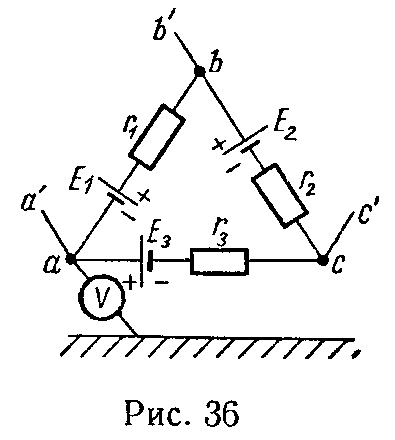
2 Два элемента с э. д. с. ε1 = 1,5 B и ε2 = 2 В и внутренними сопротивлениями r1=0,6 Ом и r2 = 0,4 Ом соединены по схеме, изображенной на рис. 119. Какую разность потенциалов между точками а и b покажет вольтметр, если сопротивление вольтметра велико по сравнению с внутренними сопротивлениями элементов?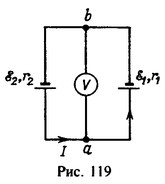
Поскольку ε2>ε1, то ток I будет идти в направлении, указанном на рис. 119. Током через вольтметр пренебрегаем ввиду
того, что его сопротивление велико по сравнению с внутренними сопротивлениями элементов. Падение напряжения на внутренних сопротивлениях элементов должно равняться разности э. д. с. элементов, так как они включены навстречу друг другу:
отсюда
Разность потенциалов между точками а и b (показание вольтметра)
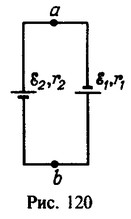
3 Два элемента с э. д. с. ε1=1.4B и ε2 = 1,1 В и внутренними сопротивлениями r =0,3 Ом и r2 = 0,2 Ом замкнуты разноименными полюсами (рис. 120). Найти напряжение на зажимах элементов. При каких условиях разность потенциалов между точками а и b равна нулю?
Решение:
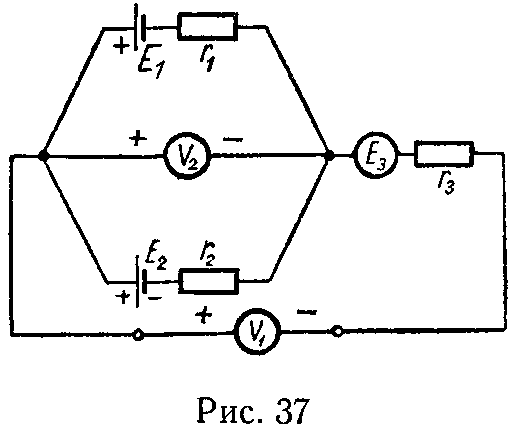
4 Два источника тока с одинаковыми э. д. с. ε = 2 В и внутренними сопротивлениями r1 =0,4 Ом и r2 = 0,2 Ом соединены последовательно. При каком внешнем сопротивлении цепи R напряжение на зажимах одного из источников будет равным нулю?
Решение: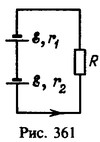
(рис.361). Напряжения на зажимах источников тока
Решая первые два уравнения при условии V1=0, получим
Условие V2=0 неосуществимо, так как совместное решение первого и третьего уравнений приводит к значению R<0.
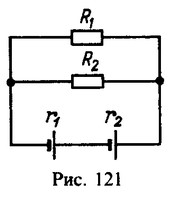
5 Найти внутреннее сопротивление r1 первого элемента в схеме, изображенной на рис. 121, если напряжение на его зажимах равно нулю. Сопротивления резисторов R1 = 3 Ом, R2 = 6 0м, внутреннее сопротивление второго элемента r2 = 0,4 Ом, э. д. с. элементов одинаковы.
Решение:
Ток в общей цепи
где внешнее сопротивление цепи
По условию задачи напряжение на зажимах первого элемента
отсюда
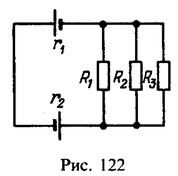
6 При каком соотношении между сопротивлениями резисторов R1, R2, R3 и внутренними сопротивлениями элементов r1, r2 (рис. 122) напряжение на зажимах одного из элементов будет равно нулю? Э. д. с. элементов одинаковы.
Решение:
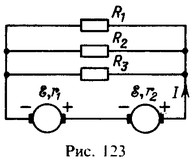
7 Два генератора с одинаковыми э. д. с. ε = 6 В и внутренними сопротивлениями r1 =0,5 Ом и r2 = 0,38 Ом включены по схеме, изображенной на рис. 123. Сопротивления резисторов R1 = 2 Ом, R2 = 4 Ом, R3 = 7 Ом. Найти напряжения V1 и V2 на зажимах генераторов.
Решение:
Ток в общей цепи
где внешнее сопротивление цепи
Напряжения на зажимах первого и второго генератора
напряжение на зажимах второго генератора
8 Три элемента с э. д. с. ε1 = 2,2 В, ε2 = 1,1 В и ε3 = 0,9 В и внутренними сопротивлениями r1 = 0,2 Ом, r2 = 0,4 Ом и r3 = 0,5 Ом включены в цепь последовательно. Внешнее сопротивление цепи R=1 Ом. Найти напряжение на зажимах каждого элемента.
Решение:
По закону Ома для полной цепи ток
Напряжение на зажимах каждого элемента равно разности э. д. с. и падения напряжения на внутреннем сопротивлении элемента:
Напряжение на зажимах батареи элементов равно падению напряжения на внешнем сопротивлении цепи:
Напряжение на зажимах третьего элемента оказалось отрицательным, так как ток определяется всеми сопротивлениями цепи и суммарной э.д.с, а падение напряжения на внутреннем сопротивлении r3 больше, чем э.д.с. ε3.
9 Батарея из четырех последовательно включенных в цепь элементов с э. д. с. ε = 1,25 В и внутренним сопротивлением r = 0,1 Ом питает два параллельно соединенных проводника с сопротивлениями R1 = 50 Ом и R2 = 200 Ом. Найти напряжение на зажимах батареи.
Решение:
10 Сколько одинаковых аккумуляторов с э. д. с. ε = 1,25B и внутренним сопротивлением r = 0,004 Ом нужно взять, чтобы составить батарею, которая давала бы на зажимах напряжение V=115 В при токе I=25 А?
Решение:
Напряжение на зажимах батареи
Следовательно,
11 Батарея из n= 40 последовательно включенных в цепь аккумуляторов с э. д. с. ε = 2,5 В и внутренним сопротивлением r = 0,2 Ом заряжается от сети с напряжением V=121 В. Найти зарядный ток, если последовательно в цепь введен проводник с сопротивлением R = 2 Ом.
Решение:
12 Два элемента с э. д. с. ε1 = 1,25 В и ε2 = 1,5 В и одинаковыми внутренними сопротивлениями r = 0,4 Ом соединены параллельно (рис. 124). Сопротивление резистора R= 10 Ом. Найти токи, текущие через резистор и каждый элемент.
Решение:
Падение напряжения на резисторе, если токи текут в направлениях, указанных на рис. 124,
Учитывая, что I=I1+I2, находим
Заметим, что I1<0. Это значит, что направление тока противоположно указанному на рис. 124.
13 Два элемента с э. д. с. ε1 =6 В и ε2 = 5 В и внутренними сопротивлениями r1 = 1 Ом и r2 = 20м соединены по схеме, изображенной на рис. 125. Найти ток, текущий через резистор с сопротивлением R= 10 Ом.
Решение: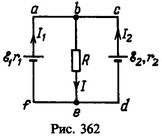
и для контура bcde (обход против часовой стрелки)
Из этих уравнений найдем
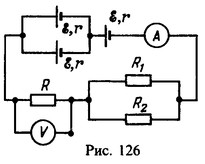
14 Три одинаковых элемента с э. д. с. ε = 1,6 В и внутренним сопротивлением r=0,8 Ом включены в цепь по схеме, изображенной на рис. 126. Миллиамперметр показывает ток I=100 мА. Сопротивления резисторов R1 = 10Ом и R2 = 15 0м, сопротивление резистора R неизвестно. Какое напряжение V показывает вольтметр? Сопротивление вольтметра очень велико, сопротивление миллиамперметра пренебрежимо мало.
Решение:
Внутреннее сопротивление элементов
Сопротивление параллельно включенных резисторов
Общая э. д. с. элементов e0=2e Согласно закону Ома для полной цепи
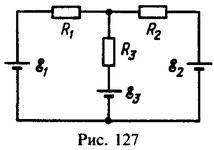
15 Сопротивления резисторов R1 и R2 и э. д. с. ε1 и ε2 источников тока в схеме, изображенной на рис. 127, известны. При какой э.д.с. ε3 третьего источника ток через резистор R3 не течет?
Решение: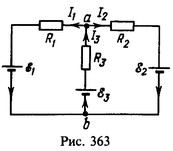
Если
Исключая I1 находим
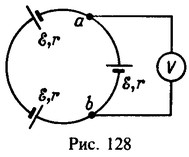
16 Цепь из трех одинаковых последовательно соединенных элементов с э.д.с. ε и внутренним сопротивлением r замкнута накоротко (рис. 128). Какое напряжение покажет вольтметр, подключенный к зажимам одного из элементов?
Решение: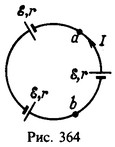
Из закона Ома для участка цепи между точками а и b получим
Подключение вольтметра к точкам, разность потенциалов между которыми равна нулю, ничего не может изменить в цепи. Поэтому вольтметр будет показывать напряжение, равное нулю.
17 Источник тока с э.д.с. ε0 включен в схему, параметры которой даны на рис. 129. Найти э.д.с. ε источника тока и направление его подключения к выводам а и b, при которых ток через резистор с сопротивлением R2 не идет.
Решение: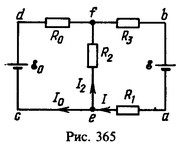
Используя условие I2 = 0, находим
Знак минус показывает, что полюсы источника тока на рис. 365 нужно поменять местами.
18 Два элемента с одинаковыми э.д.с. ε включены в цепь последовательно. Внешнее сопротивление цепи R = 5 Ом. Отношение напряжения на зажимах первого элемента к напряжению на зажимах второго элемента равно 2/3. Найти внутренние сопротивления элементов r1 и r2, если r1=2r2.
Решение:
19 Два одинаковых элемента с э.д.с. ε=1,5 В и внутренним сопротивлением r = 0,2 Ом замкнуты на резистор, сопротивление которого составляет в одном случае R1=0,2 Oм, В другом — R2 = 20 Ом. Как нужно соединить элементы (последовательно или параллельно) в первом и во втором случаях, чтобы получить наибольший ток в цепи?
Решение:
При параллельном соединении двух элементов внутреннее сопротивление и э.д.с. равны r/2 и ε при последовательном соединении они равны 2r и 2ε. Через резистор R при этом текут токи
Отсюда видно, что I2>I1, если R/2+r<R+r/2, т. е. если r1=r; следовательно, токи при параллельном и последовательном соединениях одинаковы. Во втором случае R2>r.Поэтому ток больше при последовательном соединении.
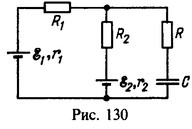
20 Два элемента с э.д.с. ε1=4В и ε2 = 2В и внутренними сопротивлениями r1 = 0,25 Ом и r2 = 0,75 Ом включены в схему, изображенную на рис. 130. Сопротивления резисторов R1 = 1 Ом и R2 = 3 Ом, емкость конденсатора С=2 мкФ. Найти заряд на конденсаторе.
Решение:
21 К батарее из двух параллельно включенных элементов с э.д.с. ε1 и ε2 и внутренними сопротивлениями r1 и r2 подключен резистор с сопротивлением R. Найти ток I, текущий через резистор R, и токи I1 и I2 в первом и втором элементах. При каких условиях токи в отдельных цепях могут быть равными нулю или изменять свое направление на обратное?
Решение: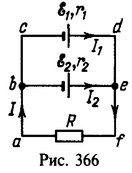
Из этих уравнений находим
Ток I=0 тогда, когда изменена полярность включения одного из элементов и, кроме того, выполнено условие
Ток I1=0 при
а ток I2 = 0 при
Токи I1 и I2 имеют направления, указанные на рис.366, если
Они меняют свое направление при
22 Батарея из n одинаковых аккумуляторов, соединенных в одном случае последовательно, в другом— параллельно, замыкается на резистор с сопротивлением R. При каких условиях ток, текущий через резистор, в обоих случаях будет один и тот же?
Решение:
При n(R-r) = R-r. Если R=r, то число элементов произвольно; если R№r, задача не имеет решения (n=1).
23 Батарея из n = 4 одинаковых элементов с внутренним сопротивлением r=2 Ом, соединенных в одном случае последовательно, в другом — параллельно, замыкается на резистор с сопротивлением R=10Ом. Во сколько раз показание вольтметра н одном случае отличается от показания вольтметра в другом случае? Сопротивление вольтметра велико по сравнению с R и r.
Решение:
где V1 — показание вольтметра при последовательном соединении элементов, V2-при параллельном.
24 Как изменится ток, текущий через резистор с сопротивлением R = 2 Ом, если n =10 одинаковых элементов, соединенных последовательно с этим резистором, включить параллельно ему? Э.д.с. элемента ε = 2 В, его внутреннее сопротивление r = 0,2 Ом.
Решение:
25 Батарея составлена из N=600 одинаковых элементов так, что n групп соединены последовательно и в каждой из них содержится т элементов, соединенных параллельно. Э.д.с. каждого элемента ε = 2 В, его внутреннее сопротивление r = 0,4 Ом. При каких значениях n и m батарея, будучи замкнута на внешнее сопротивление R = 0,6 Ом, отдаст во внешнюю цепь максимальную мощность? Найти при этом ток, текущий через сопротивление R.
Решение: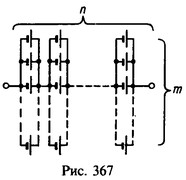
где r/m— внутреннее сопротивление группы из т параллельно соединенных элементов, а nr/m — внутреннее сопротивление n групп, соединенных последовательно. Максимальная мощность отдается во внешнюю цепь при равенстве сопротивления R внутреннему сопротивлению батареи элементов nr/m, т. е.
При этом через сопротивление R течет точек I=46 А.
26 Емкость аккумулятора Qo=80А⋅ч. Найти емкость батареи из n = 3 таких аккумуляторов, включенных последовательно и параллельно.
Решение:
При последовательном соединении через все аккумуляторы батареи течет один и тот же ток, поэтому все они разрядятся в течение одного и того же времени. Следовательно, емкость батареи будет равна емкости каждого аккумулятора:
При параллельном соединении n аккумуляторов через каждый из них течет 1/n часть общего тока; поэтому при том же разрядном токе в общей цепи батареи будет разряжаться в n раз дольше, чем один аккумулятор, т. е. емкость батареи в п раз больше емкости отдельного аккумулятора:
Заметим, однако, что энергия
отдаваемая батареей в цепь, и при последовательном и при параллельном соединении n аккумуляторов в n раз больше энергии, отдаваемой одним аккумулятором. Это происходит потому, что при последовательном соединении э. д. с. батареи в n раз больше э. д. с. одного аккумулятора, а при параллельном соединении э.д.с. батареи остается той же, что и для каждого аккумулятора, но Q увеличивается в n раз.
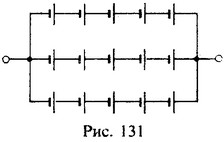
27 Найти емкость батареи аккумуляторов, включенных по схеме, изображенной на рис.131. Емкость каждого аккумулятора Q0=64 А⋅ч.
Решение:
Каждая группа из пяти аккумуляторов, включенных последовательно, имеет емкость
Три параллельно включенные группы дают общую емкость батареи
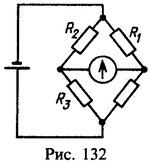
28 Мост для измерения сопротивлений сбалансирован так, что ток через гальванометр не идет (рис. 132). Ток в правой ветви I=0,2 А. Найти напряжение V на зажимах источника тока. Сопротивления резисторов R1 = 2 Ом, R2 = 4 Ом, R3 = 1 Ом.
Решение:
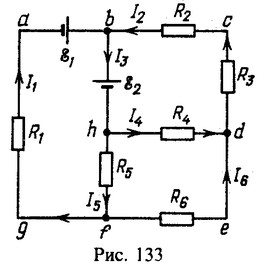
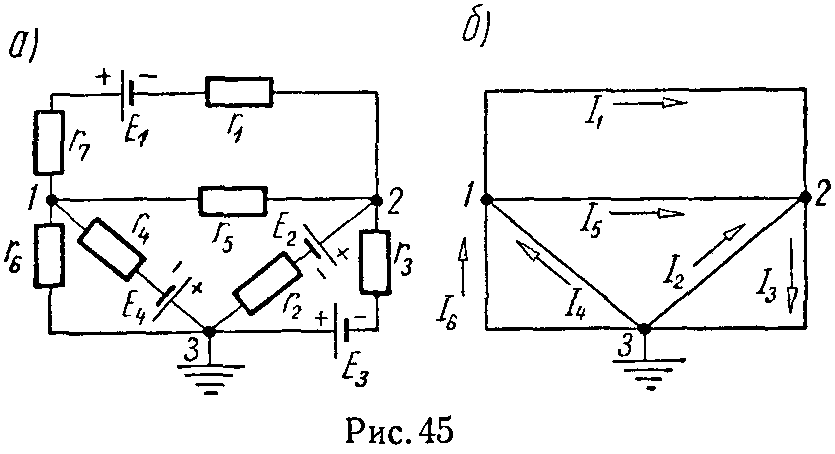
29 Найти токи, протекающие в каждой ветви цепи, изображенной на рис. 133. Э.д.с. источников тока ε1 = 6,5 В и ε2 = 3,9 В. Сопротивления резисторов R1=R2=R3=R4=R5=R6=R=10 Ом.
Решение:
Составляем уравнения Кирхгофа в соответствии с направлениями токов, указанными на рис. 133: I1 + I2 — I3 = 0 для узла b;
I3 — I4 — I5 =0 для узла h; I5 — I1 — I6 = 0 для узла f: при этом
Для контура abfg (обход по часовой стрелке),
Для контура bcdh (обход против часовой стрелки) и
для контура hdef (обход по часовой стрелке). Решая эту систему уравнений с учетом, что все сопротивления одинаковы и равны R=10 Ом, получим
Отрицательные значения токов I2, I4 и I6 показывают, что при данных э.д.с. источников и сопротивлениях резисторов эти токи текут в стороны, противоположные указанным на рис. 133.
Содержание:
Расчет электрических цепей постоянного тока:
Основная цель расчета электрической цепи заключается в определении токов в ее ветвях. Зная токи, нетрудно найти напряжения и мощности ветвей и отдельных элементов цепи.
Величины токов, напряжений, мощностей дают возможность оценить условия и эффективность работы электротехнического оборудования и приборов во всех участках электрической цепи.
Связь между э.д.с., напряжениями и токами линейных электрических цепей выражается линейными уравнениями, т. е. уравнениями первой степени, поэтому для расчета их применяются аналитические методы с обычными алгебраическими преобразованиями.
Законы Кирхгофа
Для расчета электрических цепей наряду с законом Ома применяются два закона Кирхгофа, являющиеся следствиями закона сохранения энергии.
Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлам электрических цепей:
в ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю:
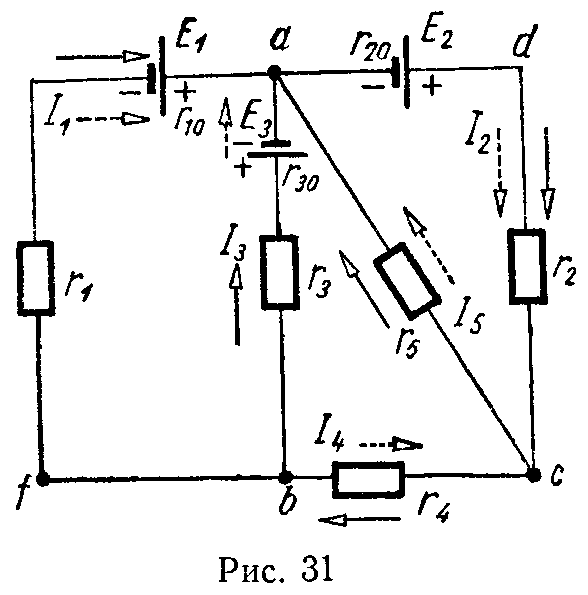
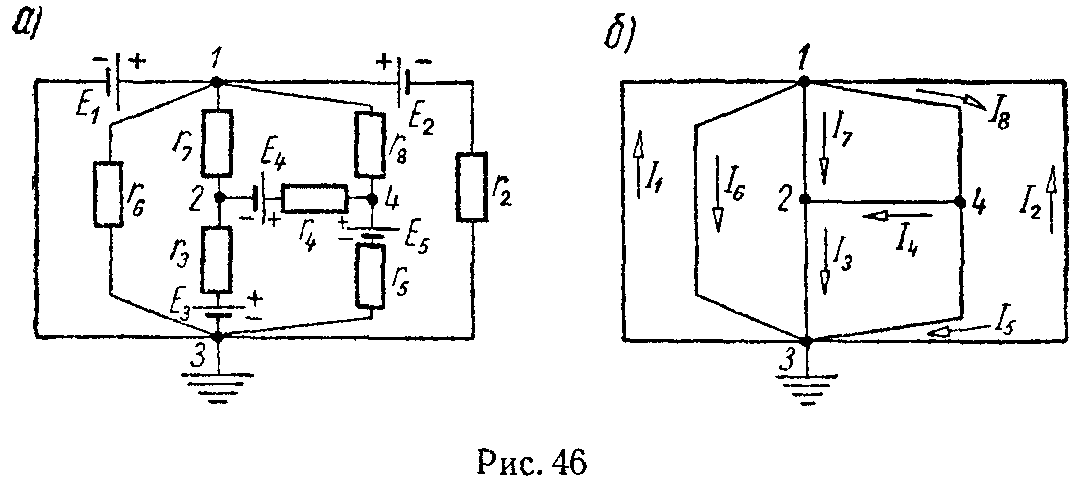
В эту сумму токи входят с разными знаками в зависимости от направления их по отношению к узлу. На основании первого закона Кирхгофа для каждого узла можно составить уравнение токов. Например, для точки 3 схемы рис. 3.16 такое уравнение имеет вид
I1 + I2 — I4 — I7 = 0.
В этом уравнении токи, направленные к узлу, условно взяты положительными, а токи, направленные от узла, — отрицательными:
I1 + I2 = I4 + I7. (4.2)
Уравнение (4.2) позволяет дать другую формулировку первого закона Кирхгофа:
сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла.
Этот закон следует из принципа непрерывности тока. Если допустить преобладание в узле токов одного направления, то заряд одного знака должен накапливаться, а потенциал узловой точки непрерывно изменяться, что в реальных цепях не наблюдается.
Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам электрических цепей:
в контуре электрической цепи алгебраическая сумма напряжений на его ветвях равна нулю:
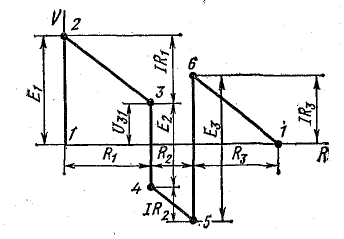
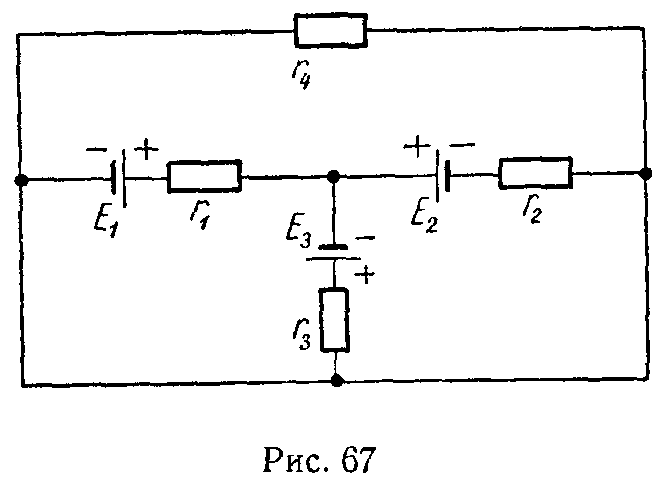
Для доказательства второго закона Кирхгофа обойдем контур 1-2-3-4-5-6-1 в схеме рис. 3.16 по часовой стрелке и запишем выражения потенциалов точек контура при указанных направлениях токов в ветвях (выбраны произвольно). Обход начнем от точки 1, потенциал которой V1. Потенциал каждой последующей точки выразим относительно точки предыдущей: V2 = V1 + Е1; V3 = V2 — I1R1; V4 = V3 — I4R4; V5 = V4 — E3; V6 = V5 + I6R6; V1 = V6 — I3R3.
Изменение потенциала по выбранному контуру должно быть равно нулю, так как оно выражает работу, затраченную на перемещение частиц, обладающих вместе единицей заряда, по замкнутому пути в электрических полях источников и приемников энергии. Таким образом, в замкнутом контуре
или
В этом уравнении напряжения ветвей
поэтому
В уравнении (4.4) напряжения, направленные по обходу контура, считаются положительными, а направленные против обхода — отрицательными.
Уравнение (4.4) перепишем в следующем виде:
Уравнение (4.5) позволяет дать другую формулировку второго закона Кирхгофа:
в контуре электрической цепи алгебраическая сумма падений напряжения на пассивных элементах равна алгебраической сумме э. д. с. этого контура:
Другим контурам соответствуют другие уравнения, которые нетрудно написать, не прибегая к выражениям потенциалов точек контура.
Для этого можно пользоваться следующим правилом. В левую часть уравнения следует записать алгебраическую сумму падений напряжения в пассивных элементах контура, а в правую—алгебраическую сумму э.д.с., встречающихся при обходе контура.
При этом положительными считаются токи и э. д. с., направление которых совпадает с направлением обхода.
Согласно этому правилу, запишем уравнения для двух других контуров схемы, представленной на рис. 3.16:
для 1-2-3-6-1
для 3-4-6-3
Неразветвленная электрическая цепь
Элементы неразветвленной электрической цепи соединены между собой последовательно.
Отличительной особенностью последовательного соединения является то, что электрический ток во всех участках цепи один и тот же.
Общий случай последовательного соединения
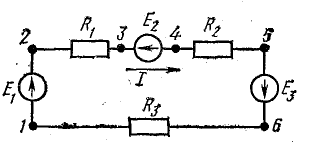
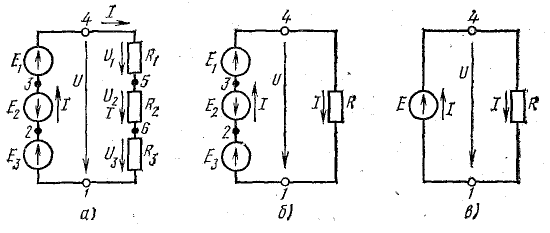
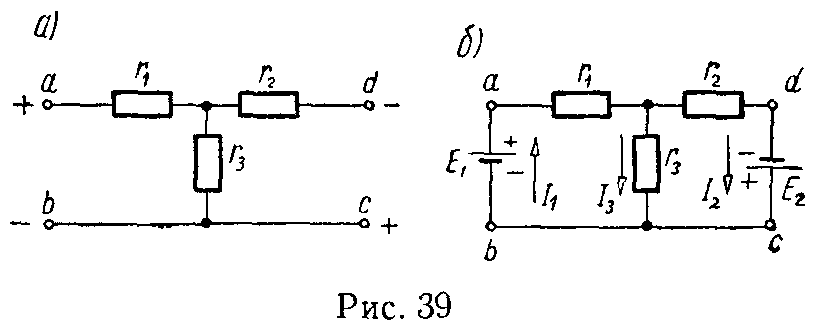
Рассмотрим общий случай последовательного соединения источников и приемников электрической энергии (рис. 4.1), пренебрегая внутренними сопротивлениями источников. Составим уравнение по второму закону Кирхгофа, произвольно задавшись направлением тока в цепи и направлением обхода контура (например, по часовой стрелке):
Ток в цепи
При обходе контура видно, что относительно направления обхода э. д. с. Е1 и Е3 направлены одинаково, т. е. согласно, а э. д. с. Е2 — им навстречу.
Ток в цепи определяется действием всех трех э.д.с., и при заданных направлениях э. д. с. и тока нетрудно установить, что элементы с э. д. с. E1 и Е3 вырабатывают электрическую энергию, а элемент с э. д. с. Е2 ее потребляет. Если в качестве источников э. д. с. в данном случае предположить аккумуляторы, то источники Е1 и Е3 разряжаются, а источник Е2 заряжается.
В элементах цепи, характеризующихся сопротивлениями R1, R2 и R3, электрическая энергия преобразуется в тепловую. Рассматривая в качестве примера схему рис. 4.1, нетрудно убедиться в том, что второй закон Кирхгофа является следствием закона сохранения энергии в применении его к контуру электрической цепи.
Рис. 4.1. Схема неразветвленной электрической цепи
Для этого достаточно умножить уравнение (4.7) на I, перенеся предварительно Е2 в левую часть:
Получим уравнение баланса мощности – для рассматриваемой цепи: сумма мощностей источников электрической энергии равна сумме мощностей приемников.
Ток в цепи с последовательным соединением элементов (рис. 4.1) не изменится и баланс мощностей сохранится, если произвести перестановку элементов цепи, сгруппировав э. д. с. и сопротивления, как показано на рис. 4.2, а.
Рис. 4.2. Преобразование схемы неразветвленной электрической цепи
Последовательное соединение пассивных элементов
Участок цепи 4-5-6-1 представляет собой последовательное соединение резисторов. На рассматриваемом участке действует напряжение U, равное алгебраической сумме э. д. с. левой части схемы [см. правую часть уравнения (4.7)]. Это напряжение равно также сумме падений напряжения в правой части схемы [см. левую часть уравнения (4.7)].
Вынеся I за скобку, получим
или
Отношение U/I = R есть некоторое сопротивление, эквивалентное по своему действию всем трем сопротивлениям:
Это равенство позволяет на участке 4-5-6-1 три сопротивления заменить одним (эквивалентным) и получить более простую схему (рис. 4.2, б) при условии неизменности тока в цепи и сохранении того же баланса мощностей. Этот вывод можно распространить на любое число последовательно включенных пассивных элементов:
т. е. общее сопротивление неразветвленной цепи равно сумме сопротивлений ее участков.
Последовательное соединение источников э.д.с.
Участок 1-2-3-4 цепи на рис. 4.2, а представляет собой последовательное соединение источников э. д. с. Напряжение между точками 4-1
Последнее равенство позволяет на участке 1-2-3-4 три э. д. с. заменить одной (эквивалентной)
и получить более простую схему (рис. 4.2, в), в которой только одна (эквивалентная) э. д. с. Е.
Этот вывод можно распространить на любое число последовательно включенных источников. Если э. д. с. всех источников равны и направлены согласно, как это имеет место при включении аккумуляторных элементов в батарее, то общая э. д. с. может быть определена по формуле
где Еn — э. д. с. одного элемента; n — число элементов в батарее.
Согласно составленной эквивалентной схеме (рис. 4.2, в),
Потенциальная диаграмма
В схеме, представленной на рис. 4.1, при переходе от точки 1 к точке 2 потенциал повышается на величину Е1, а при переходе от точки 2 к точке 3 — снижается на величину U2.3 = IR1. При переходе от точки 3 к точке 4 потенциал понижается на величину U3.4 = —E2.
Рис. 4.3. Потенциальная диаграмма электрической цепи
Изменение потенциалов в электрической цепи можно наглядно изобразить графически в виде потенциальной диаграммы.
Потенциальная диаграмма представляет собой график изменения потенциала при обходе цепи, построенный в прямоугольной системе координат, в которой по оси абсцисс откладываются в определенном масштабе сопротивления участков цепи, а по оси ординат — потенциалы соответствующих точек. Потенциальная диаграмма цепи, изображенной на рис. 4.1, показана на рис. 4.3.
Потенциалы точек цепи найдены согласно равенствам
причем потенциал точки 1 принят равным нулю.
Поскольку внутренние сопротивления источников э. д. с. приняты равными нулю, при переходе через эти элементы потенциалы изменяются скачком.
Задача 4.3.
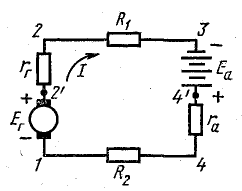
Генератор постоянного тока, аккумуляторная батарея и два резистора с постоянным сопротивлением составляют неразветвленную цепь Э. д. с. генератора Eг = 120 В; внутреннее сопротивление rг = 1,0 Ом, э. д. с. батареи Еа = 72 В, внутреннее сопротивление rа = 3 Ом, R1 = 16 Ом, R2 = 12 Ом.
Определить ток в цепи, составить баланс мощностей и построить потенциальную диаграмму цепи.
Решение. По условию задачи составлена схема (рис 4.4), из которой видно, что генератор и аккумуляторная батарея включены согласно: относительно произвольно выбранного направления обхода цепи обе э. д. с. направлены одинаково.
Рис. 4.4. К задаче 4.3
Эквивалентная э. д. с. цепи
Эквивалентное внутреннее сопротивление
Эквивалентное сопротивление нагрузки
Ток в цепи
Для составления баланса мощностей найдем мощность каждого элемента цепи:
генератора
аккумуляторной батареи
потерь внутри генератора
потерь внутри аккумуляторной батареи
потребления в резисторе R1
потребления в резисторе R2
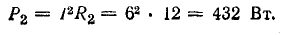
Баланс мощностей (общая мощность источников энергии равна суммарной мощности потребления)
Для построения потенциальной диаграммы найдем потенциалы точек цепи, полагая потенциал точки 1 V1 = 0:
Потенциальная диаграмма показана на рис. 4.5.
Рис. 4.5. Потенциальная диаграмма.
Разветвленная электрическая цепь с двумя узлами
Разветвленная электрическая цепь, как видно из названия, состоит из нескольких ветвей.
Ветви, присоединенные к одной паре узлов, включены параллельно (рис. 4.7, а). Отличительной особенностью параллельного соединения является то, что ко всем ветвям приложено одно и то же напряжение.
Рис. 4.7. Преобразование схемы с параллельным соединением приемников
Параллельное соединение пассивных элементов
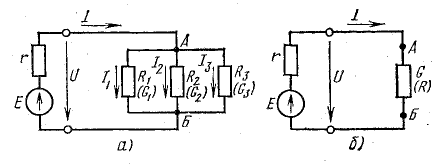
Приемники электрической энергии, представленные на схеме рис.4. 7, а сопротивлениями R1, R2, R3 и источник электрической энергии Е с внутренним сопротивлением r подключены к одной паре узлов (точки А и Б). Составим уравнение токов для узла А в соответствии с первым законом Кирхгофа:
Токи приемников можно выразить, используя напряжение между узлами и проводимости ветвей:
где
Разделим это уравнение на U:
Отношение UU есть проводимость G, соответствующая общему току цепи и общему напряжению:
Этот вывод можно распространить на любое число n параллельно соединенных приемников:
При параллельном соединении пассивных ветвей общая проводимость между двумя узлами равна сумме проводимостей всех ветвей.
Исходя из формул (4.13) и (4.14), можно заменить три проводимости (в общем случае n проводимостей) одной (эквивалентной) проводимостью GО и получить более простую схему (рис. 4.7, б).
Эквивалентное сопротивление при параллельном соединении нескольких ветвей определяется из равенства
Очень часто встречается параллельное соединение двух ветвей. В этом случае эквивалентное сопротивление определяется по формуле
или
Схема на рис. 4.7, б, полученная после замены трех проводимостей одной (эквивалентной), представляет собой простейшую схему электрической цепи.
Ток в этой схеме, равный току в неразветвленной части (рис. 4.7,а), определяется по формуле
Целью расчета электрической цепи является не только определение общего тока, но и тока в каждой ветви.
Если заданы э.д.с. и все сопротивления, то после определения общего тока по формуле (3.15) нужно определить напряжение между узловыми точками и токи в ветвях по закону Ома:
Параллельное соединение источников энергии
В практике часто встречаются случаи параллельного включения источников электрической энергии, работающих совместно на один или несколько приемников (рис. 4.8).
Рис. 4.8. Преобразование схемы с параллельным соединением источников
В таких случаях определением токов в источниках решается важная задача распределения нагрузки между ними.
Представим источники энергии в схеме рис. 4.8, а эквивалентными схемами источников тока, а сопротивление приемника заменим проводимостью G (рис. 4.8, б):
где U = Uаб — напряжение между узловыми точками А и Б.
По первому закону Кирхгофа, для узла А
или
Это равенство дает основание три источника тока заменить одним (эквивалентным), а схему рис. 4.8, б заменить более простой (рис. 4.8, в). Эквивалентный источник тока характеризуется током короткого замыкания
и внутренней проводимостью
Для схемы рис. 4.8, в
Напряжение между узлами
Токи в ветвях можно определить по следующим формулам:
Из этих выражений следует, что источники с относительно большей э. д. с. и меньшим внутренним сопротивлением имеют больший ток, т. е. принимают на себя большую нагрузку. Если э. д. с. и внутренние сопротивления источников одинаковы, нагрузка между ними распределяется поровну.
Общий ток в этом случае определяется произведением тока одного источника In на число параллельно включенных источников:
Величина тока каждого источника ограничена его номинальным значением Iном, сверх которого нагружать источник нельзя. Параллельное соединение источников применяется для увеличения общего тока, благодаря чему достигается увеличение мощности потребления энергии без изменения напряжения.
От схемы с эквивалентным источником тока можно перейти к схеме с эквивалентным источником э. д. с. (рис. 4.8, г), разделив уравнение (4.17) на g:
Так как l/g = r — внутреннее сопротивление эквивалентного источника э. д. с., то Iкr = Ir + U.
Но Iкr — Е — э. д. с. эквивалентного источника; Ir — падение напряжения во внутреннем сопротивлении, поэтому Е = U + Ir.
Рассматривается метод расчета разветвленных электрических цепей, предусматривающий замену всех источников э.д.с. одним (эквивалентным), который принято называть эквивалентным генератором.
Общий случай параллельного соединения источников и приемников электрической энергии
Выводы и формулы, полученные ранее, могут быть применены для расчета электрических цепей с двумя узловыми точками, между которыми содержится любое число параллельных ветвей с источниками и приемниками энергии, в том числе и такие ветви, которые имеют несколько элементов, соединенных последовательно (например, схема рис. 4.9).
Порядок расчета таких цепей, предусматривающий предварительное определение напряжения между узловыми точками, называется методом узлового напряжения.
Для применения этого метода должны быть заданы э.д.с. источников и проводимости ветвей (последние можно определить, если заданы сопротивления элементов каждой ветви).
Рис. 4.9. Схема с двумя узлами
В общем случае токи в ветвях и э. д. с. могут иметь различное направление, поэтому при определении узлового напряжения нужно взять алгебраическую сумму произведений ЕG и формула (4.18) примет вид
Знак э. д. с. устанавливается в соответствии с положительным направлением токов в ветвях, которое выбирается произвольно, но одинаково для всех ветвей (например, от Б к А).
Э. д. с. ветви считается положительной, если ее направление совпадает с положительным направлением тока. В противном случае э. д. с. подставляют со знаком минус в формулу (4.21) и также при определении токов по формулам (4.19).
Задача 4.8.
Для схемы, изображенной на рис. 4.7, а, известны: Е = 130 В, r = 0,5 Ом, R1 = 30 Ом, R2 = 20 Ом, R3 = 12 Ом. Определить токи в схеме, мощность передачи энергии приемникам и к. п. д. источника.
Решение. Вначале определим эквивалентное сопротивление между точками А и Б:
Ток в неразветвленной части цепи
Для определения токов в параллельных ветвях между узловыми точками определим напряжение на зажимах источника, которое в данном случае равно напряжению на приемниках:
Проверим правильность определения токов по уравнению (4.1):
Мощность передачи энергии приемникам
К. п. д. источника
Задача 4.10.
Для схемы, изображенной на рис. 4.7, а, известны: R1 = 10 Ом; R2 = 15 Ом; R3 = 6 Ом, r = 0,5 Ом, l3 = 10 А. Определить токи в схеме, мощность и к. п. д. источника.
Решение. Используя данные условия, относящиеся к третьей ветви, определим напряжение между узлами А и Б по закону Ома:
Напряжение U является общим для всех ветвей, присоединенных к точкам А и Б. Это дает возможность использовать ту же формулу для определения токов в двух ветвях:
Ток в неразветвленной части цепи
Э. д. с. источника
Мощность источника
Мощность потребления энергии приемниками
К. п. д. источника
Задача 4.12.
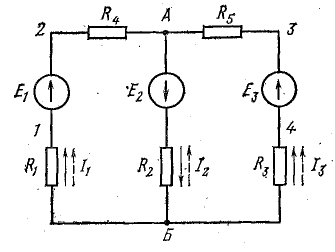
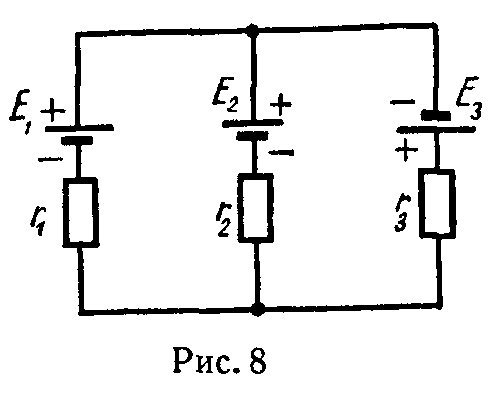
Определить токи и составить баланс мощностей для схемы, изображенной на рис. 4.9, если известны: E1 = 120 В; E2 = 80 В; E3 = 60 В; r1 = 0,5 Ом; r2 = 0,4 Ом; r3 = 0,2 Ом; R1 = 2 Ом; R2 = 15,6 Ом; R3 = 12,4 Ом; R4 = 7,5 Ом; R5 = 7,4 Ом.
Решение. Применяя метод узлового напряжения, найдем UАБ по формуле (4.21). Предварительно зададим положительное направление токов от Б к А и подсчитаем проводимости ветвей:
Токи в ветвях:
Токи l1 и l3 положительны. Их направление совпадает с выбранным ранее условно-положительным направлением от узла Б к узлу А. Направление тока l2 противоположно положительному направлению; в результате расчета этот ток получился отрицательным. На схеме рис. 4.9 пунктиром показано положительное направление токов в ветвях, а сплошной стрелкой — их действительное направление.
Для составления баланса мощностей необходимо подсчитать мощность каждого элемента схемы, в том числе и мощность потерь внутри источников. Заметим, что направления э. д. с. и токов во всех ветвях совпадают — источники Э. д. с. являются источниками энергии.
Мощности источников: P1.1 = E1I1 = 120 • 7,3 = 876 Вт; P1.2 = Е2I2 = 80 • 7,95 = 636 Вт; Р1.3 = E3I3 = 60 • 0,65 = 39 Вт.
Общая мощность источников 1551 Вт.
При определении мощности источников можно не задумываться над тем, в каком режиме работает тот или другой источник. Ответ на этот вопрос дает знак полученной мощности, если токи и э. д. с. подставлять с теми знаками, какие были приняты или получены в расчете. Например, мощность второго источника положительна: P1.2 = —80 • (—7,95) = 636 Вт. Это указывает на то, что в данной ветви работает источник энергии. Раньше Е2 и I2 сразу были взяты положительными, так как отмечено совпадение направлений напряжения и тока.
Мощность потерь внутри источников:
Общая мощность потерь внутри источников приблизительно 52 Вт. Мощность приемников:
Общая мощность приемников 1499 Вт.
Баланс мощностей (мощность источников равна мощности приемников плюс мощность потерь внутри источников) 1551 Вт = 1499 + 52 Вт.
Расчет электрических цепей методом эквивалентных сопротивлений (метод «свертывания» цепи)
Метод эквивалентных сопротивлений применяется для расчета таких электрических цепей, в которых имеются пассивные элементы, включенные между собой последовательно, параллельно или по смешанной схеме.
Определение эквивалентных сопротивлений
На схеме рис. 4.10, а сопротивления R3 и R4 включены последовательно: между ними (в точке 3) нет ответвления с током, поэтому I3 = I4. Эти два сопротивления можно заменить одним (эквивалентным), определив его как сумму
После такой замены получается более простая схема (рис. 4.10, б). Сопротивления R2 и R3.4 соединены параллельно, их можно заменить одним (эквивалентным), определив его по формуле (4.16):
и получить более простую схему (рис. 4.10, в).
Рис. 4.10. К методу эквивалентных сопротивлений
В схеме рис. 4.10, в сопротивления R1, К2.4, К5 соединены последовательно. Заменив эти сопротивления одним (эквивалентным) сопротивлением между точками 1 и 5, получим простейшую схему (рис. 4.10, г).
Подобными преобразованиями схему смешанного соединения пассивных элементов с одним источником энергии в большинстве случаев можно привести к простейшей схеме. В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает расчет.
Определение токов
В простейшей схеме (рис. 4.10, г) ток I определяется по закону Ома с использованием формулы (3.15). Токи в других ветвях первоначальной схемы определяют, переходя от схемы к схеме в обратном порядке.
Из схемы рис. 4.10, в видно, что
Кроме того, напряжение между точками 2 и 4
Зная это напряжение, легко определить токи I2 и I3 = I4:
После определения токов I1 и I5 напряжение U2.4 можно найти как разность потенциалов между точками 2 и 4. Для этого положим V4 известным (например, равным нулю), а V2 найдем так же, как при построении потенциальной диаграммы, обойдя от точки 4 неразветвленный участок цепи с током I1 =I5:
Метод преобразования треугольника и звезды сопротивлений
Пассивные элементы в электрических цепях соединяются не только последовательно или параллельно. Во многих схемах можно выделить группы из трех элементов, образующих треугольник или звезду сопротивлений.
При расчете подобных цепей упрощение схем выполняют известным методом эквивалентных сопротивлений, но предварительно проводят преобразование треугольника сопротивлений в эквивалентную звезду или наоборот.
Треугольник и звезда сопротивлений
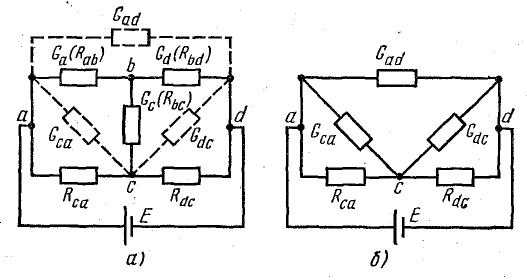
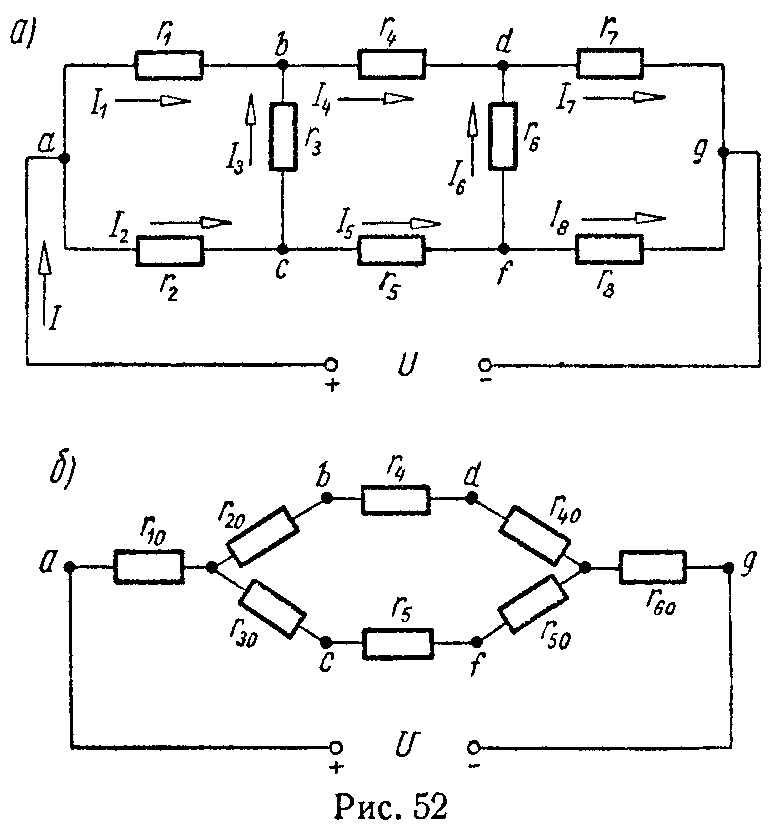
Рассмотрим в качестве примера схему рис. 4 .11, а, которая применяется для измерения сопротивлений (схема моста Уитстона).
В этой схеме нет элементов, соединенных последовательно или параллельно, но имеются замкнутые контуры из трех сопротивлений (треугольники сопротивлений), причем точки, разделяющие каждую пару смежных сопротивлений, являются узловыми.
К узловым точкам a, b, c присоединен треугольник сопротивлений Rab, Rbc, Rca. Его можно заменить эквивалентной трехлучевой звездой сопротивлений Ra, Rb, Rc (на рисунке изображены штриховыми линиями), присоединенных с одной стороны к тем же точкам a, b, c, а с другой — в общей (узловой) точке e.
Рис. 4.11. Преобразование треугольника сопротивлений в эквивалентную звезду
Смысл замены становится понятным при рассмотрении эквивалентной схемы 4.11, б, где сопротивления Rb и Rbd соединены между собой последовательно, так же как b сопротивления Rc и Rdc.
Две ветви между узловыми точками e и d с этими парами сопротивлений соединены параллельно. Соответствующими преобразованиями схему можно привести к простейшему виду.
Преобразование треугольника сопротивлений в эквивалентную звезду
Замена треугольника сопротивлений эквивалентной звездой и наоборот осуществляется при условии, что такая замена не изменяет потенциалов узловых точек a, b, c, являющихся вершинами треугольника и эквивалентной звезды.
Одновременно предполагают, что в остальной части схемы, не затронутой преобразованием, режим работы не изменяется (не меняются токи, напряжения, мощности). Для доказательства возможности перехода от треугольника к звезде и наоборот рассмотрим схемы рис. 4.11, в, г.
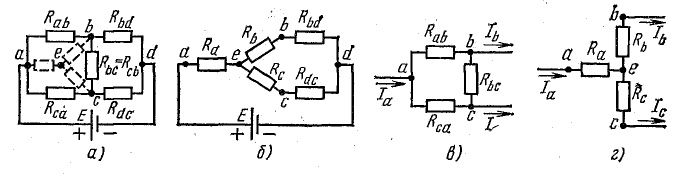
Эти схемы остаются эквивалентными для всех режимов, в том числе и для режима, при котором Ia = 0, что соответствует обрыву общего провода, ведущего к точке а. В этом случае в схеме треугольника между точками b и c включены параллельно две ветви с сопротивлениями Rbc и Rab + Rca
Общее сопротивление между этими точками
В схеме звезды между точками b и c включены последовательно сопротивления Rb и Rc. Общее сопротивление между этими точками Rb + Rc.
По условиям эквивалентности напряжение между точками b и c и токи Ib и Ic в обеих схемах должны быть одинаковыми. Следовательно, и сопротивления между точками b и c в обеих схемах одинаковы, т. е.
Полагая Ib =0, а затем Ic = 0, получим:
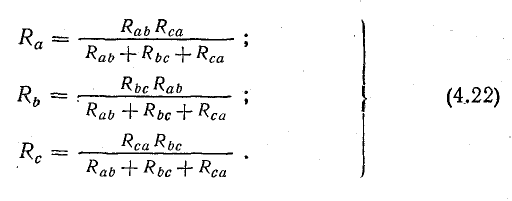
Совместное решение трех полученных уравнений приводит к следующим выражениям, которые служат для определения сопротивлений трехлучевой звезды по известным сопротивлениям эквивалентного треугольника:
Преобразование звезды сопротивлений в эквивалентный треугольник
Для расчета некоторых схем применяется преобразование трехлучевой звезды в эквивалентный треугольник, которое показано на рис. 4.12, а, где схема взята такой же, как на рис. 4.11, а.
При этом для определения параметров треугольника по заданным параметрам звезды пользуются формулами, которые записаны применительно к схемам рис. 4.12, а, б:
где Gad; Gdc; Gca — проводимости сторон треугольника; Ga; Gd; Gc — проводимости лучей звезды.
Зная проводимости, нетрудно определить сопротивления треугольника, если это необходимо.
Рис. 4.12. Преобразование трехлучевой звезды в эквивалентный треугольник
- Методы анализа сложных электрических цепей
- Метод узловых напряжений
- Метод узловых потенциалов
- Принцип и метод наложения
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Электрическая цепь
- Электрический ток
Эта
задача при расчете электрических цепей
встречается очень часто. Пусть, например,
в цепи на рис. 2.1 требуется найти напряжение
между точками m и n.
Прежде
всего необходимо показать на схеме или
мысленно представить стрелку этого
напряжения. Её направление определяется
порядком следования индексов у буквы .
Для напряжения она
направлена отточки m к
точке n.
Если мы меняем местами индексы у буквы ,
то следует изменить и направление
стрелки на схеме. При этом при расчете
меняется знак полученного напряжения,
так как .
Дальше
записываются уравнения по второму
закону Кирхгофа для любого контура,
включающего в себя эту стрелку, как было
сделано при расчете напряжений и
.
Так, для контура m31nm при
обходе его по часовой стрелке
.
Отсюда
. (7.1)
При
соответствующем навыке последняя
формула может быть записана сразу, без
составления уравнения второго закона
Кирхгофа.
В
указанном контуре напряжение складывается
из трех напряжений:
. (7.2)
Порядок
индексов у букв U соответствует
порядку, в котором мы проходим участок
электрической цепи, идя от точки m к
точке n по
элементам ,
и
.
Теперь
находим значение каждого слагаемого в
последнем уравнении.
Величина ,
определяющая напряжение между точками m и
3, представляет собой падение напряжения
на сопротивлении ,
которое мы должны взять со знаком минус,
так как от точки m к
точке 3 мы идем против тока :
.
Аналогично
.
Здесь
в правой части уравнения стоит плюс,
так как мысленная стрелка напряжения и
ток направлены
в одну сторону.
Третье
слагаемое представляет
собой напряжение на зажимах источника.
Если внутреннее сопротивление последнего
равно нулю, то это напряжение по величине
равно ЭДС, а знак его зависит от взаимного
направления стрелок напряжения и ЭДС
(рис. 7.1).
Рис.
7.1. Напряжение на зажимах источника
Рассмотрим
рис. 7.1.
При
указанной на схеме полярности зажимов
источника потенциал точки b выше
потенциала точки a на
величину ЭДС:
.
Поэтому
при одинаковых направлениях
стрелок и
(рис.
7.1, а)
.
Если
направления стрелок и
противоположны
друг другу
(рис. 7.1, б),
то
.
С
учетом сказанного напряжение на участке
1n (см.
рис. 2.1) равно
.
Подставляя
найденные значения напряжений на
участках в формулу (7.2), приходим к
выражению (7.1).
То
же самое напряжение, определяемое по
участку m2n,
будет равно
.
Разумеется,
вычисление одного и того же напряжения
по двум различным формулам должно
привести к одинаковым результатам.
8. Построение графиков
8.1. Общие требования к оформлению графиков. Зависимость мощности от тока
Правила
построения графиков рассмотрим на
примере зависимости мощности Р1, выделяющейся
в сопротивлении первой ветви, от тока I1 в
этой ветви. Эта зависимость определяется
уравнением баланса мощностей в схеме
рис. 6.1, в:
.
Так
как ,
то
. (8.1)
Это
– уравнение параболы со смещенной
вершиной и направленными вниз ветвями
(рис. 8.1).
Значения
тока, при которых парабола пересекает
горизонтальную ось, находятся из
уравнения
и
соответственно равны

.
По
смыслу –
это ток, протекающий в схеме рис.
6.1, в при
закороченном сопротивлении .
При токе, равном половине этого значения,
мощность максимальна:

Предположим,
что параметры цепи на рис. 6.1, в имеют
следующие численные значения:
=
72,4 В; =
130 В; =
43,6 Ом.
Прежде
всего находим максимальные значения
абсциссы и ординаты, которые будут
определять размеры графика. В нашем
примере – это значения и
:


Исходя
из этих величин и предполагаемых размеров
графика, выбираем масштаб, который
указываем на каждой оси графика в виде
равномерной шкалы.
В
одной единице длины (сантиметре,
миллиметре) может содержаться m × 10n именованных
единиц. Здесь n –
целое число, положительное или
отрицательное, а для mрекомендуются
числа 1, 2, 5.
Положительные
значения величин откладываются вправо
по оси абсцисс и вверх по оси ординат.
В
конце каждой оси ставится буквенное
обозначение откладываемой величины и
через запятую – ее единица измерения.
Если
график строится на белой (нелинованной)
бумаге, то чертится масштабная сетка.
Данные
для построения графика рассчитываем
по формуле (8.1) и сводим их в таблицу
(табл. 8.1).
Таблица
8.1
Данные
для построения графика
|
|
0 |
0,2 |
0,4 |
0,5 |
0,6 |
0,66 |
0,8 |
0,9 |
1 |
1,2 |
1,32 |
|
|
0 |
9,78 |
16,1 |
17,9 |
18,9 |
19 |
18,2 |
16,5 |
14 |
6,34 |
0 |
Абсциссы
точек, выбираемых для построения графика,
желательно располагать по оси равномерно.
Но вблизи характерных областей кривой
(в нашем случае у вершины параболы) точки
можно взять чаще. В таблицу внесены
также значения максимальной мощности
и тока, которому эта мощность соответствует.
При построении графика числа из таблицы
на осях не показываются (рис. 8.2).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Главная
→
Примеры решения задач ТОЭ
→
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Основные положения и соотношения
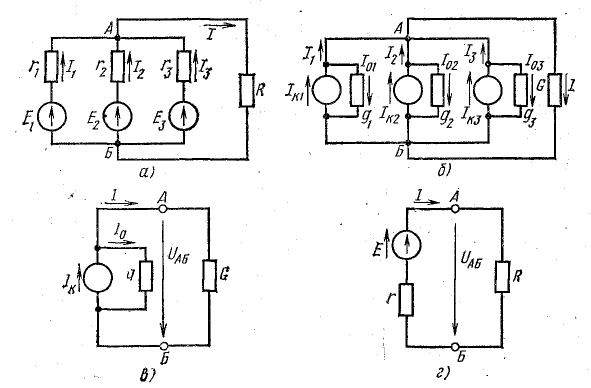
1. Источники электрической энергии
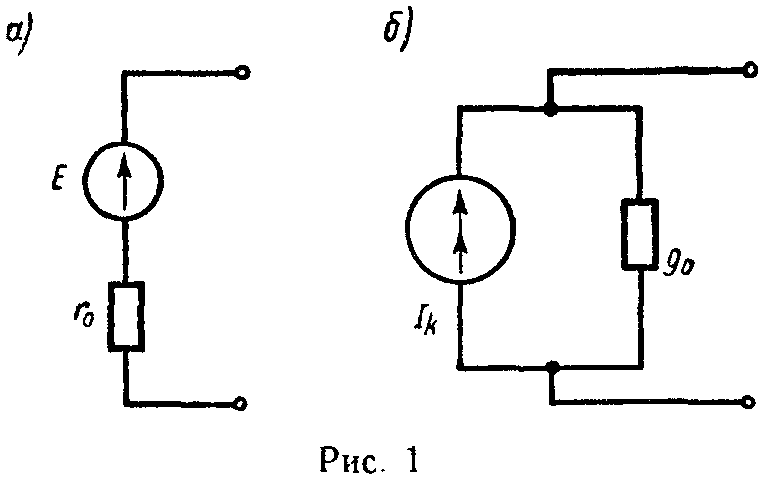
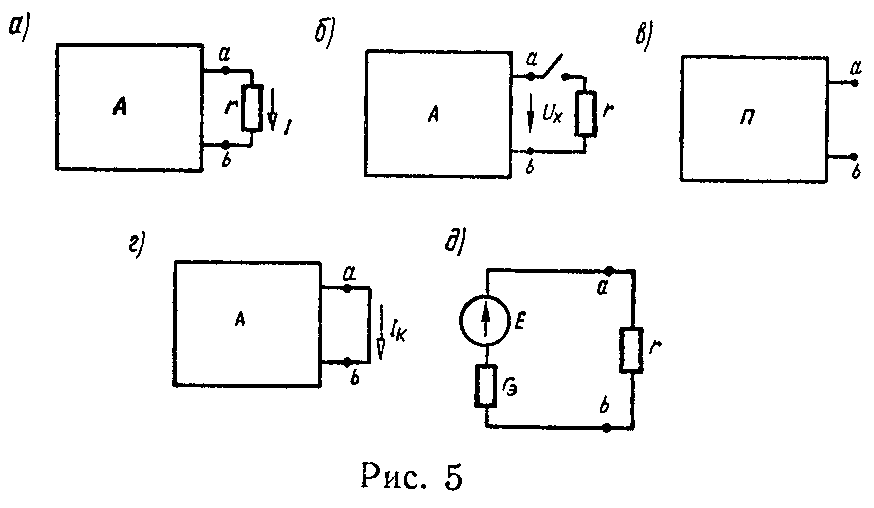
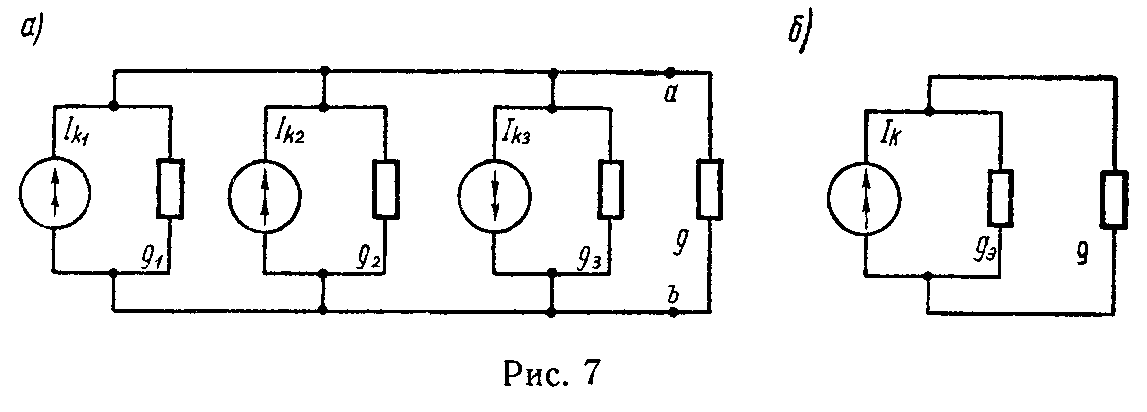
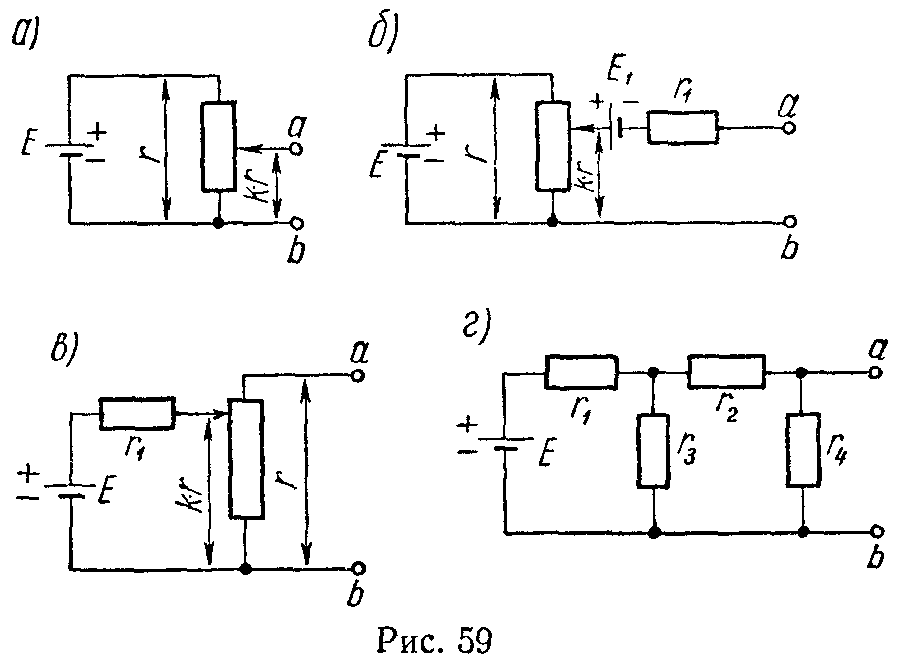
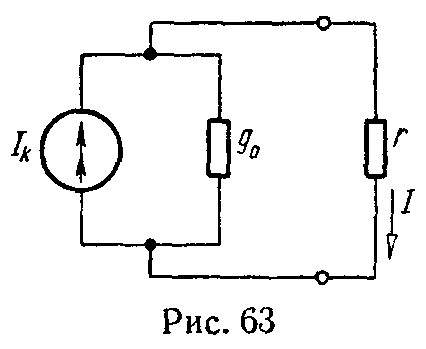
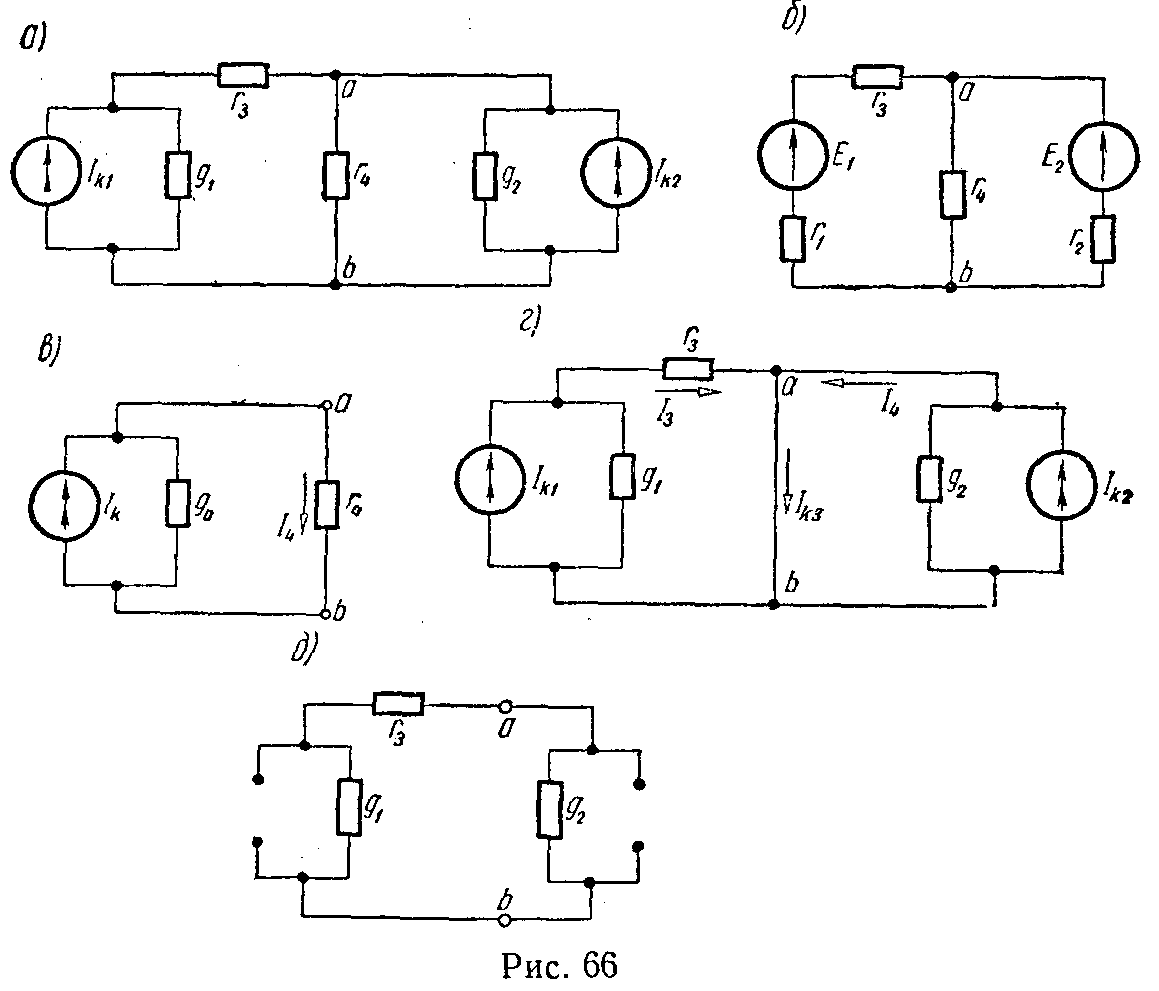
Реальный источник электрической энергии можно изобразить двояко: а) в виде генератора напряжения, который характеризуется э.д.с. Е, численно равной напряжению холостого хода источника, и включенной последовательно с сопротивлением r0 (рис. 1, а), б) в виде генератора тока, который характеризуется током Iк, численно равным току короткого замыкания реального источника, и параллельно соединенной проводимостью g0 (рис. 1, б).
Переход от генератора напряжения к эквивалентному генератору тока осуществляется по формулам
I к = E r 0 , g 0 = 1 r 0 , (1)
а обратный переход от генератора тока к эквивалентному генератору напряжения по следующим формулам
E= I к g 0 , r 0 = 1 g 0 . (2)
У идеального генератора напряжения внутреннее сопротивление равно нулю, тогда как у идеального генератора тока внутренняя проводимость равна нулю.
2. Закон Ома
Закон Ома применяется для ветви или для одноконтурной замкнутой цепи (не имеющей разветвлений).
Для написания закона Ома следует прежде всего выбрать произвольно некоторое положительное направление для тока.
а) Для ветви, состоящей только из сопротивлений и не содержащей э.д.с. (например, для ветви mn на рис. 2), при положительном направлении для тока от точки m к точке n ток равен
I= φ m − φ n r mn = U mn r mn . (3)
Здесь φm и φn — потенциалы точек m и n, Umn = φm — φn — разность потенциалов или напряжение между точками m и n, rmn = r4 + r5 — полное сопротивление ветви между точками m и n.
Пример — в задаче 17.
б) Для замкнутой одноконтурной цепи
I= ΣE Σr , (4)
где Σr — арифметическая сумма всех внешних и внутренних сопротивлений цепи, ΣE — алгебраическая сумма ее электродвижущих сил.
Со знаком плюс берут те э.д.с., направления которых совпадают с выбранным положительным направлением для тока, и со знаком минус — э.д.с. с противоположными направлениями.
Примеры — в задачах 15 и 17.
в) Для ветви, содержащей э.д.с. и сопротивления (например, для ветви acb на рис. 2),
I 1 = φ a − φ b +ΣE Σ r ab = U ab + E 1 − E 2 r 1 + r 2 + r 9 , (5)
где Uab = φa — φb — напряжение на концах ветви acb, отсчитываемое по выбранному положительному направлению тока, ΣE — алгебраическая сумма э.д.с., находящихся в этой ветви, а Σr — арифметическая сумма ее сопротивлений.
Формулу (5) называют обобщенным законом Ома.
Примеры — в задачах 15 и 17.
3. Законы Кирхгофа
Для написания законов Кирхгофа следует прежде всего задаться положительными направлениями для токов в каждой ветви.
Первый закон Кирхгофа
∑ k=1 n I k =0, (6)
Алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю. Токи, притекающие к узлу, условно принимаются положительными, а вытекающие из него — отрицательными (или наоборот).
Второй закон Кирхгофа
∑ k=1 n I k ⋅ r k = ∑ k=1 n E k . (7)
Алгебраическая сумма падений напряжений любого замкнутого контура равна алгебраической сумме э.д.с. в нем.
Направление обхода контура выбирается произвольно. При записи левой части равенства со знаком плюс берутся падения напряжения в тех ветвях, в которых положительное направление тока совпадает с направлением обхода (независимо от направления э.д.с. в этих ветвях), и со знаком минус — падения напряжения в тех ветвях, в которых положительное направление, тока противоположно направлению обхода. При записи правой части равенства э.д.с., направления которых совпадают с выбранным направлением обхода (независимо от направления тока, протекающего через них), принимаются положительными, а э.д.с., направленные против выбранного направления обхода, принимаются отрицательными.
Пример — в задаче 29.
Распределение напряжений при последовательном соединении двух сопротивлений (см. рис. 2)
I 1 = U 1 r 1 = U 2 r 2 = U r 1 + r 2 ,
U 1 =U⋅ r 1 r 1 + r 2 , U 2 =U⋅ r 2 r 1 + r 2 . (8)
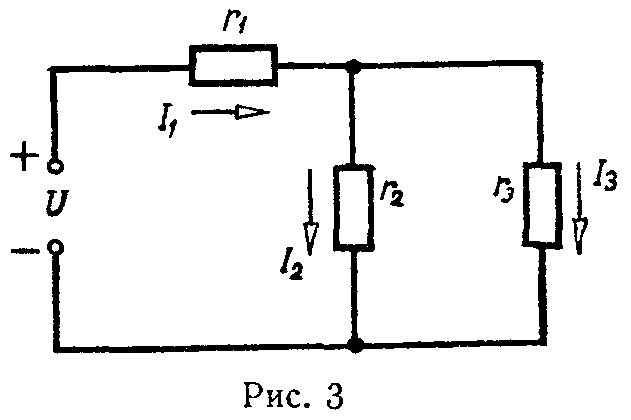
Распределение токов в двух параллельных ветвях — формула разброса токов или формула делителя токов (рис. 3)
U 2 = U 3 = U 2,3 , I 2 ⋅ r 2 = I 3 ⋅ r 3 = I 1 ⋅ r 2,3 = I 1 ⋅ r 2 ⋅ r 3 r 2 + r 3 ,
I 2 = I 1 ⋅ r 3 r 2 + r 3 , I 3 = I 1 ⋅ r 2 r 2 + r 3 . (9)
Распределение напряжений при последовательном соединении n сопротивлений
U k =U⋅ r k ∑ k=1 n r k .
Распределение токов в n параллельных ветвях
I k =I⋅ g k ∑ k=1 n g k .
4. Методы расчета сложных цепей постоянного тока
Пусть электрическая цепь состоит из p ветвей и имеет q узлов.
Применение законов Кирхгофа
Прежде всего, устанавливается число неизвестных токов, которое равно числу ветвей (p). Для каждой ветви задаются положительным направлением для тока.
Число n1 независимых уравнений, составляемых по первому закону Кирхгофа, равно числу узлов без единицы
n1 = q – 1.
Число n2 независимых уравнений, составляемых по второму закону Кирхгофа, равно числу ячеек (контуров)
n2 = p — q + 1.
Общее число уравнений n, составляемых по первому и второму законам Кирхгофа, равно числу неизвестных токов
n = n1 + n2 = p.
Решение этой системы уравнений дает значения искомых токов.
Пример — в задаче 29.
Метод контурных токов (МКТ, Максвелла).
Число n независимых контуров цепи равно числу уравнений по второму закону Кирхгофа
n = n2 = p — q + 1.
Расчет цепи методом контурных токов, состоящей из n независимых контуров, сводится к решению системы из n уравнений, составляемых для контурных токов I11, I22, …, Inn; ток в каждой ветви находится как алгебраическая сумма контурных токов, обтекающих эту ветвь.
Выбор направлений контурных токов произволен. Каждая из ветвей сложной электрической цепи должна войти хотя бы в один контур.
Система уравнений МКТ для n контурных токов имеет вид
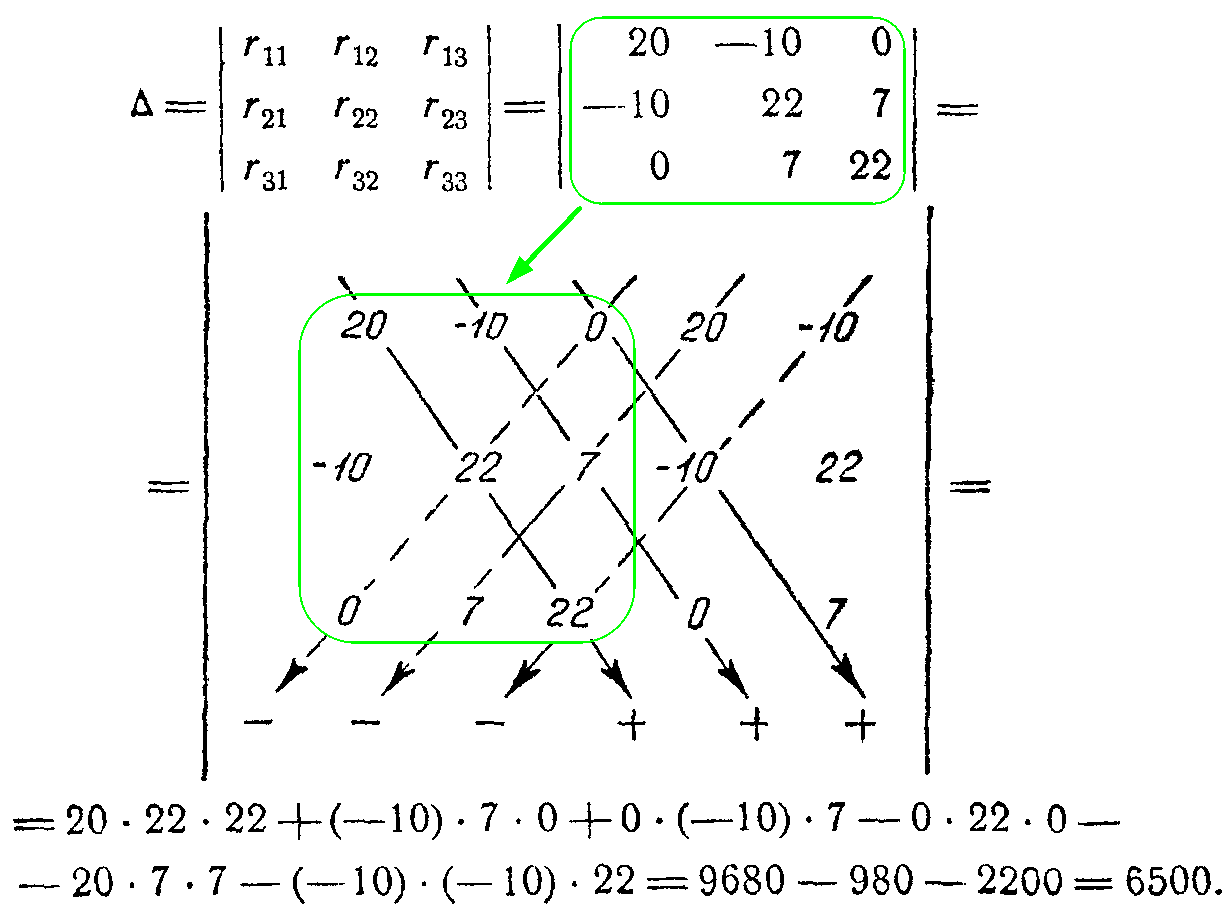
{ r 11 ⋅ I 11 + r 12 ⋅ I 22 +…+ r 1n ⋅ I nn = E 11 ; r 21 ⋅ I 11 + r 22 ⋅ I 22 +…+ r 2n ⋅ I nn = E 22 ; ………………………………………………. r n1 ⋅ I 11 + r n2 ⋅ I 22 +…+ r nn ⋅ I nn = E nn . (10)
Здесь rkk — собственное сопротивление контура k (сумма сопротивлений всех ветвей, входящих в контур k), rkl — общее сопротивление контуров k и l, причем rkl = rlk; если направления контурных токов в ветви, общей для контуров k и l, совпадают, то rkl положительно (rkl > 0), в противном случае rkl — отрицательно (rkl < 0); Ekk — алгебраическая сумма э.д.с., включенных в ветви, образующие контур k.
Пример — в задаче 41.
Метод узловых потенциалов (МУП)
Число n независимых узлов цепи равно числу уравнений по первому закону Кирхгофа
n = n1 = q — 1.
Для определения потенциалов всех узлов электрической схемы, имеющей q узлов, следует принять потенциал одного из узлов равным нулю, а для определения потенциалов остальных n = q — 1 узлов составляется следующая система уравнений
{ φ 1 ⋅ g 11 + φ 2 ⋅ g 12 +…+ φ n ⋅ g 1n = ∑ 1 Eg ; φ 1 ⋅ g 21 + φ 2 ⋅ g 22 +…+ φ n ⋅ g 2n = ∑ 2 Eg ; ……………………………………………….. φ 1 ⋅ g n1 + φ 2 ⋅ g n2 +…+ φ n ⋅ g nn = ∑ n Eg . (11)
Здесь gss — сумма проводимостей ветвей, присоединенных к узлу s; gsq — сумма проводимостей, соединяющих узел s с узлом q; – алгебраическая сумма произведений э.д.с. ветвей, примыкающих к узлу s, на их проводимости (т.е. токов короткого замыкания этих ветвей); при этом со знаком плюс берутся те из произведений Eg, в ветвях которых э.д.с. действуют в направлении узла s, и со знаком минус — в направлении от узла.
Определив потенциалы узлов, находят токи в ветвях посредством закона Ома.
Этим методом рекомендуется пользоваться в тех случаях, когда число уравнений здесь будет меньше числа уравнений, составленных по методу контурных токов.
Примеры — в задачах 44 и 45.
Метод наложения
Ток в любой ветви может быть рассчитан как алгебраическая сумма токов, вызываемых в ней каждой э.д.с. в отдельности. При этом надо иметь в виду, что когда ведется расчет для какой-либо одной действующей э.д.с., то вместо остальных источников должны быть включены сопротивления, равные внутренним сопротивлениям этих источников.
Примеры — в задачах 47 и 49.
Метод эквивалентных преобразований
Во всех случаях применения метода эквивалентных преобразований замена одних схем другими, им эквивалентными, не должна привести к изменению токов или напряжений на участках цепи, не подвергшихся преобразованию.
1) Замена последовательных сопротивлений одним эквивалентным. Сопротивления последовательны, если они обтекаются одним и тем же током. Например, на схеме цепи, изображенной на рис. 2, сопротивления r1, r2 и r9 соединены последовательно; так же последовательны сопротивления r7 и r8.
Эквивалентное сопротивление цепи, состоящей из n последовательно соединенных участков, равно сумме этих сопротивлений этих участков
r э = r 1 + r 2 +…+ r n = ∑ k=1 n r k . (12)
2) Замена параллельных сопротивлений одним эквивалентным. Сопротивления параллельны, если все они присоединены к одной паре узлов. Например (рис. 2), сопротивления r45 = r4 + r5 и r10 параллельны.
Эквивалентная проводимость цепи, состоящей из n параллельно соединенных ветвей равна сумме этих проводимостей этих ветвей. Эквивалентное сопротивление такой цепи находится как величина обратная эквивалентной проводимости этой цепи
1 r э = 1 r 1 + 1 r 2 +…+ 1 r n = ∑ k=1 n 1 r k . (13)
В частном случае параллельного соединения двух сопротивлений r1 и r2 эквивалентное сопротивление
r э = r 1 ⋅ r 2 r 1 + r 2 . (14)
3) Замена смешанного соединения сопротивлений одним эквивалентным. Смешанное соединение — это сочетание последовательного и параллельного соединения сопротивлений. Например, сопротивления r1, r2 и r3 (рис. 3) находятся в смешанном соединении. Их эквивалентное сопротивление равно
r э = r 1 + r 2,3 = r 1 + r 2 ⋅ r 3 r 2 + r 3 . (15)
При смешанном соединении сопротивлений токи ветвей цепи (рис. 3):
по закону Ома
I 1 = U r э , (16)
по формуле разброса токов (делителя токов)
I 2 = I 1 ⋅ r 3 r 2 + r 3 , I 3 = I 1 ⋅ r 2 r 2 + r 3 .
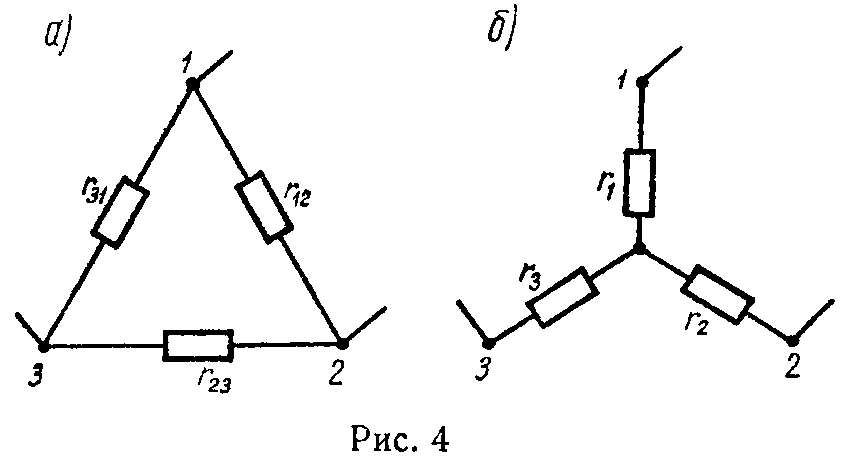
4) Формулы преобразования треугольника сопротивлений (рис. 4, а) в эквивалентную звезду сопротивлений (рис. 4, б) и наоборот имеют вид
{ r 1 = r 12 ⋅ r 31 r 12 + r 23 + r 31 ; r 2 = r 23 ⋅ r 12 r 12 + r 23 + r 31 ; r 3 = r 31 ⋅ r 23 r 12 + r 23 + r 31 , (17)
{ g 12 = g 1 ⋅ g 2 g 1 + g 2 + g 3 ; g 23 = g 2 ⋅ g 3 g 1 + g 2 + g 3 ; g 31 = g 3 ⋅ g 1 g 1 + g 2 + g 3 , (18)
где g — проводимость соответствующей ветви.
Формулы (18) можно записать через сопротивления так
r 12 = r 1 + r 2 + r 1 ⋅ r 2 r 3 ; r 23 = r 2 + r 3 + r 2 ⋅ r 3 r 1 ; r 31 = r 3 + r 1 + r 3 ⋅ r 1 r 2 . (19)
Пример — в задаче 51.
Метод эквивалентного генератора напряжения (метод холостого хода и короткого замыкания или метод активного двухполюсника)
Для нахождения тока I в ветви ab, сопротивление которой r (рис. 5, а, буква А на рисунке обозначает активный двухполюсник), надо разомкнуть эту ветвь и при этом найти (любым способом) разность потенциалов на зажимах разомкнутой ветви — Uх (рис. 5, б). Затем надо вычислить сопротивление короткого замыкания rк, равное эквивалентному сопротивлению всей остальной цепи, вычисленному в предположении, что в ней отсутствуют э.д.с. (при этом внутренние сопротивления источников сохраняются) и что она питается от постороннего источника, присоединенного непосредственно к зажимам a и b (рис. 5, в; буква П на рисунке обозначает пассивный двухполюсник).
Сопротивление rк может быть вычислено либо непосредственно по схеме рис. 5, в, либо из соотношения
r к = U х I к , (20)
где Iк — ток короткого замыкания, протекающий по ветви ab, если ее сопротивление r сделать равным нулю (рис. 5, г).
Заданная схема (рис. 5, а) может быть заменена эквивалентным генератором напряжения с э.д.с. E = Uх и внутренним сопротивлением rэ = rк, присоединенным к зажимам ab сопротивления r (рис. 5, д).
Ток в искомой ветви, имеющей сопротивление r, определяется из формулы закона Ома
I= U х r+ r к . (21)
Примеры — в задачах 55 и 56.
Метод эквивалентного генератора тока
В предыдущем пункте показано, как в любой сложной цепи можно получить эквивалентный генератор напряжения с э.д.с. E и внутренним сопротивлением rк. Этот генератор напряжения (рис. 5, д) на основании формул (1) может быть заменен эквивалентным генератором тока (рис. 1, б) по формулам
I к = U х r к , g 0 = 1 r к . (22)
где Iк — ток эквивалентного генератора тока, равный току короткого замыкания в той ветви, по отношению к которой производится эквивалентное преобразование всей остальной части цепи, g0 — внутренняя проводимость, равная эквивалентной проводимости всей остальной цепи между зажимами ab, к которым присоединен приемник энергии, в предположении, что э.д.с. всех генераторов равны нулю.
Пример — в задаче 65.
Метод замены нескольких параллельных генераторов напряжения одним эквивалентным
Если имеется несколько генераторов напряжения с э.д.с. E1, E2, …, En и внутренними сопротивлениями r1, r2, …, rn, работающие параллельно на общее сопротивление нагрузки r (рис. 6, а), то они могут быть заменены одним эквивалентным генератором напряжений, э.д.с. которого Eэ, а внутреннее сопротивление rэ (рис. 6, б),
при этом
{ E э = ∑ k=1 n E k g k ∑ k=1 n g k ; 1 r э = 1 r 1 + 1 r 2 +…+ 1 r n ; g k = 1 r k . (23)
Ток в сопротивлении r определится по формуле
I= E э r+ r э . (24)
Ток в каждой из ветвей находится по формуле
I k = E k −U r k , (25)
где U = I·r.
Пример — в задаче 60.
Метод замены параллельно соединенных генераторов тока одним эквивалентным
Если несколько генераторов тока с токами Ik1, Ik2, …, Ikn и внутренними проводимостями g1, g2, …, gn соединены параллельно (рис. 7, а) и работают на общий приемник энергии с проводимостью g то они могут быть заменены одним эквивалентным генератором тока (рис. 7, б), ток которого Ik равен алгебраической сумме токов, а его внутренняя проводимость равна сумме внутренних проводимостей отдельных генераторов
I k = I k1 + I k2 − I k3 +…= ∑ m=1 n I km , (26)
g э = g 1 + g 2 + g 3 +…= ∑ m=1 n g m . (27)
5. Принцип взаимности
Принцип взаимности гласит: если э.д.с. E, находящаяся в ветви ab сколь угодно сложной цепи, вызывает ток в другой ветви cd этой же цепи, то при переносе этой э.д.с. в ветвь cd она вызовет в ветви ab такой же ток I.
6. Принцип компенсации
Принцип компенсации: любое сопротивление в электрической цепи может без изменения распределения токов в ее ветвях быть заменено э.д.с., численно равной падению напряжения в заменяемом сопротивлении и направленной навстречу току.
7. Входное сопротивление цепи относительно ветви
Входное сопротивление цепи относительно ветви k определяется как отношение э.д.с. Ek, действующей в этой ветви, к току Ik в этой же ветви при э.д.с. в остальных ветвях равных нулю
r kk = E k I k . (28)
Входная проводимость ветви k — величина обратная входному сопротивлению этой ветви
g kk = 1 r kk . (29)
Взаимное сопротивление (передаточное сопротивление) ветвей k и l — отношение э.д.с. Ek, действующей в ветви k, к току Il, проходящему по ветви l при э.д.с. в остальных ветвях равных нулю
r kl = E k I l . (30)
Взаимная проводимость ветвей k и l — величина обратная взаимному сопротивлению тех же ветвей
g kl = 1 r kl . (31)
Пример. Для схемы рис. 8 входные сопротивления цепи относительно ветвей 1, 2 и 3 соответственно равны
r 11 = D r 2 + r 3 , r 22 = D r 1 + r 3 , r 33 = D r 1 + r 2 ,
а взаимные сопротивления ветвей 1 и 2, 2 и 3, 3 и 1 соответственно равны
r 12 = r 21 = D r 3 , r 23 = r 32 = D r 1 , r 13 = r 31 = D r 2 ,
где D = r1·r2 + r1·r3 + r2·r3.
8. Баланс мощностей
Для любой замкнутой электрической цепи сумма мощностей, развиваемых источниками электрической энергии, равна сумме мощностей, расходуемых в приемниках энергии
ΣPист = ΣPпотреб, или ΣEI = ΣI2r (32)
где ΣEI — алгебраическая сумма; здесь положительны те из слагаемых, для которых направления действия э.д.с. E и соответствующего тока I совпадают, в противном случае слагаемое отрицательно (при выборе положительных направлений токов в ветвях с э.д.с. выбираем направление тока совпадающим с действием соответствующей э.д.с.); ΣI2r — арифметическая сумма; здесь должны быть учтены как внешние сопротивления, так и сопротивления самих источников энергии.
Упражнения и задачи
Задача 1. Для цепи (рис. 9) найти эквивалентные сопротивления между зажимами a и b, c и d, d и f, если r1 = 6 Ом, r2 = 5 Ом. r3 = 15 Ом, r4 = 30 Ом, r5 = 6 Ом.
Решение
Расчет сопротивления rab.
Эквивалентное сопротивление соединенных параллельно сопротивлений r4 и r5 найдем по формуле (14)
r 45 = r 4 ⋅ r 5 r 4 + r 5 = 30⋅6 30+6 =5 Ом;
оно соединено последовательно с r2; их общее сопротивление
r’ = r2 + r45 = 5 + 5 = 10 Ом.
Сопротивление цепи состоит из сопротивления r1, последовательно с которым соединены два параллельных сопротивления r’ и r3
r ab = r 1 + r ′ ⋅ r 3 r ′ + r 3 =6+ 10⋅15 10+15 =12 Ом.
Расчет сопротивления rcd.
Сопротивления r4 и r5 теперь соединены параллельно друг другу; сопротивление r3 к ним включено последовательно
r ″ = r 3 + r 4 ⋅ r 5 r 4 + r 5 =15+ 30⋅6 30+6 =20 Ом.
Сопротивление rcd состоит из двух параллельно соединенных сопротивлений r2 и r» и равно
r cd = r 2 ⋅ r ″ r 2 + r ″ = 5⋅20 5+20 =4 Ом.
Расчет сопротивления rdf.
Эквивалентное сопротивление цепи между точками d и f состоит из трех параллельно соединенных сопротивлений: r5, r4 и r2 + r3 и может быть определено по формуле (13)
1 r df = 1 r 5 + 1 r 4 + 1 r 2 + r 3 = 1 6 + 1 30 + 1 20 = 1 4 ,
откуда rdf. = 4 ом.
Задача 2. Для цепи (рис. 10) начертить кривую зависимости эквивалентного сопротивления между точками a и b как функцию от k (0 ≤ k ≤ 10).
Ответ: при k = 0 и k = 1 rab = 0; при k = 0,5 rabмакс = 250 Ом.
Задача 3. Цепь, схема которой изображена на рис. 11, а, состоит из пяти одинаковых сопротивлений r1 = r2 = r3 = r4 = r5 = 10 кОм.
Чему равно сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К?
Решение
Ключ разомкнут.
Сопротивления r3, r4 и r5 соединены между собой последовательно; заменяющее их эквивалентное сопротивление является параллельным к сопротивлению r1; величина сопротивления, заменяющего r3, r4, r5 и r1, равна
r ′ = r 1 ⋅ ( r 3 + r 4 + r 5 ) r 1 + ( r 3 + r 4 + r 5 ) = 10⋅30 40 =7,5 кОм.
Искомое сопротивление цепи
rab = r’ + r2 = 7,5 + 10 = 17,5 кОм.
Ключ замкнут.
В этом случае сопротивления r1 и r3 соединены параллельно друг другу, а сопротивления r4 и r5 закорочены (рис. 11, б). Искомое сопротивление цепи будет
r ab = r 1 ⋅ r 3 r 1 + r 3 + r 2 = 10⋅10 20 +10=15 кОм.
Задача 4. Вычислить эквивалентное сопротивление цепи (рис. 12) между зажимами a и b, если все семь ее сопротивлений одинаковы:
Указание. Обратить внимание на закорачивающие проводники mn и np.
Ответ: 10 Ом.
Задача 5. Определить эквивалентное сопротивление цепи между точками a и b при разомкнутом и замкнутом ключе К (рис. 13, а): r1 = r2 = r3 = r4 = r5 = r6 = r7 = 10 Ом.
Решение
При разомкнутом ключе заданная схема может быть изображена согласно рис. 13, б.
Искомое сопротивление
r ab = r 1 ⋅ r 3 r 1 + r 3 = ( r 5 + r 6 + r 4 ⋅ r 7 r 4 + r 7 )⋅ r 2 r 5 + r 6 + r 4 ⋅ r 7 r 4 + r 7 + r 2 =5+ 25⋅10 35 =12,1 Ом.
При замкнутом ключе заданная схема имеет вид, изображенный на рис. 13, в.
Сопротивление цепи равно сумме двух сопротивлений
r ′ = r 1 ⋅ r 3 r 1 + r 3 10⋅10 20 =5 Ом,
и r”, определяемого из формулы
1 r ″ = 1 r 4 + 1 r 7 + 1 r 2 ,
откуда r’ = 3,33 Ом. Таким образом,
r ab = r ′ + r ″ =5+3,33=8,33 Ом.
Задача 6. Найти эквивалентное сопротивление между зажимами a и b для схемы рис. 14. Даны: r1 = 600 Ом, r2 = 360 Ом, r3 = 400 Ом, r4 = 300 Ом.
Ответ: 200 Ом.
Задача 7. Определить сопротивление каждой из цепей (рис. 15, а и б) между зажимами 1–1′ при холостом ходе (точки 2 и 2′ разомкнуты) и при коротком замыкании (точки 2 и 2′ закорочены). Сопротивления в омах даны на схеме.
Ответ: а) r1х = 120 Ом, r1к = 72 Ом; б) r1х = 20 Ом, r1к = 18 Ом.
Задача 8. Вычислить сопротивление между зажимами a и b для схемы рис. 16 при разомкнутом и замкнутом ключе К. Все семь сопротивлений одинаковы и каждое равно r = 30 Ом.
Указание. Учесть, что точки c и d равнопотенциальны.
Ответ: При разомкнутом ключе rab = 40 Ом; при замкнутом — rab = 30 Ом.
Задача 9. Найти сопротивление между зажимами a и b для схемы рис. 17, а. Значения сопротивлений в омах даны на схеме.
Решение
От данной схемы можно перейти к более простым схемам, изображенным на рис. 17, б и в. Искомое сопротивление
r ab = 240⋅ ( 180+ 300⋅450 750 ) 240+180+ 300⋅450 750 =144 Ом.
Задача 10. Имеется вольтметр, который может быть включен па три предела измерения: 3; 15 и 150 В (рис. 18). Максимально допустимый ток в измерительном механизме 30 мА.
Найти сопротивления r1, r2 и r3.
Решение
Полагаем внутреннее сопротивление измерительного механизма (ИМ) равным нулю.
На пределе измерения 3 В: ток 30 мА, сопротивление r1 = 3/0,030 = 100 Ом.
На пределе измерения 15 В: ток 30 мА, сопротивление r1 + r2 = 15/0,030 = 500 Ом, а сопротивление r2 = 500 — 100 = 400 Ом.
Аналогично находится r3 = 4500 Ом.
Задача 11. Два вольтметра, пределы измерения которых равны 150 и 100 В и внутренние сопротивления — 15000 и 7500 Ом, соединенные последовательно друг с другом и с добавочным сопротивлением 2500 Ом, подключены к сети 220 В. Чему равно показание каждого вольтметра?
Ответ: 132 и 66 В.
Задача 12. Батарея, э.д.с. которой E = 6,4 В и внутреннее сопротивление r0 = 0,1 Ом, присоединена к сопротивлению r = 3,1 Ом. Найти ток батареи и напряжение на ее зажимах.
Решение
Применяя формулу закона Ома для замкнутой цепи (формула 4), находим ток
I= E r+ r 0 = 6,1 3,1+0,1 =2 А.
Напряжение на зажимах батареи может быть найдено двумя путями: или
U = E — I·r0 = 6,4 — 2·0,1 = 6,2 В,
или
U = I·r = 2·3,1 = 6,2 В.
Задача 13. Напряжение холостого хода батареи равно 16,4 В. Чему равно внутреннее сопротивление батареи, если при токе во внешней цепи, равном 8 А, напряжение на ее зажимах равно 15,2 В?
Ответ: 0,15 Ом.
Задача 14. Источник с э.д.с. E = 100 В, внутренним сопротивлением r0 = 1 Ом замкнут на внешнее сопротивление r, которое меняется от нуля до бесконечности (рис. 19, а). Определить в функции этого сопротивления: 1) ток I; 2) напряжение на зажимах источника U; 3) мощность, отдаваемую источником во внешнюю цепь Pвнеш; 4) мощность, затрачиваемую в самом источнике Pвнутр; 5) общую мощность Pобщ; 6) коэффициент полезного действия η. При каком внешнем сопротивлении Pвнеш будет максимальным? Чему оно равно?
Построить кривые I = F1 (r), U = F2 (r), Pвнеш = F3 (r), Pвнутр = F4 (r), Pобщ = F5 (r), η = F6 (r).
Написать уравнения и построить кривые зависимостей U, Pвнеш, Pвнутр, Pобщ и η в функции тока I.
Решение
1)
I= E r+ r 0 = 100 r+1 ;
2)
I=I⋅r= E⋅r r+ r 0 = 100⋅r r+1 ;
3)
P внеш = I 2 ⋅r= E 2 ⋅r ( r+ r 0 ) 2 = 10000⋅r ( r+1 ) 2 ;
4)
P внутр = I 2 ⋅ r 0 = E 2 ⋅ r 0 ( r+ r 0 ) 2 = 10000 ( r+1 ) 2 ;
5)
P общ = I 2 ⋅ ( r+ r 0 )= E 2 ( r+ r 0 ) = 10000 r+1 ;
6)
η= P внеш P общ = r r+ r 0 = r r+1 .
Определим r, при котором Pвнеш будет максимально. Для этого вычислим производную от Pвнеш по r и приравняем ее нулю
d P внеш dr = E 2 d dr r ( r+ r 0 ) 2 = E 2 d dr r⋅ ( r+ r 0 ) 2 −r⋅ d dr ( r+ r 0 ) 2 ( r+ r 0 ) 4 = = E 2 ( r+ r 0 ) 2 −r⋅2 ( r+ r 0 ) ( r+ r 0 ) 4 = E 2 r 0 −r ( r+ r 0 ) 3 =0.
Взяв вторую производную, можно убедиться, что она отрицательна. Это соответствует условию максимума.
Отсюда найдем, что r = r0, т.е. при внешнем сопротивлении равном внутреннему сопротивлению, мощность, поступающая во внешнюю цепь, будет максимальна. При этом, по уравнению (6), коэффициент полезного действия равен 0,5. Величина максимальной мощности, поступающей во внешнюю цепь при r = r0, по уравнению (3) равна
P внеш.макс = [ E 2 ⋅r ( r+ r 0 ) 2 ] r= r 0 = E 2 4r =2500 Вт.
По написанным выше уравнениям на рис. 19, б построены кривые.
Искомые уравнения зависимостей в функции тока имеют вид
U=E−I⋅ r 0 ; P внеш =E⋅I− I 2 ⋅ r 0 ; P внутр = I 2 ⋅ r 0 ; P общ =E⋅I; η=1− I⋅ r 0 E .
По этим уравнениям на рис. 19, в построены кривые.
Задача 15. В схеме (рис. 20) э.д.с. E1 = 120 В, E2 = 40 В, а сопротивления r1 = 12 Ом, r2 = 8 Ом. Внутренние сопротивления источников энергии равны нулю. Определить напряжение между точками a и b.
Решение
Задавшись положительным направлением тока по часовой стрелке, на основании закона Ома (формула 4) имеем
I= E 1 − E 2 r 1 + r 2 = 120−40 12+8 =4 А.
Так как результат оказался положительным, то, следовательно, фактическое направление тока совпадает с выбранным. Напряжение между точками a и b можно найти по закону Ома (формула 5), примененному к участку amb
I= U ab − E 2 r 2 ,
откуда
U ab = E 2 +I⋅ r 2 =40+4⋅8=72 В.
Такой же результат можно получить, если применить ту же формулу к участку bna
I= U ba + E 1 r 1 ,
откуда
U ba =I⋅ r 1 − E 1 =4⋅12−120=−72 В,
а, следовательно, Uab = 72 В.
Замечание. Следует запомнить, что если на участке цепи, содержащем э.д.с. и сопротивление, ток и э.д.с. совпадают по направлению, то напряжение на зажимах участка меньше э.д.с. на величину падения напряжения в сопротивлении участка, а если направление тока противоположно направлению э.д.с., то напряжение на зажимах участка больше э.д.с. на величину падения напряжения в рассматриваемом участке.
Задача 16. Определить показание вольтметра (рис. 21), сопротивление которого весьма велико по сравнению с r1 и r2.
Для обоих случаев даны: E1 = 40 В, E2 = 10 В, r1 = r2 = 5 Ом. Внутренними сопротивлениями источников энергии пренебречь.
Ответ: а) 15 В, б) 25 В.
Задача 17. Построить график изменения потенциала вдоль цепи, изображенной на рис. 22, а, при замкнутом ключе и при разомкнутом ключе, предполагая в обоих случаях, что точка a заземлена (φa = 0).
В схеме найти точку, равнопотенцнальную точке a. Определить, потенциал какой точки следует принять равным нулю, чтобы потенциалы всех остальных точек были положительны (при замкнутом ключе).
Электродвижущие силы равны: E1 = 25 В, E2 = 5 В, E3 = 20 В, E4 = 35 В.
Внешние сопротивления имеют следующие значения: r1 = 8 Ом, r2 = 24 Ом, r3 = 40 Ом, r4 = 4 Ом. Внутренние сопротивления источников электрической энергии равны: r10 = 2 Ом, r20 = 6 Ом, r30 = 2 Ом, r40 = 4 Ом.
Решение
Ключ замкнут. Задавшись положительным направлением тока по часовой стрелке, на основании закона Ома (формула 4) найдем ток
I= E 1 + E 2 − E 3 + E 4 r 1 + r 10 + r 2 + r 20 + r 3 + r 30 + r 4 + r 40 = 45 90 =0,5 А.
Пользуясь формулами (3) и (5), вычислим потенциалы всех точек, обходя контур тока по часовой стрелке
φ a =0; φ b = φ a −I⋅ r 1 =0−0,5⋅8=−4 B; φ c = φ b + E 1 −I⋅ r 10 = ( −4 )+25−0,5⋅2=20 B; φ d = φ c −I⋅ r 2 =20−0,5⋅24=8 B; φ f = φ d + E 2 −I⋅ r 20 =8+5−0,5⋅6=10 B; φ g = φ f −I⋅ r 3 =10−0,5⋅40=−10 B; φ h = φ g − E 3 −I⋅ r 30 = ( −10 )−20−0,5⋅2=−31 B; φ k = φ h −I⋅ r 4 = ( −31 )−0,5⋅4=−33 B; φ a = φ k + E 4 −I⋅ r 40 = ( −33 )+35−0,5⋅4=0.
На рис. 22, б начерчен потенциальный график. По оси абсцисс отложены величины сопротивлений отдельных участков цепи, а по оси ординат — значения потенциалов в отдельных точках цепи.
Найдем точку, равнопотенциальную точке a. Из графика видно, что искомая точка m находится на участке сопротивления fg, так как в этой точке прямая падения потенциалов пересекает ось абсцисс, потенциал которой равен φa = 0. Обозначая участок сопротивления между точками f и m через rfm и применяя к участку abcdfm формулу закона Ома (5) и учитывая, что φa = φm, найдем
I= φ a − φ m + E 1 + E 2 r 1 + r 10 + r 2 + r 20 + r fm ,
или
0,5= 30 40+ r fm ,
откуда rfm = 20 Ом, т.е. точка m находится на середине сопротивления r3.
Для нахождения точки, потенциал которой следует принять равным нулю при условии, чтобы потенциалы всех остальных точек были положительны, следует обратиться к потенциальному графику, из которого видно, что такой точкой является точка k.
Ключ разомкнут. Тока в цепи нет, поэтому точки a и b равнопотенциальны, т. е. φa = φb = 0. Потенциал точки c превышает потенциал точки b на величину э.д.с. E1 и φc = E1 = 25 В; рассуждая аналогично, найдем
φ d = φ c =25 B; φ f = φ d + E 2 =25+5=30 B; φ g = φ f =30 B; φ h = φ g − E 3 =30−20=10 B; φ k = φ h =10 B; φ l = φ k + E 4 =10+35=45 B.
На основе полученных результатов на рис. 22, б начерчен график изменения потенциала при разомкнутом ключе.
Задача 18. Для схемы рис. 23 построить потенциальные графики 0abcdfghkl при разомкнутом и замкнутом ключе, если E1 = 60 В, E2 = 40 В, E3 = 25 В, E4 = 15 В, r10 = 6 Ом, r20 = 4 Ом, r30 = 3 Ом, r40 = 2 Ом, r1 = 24 Ом, r2 = 16 Ом, r3 = 25 Ом, r4 = 22 Ом, r5 = 18 Ом.
Задача 19. Определить токи в ветвях цепи (рис. 24, а) и напряжение между точками c и d и показание амперметра, включенного между точками c и d. Сопротивление амперметра считать равным нулю. Сопротивления элементов цепи r1 = 10 Ом, r2 = r3 = r5 = 25 Ом, r4 = 50 Ом, а приложенное к ней напряжение U = 120 В.
Решение
Эквивалентное сопротивление всей цепи (рис. 24, а) равно
r= r 1 + ( r 2 + r 4 )⋅ ( r 3 + r 5 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =10+ 75⋅50 125 =40 Ом.
В неразветвленной части цепи протекает ток
I= U r = 120 40 =30 А.
Токи, протекающие через сопротивления r2 + r4 и r3 + r5, можно найти различными способами.
1) В параллельных ветвях токи распределяются обратно пропорционально их сопротивлениям (формулы 9)
I 2 = I 1 ⋅ ( r 3 + r 5 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =3⋅ 50 125 =1,2 А, I 3 = I 1 ⋅ ( r 2 + r 4 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =3⋅ 75 125 =1,8 А.
2) Найдем напряжение на зажимах параллельных ветвей
U ab = I 1 ⋅ ( r 2 + r 4 )⋅ ( r 3 + r 5 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =3⋅ 75⋅50 125 =90 В.
Токи в ветвях с сопротивлениями r2 + r4 и r3 + r5 равны
I 2 = U ab r 2 + r 4 = 90 75 =1,2 А, I 3 = U ab r 3 + r 5 = 90 50 =1,8 А.
Напряжение на зажимах параллельных ветвей может быть найдена как разность между приложенным напряжением и падением напряжения на сопротивлении r1
U ab =U− I 1 ⋅ r 1 =120−3⋅10=90 В.
Найдем напряжение между точками c и d
U cd =− I 2 ⋅ r 2 + I 3 ⋅ r 3 =−1,2⋅25+1,8⋅25=15 В.
Наконец, вычислим ток, проходящий через амперметр, он равен току короткого замыкания I’cd (рис. 24, б). Для его нахождения вычислим токи
I ′ 1 = U r 1 + r 2 ⋅ r 3 r 2 + r 3 + r 4 ⋅ r 5 r 4 + r 5 = 144 47 А, I ′ 2 = I ′ 1 ⋅ r 3 r 2 + r 3 = 144 47 ⋅ 1 2 = 72 47 А, I ′ 4 = I ′ 1 ⋅ r 5 r 4 + r 5 = 144 47 ⋅ 25 75 = 48 47 А.
Искомый ток, проходящий через амперметр, равен
I A = I ′ cd = I ′ 2 − I ′ 4 = 72 47 − 48 47 = 24 47 =0.51 А.
Задача 20. Для измерения тока применены амперметры, пределы измерений которых равны 5 и 2,5 А, и шунт, сопротивление которого неизвестно. Первый амперметр, включенный с шунтом в некоторую цепь, показал 3,6 А, второй — с тем же шунтом показал в той же цепи ток 2 А. Сопротивления амперметров r1 = 0,002 Ом и r2 = 0,004 Ом. Чему равен ток в цепи?
Ответ: 18 А; rш = 0,0005 А.
Задача 21. Для цепи рис. 25 определить отношение напряжения на выходе U2 к напряжению на входе цепи U1. Сопротивления отдельных ветвей цепи в омах указаны на схеме.
Ответ: U2: U1 = 0,05.
Задача 22. В схеме (рис. 26) найти сопротивление rx, если I1 = 2,6 А, I3 = 0,6 А, r1 = 0,5 Ом, r2 =1,4 Ом, r3 = 3 Ом, r4 = 2,5 Ом. Найти э.д.с. батареи E, если ее внутреннее сопротивление r0 = 0,1 Ом.
Решение
На основании первого закона Кирхгофа найдем
I2 = I1 — I3 = 2,6 — 0,6 = 2 А.
По закону Ома, примененному к участку, содержащему сопротивление r2, найдем
Uab = I2·r2 = 2·1,4 = 2,8 В.
Применяя закон Ома к участку цепи ab, содержащему э.д.с. E и сопротивления r1 и r0, найдем искомую э.д.с.
E = Uab + I1· (r1 + r0) = 2,8 + 2,6·0,6 = 4,36 В.
Теперь найдем напряжение на параллельных ветвях с сопротивлениями r4 и rx и токи в них
Uac = Uab — I3·r3 = 2,8 — 0,6·3 = 1 В;
I4 = Uac/r4 = 1/2,5 = 0,4 А;
Ix = I3 — I4 = 0,6 — 0,4 = 0,2 А.
Искомое сопротивление
rx = Uac/Ix = 1/0,2 = 5 Ом.
Задача 23. В схеме мостика (рис. 27) известны сопротивления r1 = 1300 Ом, r2 = 800 Ом, r3 = 400 Ом. Сопротивление гальванометра rг = 600 Ом. Через, сопротивление r1 протекает ток I1 = 1 мА. К мостику приложено напряжение U = 2,5 В.
Найти сопротивление r4.
Ответ: 750 Ом.
Задача 24. В цепи (рис. 28) найти E1 и rx, если E2 = 3 В, r1 = r2 = 1 кОм, r3 = 4 кОм, r4 = 2 кОм, r5 = 1 кОм. Внутренние сопротивления батарей принять равными нулю.
Амперметр А1 показывает 4 мА, а А4 — 3 мА; полярности приборов показаны на схеме, а их сопротивлениями можно пренебречь.
Ответ: E1 = 12 В, rx = 2 Ом.
Задача 25. Однопроводная линия с сопротивлением r0 на единицу длины, питаемая батареей с э.д.с., равной E, закорочена на приемном конце (рис. 29).
В каком месте линия должна иметь утечку с сопротивлением r, чтобы ток I на приемном конце был минимальным?
Ответ: по середине линии.
Задача 26. Для определения места повреждения изоляции линии применяется схема, изображенная на рис. 30, а; r1 и r2 — магазины сопротивлений.
Правый зажим гальванометра заземлен. Свободные концы тип линии соединены между собой накоротко. Подбором сопротивлений r1 и r2 добиваются отсутствия тока в гальванометре.
Показать, что если сечения обоих проводов одинаковы, то расстояние от места повреждения изоляции a до начала линии равно
2l⋅ r 2 r 1 + r 2 .
Указание. Заданная схема может быть заменена схемой рис. 30, б.
Задача 27. При проверке постоянной C счетчика оказалось, что при силе тока 10 А и напряжении 120 В якорь его в продолжение 30 сек сделал 37 оборотов. Определить ошибку в показаниях счетчика, если на счетчике указано, что 1 ГВт·ч соответствует 400 оборотам счетчика.
Примечание. Постоянной счетчика называется число ватт-часов, приходящихся на один оборот счетчика.
Ответ: 7,5%.
Задача 28. Каково должно быть сечение медных проводов линии для передачи потребителю мощности P = 16 кВт при условии, что потеря мощности не превысит p = 5%, если длина линии l = 180 м и напряжение в конце линии равно U = 220 В?
Ответ: точное значение 41,8 мм2, по ГОСТ надо взять 50 мм2.
Задача 29. Для схемы (рис. 31), пользуясь законами Кирхгофа, найти токи и проверить баланс мощностей, если E1 = 15 В, E2 = 70 В, E3 = 5 В, r10 = r20 = 1 Ом, r30 = 2 Ом, r1 = 5 Ом, r1 = 5 Ом, r2 = 4 Ом, r3 = 8 Ом, r4 = 2,5 Ом, r5 = 15 Ом.
Решение
Всего узлов в схеме три (a, b, c), следовательно, число независимых уравнений, составляемых по первому закону Кирхгофа, будет на единицу меньше, т.е. два. Число контуров равно трем, следовательно, по второму закону Кирхгофа можно составить три взаимно независимых уравнения. Таким образом, общее число независимых уравнений, составляемых по первому и второму законам Кирхгофа, равно числу неизвестных токов в пяти ветвях схемы.
Выберем положительные направления для токов, которые обозначены пунктирными стрелками, и составим систему уравнений Кирхгофа:
для узла a
I1 — I2 + I3 + I5 = 0; (1)
для узла b
–I1 — I3 — I4 = 0; (2)
для контура abfa
E1 + E3 = I1· (r1 + r10) — I3· (r3 + r30); (3)
для контура abca
E3 = –I3· (r3 + r30) + I4·r4 + I5·r5; (4)
для контура adca
E2 = I2· (r2 + r20) + I5·r5. (5)
Уравнения (1) — (5) после подстановки в них числовых значений будут иметь следующий вид
I1 — I2 + I3 + I5 = 0,
I1 + I3 + I4 = 0,
6I1 — 10I3 = 20,
–10I3 + 2,5I4 + 15I5 = 5,
5I2 + 15I5 = 70.
Решая эту систему уравнений, получим
I1 = 5 А; I2 = 8 А; I3 = 1 А; I4 = –6 А; I5 = 2 А.
Отрицательный знак для тока I4 означает, что истинное направление этого тока противоположно принятому. При проверке баланса мощностей надо иметь в виду, что в тех ветвях цепи, где истинное направление тока совпадает с направлением э.д.с., соответствующая э.д.с. будет являться источником энергии, а в тех участках, где направления э.д.с. и тока противоположны, э.д.с. будет являться потребителем энергии. Все сопротивления как внешние, так и самих источников, независимо от направления протекающего через них тока, будут являться потребителями энергии.
Баланс мощностей для рассматриваемой схемы будет
E1·I1 + E2·I2 + E3· (–I3) = I12· (r1 + r10) + I22· (r2 + r20) + I32· (r3 + r30) + I42·r4 + I52·r5,
или
15·5 + 70·8 — 5·1 = 52·6 + 82·5 + 12·10 + 62·2,5 + 22·15,
получено тождество 630 Вт = 630 Вт.
Задача 30. В схеме (рис. 32) найти все токи, если известны: E1 = 20 В, E2 = 1,1 В, r10 = 0,2 Ом, r20 = 0,4 Ом, r1 = r2 = 5 Ом, r3 = 7 Ом.
Ответ: 2,5 А, 1,5 А, 1 А.
Задача 31. Для цепи, изображенной на рис. 33, рассчитать токи и определить показание вольтметра, если E1 = 40 В, E2 = 5 В, E3 = 25 В, r1 = 5 Ом, r2 = r3 = 10 Ом.
Внутренними сопротивлениями источников энергии и током, протекающим через вольтметр, можно пренебречь.
Ответ: I1 = 5 А, I2 = 1 А, I3 = 4 А, Uba = 30 В.
Задача 32. Аккумуляторная батарея из 20 последовательно соединенных элементов работает параллельно с генератором на сеть, имеющую нагрузку 30 А. Каждый аккумулятор имеет э.д.с. 1,82 В и сопротивление 0,001 Ом. Э.д.с. генератора 36,4 В и его сопротивление 0,04 Ом. Определить нагрузку генератора и батареи (т. е. отдаваемые ими токи) и напряжение на их зажимах.
Какую э.д.с. должен развивать генератор, чтобы нагрузка распределилась поровну между генератором и батареей?
Ответ: 20 А, 10 А, 36 В, 36,7 В.
Задача 33. По трехпроводной линии длиной 0,5 км (рис. 34) от двух генераторов 1 и 2 питаются две группы ламп 50 Вт, 110 В.
В первой группе — N1 = 200 ламп, а во второй — N2 = 600 ламп. Сечение крайних проводов q = 35 мм2, а сечение среднего (нулевого) провода q0 = 16 мм2. Каждый генератор имеет внутреннее сопротивление 0,01 Ом и развивает э.д.с. 120 В. Определить токи во всех проводах линии и напряжение на зажимах каждой группы ламп, сопротивления которых считать постоянным. Материал проводов линии — медь.
Ответ: I1 = 98 А, I2 = 144 А, I0 = 46 А, U1 = 102 В, U2 = 71 В.
Задача 34. Напряжения, измеренные электростатическим вольтметром, между узловыми точками схемы и землей, равны: U10 = –15 В, U20 = 52 В, U30 = 64 В (рис. 35).
Определить токи в ветвях и отходящих проводах при следующих данных: E1 = 80 В, E3 = 70 В, r1 = 5 Ом, r2 = 10 Ом, r3 = 12 Ом.
Решение
Вычислим напряжения между точками 1 и 2, 2 и 3, 3 и 1
U10 — U20 = U12 = (–15) — 52 = –67 В,
U20 — U30 = U23 = 52 — 64 = –12 В,
U30 — U10 = U31 = 64 — (–15) = 79 В.
Применяя к ветвям 1–2, 2–3, 3–1 закон Ома, найдем токи
I 1 = U 12 + E 1 r 1 = ( −67 )+80 5 =2,6 А, I 2 = U 32 r 2 = 12 10 =1,2 А, I 3 = U 31 − E 3 r 3 = 79−70 12 =0,75 А.
Так как все токи оказались положительными, то они имеют направления в соответствии с только что записанными уравнениями и нанесены на рис. 35.
Токи в ответвлениях от узловых точек 1–p, 2–q, 3–s находим по первому закону Кирхгофа
I4 = I1 — I3 = 1,85 А, I5 = I1 + I2 = 3,8 А, I6 = I2 + I3 = 1,95 А.
Задача 35. В цепи (рис. 36) известны э.д.с. E1 = 120 В, E2 = 40 В, E3 = 70 В и сопротивления r1 = 20 Ом, r2 = 10 Ом, r3 = 40 Ом.
Потенциалы точек a, b и c относительно земли соответственно равны (определены посредством вольтметра): Ua0 =160 В, Ub0 = 180 В, Uc0 = 50 В. Определить токи в ветвях ab, bc, ca и в проводах aa’, bb’ и cc’, подходящих к точкам a, b и c.
Ответ: I1 = 5 А, I2 = 9 А, I3 = 1 А.
Задача 36. В цепи (рис. 37) известны э.д.с. E1 = 40 В, E2 = 30 В.
Сопротивления элементов схемы r1 = 8 Ом, r2 = 5 Ом, r3 = 10 Ом. Показания вольтметров соответственно равны: U1 = 125 В, U2 = 60 В; полярность зажимов вольтметров показана на схеме. Пренебрегая внутренними сопротивлениями источников электрической энергии и считая потребляемые вольтметрами токи приближенно равными нулю, определить величину и полярность э.д.с. E3. Найти все токи.
Ответ: E3 = 20 В, I1 = 2,5 А, I2 = 6 А, I3 = 8,5 А.
Задача 37. В цепи, изображенной на рис. 38, найти токи и показания вольтметров, включенных между точками 0 и c, c и g, если известно, что E1 = 32 В, E2 = 64 В, E3 = 72 В, r1 = 9 Ом, r10 = 1 Ом, r2 = 5 Ом, r20 = 1 Ом, r3 = 2 Ом, r30 = 1 Ом, r4 = 2 Ом, r5 = 1 Ом. Сопротивления вольтметров весьма велики по сравнению с сопротивлениями элементов цепи.
Ответ: I1 = 5 А, I2 = 9 А, I3 = 1 А.
Задача 38. Для схемы (рис. 39, а) найти токи и проверить баланс мощностей, если Uab = 12 В, Ucd = 5,6 В, r1 = 4 Ом, r2 = 5 Ом, r3 = 3 Ом.
Решение
Данная схема может быть заменена эквивалентной, в которой между точками a и b, а также c и d включены э.д.с., численное значение которых E1 = Uab и E2 = Ucd, а их внутренние сопротивления равны нулю (рис. 39, б). Обращаем внимание на то, что при включении э.д.с. следует соблюдать заданные полярности напряжений.
Задавшись направлениями для токов, составим систему уравнений Кирхгофа
I1 — I2 — I3 = 0,
E1 = I1·r1 + I3·r3,
E2 = I2·r2 — I3·r3.
Подставляя сюда числовые значения и решая систему уравнений, найдем:
I1 = 2,4 А, I2 = 1,6 А, I3 = 0,8 А.
Для проверки баланса мощностей составим уравнение
Uab·I1 + Ucd·I2 = I12·r1 + I22·r2 + I32·r3,
12·2,4 + 5,6·1,6 = 2,42·4 + 1,62·5 + 0,82·3;
получено тождество 37,76 = 37,76.
Задача 39. В цепи (рис. 40) найти токи и проверить баланс мощностей, если Uab = 16 В, Ucd = 11,2 В, E = 5 В, r0 = 0, r = 10 Ом, r1 = 5 Ом, r2 = 4 Ом.
Ответ: I1 = 1,2 А, I2 = 0,3 А, I = 1,5 А.
Задача 40. Чему равно показание вольтметра на рис. 41, если током вольтметра можно пренебречь по сравнению с токами в нагрузках? Внутренние сопротивления батарей принять равными нулю.
Определить показания ваттметров и убедиться в том, что их сумма равна сумме мощностей, расходуемых в сопротивлениях r1, r2 и r3. Потерями в катушках ваттметров пренебречь.
Дано: E1 = 30 В, E2 = 21 В, E3 = 5 В, r1 = 5 Ом, r2 = 10 Ом, r3 = 50 Ом.
Ответ: 25 В, P1 = 9 Вт, P2 = 15,6 Вт.
Задача 41. Методом контурных токов найти токи в цепи, схема которой изображена на рис. 42; даны: E1 = 100 В, E2 = 30 В, E3 = 10 В, E4 = 6 В, r1 = 10 Ом, r2 = 10 Ом, r4 = 6 Ом, r5 = 5 Ом, r6 = 15 Ом, r10 = r20 = r30 = 0, r40 = 1 Ом.
Решение
Выберем направления контурных токов, которые обозначим через I11, I22, I33.
Составим систему уравнений для контуров
E1 — E2 — E3 = I11· (r1 + r10 + r2 + r20 + r30) — I22· (r2 + r20) + I33·r30,
E2 — E4 = I22· (r2 + r20 + r5 + r4 + r40) + I33· (r4 + r40) — I11· (r2 + r20),
–E3 — E4 = I33· (r30 + r6 + r4 + r40) + I22· (r4 + r40) + I11·r30.
После подстановки числовых значений будем иметь
60 = 20·I11 — 10·I22 + 0·I33,
24 = –10·I11 + 22·I22 + 7·I33,
–16 = 0·I11 + 7·I22 + 22·I33.
Решив эту систему уравнений, найдем контурные токи
I11 = 5 А, I22 = 4 А, I33 = –2 А.
Теперь найдем истинные токи во всех ветвях.
В ветви, где действует э.д.с. E1, истинный ток I1 имеет направление контурного тока I11 и равен
I1 = I11 = 5 А.
В ветви с сопротивлением r5 истинный ток I5 имеет направление контурного тока I22 и равен
I5 = I22 = 4 А.
В ветви с сопротивлением r6 истинный ток I6 имеет направление, противоположное контурному току I33, и равен
I6 = –I33 = — (–2) = 2 А.
В ветви с сопротивлением r2 истинный ток I2 получится от наложения контурных токов I11 и I22 и будет иметь направление большего контурного тока I11;
I2 = I11 — I22 = 5 — 4 = 1 А.
В ветви с сопротивлением r4 истинный ток I4 получится от наложения контурных токов I22 и I33 и будет иметь направление контурного тока I22;
I4 = I22 + I33 = 4 + (–2) = 2 А.
В ветви, где действует э.д.с. E3, истинный ток I3 получится от наложения контурных токов I11 и I33 и будет иметь направление тока I11;
I3 = I11 + I33 = 5 + (–2) = 3 А.
Эта же задача может быть решена методом определителей. Для этого уравнения для контурных токов следует записать в форме (10), а именно
{ r 11 ⋅ I 11 + r 12 ⋅ I 22 + r 13 ⋅ I 33 = E 11 ; r 21 ⋅ I 11 + r 22 ⋅ I 22 + r 23 ⋅ I 33 = E 22 ; r 31 ⋅ I 11 + r 32 ⋅ I 22 + r 33 ⋅ I 33 = E 33 ,
где контурные сопротивления
r11 = r1 + r10 + r2 + r20 + r30 = 20 Ом;
r22 = r2 + r20 + r5 + r4 + r40 = 22 Ом;
r33 = r30 + r6 + r4 + r40 = 22 Ом,
взаимные сопротивления контуров
r12 = r21 = — (r2 + r20) = –10 Ом;
r13 = r31 = r30 = 0;
r23 = r32 = r4 + r40 = 7 Ом,
контурные э.д.с.
E11 = E1 — E2 — E3 = 60 В;
E22 = E2 — E4 = 24 В;
E33 = –E3 — E4 = –16 В.
Получим численную систему уравнений метода контурных токов
{ 20⋅ I 11 − 10⋅ I 22 + 0⋅ I 33 =60; −10⋅ I 11 +22⋅ I 22 + 7⋅ I 33 =24; 0⋅ I 11 + 7⋅ I 22 +22⋅ I 33 =−16,
или в матричной форме записи
( 20 −10 0 −10 22 7 0 7 22 )⋅ ( I 11 I 22 I 33 )= ( 60 24 −16 ).
Составим главный определитель системы? и вычислим его значение
Вычислим значения вспомогательных определителей
Δ 11 =| E 11 r 12 r 13 E 22 r 22 r 23 E 33 r 32 r 33 |=| 60 −10 0 24 22 7 −16 7 22 |=32500; Δ 22 =| r 11 E 11 r 13 r 21 E 22 r 23 r 31 E 33 r 33 |=| 20 60 0 −10 24 7 0 −16 22 |=26000; Δ 33 =| r 11 r 12 E 11 r 21 r 22 E 22 r 31 r 32 E 33 |=| 20 −10 60 −10 22 24 0 7 −16 |=−13000.
Искомые контурные токи определяем по формулам
I 11 = Δ 11 Δ = 32500 6500 =5 А; I 22 = Δ 22 Δ = 26000 6500 =4 А; I 33 = Δ 33 Δ = −13000 6500 =−2 А.
Мы получили те же результаты, что и ранее.
Задача 42. Найти все токи и определить потенциалы точек a, b, c и 0 относительно земли (рис. 43).
Задачу решить методом контурных токов, Внутренние сопротивления источников электрической энергии считать равными нулю: E1 = 85 В, E2 = 84 В, E3 = 5 В, E4 = 12 В, r1 = 8 Ом, r2 = 10 Ом, r3 = 10 Ом, r4 = 10 Ом, r5 = 10 Ом, r6 = 4 Ом.
Ответ: I1 = 2 А, I2 = 2,7 А, I3 = 0,7 А, I4 = 2,2 А, I5 = 4,7 А, I6 = 2,5 А.
Задача 43. Для схемы (рис. 44) найти токи и Uab, если E1 = 70 В, E2 = 5 В, E3 = 15 В, E4 = 10 В, r1 = 5 Ом, r2 = r3 = 10 Ом, r4 = 5 Ом, r5 = 3 Ом.
Задачу решить методом контурных токов. Внутренние сопротивления источников энергии равны нулю.
Ответ: I1 = 6 А, I2 = 2 А, I3 = 4 А, I4 = 1 А, I5 = 5 А.
Задача 44. Для схемы, изображенной на рисунке 45, а, пользуясь методом узловых потенциалов, определить все токи. Данные схемы: E1 = 30 В, E2 = 10 В, E3 = 200 В, E4 = 56 В, r1 = 20 Ом, r2 = 30 Ом, r3 = 6 Ом, r4 = 8 Ом, r5 = 15 Ом, r6 = 40 Ом, r7 = 10 Ом. Внутренние сопротивления источников напряжения равны нулю.
Решение
Примем потенциал точки 3 равным нулю. Тогда, на основании формулы (11), запишем систему уравнений для определения потенциалов точек 1 и 2
φ 1 ⋅ g 11 + φ 2 ⋅ g 12 = ∑ 1 E⋅g , (1) φ 1 ⋅ g 21 + φ 2 ⋅ g 22 = ∑ 2 E⋅g . (2)
Подсчитаем g11 — сумму проводимостей, присоединенных к узлу 1
g 11 = 1 r 1 + r 7 + 1 r 5 + 1 r 4 + 1 r 6 = 1 30 + 1 15 + 1 8 + 1 40 =0,25 1 Ом .
Аналогично g22 — сумма проводимостей, присоединенных к узлу 2
g 22 = 1 r 1 + r 7 + 1 r 5 + 1 r 2 + 1 r 3 = 1 30 + 1 15 + 1 30 + 1 6 =0,3 1 Ом .
Взаимные проводимости первого и второго узлов
g 12 = g 21 =− ( 1 r 1 + r 7 + 1 r 5 )=− 1 30 − 1 15 =−0,1 1 Ом .
Подставим в уравнения (1) и (2) числовые значения
0,25⋅ φ 1 + ( −0,1 )⋅ φ 2 =30⋅ 1 30 −56⋅ 1 8 =−6, ( −0,1 )⋅ φ 1 +0,3⋅ φ 2 =−30⋅ 1 30 +10⋅ 1 30 −200⋅ 1 6 =−34.
Решив последние два уравнения, найдем потенциалы точек 1 и 2
φ1 = –80 В; φ2 = –140 В.
Наконец, применяя закон Ома для отдельных ветвей, определим искомые токи
I 1 = φ 1 − φ 2 − E 1 r 1 = ( −80 )− ( −140 )−30 30 =1 А; I 2 = φ 3 − φ 2 + E 2 r 2 = 0− ( −140 )+10 30 =5 А; I 3 = φ 2 − φ 3 + E 3 r 3 = ( −140 )−0+200 6 =5 А; I 4 = φ 3 − φ 1 − E 4 r 4 = 0− ( −80 )−56 8 =3 А; I 5 = φ 1 − φ 2 r 5 = ( −80 )− ( −140 ) 15 =4 А.
Направления найденных токов указаны на скелетной схеме (рис. 45, б).
Рекомендуем читателю решить ту же задачу, приняв за нуль потенциал узловой точки 1.
Задача 45. Методом узловых потенциалов определить токи во всех ветвях схемы, изображенной на рис. 46, а; заданы: E1 = 20 В, E2 = 30 В, E3 = 2 В, E4 = 1,2 В, E5 = 5,6 В, r2 = 50 Ом, r3 = 10 Ом, r4 = 20 Ом, r5 = 10 Ом, r6 = 100 Ом, r7 = 50 Ом, r8 = 20 Ом.
Внутренние сопротивления источников напряжения считать равными нулю.
Решение
В тех случаях, когда в цепи имеется ветвь с э.д.с., но не содержащая сопротивления, целесообразно принять равным нулю потенциал одной из узловых точек, к которой подходит указанная ветвь.
В нашем случае примем потенциал узла 3 равным нулю (φ3 = 0). Тогда потенциал точки 1 имеет значение, равное E1, т.е. φ1 = 20 В. Общее число уравнений уменьшается и равняется числу узлов минус два. В нашей задаче достаточно составить всего два уравнения для узлов 2 и 4.
Определим сумму проводимостей, присоединенных к узлу 2
g 22 = 1 r 3 + 1 r 4 + 1 r 7 =0,17 1 Ом ,
и, соответственно, к узлу 4
g 44 = 1 r 4 + 1 r 5 + 1 r 8 =0,2 1 Ом .
Найдем взаимные проводимости узлов 2 и 1, 2 и 4, 4 и 1
g 12 = g 21 =− 1 r 7 =−0,02 1 Ом , g 24 = g 42 =− 1 r 4 =−0,05 1 Ом , g 14 = g 41 =− 1 r 8 =−0,05 1 Ом .
Вычислим суммы произведений э.д,с. на проводимости, присоединенные соответственно к узлам 2 и 4
∑ 2 E⋅g = E 3 ⋅ g 3 − E 4 ⋅ g 4 =0,14 В Ом , ∑ 4 E⋅g = E 4 ⋅ g 4 + E 5 ⋅ g 5 =0,62 В Ом .
Составим систему уравнений на основании формул (11) для узла 2:
φ 1 ⋅ g 21 + φ 2 ⋅ g 22 + φ 4 ⋅ g 24 = ∑ 2 E⋅g ,
для узла 4
φ 1 ⋅ g 41 + φ 2 ⋅ g 42 + φ 4 ⋅ g 44 = ∑ 4 E⋅g .
Подставляя сюда числовые значения, получим
0,17⋅ φ 2 + ( −0,05 )⋅ φ 4 =0,54, ( −0,05 )⋅ φ 2 +0,2⋅ φ 4 =1,62.
Решая эту систему уравнений, найдем
φ2 = 6 В; φ4 = 9,6 В.
Наконец, применяя к отдельным ветвям формулы закона Ома, получим значения всех токов, которые нанесены на скелетной схеме (46, б)
I2 = 0,2 А, I3 = 0,4 А, I4 = 0,12 А, I5 = 0,4 А, I6 = 0,2 А, I7 = 0,28 А, I8 = 0,52 А.
Ток I1 определяется на основании первого закона Кирхгофа
I1 = I3 + I5 + I6 – I2 = 0,8 А.
Задача 46. Методом узловых потенциалов рассчитать токи в цепи (рис. 47). Даны: E1 = 160 мВ, E2 = 300 мВ, r3 = r4 = 100 Ом, r5 = 150 Ом, r6 = 40 Ом. Внутренние сопротивления генераторов напряжения равны нулю.
Указание. Для решения задачи достаточно составить всего одно уравнение, так как в схеме имеется две ветви с э.д.с., но не содержащие сопротивления, а узлов в схеме четыре.
Ответ: I1 = 2,25 мА, I2 = 1,4 мА, I3 = 0,85 мА, I4 = 0,75 мА, I5 = 0,1 мА, I6 = 1,5 мА.
Задача 47. Методом наложения рассчитать токи в схеме (рис. 48. а), если E1 = 10 В, E2 = 40 В, E3 = 5 В, r10 = 5 Ом, r20 = r30 = 2 Ом, r1 = 30 Ом, r2 = 3 Ом, r3 = 8 Ом.
Решение
Сначала предполагаем, что действует только э.д.с. E1, а э.д.с. E2 и E3 считаем недействующими (рис. 48, б), тогда
I ′ 1 = E 1 r 1Э ,
где
r 1Э = r 1 + r 10 + ( r 2 + r 20 )⋅ ( r 3 + r 30 ) ( r 2 + r 20 )+ ( r 3 + r 30 ) =35+ 5⋅10 15 = 115 3 Ом.
Ток
I ′ 1 = E 1 r 1Э = 10 115/3 = 6 23 А.
Токи в параллельных ветвях найдем согласно формуле (9)
I ′ 2 = I ′ 1 ⋅ ( r 3 + r 30 ) ( r 2 + r 20 )+ ( r 3 + r 30 ) = 6 23 ⋅ 10 15 = 4 23 А, I ′ 3 = I ′ 1 ⋅ ( r 2 + r 20 ) ( r 2 + r 20 )+ ( r 3 + r 30 ) = 6 23 ⋅ 5 15 = 2 23 А.
Теперь проведем расчет, предполагая, что действует э.д.с. E2, а э.д.с. E1 и E3 считаем недействующими (рис. 48, в)
I ″ 2 = E 2 r 2Э ; r 2Э = r 2 + r 20 + ( r 1 + r 10 )⋅ ( r 3 + r 30 ) ( r 1 + r 10 )+ ( r 3 + r 30 ) = 115 9 Ом; I ″ 2 = E 2 r 2Э = 40 115/9 = 72 23 А; I ″ 1 = I ″ 2 ⋅ ( r 3 + r 30 ) ( r 1 + r 10 )+ ( r 3 + r 30 ) = 72 23 ⋅ 10 45 = 16 23 А; I ″ 3 = I ″ 2 ⋅ ( r 1 + r 10 ) ( r 1 + r 10 )+ ( r 3 + r 30 ) = 72 23 ⋅ 35 45 = 56 23 А.
Аналогично рассчитываем величины токов при действии только одной э.д.с. E3 (рис. 48, г)
I ? 3 = E 3 r 3Э ; r 3Э = r 3 + r 30 + ( r 1 + r 10 )⋅ ( r 2 + r 20 ) ( r 1 + r 10 )+ ( r 2 + r 20 ) = 115 8 Ом; I ? 3 = E 3 r 3Э = 5 115/8 = 8 23 А; I ? 1 = I ? 3 ⋅ ( r 2 + r 20 ) ( r 1 + r 10 )+ ( r 2 + r 20 ) = 8 23 ⋅ 5 40 = 1 23 А; I ? 2 = I ? 3 ⋅ ( r 1 + r 10 ) ( r 1 + r 10 )+ ( r 2 + r 20 ) = 8 23 ⋅ 35 40 = 7 23 А.
Истинное значение тока в каждой ветви найдется как алгебраическая сумма токов, определяемых каждой э.д.с. в отдельности.
Ток в первой ветви
I 1 = I ′ 1 + I ″ 1 + I ? 1 = 6 23 + 16 23 + 1 23 =1 А.
Ток во второй ветви
I 2 = I ′ 2 + I ″ 2 − I ? 2 = 4 23 + 72 23 − 7 23 =3 А.
Ток в третьей ветви
I 3 =− I ′ 3 + I ″ 3 − I ? 3 =− 2 23 + 56 23 − 8 23 =2 А.
Направления этих токов показаны на рис. 48, а.
Задача 48. Найти токи в ветвях цепи, изображенной на рис. 49, если известны E1 = 125 мВ, E = 120 мВ, r1 = 40 Ом, r2 = 36 Ом, r3 = r4 = 60 Ом. Внутренними сопротивлениями источников пренебречь. Задачу решить методами наложения и контурных токов.
Ответ: I1 = 0,8 А, I2 = 0,75 А, I3 = 2 А, I4 = 1,55 А, I = 2,75 А.
Задача 49. В схеме (рис. 50, а) методом наложения найти все токи. Внутренние сопротивления источников э.д.с. принять равными нулю. Электродвижущие силы и сопротивления элементов цепи имеют следующие значения: E1 = 96 В, E2 = 75 В, r3 = 3 Ом, r4 = 15 Ом, r5 = 10 Ом, r6 = 6 Ом.
Решение
Положим, что действует только э.д.с. E1, а э.д.с. E2 не действует. В этом случае схема примет вид, изображенный на рис. 50, б. Так как внутреннее сопротивление э.д.с. E2 равно нулю, то на его месте между точками b и d показано короткое замыкание. Для большей наглядности схему рис. 50, б можно начертить в виде, показанном на рис. 50, в.
Полное сопротивление этой схемы равно
r 1экв = r 3 ⋅ r 6 r 3 + r 6 + r 4 ⋅ r 5 r 4 + r 5 = 3⋅6 9 + 15⋅10 25 =8 Ом.
Определим все токи
I ′ 1 = E 1 r 1экв = 96 8 =12 А, I ′ 3 = I ′ 1 ⋅ r 6 r 3 + r 6 =12⋅ 6 9 =8 А; I ′ 6 = I ′ 1 − I ′ 3 =4 А; I ′ 4 = I ′ 1 ⋅ r 5 r 4 + r 5 =12⋅ 10 25 =4,8 А; I ′ 5 = I ′ 1 − I ′ 4 =7,2 А; I ′ 2 = I ′ 3 − I ′ 4 =8−4,8=3,2 А или I ′ 2 = I ′ 5 − I ′ 6 =3,2 А .
Теперь положим, что действует только э.д.с. E2, а э.д.с. E1 считаем недействующей (рис. 50, г).
Схему (рис. 50, г) для большей наглядности можно представить в виде, показанном на рис. 50, д. Ее полное сонротивление
r 2экв = r 3 ⋅ r 4 r 3 + r 4 + r 5 ⋅ r 6 r 5 + r 6 = 3⋅15 18 + 6⋅10 16 =6,25 Ом.
Вычислим все токи
I ″ 2 = E 2 r 2экв = 75 6,25 =12 А, I ″ 3 = I ″ 2 ⋅ r 4 r 3 + r 4 =12⋅ 15 18 =10 А; I ″ 4 = I ″ 2 − I ″ 3 =2 А; I ″ 6 = I ″ 2 ⋅ r 5 r 5 + r 6 =12⋅ 10 16 =7,5 А; I ″ 5 = I ″ 2 − I ″ 6 =4,5 А; I ″ 1 = I ″ 3 − I ″ 6 =10−7,5=2,5 А .
Складывая алгебраически токи, полученные от действия каждой э.д.с. в отдельности (рис. 50, б и 50, г), найдем истинные токи в каждой ветви (они нанесены на рис. 50, а)
I 1 = I ′ 1 + I ″ 1 =12+2,5=14,5 А, I 2 = I ′ 2 + I ″ 2 =3,2+12=15,2 А, I 3 = I ′ 3 + I ″ 3 =8+10=18 А, I 4 = I ′ 4 − I ″ 4 =4,8−2=2,8 А, I 5 = I ′ 5 + I ″ 5 =7,2+4,5=11,7 А, I 6 = I ′ 6 − I ″ 6 =7,5−4=3,5 А.
Задача 50. Для схемы (рис. 51) методами наложения, контурных токов и при помощи законов Кирхгофа найти все токи. Внутренние сопротивления источников электрической энергии считать равными нулю.
Дано: E1 = 90 В, E2 = 54 В, r1 = 30 Ом, r3 = 60 Ом, r4 = 24 Ом, r5 = 20 Ом.
Ответ: I1 = 1,7 А, I2 = 2,5 А, I3 = 0,25 А, I4 = 2,25 А, I5 = 1,95 А.
Задача 51. Найти эквивалентное сопротивление цепи (рис. 52, а) и все токи, если U = 114 В, r1 = 30 Ом, r2 = r3 = 10 Ом, r4 = 26 Ом, r5 = 11 Ом, r6 = 10 Ом, r7 = 40 Ом, r8 = 50 Ом. Задачу решить методом преобразования треугольника сопротивлений в эквивалентную звезду.
Решение
Заменим треугольники сопротивлений abc и dfg эквивалентными звездами (рис. 52, б).
Подсчитаем сопротивления лучей звезды r10, r20 и r30, эквивалентной треугольнику abc сопротивлений r1, r2 и r3 (формулы 17)
r 10 = r 1 ⋅ r 2 r 1 + r 2 + r 3 =6 Ом, r 20 = r 1 ⋅ r 3 r 1 + r 2 + r 3 =6 Ом, r 30 = r 2 ⋅ r 3 r 1 + r 2 + r 3 =2 Ом.
Сопротивления лучей звезды r40, r50, r60 эквивалентной треугольнику dfg сопротивлений r6, r7, r8, равны
r 40 = r 6 ⋅ r 7 r 6 + r 7 + r 8 =4 Ом, r 50 = r 6 ⋅ r 8 r 6 + r 7 + r 8 =5 Ом, r 60 = r 7 ⋅ r 8 r 6 + r 7 + r 8 =20 Ом.
Эквивалентное сопротивление всей схемы
r Э = r 10 + r I ⋅ r II r I + r II + r 60 =38 Ом,
где
r I = r 20 + r 4 + r 40 =36 Ом, r II = r 3 + r 5 + r 50 =18 Ом.
Ток в неразветвленной части цепи
I= U r Э = 114 38 =3 А.
Токи в параллельных ветвях I’ (r20r4r40) и I» (r30r5r50)
I ′ =I⋅ r II r I + r II =3⋅ 18 36+18 =1 А; I ″ =I⋅ r I r I + r II =3⋅ 36 36+18 =2 А.
Теперь найдем токи в сопротивлениях заданной цепи. Для этого предварительно из схемы (рис. 52, б) найдем напряжения между точками a и b, a и c, b и c, d и g, f и g, d и f
U ab =I⋅ r 10 + I ′ ⋅ r 20 =3⋅6+1⋅6=24 В; U ac =I⋅ r 10 + I ″ ⋅ r 30 =3⋅6+2⋅2=22 В; U ab − U ac = ( φ a − φ b )− ( φ a − φ c )= φ c − φ b = U cb =24−22=2 В; U dg = I ′ ⋅ r 40 +I⋅ r 60 =1⋅4+3⋅20=64 В; U fg = I ″ ⋅ r 50 +I⋅ r 60 =2⋅5+3⋅20=70 В; U fg − U dg = ( φ f − φ g )− ( φ d − φ g )= φ f − φ d = U fd =70−64=6 В.
искомые токи будут
I 1 = U ab r 1 = 24 30 =0,8 А, I 2 = U ac r 2 = 22 10 =2,2 А, I 3 = U cb r 3 = 2 10 =0,2 А, I 4 = I ′ =1 А, I 5 = I ″ =2 А, I 6 = U fd r 8 = 6 10 =0,6 А, I 7 = U dg r 7 = 64 40 =1,6 А, I 8 = U fg r 8 = 70 50 =1,4 А.
Задача 52. В схеме (рис. 53) найти токи, применив преобразование треугольника в звезду. Определить эквивалентное сопротивление между точками a и b.
Приложенное напряжение U = 30 В; сопротивления: r1 = 60 Ом, r2 = 120 Ом, r3 = 180 Ом, r4 = 80 Ом, r5 = 120 Ом.
Определить показание ваттметра и убедиться в том, что оно равно сумме мощностей, расходуемых во всех сопротивлениях.
Ответ: I = 0,3 А, I1 = 0,2 А, I2 = 0,15 А, I3 = 0,1 А, I4 = 0,15 А, I5 = 0,05 А, rab = 100 Ом, P = 9 Вт.
Задача 53. Вычислить токи, проходящие во всех ветвях схемы (рис. 54), если E = 213 В, E1 = 90 В, r1 = 6 Ом, r2 = 40 Ом, r3 = 10 Ом, r4 = 100 Ом, r5 = 60 Ом.
Задачу решить преобразованием треугольника в эквивалентную звезду. Внутренними сопротивлениями источников напряжения пренебречь.
Определить входное сопротивление относительно ветви r1 и взаимное сопротивление ветвей r1 и r2.
Ответ: I = 3,8 А, I1 = 0,5 А, I2 = 1,5 А, I3 = 3,3 А, I4 = 1,8 А, I5 = 2 А, r11 = 33 Ом, r12 = 60 Ом.
Задача 54. Определить величины токов, проходящих по цепи, схема которой показана на рис. 55.
Данные цепи: E1 = 100 В, E2 = 140 В, r1 = 15 Ом, r2 = 5 Ом, r3 = 10 Ом, r4 = 4 Ом, r5 = 50 Ом, r10 = r20 = 0.
Задачу решить методами контурных токов и узловых потенциалов.
Ответ: I1 = 4 А, I2 = 8 А, I3 = 6 А, I4 = 10 А, I5 = 2 А.
Задача 55. Для схемы (рис. 56, а) найти методом эквивалентного генератора напряжения ток в ветви с сопротивлением r1, если E1 = 18 В, E2 = 21 В, r10 = 1 Ом, r1 = 2 Ом, r20 = 0, r2 = 9 Ом, r3 = 6 Ом.
Решение
Разомкнем цепь, содержащую сопротивление r1, и найдем напряжение между точками m и n (рис. 56, б).
Очевидно, что в разомкнутой ветви тока нет, точки m и p равнопотенциальны (φm = φp), а потенциал точки q превышает потенциал точки n на величину φq — φn = E1.
Имея это в виду, определим Ux = Umn
φm = φp, φn = φq — E1,
φm — φn = φp — φq + E1, Umn = Upq + E1.
Найдем напряжение Upq. Для этого сначала определим ток в контуре psqp
I= E 2 r 2 + r 20 + r 3 = 21 15 =1,4 А.
По закону Ома
Upq = I·r3 = 1,4·6 = 8,4 В.
Окончательно
Ux = Umn = Upq + E1 = 8,4 + 18 = 26,4 В.
Для нахождения тока в ветви r1 сначала определим сопротивление короткого замыкания (рис. 56, в)
r k = r 2 ⋅ r 3 r 2 + r 3 = 9⋅6 15 =3,6 Ом.
Искомый ток
I 1 = U x r 1 + r 10 + r k = 26,4 1+2+3,6 =4 А.
Этот ток течет от точки m к точке n.
Задача 56. Методом эквивалентного генератора напряжения найти ток (рис. 57, а), проходящий через сопротивление r5, если E = 120 В, r1 = 60 Ом, r2 = 15 Ом, r3 = 90 Ом, r4 = 60 Ом, r5 = 12 Ом. Внутреннее сопротивление источника напряжения равно нулю.
Решение
Разомкнем сопротивление r5 и. найдем напряжение между точками c и e (рис. 57, б).
Через сопротивления r1 и r2 протекает ток I’, а через r3 и r4 ток I»
I ′ = E r 1 + r 2 = 120 75 =1,6 А, I ″ = E r 3 + r 4 = 120 150 =0,8 А, φ a − φ c = U ac = I ′ ⋅ r 1 =1,6⋅60=96 В, φ a − φ d = U ad = I ″ ⋅ r 3 =0,8⋅90=72 В, ( φ a − φ c )− ( φ a − φ d )= φ d − φ c = U dc =24 В.
Но так как φd = φe, то Udc = Uec. Итак, напряжение холостого хода Ux = 24 В.
Теперь найдем сопротивление короткого замыкания. Определим его двумя способами.
1) Путем непосредственного подсчета по схеме.
В этом случае надо э.д.с. выключить, оставив ее внутреннее сопротивление, равное в данном случае нулю (рис. 57, в). Сопротивление короткого замыкания двухполюсника равно сопротивлению цепи между точками c и d
r k = r 1 ⋅ r 2 r 1 + r 2 + r 3 ⋅ r 4 r 3 + r 4 = 60⋅15 75 + 90⋅60 150 =48 Ом.
2) То же сопротивление можно найти и другим путем. Для этого надо замкнуть точки c и d накоротко, вычислить ток Iк, протекающий через короткозамкнутый участок (рис. 57, г), и сопротивление короткого замыкания определить по формуле (20).
Сопротивление схемы равно
r cx = r 1 ⋅ r 3 r 1 + r 3 + r 2 ⋅ r 4 r 2 + r 4 = 60⋅90 150 + 15⋅60 75 =48 Ом.
Найдем токи в ветвях
I 0 = E r cx = 120 48 =2,5 А, I ′ 1 = I 0 ⋅ r 3 r 1 + r 3 =2,5⋅ 90 150 =1,5 А, I ′ 2 = I 0 ⋅ r 4 r 2 + r 4 =2,5⋅ 60 75 =2 А.
Отсюда
I k = I ′ 2 − I ′ 1 =0,5 А.
Сопротивление короткого замыкания (формула 20) равно
r k = U x I k = 24 0,5 =48 Ом.
Искомый ток находим по формуле (21)
I 5 = U x r 5 + r k = 24 12+48 =0,4 А.
Задача 57. Для схемы (рис. 58) методом эквивалентного генератора напряжений найти ток в ветви с сопротивлением r3, если E1 = 5 В, E2 = 7 В, r1 = 7,5 Ом, r2 = 2,5 Ом, r3 = 5 Ом, r4 = 2 Ом, r5 = 25 Ом, r10 = r20 = 0.
Ответ: I3 = 0,6 А.
Задача 58. Пользуясь методом эквивалентного генератора напряжений, найти э.д.с. и внутреннее сопротивление источников, эквивалентных каждой из схем (рис. 59 а, б, в и г; 0 < k < 1). Внутренние сопротивления источников энергий равны нулю.
Ответ: 1) U0 = k·E, rk = k· (1 — k)·r; 2) U0 = k·E — E1, rk = r1 + k· (1 — k)·r;
3) U 0 = k⋅E⋅r r 1 +k⋅r , r k = ( 1−k )⋅r+ k⋅r⋅ r 1 k⋅r+ r 1 ;
4) U 0 = E⋅ r 3 r 4 r 1 r 2 + r 1 r 3 + r 1 r 4 + r 2 r 3 + r 3 r 4 , r k = r 4 ⋅ ( r 1 r 2 + r 1 r 3 + r 2 r 3 ) r 1 r 2 + r 1 r 3 + r 1 r 4 + r 2 r 3 + r 3 r 4 .
Задача 59. По показаниям приборов, полученным из двух опытов, найти э.д.с. и внутреннее сопротивление источника электрической энергии, эквивалентного схеме (рис. 60), в случаях:
|
1) |
U, B |
I, A |
2) |
U, B |
I, A |
3) |
U, B |
I, A |
|
20 |
2 |
20 |
12 |
20 |
3 |
|||
|
30 |
3 |
30 |
14 |
30 |
5 |
Примечание. В части схемы, обведенной на рис. 60 четырехугольником абвг и называемой двухполюсником, в действительности может быть включено большое количество различных э.д.с. и сопротивлений так, что полный расчет занял бы слишком много времени. Поэтому решено ограничиться экспериментальным исследованием двухполюсника, результаты которого помещены в таблице данных.
Ответ: 1) сопротивление 10 Ом. 2) источник энергии с э.д.с. 40 В и внутренним сопротивлением 5 Ом. 3) источник энергии с э.д.с. 5 В и внутренним сопротивлением 5 Ом.
Задача 60. Три генератора напряжений, э.д.с. которых E1 = 48 В, E2 = 45 В, E3 = 45 В, а внутренние сопротивления r1 = 1,2 Ом, r2 = 1 Ом, r3 = 1,5 Ом, работают параллельно на общую нагрузку, сопротивление которой r = 4,2 Ом (рис. 61).
Произвести замену заданных генераторов напряжений одним эквивалентным, определив его э.д.с. и внутреннее сопротивление. Чему равны токи, протекающие через каждый генератор и нагрузку?
Решение
Значения э.д.с. и внутреннего сопротивления эквивалентного генератора напряжения могут быть определены по формулам (23)
E Э = E 1 ⋅ 1 r 1 + E 2 ⋅ 1 r 2 + E 3 ⋅ 1 r 3 1 r 1 + 1 r 2 + 1 r 3 = 115 2,5 =46 В, 1 r Э = 1 r 1 + 1 r 2 + 1 r 3 =2,5 1 Ом , r Э = 1 2,5 =0,4 Ом.
Ток в нагрузке
I= E Э r+ r Э = 46 4,2+0,4 =10 А.
Напряжение на нагрузке
U=I⋅r=10⋅4,2=42 В.
Таково же напряжение на каждой из параллельных ветвей. Ток в каждой из ветвей найдем по формуле (25)
I 1 = E 1 −U r 1 = 48−42 1,2 =5 А, I 2 = E 2 −U r 2 = 45−42 1 =3 А, I 3 = E 3 −U r 3 = 45−42 1,5 =2 А.
Проверка показывает, что ток в нагрузке I равен сумме трех токов: I1, I2 и I3.
Задача 61. Для цепи, изображенной на рис. 62, проверить принцип взаимности, если э.д.с. E переместить в ветвь с сопротивлением r3.
Даны: E = 80 В, r1 = 8 Ом, r2 = 20 Ом, r3 = 30 Ом, r4 = 12 Ом.
Задача 62. Определить ток, проходящий через сопротивление r = 5 Ом, подключенное к генератору тока (рис. 63), параметры которого имеют следующие величины: ток Ik = 6 мА, внутренняя проводимость g0 = 0,04 1/Ом.
Решение
Внутреннее сопротивление генератора тока
r 0 = 1 g 0 = 1 0,04 =25 Ом.
Ток Ik распределяется по двум параллельным ветвям r и r0 обратно пропорционально их сопротивлениям. Поэтому искомый ток
I= I k ⋅ r 0 r 0 +r =6⋅ 25 25+5 =5 мА.
Задача 63. Пользуясь теоремой об эквивалентном генераторе тока, определить ток I3 в ветви r3 = 12 Ом (рис. 64, а). Электродвижущие силы генераторов напряжения равны E1 = 120 В, E2 = 100 В, их внутренние сопротивления r1 = 6 Ом, r2 = 4 Ом.
Решение
Из теории известно, что ток эквивалентного генератора тока равен току короткого замыкания Iкз, проходящему между короткозамкнутыми зажимами m и n, к которым подключена данная ветвь (рис. 64, б)
I кз = E 1 r 1 + E 2 r 2 =45 А,
а внутренняя проводимость генератора тока равна проводимости пассивной цепи между зажимами m и n при разомкнутой ветви r3 (рис. 64, в)
g 0 = 1 r 1 + 1 r 2 = 5 12 1 Ом , r 0 = 1 g 0 =2,4 Ом.
Схема эквивалентного генератора тока представлена на рис. 64 г.
Искомый ток
I 3 = I кз ⋅ r 0 r 0 + r 3 =45⋅ 2,4 2,4+12 =7,5 А.
Задача 64. Генератор тока создает в цепи ток Ik = 30 мА (рис. 65). Внутренней проводимостью генератора можно пренебречь.
Чему равны токи в ветвях, сопротивления которых равны r1 =1,8 кОм, r2 = 3 кОм, r3 = 1,5 кОм, r4 = 2 кОм.
Ответ: I1 = 10 мА, I2 = 4 мА, I3 = 20 мА, I4 = 6 мА.
Задача 65. Два генератора тока соединены в цепь, показанную на рис. 66, а. Ток первого генератора Ik1 = 3 мА, его внутренняя проводимость g1 = 0,05 1/Ом, второго — Ik2 = 2 мА, g2 = 0,01 1/Ом. Сопротивления равны: r3 = 5 Ом, r4 = 30 Ом.
Определить ток, проходящий через сопротивление r4.
Решение
1-й способ. Преобразуем генераторы тока в эквивалентные генераторы напряжения, получим схему рис. 66, б. Э.д.с. и внутренние сопротивления генераторов напряжения находим по формулам (2)
E 1 = I k1 g 1 = 3 0,05 =60 мВ, r 1 = 1 g 1 = 1 0,05 =20 Ом, E 2 = I k2 g 2 = 2 0,01 =200 мВ, r 2 = 1 g 2 = 1 0,01 =100 Ом.
Далее, любым способом находим искомый ток. Обозначим
По методу узловых потенциалов находим
U ab = E 1 ⋅ 1 r 1 + r 3 + E 2 ⋅ 1 r 2 1 r 1 + r 3 + 1 r 2 + 1 r 4 = 60⋅ 1 20+5 +200⋅ 1 100 1 20+5 + 1 100 + 1 30 =52,8 мВ.
Искомый ток
I 4 = U ab r 4 = 52,8 30 =1,76 мА.
2-й способ. Решим задачу методом эквивалентного генератора тока. Для этого заменим всю цепь, за исключением ветви с r4 эквивалентным генератором тока (рис. 66, в). Для определения его параметров Ik и g0 сначала исключим ветвь с r4, а точки a и b закоротим (рис. 66, г). Найдем ток короткого замыкания Iкз. Предварительно определим токи I3 и I4
I 3 = I k1 ⋅ 1 g 1 1 g 1 + r 3 =3⋅ 20 25 =2,4 мА, I 4 = I k2 =2 мА .
Следовательно, ток эквивалентного генератора тока
Ik = I3 + I4 = 2,4 + 2 = 4,4 А.
Теперь определим внутреннюю проводимость эквивалентного генератора тока g0 между точками a и b. Для этого исключим генераторы токов и оставим лишь их внутренние сопротивления (рис. 66, д)
g 0 = g ab = 1 1 g 1 + r 3 + g 2 = 1 20+5 +0,01=0,05 См .
Ток в искомой ветви (рис. 66, в) равен
I 4 = I k ⋅ 1 g 0 1 g 0 + r 4 =4,4⋅ 20 20+30 =1,76 мА .
Задача 66. В схеме рис. 67 простейшим способом вычислить токи. Даны: E1 = 100 В, E2 = 80 В, E3 = 40 В, r1 = 10 Ом, r2 = 10 Ом, r3 = 20 Ом, r4 = 30 Ом.
Внутренние сопротивления источников напряжения равны нулю.
Ответ: I1 = 3,6 А, I2 = 1,6 А, I3 = 5,2 А, I4 = 0.
В начало статьи Линейные электрические цепи постоянного тока

Генератор напряжения,
закон Ома,
обобщенный закон Ома,
Законы Кирхгофа,
первый закон Кирхгофа,
второй закон Кирхгофа,
метод контурных токов,
метод узловых потенциалов,
метод наложения,
Метод эквивалентных преобразований,
метод эквивалентного генератора,
метод активного двухполюсника,
принцип взаимности,
принцип компенсации,
входная проводимость,
взаимная проводимость,
баланс мощностей