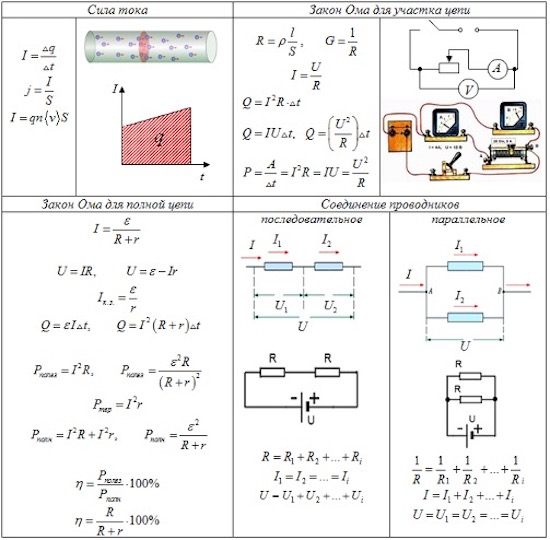
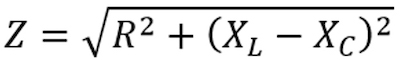Закон
Ома для участка цепи: сила
тока I
на участке электрической цепи прямо
пропорциональна напряжению U
на концах участка и обратно пропорциональна
его сопротивлению
R.
Формула
закона:
I=.
Отсюда запишем формулыU= IR
и R
=.
Рис.1.
Участок
цепи
Полная
цепь
Закон
Ома для полной цепи: сила
тока I
полной электрической цепи равна
ЭДС
(электродвижущей силе) источника тока
Е,
деленной на полное сопротивление цепи
(R
+ r). Полное
сопротивление цепи равно сумме
сопротивлений внешней цепи R
и внутреннего r
источника тока.
Формула
закона I
=
.
На
рис. 1 и 2 приведены схемы электрических
цепей.
3. Последовательное и параллельное соединение проводников
Проводники
в электрических цепях могут соединяться
последовательно
и параллельно.
Смешанное соединение сочетает оба эти
соединения.
Сопротивление,
при
включении которого
вместо всех других проводников,
находящихся между двумя точками цепи,
ток и напряжение остаются неизменными,
называют
эквивалентным
сопротивлением
этих
проводников.
Последовательное соединение
Последовательным
называется соединение, при котором
каждый
проводник соединяется только с одним
предыдущим и одним последующим
проводниками.
Как
следует из первого правила
Кирхгофа,
при последовательном
соединении проводников сила электрического
тока, протекающего по всем проводникам,
одинакова (на основании закона сохранения
заряда).
1.
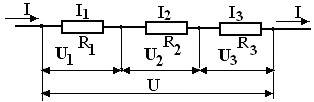
При последовательном соединении
проводников
(рис. 1)
сила
тока во всех проводниках одинакова:
I1 = I2 =
I3
=
I
Рис.
1.
Последовательное
соединение двух проводников.
2.
Согласно закону Ома, напряжения
U1
и
U2
на
проводниках равны U1 = IR1, U2 = IR2,
U3 = IR3.
Напряжение
при последовательном соединении
проводников равно сумме напряжений на
отдельных участках (проводниках)
электрической цепи.
U = U1
+
U2 + U3
По
закону
Ома, напряжения U1,
U2
на
проводниках равны
U1 = IR1, U2 = IR2,
В
соответствии вторым правилом Кирхгофа
напряжение на всем участке:
U = U1
+
U2 =
IR1+ IR2
=
I(R1+
R2)=
I·R.
Получаем:
R =
R1 + R2
Общее
напряжение U
на проводниках равно сумме напряжений
U1,
U2
,U3
равно: U =
U1 + U2 + U3 = I·(R1 + R2
+ R3)
= IR
где
RЭКВ
–
эквивалентное
сопротивление всей цепи. Отсюда: RЭКВ
=
R1 + R2 + R3
При
последовательном соединении эквивалентное
сопротивление цепи равно сумме
сопротивлений отдельных участков цепи:
R ЭКВ=
R1 + R2 + R3+…
Этот
результат справедлив для
любого числа
последовательно соединенных проводников.
Из
закона Ома
следует:
при равенстве сил тока при последовательном
соединении:
I = ,I =
.
Отсюда
=
или
=
,
т. е. напряжения на отдельных участках
цепи прямо пропорциональны сопротивлениям
участков.
При
последовательном соединении n
одинаковых
проводников общее напряжение равно
произведению напряжению одного U1
на
их количество n:
UПОСЛЕД=
n
·U1.
Аналогично
для сопротивлений:
RПОСЛЕД
= n·
R1
При размыкании
цепи одного из последовательно
соединенных потребителей ток исчезает
во всей цепи, поэтому последовательное
соединение на практике не всегда удобно.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основой прикладной электротехники безусловно является закон Ома для участка цепи. Не зная его основных положений, можно допустить серьезные ошибки в практической работе. О самом физическом явлении всем известно еще со школы. Но с помощью базовых положений может формулироваться много других вариантов, так или иначе затрагивающих особенности применения закона в реальных условиях. Именно здесь возникают сложности, требующие точных знаний и навыков оперирования физическими величинами.
Как звучит закон Ома для участка цепи
Ток в проводнике возникает в электрическом поле, которое, в свою очередь, появляется при наличии разности потенциалов или напряжения. Движение тока направлено в сторону меньшего потенциала. Условно считается, что в этом направлении двигаются положительные заряды, а в обратную сторону происходит движение свободных электронов.
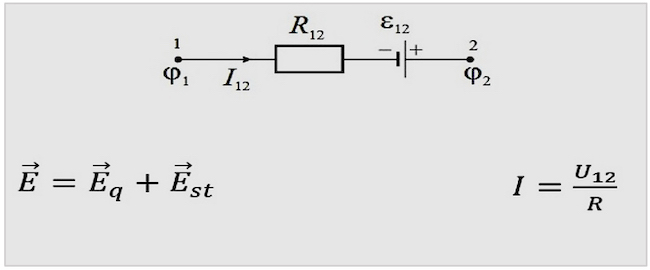
На участке металлического проводника данный процесс будет выглядеть следующим образом. На каждом конце присутствует потенциал – ϕ1 и ϕ2, при этом ϕ1 > ϕ2. Следовательно, напряжение в этом месте равно U = ϕ1 – ϕ2. Немецкий ученый Ом практически установил зависимость, при которой с увеличением напряжения, возрастает и сила тока, протекающего через неполный участок.
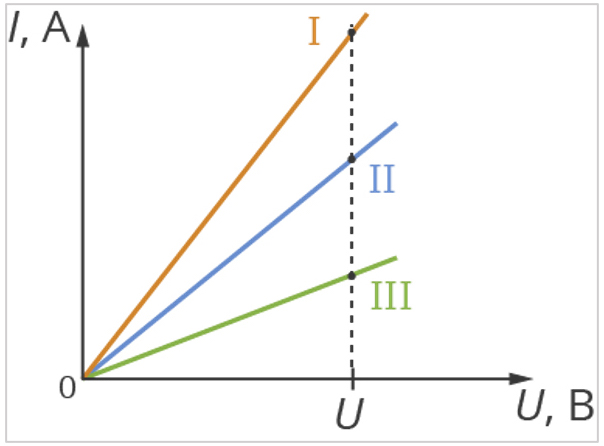
Для каждого из проводников, отличающихся материалами, был построен свой график, отражающий зависимость силы тока от напряжения. В дальнейшем, эти графики стали известны, как вольт-амперные характеристики. В результате, было установлено наличие линейной связи между обеими величинами – силой тока и напряжением. То есть, они находятся в прямой пропорциональной зависимости.
Но, как показывают графики, все проводники обладают разными коэффициентами пропорциональности. Следовательно, у них разная степень проводимости, получившая название электрического сопротивления (R). Поэтому, чем ниже будет сопротивление проводника, тем выше сила тока, проходящего через него. При том, что напряжение для всех проводников будет одинаковым.
После всех опытов ученый смог окончательно сформулировать свой закон для участка цепи:
Сила тока в однородном проводнике на отдельном участке, находится в прямой пропорции с напряжением на этом же участке и в обратной пропорциональной зависимости с сопротивлением данного проводника.
Принятые единицы измерения
При использовании закона Ома для практических расчетов все математические вычисления выполняются в установленных единицах измерений для всех 3-х величин:
- Сила тока – в амперах (А).
- Напряжение – в вольтах (В/V).
- Сопротивление – в омах (Ом).
Исходные данные и другие параметры, представленные в единицах, должны переводиться в общепринятые значения.
Действие основных единиц и физическое соблюдение закона Ома невозможно в следующих ситуациях:
- Наличие высоких частот, при которых электрическое поле изменяется с большой скоростью.
- Низкотемпературный режим и сверхпроводимость.
- Сильно разогретые спирали ламп накаливания, когда отсутствует линейность напряжения.
- Пробой проводника или диэлектрика, вызванный высоким напряжением.
- Электронные и вакуумные лампы, заполненные газами.
- Полупроводники с р-п-переходами, в том числе, диоды и транзисторы.
Сила тока
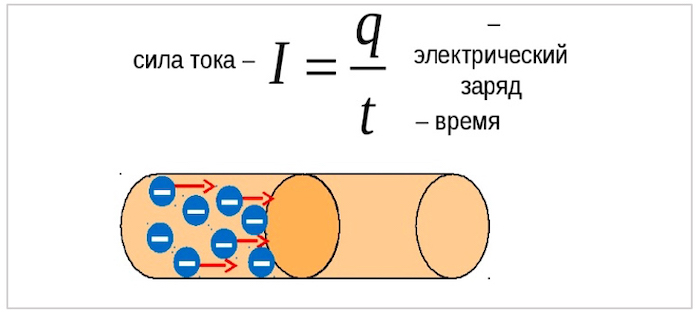
Сила тока возникает при наличии частиц со свободными зарядами. Они перемещаются через поперечное сечение проводника из одной точки в другую. Источник питания создает электрическое поле, под действием которого электроны начинают двигаться упорядоченно.
Таким образом, сила тока является количеством электричества, проходящего через определенное сечение за единицу времени. Увеличить этот показатель можно путем увеличения мощности источника тока или изъятия из цепи резистивных элементов.
Международная единица СИ для тока – ампер. Это довольно большая величина, поскольку для человека смертельно опасными считаются всего 0,1 А. В электротехнике малые величины могут выражаться в микро- и миллиамперах.
Определение силы тока можно окончательно сформировать в виде формулы I = q/t, в которой q является зарядом, проходящим через сечение, t – отрезок времени, затраченный на перемещение этого заряда.
Кроме того, сила тока может записываться с помощью основной формулы, когда известны значения напряжения и сопротивления. В числом виде она будет гласить следующее:
- I = U/R
Сопротивление
Рассматривая закон ома для участка цепи, нельзя забывать о таком понятии, как сопротивление. Данная величина считается основной характеристикой проводника, поскольку именно сопротивление влияет на качество проводимости. Разные материалы проводят ток лучше или хуже. Это объясняется неоднородностью их структуры, различиями в кристаллических решетках. Поэтому в одних случаях электроны движутся с большей скоростью, а в других – с меньшей.
Собственным электрическим сопротивлением обладают все проводники, находящиеся в твердом, жидком, газообразном и плазменном состоянии. У каждого из них своя характеристика, называемая удельным сопротивлением. Данная величина отражает способность каждого материала к сопротивлению. За эталон принимается проводник длиной 1 м с поперечным сечением 1 м².
Чтобы найти сопротивление проводника из данного материала нужно воспользоваться формулой: R = ρ x (l/S). В ней l является длиной проводника, S – площадью его поперечного сечения, ρ – удельным сопротивлением.
По закону Ома на участке цепи эта величина определяется: R = U/I.
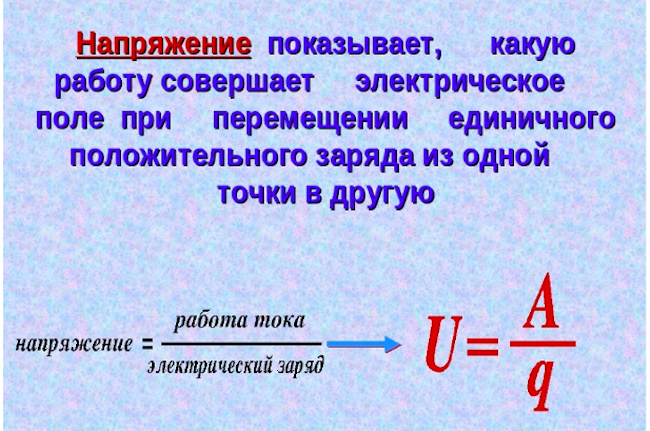
Напряжение
Напряжение относится к важным характеристикам электрического тока, протекающего в проводнике. С физической точки зрения, это работа электрического поля, которое перемещает заряд на какое-то расстояние. В электротехнике напряжением считается разность потенциалов между двумя точками участка цепи. На практике эта величина служит для определения возможности подключения к сети потребителей электроэнергии, продолжительность их работы в этом состоянии.
В электрической цепи напряжение возникает следующим образом:
- Вначале цепь подключается к источнику тока путем соединения с двумя полюсами. Это может быть генератор или батарея.
- На одном полюсе или клемме – избыточное количество электроном, а на другом – их недостает. Первый условно считается положительным, второй – отрицательным.
- Электрическое поле источника энергии воздействуют на электроны положительного полюса и самого проводника, заставляя их двигаться в сторону отрицательного полюса и притягиваться к нему. Такое притяжение происходит из-за положительного заряда на этом полюсе, поскольку электроны здесь отсутствуют.
- Между обеими клеммами возникает разность потенциалов с определенным значением, что приводит к упорядоченному движению электронов в проводниках и подключенных нагрузках. Постепенно избыток электронов положительного полюса уменьшается, соответственно, снижается и потенциал. Характерным примером служит аккумуляторная батарея. При подключении нагрузки, ее потенциал будет падать, вплоть до полной разрядки. Для восстановления первоначальных свойств, потребуется подзарядка от постороннего источника тока.
При неизменной мощности источника энергии, значение напряжения может быть разным под действием следующих факторов:
- Материал соединительных проводников. У каждого свой вольтамперный график.
- Количество потребителей, подключенных к сети.
- Температура окружающей среды.
- Качество монтажа самой сети.
Закон Ома для участка цепи — расчет цепей
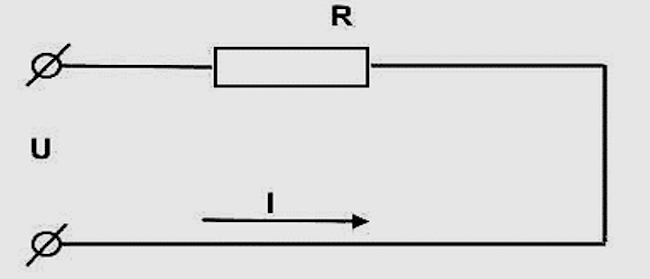
Простейший вариант наглядно представлен на рисунке. Это однородный участок цепи открытого типа.
Для его описания применяется известная формула, которая будет иметь следующую форму:
- I = U/R, где I является силой тока, U – напряжением, R – сопротивлением.
Данная формула является интегральной. С ее помощью хорошо видно, как при возрастании напряжения, увеличивается и сила тока. Но, если увеличить сопротивление, то сила тока, наоборот, будет понижаться.
На схеме изображен всего один элемент, обладающий сопротивлением. На практике, их может быть любое количество. Они могут соединяться последовательно, параллельно и смешанным способом.
Неоднородный участок цепи постоянного тока
Неоднородную структуру имеет такой участок цепи, где помимо проводников и элементов, присутствует источник тока. Его ЭДС необходимо учитывать при расчетах общей силы тока на данном участке.
Существует формула, которая дает определение основным параметрам и процессам неоднородного участка: q = q0 x n x V. Ее показатели характеризуются следующим образом:
- В процессе перемещения зарядов (q) они приобретают определенную плотность. Ее показатели зависят от силы тока и площади поперечного сечения проводника (S).
- В условиях определенной концентрации (n) можно точно указать численность единичных зарядов (q0), которые были перемещены за единичный отрезок времени.
- Для расчетов проводник условно считается цилиндрическим участком, имеющим какой-то объем (V).
При подключении проводника к аккумулятору, последний через некоторое время будет разряжен. То есть, движение электронов постепенно замедляется и, в конце концов, прекратится совсем. Этому способствует молекулярная решетка проводника, оказывающая противодействие, столкновения электронов между собой и другие факторы. Для преодоления такого сопротивления следует дополнительно приложить определенные сторонние силы.
Во время расчетов эти силы суммируются с кулоновскими. Кроме того, для перенесения единичного заряда q из 1-й точки во 2-ю потребуется выполнение работы А1-2 или просто А12. С этой целью создается разница потенциалов (ϕ1 – ϕ2). Под действием источника постоянного тока возникает ЭДС, перемещающая заряды по цепи. Величина общего напряжения будет состоять из всех сил, отмеченных выше.
Полярность подключения к источнику постоянного тока нужно учитывать в расчетах. При изменении клемм будет меняться и ЭДС, ускоряющая или замедляющая перемещение зарядов.
Формулировка закона Ома для полной цепи
Закон Ома для полной цепи выражается поведением основных величин, был выведен опытным экспериментальным путем. Результатом стало выявление связей, объединяющих силу тока (I), электродвижущую силу – ЭДС (Е), внешнее (R) и внутреннее (r) сопротивления в цепи.
В теоретических расчетах с точки зрения чистой физики, в цепях предполагался так называемый идеальный источник постоянного тока. После того, как были проведены реальные исследования, выяснилось, что источник тока обладает собственным сопротивлением.
Формулировка закона Ома для полной цепи приобрела следующий вид: Сила тока находится в прямой пропорции с суммой ЭДС цепи, и в обратной пропорции с суммой сопротивлений самой цепи и источника тока.
Следует сразу же выяснить, что такое электродвижущая сила. По сути, она является физической величиной, характеризующей действие внешних сил источника ЭДС. Например, в простой батарейке перемещение зарядов происходит в результате химической реакции. То есть, данная сила двигает заряд, обеспечивая общее течение электрического тока.
Формулу закона Ома можно записать по-другому. ЭДС источника тока полной цепи представляет собой суммарные падения напряжений у самого источника и во внешней цепи:
- E = Ir + IR = Ur + UR
Переменный ток
В отличие от цепей, по которым течет постоянный ток, в цепи переменного тока кроме активной нагрузки в виде потребителей, входят элементы с реактивным сопротивлением. Это различные типы катушек и конденсаторов, обладающих индуктивностью и емкостью.
С увеличением напряжения будет расти и сила тока. Однако, к активному сопротивлению здесь добавляются реактивные. С связи с этим, полный расклад для такой цепи будет выглядеть так:
- I = U/Z, где I и U – это сила тока и напряжение, а Z – является полным сопротивлением цепи.
Показатель Z следует рассмотреть более подробно. Прежде всего, это сумма, включающая активное, индуктивное и емкостное сопротивления. То есть, на электрический ток оказывает влияние не только обычная омическая нагрузка, но также емкость (С) и индуктивность (L).
В результате, краткая формула полного сопротивления примет следующий вид:
Опытным путем было установлено, что в цепях переменного тока наблюдается несовпадение по фазе колебаний тока и напряжения. Величина этих несовпадений она же разница фаз находится под непосредственным влиянием индуктивности и емкости.
Использование на практике
Закон Ома лежит в основе всех расчетов производимых в электронике и электротехнике. Будущих специалистов с первых дней учат, как использовать так называемый треугольник. Чтобы найти какую-то искомую величину, должны выполняться простые арифметические действия. Если два оставшихся параметра находятся в одной строке – они перемножаются. Если на разных уровнях, то верхний всегда делится на нижний.
Практически данная схема выглядит так:
- U = I x R, I = U/R, R = U/I.
Самые простые вычисления производятся на основе данных измерительных приборов. На участке цепи измерение тока выполняется амперметром, а напряжения – вольтметром. После этого найти сопротивление математическим путем не составит труда.
Для замеров сопротивления тоже есть прибор – омметр. Полученное выражение, подставляется в одну из формул, после чего находятся величины силы тока или напряжения. Точность омметра зависит от стабильности напряжения, подаваемого источником тока. Стабилизация проводится путем добавления резистора, выполняющего функцию регулятора.
Иногда требуется исключить из схемы какой-нибудь элемент без демонтажа. С этой целью проводится шунтирование, когда приходится устанавливать проводник на входных клеммах ненужного резистора. Ток начинает идти через шунт с меньшим сопротивлением, а напряжение на резисторе падает до нуля.
Закон Ома используется в защитных системах. Это делается с помощью уставок, обеспечивающих нормальную работу и отключающих питание лишь в аварийных ситуациях.
Формулы для закона Ома
Представленные на рисунке формулы, начали формироваться из основных формул для полной цепи и отдельного участка. С их помощью можно выполнять все основные расчеты, при составлении проектов и в других ситуациях. Формулы полностью пригодны для работы с цепями как постоянного, так и переменного тока.
Видеоинструкция
Закон Ома для участка цепи — одна из основ электротехники. Данный закон указывает на соотношение между током, напряжением и сопротивлением.
Сам Закон Ома для участка цепи гласит так:
Сила тока в проводнике (участке электрической цепи) прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника (участка электрической цепи)
[Г.С. Ом, 1826]
Из этого определения Георг Ом вывел следующую формулу:
I = U/R или U = R*I
Формула, вытекающая из закона Ома, также известна в просторечии как формула URI. Такое название появилось от последовательности букв в формуле:
U = R*I
- R — сопротивление проводника (Ом);
- I — сила тока в проводнике (Ампер);
- U — напряжение приложенное к проводнику (Вольт).
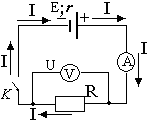
Электрическая цепь и закон Ома
Три величины — напряжение, электрический ток и сопротивление — могут быть четко представлены в электрической цепи. В простейшем случае она состоит из источника постоянного напряжения и резистора. Резистор подключен к источнику напряжения, а для упрощения возьмем, что сопротивление проводов равно 0 Ом.
Направление электрического тока.
В электротехнике ток течет от плюса до минуса (смотрите рисунок 1). Другими словами, как только возникает замкнутая цепь, ток начинает течь от положительного полюса к отрицательному полюсу источника напряжения. Мы говорим о замкнутой цепи, когда два полюса источника напряжения соединены друг с другом сопротивлением.
Как и чем измерять ток и напряжение?
Есть два способа определения силы тока и напряжения. С одной стороны, их можно определить арифметически с помощью закона Ома для участка цепи. С другой стороны, две переменные также могут быть определены путем измерения.
Однако для арифметического определения тока или напряжения должны быть известны две другие величины (напряжение и сопротивление либо ток и сопротивление).
С другой стороны, метрологический метод также работает с любой электрической цепью. Для этого в электрическую цепь необходимо вставить амперметр и вольтметр . Они используются для измерения силы тока и напряжения. Но здесь также применяется закон Ома, поскольку сопротивление нельзя измерить напрямую, но его можно будет рассчитать, когда будут измерены значения тока и напряжения.
Итак, ток измеряется так амперметром, который последовательно подключается к потребителю (резистору, лампе накаливания и т. д.), Через который нужно определять ток. На принципиальной схеме он изображен как A внутри круга (см. рисунок 1). Амперметр имеет очень низкое внутреннее сопротивление, чтобы не влиять на ток, который должен протекать через потребителя. В идеале, внутреннее сопротивление амперметра принимается равным 0 Ом и поэтому просто опускается.
Измерение напряжения производится с помощью вольтметра, который замеряет разность потенциалов между двумя его точками подключения. На электрической схеме он обозначен буквой V внутри круга (см. рисунок 1). В отличие от амперметра, вольтметр подключается параллельно нагрузке, на которой измеряется напряжение. Добавление вольтметра параллельно некоторому потребителю (например, резистору) создает току еще один «обходной» путь, что резко изменяет параметры цепи. Чтобы избежать этих нежелательных последствий, надо применять вольтметры с максимально большим сопротивлением.
Вольт-амперная характеристика (ВАХ).
Вольт-амперная характеристика или характеристика UI резистора может быть записана путем приложения к нему различных напряжений и последующего измерения тока. Обычно при омическом сопротивлении достаточно одной точки измерения, которая затем соединяется с началом системы координат. Однако на практике, для целей контроля, выполняют серию измерений с тремя точками измерения.
Затем эти точки измерения отмечаются в системе координат и соединяются. Напряжение откладывают по оси абсцисс, а ток — по оси ординат. Пример ВАХ смотрите на рисунке ниже

ВАХ может быть использована для определения тока через резистор при определенном напряжении.
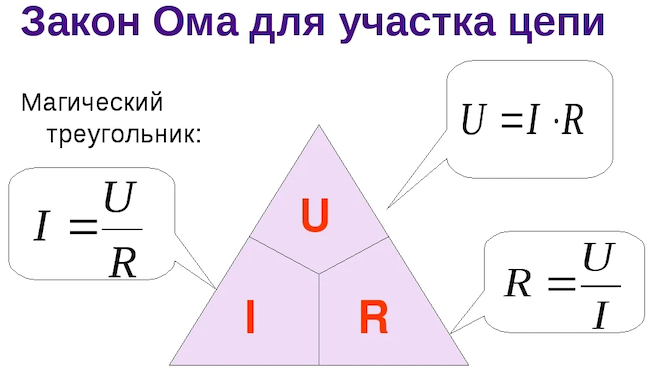
«Треугольник Ома»
Связь между отдельными величинами из закона Ома может быть показана в так называемом «треугольнике Ома».
Вверху треугольника вы найдете напряжение U, слева — сопротивление R, а справа — ток I.
Если вы хотите определить недостающую величину, то прикройте эту величину мысленно или пальцем, а затем посмотрите на две другие величины. Если две «не закрытые» величины находятся рядом друг с другом, то они умножаются. С другой стороны, если они расположены друг над другом, то верхняя величина делится на нижнюю.
Например, вы «закрываете» напряжение U в вершине «треугольника Ома». Две оставшиеся величины, то есть сопротивление R и ток I, находятся рядом. Соответственно, чтобы получить напряжение U, нужно умножить сопротивление R на ток I. Это в точности соответствует формуле закона Ома для участка электрической цепи.
Калькулятор, который основан на законе Ома
Используйте этот калькулятор, который основан на законе Ома для расчета соотношений между током, напряжением, сопротивлением и мощностью в электрических цепях. Чтобы воспользоваться калькулятором, введите значения в 2 любых поля и нажмите кнопку «рассчитать».

Таблица-шпаргалка
Используя закон Ома для участка цепи, а также формулу для мощности электрического тока: P = U*I – я подготовил для вас полезную таблицу-шпаргалку, которая позволяет соотносить между собой сопротивление (R), силу тока (I), напряжение (U) и мощность электрического тока (P). Будет точно полезно не только школьникам!
| Известные величины | R (сопротивление) | I (сила тока) | U (напряжение) | P (мощность) |
| Ток и сопротивление | U = I × R | P = I2 × R | ||
| Напряжение и ток | R = U / I | P = U × I | ||
| Мощность и ток | R = P / I2 | U = P / I | ||
| Напряжение и сопротивление | I = U / R | P = U2 / R | ||
| Мощность и сопротивление | I = P / R | |||
| Напряжение и мощность | R = U2 / R | I = P / U |
Пример применения закона Ома
В этом примере лампочка накаливания подключена к источнику постоянного напряжения с U=12 В. Цель – определить сопротивление лампочки. Для измерения силы тока также имеется амперметр.
Первая часть задачи – определить силу тока с помощью амперметра. Для этого его необходимо правильно вставить в цепь. Поскольку мы будем вычислять электрический ток, который протекает через лампочку, амперметр должен быть подключен последовательно с ней.
Непосредственно после включения источника напряжения измеряется ток I, равный 1A. Сопротивление лампочки можно рассчитать по закону Ома:
R = U / I = 12В / 1А = 12 Ом.
Через некоторое время вы снова смотрите на амперметр и замечаете, что ток упал до 200 мА.
Сопротивление лампочки изменилось. Почему так произошло? Это связано с разной температурой в момент включения и во время обычной работы, так как лампочка нагревается. Поэтому сопротивление холодной лампы ниже, чем теплой. Именно поэтому лампочку часто называют терморезистором.
Список использованной литературы
- Физика, 8 класс. Л.А. Исаченкова, Ю.Д. Лещинский, В.В. Дорофейчик. Издательство «Народная асвета»
- Физика. 8 класс. Учебник для общеобразовательных учреждений. Перышкин А.В.
Профессиональному электрику, специалисту электронщику никак не обойти в собственной деятельности закон Ома, решая любые задачи, связанные с наладкой, настройкой, ремонтом электронных и электрических схем.
Собственно, понимание этого закона необходимо каждому. Потому что каждому в быту приходится иметь дело с электричеством.
И хотя учебным курсом средней школы закон немецкого физика Ома и предусмотрен, но на практике не всегда своевременно изучается. Поэтому рассмотрим в нашем материале такую актуальную для жизни тему и разберемся с вариантами записи формулы.
Содержание статьи:
- Отдельный участок и полная электрическая цепь
- Расчет тока участка электрической схемы
- Вариант расчета для полной цепи
- Рассмотрение действия закона к переменной величине
- Последовательное и параллельное включение элементов
- Цепь последовательно включенных резистивных элементов
- Цепь параллельно включенных резистивных элементов
- Интегральная и дифференциальная формы закона
- Выводы и полезное видео по теме
Отдельный участок и полная электрическая цепь
Рассматривая электрическую цепь с точки зрения применения к схеме закона Ома, следует отметить два возможных варианта расчета: для отдельно взятого участка и для полноценной схемы.
Расчет тока участка электрической схемы
Участком электрической цепи, как правило, рассматривается часть схемы, исключающая источник ЭДС, как обладающий дополнительным внутренним сопротивлением.
Поэтому расчетная формула, в данном случае, выглядит просто:
I = U/ R,
Где, соответственно:
- I – сила тока;
- U – приложенное напряжение;
- R – сопротивление.
Трактовка формулы простая – ток, протекающий по некоему участок цепи, пропорционален приложенному к нему напряжению, а сопротивлению – обратно пропорционален.
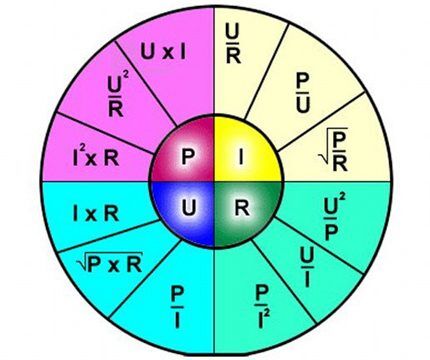
Так называемая графическая «ромашка», посредством которой представлен весь набор вариаций формулировок, основанных на законе Ома. Удобный инструмент для карманного хранения: сектор «P» — формулы мощности; сектор «U» — формулы напряжения; сектор «I» — формулы тока; сектор «R» — формулы сопротивления
Таким образом, формулой чётко описывается зависимость протекания тока по отдельному участку электрической цепи относительно определенных значений напряжения и сопротивления.
Формулой удобно пользоваться, например, рассчитывая параметры сопротивления, которое требуется впаять в схему, если заданы напряжение с током.
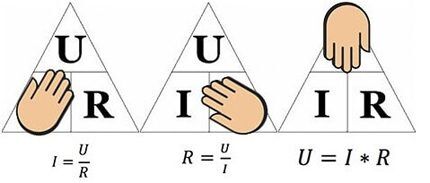
Закон Ома и два следствия, которыми необходимо владеть каждому профессиональному электромеханику, инженеру-электрику, электронщику и всем, кто связан с работой электрических цепей. Слева направо: 1 — определение тока; 2 — определение сопротивления; 3 — определение напряжения, где I — сила тока, U — напряжение, R — сопротивление
Вышеприведенный рисунок поможет определить, например ток, протекающий через 10-омное сопротивление, к которому приложено напряжение 12 вольт. Подставив значения, найдем – I = 12 / 10 = 1.2 ампера.
Аналогично решаются задачи поиска сопротивления (когда известны ток с напряжением) или напряжения (когда известны напряжение с током).
Тем самым всегда можно подобрать требуемое рабочее напряжение, нужную силу тока и оптимальный резистивный элемент.
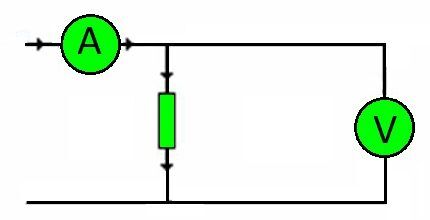
Формула, которой предложено пользоваться, не требует учитывать параметры источника напряжения. Однако, схема, содержащая, например, аккумулятор, будет рассчитываться по другой формуле. На схеме: А – включение амперметра; V – включение вольтметра.
Кстати, соединительные провода любой схемы – это сопротивления. Величина нагрузки, которую им предстоит нести, определяется напряжением.
Соответственно, опять же пользуясь законом Ома, становится допустимым точный подбор необходимого сечения проводника, в зависимости от материала жилы.
У нас на сайте есть подробная инструкция по расчету сечения кабеля по мощности и току.
Вариант расчета для полной цепи
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС.
Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС.
Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
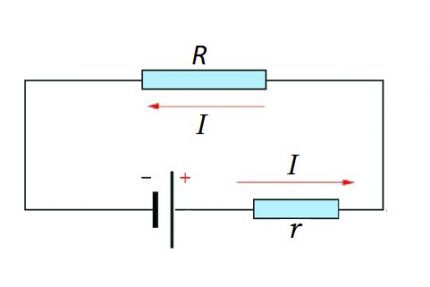
Для расчетов в условиях полноценной электрической цепи всегда берется к учету резистивное значение источника ЭДС. Это значение суммируется с резистивным сопротивлением непосредственно электрической цепи. На схеме: I — прохождение тока; R — резистивный элемент внешний; r — резистивный фактор ЭДС (источника энергии)
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины.
Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Рассмотрение действия закона к переменной величине
Понятие «сопротивление» к условиям прохождения переменного тока следует рассматривать уже больше как понятие «импеданса». Здесь имеется в виду сочетание активной резистивной нагрузки (Ra) и нагрузки, образованной реактивным резистором (Rr).
Обусловлены подобные явления параметрами индуктивных элементов и законами коммутации применительно к переменной величине напряжения — синусоидальной величине тока.

Такой видится эквивалентная схема электрической цепи переменного тока под расчет с применением формулировок, исходящих из принципов закона Ома: R — резистивная составляющая; С — емкостная составляющая; L — индуктивная составляющая; ЭДС -источник энергии; I -прохождение тока
Другими словами, имеет место эффект опережения (отставания) токовых значений от значений напряжения, что сопровождается появлением активной (резистивной) и реактивной (индуктивной или емкостной) мощностей.
Расчёт подобных явлений ведётся при помощи формулы:
Z = U / I или Z = R + J * (XL — XC)
где: Z – импеданс; R – активная нагрузка; XL , XC – индуктивная и емкостная нагрузка; J – коэффициент.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.
Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1 = I2 ;
- U = U1 + U2 ;
- R = R1 + R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.
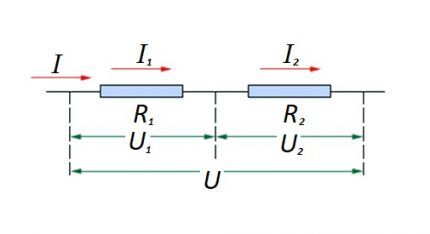
Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U, U1, U2 — приложенное напряжение
Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.
Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1 + I2 … ;
- U = U1 = U2 … ;
- 1 / R = 1 / R1 + 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.
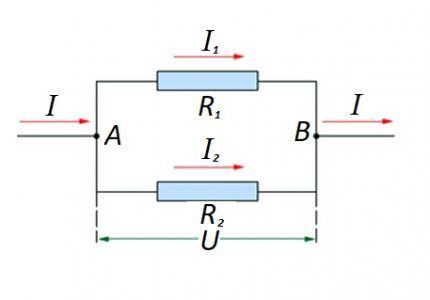
Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U — подведённое напряжение; А, В — точки входа/выхода
Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.
Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E
Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ
Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Выводы и полезное видео по теме
Подробный разбор закона Ома в видеоролике, представленном ниже, поможет окончательно закрепить знания в этом направлении.
Своеобразный видеоурок качественно подкрепляет теоретическое письменное изложение:
Работа электрика или деятельность электронщика неотъемлемо связана с моментами, когда реально приходится наблюдать закон Георга Ома в действии. Это своего рода прописные истины, которые следует знать каждому профессионалу.
Объёмных знаний по данному вопросу не требуется — достаточно выучить три основных вариации формулировки, чтобы успешно применять на практике.
Хотите дополнить изложенный выше материал ценными замечаниями или выразить свое мнение? Пишите, пожалуйста, комментарии в блоке под статьей. Если у вас остались вопросы, не стесняйтесь задавать их нашим экспертам.
Закон Ома назван в честь своего открывателя это ученый Георг Симон Ом. Свои эксперименты в области электричества он начал вдохновляясь опытами Фурье. Ом проводил свои опыты с различными материалами и изучение их электропроводности. Так была разработана знаменитая формула, которая стала краеугольной в современной физике, которая вошла в школьные учебники: I=U/R. Сила тока пропорциональна величине напряжения и имеет обратную пропорциональность сопротивлению.
В статье подробно разобраны области теории и практического применения принципов закона Ома в современной электротехнике. В качестве дополнения, в материале содержатся два обучающих видеоролика и один научный материал на тему статьи.
Закон Ома
Закон Ома показывает отношения между напряжением (U), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:
U = I × R
или
I = V/R
или
R = V/I
Где:
- V – напряжение в вольтах (В);
- I – сила тока в амперах (А);
- R – сопротивление в омах (Ом);
Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.
Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».
- Если надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
- Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление: I = V/R .
- Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .
Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
Для замкнутой цепи
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.