Содержание:
Переходные процессы в электрических цепях:
Переходный процесс в электрической цепи — это электромагнитный процесс, возникающий в электрической цепи при переходе от одного установившегося (принужденного) режима к другому. Установившимся (принужденным) называется режим работы электрической цепи, при котором напряжение и токи цепи в течение длительного времени остаются неизменными.
Такой режим в электрической цепи устанавливается при длительном действии источников постоянной или переменной ЭДС при неизменных параметрах этой цепи R, L и С.
Переходный процесс вызывается коммутацией в цепи. Коммутацией называется процесс замыкания или размыкания рубильников или выключателей. Переходный процесс может быть вызван изменением параметров электрической цепи R, L или С.
Переходный процесс базируется на двух законах коммутации:
- ток в индуктивности не может изменяться скачком;
- напряжение на емкости не может изменяться скачком.
Действительно, если ток в индуктивности L изменяется скачком, т. е. мгновенно, то ЭДС самоиндукции eL становится бесконечно большой (при 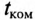
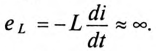
В реальных цепях ЭДС самоиндукции может иметь только конечные значения.
Если в цепи с емкостью С напряжение на ее обкладках изменяется скачком, т. е. мгновенно, то появляется бесконечно большой зарядный (или разрядный) ток (при 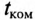 = 0):
= 0):
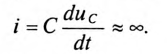
Ток в электрических цепях может иметь только конечные значения.
Переходный процесс является быстропротекающим процессом, длительность которого обычно составляет десятые, сотые и даже миллионные доли секунды и сравнительно редко — секунды и даже десятки секунд.
Таким образом, один установившийся режим цепи отделяется от другого некоторым промежутком времени, в течение которого происходит постепенный переход от прежнего состояния цепи к новому.
Переходный процесс в линейных цепях можно рассматривать как результат наложения двух процессов:
- нового установившегося режима, который наступает после коммутации;
- свободного процесса, обеспечивающего переход цепи от прежнего установившегося режима к новому установившемуся режиму.
Таким образом, ток i цепи в течение переходного процесса можно представить суммой двух токов: нового установившегося 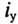 и свободного
и свободного 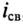 , возникающего после коммутации:
, возникающего после коммутации:

Аналогично напряжение в течение переходного процесса равно

В результате переходного процесса происходят изменения тока, напряжения, фазы, частоты и т.д.
Изучение переходных процессов очень важно, так как оно позволяет выявить возможные превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, позволяет выявить возможные броски токов, величина которых в десятки раз превышает установившийся. Изучение переходных процессов позволяет выявить ситуации, возникающие в электрических цепях при коротком замыкании, резком включении и выключении рубильников, и прочие режимы работы цепи.
Переходный процесс в электрической цепи
Переходный процесс в электрической цепи — это процесс, возникающий в электрической цепи при различных воздействиях, приводящих их из стационарного состояния в новое стационарное состояние, когда при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.
Подключение катушки индуктивности к источнику с постоянным напряжением
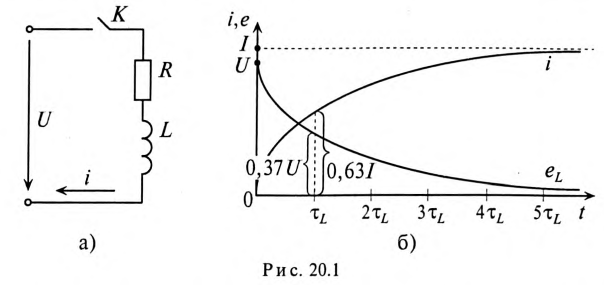
Если катушку индуктивности (RL) подключить к источнику с постоянным напряжением U (замыкание ключа К), то ток i в не-разветвленной цепи (рис. 20.1а) будет увеличиваться от нуля (в начале переходного процесса) до установившегося значения

Установившийся, т.е. постоянный, ток I не индуктирует в катушке ЭДС самоиндукции, поэтому индуктивное сопротивление в установившемся режиме при условии (20.3) отсутствует.
Этот увеличивающийся ток i индуктирует в индуктивности L катушки ЭДС самоиндукции (см. (9.11))
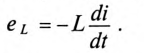
Следовательно, для любого момента времени переходного процесса по второму закону Кирхгофа можно записать
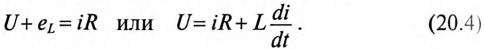
Разделив уравнение (20.4) на R, получают

В уравнении (20.5) 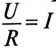 — установившийся в конце переходного процесса ток (
— установившийся в конце переходного процесса ток (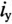 ).
).
Отношение — 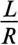 имеет размерность времени
имеет размерность времени 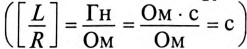 обозначается буквой
обозначается буквой 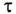 (тау) и называется постоянной времени
(тау) и называется постоянной времени 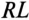 -цепи, т. е.
-цепи, т. е.

Тогда уравнение (20.5) можно записать в виде

Если это уравнение проинтегрировать, предварительно разделив переменные (ток и время), а затем спотенцировать, то получим выражение
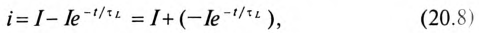
где е — основание натурального логарифма (е=2,71); I — установившийся ток (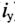 ); (
); (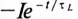 ) – свободный ток (
) – свободный ток (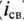 ), так как
), так как 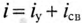 , т.е.
, т.е.

Таким образом, уравнение, которое позволяет определить вели-шу тока в цепи с индуктивностью L в любой момент переходно-процесса RL-цепи при подключении реальной катушки индук-1Вности к источнику с постоянным напряжением U, записывается в виде

Воспользовавшись Приложением 9, по выражению (20.10) можно определить, что за время t=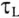 ток в цепи увеличивается до 0,63I, а за время t= 4,6
ток в цепи увеличивается до 0,63I, а за время t= 4,6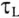 — до 0,99I, т. е. до 99 % установившегося тока I.
— до 0,99I, т. е. до 99 % установившегося тока I.
Теоретически переходный процесс происходит бесконечно долго. Практически переходный процесс в рассматриваемой цепи считается законченным, когда ток i увеличивается до 99 % установившегося тока I.
Как видим, чем больше xL, тем больше времени t длится перечный процесс.
Таким образом, постоянная времени xL определяет скорость греховного процесса или его длительность.
ЭДС самоиндукции в рассматриваемой цепи, вызванная свободным током 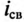 , определяется выражением
, определяется выражением

Таким образом, ЭДС самоиндукции в 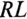 -цепи, подключенной к источнику с постоянным напряжением U, будет уменьшаться. Так, за время t=
-цепи, подключенной к источнику с постоянным напряжением U, будет уменьшаться. Так, за время t=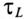 , ЭДС самоиндукции согласно (20.11) уменьшатся до 0,37U, а за время t = 4,6
, ЭДС самоиндукции согласно (20.11) уменьшатся до 0,37U, а за время t = 4,6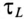 – до 0,01 U, т.е. до 1 % постоянного напряжения U.
– до 0,01 U, т.е. до 1 % постоянного напряжения U.
Увеличение тока и уменьшение ЭДС самоиндукции катушки при подключении катушки к источнику с постоянным напряжением U показаны на графике рис. 20.1б.
Отключение и замыкание RL-цепи
Если цепь с катушкой, в которой проходит установившийся ток I (рис. 20.1а), разомкнуть, то ток i в такой цепи с большой скоростью уменьшается до нуля и в катушке индуктируется большая ЭДС самоиндукции eL
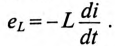
Эта ЭДС полностью приложена к клеммам ключа, так как при размыкании сопротивление ключа становится бесконечно большим. Эта ЭДС вызывает значительное увеличение электрического поля между контактами ключа, а следовательно, и напряженности поля. Большая напряженность электрического поля может вызвать искровой и даже дуговой разряд между размыкающимися контактами ключа, в результате чего обгорают контакты ключа.
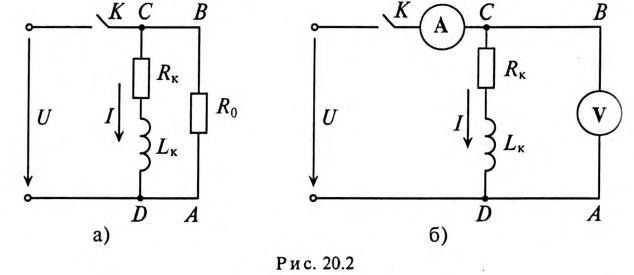
Поэтому рубильники в RL-цепях шунтируются специальными устройствами, которые обеспечивают гашение дугового разряда. Для гашения дугового разряда необходимо одновременно с отключением катушки индуктивности от источника замкнуть ее на разрядное сопротивление R0 (рис. 20.2а).
Уменьшение тока 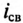 при отключении катушки от источника (рис. 20.1а) происходит по закону
при отключении катушки от источника (рис. 20.1а) происходит по закону
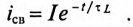
Наглядно это уменьшение можно наблюдать на рис. 20.1б, если кривую изменения eL считать кривой уменьшения тока 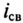 в соответствующем масштабе.
в соответствующем масштабе.
Постоянная времени при отключении катушки от источника с постоянным напряжением U определяется как и при включении катушки на это напряжение, т.е. 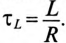
Если катушку с установившимся током I, зашунтированную сопротивлением Ro (рис. 20.2а), отключить от источника (разомкнуть ключ К), то в замкнутом контуре ABCD в начальный момент коммутации 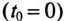 пройдет ток
пройдет ток 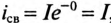 , т.е. установившийся ток. Этот ток I может оказаться недопустимо большим резистора с сопротивлением Ro.
, т.е. установившийся ток. Этот ток I может оказаться недопустимо большим резистора с сопротивлением Ro.
Для определения активного сопротивления катушки 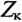 и полного ее сопротивления включают амперметр А и вольтметр V (рис. 20.26), т.е. вместо резистора с сопротивлением Ro в контур CD (рис. 20.26) включен вольтметр V. Этот вольтметр может не быть рассчитан на установившийся ток I, проходящий через него и размыкании ключа, в результате чего может сгореть. Чтобы «сжечь» вольтметр (рис. 20.26), сначала необходимо отключить вольтметр, а затем разомкнуть ключ К.
и полного ее сопротивления включают амперметр А и вольтметр V (рис. 20.26), т.е. вместо резистора с сопротивлением Ro в контур CD (рис. 20.26) включен вольтметр V. Этот вольтметр может не быть рассчитан на установившийся ток I, проходящий через него и размыкании ключа, в результате чего может сгореть. Чтобы «сжечь» вольтметр (рис. 20.26), сначала необходимо отключить вольтметр, а затем разомкнуть ключ К.
Как видно, за счет переходных процессов в цепях с индуктивностью возникают большие токи и напряжения. С этим необходимо считаться и учитывать при проектировании и эксплуатации цепей с индуктивностью.
Зарядка, разрядка и саморазрядка конденсатора
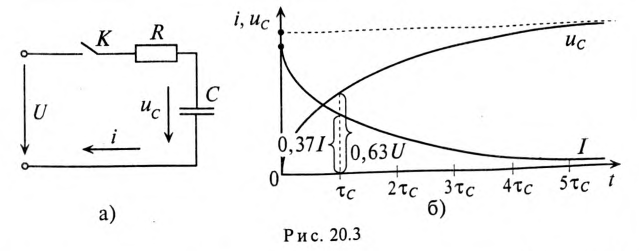
Если конденсатор с сопротивлением (утечки) R и емкостью С подключить к источнику с постоянным напряжением U (замыканием ключа К), то в цепи (рис. 20.3а) появится ток зарядки конденсатора (см. (11.16)):

где 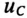 – напряжение на конденсаторе в любой момент времени переходного процесса.
– напряжение на конденсаторе в любой момент времени переходного процесса.
По второму закону Кирхгофа для цепи зарядки конденсатора (рис. 20.3а) можно записать уравнение
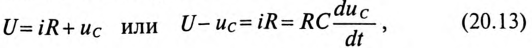
где произведение RC имеет размерность времени, обозначается буквой 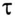 и называется постоянной времени переходного процесса в RC-цепи, т. е.
и называется постоянной времени переходного процесса в RC-цепи, т. е.

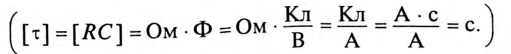
Уравнение (20.13) можно записать в виде

Если в уравнении (20.15) разделить переменные, проинтегрировать, а затем спотенцировать, то получится выражение
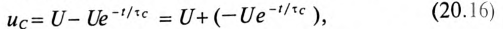
где U — установившееся напряжение 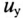 RC-цепи;
RC-цепи; 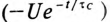 -свободная составляющая напряжения
-свободная составляющая напряжения 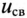 на конденсаторе; т.е.
на конденсаторе; т.е. 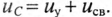
Следовательно, напряжение на заряжающемся конденсаторе в любой момент времени t переходного процесса определяется выражением

По (20.17), пользуясь Приложением 9, можно определить, что за время t=  конденсатор зарядится до напряжения
конденсатор зарядится до напряжения 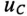 = 0,63 U, а за время t=4,6
= 0,63 U, а за время t=4,6 — до напряжения
— до напряжения 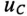 =0,99U.
=0,99U.
Теоретически зарядка конденсатора длится бесконечно долю а практически конденсатор считается заряженным, когда напряжение на нем достигает 99 % напряжения источника U.
Таким образом, и в RC-цепи, чем больше постоянная времени  , тем больше времени t тратится на зарядку конденсатор, т. е. и в данном случае постоянная времени
, тем больше времени t тратится на зарядку конденсатор, т. е. и в данном случае постоянная времени  характеризует дли тельность зарядки и разрядки конденсатора.
характеризует дли тельность зарядки и разрядки конденсатора.
Ток i при зарядке конденсатора (см. (20.13)) уменьшается по за кону
(20. IS)

где 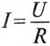 – максимальный ток, который имеет место в начальный момент t=0 зарядки конденсатора (момент коммутации).
– максимальный ток, который имеет место в начальный момент t=0 зарядки конденсатора (момент коммутации).
За время t= ток в цепи заряжающегося конденсатора уменьшится до 0,37 I, а за время t= 4,6
ток в цепи заряжающегося конденсатора уменьшится до 0,37 I, а за время t= 4,6 — до 0,01 I, при котором переходный процесс можно считать законченным.
— до 0,01 I, при котором переходный процесс можно считать законченным.
Графики изменения напряжения на конденсаторе и тока в цепи арядки конденсатора изображены на рис. 20.36.
Если конденсатор емкостью С, заряженный предварительно до напряжения U, разряжать через резистор с сопротивлением R рис. 20.4а), то напряжение 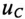 на конденсаторе и ток в цепи разрядки будут уменьшаться по закону
на конденсаторе и ток в цепи разрядки будут уменьшаться по закону

где U — напряжение на конденсаторе до начала разрядки (при t= 0), а 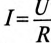 – максимальный ток в начальный момент разрядки R (при t=0),
– максимальный ток в начальный момент разрядки R (при t=0),  = RC – постоянная времени в цепи разрядки конденсатора.
= RC – постоянная времени в цепи разрядки конденсатора.
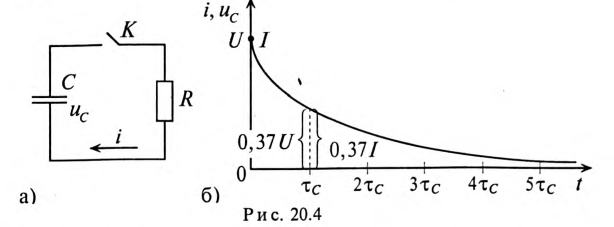
За время t=  напряжение и ток уменьшатся до 37 % своих максимальных значений. Изменение напряжения и тока на разряжающемся конденсаторе показаны на рис. 20.46 (в разных масштабах).
напряжение и ток уменьшатся до 37 % своих максимальных значений. Изменение напряжения и тока на разряжающемся конденсаторе показаны на рис. 20.46 (в разных масштабах).
Если конденсатор емкостью С, заряженный до напряжения U, отсоединить от источника, то он будет разряжаться через свой диэлектрик. Напряжение на нем будет уменьшаться по закону 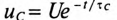 . Процесс разрядки конденсатора через свой диэлектрик называется саморазрядом.
. Процесс разрядки конденсатора через свой диэлектрик называется саморазрядом.
Постоянная времени саморазряда зависит от физических свойств диэлектрика

где р — удельное сопротивление диэлектрика; 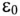 — электрическая постоянная;
— электрическая постоянная; 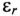 — диэлектрическая проницаемость диэлектрика (относительная).
— диэлектрическая проницаемость диэлектрика (относительная).
Для определения напряжения, тока, ЭДС в любой момент переходного процесса 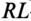 -цепи и
-цепи и 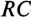 -цепи можно воспользоваться таблицей показательных функций (Приложение 9).
-цепи можно воспользоваться таблицей показательных функций (Приложение 9).
Пример 20.1
Катушка электромагнита с параметрами 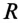 =11 Ом и
=11 Ом и 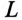 = 0,11 мГн подключена к сети постоянного тока с напряжением
= 0,11 мГн подключена к сети постоянного тока с напряжением 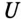 =110 В. Определить время t, за которое ток в катушке i увеличится от нуля до 8 А. Определить, какого значение достигнет ЭДС самоиндукции eL за время t.
=110 В. Определить время t, за которое ток в катушке i увеличится от нуля до 8 А. Определить, какого значение достигнет ЭДС самоиндукции eL за время t.
Решение
Установившийся ток 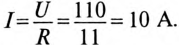
Постоянная времени для катушки 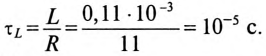
Подставляем значение величин в (20.10):
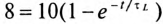 , откуда
, откуда 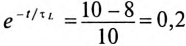 .
.
По Приложению 9 определяется 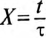 = 1,6, откуда
= 1,6, откуда
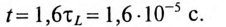
ЭДС самоиндукции за время 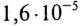 с уменьшается со 110 В до значения
с уменьшается со 110 В до значения
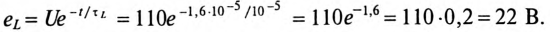
Пример 20.2
К зажимам катушки индуктивности с параметрами 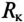 = 100 Ом,
= 100 Ом, 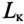 = 10 Гн подключен вольтметр V (рис. 20.26) электродинамической системы. Сопротивление вольтметра
= 10 Гн подключен вольтметр V (рис. 20.26) электродинамической системы. Сопротивление вольтметра 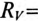 5000 Ом. Напряжение на клеммах источника U= 200 В.
5000 Ом. Напряжение на клеммах источника U= 200 В.
Определить напряжение на зажимах вольтметра и ток в обмотках прибора (обмотки соединены последовательно) при t=0, если размыкание рубильника К произойдет мгновенно и дуги не возникнет.
Решение
До размыкания рубильника через катушку проходил ток
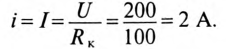
В момент размыкания рубильника (t = 0) весь этот ток проходит обмоткам вольтметра. При этом на вольтметре напряжение cтанет равным
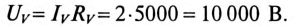
Такого напряжения (10 кВ) и такого тока (2 А) обмотка вольтметра (обычно подвижная обмотка электродинамического прибора рассчитана на ток порядка десятков, максимум, сотен миллиампер) не выдержит и сгорит.
При размыкании рубильника с конечной скоростью между расходящимися контактами рубильника К (рис. 20.26) возникнет электрическая дуга. Это приведет к тому, что увеличение напряжения на вольтметре и тока через обмотки вольтметра будет меньше, чем в рассмотренном выше случае (мгновенное размыкание рубильника). Однако меры предосторожности для сохранения вольтметра и рубильника, описанные выше, нужно соблюдать.
Пример 20.3
Конденсатор емкостью С= 2 мкФ через сопротивление R= 500 кОм подключается к источнику с постоянным напряжением U= 220 В.
Определить напряжение на конденсаторе 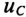 и ток в цепи заряда конденсатора i через 2 с от начала заряда конденсатора t= 2 с), а также время t’, за которое этот конденсатор зарядится р напряжения Uc= 150 В.
и ток в цепи заряда конденсатора i через 2 с от начала заряда конденсатора t= 2 с), а также время t’, за которое этот конденсатор зарядится р напряжения Uc= 150 В.
Решение
Постоянная времени заряда конденсатора
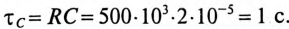
Напряжение на конденсаторе через 2 с от начала заряда
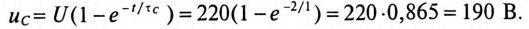
Ток в цепи заряда конденсатора через 2 с от начала заряда
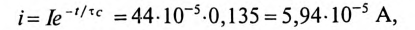
так как 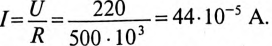
Время t’ заряда конденсатора до напряжения 150 В определяется по формуле (20.17):
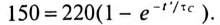
Откуда 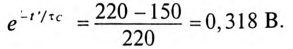
Из таблицы показательных функций (Приложение 9) находят t’= 1,14 с.
Пример 20.4
Параметры цепи, изображенной на рис. 20.5, следующие: 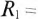
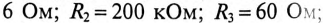
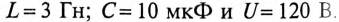
Определить значение токов в ветвях через время t= 2 с после замыкания ключа К.
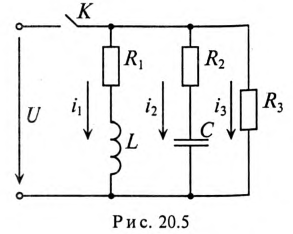
Решение
Для ветви (1) с индуктивностью определяются:
установившийся ток 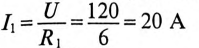
и постоянная времени 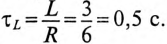
Тогда ток через 2 с будет равен
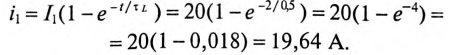
Для ветви (2) с емкостью определяются:
максимальный установившийся ток по окончании переходного процесса
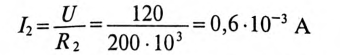
и постоянная времени 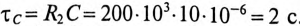 .
.
Тогда ток зарядки через 2 с будет равен
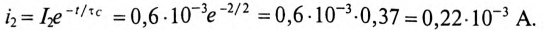
Для ветви (3) с активным сопротивлением 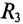 определяется ток ветви
определяется ток ветви
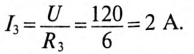
Постоянная времени 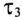 = 0, так как отсутствуют L и С.
= 0, так как отсутствуют L и С.
Через 2 с значение тока будет таким же, т. е. 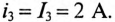
Переходные процессы в электрических цепях. Классический метод расчета
Возникновение переходных процессов:
В предыдущих главах рассматривались установившиеся процессы в линейных электрических цепях, т. е. такие процессы, при которых напряжения и токи либо неизменны во времени (цепи постоянного тока), либо представляют собой периодические функции времени (цепи переменного тока).
Наступлению установившегося процесса, отличного от первоначального режима работы цепи, предшествует, как правило, переходный процесс, при котором напряжения и токи изменяются непериодически.
Переход от одного режима работы цепи к другому может быть вызван изменением параметров или схемы цепи, называемым в общем случае в электротехнике коммутацией.
Можно теоретически считать, что коммутация цепи производится мгновенно, т. е. на включение, выключение или переключение цепи время не расходуется. Тем не менее переход от исходного режима работы цепи к последующему установившемуся процессу происходит не мгновенно, а в течение некоторого времени. Объясняется это тем, что каждому состоянию цепи соответствует определенный запас энергии электрических и магнитных полей. Переход к новому режиму связан с нарастанием или убыванием энергии этих полей. Энергия 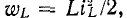 запасаемая в магнитном поле индуктивности L, и энергия
запасаемая в магнитном поле индуктивности L, и энергия 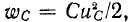 запасаемая в электрическом поле емкости С, не могут изменяться мгновенно: энергия может изменяться непрерывно, без скачков, так как в противном случае мощность, равная производной энергии по времени, достигала бы бесконечных значении, что физически невозможно. Именно поэтому, например, в случае размыкания ветви с индуктивной катушкой в месте размыкания неизбежно возникает искра, в сопротивлении которой расходуется энергия, накопленная в магнитном поле индуктивной катушки. Аналогично если замкнуть накоротко выводы конденсатора, который был предварительно заряжен, то запасенная в нем электрическая энергия рассеется в сопротивлении соединяющего провода и между контактами.
запасаемая в электрическом поле емкости С, не могут изменяться мгновенно: энергия может изменяться непрерывно, без скачков, так как в противном случае мощность, равная производной энергии по времени, достигала бы бесконечных значении, что физически невозможно. Именно поэтому, например, в случае размыкания ветви с индуктивной катушкой в месте размыкания неизбежно возникает искра, в сопротивлении которой расходуется энергия, накопленная в магнитном поле индуктивной катушки. Аналогично если замкнуть накоротко выводы конденсатора, который был предварительно заряжен, то запасенная в нем электрическая энергия рассеется в сопротивлении соединяющего провода и между контактами.
Если исключить случаи размыкания индуктивности и замыкания накоротко емкости и рассматривать цепи, в которых энергия, накапливаемая в магнитном или электрическом поле, может рассеиваться в виде теплоты в сопротивлениях, то, считая, что коммутация происходит мгновенно, можно искрообразование не учитывать.
Для завершения переходного и наступления установившегося процессов теоретически требуется бесконечно большое время. Практически, однако, время переходного процесса определяется малым интервалом, по истечении которого токи и напряжения настолько приближаются к установившимся значениям, что разница оказывается практически неощутимой. Чем интенсивнее происходит рассеяние энергии в сопротивлениях, тем быстрее протекает переходный процесс.
Если бы электрическая цепь состояла только из сопротивлений и не содержала индуктивностей и емкостей, то переход от одного установившегося состояния к другому совершался бы мгновенно, без затраты времени. В реальных электротехнических устройствах тепловые потери, обусловленные током, магнитные и электрические поля сопутствуют друг другу. Применяя специальные схемы и подбирая соответствующие параметры цепи, можно в зависимости от необходимости ускорить или замедлить переходный процесс.
В одних случаях переходные процессы в электрических цепях нежелательны и опасны (например, при коротких замыканиях в энергетических системах). В других случаях переходный процесс представляет собой естественный, нормальный режим работы цепи, как это, например, имеет место в радиопередающих и радиоприемных устройствах, системах автоматического регулирования и других цепях.
Существуют различные методы расчета переходных процессов в линейных электрических цепях. Настоящая глава посвящена классическому методу решения дифференциальных уравнений, описывающих переходные процессы.
Законы коммутации и начальные условия
Высказанные выше положения о том, что запас энергии магнитного или электрического поля может изменяться только плавно, без скачков, выражают принцип непрерывности во времени потокосцепления индуктивности и электрического заряда емкости и называются законами коммутации.
Невозможность скачкообразного изменения потокосцепления следует из того, что в противном случае на индуктивности появилось бы бесконечно большое напряжение 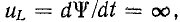 что лишено физического смысла. Ввиду равенства
что лишено физического смысла. Ввиду равенства 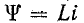 принцип непрерывности потокосцепления означает, что при неизменном L ток i не может изменяться скачком. Итак, в начальный момент после коммутации ток в индуктивности остается таким же, каким он был непосредственно перед коммутацией, а затем плавно изменяется.
принцип непрерывности потокосцепления означает, что при неизменном L ток i не может изменяться скачком. Итак, в начальный момент после коммутации ток в индуктивности остается таким же, каким он был непосредственно перед коммутацией, а затем плавно изменяется.
Аналогично невозможность скачкообразного изменения электрического заряда q следует из того, что в противном случае через емкость проходил бы бесконечно большой ток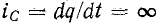 , что также лишено физического смысла. Ввиду равенства
, что также лишено физического смысла. Ввиду равенства 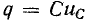 принцип непрерывности электрического заряда означает, что при неизменном С напряжение
принцип непрерывности электрического заряда означает, что при неизменном С напряжение 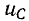 не может изменяться скачком. Итак, в начальный момент после коммутации напряжение на емкости остается таким же, каким оно было непосредственно перед коммутацией, а затем плавно изменяется.
не может изменяться скачком. Итак, в начальный момент после коммутации напряжение на емкости остается таким же, каким оно было непосредственно перед коммутацией, а затем плавно изменяется.
При этом следует отметить, что в цепях с идеализированными сосредоточенными параметрами скачкообразно могут изменяться: 1) токи в сопротивлениях и емкостях и 2) напряжения на сопротивлениях и индуктивностях.
Значения тока в индуктивности и напряжения на емкости в момент коммутации называются независимыми начальными условиями.
Обычно принимают, что коммутация происходит в момент времени t= 0; тогда ток в индуктивности и напряжение на емкости в момент времени непосредственно перед коммутацией обозначаются через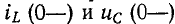 а в начальный момент переходного процесса после коммутации — через
а в начальный момент переходного процесса после коммутации — через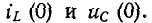
На основании законов коммутации:
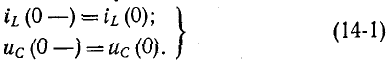
Эти равенства выражают начальные условия цепи, в которых происходит коммутация.
При нулевых начальных условиях, т. е. косца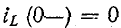
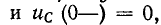 индуктивность в начальный момент после коммутации равносильна разрыву цепи, а емкость равносильна короткому замыканию.
индуктивность в начальный момент после коммутации равносильна разрыву цепи, а емкость равносильна короткому замыканию.
В случае ненулевых начальных условий, т. е. когда 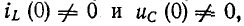 индуктивность в первый момент равносильна источнику тока
индуктивность в первый момент равносильна источнику тока 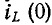 , а емкость равносильна источнику э. д. с.
, а емкость равносильна источнику э. д. с. 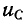 (0).
(0).
Независимые начальные условия характеризуют энергию магнитного и электрического полей, запасенную к моменту коммутации, и для расчета переходного процесса обязательно требуется знание этих начальных условий, причем совершенно безразлично, каким образом эти условия в цепи были созданы.
При расчете переходных процессов в разветвленных электрических цепях наряду с независимыми начальными условиями используются так называемые зависимые начальные условия, а именно: значения токов, напряжений и их производных в начальный момент времени (t = 0).
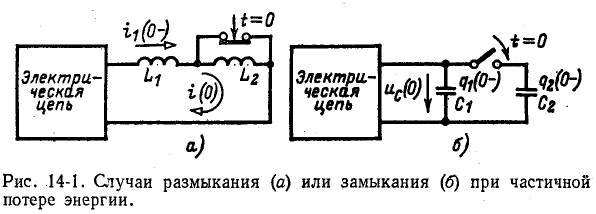
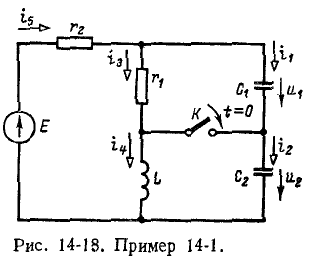
До сих пор нами исключались из рассмотрения случаи коммутации, при которых неизбежно между контактами возникает искра или дуга. Один из таких случаев показан на рис. 14-1, а. До коммутации ток проходит через индуктивность 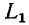 и контакт, шунтирующий индуктивность
и контакт, шунтирующий индуктивность 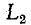 ток в
ток в 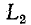 равен нулю. В момент t = 0 контакт размыкается и индуктивности
равен нулю. В момент t = 0 контакт размыкается и индуктивности 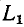 и
и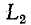 оказываются включенными последовательно; ток в них принудительно становится одинаковым. Поскольку в момент коммутации ток в
оказываются включенными последовательно; ток в них принудительно становится одинаковым. Поскольку в момент коммутации ток в 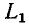 не изменяется, а ток в
не изменяется, а ток в 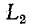 равен нулю, в силу первого закона Кирхгофа ток должен замкнуться через дугу, образовавшуюся между контактами. Кроме того, если под
равен нулю, в силу первого закона Кирхгофа ток должен замкнуться через дугу, образовавшуюся между контактами. Кроме того, если под 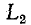 подразумевать реальную индуктивную катушку, то ток может частично
подразумевать реальную индуктивную катушку, то ток может частично
замкнуться и через межвитковую емкость. После быстрого погасания дуги токи в 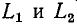 уравниваются. Эта начальная стадия переходного процесса протекает столь быстро, что ею практически можно пренебречь, считая, что токи в
уравниваются. Эта начальная стадия переходного процесса протекает столь быстро, что ею практически можно пренебречь, считая, что токи в 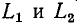 уравниваются мгновенно. Именно в этом смысле можно условно говорить о скачкообразном изменении токов в индуктивностях, которое предшествует исследуемому переходному процессу в цепи. При этом для расчета переходного процесса используется принцип непрерывности суммарного потокосцепления при коммутации, т. е.
уравниваются мгновенно. Именно в этом смысле можно условно говорить о скачкообразном изменении токов в индуктивностях, которое предшествует исследуемому переходному процессу в цепи. При этом для расчета переходного процесса используется принцип непрерывности суммарного потокосцепления при коммутации, т. е. 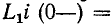
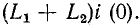 . Скачкообразное изменение токов и соответствующих им потоков в Lx и L2 в момент коммутации не сопряжено в данном случае с наведением бесконечно большой суммарной э. д. с. самоиндукции, поскольку суммарное лотокосцепление не претерпевает скачкообразного изменения. При новых значениях токов в
. Скачкообразное изменение токов и соответствующих им потоков в Lx и L2 в момент коммутации не сопряжено в данном случае с наведением бесконечно большой суммарной э. д. с. самоиндукции, поскольку суммарное лотокосцепление не претерпевает скачкообразного изменения. При новых значениях токов в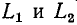 магнитная энергия, запасенная в катушках, будет меньше энергии, запасенной в первой катушке до коммутации. Часть энергии превратится в тепло в искре, а также излучится.
магнитная энергия, запасенная в катушках, будет меньше энергии, запасенной в первой катушке до коммутации. Часть энергии превратится в тепло в искре, а также излучится.
Найденный таким образом ток 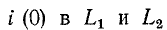 может рассматриваться как независимое начальное условие для расчета переходного процесса во всей цепи на рис. 14-1, а после разрыва дуги.
может рассматриваться как независимое начальное условие для расчета переходного процесса во всей цепи на рис. 14-1, а после разрыва дуги.
При коммутациях в цепях с емкостями при отсутствии сопротивлений также возможны весьма быстрые перераспределения зарядов, условно рассматриваемые как мгновенные. В этом случае применим принцип непрерывности суммарного заряда. Полученные при этом значения зарядов и напряжений на отдельных емкостях используются в расчете последующего переходного процесса как независимые начальные условия.
Например, в случае схемы на рис. 14-1, б принцип непрерывности суммарного заряда до и после коммутации выражается равенством
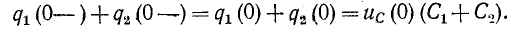
При сделанном допущении в остальной электрической цепи, соединенной с емкостями, не возникает бесконечно большого тока, так как суммарный заряд не изменяется скачкообразно при t=0.
В процессе рассматриваемой коммутации энергия электрического поля уменьшится, так как часть ее превратится в тепло в очень малом сопротивлении проводника при очень большом токе, а также сможет выделиться в искре и излучиться.
Установившийся и свободный режимы
В общем случае анализ переходного процесса в линейной цепи с сосредоточенными параметрами r, L, С и М сводится к решению обыкновенных линейных неоднородных дифференциальных уравнений, выражаюших законы Кирхгофа. Эти уравнения представляют собой линейную комбинацию напряжений, токов, их первых производных и интегралов по времени.
Например, если какая-нибудь э. д. с. е (t) включается в цепь, состоящую из последовательно соединенных r, L и С, то интегродифференциальное уравнение имеет вид:
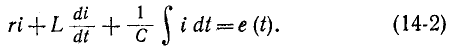
Это уравнение после дифференцирования приводится к неоднородному дифференциальному уравнению второго
порядка
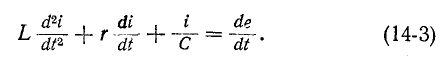
Как известно, общий интеграл такого^ уравнения равен сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Частное решение выражает установившийся режим, задаваемый источником.
Расчеты установившихся токов рассмотрены в предыдущих главах.
Общее решение физически определяет поведение цепи при отсутствии внешних источников электрической энергии и заданных начальных условиях. Функции, определяемые общим решением, называются свободными составляющими (токов, напряжений и пр.).
В случае, рассмотренном выше, однородное уравнение имеет вид:
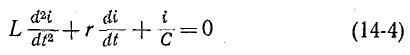
и соответствующее ему характеристическое уравнение
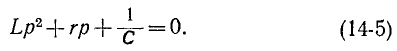
Если корни характеристического уравнения обозначить через 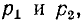 , то общее решение запишется в виде:
, то общее решение запишется в виде:
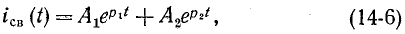
где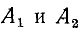 — постоянные интегрирования, которые определяются из начальных условий .
— постоянные интегрирования, которые определяются из начальных условий .
Полный переходный ток в цепи равен сумме установившегося и свободного токов:
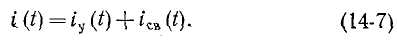
Аналогично напряжение, заряд, магнитный поток и другие функции на любом участке цепи в переходном режиме состоят из установившейся и свободной составляющих.
На основании законов коммутации можно найти начальные независимые условия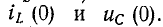 После этого можно написать согласно (14-7):
После этого можно написать согласно (14-7):
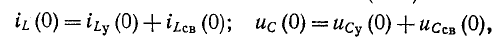
откуда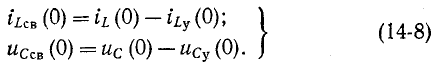
Итак, начальные значения свободных функций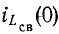 и
и 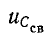 (0) определяются изменениями в момент коммутации соответствующих установившихся функций.
(0) определяются изменениями в момент коммутации соответствующих установившихся функций.
В частном случае при нулевых начальных условиях:
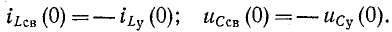
В зависимости от порядка дифференциальных уравнений, описывающих исследуемые переходные процессы, различают цепи первого, второго и более высокого порядков.
В цепях первого порядка накопление энергии происходит только в одном элементе, L или С в форме магнитной энергии, или электрической энергии . Одноконтурная цепь, содержащая элементы, в которых накапливается энергия обоих видов — магнитная « электрическая, представляет собой цепь второго порядка . Разветвленные цепи могут быть более высокого порядка.
Переходный процесс в цепи r, L
Положим, что в момент t = 0 цепь, состоящая из сопротивления r и индуктивности L, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-2).
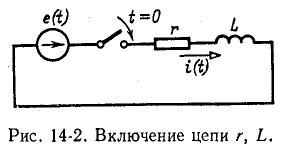
Дифференциальное уравнение для времени записывается в виде
записывается в виде
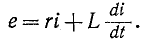
Характеристическое уравнение имеет вид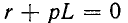 и соответственно корень уравнения
и соответственно корень уравнения 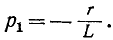
Отсюда свободный ток
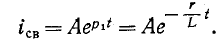
Переходный ток в цепи определится суммой установившегося и свободного токов:
Установившийся ток может быть найден, если задана э. д. с. е (t).
Рассмотрим три случая:
1) включение в цепь г, L постоянной э. д. с. £;
2) короткое замыкание цепи г, L
3) включение в цепь г, L синусоидальной э. д. с. 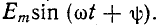
1. Включение в цепь г, L постоянной э. д. с.
При включении в цепь г, L постоянной э. д. с. Е установившийся ток равен Е’/г. Поэтому согласно (14-9)
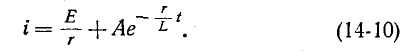
Постоянная интегрирования А находится по начальному условию
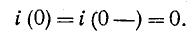
Согласно уравнению (14-10) при t — 0
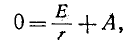
откуда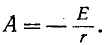 Следовательно,
Следовательно,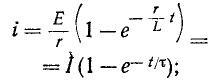
здесь 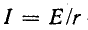 — предельное значение, к которому стремится ток i (t) по мере неограниченного возрастания t, называемое установившимся током.
— предельное значение, к которому стремится ток i (t) по мере неограниченного возрастания t, называемое установившимся током.
В начальный момент t = 0 э. д. с. самоиндукции 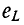 =
=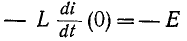 и полностью компенсируется э. д. с. источника, так как ток i (0) равен нулю.
и полностью компенсируется э. д. с. источника, так как ток i (0) равен нулю.
С течением времени э. д. с. самоиндукции убывает, а ток в цепи возрастает, асимптотически приближаясь к установившемуся значению.
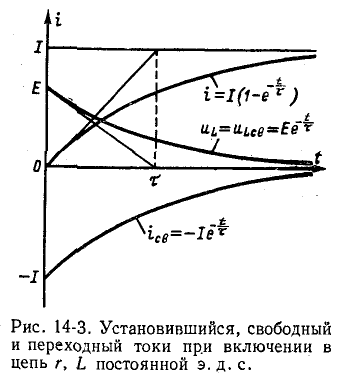
На рис. 14-3 показаны кривые установившегося, свободного и переходного токов; на том же рисунке изображена кривая напряжения на индуктивности
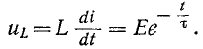
Из курса математического анализа известно, что если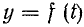 , то подкасательная равна
, то подкасательная равна 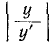 . В данном случае при любом значении t
. В данном случае при любом значении t
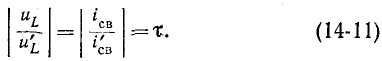
Величина 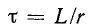 носит название постоянной времени. Постоянная времени измеряется в секундах:
носит название постоянной времени. Постоянная времени измеряется в секундах:
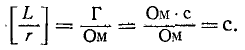
Выражение (14-11) показывает, что постоянная времени графически определяется длиной подкасательной к кривой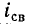 или
или 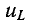 при любом значении t.
при любом значении t.
Нарастание тока происходит тем быстрее, чем меньше постоянная времени и соответственно чем быстрее убывает э. д. с. самоиндукции. Для различных моментов времени ток в цепи, выраженный в процентах конечного (установившегося) значения составляет:
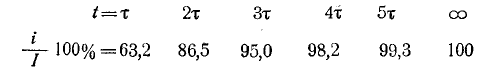
Следовательно, постоянная времени цепи г, L равна промежутку времени, в течение которого свободная составляющая тока убывает в е = 2,718 раза и соответственно ток в этой цепи, включенной на постоянное напряжение, достигает 63,2% своего установившегося значения.
Как видно из рис. 14-3 и приведенной выше таблицы”, переходный процесс теоретически длится бесконечно долго. Практически же можно считать, что он заканчивается спустя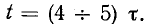
2. Короткое замыкание цепи r, L.
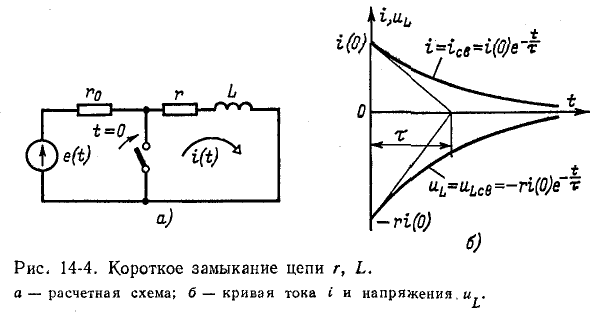
Положим, что цепь r, L, присоединенная к источнику постоянного или переменного напряжения, замыкается при t = 0 накоротко (рис. 14-4, а). В образовавшемся при этом контуре r, L благодаря наличию магнитного поля индуктивной катушки ток исчезает не мгновенно: э. д. с. самоиндукции, обусловленная убыванием магнитного потока, стремится поддержать ток в контуре за счет энергии исчезающего магнитного поля.
По мере того как энергия магнитного поля постепенно рассеивается, превращаясь в сопротивлении г в тепло, ток в контуре приближается к нулю.
Процесс, происходящий в короткозамкнутом контуре г, L, является свободным; установившийся ток в данном случае равен нулю.
Положив в (14-9)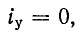 получим:
получим:
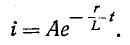
Постоянная интегрирования А находится из начального условия
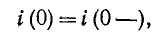
откуда
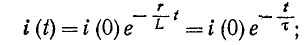
здесь i (0—) — значение тока в индуктивности в момент, непосредственно предшествовавший короткому замыканию; оно может быть положительным или отрицательным.
На рис. 14-4, б изображены кривые спада тока в короткозамкнутом контуре и кривая напряжения на индуктивности
 в предположении, что i (0) > 0.
в предположении, что i (0) > 0.
Постоянная времени контура 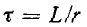 может быть найдена графически как подкасательная к кривой i (t) (например-, в момент t = 0).
может быть найдена графически как подкасательная к кривой i (t) (например-, в момент t = 0).
Переходный процесс в короткозамкнутом контуре заканчивается теоретически при 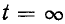 . За это время в сопротивлении г выделяется в виде тепла энергия
. За это время в сопротивлении г выделяется в виде тепла энергия
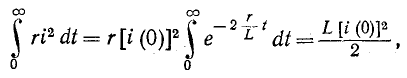
т. е. вся энергия, запасенная в магнитном поле катушки до коммутации.
Так же как и в предыдущем случае, переходный процесс в короткозамкнутом контуре можно практически считать законченным спустя 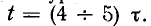
3. Включение в цепь r, L синусоидальной э. д. с.
При включении в цепь r, L синусоидальной э. д. с. 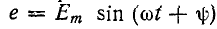 установившийся ток будет:
установившийся ток будет:
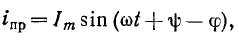
где
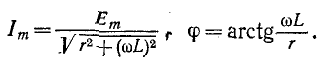
На основании (14-9)
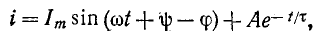
где
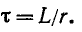
Постоянная интегрирования определяется по начальному условию 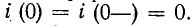
Следовательно, 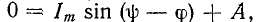 откуда А =
откуда А =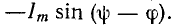 Поэтому искомый ток будет:
Поэтому искомый ток будет:
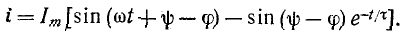
На рис. 14-5, а изображены кривые 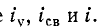 Начальные ординаты
Начальные ординаты 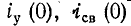 одинаковы и противоположны по знаку; поэтому ток в начальный момент равен нулю. Свободный ток убывает по показательному закону. По истечении времени
одинаковы и противоположны по знаку; поэтому ток в начальный момент равен нулю. Свободный ток убывает по показательному закону. По истечении времени 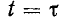 свободный ток уменьшается в е=2,718 раза по сравнению с начальным значением
свободный ток уменьшается в е=2,718 раза по сравнению с начальным значением 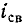 (0). Постоянная времени прямо пропорциональна добротности
(0). Постоянная времени прямо пропорциональна добротности
контура Q и обратно пропорциональна частоте 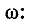
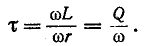
Если в момент коммутации (t = 0) ток 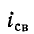 проходит через нуль, т. е. выполняется условие
проходит через нуль, т. е. выполняется условие 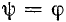 или
или 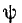 =
= 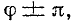 , то свободный ток не возникает и в цепи сразу наступает установившийся режим без переходного процесса.
, то свободный ток не возникает и в цепи сразу наступает установившийся режим без переходного процесса.
Если же коммутация происходит при 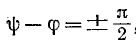 то начальный свободный ток максимален (рис. 14-5, б),
то начальный свободный ток максимален (рис. 14-5, б),
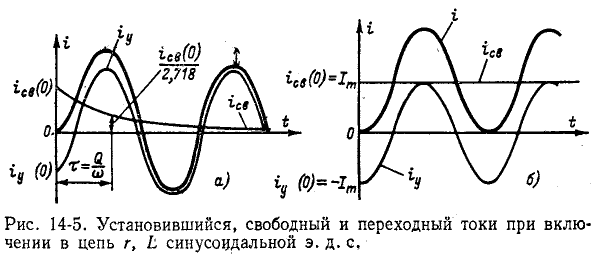
а именно  и ток переходного режима дости-
и ток переходного режима дости-
гает экстремального значения (положительного или отрицательного) в конце первого полупёриода. Однако даже в предельном случае, когда r= 0 и, следовательно, 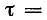
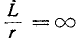 ток не может превышать амплитуды установившегося режима более чем вдвое.
ток не может превышать амплитуды установившегося режима более чем вдвое.
При достаточно большой постоянной времени 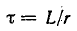 первым слагаемым в правой части дифференциального уравнения
первым слагаемым в правой части дифференциального уравнения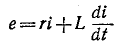
можно пренебречь по сравнению со вторым слагаемым, приняв приближенно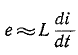 , откуда
, откуда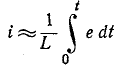 и соответственно
и соответственно 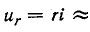
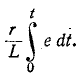
Следовательно, цепь с последовательно соединенными сопротивлением и индуктивностью при большой постоянной времени можно рассматривать как интегрирующее звено.
В свою очередь при достаточно малой постоянной времени, пренебрегая вторым слагаемым уравнения, приближенно получаем:
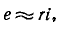
откуда
.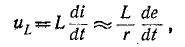
т. e. цепь с последовательно соединенными сопротивлением и индуктивностью при малой постоянной времени представляет собой дифференцирующее звено.
В обоих случаях функция е(t) может быть произвольной.
Интегрирующие и дифференцирующие звенья входят в качестве элементов в системы автоматического управления и регулирования.
Переходный процесс в цепи r, С
Положим, что в момент t = О цепь, состоящая из сопротивления г и емкости С, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-6).
На основании второго закона Кирхгофа уравнение для времени t 0 имеет вид:
0 имеет вид:
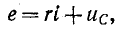
где 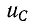 — напряжение на емкости.
— напряжение на емкости.
С учетом того, что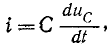
получим:
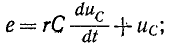
здесь искомой величиной является напряжение на емкости.
Характеристическое уравнение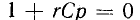 и соответственно корень уравнения
и соответственно корень уравнения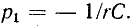 Следовательносвободная слагающая напряжения на емкости
Следовательносвободная слагающая напряжения на емкости
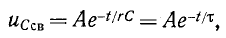 где
где 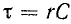 — постоянная времени контура r, С (измеряется в секундах:
— постоянная времени контура r, С (измеряется в секундах: 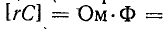
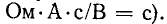
Переходное напряжение на емкости равно сумме принужденного и свободного напряжений:
В свою очередь ток в контуре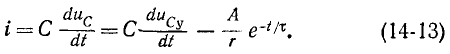
Рассмотрим три случая:
1) включение в цепь г, С постоянной э. д. с.
2) короткое замыкание цепи r, С
3) включение в цепь r, С синусоидальной э. д. с.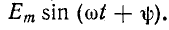
Включение в цепь r, С постоянной э. д. с.
Включим постоянную э. д. с. Е в цепь с сопротивлением г и предварительно заряженной емкостью С (полярности заряженной емкости указаны на рис. 14-6 знаками + и —); начальное напряжение на емкости
(0) обозначим для простоты через U.
Установившееся напряжение на емкости равно э. д. с. источника. Поэтому согласно (14-12)

Постоянная интегрирования А, входящая в (14-14), находится по начальному условию:
При t = 0 имеем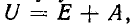 откуда
откуда 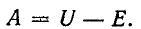 Следовательно,
Следовательно,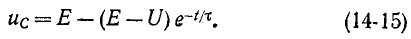
Согласно (14-13) ток в контуре
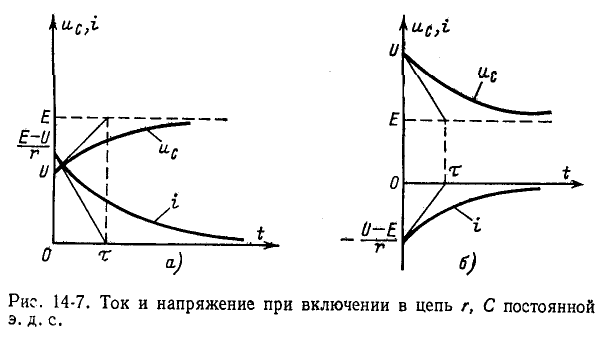
Если Е > U, то с течением времени напряжение на емкости возрастает, стремясь к установившемуся значению Е, а ток убывает, стремясь в пределе к нулю; на рис. 14-7, а изображены кривые нарастания 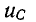 и спада i. Чем больше постоянная времени, тем медленнее происходят нарастание
и спада i. Чем больше постоянная времени, тем медленнее происходят нарастание 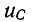 и спад i.
и спад i.
Если Е < U, то кривые 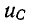 и i имеют вид, показанный на рис. 14-7, б.
и i имеют вид, показанный на рис. 14-7, б.
Постоянная времени 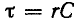 может быть найдена так же, как раньше, графически как подкасательная к кривой i в любой точке (например, при t = 0).
может быть найдена так же, как раньше, графически как подкасательная к кривой i в любой точке (например, при t = 0).
Закон изменения напряжения на емкости и тока в данной цепи аналогичен закону изменения тока и напряжения 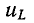 в контуре r, L, рассмотренном ранее. Поэтому все сказанное о постоянной времени в предыдущем случае сохраняет силу для данного случая.
в контуре r, L, рассмотренном ранее. Поэтому все сказанное о постоянной времени в предыдущем случае сохраняет силу для данного случая.
Короткое замыкание цепи r, С
Замыкание накоротко цепи, состоящей из последовательно соединенных г и С, равносильно принятию в предыдущем случае э. д. с., равной нулю. Предполагается, что емкость С заряжена, т. е. в момент включения на выводах имеется напряжение U.
Положив в (14-15) и (14-16) э. д. с. Е равной нулю, получим:
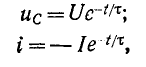
где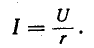
При коротком замыкании цепи r, С электрический ток идет от вывода + к выводу — Следовательно, при выбранной на рис. 14-6 полярности емкости ток проходит через сопротивление r в направлении, противоположном тому, которое принято на рис. 14-6 за положительное. Поэтому в выражении для тока стоит знак минус. На рис. 14-8 изображены кривые спала 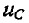 и i.
и i.
В отличие от напряжения на емкости, которое изменяется непрерывно, ток в контуре r, С, пропорциональный скорости изменения 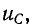 совершает при t = 0 скачок.
совершает при t = 0 скачок.
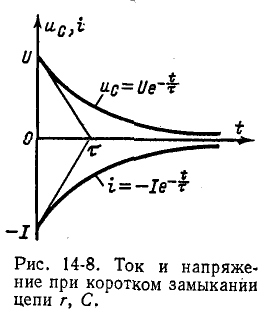
Энергия, рассеиваемая в сопротивлении г в течение всего переходного процесса, равна энергии, запасенной в электрическом поле до коммутации:
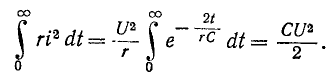
Так же как и в случае цепи r, L, переходный процесс может считаться законченным спустя 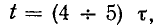 так как
так как
к этому времени емкость разрядится на 98,2—99,3% и напряжение на емкости снизится до 1,8—0,7% первоначального.
Включение в цепь г, С синусоидальной э. д. с.
При включении в цепь r, С синусоидальной э. д. с. установившееся напряжение на емкости
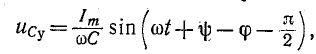
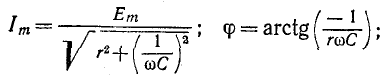
на основании (14-12)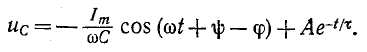
Если предполагать, что конденсатор не был заряжен, то постоянная интегрирования определится по начальному условию 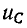 (0) = 0:
(0) = 0:
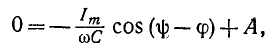
откуда
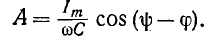
Тогда искомое напряжение на емкости будет: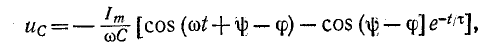
а ток в цепи
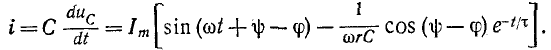
Из написанных выражений видно, что если включение цепи r, С происходит в момент, когда установившийся ток должен достигать максимума — положительного или
отрицательного (т. е. 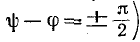 а установившееся
а установившееся
напряжение на емкости должно быть равно нулю, то свободной слагающей напряжения на емкости не возникает и в цепи сразу же без переходного процесса наступает установившийся режим.
Так как цепь г, С по протеканию переходного процесса подобна цепи г, L, то при соответствующем подборе параметров г и С она также может служить дифференцирующим и интегрирующим звеном.
Переходный процесс в цепи r, L, С
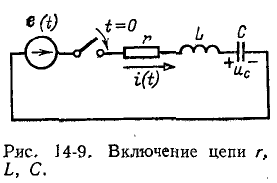
При включении в цепь г, L, С э. д. с. е (t) (рис. 14-9) переходный процесс исследуется с помощью дифференциального уравнения (14-3):
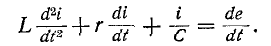
Соответствующее ему характеристическое уравнение (14-5)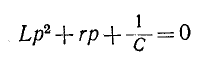
имеет корни
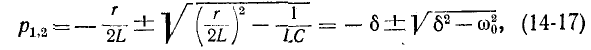
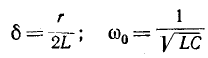 -резонансная частота.
-резонансная частота.
Свободный ток согласно (14-6) равен:
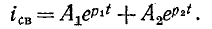
Ток в цепи определяется суммой установившегося и свободного токов:
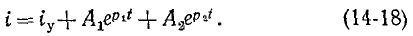
Установившийся ток находится в соответствии с заданной э. д. с. е (t). Что касается свободного тока, то его характер зависит от знака подкоренного выражения (14-17).
Включение в цепь г, L, С постоянной э. д. с.
Рассмотрим сначала случай, когда э. д. с. источника постоянна: е = Е, и емкость имеет начальное напряжение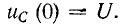
Ввиду наличия индуктивности начальное значение тока i (0) = 0.
Исходное уравнение
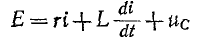
для начального момента записывается в виде
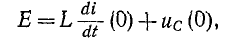
откуда находится начальное значение производной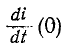 ,
,
которое является зависимым начальным условием, необходимым для вычисления 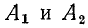 :
:

При установившемся режиме ток будет равен нулю, что следует как из физического смысла, так и из вида правой части дифференциального уравнения (14-3). Продифференцировав (14-18) с учетом того, что 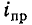 = 0, получим:
= 0, получим:
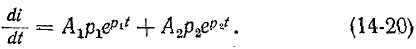
Подставляя в (14-18) и (14-20) t = 0 и используя (14-19), получаем:
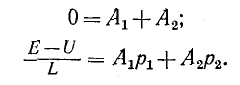
Из этих уравнений следует:
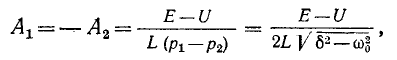
поэтому
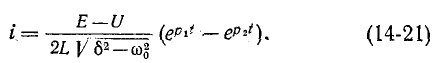
Рассмотрим возможные три случая.
Случай 1. 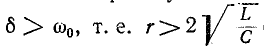 {апериодический процесс).
{апериодический процесс).
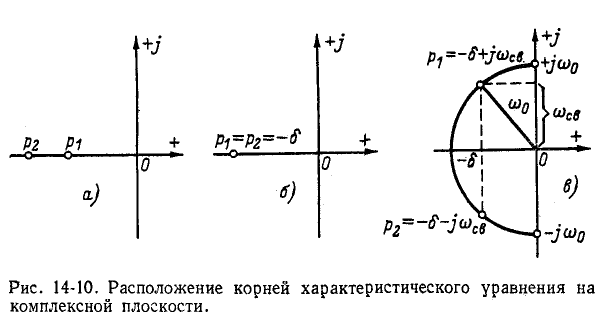
Согласно (14-17) корни характеристического уравнения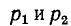 — отрицательные действительные числа (рис. 14-10, а). Если индекс 1 соответствует верхнему знаку перед корнем, т0
— отрицательные действительные числа (рис. 14-10, а). Если индекс 1 соответствует верхнему знаку перед корнем, т0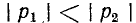 и поэтому кривая
и поэтому кривая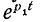 спадает медленнее, чем
спадает медленнее, чем 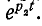 На рис. 14-11 показана кривая i, построенная по выражению (14-21).
На рис. 14-11 показана кривая i, построенная по выражению (14-21).
При больших значениях С влияние емкости мало и кривая тока приближается к кривой тока в цепи r, L (см. рис. 14-3); при малых значениях L влияние индуктивности незначительно и кривая тока близка к кривой тока в цепи г, С (рис. 14-7).
Выражение (14-21) может быть преобразовано в гиперболическую форму
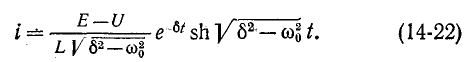
Следует заметить, что при коротком замыкании цепи г, L, С, т. е. при Е = О, ток в цепи обусловливается разрядом емкости.
Случай 2.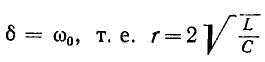 {критический случай).
{критический случай).
Согласно (14-17) корни характеристического уравнения одинаковы:
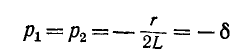
(см. рис. 14-10, б).
Выражение (14-21) приводит в этом случае к неопределенности вида 0/0.
Раскрывая неопределенность по правилу Лопиталя дифференцированием числителя и знаменателя по 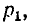 получаем:
получаем:
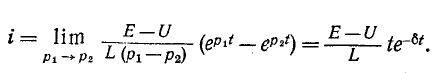
To же выражение получится, если воспользоваться общим решением однородного дифференциального уравнения с кратными корнями:
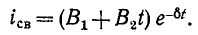
В рассматриваемом случае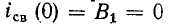 и
и
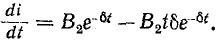
Следовательно,
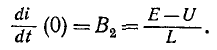
Кривая тока аналогична кривой i на рис. 14-11.
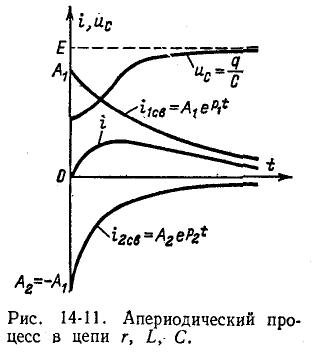
Случай 3. 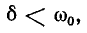 т. е.
т. е.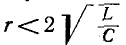 (колебательный процесс).
(колебательный процесс).
Корни характеристического уравнения комплексные и сопряженные:
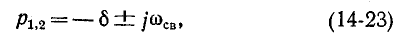

Согласно (14-24) 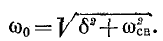
Корни характеристического уравнения располагаются симметрично относительно действительной оси в левой полуплоскости, на полуокружности, центр которой совпадает с началом координат, а радиус равен 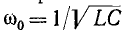 (см. рис. 14-10, в).
(см. рис. 14-10, в).
Сопоставление рис. 14-10, а, б к в показывает, что о характере переходного процесса в цени г, L, С можно судить по расположению корней характеристического уравнения, т. е. нулей функции Z (р), на комплексной плоскости.
Если расположенные в левой полуплоскости нули функции Z (р) лежат на действительной оси, то имеет место апериодический процесс: совмещению нулей в одной точке отвечает критический случай; наконец, если нули функции Z (р) являются комплексно-сопряженными, то имеет место колебательный процесс.
Величина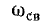 (рис. 14-10, в) называется угловой частотой свободных или собственных колебаний в цепи г, L, С, а
(рис. 14-10, в) называется угловой частотой свободных или собственных колебаний в цепи г, L, С, а 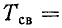
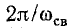 периодом этих колебаний Ток в цепи согласно (14-22)
периодом этих колебаний Ток в цепи согласно (14-22)
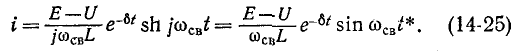
Полученное выражение показывает, что при включении цепи г, L, С на постоянное напряжение, когда 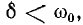 в цепи возникают затухающие синусоидальные колебания,причем огибающими кривой тока служат кривые:
в цепи возникают затухающие синусоидальные колебания,причем огибающими кривой тока служат кривые: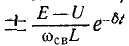
(рис. 14-12). Колебания возникают вследствие периодического преобразования энергии электрического поля в энергию
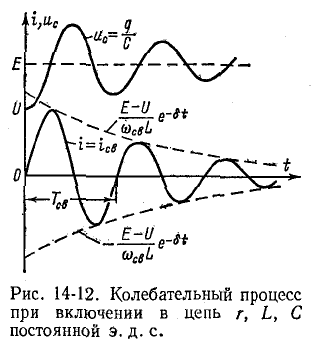
* Тот же результат получится, если исходить из общего решения однородного дифференциального уравнения с комплексно-сопряженными корнями:
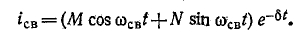
магнитного поля и обратно, причем эти колебания сопровождаются потерей энергии в сопротивлении.
При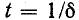 ордината огибающей в е = 2,718 раза меньше начального значения огибающей. Поэтому величину
ордината огибающей в е = 2,718 раза меньше начального значения огибающей. Поэтому величину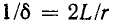 называют постоянной времени колебательного контура.
называют постоянной времени колебательного контура.
На рис. 14-12 показана также кривая напряжения 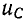 на емкости, которая в другом масштабе выражает также зависимость электрического заряда q от времени. Функции
на емкости, которая в другом масштабе выражает также зависимость электрического заряда q от времени. Функции 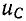 и i имеют одинаковый множитель затухания. При нулевых начальных условиях (U = 0) кривая
и i имеют одинаковый множитель затухания. При нулевых начальных условиях (U = 0) кривая 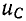 начинается с нуля.
начинается с нуля.
Как видно из (14-23) и рис. 14-10, в, угловая частота этих колебаний 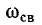 определяется абсолютным значением ординаты корня характеристического уравнения, которая при
определяется абсолютным значением ординаты корня характеристического уравнения, которая при 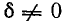 всегда меньше резонансной частоты
всегда меньше резонансной частоты 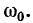
Чем меньше 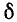 по сравнению с
по сравнению с 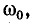 , тем медленнее затухает колебательный процесс и тем больше частота собственных колебаний цепи г, L, С приближается к резонансной частоте.
, тем медленнее затухает колебательный процесс и тем больше частота собственных колебаний цепи г, L, С приближается к резонансной частоте.
В пределе, при 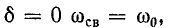 колебания не затухают и корни характеристического уравнения располагаются на мнимой оси (см. рис. 14-10, в).
колебания не затухают и корни характеристического уравнения располагаются на мнимой оси (см. рис. 14-10, в).
О быстроте затухания колебательного процесса судят по величине 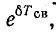 называемой декрементом колебания, или величине 8
называемой декрементом колебания, или величине 8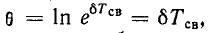 называемой логарифмическим декрементом колебания.
называемой логарифмическим декрементом колебания.
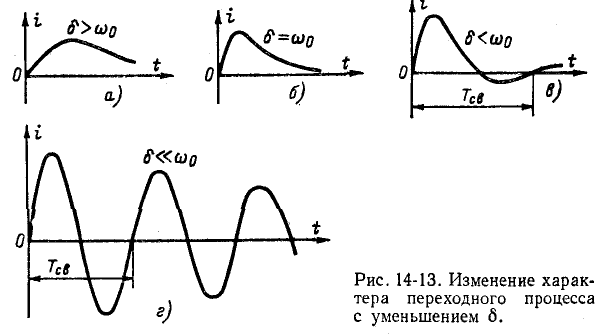
На рис. 14-13, а—г показано изменение характера переходного процесса при уменьшении 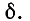
Приведенные выше величины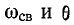 связаны с параметрами последовательного резонансного контура — добротностью
связаны с параметрами последовательного резонансного контура — добротностью 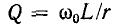 и затуханием d = 1 /Q,:
и затуханием d = 1 /Q,:
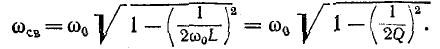
При достаточно высокой добротности 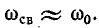 В этом случае
В этом случае 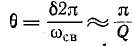
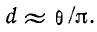 Для контура среднего качества
Для контура среднего качества 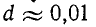 и логарифмический декремент
и логарифмический декремент 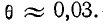 .
.
Включение в цепь г, L, С синусоидальной э. д. с.
Если цепь г, L, С присоединяется к источнику синусоидальной э. д. с.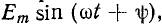 , то установившийся
, то установившийся
ток равен:
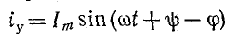
и переходный ток согласно (14-18) равен:
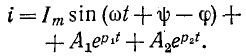
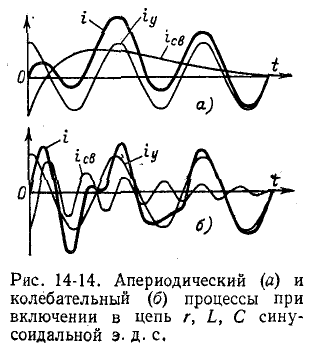
Кривые установившегося, свободного и- переходного токов при апериодическом и колебательном процессах показаны в виде примера на рис. 14-14.
Частота установившегося тока равна частоте источника синусоидального напряжения, свободный же ток при 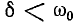 изменяется с собственной частотой цепи
изменяется с собственной частотой цепи 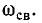 Частота
Частота 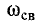 может быть в зависимости от параметров r, L и С меньше, больше или равна частоте
может быть в зависимости от параметров r, L и С меньше, больше или равна частоте 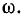
Свободные колебания тока накладываются на установившийся ток и затухают пропорционально множителю 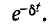 По мере затухания свободного тока кривая переходного тока приближается к кривой установившегося тока.
По мере затухания свободного тока кривая переходного тока приближается к кривой установившегося тока.
Та из двух слагающих тока i, частота которой меньше, служит как бы криволинейной осью для другой слагающей, колеблющейся относительно нее (рис. 14-14, б). При близком совпадении частот 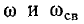 в цепи возникают биения.
в цепи возникают биения.
Расчет переходного процесса в разветвленной цепи
Переходный процесс в разветвленной линейной электрической цепи описывается системой линейных дифференциальных уравнений с постоянными коэффициентами, общее решение которых находится как сумма установившейся и свободной составляющих.
Рассмотрим сначала методику расчета установившегося режима.
Во многих случаях воздействующая функция, например
э. д. с. источника, может быть представлена в обобщенной форме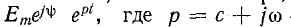 — комплексное число. В зависимости от значений буквенных величин, входящих в приведенное выражение, получается тот или иной закон изменения э. д. с., причем мгновенные значения э. д. с. определяются мнимой или действительной частью выражения.
— комплексное число. В зависимости от значений буквенных величин, входящих в приведенное выражение, получается тот или иной закон изменения э. д. с., причем мгновенные значения э. д. с. определяются мнимой или действительной частью выражения.
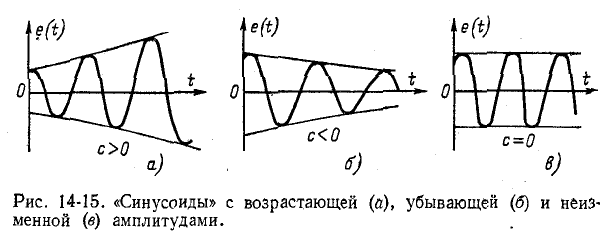
Условие 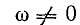 соответствует гармонической э. д. с. с возрастающей (с > 0), убывающей (с < 0) или неизхменной (с = 0) амплитудой (рис. 14-15).
соответствует гармонической э. д. с. с возрастающей (с > 0), убывающей (с < 0) или неизхменной (с = 0) амплитудой (рис. 14-15).
Условие 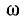 = 0 соответствует возрастающей (с > 0) или убывающей (с < 0) показательной функции; при с = 0 э. д. с. постоянна (рис. 14-16).
= 0 соответствует возрастающей (с > 0) или убывающей (с < 0) показательной функции; при с = 0 э. д. с. постоянна (рис. 14-16).
Задавшись э. д. с. 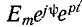 , ищем установившийся ток. в виде
, ищем установившийся ток. в виде 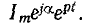 Данная функция при дифференцировании (по переменной t) умножается на р, а при интегрировании делится на р. Поэтому подстановка выражения
Данная функция при дифференцировании (по переменной t) умножается на р, а при интегрировании делится на р. Поэтому подстановка выражения 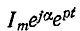 в исходное дифференциальное (или интегродифференциаль-ное) уравнение приводит к алгебраическому’ уравнению, которое отличается от уравнения для установившегося режима, записанного в комплексной форме, только тем, что
в исходное дифференциальное (или интегродифференциаль-ное) уравнение приводит к алгебраическому’ уравнению, которое отличается от уравнения для установившегося режима, записанного в комплексной форме, только тем, что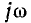 заменяется на р. Таким образом, установившийся ток получается равным
заменяется на р. Таким образом, установившийся ток получается равным
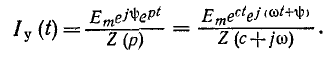
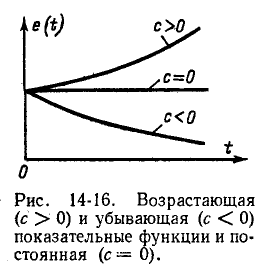
В зависимости от схемы и постановки задачи Z (р) означает обобщенное входное сопротивление или величину, обратную обобщенной передаточной проводимости;Z (р) получается из соответствующего комплексного сопротивления заменой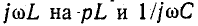
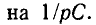
Мгновенные значения тока определяются мнимой или действительной частью 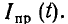
В случае синусоидальной э. д. с. (с = 0; р 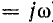 ) установившийся ток также синусоидальный
) установившийся ток также синусоидальный
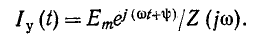
Если э. д. с. есть показательная функция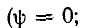
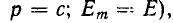 то установившийся ток изменяется также по показательному закону
то установившийся ток изменяется также по показательному закону
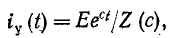
где
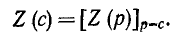
При постоянной э. д. с. 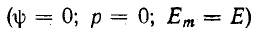 установившийся ток равен постоянному току
установившийся ток равен постоянному току
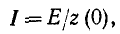
где z (0) — сопротивление при постоянном токе.
Перейдем теперь к рассмотрению свободного режима.
Свободные составляющие представляют собой общее решение системы однородных линейных дифференциальных уравнений. Для заданной цепи степень характеристического уравнения не зависит от выбора контуров, для которых составляются уравнения по второму закону Кирхгофа. Однако если выбрать контуры так, чтобы порядок дифференциальных уравнений был наименьшим, то степень характеристического уравнения не будет превышать суммы порядков исходных дифференциальных уравнений системы. При этом, как будет показано ниже, для получения характеристического уравнения отнюдь не обязательно приводить систему дифференциальных уравнений к одному уравнению относительно одной неизвестной функции.
Корни характеристического уравнения могут быть действительными или комплексными. Если корни комплексные, то они всегда образуют комплексно сопряженные пары. В связи с этим характеристическое уравнение нечетной степени всегда имеет хотя бы один действительный корень, остальные же корни могут быть действительными или комплексно-сопряженными; характеристическое уравнение четной степени имеет четное число действительных или комплексно-сопряженных корней. Действительные части всех корней характеристического уравнения всегда отрицательны, что физически обусловлено затуханием свободных составляющих в пассивных цепях с течением времени. При этом все коэффициенты характеристического уравнения должны быть действительными и положительными.
Корни единого характеристического уравнения используются для нахождения в данной цепи свободных составляющих как токов, так и напряжений.
Допустим, что характеристическое уравнение имеет п корней. Тогда свободный ток в любой ветви
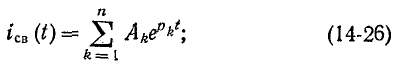
здесь 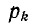 — корни характеристического уравнения,
— корни характеристического уравнения, 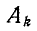 — постоянные интегрирования.
— постоянные интегрирования.
Аналогичная структура решения получается и для свободных составляющих напряжений.
В случае, когда 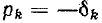 является действительным корнем т-й кратности, решение для этого корня записывается в виде
является действительным корнем т-й кратности, решение для этого корня записывается в виде
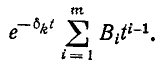
Если имеются сопряженные комплексные корни, например 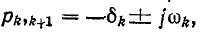 то выражение
то выражение 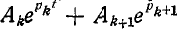
преобразуется в 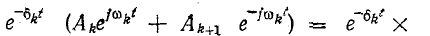
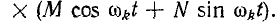
Для m-кратных сопряженных комплексных корней решение принимает вид:
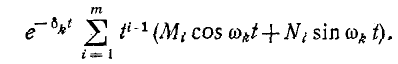
Методика получения характеристического уравнения иллюстрирована ниже на примере двухконтурной схемы, изображенной на рис. 14-17.
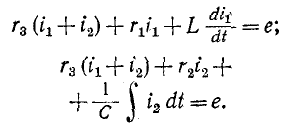
Первый контур содержит сопротивления 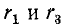 и индуктивность L, второй контур содержит сопротивления
и индуктивность L, второй контур содержит сопротивления 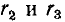 и емкость С; поэтому порядок дифференциального уравнения для каждого из этих контуров равен единице:
и емкость С; поэтому порядок дифференциального уравнения для каждого из этих контуров равен единице:
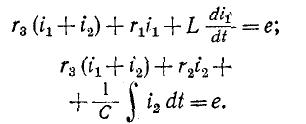
Соответственно степень характеристического уравнения равна 2.
Для получения характеристического уравнения применяется следующий прием. Система дифференциальных уравнений для свободных слагающих токов
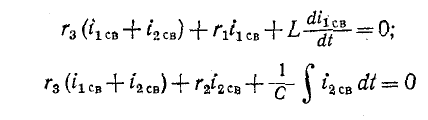
записывается в символической алгебраической форме, при которой символ р заменяет операцию дифференцирования, а символ 1/р — операцию интегрирования:
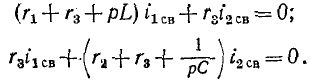
Данная система уравнений имеет решение, отличное от нулевого, если определитель системы равен нулю, т. е.
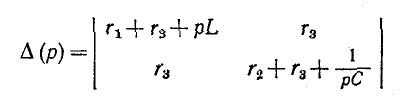
или
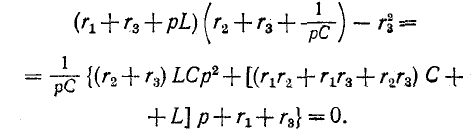
Таким образом, получается характеристическое уравнение второй степени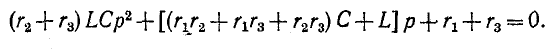
Ввиду прямой пропорциональности, существующей между входным сопротивлением цепи Z (р) и определителем системы 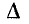 (р), то же характеристическое уравнение получается и по формуле Z (р) = 0.
(р), то же характеристическое уравнение получается и по формуле Z (р) = 0.
Операторное сопротивление Z (р) получается из комплексного сопротивления 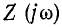 заменой
заменой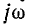 на р. При этом, разомкнув любую ветвь в пассивной цепи, находим в месте размыкания входное сопротивление Z (р) *.
на р. При этом, разомкнув любую ветвь в пассивной цепи, находим в месте размыкания входное сопротивление Z (р) *.
Если характеристическое уравнение имеет степень л, то искомыми являются п постоянных интегрирования 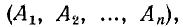 входящих в выражение (14-26)
входящих в выражение (14-26)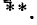 . Постоянные интегрирования находятся в результате решения системы n уравнений, соответствующих моменту времени t = 0. Эта система уравнений получается путем
. Постоянные интегрирования находятся в результате решения системы n уравнений, соответствующих моменту времени t = 0. Эта система уравнений получается путем
(n — 1)-кратного дифференцирования уравнения (14-26):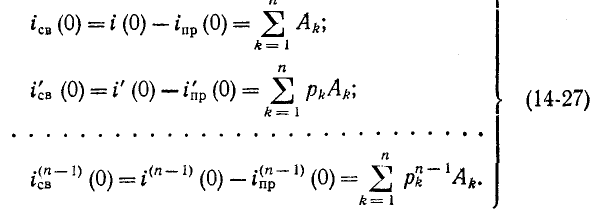
Значения свободного тока и его производных при t =0, входящие в (14-27), находятся предварительно на основании законов коммутациии уравнений Кирхгофа.
Для определения начальных значений токов и напряжений в цепи можно для наглядности воспользоваться схемой замещения, которая составляется из исходной схемы после коммутации, если заменить индуктивности идеальными источниками тока с токами, равными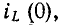 а емкости — идеальными источниками э. д. с.
а емкости — идеальными источниками э. д. с. 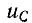 (0). Эта схема замещения справедлива только для t = 0.
(0). Эта схема замещения справедлива только для t = 0.
При нулевых начальных условиях индуктивность равносильна разрыву ветви, а емкость — короткому замыканию.
По этой схеме замещения можно найти другие токи и напряжения в момент t=0, если воспользоваться уравнениями Кирхгофа или правилами преобразования схем.
Итак, в соответствии со сказанным выше расчет переходного процесса классическим методом проводится в следующем порядке:
- Производится расчет режима до коммутации, из которого определяются конечные значения (т. е. при t=0—) функций, не меняющихся скачком (токов в индуктивностях, напряжений на емкостях). Далее с использованием законов коммутации находятся независимые начальные условия, т. е.
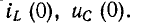
- Составляется система дифференциальных уравнений Кирхгофа, описывающая процесс в цепи после коммутации.
- Находится общее решение системы однородных дифференциальных уравнений.
- Находится тем или иным методом частное решение системы неоднородных дифференциальных уравнений, указанных в n. 2, соответствующее принужденному режиму цепи.
- Определяются зависимые начальные условия для искомых функций на основании найденных в п. 1 независимых начальных условий и уравнений Кирхгофа из п. 2, примененных для t = 0.
- По начальным условиям определяются постоянные интегрирования, содержащиеся в общем решении.
- Найденные установившиеся и свободные токи и напряжения складываются
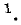
Приведенный ниже пример 14-1 иллюстрирует нахождение начальных условий; в примере 14-2 дан численный расчет переходного процесса в цепи на рис. 14-17.
Пример 14-1. В цепи, изображенной на рис. 14-18, моменту t= 0 предшествовал установившийся режим постоянного тока. При t = 0 замкнулся контакт К. Найти начальные значения тока в.индук- is & тивности и напряжений на емкостях и их первых производных.
Независимыми начальными условиями будут ток в индуктивности 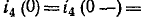
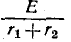 и напряжения на емкостях иг
и напряжения на емкостях иг 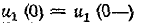 и
и
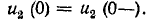
Напряжения на емкостях до коммутации находятся из условий равенства их зарядов (так как емкости соединены последовательно) и равенства суммарного напряжения на емкостях напряжению на сопротивлении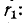
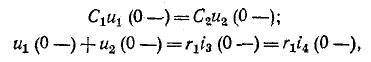
откуда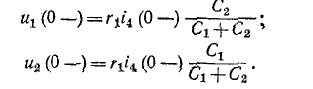
Требуемые зависимые начальные условия определятся из уравнений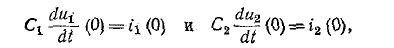
1В случае, когда э. д. с. изменяется в виде импульса, имеющего кусочно-аналитическую форму, представляется часто целесообразным применять интеграл Дюамеля
токи же 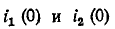 — из уравнений Кирхгофа после коммутации:
— из уравнений Кирхгофа после коммутации: 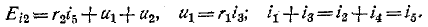
Подстановка в эти уравнения найденных значений 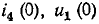 и
и
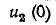 дает:
дает:
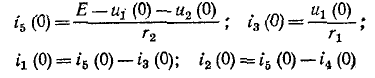
и далее
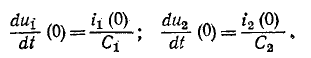
Начальное значение производной тока в индуктивности определяется также из уравнения Кирхгофа:
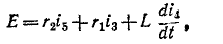
откуда при t = О
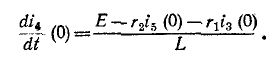
Пример (4-2. Определить ток i в иепи на рис. 14-17, если известно, что е = E = 100 В, 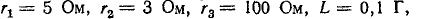
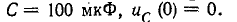
Подстановка заданных значений в приведенное выше характеристическое уравнение дает:
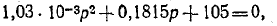
или
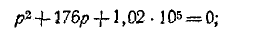
корни характеристического уравнения комплексные:
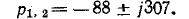
Искомый ток
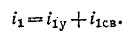
Установившийся ток
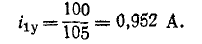
Свободный ток
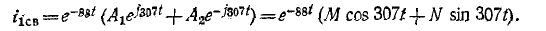
В начальный момент 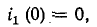 следовательно, 0 = 0,952 + М, откуда М= — 0,952.
следовательно, 0 = 0,952 + М, откуда М= — 0,952.
Производная тока по времени
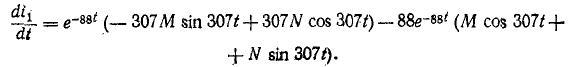
В начальный момент 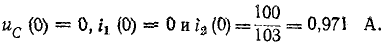
Следовательно, в начальный момент напряжение на ветви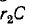 (и параллельной ей ветви
(и параллельной ей ветви 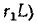 равно
равно 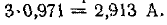 Начальное значение
Начальное значение
производной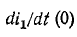 ) определяется из уравнений
) определяется из уравнений 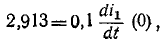 откуда
откуда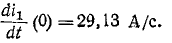
Следовательно, подставляя значение 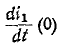 в выражение для производной при t= 0, получаем:
в выражение для производной при t= 0, получаем:
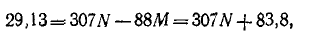
откуда
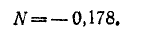
Итак,
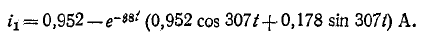
Переходные процессы в цепях с распределенными параметрами
Переходные процессы в цепях с распределенными параметрами (в линиях, обмотках электрических машин и т. п.) возникают при коммутациях, передаче непериодических сигналов или под влиянием внешнего электромагнитного поля (например, при грозовых разрядах). Для исследования переходных процессов в однородных цепях с распределенными параметрами пользуются дифференциальными уравнениями (11-2) в частных производных:
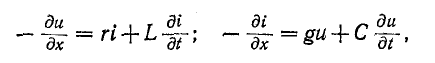
где r, L, g и С — параметры цепи на единицу длины; х — координата рассматриваемой точки, отсчитываемая от начала цепи.
В общем виде решение этих дифференциальных уравнений достаточно сложно. Решение упрощается, если пренебречь потерями В этом случае
е. считать, что r и g равны нулю.
В этом случае
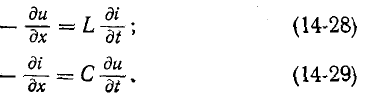
Дифференцируя (14-28) по х:
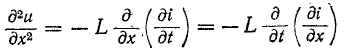
и используя (14-29), получаем:

Дифференциальное уравнение (14-30) известно в математической физике под названием уравнения ко–лебаний струны. Его решение дано Даламбером и имеет вид:
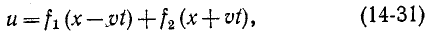
где
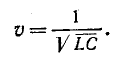
Первая слагающая представляет собой одиночную прямую волну напряжения, которая без изменения перемещается в сторону возрастающих х, т. е. от начала к концу цепи. Для всех значений х, при которых 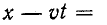 const, эта слагающая имеет одно и-то же значение, т. е. волна движется со скоростью
const, эта слагающая имеет одно и-то же значение, т. е. волна движется со скоростью 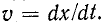
Вторая слагающая представляет собой одиночную о б -ратную волну напряжения, которая без изменения перемещается в противоположном направлении.
Для нахождения тока произведем замену переменных, обозначив 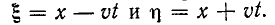 На основании (14-29) и (14-31)
На основании (14-29) и (14-31)
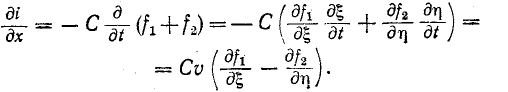
Но
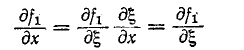
и
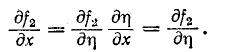
Следовательно,
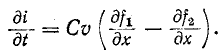
Интегрирование последнего уравнения дает 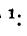
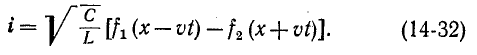
Выражения (14-31) и (14-32) записываются сокращенно:
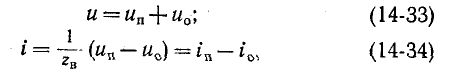
здесь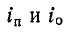 — прямая и обратная волны тока;
— прямая и обратная волны тока; 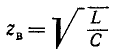 — волновое сопротивление.
— волновое сопротивление.
Следовательно, напряжение и ток прямой и соответственно обратной волн связаны законом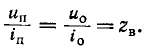
Аналогичный результат был получен для установившихся прямой и обратной волн при рассмотрении синусоидального режима в однородной линии. Физически установившиеся волны представляют собой бесконечные суммы прямых и обратных одиночных волн, отраженных от обоих концов линии.
Итак, при отсутствии потерь в однородной цепи с распределенными параметрами напряжение и ток могут быть представлены как сумма и разность двух волн, движущихся с одинаковой скоростью 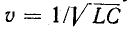 в противоположных напряжениях, без изменения их формы. При этом в любой точке однородной цепи отношение, напряжения и тока для прямой и обратной волн равно волновому сопротивлению гв.
в противоположных напряжениях, без изменения их формы. При этом в любой точке однородной цепи отношение, напряжения и тока для прямой и обратной волн равно волновому сопротивлению гв.
Если на пути распространения волны встречается неоднородность, например воздушная линия переходит в кабельную или волна достигает конца линии (разомкнутого или замкнутого через сопротивление или на короткое), происходит отражение волны. В зависимости от характера неоднородности отражение может быть частичным или полным. В первом случае наряду с отраженной волной возникает преломленная волна, распространяющаяся за место нарушения однородности; во втором случае преломленная волна отсутствует.
Обозначим 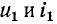 — напряжение и ток в месте отражения;
— напряжение и ток в месте отражения;
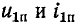 — напряжение и ток падающей (прямой) волны;
— напряжение и ток падающей (прямой) волны;
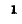 Постоянная интегрирования может быть отнесена к функциям
Постоянная интегрирования может быть отнесена к функциям
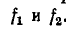
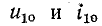 — напряжение и ток отраженной (обратной) волны;
— напряжение и ток отраженной (обратной) волны;
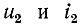 — напряжение и ток преломленной (прямой) волны;
— напряжение и ток преломленной (прямой) волны;
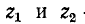 — волновые сопротивления для прямой и обратной волн
— волновые сопротивления для прямой и обратной волн 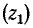 и преломленной волны
и преломленной волны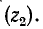
В месте неоднородности выполняется условие равенства
напряжений и токов:
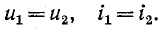
Следовательно,

Подстановка в (14-36) значений 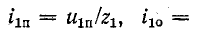
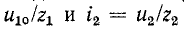 дает:
дает: 
В результате совместного решения уравнений (14-35) — (14-37) находятся отраженная 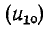 и преломленная
и преломленная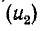 волны:
волны:
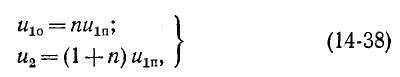
где 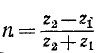 — коэффициент отражения.
— коэффициент отражения.
Соответственно ток отраженной волны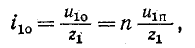
а ток преломленной волны
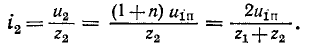
Последнее выражение показывает, что ток в конце линии после отражения можно найти как ток в эквивалентной цепи, в которую включается напряжение, равное двойному напряжению падающей волны, и которая состоит из волнового сопротивления первой линии 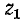 и последовательно соединенного с ним сопротивления нагрузки (в которое входит вторая линия своим волновым сопротивлением
и последовательно соединенного с ним сопротивления нагрузки (в которое входит вторая линия своим волновым сопротивлением 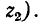
Опишем процесс включения однородной линии без потерь. После присоединения линии к источнику э. д. с. по линии начнет распространяться зарядная волна, создающая напряжение и ток. Если в конце линии присоединена нагрузка, равная волновому сопротивлению линии,
то падающая волна, достигнув ее, не отразится и в линии сразу наступит установившийся режим. Если же нагрузка с линией не согласована, то падающая зарядная волна, достигнув конца линии, претерпит отражение. Распространяясь в обратную сторону, отраженная волна сложится с падающей, причем напряжения волн суммируются, а токи вычитаются (алгебраически). Достигнув начала линии, обратная волна снова отразится от источника э. д. с., как от короткозамкнутого конца; появится новая прямая волна напряжения и тока, которая также отразится от конца, и т. д. Процесс будет продолжаться до наступления установившегося режима. Теоретически в идеальной линии без потерь при чисто реактивной нагрузке процесс колебаний будет продолжаться бесконечно долго. В реальной линии при наличии потерь волны напряжения и тока будут постепенно затухать в направлении распространения.
Напряжение и ток в линии в произвольный момент времени определятся как алгебраические суммы и соответственно разности напряжений и токов прямых и обратных волн.
Пользуясь формулами и схемой замещения, описанной выше, можно найти напряжение и ток, возникающие в месте присоединения сосредоточенной нагрузки или перехода одной линии в другую (см. пример 14-3).
Следует отметить что индуктивность, включенная последовательно в линию, или емкость, включенная параллельно проводам линии, сглаживает фронт преломленных волн; активное сопротивление, включенное в линию параллельно, уменьшает преломленную волну.
Пример 14-3. К концу линии, имеющей волновое сопротивление 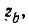 присоединена индуктивная катушка r, L. Определить ток в катушке и напряжение на ней под воздействием прямоугольной волны U
присоединена индуктивная катушка r, L. Определить ток в катушке и напряжение на ней под воздействием прямоугольной волны U
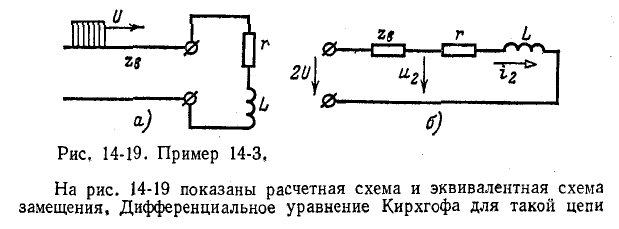
запишите так:
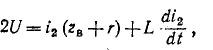
откуда
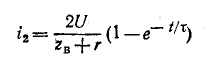
и
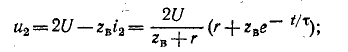
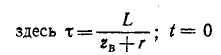 соответствует моменту падения волны на катушках
соответствует моменту падения волны на катушках
- Переходные процессы в линейных цепях
- Переходные процессы в нелинейных цепях
- Переходные процессы в электрических цепях с сосредоточенными параметрами
- Переходные процессы в колебательных контурах
- Цепи с взаимной индукцией
- Трехфазные цепи
- Периодические несинусоидальные напряжения и токи в линейных цепях
- Нелинейные цепи переменного тока
При всех изменениях в электрической цепи: включении, выключении, коротком замыкании,
колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные
процессы, которые не могут протекать мгновенно, так как невозможно мгновенное
изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный
процесс обусловлен несоответствием величины запасенной энергии в магнитном поле
катушки и электрическом поле конденсатора ее значению для нового состояния цепи.
При переходных процессах могут возникать большие перенапряжения, сверхтоки,
электромагнитные колебания, которые могут нарушить работу устройства вплоть
до выхода его из строя. С другой стороны, переходные процессы находят полезное
практическое применение, например, в различного рода электронных генераторах.
Все это обусловливает необходимость изучения методов анализа нестационарных
режимов работы цепи.
Основные методы анализа переходных процессов в линейных цепях:
- Классический метод, заключающийся в непосредственном интегрировании
дифференциальных уравнений, описывающих электромагнитное состояние цепи. - Операторный метод, заключающийся в решении системы алгебраических
уравнений относительно изображений искомых переменных с последующим переходом
от найденных изображений к оригиналам. - Частотный метод, основанный на преобразовании Фурье и находящий широкое
применение при решении задач синтеза. - Метод расчета с помощью интеграла Дюамеля, используемый при сложной
форме кривой возмущающего воздействия. - Метод переменных состояния, представляющий собой упорядоченный способ
определения электромагнитного состояния цепи на основе решения системы дифференциальных
уравнений первого прядка, записанных в нормальной форме (форме Коши).
Классический метод расчета
Классический метод расчета переходных процессов заключается в непосредственном
интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений
на участках цепи в переходном процессе.
В общем случае при использовании классического метода расчета составляются
уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных
значений напряжений и токов, связанных между собой на отдельных элементах цепи
соотношениями, приведенными в табл. 1.
Таблица 1. Связь мгновенных значений напряжений и токов на элементах электрической цепи
| Резистор (идеальное активное сопротивление) |
|
|
| Катушка индуктивности (идеальная индуктивность) |
|
при наличии магнитной связи с катушкой, обтекаемой током |
| Конденсатор (идеальная емкость) |
|
|

Для последовательной цепи,
содержащей линейные резистор R, катушку индуктивности L и конденсатор С, при
ее подключении к источнику с напряжением u (см. рис. 1) можно записать
| (1) |
Подставив в (1) значение тока через конденсатор
![]() ,
,
получим линейное дифференциальное уравнение второго порядка относительно ![]()
 .
.
В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми
накопителями энергии, имеет вид:
 , , |
(2) |
где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.);
![]() – известное возмущающее воздействие
– известное возмущающее воздействие
(напряжение и (или) ток источника электрической энергии); ![]() – к-й постоянный коэффициент,
– к-й постоянный коэффициент,
определяемый параметрами цепи.
Порядок данного уравнения равен числу независимых накопителей энергии в цепи,
под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме,
получаемой из исходной путем объединения индуктивностей и соответственно емкостей
элементов, соединения между которыми являются последовательными или параллельными.
В общем случае порядок дифференциального уравнения определяется соотношением
| (3) |
где ![]() и
и ![]() – соответственно число катушек
– соответственно число катушек
индуктивности и конденсаторов после указанного упрощения исходной схемы; ![]() – число узлов, в которых сходятся
– число узлов, в которых сходятся
только ветви, содержащие катушки индуктивности (в соответствии с первым законом
Кирхгофа ток через любую катушку индуктивности в этом случае определяется токами
через остальные катушки); ![]() – число контуров схемы, ветви
– число контуров схемы, ветви
которых содержат только конденсаторы (в соответствии со вторым законом Кирхгофа
напряжение на любом из конденсаторов в этом случае определяется напряжениями
на других).
Наличие индуктивных связей на порядок дифференциального уравнения не влияет.
Как известно из математики, общее решение уравнения (2) представляет собой
сумму частного решения исходного неоднородного уравнения и общего решения однородного
уравнения, получаемого из исходного путем приравнивания его левой части к нулю.
Поскольку с математической стороны не накладывается каких-либо ограничений на
выбор частного решения (2), применительно к электротехнике в качестве последнего
удобно принять решение ![]() , соответствующее искомой переменной
, соответствующее искомой переменной
х в установившемся послекоммутационном режиме (теоретически для ![]() ).
).
Частное решение ![]() уравнения (2) определяется видом
уравнения (2) определяется видом
функции ![]() , стоящей в его правой части,
, стоящей в его правой части,
и поэтому называется принужденной составляющей. Для цепей с заданными
постоянными или периодическими напряжениями (токами) источников принужденная
составляющая определяется путем расчета стационарного режима работы схемы после
коммутации любым из рассмотренных ранее методов расчета линейных электрических
цепей.
Вторая составляющая ![]() общего решения х уравнения (2)
общего решения х уравнения (2)
– решение (2) с нулевой правой частью – соответствует режиму, когда внешние
(принуждающие) силы (источники энергии) на цепь непосредственно не воздействуют.
Влияние источников проявляется здесь через энергию, запасенную
в полях катушек индуктивности и конденсаторов. Данный режим работы схемы называется
свободным, а переменная ![]() – свободной составляющей.
– свободной составляющей.
В соответствии с вышесказанным, общее решение уравнения (2) имеет
вид
| (4) |
Соотношение (4) показывает, что при классическом методе расчета послекоммутационный
процесс рассматривается как наложение друг на друга двух режимов – принужденного,
наступающего как бы сразу после коммутации, и свободного, имеющего место только
в течение переходного процесса.
Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только
для линейных систем, метод решения, основанный на указанном разложении искомой
переменной х, справедлив только для линейных цепей.
Начальные условия. Законы коммутации
В соответствии с определением свободной составляющей ![]() в ее выражении имеют место постоянные
в ее выражении имеют место постоянные
интегрирования ![]() , число которых равно порядку
, число которых равно порядку
дифференциального уравнения. Постоянные интегрирования находятся из начальных
условий, которые принято делить на независимые и зависимые. К независимым начальным
условиям относятся потокосцепление (ток) для катушки индуктивности и заряд (напряжение)
на конденсаторе в момент времени ![]() (момент коммутации). Независимые
(момент коммутации). Независимые
начальные условия определяются на основании законов коммутации (см. табл. 2).
Таблица 2. Законы коммутации
|
Название закона |
Формулировка закона |
|
Первый закон коммутации (закон сохранения потокосцепления) |
Магнитный поток, сцепленный с катушками индуктивности контура, в момент |
|
Второй закон коммутации (закон сохранения заряда) |
Электрический заряд на конденсаторах, присоединенных к любому узлу, в |
Доказать законы коммутации можно от противного: если допустить обратное, то
получаются бесконечно большие значения ![]() и
и ![]() , что приводит к нарушению законов
, что приводит к нарушению законов
Кирхгофа.
На практике, за исключением особых случаев (некорректные коммутации), допустимо
использование указанных законов в другой формулировке, а именно:
первый закон коммутации – в ветви с катушкой индуктивности
ток в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем
начинает изменяться с него: ![]() .
.
второй закон коммутации – напряжение на конденсаторе
в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем
начинает изменяться с него: ![]() .
.
Необходимо подчеркнуть, что более общей формулировкой законов коммутации является
положение о невозможности скачкообразного изменения в момент коммутации для
схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами
– зарядов на них. В качестве иллюстрации сказанному могут служить схемы на рис.
2, переходные процессы в которых относятся к так называемым некорректным
коммутациям (название произошло от пренебрежения в подобных схемах малыми
параметрами, корректный учет которых может привести к существенному усложнению
задачи).

Действительно, при переводе в схеме на рис. 2,а ключа
из положения 1 в положение 2 трактование второго закона коммутации как невозможность
скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа ![]() . Аналогично при размыкании ключа
. Аналогично при размыкании ключа
в схеме на рис. 2,б трактование первого закона коммутации как невозможность
скачкообразного изменения тока через катушку индуктивности приводит к невыполнению
первого закона Кирхгофа ![]() . Для данных схем, исходя из сохранения
. Для данных схем, исходя из сохранения
заряда и соответственно потокосцепления, можно записать:

Зависимыми начальными условиями называются значения остальных токов и напряжений,
а также производных от искомой функции в момент коммутации, определяемые по
независимым начальным условиям при помощи уравнений, составляемых по законам
Кирхгофа для ![]() . Необходимое число начальных
. Необходимое число начальных
условий равно числу постоянных интегрирования. Поскольку уравнение вида (2)
рационально записывать для переменной, начальное значение которой относится
к независимым начальным условиям, задача нахождения начальных условий обычно
сводится к нахождению значений этой переменной и ее производных до (n-1) порядка
включительно при  .
.

Пример. Определить токи
и производные ![]() и
и ![]() в момент коммутации в схеме на
в момент коммутации в схеме на
рис. 3, если до коммутации конденсатор был не заряжен.
В соответствии с законами коммутации
![]() и
и  .
.
На основании второго закона Кирхгофа для момента коммутации имеет место
![]() ,
,
откуда

и ![]() .
.
Для известных значений ![]() и
и ![]() из уравнения
из уравнения

определяется ![]() .
.
Значение производной от напряжения на конденсаторе в момент коммутации (см.
табл. 1)
 .
.
Корни характеристического уравнения. Постоянная времени
Выражение свободной составляющей ![]() общего решения х дифференциального
общего решения х дифференциального
уравнения (2) определяется видом корней характеристического уравнения (см. табл.
3).
Таблица 3. Выражения свободных составляющих общего решения
|
Вид корней характеристического уравнения |
Выражение свободной составляющей |
|
Корни |
|
|
Корни |
|
|
Пары комплексно-сопряженных корней |
|
Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная
составляющая затухает, вещественные части корней характеристического уравнения
не могут быть положительными.
При вещественных корнях ![]() монотонно затухает, и имеет место
монотонно затухает, и имеет место
апериодический переходный процесс. Наличие пары комплексно сопряженных
корней обусловливает появление затухающих синусоидальных колебаний (колебательный
переходный процесс).
Поскольку физически колебательный процесс связан с периодическим обменом энергией
между магнитным полем катушки индуктивности и электрическим полем конденсатора,
комплексно-сопряженные корни могут иметь место только для цепей, содержащих
оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением
 ,
,
которое называется декрементом колебания, или натуральным логарифмом
этого отношения
![]() ,
,
называемым логарифмическим декрементом колебания, где ![]() .
.
Важной характеристикой при исследовании переходных процессов является постоянная
времени t, определяемая для цепей первого порядка, как:
![]() ,
,
где р – корень характеристического уравнения.
Постоянную времени можно интерпретировать как временной интервал, в течение
которого свободная составляющая уменьшится в е раз по сравнению со своим начальным
значением. Теоретически переходный процесс длится бесконечно долго. Однако на
практике считается, что он заканчивается при 
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с. - Теоретические основы электротехники. Учеб. для вузов. В трех т. Под
общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи
с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
- Чем обусловлены переходные процессы?
- Как определяется порядок дифференциального уравнения, описывающего переходный
процесс? - Для каких цепей применим классический метод расчета переходных процессов?
- Доказать законы коммутации:
 и
и  – с энергетических позиций.
– с энергетических позиций. - В каких цепях и почему возможен колебательный процесс?
- Определить величину токов
 и напряжений
и напряжений  на конденсаторе и
на конденсаторе и  на катушке индуктивности в момент коммутации в
на катушке индуктивности в момент коммутации в
цепи на рис. 4, если .
.
Для
анализа переходного процесса предварительно
следует привести схему к минимальному
числу накопителей энергии, исключив
параллельные и последовательные
соединения однотипных реактивных
элементов (индуктивностей или емкостей).
Система интегродифференциальных
уравнений, составленных в соответствии
с законами Кирхгофа или методом контурных
токов, может быть сведена путем подстановки
к одному дифференциальному уравнению,
которое используется для составления
характеристического уравнения.
Порядок
дифференциального, следовательно, и
характеристического уравнения зависит
от числа реактивных элементов приведенной
схемы. Главная трудность в решения
задачи классическим методом для уравнений
высоких порядков состоит в отыскании
корней характеристического уравнения
и постоянных интегрирования. Поэтому
для решения уравнений порядка выше
второго применяют другие методы, в
частности операторный метод, основанный
на применении преобразования Лапласа
и исключающий трудоемкую процедуру
отыскания постоянных интегрирования.
Для
практических целей при анализе переходных
процессов в любой схеме классическим
методом может быть рекомендован следующий
алгоритм.
-
Рассчитать
принужденный (установившийся) режим
при t→∞. Определить принужденные токи
и напряжения. -
Рассчитать
режим до коммутации. Определить токи
в ветвях с индуктивностью и напряжения
на конденсаторах. Значения этих величин
в момент коммутации является независимыми
начальными условиями. -
Составить
дифференциальные уравнения для
свободного процесса (Е = 0) в схеме
после коммутации по законам Кирхгофа
или по методу контурных токов.
Алгебраизировать данные уравнения,
получить характеристическое уравнение
и найти его корни. Существуют приемы,
упрощающие операцию отыскания корней
характеристического уравнения, например,
приравнивание нулю входного операторного
сопротивления цепи, которое получается
путем замены в выражении комплексного
сопротивления цепи множителя “jω”
на оператор “р”. -
Записать
общие выражения для искомых напряжений
и токов в соответствии с видом корней
характеристического уравнения. -
Переписать
величины, полученные в п. 4, и производные
от них при t = 0. -
Определить
необходимые зависимые начальные
условия, используя независимые начальные
условия. -
Подставив
начальные условия в уравнения п. 5,
найти постоянные интегрирования. -
Записать
законы изменения искомых токов и
напряжений.
5.4. Переходные процессы в электрических цепях с последовательно соединенными резисторами и катушками
В
данном разделе предполагается не только
практическое знакомство с классическим
методом расчета переходных процессов,
но и с особенностями самих процессов в
рассматриваемых задачах.
5.4.1. Короткое замыкание в цепи с резистором и катушкой

Рис.
5.2
Исследуем
электромагнитные процессы в цепи,
изображенной на рис. 5.2, происходящие
после замыкания ключа.
Рассчитаем
установившийся режим в цепи до коммутации
(до замыкания ключа) и определим из него
независимое начальное условие — ток в
катушке в момент t = 0–,
непосредственно предшествующий
коммутации
i(0–)
= i(0+)
= E / (Rвн
+ R).
Найдем
установившийся ток i после коммутации.
Так как во вновь образованном контуре
из катушки L и резистора R нет источника,
то iy = 0.
Для
определения свободной составляющей
тока запишем по второму закону Кирхгофа
уравнение электрического состояния
цепи после коммутации:
![]() .
.
Характеристическое
уравнение имеет вид:
pL
+ R = 0.
Общее
решение уравнения для свободной
составляющей:
iсв
= A ept,
где:
А – постоянная интегрирования;
p = –
R/L, c-1
– корень характеристического уравнения.
Записав
общий вид переходного тока катушки
i
= iу
+ iсв
= A ept,
приравниваем
его значение i(0+) = A
в точке t = 0+
к значению i(0–),
найденному в п. 1. Получаем искомую
константу
A
= E / (Rвн
+ R) = I0.
Переходный
ток i = iу
+ iсв
при этом равен
![]() ,
,
где
τ = L / R – постоянная времени цепи.
Постоянная
времени
– это время, в течение которого свободная
составляющая процесса уменьшается в
е = 2,72 раза по сравнению с начальным
значением.

Рис.
5.3
График
изменения переходного тока показан на
рис. 5.3.
Определим
э.д.с. самоиндукции катушки
 t ≥ 0.
t ≥ 0.
В
момент коммутации эта э.д.с. равна
напряжению на сопротивлении R, а в
дальнейшем уменьшается по экспоненциальному
закону. На основании изложенного можно
сделать следующие выводы.
-
При
коротком замыкании в рассматриваемой
цепи ток в ней изменяется по
экспоненциальному закону, уменьшаясь
от начального значения до нуля. -
Скорость
изменения тока определяется постоянной
времени цепи, которая равна индуктивности
катушки, деленной на активное сопротивление
цепи. -
Практически
можно считать, что переходный процесс
заканчивается при t ≈ (3…5)τ , когда
первоначальное значение тока уменьшается
по модулю на порядок. -
Напряжение
на катушке в начальный момент времени
равно напряжению на активном сопротивлении:
uL(0+)
= I0R.
-
С
энергетической точки зрения рассматриваемый
переходный процесс характеризуется
расходом энергии магнитного поля
катушки на тепловые потери в резисторе.
Следует отметить, что сопротивление
резистора влияет не на количество
выделенной теплоты W, а на начальное
значение напряжения катушки и длительность
процесса. В самом деле
 .
.
Название метода «классический» отражает использование в нем решений дифференциальных уравнений с постоянными параметрами методами классической математики. Данный метод обладает физической наглядностью и удобен для расчета простых цепей (расчет сложных цепей упрощается операторным методом).
Методика[править | править код]
Этапы расчета переходного процесса в цепи классическим методом:
- Найти независимые начальные условия, то есть, напряжения на ёмкостях и токи на индуктивностях в момент начала переходного процесса.
- Далее необходимо составить систему уравнений на основе законов Кирхгофа, Ома, электромагнитной индукции и т.д., описывающих состояние цепи после коммутации, и исключением переменных получить одно дифференциальное уравнение, в общем случае неоднородное относительно искомого тока
или напряжения
. Для простых цепей получается дифференциальное уравнение первого или второго порядка, в котором в качестве искомой величины выбирают либо ток в индуктивном элементе, либо напряжение на емкостном элементе.
- Далее следует составить общее решение полученного неоднородного дифференциального уравнения цепи в виде суммы частного решения неоднородного дифференциального уравнения и общего решения соответствующего однородного дифференциального уравнения.
- Наконец, в общем решении следует найти постоянные интегрирования из начальных условий, т. е. условий в цепи в начальный момент времени после коммутации.
Применительно к электрическим цепям в качестве частного решения неоднородного дифференциального уравнения выбирают установившийся режим в рассматриваемой цепи (если он существует), т. е. постоянные токи и напряжения, если в цепи действуют источники постоянных ЭДС и токов, или синусоидальные напряжения и токи при действии источников синусоидальных ЭДС и токов. Токи и напряжения установившегося режима называют установившимися.
Общее решение однородного дифференциального уравнения описывает процесс в цепи без источников ЭДС и тока, который поэтому называют свободным процессом. Токи и напряжения свободного процесса называют свободными, а их выражения должны содержать постоянные интегрирования, число которых равно порядку однородного уравнения.
Пример расчёта простейшего переходного процесса классическим методом[править | править код]

Задача[править | править код]
На рисунке изображена коммутируемая RL-цепочка. В некоторый момент времени t=0 ключ К замыкается. Определить зависимость тока в RL-цепочке от времени.
Решение[править | править код]
Согласно второму закону Кирхгофа, схема описывается следующим дифференциальным уравнением:
где первый член описывает падение напряжения на резисторе R, а второй — на индуктивности L.
Делаем замену переменной 
Поскольку один из сомножителей a, b можно выбрать произвольно, выберем b так, чтобы выражение в скобках было равно нулю:
Разделяем переменные:
С учётом выбранного значения b дифференциальное уравнение приводится к виду
Интегрируя, получаем
Получаем выражение для тока
Значение постоянной интегрирования находим из условия, что в момент t=0 тока в цепи не было:
Окончательно получаем
См. также[править | править код]
- Переходные процессы в электрических цепях
Литература[править | править код]
- Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6
Ссылки[править | править код]
- Классический метод расчета переходных процессов Архивная копия от 4 октября 2006 на Wayback Machine на http://www.ups-info.ru Архивная копия от 14 июня 2008 на Wayback Machine
- Методика и примеры расчета переходных процессов классическим методом. Архивная копия от 4 октября 2006 на Wayback Machine на http://www.ups-info.ru Архивная копия от 14 июня 2008 на Wayback Machine
6.1. Переходный режим электрических цепей. Законы коммутации
6.2. Классический метод расчета переходных процессов
6.3. Переходные процессы в цепях первого порядка
6.4. Переходные процессы в цепях второго порядка
6.5. Включение RLC-контура на постоянное и гармоническое напряжение
6.6. Переходные процессы в разветвленных цепях
6.7. Метод переменных состояния
6.8. Вопросы и задания для самопроверки
6.1. Переходный режим электрических цепей. Законы коммутации
В предыдущих главах рассматривались процессы в электрических цепях и методы их расчета в установившемся режиме, т. е. в режиме, при котором напряжения и токи в цепях либо не зависят от времени, либо являются периодическими функциями времени в зависимости от вида приложенного воздействия. Установившийся режим в цепи достигается обычно через определенный промежуток времени после начала воздействия, поэтому рассмотренные ранее методы анализа не охватывают так называемый переходный режим от начала воздействия до установившегося состояния цепи. Переходной режим работы цепи обусловлен наличием в ней реактивных элементов (индуктивности, емкости), в которых накапливается энергия магнитного и электрического полей. При различного рода воздействиях (подключении к цепи или исключении источников электрической энергии, изменении параметров цепи) изменяется энергетический режим работы цепи, причем эти изменения не могут осуществляться мгновенно в силу непрерывности изменения энергии электрического и магнитного полей (принцип непрерывности), что и приводит к возникновению переходных процессов. Следует подчеркнуть, что переходные процессы во многих устройствах и системах связи являются составной “нормальной” частью режима их работы. В то же время в ряде случаев переходные процессы могут приводить к таким нежелательным явлениям, как возникновение сверхтоков и перенапряжений. Все это определяет важность рассмотрения методов анализа переходных процессов в электрических цепях.
В основе методов расчета переходных процессов лежат законы коммутации. Коммутацией принято называть любое изменение параметров цепи, ее конфигурации, подключение или отключение источников, приводящее к возникновению переходных процессов. Коммутацию будем считать мгновенной, однако переходный процесс, как было отмечено выше, будет протекать определенное время. Теоретически для завершения переходного процесса требуется бесконечно большое время, но на практике его принимают конечным, зависящим от параметров цепи. Будем считать, что коммутация осуществляется с помощью идеального ключа К (рис. 6.1), сопротивление которого в разомкнутом состоянии бесконечно велико, а в замкнутом равно нулю. Направление замыкания или размыкания ключа будем показывать стрелкой. Будем также считать, если не оговорено иное, что коммутация осуществляется в момент t = 0.
Различают первый и второй законы коммутации. Первый закон коммутации связан с непрерывностью изменения магнитного поля катушки индуктивности WL = Li2/2 и гласит: в начальный момент t = 0+ непосредственно после коммутации ток в индуктивности имеет то же значение, что и в момент t = 0– до коммутации и с этого момента плавно изменяется (здесь и далее под f(0– ) понимается левосторонний предел функции f(t) при t ![]() 0– , а под f(0+ ) – правосторонний предел f(t) при t
0– , а под f(0+ ) – правосторонний предел f(t) при t![]() 0+ )
0+ ) ![]() (6.1)
(6.1)
Второй закон коммутации связан с непрерывностью изменения электрического поля емкости WC = Cu2/2: в начальный момент t = 0+ непосредственно после коммутации напряжение на емкости имеет то же значение, что и в момент t = 0– до коммутации и с этого момента плавно изменяется: ![]() (6.2)
(6.2)
В отличие от тока в индуктивности iL и напряжения на емкости uC напряжение на индуктивности uL и ток в емкости iC могут изменяться скачком, так как согласно (1.9) и (1.12) они являются производными от iL и uC и с ними непосредственно не связана энергия магнитного и электрического полей. Значения токов в индуктивности iL(0+) и напряжений на емкостях uC(0+) образуют начальные условия задачи. В зависимости от начального энергетического состояния цепи различают два типа задач расчета переходных процессов: задачи с нулевыми начальными условиями, когда непосредственно после коммутации (при t = 0+) iL(0+) = 0; uC(0+) = 0 (т. е. WL(0+) + WC(0+) = 0) и задачи с ненулевыми начальными условиями, когда iL(0+) ![]() 0 и (или) uC(0+)
0 и (или) uC(0+) ![]() 0 (т. е. WL(0+) + WC(0+)
0 (т. е. WL(0+) + WC(0+) ![]() 0). Нулевые и ненулевые значения начальных условий для iL и uC называются независимыми, а начальные условия остальных токов и напряжений зависимыми. Независимые начальные условия определяются с помощью законов коммутации (6.1) и (6.2).
0). Нулевые и ненулевые значения начальных условий для iL и uC называются независимыми, а начальные условия остальных токов и напряжений зависимыми. Независимые начальные условия определяются с помощью законов коммутации (6.1) и (6.2).
6.2. Классический метод расчета переходных процессов
В основе классического метода расчета переходных процессов в электрических цепях лежит составление интегрально-дифференциальных уравнений для мгновенных значений токов и напряжений. Эти уравнения составляются на основе законов Кирхгофа, методов контурных токов, узловых напряжений и могут содержать как независимые, так и зависимые переменные. Для удобства решения обычно принято составлять дифференциальные уравнения относительно независимой переменной, в качестве которой может служить iL или uC. Решение полученных дифференциальных уравнений относительно выбранной переменной и составляет сущность классического метода.
Учитывая, что в ряде случаев решение дифференциальных уравнений проще интегрально-дифференциальных, полученную систему сводят к одному дифференциальному уравнению соответствующего порядка относительно выбранной независимой переменной iL или uC. Порядок дифференциального уравнения определяется числом независимых накопителей энергии электрического и магнитного полей.
Обозначим независимую переменную (iL или uC) через x = x(t).
Дифференциальное уравнение m-гo порядка, описывающее переходный процесс в электрической цепи, находящейся под воздействием источника w(t), описывается уравнением: ![]() (6.3) где b0, b1, …, bm–1, bm — коэффициенты параметров цепи; w(t) — функция, описывающая характер воздействия на цепь.
(6.3) где b0, b1, …, bm–1, bm — коэффициенты параметров цепи; w(t) — функция, описывающая характер воздействия на цепь.
Цепь, параметры которой b0, b1, …, bm–1, bm – неизменны, называют цепью с постоянными параметрами. Если же какой-либо из коэффициентов b0, b1, …, bm–1, bm — переменен, то цепь называют параметрической. В дальнейшем будем рассматривать цепи с постоянными параметрами.
Дифференциальное уравнение (6.3) относится к линейным неоднородным уравнениям m-го порядка. Как известно, его решение находится как сумма общего решения xсв однородного дифференциального уравнения m-го порядка: ![]() (6.4) и частного решения xпр уравнения (6.3):
(6.4) и частного решения xпр уравнения (6.3): ![]() (6.4) где xсв и xпр — общее и частное решения. Общее решение xсв определяет свободные процессы, которые протекают в цепи без участия источника w(t) (отсюда индекс “св”). Частное решение xпр определяет принудительный процесс (отсюда индекс “пр”), который протекает в цепи под влиянием w(t). В теории цепей xпр обычно находят одним из ранее рассмотренных методов расчета цепей в установившемся режиме.
(6.4) где xсв и xпр — общее и частное решения. Общее решение xсв определяет свободные процессы, которые протекают в цепи без участия источника w(t) (отсюда индекс “св”). Частное решение xпр определяет принудительный процесс (отсюда индекс “пр”), который протекает в цепи под влиянием w(t). В теории цепей xпр обычно находят одним из ранее рассмотренных методов расчета цепей в установившемся режиме.
Свободная составляющая переходного процесса xсв будет зависеть от характера корней характеристического уравнения: ![]() (6.6)
(6.6)
В случае, когда корни p1, p2, …, рm характеристического уравнения (6.6) вещественные и различные, решение (6.4) имеет вид ![]() (6.7) где A1, A2, …, Am — постоянные интегрирования, которые находятся из начальных условий.
(6.7) где A1, A2, …, Am — постоянные интегрирования, которые находятся из начальных условий.
В случае, когда корни уравнения (6.6) вещественные и равные, т. е. p1 = p2 = … = рm = p, свободная составляющая определяется уравнением ![]() (6.8)
(6.8)
Представляет практический интерес и случай, когда корни попарно комплексно-сопряженные рk,k–1= —a ± j![]() с. При этом в формуле (6.7) соответствующая пара корней рk,k–1заменяется слагаемыми вида
с. При этом в формуле (6.7) соответствующая пара корней рk,k–1заменяется слагаемыми вида ![]() (6.9) где A,
(6.9) где A, ![]() — постоянные интегрирования, определяемые также из начальных условий.
— постоянные интегрирования, определяемые также из начальных условий.
6.3. Переходные процессы в цепях первого порядка
Рассмотрим применение классического метода к расчету переходных процессов в цепях первого порядка. Это цепи, содержащие только однотипные реактивные элементы (емкости или индуктивности), процессы, в которых описываются дифференциальными уравнениями первого порядка ![]() (6.10)
(6.10)
Примером цепей первого порядка являются простейшие RL и RC цепи.
Переходные процессы в RL-цепях
Рассмотрим включение RL-цепи к источнику напряжения u(t) (рис. 6.1).
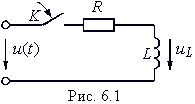
Из рис. 6.1 следует, что до коммутации ключ К разомкнут, поэтому ток iL(0–) = 0 и цепь находится при нулевых начальных условиях. В момент t = 0 ключом К замыкаем (осуществим коммутацию) цепь, подключив ее к источнику напряжения u(t). После замыкания ключа К в цепи начнется переходный процесс. Для его математического описания выберем в качестве независимой переменной iL = i и составим относительно нее дифференциальное уравнение по ЗНК: ![]() (6.11)
(6.11)
Уравнение (6.11) относится к линейным неоднородным дифференциальным уравнениям первого порядка типа (6.3), решение которого можно записать согласно (6.5) в форме ![]() (6.12) где iсв — свободная составляющая тока, обусловленная свободными процессами, протекающими в цепи без участия источника u(t); inp — принужденная составляющая тока, обусловленная действием источника напряжения u(t).
(6.12) где iсв — свободная составляющая тока, обусловленная свободными процессами, протекающими в цепи без участия источника u(t); inp — принужденная составляющая тока, обусловленная действием источника напряжения u(t).
Свободная составляющая тока iсв есть общее решение однородного дифференциального уравнения ![]() (6.13) и согласно (6.7)
(6.13) и согласно (6.7) ![]() (6.14) где А — постоянная интегрирования; р — корень характеристического уравнения типа (6.6);
(6.14) где А — постоянная интегрирования; р — корень характеристического уравнения типа (6.6); ![]() (6.15)
(6.15)
Отсюда p = —R/L. Величина 1/|р| носит название постоянной времени цепи. В неразветвленной RL-цепи ![]() = L/R.
= L/R.
Принужденная составляющая iпp может быть определена как частное решение уравнения (6.11). Однако, как было указано выше, iпp можно найти более просто методами расчета установившегося режима цепи. Рассмотрим два частных случая: ![]()
В первом случае принужденная составляющая может быть определена из установившегося режима: iпp = U/R. Для нахождения постоянной интегрирования A перепишем (6.12) в форме i = Ае–t /![]() + U/R и учтем начальные условия для i, а также первый закон коммутации (6.1):
+ U/R и учтем начальные условия для i, а также первый закон коммутации (6.1): ![]()
Отсюда А = —U/R. Таким образом, закон изменения тока в RL-цепи определяется уравнением ![]() (6.16)
(6.16)
Напряжение на индуктивности согласно (1.9) ![]() (6.17)
(6.17)
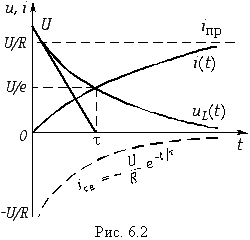
На рис. 6.2 изображены графики зависимости i(t) и uL(t). Анализ полученных уравнений (6.16) и (6.17) показывает, что чем больше постоянная времени цепи ![]() , тем медленнее затухает переходной процесс. На практике принято считать переходной процесс законченным при t = (3…5)
, тем медленнее затухает переходной процесс. На практике принято считать переходной процесс законченным при t = (3…5)![]() , при t = 3
, при t = 3![]() ток достигает 95% своего установившегося значения, а при t = 5
ток достигает 95% своего установившегося значения, а при t = 5![]() — более 99%. Графически постоянная времени
— более 99%. Графически постоянная времени ![]() может определиться как интервал времени на оси t от t = 0 до точки пересечения касательной к uL (рис. 6.2), в указанный момент напряжение на uL уменьшается в е раз по сравнению с начальным.
может определиться как интервал времени на оси t от t = 0 до точки пересечения касательной к uL (рис. 6.2), в указанный момент напряжение на uL уменьшается в е раз по сравнению с начальным.
Анализ полученных результатов показывает, что при нулевых начальных условиях в момент t = 0+ индуктивность ведет себя как бесконечно большое сопротивление (разрыв цепи), а при t = ![]() как бесконечно малое сопротивление (короткое замыкание цепи).
как бесконечно малое сопротивление (короткое замыкание цепи).
Для второго случая принужденная составляющая тока ![]() где
где ![]() ,
, ![]() = arctg(
= arctg(![]() L/R). Постоянная интегрирования определяется из уравнения
L/R). Постоянная интегрирования определяется из уравнения ![]()
Откуда ![]() . Следовательно, закон изменения тока в цепи в этом случае будет
. Следовательно, закон изменения тока в цепи в этом случае будет ![]() (6.18)
(6.18)
На рис. 6.3 изображена временная зависимость тока (6.18). Напряжение на индуктивности 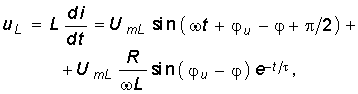 (6.19) где UmL =
(6.19) где UmL = ![]() LIm.
LIm.
Анализ уравнения (6.18) показывает, что в случае подключения цепи к источнику u(t) в момент, когда ![]() u =
u = ![]() ±
± ![]() /2 в последней могут возникать сверхтоки. Если постоянная времени цепи
/2 в последней могут возникать сверхтоки. Если постоянная времени цепи ![]() достаточно велика, то скачок тока в начальный период может достигать imax
достаточно велика, то скачок тока в начальный период может достигать imax ![]() 2Im. Напротив, при включении цепи в момент, когда
2Im. Напротив, при включении цепи в момент, когда ![]() u =
u = ![]() , в ней сразу наступает установившийся режим. Аналогичная картина наблюдается и с напряжением на индуктивности (6.19).
, в ней сразу наступает установившийся режим. Аналогичная картина наблюдается и с напряжением на индуктивности (6.19).
В качестве второго примера расчета рассмотрим случай ненулевых начальных условий в RL-цепи (рис. 6.4). К моменту коммутации в данной цепи была запасена энергия магнитного поля, равная WL = Li2(0– )/2, где i(0– ) = U/(R0 + R). После коммутации в RL-цепи возникает переходный процесс, описываемый уравнением: ![]() (6.20) т. е. iпp = 0. Решая уравнение (6.20), находим с учетом (6.13) – (6.15):
(6.20) т. е. iпp = 0. Решая уравнение (6.20), находим с учетом (6.13) – (6.15): ![]()
Постоянную А находим из начального условия i(0– ) и закона коммутации (6.1): ![]()
Окончательно закон изменения тока в переходном режиме описывается уравнением 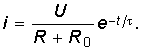 (6.21)
(6.21)
Напряжение uL определяется как 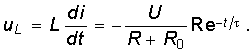 (6.22)
(6.22)
На рис. 6.5 изображены графики i и uL. Следует отметить, что вся энергия WL, запасенная в индуктивности с течением времени, расходуется на тепловые потери в R. При ненулевых начальных условиях L ведет себя как источник тока.
Переходные процессы в RС-цепях
При расчете переходных процессов в RС-цепях в качестве независимой переменной выбирают uC. Затем также составляют дифференциальное уравнение для заданной RС-цепи, решение которого с учетом начальных условий для uC(0) и определяет закон изменения напряжения на емкости.
Рассмотрим вначале RC-цепь при нулевых начальных условиях (рис. 6.6), которая подключается в момент t = 0 к источнику постоянного и(t) = U или синусоидального и(t) = Umsin(![]() t +
t + ![]() u ) напряжения. Переходный процесс в данной цепи описывается дифференциальным уравнением
u ) напряжения. Переходный процесс в данной цепи описывается дифференциальным уравнением ![]() (6.23) решение которого ищем также в форме суммы общего и частного решений, определяющих свободную и принужденную составляющие:
(6.23) решение которого ищем также в форме суммы общего и частного решений, определяющих свободную и принужденную составляющие: ![]() (6.24)
(6.24)
Свободная составляющая является решением однородного дифференциального уравнения 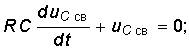 (6.25)
(6.25) ![]() (6.26) где р определяется из характеристического уравнения
(6.26) где р определяется из характеристического уравнения ![]()
Величина RC носит название постоянной времени RC-цепи и обозначается через ![]() .
.
Определим принужденную составляющую uC пp для случая, когда u(t) = U = const. Из рис. 6.6 следует, что в установившемся режиме uC пp = U. Следовательно, с учетом (6.24) и (6.26) уравнение для иC примет вид иC = Ae–t /![]() + U. Для нахождения постоянной интегрирования А учтем нулевые начальные условия для uC(0–) и второй закон коммутации (6.2): uC(0–) = uC(0+) = 0 = A + U, откуда А = —U. Таким образом, получаем окончательно:
+ U. Для нахождения постоянной интегрирования А учтем нулевые начальные условия для uC(0–) и второй закон коммутации (6.2): uC(0–) = uC(0+) = 0 = A + U, откуда А = —U. Таким образом, получаем окончательно: ![]() (6.27)
(6.27)
Ток в цепи определяется согласно (1.12): ![]() (6.28)
(6.28)
На рис. 6.7 изображены графические зависимости uС(t) и i(t).
Анализ полученных результатов показывает, что в момент t = 0+ емкость С (при нулевых начальных условиях) ведет себя как короткозамкнутый участок. Напротив, при t = ![]() емкость представляет собой бесконечно большое сопротивление (разрыв цепи для постоянного тока).
емкость представляет собой бесконечно большое сопротивление (разрыв цепи для постоянного тока).
Рассмотрим случай гармонического воздействия. Нетрудно видеть что при этом ![]() (6.29) где
(6.29) где 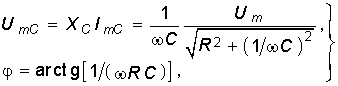 (6.30) а напряжение
(6.30) а напряжение ![]()
Постоянная А находится из начальных условий для uC(0+) при t = 0+: ![]()
Окончательно закон изменения напряжения 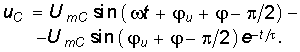 (6.31)
(6.31)
На рис. 6.8 изображен график зависимости uC(t). Анализ уравнения (6.31) показывает, что в случае неудачного включения при ![]() u =
u = ![]() –
– ![]() и большой
и большой ![]() в цепи могут возникать перенапряжения, достигающие на емкости величины uCmax
в цепи могут возникать перенапряжения, достигающие на емкости величины uCmax ![]() 2UmC. В случае удачного включения, когда
2UmC. В случае удачного включения, когда ![]() u =
u = ![]() /2 –
/2 – ![]() , в цепи сразу наступает установившийся режим.
, в цепи сразу наступает установившийся режим.
Ток в цепи 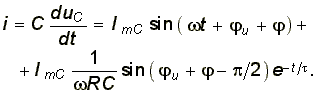 (6.32)
(6.32)
Рассмотрим теперь случай ненулевых начальных условий, когда емкость С, заряженная до напряжения U, разряжается на сопротивление R (рис. 6.9). К моменту коммутации в емкости была запасена энергия WC = CU2/2. После коммутации возникает переходный процесс, определяемый уравнением ![]() (6.33) т. е. имеет место свободный режим разряда (емкости):
(6.33) т. е. имеет место свободный режим разряда (емкости): ![]() (6.34)
(6.34)
Постоянную интегрирования А находим из начального условия для uC(0+) = U и закона коммутации (6.2): ![]()
Таким образом, получаем закон изменения напряжения на емкости ![]() (6.35) и тока в цепи
(6.35) и тока в цепи ![]() (6.36)
(6.36)
Знак “–” в уравнении (6.36) для тока свидетельствует о том, что ток разряда направлен противоположно опорному направлению напряжения иС в емкости. На рис. 6.10 приведены графики изменения напряжения иС(t) и тока i(t) данной RС-цепи. Следует подчеркнуть, что вся запасенная энергия WC емкости с течением времени преобразуется в элементе R в тепло. При ненулевых начальных условиях С ведет себя как источник напряжения.
6.4. Переходные процессы в цепях второго порядка
Ранее рассматривались переходные процессы в RL- и RС-цепях, которые относятся к цепям первого порядка, так как описываются дифференциальными уравнениями первого порядка (6.11), (6.23). При наличии в цепи двух независимых накопителей энергии переходные процессы в них описываются уравнением второго порядка. Простейшим примером такой цепи является последовательный колебательный контур (рис. 6.11).
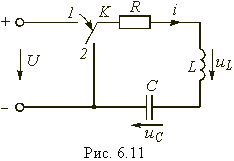
Для этого контура можно по аналогии с RL- и RС-цепью составить дифференциальное уравнение второго порядка, выбрав в качестве независимой переменной напряжение на емкости ![]()
Учитывая, что i = CduC/dt окончательно получаем ![]() (6.37)
(6.37)
Решение дифференциального уравнения (6.37) ищется согласно (6.5) в форме суммы свободной uCсв и принужденной uCпр составляющих: ![]() (6.38)
(6.38)
Вид uCпр зависит от характера приложенного напряжения, а uCсв определится решением однородного дифференциального уравнения второго порядка: 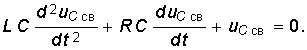 (6.39)
(6.39)
Решение уравнения (6.39) зависит от вида корней характеристического уравнения ![]() (6.40)
(6.40)
Корни уравнения (6.40) определяются только параметрами цепи независимо от выбранной переменной: 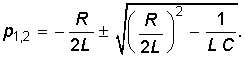 (6.41)
(6.41)
Величина a = R/2L носит название коэффициента затухания контура, а ![]() есть резонансная частота контура (см. § 4.2). Таким образом, уравнение (6.41) можно переписать в виде
есть резонансная частота контура (см. § 4.2). Таким образом, уравнение (6.41) можно переписать в виде ![]() (6.42)
(6.42)
Характер переходного процесса существенным образом зависит от вида корней р1, р2, которые могут быть: 1) вещественными и различными (при R > 2![]() ); 2) комплексно-сопряженными (при R < 2
); 2) комплексно-сопряженными (при R < 2![]() ); 3) вещественными и равными (при R = 2
); 3) вещественными и равными (при R = 2![]() ).
).
Здесь ![]() =
= ![]() — характеристическое сопротивление контура (см. формулу (4.22)).
— характеристическое сопротивление контура (см. формулу (4.22)).
Разряд емкости на RL-цепь
Для исследования характера переходного процесса во всех этих случаях рассмотрим разряд емкости С на цепь RL (см. рис. 6.11). Так как до коммутации емкость С была заряжена до напряжения U, то имеем ненулевые начальные условия: ![]()
После коммутации (переключение ключа К из положения 1 в положение 2 емкость начнет разряжаться и в цепи возникнет свободный переходный процесс. Найдем закон изменения тока и напряжений на отдельных элементах цепи для случая 1)—3).
В первом случае, когда R > 2![]() , корни p1 и р2 в (6.41) будут вещественными и различными, и решение уравнения определится согласно (6.7):
, корни p1 и р2 в (6.41) будут вещественными и различными, и решение уравнения определится согласно (6.7): ![]() (6.43) где A1 и A2 — постоянные интегрирования. Для определения A1 и A2 запишем еще уравнение для тока в цепи:
(6.43) где A1 и A2 — постоянные интегрирования. Для определения A1 и A2 запишем еще уравнение для тока в цепи: ![]() (6.44)
(6.44)
Постоянные A1 и A2 можно найти из начальных условий для uC(0–) = U и i(0–) = 0 (при t = 0–) и законов коммутации (6.1), (6.2): ![]() (6.45)
(6.45)
Из решения системы уравнение (6.45) ![]()
В результате получаем уравнения для напряжения UC и тока i: 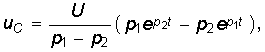 (6.46)
(6.46) 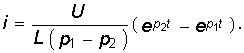 (6.47)
(6.47)
Закон изменения напряжения на индуктивности определяется при этом уравнением 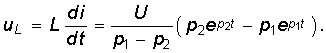 (6.48)
(6.48)
Из уравнений (6.46)—(6.48) следует, что каждая из найденных величин uC, i, uL состоит из двух слагаемых, затухающих по экспоненте с коэффициентами p1 < 0 и p2 < 0. На рис. 6.12 показан характер зависимостей (6.46)—(6.48). Момент времени t1, соответствующий точке перегиба uC, максимуму | i | и нулевому значению uL определяется из решения уравнения di / dt = 0, а момент t2 из решения уравнения duL / dt = 0: 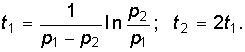 (6.49)
(6.49)
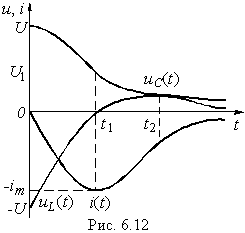
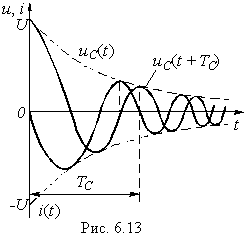
Анализ полученных кривых показывает, что в рассматриваемом случае происходит апериодический разряд емкости С, причем в интервале от 0 до t1 энергия WC расходуется на покрытие тепловых потерь в резистивном сопротивлении R и создание магнитного поля в индуктивности ( pC = uC i < 0; pL = uL i > 0). В дальнейшем (при t > t1) как энергия электрического поля емкости WC, так и запасенная к моменту t = t1 магнитная энергия индуктивности WL расходуется на покрытие тепловых потерь в сопротивлении R. Отрицательное значение тока свидетельствует о противоположном направлении тока разряда относительно опорного направления.
Во втором случае при R < 2![]() , когда корни p1 и p2 носят комплексно-сопряженный характер,
, когда корни p1 и p2 носят комплексно-сопряженный характер, ![]() (6.50) где
(6.50) где ![]() называют частотой собственных затухающих колебаний. Решение уравнения (6.39) имеет вид (6.9)
называют частотой собственных затухающих колебаний. Решение уравнения (6.39) имеет вид (6.9) ![]() (6.51) где A и
(6.51) где A и ![]() — постоянные интегрирования. Закон изменения тока в цепи
— постоянные интегрирования. Закон изменения тока в цепи ![]() (6.52)
(6.52)
Постоянные A и ![]() определяются из начальных условий для uC и i и законов коммутации (6.1), (6.2):
определяются из начальных условий для uC и i и законов коммутации (6.1), (6.2): 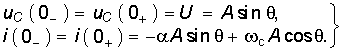 (6.53)
(6.53)
Отсюда ![]()
Окончательно уравнения для uC, i и и принимают вид  (6.54)
(6.54) 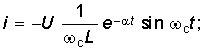 (6.55)
(6.55) 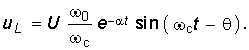 (6.56)
(6.56)
Полученные уравнения показывают, что в данном случае имеет место колебательный разряд емкости с частотой ![]() с, зависящей только от параметров R, L, С цепи. Интервал времени Тc = 2
с, зависящей только от параметров R, L, С цепи. Интервал времени Тc = 2![]() /
/![]() с носит название квазипериода. На рис. 6.13 изображены графики зависимостей uC(t) и i(t) определяемых уравнениями (6.54) и (6.55). Скорость затухания периодического процесса принято характеризовать декрементом затухания, который определяют как отношение двух соседних амплитуд тока или напряжения одного знака (см. рис. 6.13):
с носит название квазипериода. На рис. 6.13 изображены графики зависимостей uC(t) и i(t) определяемых уравнениями (6.54) и (6.55). Скорость затухания периодического процесса принято характеризовать декрементом затухания, который определяют как отношение двух соседних амплитуд тока или напряжения одного знака (см. рис. 6.13): 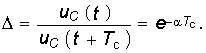 (6.57)
(6.57)
На практике чаще используется логарифмический декремент затухания 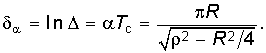 (6.58)
(6.58)
Из уравнений (6.57) и (6.58) следует, что затухание тем больше, чем больше R. При R = 2![]() колебания прекращаются и переходной процесс становится апериодическим. При R = 0 оказываются незатухающие гармонические колебания с частотой
колебания прекращаются и переходной процесс становится апериодическим. При R = 0 оказываются незатухающие гармонические колебания с частотой ![]() с =
с = ![]() 0 =
0 = ![]() . Очевидно, что этот случай представляет чисто теоретический интерес, так как в любом реальном контуре имеются потери. В процессе колебательного разряда емкости (свободных колебаний в RLC-контуре) имеет место попеременное запасание энергии WC в электрическом поле емкости и магнитном поле индуктивности WL: в начале энергия WC расходуется на создание магнитного поля WL индуктивности и покрытие тепловых потерь сопротивления R, затем запасенная энергия WL, расходуется на перезаряд емкости и покрытие потерь в R и т. д. до полного перехода первоначальной энергии Wc(0) в тепловые потери в резисторе R.
. Очевидно, что этот случай представляет чисто теоретический интерес, так как в любом реальном контуре имеются потери. В процессе колебательного разряда емкости (свободных колебаний в RLC-контуре) имеет место попеременное запасание энергии WC в электрическом поле емкости и магнитном поле индуктивности WL: в начале энергия WC расходуется на создание магнитного поля WL индуктивности и покрытие тепловых потерь сопротивления R, затем запасенная энергия WL, расходуется на перезаряд емкости и покрытие потерь в R и т. д. до полного перехода первоначальной энергии Wc(0) в тепловые потери в резисторе R.
Третий случай R = 2![]() является пограничным между колебательным и апериодическим и соответствует критическому разряду емкости. Решение уравнения (6.39) при этом имеет вид (6.8)
является пограничным между колебательным и апериодическим и соответствует критическому разряду емкости. Решение уравнения (6.39) при этом имеет вид (6.8) ![]() (6.59)
(6.59)
Ток определяется уравнением ![]() (6.60) где p1 = p2 = p = -a — корни характеристического уравнения (6.40); А1, А2 — постоянные интегрирования, определяемые из начальных условий для uC и i и законов коммутации (6.1), (6.2):
(6.60) где p1 = p2 = p = -a — корни характеристического уравнения (6.40); А1, А2 — постоянные интегрирования, определяемые из начальных условий для uC и i и законов коммутации (6.1), (6.2): ![]()
Отсюда А2 = aU. Окончательные выражения для напряжения и тока принимают вид ![]() (6.61)
(6.61) ![]() (6.62)
(6.62) ![]() (6.63)
(6.63)
По своей форме графики зависимостей (6.61)—(6.63) аналогичны кривым, изображенным на рис. 6.12 с той лишь разницей, что их скорость изменения больше, чем при R > 2![]() . Значение R = 2
. Значение R = 2![]() носит название критического сопротивления контура.
носит название критического сопротивления контура.
6.5. Включение RLC-контура на постоянное и гармоническое напряжение
Включение RLC-контура на постоянное напряжение
Рассмотрим случай нулевых начальных условий uC(0–) = 0, i(0–) = 0, когда RLC-контур включается на постоянное напряжение (рис. 6.14).
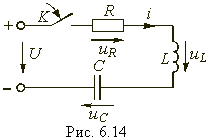
Отличие данного случая от рассмотренного выше заключается в нулевых начальных условиях и наличии принужденной составляю щей uCпр = U. Свободная составляющая uCсв определяется, как и ранее, уравнениями (6.43), (6.51) или (6.59) в зависимости от вида корней р1 и р2. Постоянные интегрирования А1 и А2 находятся при этом из начальных условий i(0–) = 0, uC(0–) = 0 и законов коммутации для i и uC. Определим, например, закон изменения uC, i и uL в случае, когда корни р1 и р2 — вещественные и различные. При этом uC св определяются уравнением (6.43), а напряжение uC и ток i имеют следующий вид: 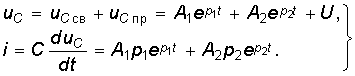 (6.64)
(6.64)
Для нахождения коэффициентов А1 и А2 используем начальные условия uC(0– ) = 0 и i(0– ) = 0, а также законы коммутации, определяемые выражениями (6.1),(6.2): ![]() (6.65)
(6.65)
Тогда ![]() (6.66)
(6.66)
Окончательные уравнения для иС, i, иL имеют вид 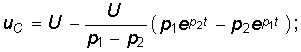 (6.67)
(6.67) 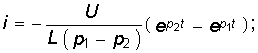 (6.68)
(6.68) 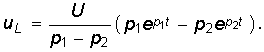 (6.69)
(6.69)
На рис. 6.15 изображены графики зависимостей (6.67)—(6.69), где моменты времени t1 и t2 определяются уравнениями (6.49). Сравнение формул (6.67)—(6.69) с (6.46)—(6.48) показывает, что ток i и напряжение иL отличаются только знаком, а напряжение иС — наличием постоянной составляющей U.
Аналогичным можно найти уравнения напряжений и тока для случая R < 2![]() :
: 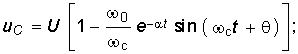 (6.70)
(6.70) 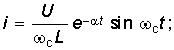 (6.71)
(6.71) 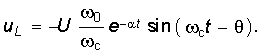 (6.72)
(6.72)
На рис. 6.15 штриховой линией показана зависимость (6.70), которая свидетельствует о колебательном характере заряда емкости. Таким же образом можно получить уравнения для uC, i и uL для случая критического заряда емкости С при R = 2![]() .
.
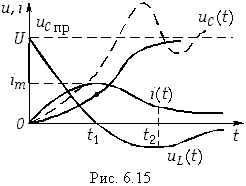
Включение RLC-контура на гармоническое напряжение
При включении RLC-контура на гармоническое напряжение u = Umsin(![]() t +
t + ![]() u ) принужденная составляющая напряжения на емкости
u ) принужденная составляющая напряжения на емкости ![]() (6.73) где
(6.73) где ![]() C =
C = ![]() u +
u + ![]() —
— ![]() /2. Здесь фазовый сдвиг между током в контуре и приложенным напряжением
/2. Здесь фазовый сдвиг между током в контуре и приложенным напряжением ![]() (6.74) а амплитуда принужденного напряжения на емкости
(6.74) а амплитуда принужденного напряжения на емкости 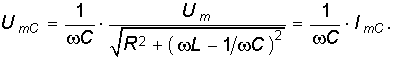 (6.75)
(6.75)
Учитывая, что колебательный контур в радиотехнических устройствах, как правило имеет высокую добротность, т. е. выполняется условие R ![]() 2
2![]() , то свободная составляющая uCсв определяется уравнением (6.51), и закон изменения напряжения на емкости будет иметь вид
, то свободная составляющая uCсв определяется уравнением (6.51), и закон изменения напряжения на емкости будет иметь вид ![]() (6.76)
(6.76)
Взяв производную от выражения (6.76), и учтя, что для заданного контура ![]() , получим уравнение тока
, получим уравнение тока ![]() (6.77)
(6.77)
Постоянные интегрирования A и ![]() находим из начальных условий и законов коммутации:
находим из начальных условий и законов коммутации:  (6.78)
(6.78)
Откуда 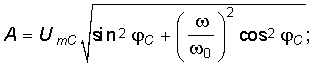 (6.79)
(6.79) ![]() (6.80)
(6.80)
Подставив значения А и ![]() из уравнений (6.79), (6.80) в (6.76) и (6.77), получим окончательный закон изменения напряжения на емкости и тока в RLC-контуре:
из уравнений (6.79), (6.80) в (6.76) и (6.77), получим окончательный закон изменения напряжения на емкости и тока в RLC-контуре: 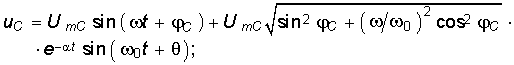 (6.81)
(6.81) 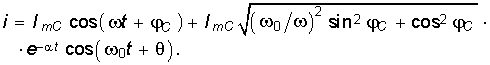 (6.82)
(6.82)
Анализ уравнений (6.81), (6.82) показывает, что в случае, когда частота приложенного напряжения ![]() существенно превышает резонансную частоту контура
существенно превышает резонансную частоту контура ![]() 0 при
0 при ![]() C
C ![]() 0 в цепи могут возникнуть сверхнапряжения, а в случае
0 в цепи могут возникнуть сверхнапряжения, а в случае ![]() и
и ![]() C
C ![]()
![]() /2 — сверхтоки.
/2 — сверхтоки.
Если частота задающего напряжения ![]() =
= ![]() 0, то при этом в цепи возникают явления изохронизма, когда напряжение на емкости и ток в контуре плавно изменяется в соответствии с уравнениями:
0, то при этом в цепи возникают явления изохронизма, когда напряжение на емкости и ток в контуре плавно изменяется в соответствии с уравнениями: ![]() (6.83)
(6.83) ![]() (6.84)
(6.84)
При этом переходный процесс протекает без перенапряжений и сверхтоков (рис. 6.16, а).
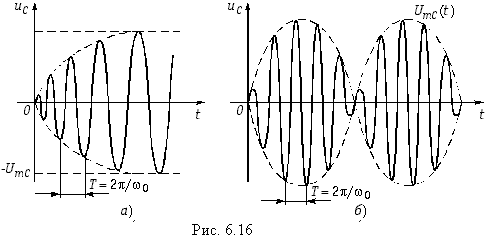
В случае, когда частота заданного напряжения ![]() и резонансная частота контура
и резонансная частота контура ![]() 0 близки между собой, то в контуре возникают явления биений. Положим, что a = 0, тогда
0 близки между собой, то в контуре возникают явления биений. Положим, что a = 0, тогда 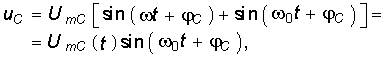 (6.85) где UmС(t) = 2UmСсos
(6.85) где UmС(t) = 2UmСсos![]() t — амплитуда биений с угловой частотой
t — амплитуда биений с угловой частотой ![]() = (
= (![]() —
— ![]() 0 )/2. На рис. 6.16, б, показан график изменения напряжений биений (6.85).
0 )/2. На рис. 6.16, б, показан график изменения напряжений биений (6.85).
При расчете переходных процессов в разветвленных цепях классическим методом составляется система уравнений для мгновенных значений токов и напряжений по ЗТК и ЗНК. Затем полученная система сводится к дифференциальному уравнению соответствующего порядка относительно выбранной независимой переменной (иС или iL). После этого полученное уравнение решается по аналогии с уравнениями, рассмотренными в 6.2. Классический метод расчета переходных процессов, 6.3. Переходные процессы в цепях первого порядка, 6.4. Переходные процессы в цепях второго порядка, 6.5. Включение RLC-контура на постоянное и гармоническое напряжение.
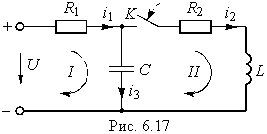
В качестве примера рассмотрим разветвленную цепь второго порядка, изображенную на рис. 6.17. Для данной цепи имеем ненулевые начальные условия: uC(0– ) = U; iL(0– ) = 0. Составим для нее систему уравнений по законам Кирхгофа: 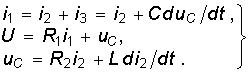 (6.86)
(6.86)
Выберем в качестве независимой переменной i2 = iL и, решая (6.86) относительно i2, получаем: 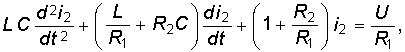 (6.87) т. е. выражение (6.87) есть неоднородное дифференциальное уравнение второго порядка, аналогичное (6.37). Его решение, как обычно, находим в виде
(6.87) т. е. выражение (6.87) есть неоднородное дифференциальное уравнение второго порядка, аналогичное (6.37). Его решение, как обычно, находим в виде ![]() (6.88) где i2np = U/(R1 + R2), а i2св определим из решения однородного дифференциального уравнения
(6.88) где i2np = U/(R1 + R2), а i2св определим из решения однородного дифференциального уравнения 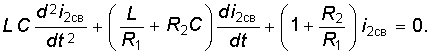 (6.89)
(6.89)
Решение последнего имеет вид, аналогичный (6.43), (6.51) или (6.59) в зависимости от вида корней характеристического уравнения 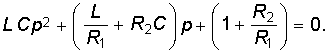 (6.90)
(6.90)
Постоянные интегрирования определяются из начальных условий и законов коммутации, причем для нахождения иС используется система уравнений (6.86). Например, для случая вещественных и различных корней при R1 = R2 = R получим 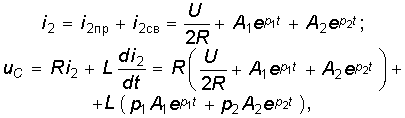 где A1 и А2 определяются из начальных условий и законов коммутации:
где A1 и А2 определяются из начальных условий и законов коммутации: 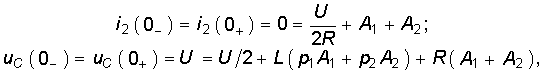
откуда 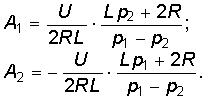
На рис. 6.18 изображены графики uC(t) и i2(t).
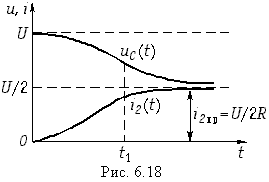
Как следует из вышеуказанного, для определения характера переходного процесса и записи уравнения свободной составляющей независимой переменной необходимо располагать характеристическим уравнением цепи. Это уравнение может быть получено из соответствующего дифференциального уравнения цепи или из анализа ее операторного сопротивления. Последнее может быть получено, если в уравнении для комплексного сопротивления цепи Z = Z(j![]() ) заменить оператор j
) заменить оператор j![]() на р и приравнять его к нулю:
на р и приравнять его к нулю: ![]() (6.91)
(6.91)
Например для цепи, изображенной на рис. 6.17, имеем: 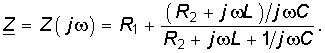
Отсюда 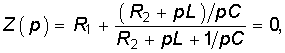 или после преобразований
или после преобразований 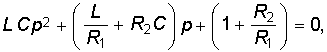 что полностью совпадает с (6.90).
что полностью совпадает с (6.90).
Таким образом, отпадает необходимость преобразовывать систему уравнений к одному уравнению для выбранной независимой переменной.
В заключение следует отметить, что применение классического метода расчета к цепям более высокого порядка встречает определенные трудности. Главное из них резко возрастающий объем необходимых вычислений, связанных с решением задач уравнений высокого порядка. В этой связи в последнее время все большее применение находят другие методы расчета переходных процессов: метод переменных состояний, операторный и частотные методы, которые будут рассмотрены ниже.
6.7. Метод переменных состояния
В настоящее время для анализа переходных процессов в цепях широкое применение находит метод переменных состояния, позволяющий при расчетах эффективно использовать ЭВМ. Суть метода заключается в том, что переходный процесс в цепи рассматривается как траектория в m-мерном пространстве (где т — порядок цепи) с начальной точкой при t = 0 (начальное состояние) и конечной при t = ![]() . Например, переходный процесс в последовательном RLC-контуре (см. 6.4. Переходные процессы в цепях второго порядка, апериодический разряд и рис. 6.12) можно в пространстве состояний представить кривой, изображенной на рис. 6.19, где iL(0) = 0 и uC(0) = U характеризуют начальное состояние цепи, а iL(t) и uC(t) определяют состояние цепи в любой заданный момент времени. Достоинства этого метода — наглядность, простота, удобство программирования на ЭВМ, возможность анализа как линейных, так и нелинейных цепей, а также цепей с переменными параметрами.
. Например, переходный процесс в последовательном RLC-контуре (см. 6.4. Переходные процессы в цепях второго порядка, апериодический разряд и рис. 6.12) можно в пространстве состояний представить кривой, изображенной на рис. 6.19, где iL(0) = 0 и uC(0) = U характеризуют начальное состояние цепи, а iL(t) и uC(t) определяют состояние цепи в любой заданный момент времени. Достоинства этого метода — наглядность, простота, удобство программирования на ЭВМ, возможность анализа как линейных, так и нелинейных цепей, а также цепей с переменными параметрами.
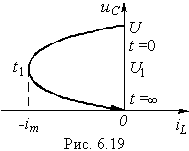
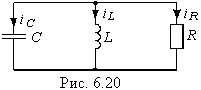
Поясним сущность данного метода на примере цепи, находящейся при ненулевых начальных условиях: iL(0) = i0, uC(0) = u0 (рис. 6.20). Для этой цепи при t ![]() 0 можно записать:
0 можно записать: 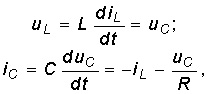 или
или 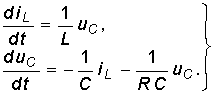 (6.92)
(6.92)
Уравнения (6.92) называются уравнениями состояния цепи, а iL и uC — переменными состояния. Начальные условия iL(0) = i0 и uC(0) = u0 определяют с помощью (6.92) состояния цепи в любой момент t ![]() 0. Величины iL и uC можно считать компонентами вектора состояния х:
0. Величины iL и uC можно считать компонентами вектора состояния х: ![]()
Тогда (6.92) можно переписать в матричной форме: ![]() (6.93) где
(6.93) где ![]()
В случае, если цепь находится после коммутации под воздействием источников, уравнение состояния принимает вид ![]() (6.94) где w(t) — вектор воздействий источников; В — матрица параметров цепи.
(6.94) где w(t) — вектор воздействий источников; В — матрица параметров цепи.
Например, для случая включения RLC-контура на постоянное напряжение уравнение состояния имеет вид (6.94), где ![]()
Зная состояние цепи х(t), реакцию цепи y(t) (токи и напряжения в любой ветви) можно найти как линейную комбинацию векторов состояния х(t) и входных воздействий w(t): ![]() (6.95) где у(t) — вектор искомых реакций цепи; С, D — матрицы, зависящие только от параметров цепи. Уравнение (6.95) называют уравнением реакции цепи.
(6.95) где у(t) — вектор искомых реакций цепи; С, D — матрицы, зависящие только от параметров цепи. Уравнение (6.95) называют уравнением реакции цепи.
Так, если в качестве компонентов вектора у(t) в предыдущем примере RLC-контура взять uR и uL, то искомые реакции цепи (uR и uL) определяются согласно системе уравнений: ![]() которую можно переписать в форме (6.95), где
которую можно переписать в форме (6.95), где ![]()
Следует подчеркнуть, что уравнения (6.93)—(6.95) справедливы для линейных цепей с постоянными параметрами (матрицы А, В, С, D не зависят от t). Для цепей с переменными параметрами (параметрические цепи) матрицы А(t), B(t), C(t), D(t) являются функциями времени.
Уравнения (6.94), (6.95) — основные в методе переменных состояний. Для решения уравнений состояния могут использоваться как аналитические, так и численные методы. Аналитически уравнение (6.94) может быть решено в области как действительного переменного t, так и комплексного переменного р. Рассмотрим некоторые основные методы решения уравнения состояния.
Метод матричных экспонент
Решение этим методом ищут в форме 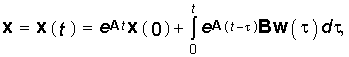 (6.96) где е At — матричная экспонента (матрица перехода). Из (6.96) следует, что решение уравнения состояния содержит два слагаемых: первое — реакция цепи при нулевом входном сигнале; второе — реакция цепи при нулевом начальном состоянии.
(6.96) где е At — матричная экспонента (матрица перехода). Из (6.96) следует, что решение уравнения состояния содержит два слагаемых: первое — реакция цепи при нулевом входном сигнале; второе — реакция цепи при нулевом начальном состоянии.
Для вычисления е At обычно используют разложение ![]() (6.97)
(6.97)
Пример. Найдем матрицу перехода для схемы, изображенной на рис. 6.21.
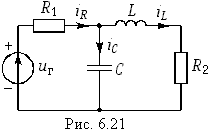
Матрицы А и В для данной схемы имеют следующий вид: ![]()
Примем L = 0,55 Гн, С = 0,5 Ф, R1 = 1 Ом, R2 = 3,5 Ом, е(t) = 1 В, iL = 0, uC = 1 В. Тогда ![]()
Согласно (6.97) матрица перехода примет вид 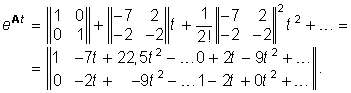
Таким образом, матрица перехода представляет собой квадратную матрицу порядка п с элементами в форме рядов от t. Подставив значение е At в уравнение (6.96), можно определить после интегрирования искомое решение x(t).
Следует, однако, отметить, что ряд (6.97) сходится медленно и использование уравнения (6.96) требует большого объема вычислений, поэтому вместо (6.96) обычно используют итерационную процедуру для дискретных моментов времени tn = n![]() t = nh, где h =
t = nh, где h = ![]() t достаточно малый шаг:
t достаточно малый шаг: 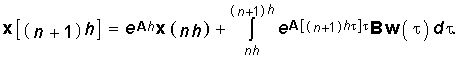 (6.98)
(6.98)
Интеграл в (6.98) вычисляется численными методами (методом прямоугольников, трапеций, Симпсона и др.). Так, при использовании метода прямоугольников алгоритм (6.98) приобретает вид ![]() (6.99)
(6.99)
При нулевом входном сигнале w = 0 (свободные колебания) ![]() (6.100)
(6.100)
Если ограничиться в разложении (6.97) только первыми двумя членами e Ah ![]() I + Ah, то получим
I + Ah, то получим ![]() (6.101)
(6.101)
Алгоритм (6.101) легко программируется на ЭВМ и имеет ясный физический смысл. Он определяет положение точки в пространстве состояний на (n + 1)-м шаге, исходя из ее состояния на n-м шаге при аппроксимации траектории на участке h прямолинейным отрезком с постоянной скоростью ![]() (h).
(h).
Пример. Рассчитать траекторию состояний, изображенную на рис. 6.19, используя аппроксимацию ее на каждом из m участков величины h в форме прямолинейных отрезков. Скорость изменения состояния ![]() (h) на каждом из выделенных участков остается постоянной.
(h) на каждом из выделенных участков остается постоянной.
На основании уравнения состояния (6.93) имеем: для момента t = 0; ![]() (0) = Ах(0); для момента t = h
(0) = Ах(0); для момента t = h ![]() для момента t = 2h
для момента t = 2h ![]() для момента t = (n + 1)h
для момента t = (n + 1)h ![]() т. е. полученное уравнение полностью совпадает с (6.101).
т. е. полученное уравнение полностью совпадает с (6.101).
Метод Рунге—Кутта — метод численного решения уравнения состояния (6.94), при котором интервал 0…t разбивается на ” т ” малых участков ![]() t = h, на каждом из которых значение переменной х определяется с помощью линейной комбинации некоторых вспомогательных функций ki (h) с постоянными коэффициентами. В зависимости от способа выбора коэффициентов и требуемой точности решения существуют различные модификации алгоритмов Рунге — Кутта.
t = h, на каждом из которых значение переменной х определяется с помощью линейной комбинации некоторых вспомогательных функций ki (h) с постоянными коэффициентами. В зависимости от способа выбора коэффициентов и требуемой точности решения существуют различные модификации алгоритмов Рунге — Кутта.
Проиллюстрируем суть метода Рунге—Кутта на примере скалярного уравнения состояния ![]() (6.102)
(6.102)
Наиболее распространенный алгоритм Рунге—Кутта имеет вид 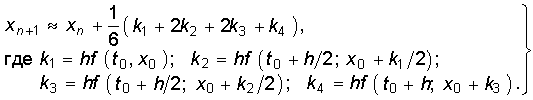 (6.103)
(6.103)
При этом порядок погрешности составляет h 5.
Пример. Решить скалярное уравнение состояния (6.102) на интервале [0; t ] методом Рунге—Кутта при условии A = 1; х(0) = 1.
Разобьем интервал [0; t ] на 10 участков с шагом h = 0,1. Тогда в соответствии с алгоритмами (6.103) можем получить для t = 0, х(0) = 1 (первый шаг): 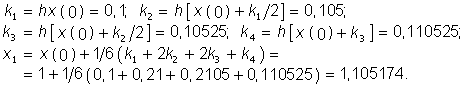
Аналогично на втором шаге ![]()
Как следует из (6.103), для определения х необходимо вычислить f (t, x) в четырех точках.
Аналогично записывается алгоритм Рунге—Кутта для системы уравнений типа (6.102). Например, для случая системы из двух уравнений 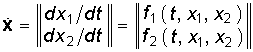 алгоритм (6.103) примет вид
алгоритм (6.103) примет вид 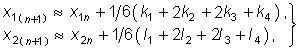 (6.104) где
(6.104) где 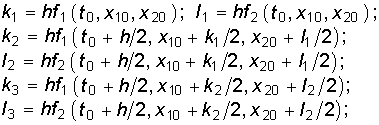
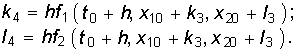
Частным случаем метода Рунге—Кутта является прямой алгоритм Эйлера (при k2 = k3 = k4 = 0). Однако он имеет малую точность и не нашел широкого применения.
Разностные методы
Существенным недостатком метода Рунге—Кутта является то, что для получения каждого значения решения х необходимо вычислять правую часть уравнения (6.94) в нескольких точках (для алгоритма (6.103) — в четырех точках). Это приводит к большому объему вычислений, особенно для сложной правой части. Применение разностных методов позволяет существенно сократить объем вычислений и затраты машинного времени, так как на каждом шаге правая часть вычисляется только один раз.
В основе разностных методов лежит использование различных интерполяционных алгебраических многочленов (многочлены Ньютона, Стирлинга, Эрмита и др.). При этом решение x на (n + 1) шаге определяется алгоритмом 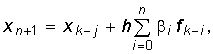 (6.105) где h — шаг;
(6.105) где h — шаг; ![]() i — постоянные коэффициенты; fk — значение алгебраического многочлена в точке k. Как следует из (6.105) для определения решения хk+j; необходимо знать значения х1, х2, …, хj — они находятся обычно либо аналитически, либо методом Рунге—Кутта.
i — постоянные коэффициенты; fk — значение алгебраического многочлена в точке k. Как следует из (6.105) для определения решения хk+j; необходимо знать значения х1, х2, …, хj — они находятся обычно либо аналитически, либо методом Рунге—Кутта.
6.8. Вопросы и задания для самопроверки
- Каковы причины возникновения переходных процессов?
- Сформулировать законы коммутации.
- Дать понятия переходного, установившегося и свободного режимов в электрических цепях.
- Что такое нулевые и ненулевые начальные условия?
- Какой вид имеет свободная составляющая переходных колебаний в цепях первого порядка?
- Что представляет собой принужденная составляющая?
- Как рассчитываются постоянные интегрирования в цепях первого порядка?
- Что такое постоянная времени цепи?
- Для схемы, изображенной на рис. 6.22, определить ток i(t) и напряжение на катушке индуктивности uL(t), если U = 90 В; L = 0,25 Гн; R1 = 20 Ом; R2 = R3 = 5 Ом.
Ответ: i(t) = 3,6 – 1,6е–100t, А; uL(t) = 40е–j100t, В.
- Для схемы, изображенной на рис. 6.23, найти uС(t), если U = 60 В; R1 = R2 = R3 = 5 кОм; С = 2,5 мкФ.
Ответ: uС(t) = 60 – 30е–40t, В.
- Как зависит характер свободных колебаний в RLC-контуре от расположения на комплексной плоскости корней характеристического уравнения?
- Как определяются частота и период свободных колебаний?
- Что такое логарифмический декремент затухания?
- Какова последовательность анализа переходных процессов в разветвленных цепях второго порядка?
- Для схемы, приведенной на рис. 6.24, найти iL(t) и uС(t), если U = 100 В; L = 50 мГн; С = 5 мкФ; R = 25 Ом.
Ответ: iL(t) = 0,29е–540t – 0,29е–7460t, А; uС(t) = 100 + 8е–540t – 108е–7460t, В.
- Для схемы, приведенной на рис. 6.25, найти i(t) и uС(t), если U = 60 В; R1 = 250 Ом; R2 = 50 Ом; L = 50 мГн; C = 0,5 мкФ.
Ответ: i(t) = 0,22е–2500tsin(5800t + 67°), А; uС(t) = 60 + 69е–2500tsin(5800t – 46,5°), В.
- В чем заключается суть метода переменных состояния? Что понимают под переменными состояния?
- Что такое уравнения состояния цепи? Какова его матричная форма записи?
- В чем сущность метода матричных экспонент?
- Суть метода Рунге-Кутта.
- Что лежит в основе методов решения уравнения состояния цепи?

 ,
,
 ;
;












