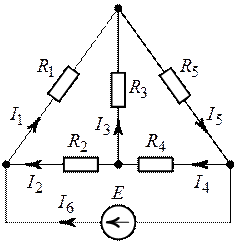
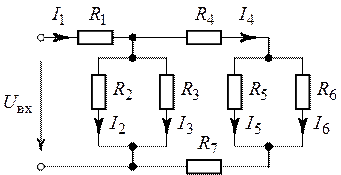Рассмотрим типовую задачу с ключом, который немного изменяет электрическую схему. Основной материал для повторения: формулы последовательного и параллельного подключения резисторов, закон Ома, выражение для мощности.
Задача:
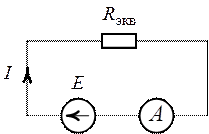
Источник тока, два резистора и ключ включены в цепь, как показано на рисунке. При разомкнутом ключе на резисторе R₁ выделяется мощность P₁ = 2 Вт, а на резисторе R₂ — мощность P₂ = 1 Вт. Какая мощность будет выделяться на резисторе R₂ после замыкания ключа К? Внутренним сопротивлением источника пренебречь. Ответ дайте в ваттах.
Решение:
Схема с ключами всегда пугает учащихся. По началу кажется, что контуров такой цепи больше, чем на самом деле. Здесь нужно понимать, что разомкнутый ключ представляет собой обычный разрыв цепи. При этом даже не конденсатор, способный накапливать заряд и влиять на переходной процесс, а просто разрыв цепи. То есть ток туда не идет. Это и есть наш первый случай. В первой ситуации мы имеем два последовательных резистора, соединенных с ЭДС, при этом в цепи идет один ток, цепь состоит их одного контура.
Что меняется, когда мы замыкаем ключ К ? Ток начинает течь через меньшее сопротивление, то есть через провод с ключом. Это называется шунтированием резистора R₁. Ток через R₁ уже не течет, а обходит его через параллельный провод. Ток – существо ленивое, всегда идет в обход 🙂
Давайте я перерисую схему, чтобы было наглядно:
Как видите, схемы заметно упростились, что дает нам возможность приступить к решению задачи, расписывая основные законы электричества для двух разных случаев.
До замыкания ключа:
Имеем последовательное соединение двух резисторов. Выразим мощности, которые на них выделяются и которые изначально даны в условии.
Возьмем отношение этих мощностей, выразим через него отношение сопротивлений, которое нам понадобится в дальнейшем:
После замыкания ключа:
Шунтируется резистор R₁. Схема начинает работать только через резистор R₂. Выразим мощность, которая на нем выделяется.
Теперь рассмотрим отношение мощности, выделяемом на резисторе R₂ до замыкания ключа, к мощности, выделяемой на этом же резисторе R₂ после замыкания ключа. Отношения этих мощностей выражаются через отношение сопротивлений резисторов R₁/R₂, а это отношение соответственно выражается через отношение мощностей P₁/P₂, которое нам известно из условия (до замыкания ключа). Собираем всё вместе и получаем:
Ответ: на резисторе R₂ будет выделяться 9 Ватт после замыкания ключа.
Решение целиком:
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
1
.
Рассмотрим электрическую цепь (рис.
20.4.1), состоящую из двух параллельных
ветвей, в одну из которых подключена
катушка индуктивности L,
а во вторую ветвь проводник сопротивлением
R. В каждую
ветвь цепи подключена лампочка. ЭДС
источника тока обозначена Е.
При замыкании
ключа К лампа Л2 загорается после лампы
Л1. В катушке с ростом силы тока в цепи
от 0 появляется ток самоиндукции
,
направленный противоположно току
I.
Поэтому сила тока в катушке позже
достигает максимального значения.
Выведем формулу изменения силы тока.
По второму закону Кирхгофа для замкнутого
контура можно записать
.
Подставляя ЭДС
индукции
получаем
,
.
Умножив и разделив
правую часть соотношения на величину
сопротивления
,
получаем
.
Проводя преобразования,
учли, что ЭДС источника тока можно
считать постоянной величиной, поэтому
ее дифференциал равен нулю
.
Проведем разделение
переменных и проинтегрируем обе части
уравнения
.
Неопределенный
интеграл определяется с точностью до
постоянной С,
поэтому можно записать
или
.
(20.4.1)
В начальный момент
времени t
= 0 и тока нет
= 0. Подставим
эти значения в формулу (20.4.1), получим
.
(20.4.2)
Учитывая (20.4.2),
можно записать
.
Найдем силу тока
(20.4.3)
Из соотношения
(20.4.3) следует, что сила тока в цепи
постепенно увеличивается от 0 до
максимального значения, которое равно
.
Подставляя в
формулу (20.4.3) значения силы тока I
= 0 в начальный момент времени t=
0, получаем
П
ри
увеличении времени
сила тока достигает значения
.
График возрастания
силы тока со временем представлен на
(рис. 20.4.2). Чем больше индуктивность
катушки (
),
тем позже сила тока принимает максимальное
значение.
2
.
Рассмотрим электрическую цепь, содержащую
последовательно соединенные лампу Л и
катушку большой индуктивности L (рис.
20.4.3). В цепи первоначально идет ток силой
тока I.
При размыкании ключа сила тока в цепи
уменьшается. В катушке возникает ток
самоиндукции
,
сонаправленный с током I,
поэтому сила тока в цепи уменьшается
до нуля не сразу, а постепенно. При
большой индуктивности катушки L сила
тока самоиндукции может стать больше
чем I,
тогда лампа Л вспыхивает, а затем гаснет.
Выведем формулу изменения силы тока в
цепи. Запишем второй закон Кирхгофа
(20.4.4)
При размыкании
ключа
.
Подставим ЭДС
самоиндукции
,
в формулу (20.4.4)
.
Проведем разделение
переменных
I и t
.
Проинтегрируем
полученное выражение
.
Учтем, что
неопределенный интеграл определен с
точность до постоянной С
.
Найдем силу тока
.
Постоянную С
определим из начальных условий: при
значение
;
.
Подставляя
постоянную, получаем формулу изменения
силы тока при размыкании цепи
(20.4.5)
Из выражения
(20.4.5) следует, что при
размыкании цепи cила
тока уменьшается со временем по
экспоненциальному закону:
при
,
.
Чем больше индуктивность катушки
,
тем позже сила тока в цепи уменьшается
до нуля (рис. 20.4.4).
В
ремя
релаксации
– это время, за которое сила тока в цепи
уменьшается в e = 2,71 раз. Подставим данное
условие в формулу (20.4.3) и, преобразуя,
получим
. (20.4.4)
С другой стороны
по определению
времени релаксации
.
.
(20.4.5)
Сравнивая формулы
(20.4.4) и (20.4.5), получаем
;
.
Время релаксации
зависит от параметров цепи: индуктивности
катушки и сопротивления. На практике
сила тока в цепи уменьшается до нуля за
время равное
.
В промышленности
при больших индуктивностях катушек ток
самоиндукции
может стать очень большим, что приведет
к пробою изоляции и аварии. Поэтому силу
тока в цепи уменьшают постепенно,
увеличивая сопротивление с помощью
реостатов.
Оба рассмотренных
случая размыкания и замыкания цепи
показывают: чем больше индуктивность
(L),
тем позже ток достигает максимального
или минимального значений. Этим свойством
индуктивность похожа на массу в механике.
Индуктивность является мерой инертности
в электромагнитных явлениях.
Соседние файлы в предмете Физика
- #
- #
- #
ЭДС разомкнутой и замкнутой цепи



Теоретические сведения
В одной из прошлых тем (условия существования электрического тока) уже затрагивался вопрос о необходимости источника питания для длительного поддержания существования электрического тока. Сам по себе ток, конечно же, можно получать и без таких источников питания. Например, разрядка конденсатора при вспышке фотоаппарата. Но такой ток будет слишком скоротечным. Кулоновские силы всегда стремятся свести разноименные заряды, выровняв тем самым потенциалы по всей цепи. А, как известно, для наличия поля и тока необходима разность потенциалов. Поэтому никак нельзя обойтись без каких-либо других сил, разводящих заряды и поддерживающих разность потенциалов.
Определение. Сторонние силы – силы неэлектрического происхождения, направленные на разведение зарядов.
Эти силы могут быть разной природы в зависимости от типа источника. В батареях они химического происхождения, в электрогенераторах – магнитного. Они-то и обеспечивают существование тока, так как работа электрических сил по замкнутому контуру всегда равна нулю.
Вторая задача источников энергии, помимо поддержания разности потенциалов, – это восполнение потерь энергии на столкновении электронов с другими частицами, вследствие чего первые теряют кинетическую энергию, а внутренняя энергия проводника повышается.
Сторонние силы внутри источника выполняют работу против электрических сил, разводя заряды в стороны, противоположные их естественному ходу (как они движутся во внешней цепи) (рис. 2).
Роль источника тока: разделить заряды за счет совершения работы сторонними силами. Любые силы, действующие на заряд, за исключением потенциальных сил электростатического происхождения (т. е. кулоновских) называют сторонними силами. (Сторонние силы объясняются электромагнитным взаимодействием между электронами и ядрами)
Рис. 2. Схема действия сторонних сил
Аналогом действия источника питания можно считать водяной насос, который пускает воду против ее естественного хода (снизу вверх, в квартиры). Обратно же вода естественным образом под действием силы тяжести спускается вниз, но для непрерывной работы водоснабжения квартиры необходима непрерывная работа насоса.
Электродвижущая сила
ЭДС — энергетическая характеристика источника. Это физическая величина, равная отношению работы, совершенной сторонними силами при перемещении электрического заряда по замкнутой цепи, к этому заряду:
Измеряется в вольтах (В).

Еще одна характеристика источника — внутреннее сопротивление источника тока: r.
ЭДС разомкнутой и замкнутой цепи
Рассмотрим следующую цепь (рис. 3):
Рис. 3. ЭДС разомкнутой цепи
При разомкнутом ключе и идеальном вольтметре (сопротивление бесконечно велико) никакого тока в цепи не будет, и внутри гальванического элемента будет совершаться только работа по разделению зарядов. В этом случае вольтметр покажет значение ЭДС.

Здесь: U – напряжение на внешней цепи (на нагрузке и подводящих проводах); U1 – напряжение внутри гальванического элемента.
3) 
Энергетические преобразования в цепи:

(А — работа сторонних сил; Авнеш.— работа тока на внешнем участке цепи сопротивлением R; Авнутр.— работа тока на внутреннем сопротивлении источника r.)
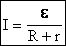
1. Если R>>r, то ε=U. Измеряют высокоомным вольтметром при разомкнутой внешней цепи.
3. На внутреннем участке цепи: Aвнутр=U1q , на внешнем участке цепи: Aвнеш=U2q.
A=Aвнутр+ Aвнеш. Тогда: εq=U1q+U2q. Следовательно: ε= U1+U2
ЭДС источника тока равна сумме падений напряжений на внешнем и внутреннем участках цепи.
4. Если R растет, то I уменьшается. 
Источник
Напряжение при разомкнутом ключе формула
На рисунке показана цепь постоянного тока, содержащая источник тока с ЭДС и два резистора:
и
В начальный момент времени ключ К был замкнут. Если ключ К разомкнуть, то как изменятся следующие три величины: сила тока через резистор
; напряжение на резисторе
; суммарная тепловая мощность, выделяющаяся на внешнем участке цепи? Внутренним сопротивлением источника тока пренебречь.
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
резистор Напряжение
на резисторе Суммарная
Если ключ К замкнут, то резистор закорочен (к нему параллельно подсоединён провод с нулевым сопротивлением). При этом ток через него не течёт, напряжение на нём равно нулю. Если ключ К разомкнут, то через резистор
течёт ток, а значит, на нём, согласно закону Ома для участка цепи
падает ненулевое напряжение. Таким образом, напряжение на резисторе
при размыкании ключа увеличивается.
Сила тока в цепи связана с ЭДС и сопротивлением нагрузки соотношением: При размыкании ключа сопротивление нагрузки увеличивается (было
а стало
). Следовательно, сила тока через резистор
уменьшается.
Остается разобраться с суммарной тепловой мощностью. Она зависит от полного сопротивления нагрузки:
Так как сопротивление нагрузки увеличивается, выделяющаяся мощность уменьшается.
Источник
Замкнутая и разомкнутая электрическая цепь
Вы будете перенаправлены на Автор24
Электрической цепью называют совокупность различных устройств, которые соединены конкретным способом. Устройства должны обеспечивать путь для протекания электрического тока. Существуют различные элементы цепей, служащие для множества целей. Для описания цепей используют специальные электрические схемы.
В состав любой электрической цепи входят различные элементы:
- Источник тока. Им, например, может быть катушка индуктивности, по которой какое-то время шёл ток внешнего источника.
- Проводники;
- Нагрузка (в случае, когда она постоянна, вольтамперная характеристическая кривая представляет собой прямую линию, а такая нагрузка зовётся линейной;
- Устройства защиты;
- Устройства коммутации.
Различают два вида элементов цепей: пассивные и активные. Пассивные представляют собой соединительные элементы и приборы-потребители электроэнергии, также к пассивным элементам относятся конденсаторы. Активные элементы — это электродвигатели, заряжающиеся аккумуляторы и различные источники ЭДС.
Основными видами электрической цепи являются:
- замкнутая цепь;
- разомкнутая цепь.
Замкнутая электрическая цепь
Замкнутая электрическая цепь представляет собой наиболее простой вариант соединения. Она состоит из источника электроэнергии, потребителя энергии и соединительных элементов в виде обычных проводов. Провода в цепи обязательно должны иметь соответствующую изоляцию.
Для обеспечения стабильной и безопасной работы электрической цепи ее снабжают дополнительными элементами. Обычно это различные электроизмерительные приборы, с помощью которых можно узнать величину токов и напряжения в системе, а также оборудование, предназначенное для замыкания и размыкания цепи.
Все замкнутые электрические цепи делят на две основные части:
Готовые работы на аналогичную тему
Внутренний участок цепи – непосредственно источник электроэнергии у потребителя.
Внешний участок цепи – система, которая состоит из одного или многих потребителей электроэнергии, а также соединительных проводов и приборов. Все они должны иметь отношение к функционированию замкнутой электрической цепи.
Закон Ома для замкнутой цепи
Закон Ома для замкнутой цепи показывает определенное значение тока. Оно зависит от сопротивления источника, а также от сопротивления нагрузки.
Величина тока в замкнутой цепи, которая состоит из источника цепи, будет равняться отношению электродвижущей силы источника к сумме внешнего и внутреннего сопротивлений. При этом источник тока должен обладать внешним и внутренним нагрузочным сопротивлением.
Такая зависимость была установлена экспериментальным путем в начале 19 века известным ученым Георгом Омом. Он смог описать результаты собственных опытов на математическом уровне.
Закон Ома для замкнутой цепи можно записать следующим образом:
- $varepsilon$ — электродвижущая сила источника напряжения;
- $R$ — сопротивление всех внешних элементов цепи, например, проводников;
- $r$ — внутреннее сопротивление источника напряжения;
- $I$ – сила тока в цепи.
Расчет для определенного сопротивления:
После подстановки полученных значений, формула приобретает такой вид:
Физический смысл закона Ома для замкнутой цепи
Замкнутую электрическую цепь образуют потребители энергии только в совокупности с источником тока. Проходящий через потребителя ток течет обратно на его источник. Поэтому току достается сопротивление проводника и источника. Из этого складывается общее сопротивление замкнутой цепи, предполагающее наличие двух основных компонентов: сопротивления источника и сопротивления потребителя.
Зависимость тока от электродвижущей силы источника и сопротивления цепи состоит в следующем: при увеличении электродвижущей силы увеличивается энергия носителей зарядов. Это означает, что становится больше скорость движения зарядов в упорядоченном виде. Если увеличивать размер сопротивления цепи, то величина тока будет уменьшаться.
Электрический ток проходит непосредственно по замкнутой цепи. Необходимым условием присутствия электрического тока в цепи является надежное соединение проводниками источника электрической энергии с ее потребителями.
Источники электроэнергии для различной аппаратуры: генераторы, аккумуляторы, гальванические элементы.
В различных устройствах могут быть определенные потребители электрической энергии. Чаще всего их представляют в виде ламп или электродвигателей.
Для соединения источников и потребителей в единую цепь применяют проводники из металлических материалов. Они могут быть различной формы, длины, толщины, обладать определенными техническими характеристиками. Часто применяются проводники, которые изолированы друг от друга.
Для возникновения тока нужно соединить две точки. Одна из точек должна иметь избыток электронов по отношению ко второй точке. Специалисты называют это действие созданием разности потенциалов между точками. Источник тока служит основным элементом для создания разности потенциалов в электрической цепи.
Любой потребитель электрической энергии может являться нагрузкой в цепи. Нагрузка создает сопротивление электрическому току.
Электрический ток активно используют при создании искусственного освещения. Электрические простые лампы служат примером замкнутой цепи.
Разомкнутая электрическая цепь
При отсутствии потока электронов необходимое напряжение источника цепи проявляется на концах точек. В этом случае происходит процесс ожидания момента соединения концов точек, чтобы возобновился поток электронов. Подобную цепь принято называть разомкнутой.
При связывании концов проводов, где существует разрыв, непрерывность всей цепи восстановится. Это основная разница между замкнутой и разомкнутой цепью.
При включении и выключении электрического освещения (лампы) требуется постоянно осуществлять похожие процессы. Для удобства были созданы специальные устройства. Их называют выключателями или рубильниками. Они в автоматическом режиме по сигналу управляют потоками электронов в цепи, контролируя начало и завершение работы электрооборудования.
Рубильники практически идеально подходят для демонстрации принципов работы выключателей и переключателей. Однако при использовании их в больших электрических цепях существует немало проблем, связанных с безопасной эксплуатацией. Так как некоторые части рубильников открыты, то существует вероятность воспламенения горючих материалов. В современных выключателях применяются подвижные и неподвижные контакты, которые защищены изоляционным корпусом.
Источник
Окончательно для токов ,
получим (рис. 1.8)
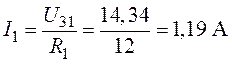

5. Ток определим из
уравнения, составленного по первому закону Кирхгофа для узла 1 (рис.1.6)
.
6. Из уравнений, составленных по первому закону
Кирхгофа, для узлов 3 и 2 (рис. 1.6) определим токи и
:
;
.
Задача 1.3.
Определить показание амперметра, установленного в
ветви с источником ЭДС (рис. 1.12), если ,
,
,
,
,
,
.
Внутренним сопротивлением амперметра можно пренебречь ().
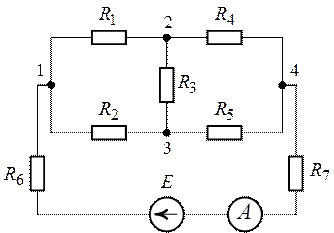
Рис. 1.12. Рис.
1.13.
Решение.
1. Методом свертывания цепи преобразуем схему рис.
1.12 к виду, приведенному на рис. 1.13.
Заменим треугольник сопротивлений, подключенный к
точкам 1, 2 и 3 (рис. 1.12), эквивалентной звездой с вершинами 1, 2 и 3 (рис.
1.14).
Величины сопротивлений эквивалентной звезды:
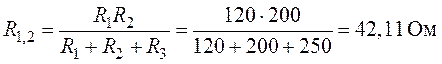
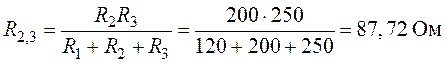
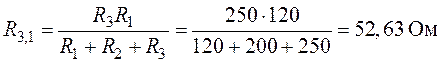
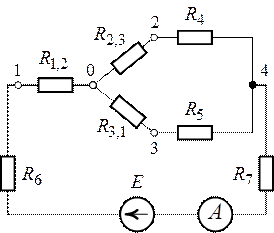
Рис. 1.14. Рис.
1.15.
Сопротивление соединено
последовательно с , а сопротивление
последовательно с
(рис. 1.14). Участок цепи с сопротивлениями
и
включен
параллельно участку с сопротивлениями и
(рис. 1.14).
Общее сопротивление обоих участков схемы (рис. 1.15)
равно:
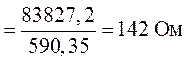
Сопротивления ,
,
,
(рис. 1.15) включены последовательно.
Эквивалентное сопротивление всей цепи (рис. 1.13)
.
2. Показание амперметра соответствует току (рис. 1.13):

Задача 1.4.
Определить величину источника тока, установленного на
входе цепи (рис. 1.16), если показание амперметра в разветвленной части схемы
составляет . Сопротивления резисторов
равны
.
Внутреннее сопротивление источника . Внутренним сопротивлением
амперметра можно пренебречь ().
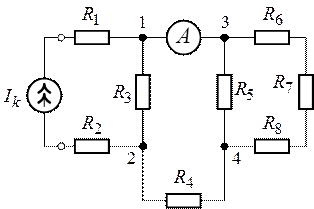
Рис. 1.16. Рис.
1.17.
Решение.
1. Пользуясь методом свертывания, приведем участок
цепи (рис. 1.16) относительно узлов 3 и 4 к виду, представленному на рис. 1.17.
Общее сопротивление участка цепи

2. Напряжение между
узлами 1 и 2 (рис. 1.17)
.
3. Ток в ветви с
сопротивлением (рис. 1.17)

4. Ток источника на
входе цепи определим на основании первого закона Кирхгофа:
.
Задача 1.5.
В схеме (рис. 1.18) найти токи, применив метод
пропорционального пересчета, если ,
,
,
,
,
.
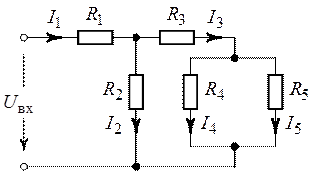
Рис. 1.18. Рис.
1.19.
Решение.
1. В рассматриваемой цепи зададим ток в одной из
удаленных от источника ветвей, например, с сопротивлением , равным
и
определим некоторое напряжение источника на входе цепи ,
при котором (рис. 1.19)
2. Определим токи (рис.
1.19)
Напряжение
.
Ток равен:
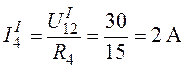
Ток определим как
сумму токов и
.
Напряжение на сопротивлении
.
Напряжение между узловыми
точками 3 и 4
.
Ток определим как
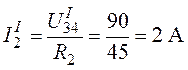
Ток на входе цепи
определим как сумму токов и
:
.
Напряжение на сопротивлении
.
Напряжение на входе цепи
.
3. Определим коэффициент пересчета как отношение
напряжения на входе цепи, заданного по условию задачи ,
к найденному при расчетах :
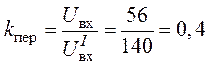
4. Действительные токи в ветвях цепи найдем как
,
,
,
,
.
Задачи для
самостоятельного решения
Задача 1.6. Определить
эквивалентное сопротивление электрической цепи, представленной на рис. 1.20,
относительно зажимов 1 и 2, в которой сопротивления равны
.
О т в е т: .
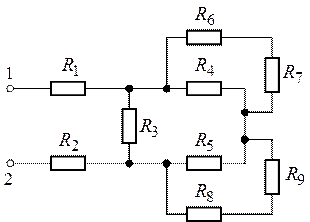
Рис. 1.20. Рис.
1.21.
Задача 1.7. Определить
эквивалентное сопротивление цепи (рис.1.21) между входными зажимами 1 и 2 при
разомкнутом и замкнутом положениях ключа (),
если ,
,
,
,
,
.
О т в е т: при разомкнутом ключе ; при замкнутом ключе
.
Задача 1.8. Определить
токи в ветвях цепи (рис. 1.22), если задано ,
,
,
,
,
.
О т в е т: ,
,
,
,
,
.
Задача 1.9. В
схеме (рис. 1.23) определить токи во всех ветвях, если ,
,
,
,
,
.
О т в е т: ,
,
,
,
,
.
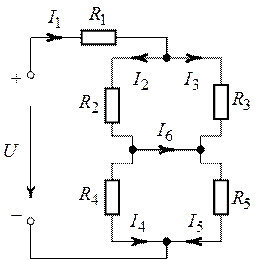
Рис. 1.22. Рис.
1.23.
Задача 1.10. Определить
токи во всех ветвях схемы (рис. 1.24), если задано ,
,
,
.
О т в е т: ,
,
,
,
,
.
Задача 1.11. В
электрической схеме рис. 1.25 определить токи во всех ветвях, если задано ,
,
,
,
.
О т в е т: ,
,
,
,
,
.

Рис. 1.24.
Рис. 1.25.
Задача 1.12. Определить
показание амперметра для схемы рис. 1.26, если ,
,
,
,
.
Принять .
О т в е т: .
Задача 1.13. Определить
показание амперметра для схемы рис. 1.27, если ,
,
,
,
.
Принять .
О т в е т: .
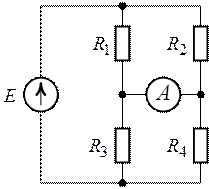
Рис. 1.26.
Рис. 1.27.
Задача 1.10. Показание
амперметра (рис. 1.28), установленного в разветвленной части схемы, составляет . Найти величину источника тока
, если
,
,
,
. Сопротивление источника считать
, амперметра
.
О т в е т: .
Задача 1.11. Найти
все токи в ветвях цепи, схема которой приведена на рис. 1.29, если ,
,
,
,
. Принять сопротивление источника
.
О т в е т: ,
,
,
,
.

Рис. 1.28. Рис.
1.29.
Задача 1.12. Определить
показание амперметра в схеме (рис. 1.30), если ,
,
,
,
.
Принять .
О т в е т: .
Задача 1.13. Методом
пропорционального пересчета найти все токи в схеме рис. 1.31, если ,
,
,
,
,
,
,
.
В расчетах принять ток в сопротивлении равным
.
О т в е т: ,
,
,
,
,
,
.
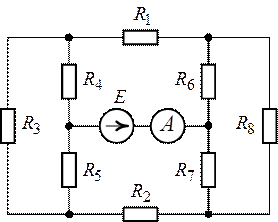
Рис. 1.30. Рис.
1.31.
2.
РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ С ПОМОЩЬЮ ПРЯМОГО ПРИМЕНЕНИЯ ЗАКОНОВ КИРХГОФА
Законы Кирхгофа лежат в основе расчета сложных цепей содержащих несколько
источников энергии. С помощью двух законов Кирхгофа устанавливаются соотношения
между токами и ЭДС в ветвях электрической цепи и напряжениями на элементах
цепи.
Задача 2.1.
Пользуясь законами Кирхгофа, рассчитать токи в
ветвях схемы рис.2.1, если ,
,
,
,
,
,
.
Решение.
1. Цепь рис. 2.1 содержит три ветви (), два узла (
).
Цепь питает два источника ЭДС и
. Источники тока в цепи отсутствуют (
).
Выберем произвольно положительные направления токов в
ветвях схемы и обозначим их как указано на рис. 2.2.
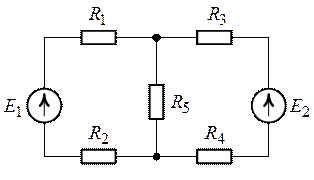
Рис. 2.1.
Рис. 2.2.
2. Определим достаточное количество уравнений для
расчета цепи по законам Кирхгофа.
По первому закону Кирхгофа:
.
По второму закону Кирхгофа:
.
Достаточное количество уравнений равно трем, что
соответствует количеству неизвестных токов, обозначенных в ветвях схемы как ,
и
(рис. 2.2).
3. Составим систему уравнений по первому и второму
закону Кирхгофа. Одно уравнение по первому закону Кирхгофа, например, для узла
1 и два уравнения по второму закону Кирхгофа для двух независимых контуров. Положительные
направления обхода контуров соответствуют направлениям, указанным на рис. 2.2.
для узла 1: ;
для контура :
;
для контура :
.
4. После подстановки числовых значений имеем:
5. Решение системы получим с помощью определителей:
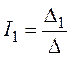
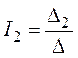
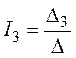
где– главный
определитель системы, ,
,
– алгебраические дополнения.
Главный определитель системы равен:
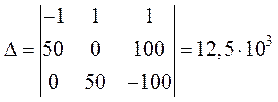
Дополнительные определители равны:
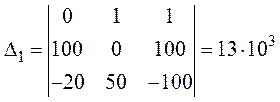
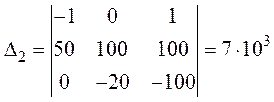

6. Токи в ветвях:

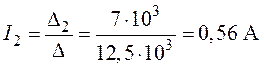
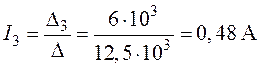
Задача 2.2.
Рассчитать с использованием законов Кирхгофа токи в
ветвях схемы изображенной на рис. 2.3, если известны ,
,
,
,
,
. Выполнить правильность расчета цепи
путем проверки баланса мощностей.
Печатать книгу
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 26. Закон Ома для полной электрической цепи. КПД источника тока |
| Напечатано:: | Гость |
| Дата: | Понедельник, 15 Май 2023, 00:39 |
Оглавление
- Закон Ома для полной электрической цепи
- Различные режимы работы электрической цепи
- Коэффициент полезного действия источника тока
- Примеры решения задач
- Упражнение 19
В 1826 г. немецкий физик Георг Симон Ом (1787–1854) опытным путём установил, что при постоянной температуре отношение напряжения между концами металлического проводника к силе тока в нём является величиной постоянной. На основании этого был сформулирован закон, названный законом Ома для участка электрической цепи: , где R — сопротивление участка цепи. От чего и как зависит сила тока в замкнутой цепи, содержащей источник тока, т. е. в полной электрической цепи?
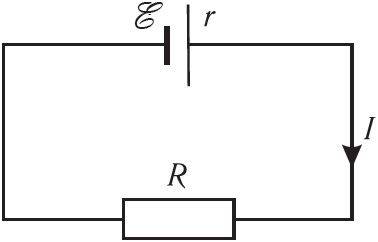
Закон Ома для полной электрической цепи. Рассмотрим электрическую цепь, состоящую из источника тока (гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R. Известны ЭДС источника тока и его сопротивление r, которое называют внутренним. Схема цепи представлена на рисунке 132. Пусть сила тока в цепи I, а напряжение между концами проводника U.
Закон Ома для полной цепи связывает силу тока I в цепи, ЭДС источника тока и полное сопротивление цепи R + r, которое складывается из сопротивлений внешнего (резистор) и внутреннего (источник тока) участков цепи (сопротивлением соединительных проводов пренебрегаем). Эту связь можно установить теоретически на основании закона сохранения энергии.
Если через поперечное сечение проводника за промежуток времени t проходит заряд q, то работу сторонней силы по перемещению электрического заряда можно определить по формуле
Поскольку сила тока , то
(26.1)
В неподвижных проводниках неизменного химического состава в результате работы сторонних сил происходит увеличение только внутренней энергии внешнего и внутреннего участков цепи. Таким образом, при прохождении электрического тока в резисторе и источнике тока выделяется количество теплоты Q, которое можно определить по закону Джоуля–Ленца:
На основании закона сохранения энергии:
Подставим формулы (26.1) и (26.2) в равенство (26.3) и в результате математических преобразований получим:
= IR + Ir.
(26.4)
Произведение силы тока на сопротивление участка цепи часто называют падением напряжения на этом участке. Поэтому IR = U — падение напряжения (напряжение) на внешнем участке цепи, Ir — падение напряжения на внутреннем участке цепи.
Выражая силу тока из формулы (26.4), получим:
(26.5)
Формула (26.5) является математическим выражением закона Ома для полной электрической цепи, согласно которому сила тока в полной электрической цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи.
От теории к практике
Аккумулятор, внутреннее сопротивление которого r = 0,80 Ом, подсоединён к резистору. Чему равна ЭДС аккумулятора, если напряжение на его полюсах U = 6,0 В, а сила тока в цепи I = 0,50 А?
Различные режимы работы электрической цепи. Преобразуем формулу (26.4):
IR = – Ir,
так как IR = U, то
U = − Ir.
(26.6)
Из выражения (26.6) следует, что при разомкнутой цепи (I = 0) напряжение между полюсами источника тока равно его ЭДС: U = . Следовательно, измерить ЭДС источника тока можно, подключив к его полюсам вольтметр с бесконечно большим собственным сопротивлением (чтобы не нарушать режим разомкнутой цепи).
В случае, если сопротивление внешнего участка цепи стремится к нулю (R 0), сила тока возрастает и достигает максимального значения. Падение напряжения на источнике тока при этом равно ЭДС, а напряжение между его полюсами — нулю.
Такой режим работы источника тока называют коротким замыканием, а максимально возможную для данного источника силу тока называют силой тока короткого замыкания:
где r — внутреннее сопротивление источника тока.
Для источников тока с незначительным внутренним сопротивлением (например, у автомобильных аккумуляторов r ≈ 0,01 Ом) режим короткого замыкания чрезвычайно опасен, поскольку может привести к повреждению источника тока и даже быть причиной пожара.
От теории к практике
Сила тока при коротком замыкании батарейки Iк.з = 2 А. Когда к батарейке подключили резистор с сопротивлением R = 3 Ом, сила тока стала I = 1 А. Как изменилось полное сопротивление цепи? Чему равно внутреннее сопротивление батарейки?
Коэффициент полезного действия источника тока. При перемещении заряда q на внешнем участке цепи, напряжение на котором U, за промежуток времени t сила электрического поля совершает работу:
A = Uq.
Используя выражение , получим формулу для расчёта работы электрического тока, совершённой на внешнем участке
A = IUt.
В общем случае работа тока может превращаться в механическую работу Амех электродвигателей, расходоваться на увеличение внутренней энергии участка цепи (выделение количества теплоты Q), обеспечивать увеличение химической энергии ΔEхим , а также преобразовываться в энергию возникающего электромагнитного излучения Eизл:
IUt = Aмех + Q + ΔEхим + Eизл.
Если к источнику тока подключён только электродвигатель, то IUt = Aмех + Q и полезной работой будет Амех.
Если прохождение тока сопровождается химическими реакциями (например, зарядка аккумулятора), то IUt = ΔEхим + Q и полезная работа будет равна ΔEхим.
При работе электроосветительного оборудования IUt = Eизл + Q и полезная работа равна Eизл.
При включении в цепь только электронагревательных приборов IUt = Q и полезная работа равна Q.
При изучении физики в 8-м классе вы узнали, что, согласно экспериментально установленному закону Джоуля‒Ленца, количество теплоты, которое выделяется в проводнике при прохождении электрического тока, определяют по формуле Q = I2Rt.
Следовательно, работа тока на произвольном участке цепи в общем случае не равна количеству теплоты, выделяющемуся на этом участке при прохождении тока, т. е. IUt ≠ I2Rt.
Равенство IUt = I2Rt выполняется только в том случае, если на участке цепи имеет место превращение энергии электрического поля, поддерживаемого источником тока, во внутреннюю энергию этого участка.
Если внешним участком цепи является нагревательный элемент (или резистор), то с учётом закона Джоуля–Ленца формула для расчёта полезной работы электрического тока на внешнем участке цепи:
Aполезн = I2Rt.
Учитывая, что мощность , получим выражение для определения полезной мощности тока на тепловом потребителе, являющемся внешним участком цепи:
Pполезн = I2R = IU.
Поскольку работа сторонних сил источника тока:
Aст = Aполн = It,
то мощность, развиваемая сторонними силами источника тока при наличии в цепи только нагревательного элемента:
Pст = Pполн = I = IU + I2r.
Следовательно, Pполн = Pполезн + I2r.
Коэффициент полезного действия (КПД) источника тока — отношение полезной мощности тока на внешнем участке цепи к полной мощности, развиваемой сторонними силами источника тока:
Согласно формуле :
Так, например, при зарядке аккумулятора источником тока с ЭДС при силе зарядного тока I КПД этого источника определяют по формуле
.
Если внешний участок цепи — нагревательный элемент, то
Pполезн = I2R,
Pполн = I2(R + r).
Тогда КПД источника тока
1. Сформулируйте закон Ома для полной цепи.
2. Как можно измерить ЭДС источника тока?
3. Какой режим работы электрической цепи соответствует короткому замыканию?
4. Что понимают под силой тока короткого замыкания?
5. Что понимают под полезной работой электрического тока? полной работой источника тока?
6. Как определить полезную мощность электрического тока? полную мощность источника тока?
7. Что называют коэффициентом полезного действия (КПД) источника тока?
Примеры решения задач
Пример 1. Резистор с сопротивлением R = 3,0 Ом подключён к источнику тока с ЭДС = 8,0 В и внутренним сопротивлением r = 1,0 Ом. Определите полезную мощность тока и КПД источника тока в данной цепи.
Дано:
R = 3,0 Ом = 8,0 В
r = 1,0 Ом
Pполезн — ?
η — ?
Решение: Полезной является мощность тока на внешнем участке цепи, т. е. на резисторе: Pполезн = I2R. С учётом закона Ома для полной цепи получим:
КПД источника тока в данной цепи определим по формуле
Ответ: Pполезн = 12 Вт, η = 75 %.
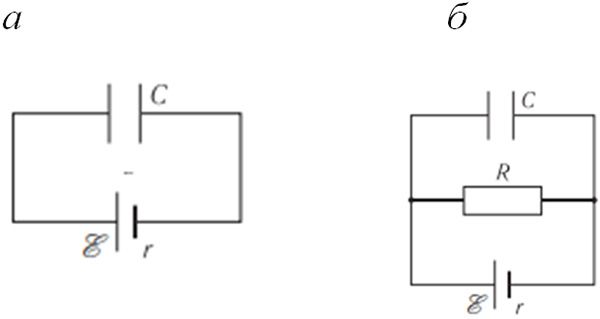
Пример 2. Конденсатор подключён к источнику тока (рис. 132.1, а). При подключении параллельно конденсатору резистора с сопротивлением R = 20 Ом (рис. 132.1, б) заряд на конденсаторе уменьшился в α = 1,4 раза. Определите внутреннее сопротивление источника тока.
Дано:
R = 20 Ом
α = = 1,4
R — ?
Решение: При подключении конденсатора к источнику тока напряжение на конденсаторе равно напряжению на полюсах источника (цепь разомкнута, см. рис. 132.1, а) . После того, как параллельно конденсатору подключили резистор (см. рис. 132.1, б), в цепи возник электрический ток. Силу тока можно определить, используя закон Ома для полной цепи:
. В этом случае напряжение на конденсаторе стало равно напряжению на резисторе:
. Поскольку напряжение на конденсаторе прямо пропорционально его заряду
и
, то
и r = 0,40 R. Таким образом,
r = 0,40 · 20 Ом = 8,0 Ом.
Ответ: r = 8,0 Ом.
Пример 3. Электродвигатель в сети постоянного тока с напряжением U = 120 В потребляет ток силой I = 6,0 А. Определите сопротивление его обмотки, если КПД электродвигателя η = 80 %.
Дано:
U = 120 В
I = 6,0 А
η = 80 %
R — ?
Решение: Мощность, потребляемую электродвигателем, определим по формуле Pполн = IU (1). Часть этой мощности затрачивается на нагревание обмотки: P = I2R, а часть — превращается в полезную механическую мощность Pполезн электродвигателя. На основании закона сохранения энергии
Pполн = I2R + Pполезн.
(2)
Используя формулы (1) и (2), запишем выражение для нахождения полезной мощности электродвигателя:
Pполезн = Pполн – I2R = IU – I2R.
(3)
КПД электродвигателя определим по формуле .
С учётом формул (1) и (3) получим:
.
(4)
Сопротивление обмотки электродвигателя выразим из формулы (4):
Ответ: R = 4,0 Ом.
Упражнение 19
1. Резистор с сопротивлением R = 2 Ом подключён к источнику тока с ЭДС = 5 В и внутренним сопротивлением r = 0,5 Ом. Определите силу тока в цепи и падение напряжения на внешнем и внутреннем участках электрической цепи.
2. Реостат подключён к источнику тока с ЭДС = 4 В и внутренним сопротивлением r = 1 Ом. Постройте график зависимости силы тока от сопротивления той части реостата, по которой проходит ток, I = I(R).
3. При подключении к источнику тока с ЭДС = 2,2 В резистора с сопротивлением R = 4,0 Ом сила тока в цепи I = 0,50 А. Определите силу тока при коротком замыкании источника тока.
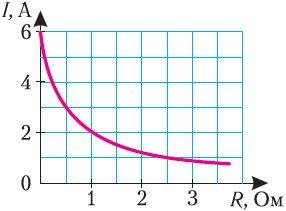
4. На рисунке 133 представлен график зависимости силы тока в реостате от его сопротивления. Определите силу тока при коротком замыкании источника тока и его внутреннее сопротивление.
5. Определите полную мощность, развиваемую источником тока с внутренним сопротивлением r = 0,50 Ом, при подключении к нему резистора с сопротивлением R = 2,0 Ом, если напряжение на резисторе U = 4,0 В.
6. Спираль нагревательного элемента, сопротивление которой R = 38 Ом, подключена к источнику тока с ЭДС = 12 В и внутренним сопротивлением r = 2,0 Ом. Определите количество теплоты, которое выделится в спирали за промежуток времени t = 10 мин.
7. Два параллельно соединённых резистора, сопротивления которых R1 = 4,0 Ом и R2 = 6,0 Ом, подключили к источнику тока с ЭДС = 12 В и внутренним сопротивлением r = 0,60 Ом. Определите напряжение на резисторах и силу тока в каждом из них.
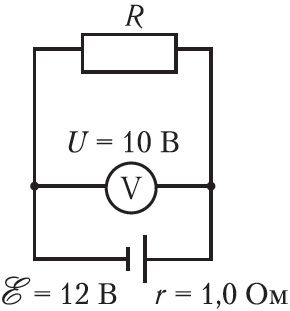
8. На рисунке 134 представлена схема электрической цепи, состоящей из источника тока, резистора и идеального вольтметра. Определите работу электрического тока на внешнем участке цепи за промежуток времени t = 10 мин и КПД источника тока.

9. На рисунке 135 представлена схема электрической цепи, состоящей из источника тока, ключа и трёх резисторов. Выберите из предложенного перечня три верных утверждения. Укажите их номера.
1) Полезную мощность тока на внешнем участке цепи при разомкнутом ключе можно определить по формуле .
2) Мощность, развиваемую сторонними силами источника тока при замкнутом ключе, можно определить по формуле .
3) Полезную работу тока на внешнем участке цепи при замкнутом ключе можно определить по формуле .
4) Работу сторонних сил источника тока при разомкнутом ключе можно определить по формуле .
5) КПД источника тока при разомкнутом ключе η = 80 %.
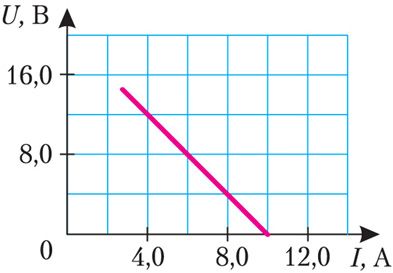
10. Вольт-амперная характеристика, построенная по результатам экспериментального исследования зависимости напряжения на реостате от силы тока в нём, представлена на рисунке 135.1. Определите силу тока при коротком замыкании источника тока и его ЭДС.
11. Для проведения экспериментального исследования была собрана электрическая цепь, состоящая из источника тока, ключа, соединительных проводов, реостата, амперметра и вольтметра. В ходе исследования зависимости напряжения на реостате от силы тока в нём была составлена таблица.
| U, В | 0,50 | 0,70 | 0,80 | 0,90 |
| I, А | 0,70 | 0,50 | 0,40 | 0,30 |
Определите ЭДС источника тока и его внутреннее сопротивление.
13. Электродвигатель в сети постоянного тока с напряжением U = 220 В потребляет ток силой I = 12 А. Сопротивление обмотки электродвигателя R = 5,0 Ом. Определите механическую мощность и КПД электродвигателя.
14. В электрический чайник налили воду и подключили к источнику тока с ЭДС = 140 В и внутренним сопротивлением r = 4,0 Ом. Вольтметр, подключённый к полюсам источника тока, показывает напряжение U = 120 В. Определите, на сколько увеличится температура воды за промежуток времени τ = 2,0 мин, если её объём V = 1,0 л и КПД чайника η = 70 %. Плотность воды ρ = 1,0 · 103
, удельная теплоёмкость воды c = 4,2 · 103
.