Статический ток Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Статическая мощность: 5.94 Милливатт –> 0.00594 Ватт (Проверьте преобразование здесь)
Напряжение стока: 1.45 вольт –> 1.45 вольт Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.00409655172413793 Ампер –>4.09655172413793 Миллиампер (Проверьте преобразование здесь)
13 Основные параметры Калькуляторы
Статический ток формула
Статический ток = Статическая мощность/Напряжение стока
Istatic = Pstatic/vds
Что такое динамическая и статическая мощность?
Для зарядки и разрядки емкости нагрузки требуется энергия. Это называется динамической мощностью, потому что она потребляется, когда цепь активно переключается. Даже когда ворота не переключаются, они потребляют некоторую статическую энергию. Поскольку закрытый транзистор имеет утечку, между питанием и землей протекает небольшой ток Istatic, что приводит к рассеиванию статической мощности.
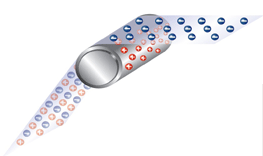
Когда синтетическая пленка касается подающего/приемного вала, невысокий заряд, перетекающий от материала к валу, провоцирует дисбаланс. По мере того, как материал преодолевает зону контакта с валом, напряжение возрастает точно также как в случае с конденсаторными пластинами в момент их разделения. Практика показывает, что амплитуда результирующего напряжения ограничена вследствие электрического пробоя, возникающего в промежутке между соседними материалами, поверхностной проводимости и других факторов. На выходе пленки из контактной зоны часто можно слышать слабое потрескивание или наблюдать искрение. Это происходит в момент, когда статический заряд достигает величины, достаточной для пробоя окружающего воздуха. До контакта с валом синтетическая пленка с точки зрения электричества нейтральна, но в процессе перемещения и контакта с подающими поверхностями поток электронов направляется на пленку и заряжает ее отрицательным зарядом. Если вал металлический и заземленный его положительный заряд быстро стекает.
Большая часть оборудования имеет много валов, поэтому величина заряда и его полярность могут часто меняться. Наилучший способ контроля статического заряда – это его точное определение на участке непосредственно перед проблемной зоной. Если заряд нейтрализован слишком рано, он может восстановиться до того, как пленка достигнет этой проблемной зоны.
В теории возникновение статического заряда может быть проиллюстрировано простой электрической схемой:
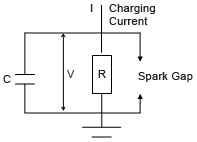
C – выполняет функцию конденсатора, который накапливает заряд, как батарея. Это обычно поверхность материала или изделия.
R – сопротивление, способное ослабить заряд материала/механизма (обычно при слабой циркуляции тока). Если материал является проводником, заряд стекает на землю и не создает проблем. Если же материал является изолятором, заряд не сможет стекать, и возникают сложности. Искровой разряд возникает в том случае, когда напряжение накопленного заряда достигает предельного порога.
Токовая нагрузка — заряд, сгенерированный, например, в процессе перемещения пленки по валу. Ток заряда заряжает конденсатор (объект) и повышает его напряжение U. В то время как напряжение повышается, ток течет через сопротивление R. Баланс будет достигнут в момент, когда ток заряда станет равен току, циркулирующему по замкнутому контуру сопротивления. (Закон Ома: U = I х R).
Если объект имеет способность накапливать значительный заряд, и если имеет место высокое напряжение, статическое электричество приводит к возникновению таких серьезных проблем, как искрение, электростатическое отталкивание/притягивание или электропоражение персонала.
Полярность заряда
Статический заряд может быть либо положительным, либо отрицательным. Для разрядников постоянного тока (AC) и пассивных разрядников (щеток, шнуров, мишуры) полярность заряда обычно не важна.
Вернуться к списку для выбора раздела.
IV. Измерение статического заряда
Измерение величины статического заряда является очень важной процедурой, которая позволяет обнаружить присутствие заряда, определить его амплитуду и породивший источник.
Как уже отмечалось выше, статическое электричество возникает при дефиците или избытке электронов в атоме. Вследствие того, что измерить величину заряда на поверхности объекта в кулонах невозможно, измеряют сопротивление или напряженность электрического поля, связанную со статическим зарядом. Этот способ измерения широко применяется в промышленности.
Зависимость между сопротивлением поля и напряженностью заключается в том, что в любой точке сопротивление является составляющей градиента напряженности.
Приборы Fraser серии 710 собраны по представленной ниже схеме и измеряют напряжение на поверхности объекта.
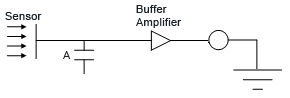
А – напряжение в конденсаторе изменяется вместе с изменением величины заряда.
Проводя измерения с расстояния 100 мм, и пользуясь формулой Q (заряд) = С (емкостное сопротивление) х U (напряжение), можно вычислить емкостное сопротивление.
Измерительные приборы Fraser просты в использовании и очень полезны для анализа возникших проблем или прогноза их появления в будущем.
При измерениях параметров статического электричества важно следовать инструкциям по эксплуатации приборов. Электрическое поле действует в единственном направлении, поэтому его практическое изучение не представляет сложностей. Одними из наиболее интересных и важных для измерения заряда характеристик электрического поля являются:

- Электрическое поле — участок пространства, на котором действуют электрические силы, величины которых выражены в кулонах.
- Все заряженные объекты окружены электрическим полем.
- Силовые линии поля проходят перпендикулярно поверхности объекта и указывают направление, по которому действует сила.
- Электрическое поле может охватывать несколько объектов, что важно учитывать при проведении измерений и осуществлении мероприятий по нейтрализации статического заряда.
Как отмечалось выше, в воздушном пространстве силовые линии электрического поля проходят перпендикулярно поверхности заряженного объекта. Это позволяет производить измерения с очень высокой точностью.
В случае с производством и обработкой синтетической пленки следует отметить важную деталь. Когда материал перемещается по валу, электрический заряд переходит к валу, и кажется, что поле исчезло. Поэтому вблизи вала нет возможности производить точные измерения. Электрическое поле появляется вновь, когда материал преодолевает зону контакта, и статический заряд можно снова измерить точно.
Вернуться к списку для выбора раздела.
V. Четыре основные проблемы, связанные со статическим электричеством
1. Статический разряд в электронике
На эту проблему необходимо обратить внимание, т.к. она часто возникает в работе с электронными блоками и компонентами, использующимися в современных контрольно-измерительных устройствах.
В электронике основная опасность, связанная со статическим зарядом, исходит от человека, несущего заряд, и пренебрегать этим нельзя. При разряде образуется тепло, которое приводит к выжиганию соединений, прерыванию контактов и разрыву дорожек микросхем. Высокое напряжение уничтожает также тонкую оксидную пленку на полевых транзисторах и других элементах, имеющих покрытие.
Часто компоненты не полностью выходят из строя, что можно считать еще более опасным, т.к. неисправность проявляется не сразу, а в непредсказуемый момент в процессе эксплуатации устройства.
Общее правило: при работе с чувствительными к статическому электричеству деталями и устройствами необходимо всегда принимать меры для нейтрализации заряда, накопленного на теле человека. Подробная информация по этому вопросу содержится в документах европейского стандарта CECC 00015.
2. Электростатическое притяжение/отталкивание
Это, возможно, наиболее широко распространенная проблема, возникающая на предприятиях, связанных с производством и обработкой пластмасс, бумаги, текстиля и в смежных отраслях. Она проявляется в том, что материалы самостоятельно меняют свое поведение — склеиваются между собой или, наоборот, отталкиваются, прилипают к оборудованию, притягивают пыль, неправильно наматываются на приемное устройство и пр.
Притягивание/отталкивание происходит в соответствии с законом Кулона, в основе которого лежит принцип обратной пропорциональности квадрата расстояния. В простой форме он выражается следующим образом:
Сила притяжения или отталкивания = Заряд А * Заряд В / Расстояние между объектами2
Следовательно, интенсивность проявления этого эффекта напрямую связана с амплитудой статического заряда и расстоянием между притягивающимися или отталкивающимися объектами. Притягивание и отталкивание происходят в направлении силовых линий электрического поля.

Если два заряда имеют одинаковую полярность – они отталкиваются, если противоположную – притягиваются. Если один из объектов заряжен, он будет провоцировать притягивание, создавая зеркальную копию заряда на нейтральных объектах.
3. Риск возникновения пожара
Риск возникновения пожара не является общей для всех производств проблемой. Но вероятность возгорания очень велика на полиграфических и других предприятиях, где используются легковоспламеняющиеся растворители.
В опасных зонах наиболее распространенными источниками возгорания являются незаземленное оборудование и подвижные проводники. Если на операторе, находящемся в опасной зоне, надета спортивная обувь или туфли на токонепроводящей подошве, существует риск, что его тело будет генерировать заряд, способный спровоцировать возгорание растворителей. Незаземленные проводящие детали машин также представляют опасность. Все, что находится в опасной зоне должно быть хорошо заземлено.
Нижеследующая информация дает краткое пояснение способности статического разряда провоцировать возгорание в легковоспламеняющихся средах. Важно, чтобы неопытные продавцы были заранее осведомлены о видах оборудования, чтобы не допустить ошибки в подборе устройств для применения в таких условиях.
Способность разряда провоцировать возгорание зависит от многих переменных факторов:
- типа разряда;
- мощности разряда;
- источника и энергии разряда;
- минимальной энергии воспламенения (МЭВ) легковоспламеняющейся среды;
- наличия легковоспламеняющейся среды (растворителей в газовой фазе, пыли или горючих жидкостей).
Типы разряда
Существует три основных типа — искровой, кистевой и скользящий кистевой разряды. Коронный разряд в данном случае во внимание не принимается, т.к. он отличается невысокой энергией и происходит достаточно медленно. Коронный разряд чаще всего неопасен, его следует учитывать только в зонах очень высокой пожаро- и взрывоопасности.
Искровой разряд в основном исходит от умеренно проводящего, электрически изолированного объекта. Это может быть тело человека, деталь машины или инструмент. Предполагается, что вся энергия заряда рассеивается в момент искрения. Если энергия выше МЭВ паров растворителя, может произойти воспламенение.
Энергия искры рассчитывается следующим образом: Е (в Джоулях) = 1/2 С U2
Кистевой разряд возникает, когда заостренные части деталей оборудования концентрируют заряд на поверхностях диэлектрических материалов, изоляционные свойства которых приводят к его накоплению. Кистевой разряд отличается более низкой энергией по сравнению с искровым и, соответственно, представляет меньшую опасность в отношении воспламенения.
Скользящий кистевой разряд происходит на листовых или рулонных синтетических материалах с высоким удельным сопротивлением, имеющих повышенную плотность заряда и разную полярность зарядов с каждой стороны полотна. Такое явление может быть спровоцировано трением или распылением порошкового покрытия. Эффект сравним с разрядкой плоского конденсатора и может представлять такую же опасность, как искровой разряд.
Мощность разряда
Если объект, имеющий энергию, не очень хорошо проводит электрический ток, например, человеческое тело, сопротивление объекта будет ослаблять разряд и понижать опасность. Для человеческого тела существует эмпирическое правило: считать, что любые растворители с внутренней минимальной энергией воспламенения менее 100 мДж могут воспламениться несмотря на то, что энергия, содержащаяся в теле, может быть выше в 2 – 3 раза.
Источник и энергия разряда
Величина и геометрия распределения заряда являются важными факторами. Чем больше объем тела, тем больше энергии оно содержит. Острые углы повышают мощность поля и поддерживают разряды.
Минимальная энергия воспламенения МЭВ
Минимальная энергия воспламенения растворителей и их концентрация в опасной зоне являются очень важными факторами. Если минимальная энергия воспламенения ниже энергии разряда, возникает риск возгорания.
4. Удар электрическим током
Вопросу риска статического удара в условиях промышленного предприятия уделяется все больше внимания. Это связано с существенным повышением требований к гигиене и безопасности труда.
Удар током, спровоцированный статическим электричеством, в принципе, не представляет особой опасности. Он просто неприятен, если только не вызывает резкой реакции отклонения от объекта удара.
Существуют две общие причины статического удара.
Наведенный заряд
Если человек находится в электрическом поле и держится за заряженный объект, например, за намоточную бобину для пленки, возможно, что его тело зарядится от наведенной индукции.

Заряд остается в теле оператора, если он находится в обуви на изолирующей подошве, до того момента, пока он не дотронется до заземленного оборудования. Заряд стекает на землю и поражает человека. Такое происходит и в случае, когда оператор дотрагивается до заряженных объектов или материалов – из-за изолирующей обуви заряд накапливается в теле. Когда оператор трогает металлические детали оборудования, заряд может стечь и спровоцировать электроудар.
При перемещении людей по синтетическим ковровым покрытиям порождается статический заряд при контакте между ковром и обувью. Электроудары, которые получают водители, покидая свою машину, провоцируются зарядом, возникшим между сиденьем и их одеждой в момент подъема. Решение этой проблемы – дотронуться до металлической детали автомобиля, например, до рамы дверного проема, до момента подъема с сиденья. Это позволяет заряду безопасно стекать на землю через кузов автомобиля и его шины.
Удар, спровоцированный оборудованием
Такой электроудар возможен, хотя происходит значительно реже, чем поражение, спровоцированное материалом.
Если намоточная бобина имеет значительный заряд, случается, что пальцы оператора концентрируют заряд до такой степени, что он достигает точки пробоя, и происходит разряд. Помимо этого, если металлический незаземленный объект находится в электрическом поле, он может зарядиться наведенным зарядом. По причине того, что металлический объект является токопроводящим, подвижный заряд разрядится в человека, который дотрагивается до объекта.
Вернуться к списку для выбора раздела.
VI. Оценка минимального заряда, достаточного для воспламенения опасных атмосфер
При определении эффективности применения антистатического ионизатора ЕХ1250 во взрывоопасной среде может возникнуть вопрос о количественной оценке остаточного статического поля на предмет возможности привести к воспламенению или взрыву в опасной атмосфере, возникающей в производственном процессе.
Увы, на этот вопрос вряд ли есть точный и однозначный ответ, так как степень опасности зависит от того, способен ли накопленный заряд генерировать электрическое поле с достаточным напряжением, чтобы сформировать пробой на материале с последующим разрядом, содержащим энергию, большую, чем минимальная энергия воспламенения горючей атмосферы данного процесса.
Конечно, различные виды разрядов требуют различных условий для их возникновения, например, искровой разряд, кистевой разряд и т.д.
Самый лучший международный источник информации по теме, касающейся статических опасностей — это руководство IEC60079-32-1, но и оно не дает никаких точных значений напряжений, но тем не менее в разделе 7.1.5. “Невоспламеняющие разряды при операциях с жидкостями” утверждает следующее:
Опасность воспламенения может возникнуть при гораздо более низких напряжениях (обычно от 5 до 10 кВ), если изолированные проводники, такие, как плавающие металлические объекты или неправильно закрепленные элементы, находятся в емкости, или если контейнер имеет изолирующую подложку без точки контакта для заземления находящейся в нем жидкости и наполняется жидкостью, которая имеет достаточную проводимость для создания разрядов.
Далее раздел A.3. “Электростатические разряды” дает описание статического разряда:
А.3.2. Искры
Искра — это разряд между двумя проводниками, жидкими или твердыми. Она характеризуется ярко выраженным световым каналом разряда, несущим ток высокой плотности. Газ ионизирован на всю длину канала. Разряд очень быстрый и вызывает резкий треск.
Искра происходит между двумя проводниками, когда напряженность поля между ними превышает электрическую напряженность атмосферы. Разница потенциалов между проводниками, необходимая для пробоя, зависит как от формы так и от расстояния между проводниками. Для сравнения: напряженность пробоя для поверхностей плоских или с большим радиусом искривления при расстоянии 10 мм или более между ними составляет 3 МВм-1 (300 В на мм) в нормальном воздухе и увеличивается при увеличении расстояния.
Поскольку объекты, между которыми проскакивает искра, являются проводниками, преобладающая часть сохраненного заряда проходит через искру. В большинстве случаев на практике это рассеивает почти всю сохраненную энергию. Энергия искры между проводящим телом и проводящим заземленным объектом может быть вычислена по следующей формуле:
W = ½ Q V = ½ C V2,
где
- W — рассеянная энергия в джоулях,
- Q — количество заряда на проводнике в кулонах,
- V — его потенциал в вольтах,
- C — его емкость в фарадах.
Результатом расчета является максимальное количество энергии. Энергия искры будет меньше, если есть сопротивление в пути разряда на заземление. Типичные значения емкостей проводников даны в таблице ниже:
| Таблица А.2 Значения емкостей типичных проводников | |
| Объект | Емкость в пФ (1 пФ = 1х10-12 Ф) |
| Мелкие металлические предметы (наконечник шланга, ковш) | от 10 до 20 |
| Малые контейнеры (корзина, барабан до 50 л) | от 10 до 100 |
| Средние контейнеры (250 — 500 л) | от 50 до 300 |
| Крупные объекты (реакторы, окруженные заземленными структурами) | от 100 до 1000 |
| Тело человека | от 100 до 200 |
Исходя из того, что искра может возникать как между жидкими, так и твердыми проводниками, мы можем принять в качестве примерной оценки нижнего порога для разряда в 5-10 кВ, что очень приблизительно и не учитывает ни форму проводников, ни состав и концентрацию газовой смеси.
Также в заключение можно сказать, что фактическая возможность пожара или взрыва всегда зависит не только от напряжения, но и емкости проводника и минимальной энергии воспламенения окружающей атмосферы данного производственного процесса.
Вернуться к списку для выбора раздела.
Static electricity is defined as an imbalance of electric charges in a body, especially the negative and positive charges. In other words, the discharge of an electrical pulse is known as static electricity. Physical techniques are used to create the charge imbalance. Contact between solid things is one of the most prominent sources of static electricity. The static electricity generates a force during its creation which is directly proportional to the charges of both the bodies in contact and inversely proportional to the square of the distance between them. It is known as electrostatic force and is denoted by the symbol F. Its standard unit of measurement is Newtons (N), and the dimensional formula is given by [M1L1T-2].
Static Electricity Formula
F = 1/4πε0 (q1q2 / r2)
Where,
- F is the electrostatic force,
- 1/4πε0 = k0 is the Coulomb’s constant with a value of 9 × 109 Nm2C-2,
- q1, q2 are the charge values,
- r is the distance between the bodies.
Derivation
Consider a system of two bodies of charges q1 and q2 such that they are separated by a distance r. It is known that the static electricity force between these two bodies is directly proportional to the product of the charges of the bodies.
F ∝ q1q2 ⇢ (1)
Also, the force is indirectly proportional to the square of the distance between the two bodies. So we get,
F ∝ 1/r2 ⇢ (2)
From (1) and (2),
F ∝ q1q2/r2
Replacing the proportionality sign with a constant, we get,
F = k0q1q2/r2
Here, k0 is known as the Coulomb’s constant.
This derives the formula for static electricity force between two charged bodies.
Sample Problems
Problem 1: Calculate the static electricity force between two bodies of charge, 0.2 C and 0.4 C, separated by a distance of 0.1 m.
Solution:
We have,
q1 = 0.2
q2 = 0.4
r = 0.1
Using the formula we have,
F = 1/4πε0 (q1q2 / r2)
= (9 × 109 × 0.2 × 0.4)/0.01
= 2.87 × 109 N
Problem 2: Calculate the static electricity force between two bodies of charge, 1.5 C and 4 C, separated by a distance of 0.1 m.
Solution:
We have,
q1 = 1.5
q2 = 4
r = 0.1
Using the formula we have,
F = (9 × 109 × 1.5 × 4)/0.01
= 215.7 × 109 N
Problem 3: Calculate the static electricity force between two bodies of charge, 2 C and 3 C, separated by a distance of 1 m.
Solution:
We have,
q1 = 2
q2 = 3
r = 1
Using the formula we have,
F = (9 × 109 × 2 × 3)/1
= 53.92 × 109 N
Problem 4: Calculate the static electricity force between two bodies of charge, 4 C and 6 C, separated by a distance of 8 m.
Solution:
We have,
q1 = 4
q2 = 6
r = 8
Using the formula we have,
F = (9 × 109 × 4 × 6)/64
= 3.37 × 109 N
Problem 5: Calculate the static electricity force between two bodies of charge, 10 C and 3 C, separated by a distance of 2 m.
Solution:
We have,
q1 = 10
q2 = 3
r = 2
Using the formula we have,
F = (9 × 109 × 10 × 3)/4
= 67.4 × 109 N
Problem 6: Calculate the static electricity force between two bodies of charge, 3 C and 7 C, separated by a distance of 4 m.
Solution:
We have,
q1 = 3
q2 = 7
r = 4
Using the formula we have,
F = (9 × 109 × 3 × 7)/16
= 11.79 × 109 N
Problem 7: Calculate the static electricity force between two bodies of charge, 4 C and 9 C, separated by a distance of 12 m.
Solution:
We have,
q1 = 4
q2 = 9
r = 12
Using the formula we have,
F = (9 × 109 × 4 × 9)/144
= 2.24 × 109 N
Last Updated :
25 Jun, 2022
Like Article
Save Article

Волосы ребёнка наэлектризовались от трения.
Стати́ческое электри́чество — совокупность явлений, связанных с возникновением, сохранением и релаксацией свободного электрического заряда на поверхности или в объёме диэлектриков или на изолированных проводниках[1].
Происхождение[править | править код]
Электризация диэлектриков трением может возникнуть при соприкосновении двух разнородных веществ из-за различия атомных и молекулярных сил (из-за различия работы выхода электрона из материалов). При этом происходит перераспределение электронов (в жидкостях и газах ещё и ионов) с образованием на соприкасающихся поверхностях электрических слоёв с разными знаками электрических зарядов. Фактически атомы и молекулы одного вещества, обладающие более сильным притяжением, отрывают электроны от другого вещества, создавая вихревое движение ионов среды, в которой они заключены.
Полученная разность потенциалов соприкасающихся поверхностей зависит от ряда факторов — диэлектрических свойств материалов, значения их взаимного давления при соприкосновении, влажности и температуры поверхностей этих тел, климатических условий. При последующем разделении этих тел каждое из них сохраняет свой электрический заряд, а с увеличением расстояния между ними за счёт совершаемой работы по разделению зарядов, разность потенциалов возрастает и может достигнуть десятков и сотен киловольт.
Электрические разряды могут образовываться вследствие некоторой электропроводности влажного воздуха. При влажности воздуха более 85 % статическое электричество практически не возникает.
Статическое электричество в быту[править | править код]

Пенопластовые кусочки прилипли к шерсти кошки из-за статического электричества
Статическое электричество широко распространено в обыденной жизни. Если, например, на полу лежит ковер из шерсти, то при трении об него человеческое тело может получить отрицательный электрический заряд, в то время как ковёр получит положительный. Другим примером может служить электризация пластиковой расчески, которая после причёсывания получает отрицательный заряд, а волосы получают положительный заряд. Накопителем отрицательного заряда нередко являются полиэтиленовые пакеты, полистироловый пенопласт. Накопителем положительного заряда может являться сухая полиуретановая монтажная пена, если её сжать рукой.
Когда человек, тело которого наэлектризовано, дотрагивается до металлического предмета, например, трубы отопления, кухонной плиты или холодильника, — накопленный заряд моментально разрядится, а человек почувствует лёгкий удар током.
Электростатический разряд происходит при очень высоком напряжении и чрезвычайно низких токах. Даже простое расчёсывание волос в сухой день может привести к накоплению статического заряда с напряжением в десятки тысяч вольт, однако ток его освобождения будет настолько мал, что его зачастую невозможно будет даже почувствовать. Именно низкие значения тока мгновенного разряда делают статический заряд безвредным для человека.[2]
С другой стороны, такие напряжения могут быть опасны для элементов различных электронных приборов — микропроцессоров, транзисторов и т.п. Поэтому при работе с радиоэлектронными компонентами рекомендуется принимать меры по предотвращению накопления статического заряда: браслеты электрозаземления, повышенная влажность и проч.
Молнии[править | править код]
В результате движения воздушных потоков, насыщенных водяными парами, образуются грозовые облака, являющиеся носителями статического электричества. Электрические разряды образуются между разноименными заряженными облаками или, чаще, между заряженным облаком и озоновым слоем земли, с последующим разрядом на землю. При достижении критической разности потенциалов происходит разряд молнии между облаками, на земле или в околокосмическом слое планеты. Для защиты от молний устанавливаются молниеотводы, проводящие разряд напрямую в землю.
Помимо молний, грозовые облака могут вызывать на изолированных металлических предметах опасные электрические потенциалы из-за электростатической индукции.
В 1872 году экспедицией под руководством географа Генри Ганнетта[en] была покорена 13-я по высоте гора штата Монтана (США)[en]. Ей дали название Электрический пик, так как у первопроходцев-покорителей, находящихся на вершине, после грозы начали сыпаться искры из пальцев рук и волос на голове[3][4][5].
См. также[править | править код]
- Заземление
- Зануление
- Электрическое поле
- Электростатическое поле
Примечания[править | править код]
- ↑ ГОСТ 12.1.018-93 «Пожаровзрывобезопасность статического электричества». Дата обращения: 22 марта 2010. Архивировано 15 июля 2010 года.
- ↑ Гордон Мак-Комб, Эрл Бойсен. Радиоэлектроника для «чайников». — М.: ИД «Вильямс», 2007. — 387 с.
- ↑ The Father of Government Mapmaking: Henry Gannett Архивная копия от 1 декабря 2017 на Wayback Machine (англ.) на сайте amerisurv.com
- ↑ Электрик-Пик Архивная копия от 28 мая 2018 на Wayback Machine (англ.) на сайте summitpost.org
- ↑ Генри Ганнетт[en]. The Origin of Certain Place Names in the United States (англ.). — Govt. Print. Off., 1905. — P. 116. Архивная копия от 12 января 2016 на Wayback Machine
Ссылки[править | править код]
- Боргман И. И. Электризация тел // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- [www.electrik.info/main/fakty/48-staticheskoe-jelektrichestvo-v-prirode.html Статическое электричество в природе и технике]
- Электротехническая энциклопедия #143. Война со ‘статикой’ в автомобиле и дома
- Физические основы электростатики и ЭСР
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок
|

В этой главе…
- Оцениваем электрический заряд и электрическую силу
- Сканируем электрическое поле
- Изучаем электрическое поле с помощью точечных зарядов
- Создаем простое электрическое поле между пластинами конденсатора
- Постигаем электрические потенциалы, измеряя напряжение
- Связываем электрический потенциал с точечными зарядами
Вокруг нас все пронизано электричеством. В каждом атоме его собственные заряды вращаются с невероятной скоростью. Иногда электрические заряды проявляются совершенно неожиданно, например, ощущаются, как острое покалывание в момент касания наэлектризованной металлической дверной ручки или дверцы автомашины. А порой, наоборот, включая электрический свет, мы внезапно узнаем, что так остро необходимые электрические заряды куда-то пропали.
В этой главе повествование курса постепенно “электризуется”: в ней описываются причины того, почему избыток заряда на нашей одежде (например, из-за скопления слишком большого количества электронов) доставляет нам столь острые ощущения в момент разряда. Это пример типичного проявления статического электричества. Кроме того, в этой и следующей главах говорится о том, как ведут себя электрические заряды и как они становятся тем, что принято называть электрическим током. В данной главе речь идет об электрических зарядах, электрическом потенциале, электрических полях, силах, действующих между зарядами, и о многом другом. А все это начинается с мельчайших носителей заряда.
Содержание
- Плюс и минус: заряды электрона и протона
- Тяни и толкай: электрические силы
- Подбираемся к закону Кулона
- Притягиваем заряды
- Вычисляем скорость электронов
- Изучаем силы, действующие между несколькими зарядами
- Действие на расстояние: электрические поля
- По всем направлениям: электрические поля от точечных зарядов
- Заряжаем конденсатор: электрические поля между плоскими пластинами
- Повышаем напряжение: электрический потенциал
- Вычисляем потенциальную энергию электрического поля
- Потенциалы и напряжение
- Оказывается, энергия сохраняется даже в электрическом поле
- Электрический потенциал точечных зарядов
- Сохраняем заряд с помощью емкости
Плюс и минус: заряды электрона и протона
Атомы состоят из ядра с заряженными протонами и нейтральными нейтронами, а также из легких заряженных электронов, стремительно вращающихся вокруг ядра.
У заряженных частиц, электронов и протонов одинаковая величина заряда, равная:
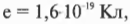
где Кл означает кулон — используемая в СИ единица заряда (см. главу 2). Заряды протона и электрона соответственно равны +1,6·10-19 Кл и -1,6·10-19 Кл (считать заряд электрона отрицательным — это не более чем достигнутая в свое время договоренность). Таким образом, электроны — это частицы-носители электричества: как статического — при отсутствии движения заряженных частиц, так и динамического — с учетом движения заряженных частиц (например, электрический ток, который протекает по проводам). Итак, если имеется заряд, равный целому кулону, то какому количеству электронов он соответствует? Поскольку величина заряда каждого электрона равна 1,6·10-19 Кл, то получается, что:
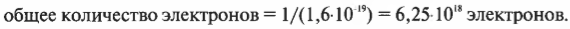
Итак, чтобы получить заряд в 1 Кл, надо собрать 6,25·1018 электронов. Но если собрать вместе огромное количество электронов, то произойдет интересная вещь. Электроны разлетятся в сторону, подобно родственникам, разбегающимся в конце скучного семейного мероприятия.
Тяни и толкай: электрические силы
Воздействие электрических зарядов друг на друга проявляется в виде силы. Например, чтобы удержать в одном месте 6,25·1018 электронов, придется приложить немало усилий. Все объекты вокруг нас содержат электрические заряды, но если некий объект имеет избыточное количество электронов, то он обладает суммарным отрицательным зарядом, а если, наоборот, электронов ему не хватает, то этот объект обладает суммарным положительным зарядом.
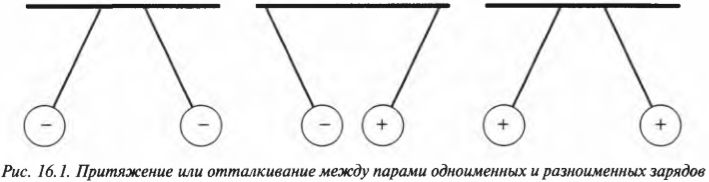
Как известно, одноименные полюсы магнитов отталкиваются, а разноименные — притягиваются. На рис. 16.1 показаны шарики, подвешенные на ниточках и имеющие электрический заряд. Так вот, как и в случае с магнитами, пары шариков с одноименными зарядами (+ и + или — и -) будут отталкиваться друг от друга, а пары с разноименными зарядами (+ и — или — и +) — наоборот, притягиваться друг к другу.
Подбираемся к закону Кулона
Недостаточно просто говорить о положительности или отрицательности заряда, надо еще указывать их числовые значения. Насколько велики силы, действующие между заряженными телами? Это зависит от того, насколько велики заряды и насколько далеко они находятся друг от друга. В главе 5 говорится о другой силе, действующей между телами, — силе всемирного тяготения:
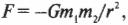
где ( F ) — это сила, ( G ) — универсальная гравитационная постоянная, ( m_1 ) — масса первого тела, ( m_2 ) — масса второго, а ( r ) — расстояние между ними. Аналогично, в результате лабораторных измерений можно убедиться, что сила взаимодействия электрических зарядов выражается таким образом:
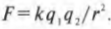
В данном случае ( q_1 ) и ( q_2 ) — это два взаимодействующих заряда, измеренных в кулонах, ( r ) — расстояние между ними, а ( k ) — коэффициент пропорциональности.
(В системе СГСЭ единица измерения заряда выбрана таким образом, что коэффициент ( k ) = 1, а сам символ ( k ) принято опускать в формуле закона Кулона. В системе СИ ( k ) ≈ 8,99·109 Н·м2·Кл-2, причем обычно он выражается формулой:
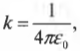
где ( delta_0 ) ≈ 8,85·10-12 Кл2·Н-1·м-2 — электрическая постоянная. Здесь и далее автор использует систему СИ. — Примеч. ред.)
Формула ( F=kq_1q_2/r^2 ) называется законом Кулона. Этот закон определяет величину силы, действующей между электрическими зарядами. Обратите внимание, что если заряды имеют одинаковый знак, то действующая между ними сила является положительной, т.е. заряды будут отталкиваться друг от друга. А если заряды имеют противоположные знаки, то действующая между ними сила является отрицательной, т.е. заряды будут притягиваться друг к другу.
Притягиваем заряды
Важным компонентом закона Кулона является расстояние между заряженными телами (см. два предыдущих раздела). Допустим, два точечных объекта разнесли на 1 м друг от друга и придали каждому из них заряд в 1 Кл: одному — отрицательный, а другому — положительный. Какую силу нужно приложить, чтобы преодолеть их притяжение друг к другу? Подставим численные значения в формулу закона Кулона:
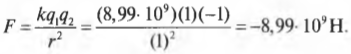
Чтобы не дать шарикам сойтись, нужно приложить силу в 8,99·109Н. Значение неправдоподобно большое — оно равносильно весу груза с массой примерно 560000 т или весу 10 наполненных нефтяных танкеров. Забавный вывод: следует хорошо подумать, прежде чем придавать точечным объектам заряды в 1 Кл. Как видите, между такими зарядами возникает чудовищно большое электрическое взаимодействие.
Вычисляем скорость электронов
Благодаря круговой орбите электрона можно связать между собой две силы: электростатическую и центростремительную (глава 10). Известно, что каждый атом водорода состоит из одного электрона, который вращается вокруг одного протона. Размеры атома водорода слишком малы, чтобы все это увидеть, но известно, что электрон носится вокруг протона очень быстро. Тогда возникает вопрос — насколько быстро? Как известно, между протоном и электроном действует электростатическая сила притяжения. При условии, что орбита электрона круговая, эта сила обеспечивает центростремительную силу (глава 10). Таким образом, электростатическую силу по закону Кулона можно приравнять к центростремительной силе:
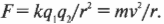
Масса электрона и радиус его орбиты равны соответственно 9,1·10-31 кг и 5,29·10-11 м. Итак, взяв значения, требуемые для вычисления электростатической силы (константу ( k ), а также заряды электрона и протона), получим:
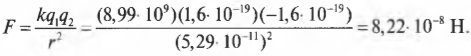
Полученная сила, действующая между электроном и протоном, обеспечивает центростремительную силу, поэтому:
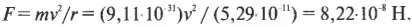
Вычисление дает для ( v ) значение 2,19·106 м/с или около 7,88 млн. км/ч! Попробуйте представить себе эту скорость; она равна где-то 1% от скорости света.
Изучаем силы, действующие между несколькими зарядами
Если в задаче рассматривается взаимодействие зарядов, то совсем не обязательно, что их будет только два. И если зарядов все-таки больше двух, то для вычисления результирующей силы, приложенной к любому из них, придется использовать векторы. (Подробнее о векторах можно узнать в главе 4.)
Посмотрите на рис. 16.2, где показаны три взаимодействующие заряда: один положительный и два отрицательных. Какова результирующая сила, действующая на положительный заряд?
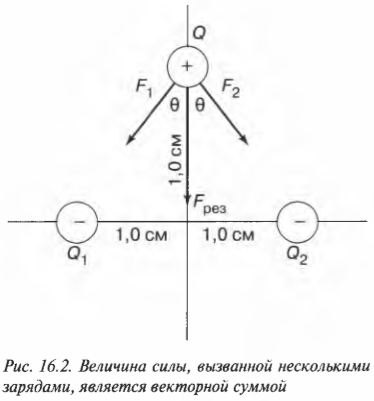
На положительный заряд ( Q ) действуют силы, вызванные двумя отрицательными зарядами ( Q_1 ) и ( Q_2 ); на рис. 16.2 эти силы обозначены, как ( F_1 ) и ( F_2 ). Суммой ( F_1 ) и ( F_2 ) является ( F_{рез} ). Пусть ( Q_1 ) = ( Q_2 ) = -1,0·10-8 Кл, ( Q ) = 3,0·10-8 Кл, а все заряды, как показано на рисунке, расположены на осях X и Y в 1,0 см от начала координат. Чему равна( F_{рез} )? С помощью теоремы Пифагора (глава 2) получаем ( theta ) = 45°. По величине ( F_1=F_2 ), поэтому:
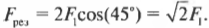
Какова величина ( F_1 )?
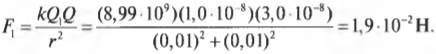
Итак, ( F_1 ) равняется 1,9·10-2 Н, и можно найти результирующую силу, действующую на положительный заряд:
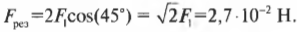
Итак, величина результирующей силы, действующей на положительный заряд, получена в виде векторной суммы (глава 4) и равняется 2,7·10-2 Н.
Действие на расстояние: электрические поля
Чтобы найти силу, действующую между двумя зарядами, надо знать величину (значение) каждого из них. А когда зарядов целое множество, то не исключено, что и их значений также целое множество. Что если к имеющемуся множеству зарядов кто-то другой захочет добавить еще и пробный заряд (т.е. заряд, используемый специально для измерения действующих на него сил)? Допустим, что величина этого нового пробного заряда не известна. Может, 1 Кл? А почему бы не 1,0·10-8 Кл или 1,0·103 Кл?
Чтобы описать, как имеющееся множество зарядов будет воздействовать на чей-то другой пробный заряд, физики ввели понятие электрическое поле. Для определения силы взаимодействия поля от имеющегося множества зарядов достаточно умножить величину пробного заряда на величину напряженности поля в той точке, где он находится. Вот как определяется напряженность ( mathbf{E} ) электрического поля:
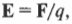
где ( mathbf{F} ) обозначает силу, действующую на пробный заряд со стороны имеющегося множества зарядов, a ( q ) — величина пробного заряда. Напряженность выражается в ньютонах на один кулон (Н·Кл-1). Обратите внимание, что речь идет о векторной величине, т.е. имеющей модуль и направление (глава 4).
Другими словами, напряженность электрического поля в той или иной точке — это сила, которая бы действовала в ней на пробный заряд в один кулон. Направление напряженности совпадает с направлением силы, вызываемой в данной точке каким-либо положительным зарядом.
Представим, что вы перемещаете по горизонтали заряд в 1 Кл. День солнечный, погода прекрасна, но тут нежданно-негаданно заряд оказывается в электрическом поле с напряженностью 5 Н/Кл, направленной противоположно его движению (рис. 16.3).
Что же происходит? На объект с зарядом 1 Кл внезапно действует сила, направленная противоположно его движению:
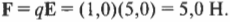
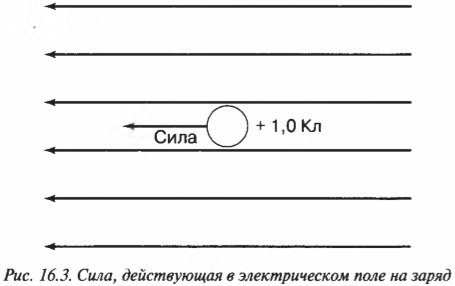
Если изменить направление движения объекта с зарядом 1 Кл, то эта сила будет направлена уже по ходу его движения. Польза понятия “электрическое поле” состоит в следующем: по напряженности поля можно определить силу, действующую на заряд в этом поле. Если заряд в точке положительный, то направление этой силы будет совпадать с направлением напряженности поля в этой точке, а если заряд отрицательный, то сила будет направлена в противоположную сторону.
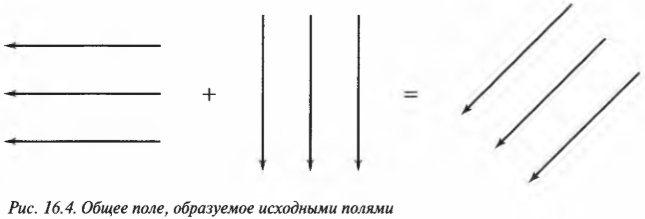
Так как напряженность электрического поля в любой точке — это результирующий вектор (обладающий, как известно, величиной и направлением), то его можно вычислить путем сложения составляющих его векторов (об особенностях такого сложения говорится в главе 4). Посмотрите на рис. 16.4, где показаны (в виде векторов напряженности) два исходных электрических поля, “горизонтальное” и “вертикальное”, расположенные в одной и той же области. Образуемое ими общее электрическое поле имеет напряженность, равную векторной сумме их напряженностей.
По всем направлениям: электрические поля от точечных зарядов
Не все электрические поля выглядят так просто как те, что показаны на рис. 16.3. Как, например, выглядит электрическое поле от точечного заряда? Под точечным подразумевается заряд очень малого физического объекта. Известно, что заряд ( Q ) создает электрическое поле, но какое? Благодаря формуле напряженности электрического поля, ( E=F/q ), ответить на этот вопрос достаточно просто. Пусть имеется пробный заряд ( q ), с помощью которого можно в разных точках измерять силу, вызываемую зарядом ( Q ). Вот эта сила, вычисляемая по формуле из предыдущего раздела этой главы:
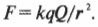
Итак, чему равна напряженность электрического поля? Надо разделить эту силу на величину пробного заряда ( q ):
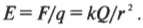
Напряженность электрического поля от точечного заряда — это ( E=kQ/r^2 ). Она является вектором (глава 4), но куда направлен этот вектор? Чтобы узнать это, вернемся к пробному заряду ( q ) и предположим, что он является положительным (помните, что напряженность электрического поля определяется как сила, действующая на положительный заряд в один кулон).
В любом месте электрического поля сила, действующая из ( Q ) на ( q ), является радиальной, т.е. направленной по прямой, которая соединяет центры двух зарядов. Если заряды ( Q ) и ( q ) положительны, то сила, действующая на ( q ), будет направлена не к ( Q ), а в противоположную сторону. Таким образом, напряженность электрического поля в любой точке будет также направлена в противоположную от ( Q ) сторону. Это можно увидеть на рис. 16.5, где электрическое поле изображено в виде так называемых линий поля, использовать которые впервые предложил Майкл Фарадей в XIX веке.
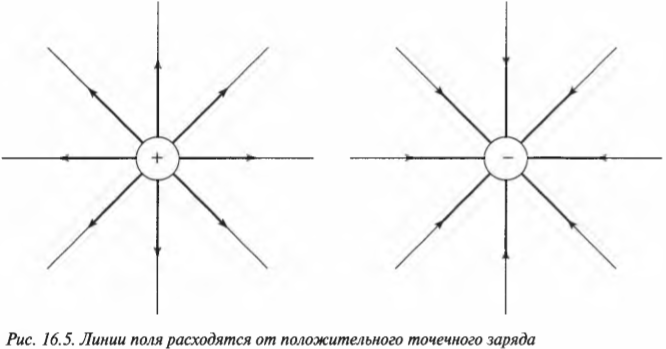
Глядя на линии поля, можно получить хорошее качественное представление электрического поля (не путать с количественным представлением, т.е. в виде У ^ / чисел). И когда в точке А линии поля ближе друг к другу, чем в точке В, то это значит, что в точке А поле сильнее, чем в точке В. Кроме того, обратите внимание, что линии поля расходятся от положительных зарядов и, наоборот, сходятся к отрицательным зарядам (рис. 16.5).
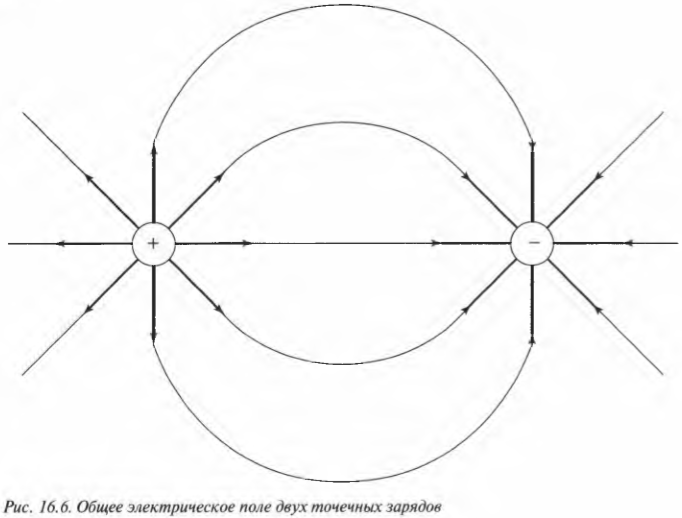
Как определить величину электрического поля от нескольких зарядов? В таком случае напряженности полей в каждой точке надо складывать как векторы. Например, имея два точечных заряда, положительный и отрицательный, получим электрическое поле, показанное на рис. 16.6.
Линии поля (как те, что показаны на рис. 16.6) начинаются на положительном заряде и заканчиваются на отрицательном заряде, т.е. они не могут начинаться или заканчиваться в точке пространства без заряда.
Заряжаем конденсатор: электрические поля между плоскими пластинами
Вычисление электрического поля от множества точечных зарядов, о котором говорилось в предыдущем разделе, в общем случае представляет собой довольно сложную задачу сложения векторов (глава 4). Чтобы облегчить себе жизнь, физики используют модели простых полей. Рассмотрим модель простого поля в плоском конденсаторе. Вообще говоря, конденсатором (не обязательно плоским) называется объект, способный сохранять заряд: положительный и отрицательный заряды хранятся отдельно, чтобы они притягивались друг к другу, но не могли самостоятельно соединиться.
На рис. 16.7 показан пример конденсатора с двумя плоскими пластинами: на одной пластине равномерно распределен заряд ( +q ), а на другой — заряд ( -q ). Все компоненты напряженностей полей, созданных точечными зарядами, на этих пластинах взаимно компенсируют друг друга, за исключением тех компонент, которые направлены перпендикулярно пластинам. Другими словами, между параллельными пластинами конденсатора создаются постоянные электрические поля, работать с которыми легче, чем с полями точечных зарядов.
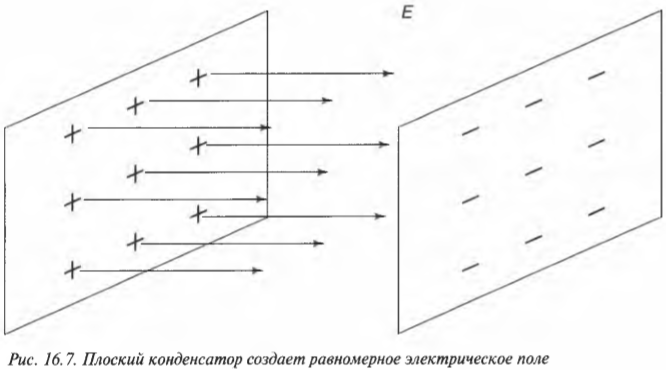
В результате достаточно долгих вычислений можно сделать вывод, что электрическое поле между пластинами постоянно (если пластины находятся друг от друга достаточно близко), а его напряженность равна:
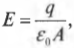
где ( varepsilon_0 ) — это электрическая постоянная, равная 8,85·10-12 Кл2·Н-1·м-2 (см. один из предыдущих разделов этой главы), ( q ) — общий заряд на каждой из пластин (на одной и на другой из них заряд соответственно равен ( +q ) и ( -q )), ( A ) — это площадь каждой пластины. Формулу еще можно записать с помощью плотности заряда ( sigma ) на каждой пластине, где ( sigma=q/A ) (заряд, приходящийся на единицу площади). Тогда формула будет выглядеть таким образом:
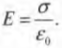
Модель плоского конденсатора значительно облегчает жизнь физика потому, что напряженность электрического поля постоянна и имеет постоянное направление (с положительной пластины на отрицательную), поэтому для вычисления напряженности поля не важно, в каком месте между пластинами измеряется напряженность поля.
Повышаем напряжение: электрический потенциал
Электрические поля (см. предыдущий раздел) — это еще не все, что относится к электричеству. Для изучения электричества придется использовать и другие понятия. Например, для работы с электрическими силами удобно использовать понятие потенциальной энергии, или энергии, “запасенной” в теле или в системе тел. В механике вполне естественно связывают работу силы и потенциальную энергию: например, подъем груза в поле силы тяжести связывается с увеличением потенциальной энергии ( Delta W ), т.е. энергии, накапливаемой в теле благодаря его новому положению:
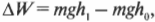
где ( m ) означает массу, ( g ) — ускорение свободного падения в поле силы тяжести, ( h_1 ) и ( h_2 ) — соответственно конечную и начальную высоту. Так как в электрическом поле на заряды действует сила, то можно говорить о потенциальной энергии и в электрических полях. Такой энергией является потенциальная энергия электрического поля, а ее изменение создает новую величину, которая называется напряжением и является движущей силой электрического тока.
Вычисляем потенциальную энергию электрического поля
Потенциальная энергия электрического поля — это потенциальная энергия, “запасенная” в электрическом поле. При знакомстве с понятием энергии в главе 8 мы также познакомились с понятием работы. Предположим, что положительный заряд перемещается по направлению к положительно заряженной пластине, как показано на рис. 16.8. Как они будут взаимодействовать друг с другом? Линии поля идут от положительных зарядов к отрицательным, а показанный на рисунке одиночный положительный заряд взаимодействует с положительно заряженной пластиной. Поскольку этот заряд имеет положительный знак, то действующая на него сила будет отталкивать его от положительно заряженной пластины, то есть вправо в плоскости рисунка. Кроме того, одиночный заряд будет притягиваться отрицательно заряженной пластиной справа от него.
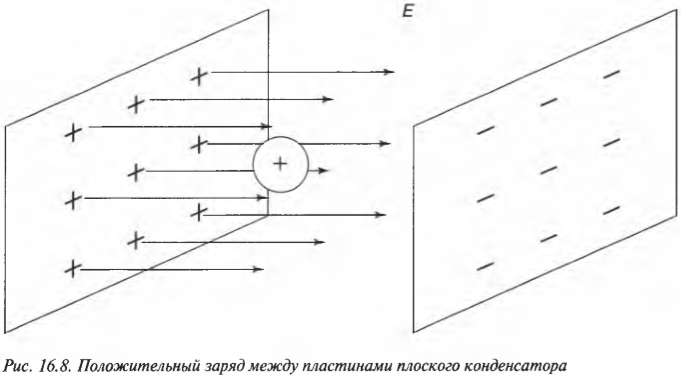
Итак, каким будет изменение потенциальной энергии положительного заряда при перемещении его между пластинами справа налево против силы, направленной в обратную сторону? Работа ( A ) по перемещению заряда должна равняться увеличению его потенциальной энергии. Формула такой работы имеет следующий вид:
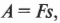
где ( F ) и ( s ) означают соответственно силу и перемещение. Сила, приложенная к положительному заряду, равна ( qE ), где ( q ) — это величина заряда, а ( E ) — напряженность электрического поля, в котором он находится. В результате получаем для формулы работы следующее выражение:
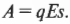
Эта величина работы равна увеличению потенциальной энергии заряда ( Delta W ). Если электрическое поле постоянно по направлению к модулю напряженности, то можно сказать, что изменение потенциальной энергии:
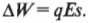
Для характеристики электрического поля физики придумали понятие напряженность электрического поля, которая определяется, как сила, действующая со стороны поля на точечный объект с зарядом 1 Кл (см. один из предыдущих разделов этой главы о действии на расстоянии с помощью электрического поля). Аналогично, для характеристики изменения потенциальной энергии электрического поля между точками А и Б физики ввели понятие электрическое напряжение.
Потенциалы и напряжение
На языке физики напряжение — это разность электрических потенциалов (т.е. потенциальной энергии электрического поля, приходящейся на единицу заряда), или просто разность потенциалов. Эта величина определяется как отношение работы электрического поля при переносе пробного заряда из точки А в точку Б к величине пробного заряда. Единицей измерения напряжения в системе СИ является вольт (В), 1 В = 1 Дж/1 Кл. Напряжение обозначается символом ( U ).
Электрический потенциал ( U ) в определенной точке представляет собой электрическую потенциальную энергию ( W ) пробного заряда, деленную на величину этого заряда ( q ):
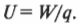
Таким образом, напряжение — это изменение потенциальной энергии заряда в один кулон. Работа ( A ) по перемещению в плоском конденсаторе положительного заряда ( q ) с отрицательной пластины на расстояние ( s ) по направлению к положительной пластине (см. выше) равна:
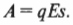
Эта работа равна изменению потенциальной энергии заряда при перемещении на расстояние ( s ) от отрицательной пластины, поэтому потенциал в месте нахождения заряда вычисляется по следующей формуле:
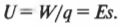
Предположим, что ваше внимание привлекла машина, стоящая на обочине дороги с открытым капотом. На вопрос: “В чем дело?” водитель отвечает: “Машина не едет”.
Желая помочь бедняге, вы достаете свой вольтметр и пытаетесь протестировать аккумулятор машины. Вольтметр показывает 12 В и, похоже, проблема совсем не в этом, но поскольку вы увлечены самим процессом изучения электричества, то вас уже не остановить.
Если 12 В — это изменение потенциальной энергии при перемещении заряда в один кулон от одной клеммы аккумулятора к другой, то какую работу нужно выполнить для перемещения между этими клеммами одного электрона? Как известно:
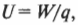
поэтому
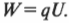
Попавший в затруднение водитель с интересом наблюдает за этими манипуляциями. Поскольку величина заряда электрона равна 1,6·10-19 Кл (см. выше первый раздел в этой главе о заряде электрона и протона), то, подставляя в эту формулу численные значения, получим:
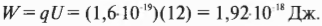
Спустя несколько мгновений вы гордо заявляете: “На перемещение одного электрона между клеммами аккумулятора требуется 1,92·10-18 джоулей”.
У водителя пропадает всякая надежда, и не удивительно, что после ваших слов он смотрит на вас со странным выражением лица…
Оказывается, энергия сохраняется даже в электрическом поле
Как известно, при переходе системы объектов из состояния 1 с полной энергией ( E_1 ) в состояние 2 с полной энергией ( E_2 ) (где полная энергия является суммой кинетической ( K ) и потенциальной ( W ) энергии, см. главу 8) полная энергия сохраняется:
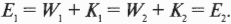
Оказывается, что полная энергия системы объектов сохраняется и в электрическом поле. Допустим, что пылинка с массой 1,0·10-5 кг столкнулась с отрицательно заряженной пластиной плоского конденсатора и получила заряд —1,0·10-5 Кл. Очевидно, что отрицательно заряженная пылинка будет притягиваться положительной пластиной и начнет движение к ней.
Разность потенциалов между пластинами составляет 30 В. Какова будет скорость пылинки, когда она столкнется с положительной пластиной (если не учитывать сопротивление воздуха)? Так как полная энергия сохраняется, то потенциальная энергия пылинки на отрицательной пластине к моменту ее столкновения с положительной пластиной уменьшится на величину возрастания кинетической энергии (( Delta K={}^1!/!_2mv^2 )). Величину уменьшения потенциальной энергии пылинки можно найти с помощью формулы:
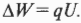
Подставляя в нее численные значения, получим:
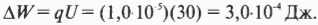
Это уменьшение потенциальной энергии превращается в увеличение кинетической энергии:
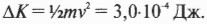
Подставляя численные значения, получим:
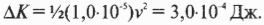
В результате несложных вычислений получим:
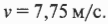
Иными словами, пылинка столкнется с положительной пластинкой на скорости, примерно равной 7,75 м/с, или 27,9 км/ч.
Электрический потенциал точечных зарядов
Разность потенциалов, или напряжение ( U ) (см. предыдущий раздел), между пластинами конденсатора зависит от расстояния ( s ) между положительно и отрицательно заряженными пластинами (подробнее о конденсаторах рассказывается выше в этой главе):
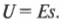
Сложнее определить потенциал точечного объекта с зарядом ( Q ), ведь его электрическое поле совсем не такое постоянное, как между пластинами конденсатора. Как вычислить потенциал на произвольном расстоянии от точечного заряда? Сила, действующая на пробный заряд ( q ), вычисляется по формуле:
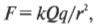
где ( k ) означает константу, равную 8,99·109 Н·м2/Кл2, а ( r ) — расстояние между точечным объектом с зарядом ( Q ) и пробным зарядом ( q ).
Напомним, что напряженность ( E ) в любой точке вокруг точечного заряда ( Q ) выражается формулой:
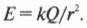
Итак, чему равен электрический потенциал точечного заряда? На бесконечности он равен нулю.
Если перенести пробный заряд на более близкое расстояние ( r ) от точечного заряда, то изменение его потенциала ( U ) будет равно выполненной работе ( A ), деленной на величину пробного заряда ( q ):
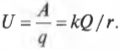
Это потенциал в вольтах, полученный для любой точки на расстоянии ( r ) от точечного заряда ( Q ) и равный нулю на расстоянии ( r=infty ). Сказанное имеет смысл, если не забывать, что потенциал — это работа по переносу пробного заряда в определенное место, деленная на величину пробного заряда. Возьмем, например, протон ( Q ) = +1,6·10-19 Кл, расположенный в центре атома водорода. На расстоянии 5,29·10-11 м от протона по свой обычной орбите движется электрон. Какой потенциал будет на таком расстоянии от протона? Вам известно, что:
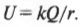
Подставив в формулу числа, получаем:
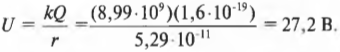
Итак, электрический потенциал на указанном расстоянии от протона равен 27,2 В. А это немало для столь крошечного (почти точечного) заряда.
Как и электрические поля, электрический потенциал можно представить графически (только не в виде линий поля, а в виде эквипотенциальных поверхностей). Эквипотенциальными называются поверхности с одинаковым потенциалом. Так как, например, потенциал точечного заряда зависит от расстояния (или радиуса сферы), то эквипотенциальными поверхностями точечного заряда являются сферы, расположенные вокруг этого заряда (рис. 16.9).
А как насчет эквипотенциальных поверхностей между пластинами плоского конденсатора? Как вам известно, при перемещении положительного заряда с отрицательно заряженной пластины на расстояние ( s ) по направлению к положительно заряженной пластине разность потенциалов имеет вид:
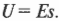
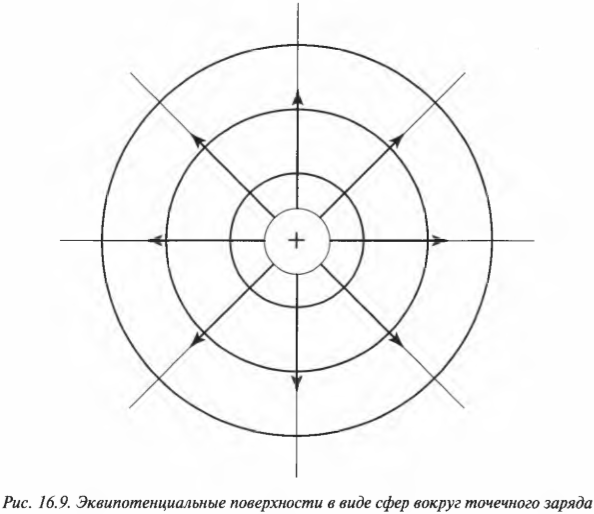
Иначе говоря, потенциал на эквипотенциальной поверхности зависит только от расстояния до пластин. Например, на рис. 16.10 две эквипотенциальные поверхности показаны между пластинами конденсатора.
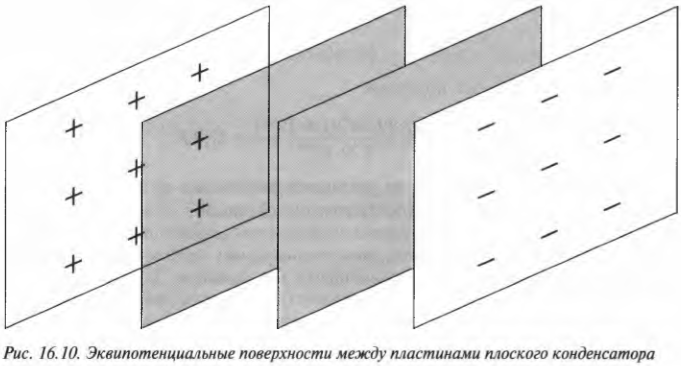
Сохраняем заряд с помощью емкости
Конденсатор способен хранить противоположные электрические заряды. Они удерживаются отдельно так, чтобы они притягивались друг к другу, но не могли самостоятельно соединиться, например перейти с одной пластины на другую в плоском конденсаторе.
Каков заряд конденсатора? Он зависит от емкости ( C ) конденсатора. Заряды на обеих пластинах конденсатора равны друг другу (только противоположны по знаку) и связаны с напряжением ( U ) между пластинами и емкостью ( C ) конденсатора следующей формулой:
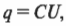
где ( q ) и ( C ) — это соответственно заряд и емкость. В плоском конденсаторе напряженность ( E ) электрического поля определяется следующей формулой:
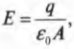
где ( varepsilon_0 ) — электрическая постоянная, а ( A ) — площадь пластины. Для связи напряжения ( U ) между пластинами, расположенными на расстоянии ( s ) друг от друга, и напряженности ( E ) электрического поля используется следующая формула:
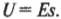
Поэтому:
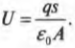
Так как ( q = CU ), то из предыдущей формулы получим:
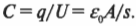
В системе СИ единицей измерения емкости является фарада (Ф), 1 Ф = 1 Кл/1 В.
Неплохо, но это еще не все. В большинстве конденсаторов между пластинами находится не воздух, а специальный наполнитель — диэлектрик. Диэлектрик — это материал, который плохо проводит электрический ток и увеличивает емкость конденсатора пропорционально своей диэлектрической проницаемости ( varepsilon ). Итак, если пространство между пластинами плоского конденсатора заполнено диэлектриком с диэлектрической проницаемостью ( varepsilon_0 ), то емкость увеличивается в соответствии с формулой:
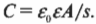
Например, диэлектрическая проницаемость слюды (минерала, широко используемого в конденсаторах) примерно равна 5,4, таким образом делая емкость конденсатора примерно в 5,4 раза большей, чем у того же конденсатора с вакуумом между пластинами, потому что диэлектрическая константа вакуума равна 1.
Конденсатор содержит заряды, расположенные отдельно друг от друга, но способные соединиться, и потому обладает связанной с этим потенциальной энергией. Ведь, чтобы разделить эти заряды, нужно затратить определенную работу. Чему равна энергия конденсатора? Путем несложных вычислений можно определить, что энергия конденсатора ( W_c ) равна:
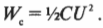
Пусть имеется две незаряженные пластины конденсатора с разностью потенциалов ( U ). Чтобы перенести часть заряда ( dq ) с одной пластины на другой (и таким образом создать заряд ( +dq ) на одной пластине и ( -dq ) на другой), нужно совершить работу ( A=dq!cdot!U ). Поскольку ( q = CU ), то работа ( A=q!cdot!dq/C ) и для определения полной работы по перенесению заряда ( Q ) нужно вычислить интеграл:
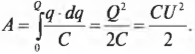
Теперь по формуле ( W_c={}^1!/!_2CU^2 ) можно вычислять энергию, хранящуюся в плоском конденсаторе, и выражать ее в джоулях (Дж).
Глава 16. Электризуемся: изучаем статическое электричество
Оценка
