Как найти ток в круговом витке

1. Магнитное поле кругового витка с током.

Согласно
закону Био-Савара-Лапласа, индукция
магнитного поля, создаваемого элементом
тока dl на расстоянии r от него есть

где
α – угол между элементом тока

и
радиус-вектором

,
проведенным из этого элемента в точку
наблюдения; r – расстояние от элемента
тока до точки наблюдения.

В
нашем случае α = π/2, sinα = 1;

, где а – расстояние, отсчитываемое от
центра витка до рассматриваемой точки
на оси витка. Векторы

образуют
в этой точке конус с углом раствора при
вершине 2

=
π – 2β, где β – угол между отрезками а и
r.

Из
соображений симметрии ясно, что
результирующее магнитное поле на оси
витка будет направлено вдоль этой оси,
то есть вклад в него дают только те
составляющие, которые параллельны оси
витка:

Результирующую
величину индукции магнитного поля B на
оси витка получим, проинтегрировав это
выражение по длине контура от 0 до 2πR:

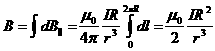
или,
подставив значение r:

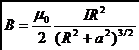
В
частности, при а = 0 находим индукцию
магнитного поля в центре кругового
витка с током:

Этой
формуле можно придать другой вид,
воспользовавшись определением магнитного
момента витка с током:

Последнюю
формулу можно записать в векторном виде
(см. рис.9.1):

.

1. Действие магнитного поля на проводник с током. Закон Ампера.

Магнитное
поле действует с некоторой силой на
любой проводник с током, находящийся
в нем.

Если
проводник, по которому протекает
электрический ток подвесить в магнитном
поле, например, между полюсами магнита,
то магнитное поле будет действовать на
проводник с некоторой силой и отклонять
его.

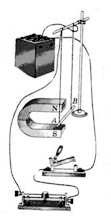
Направление
движения проводника зависит от
направления тока в проводнике и от
расположения полюсов магнита.

Сила,
с которой магнитное поле действует на
проводник с током, называется силой
Ампера.

Французский
физик А. М. Ампер был первым, кто обнаружил
действие магнитного поля на проводник
с током. Правда, источником магнитного
поля в его опытах был не магнит, а другой
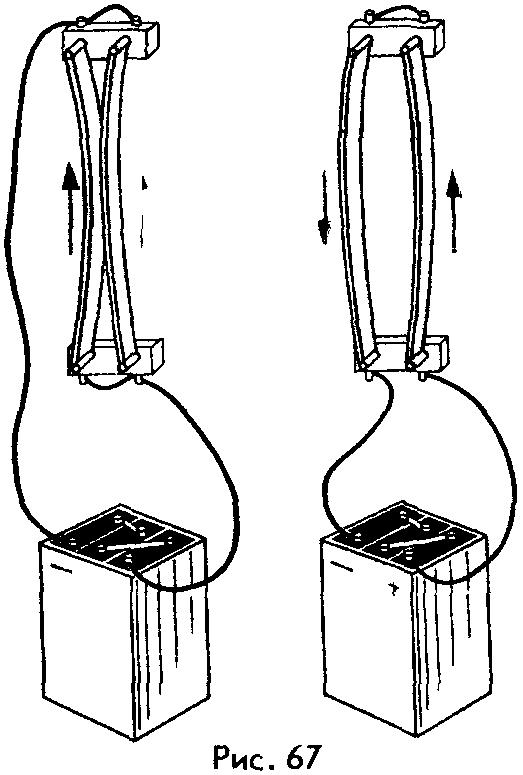
проводник с током. Помещая проводники
с током рядом друг с другом, он обнаружил
магнитное взаимодействие токов (рис.
67) – притяжение параллельных токов и
отталкивание антипараллельных (т. е.
текущих в противоположных направлениях).
В опытах Ампера магнитное поле первого
проводника действовало на второй
проводник, а магнитное поле второго
проводника – на первый. В случае
параллельных токов силы Ампера оказывались
направленными навстречу друг другу и
проводники притягивались; в случае
антипараллельных токов силы Ампера
изменяли свое направление и проводники
отталкивались друг от друга.

Направление
силы Ампера можно определить с помощью
правила левой руки:

если
расположить левую ладонь руки так, чтобы
четыре вытянутых пальца указывали
направление тока в проводнике, а силовые
линии магнитного поля входили в ладонь,
то отставленный большой палец укажет
направление силы, действующей на
проводник с током (рис. 68).

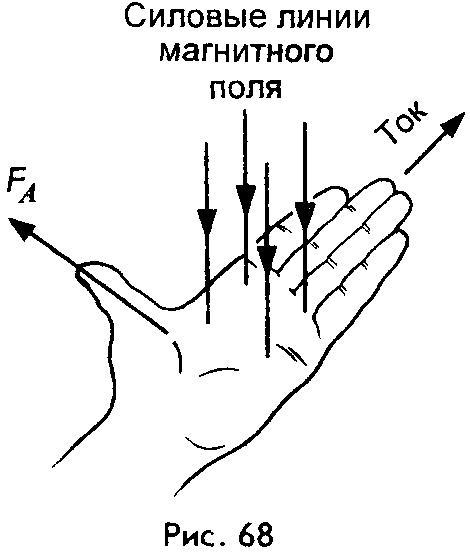
Эта
сила (сила Ампера) всегда перпендикулярна
проводнику, а также силовым линиям
магнитного поля, в котором этот проводник
находится.

Сила
Ампера действует не при любой ориентации
проводника. Если проводник с током
расположить вдоль си

Зако́н
Ампе́ра — закон взаимодействия
электрических токов. Впервые был
установлен Андре Мари Ампером в 1820 для
постоянного тока. Из закона Ампера
следует, что параллельные проводники
с электрическими токами, текущими в
одном направлении, притягиваются, а в
противоположных — отталкиваются.
Законом Ампера называется также закон,
определяющий силу, с которой магнитное
поле действует на малый отрезок проводника
с током. Сила

,
с которой магнитное поле действует на
элемент объёма

проводника с током плотности

,
находящегося в магнитном поле с индукцией
:

.

Если
ток течёт по тонкому проводнику, то

,
где —

«элемент длины» проводника — вектор,
по модулю равный и совпадающий по
направлению с током. Тогда предыдущее
равенство можно переписать следующим
образом:

Сила

,
с которой магнитное поле действует на
элемент

проводника
с током, находящегося в магнитном поле,
прямо пропорциональна силе тока

в проводнике и векторному произведению
элемента длины

проводника на магнитную индукцию :

.

Направление
силы

определяется по правилу вычисления
векторного произведения, которое удобно
запомнить при помощи правила правой
руки.

Модуль
силы Ампера можно найти по формуле:

,

где

—
угол между векторами магнитной индукции
и тока.

Сила

максимальна когда элемент проводника
с током расположен перпендикулярно
линиям магнитной индукции

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Французские ученые Ж. Био и Ф. Савар изучали магнитные поля, создаваемые постоянными токами разной формы. Результаты их работы обобщил известный математик и физик П. Лаплас.

Применение закона Био – Савара – Лапласа к вычислению магнитного поля кругового тока

Закон Био-Савара–Лапласа описывает порождение магнитного поля током $I$ на элементе проводника длиной $dl$ в некоторой точке пространства ($mu$ – магнитная проницаемость вещества в котором локализовано поле):

$dvec{B}=frac{mu_{0}mu }{4pi }frac{Ileft[ dvec{l}vec{r}right]}{r^{3}}left( 1 right)$

где $d vec l ⃗$ – вектор, длина которого равна длине элемента проводника $dl$, направленный по току; $vec r$ – радиус-вектор, который проведен от элемента $dl$ в точку, в которой исследуется магнитное поле. Поскольку в правой части формулы (1) находится векторное произведение, очевидно, что индукция элементарного магнитного поля будет направлена перпендикулярно плоскости, в которой находятся векторы $vec r$ и $vec l$ и при этом является касательной к силовой линии поля.

Величину вектора $vec{dB}$ из выражения (1) найдем как:

$dB=frac{mu_{0}mu }{4pi }frac{Idlsin alpha }{r^{2}}left( 2 right)$.

где $ alpha $– угол между векторами $vec r$ и $vec l$ .

Конкретное направление $vec{dB}$ находят по правилу буравчика (правилу правой руки):

Если правый винт вращать так, что его поступательное движение будет совпадать с направлением течения тока в избранном элементе, то вращение его головки укажет направление $vec{dB}$.

Магнитные поля подчиняются принципу суперпозиции:

Суммарную магнитную индукцию поля, создаваемого несколькими источниками, находят как геометрическую сумму векторов магнитной индукции отдельных полей:

$vec{B}=sumlimits_{i=1}^N vec{B}_{i} left( 3 right). $

Если распределение токов можно считать непрерывным, то принцип суперпозиции можно записать:

$vec{B}=int {dvec{B}_{i}} left( 4 right).$

Вычисление магнитной индукции поля с применением закона Био-Савара-Лапласа довольно сложная процедура. Но при существовании определенной симметрии в распределении токов, используя, рассмотренный нами закон и принцип суперпозиции, рассчитать конкретные поля просто. В любом случае следует придерживаться следующей схемы действий:

1. Выделить на проводнике с током элементарный отрезок $dl$.
2. Записать для исследуемой точки поля закон Био – Савара – Лапласа.
3. Определить направление элементарного поля $vec{dB}$ в избранной точке.
4. Воспользоваться принципом суперпозиции для магнитных полей (учесть, что суммируются векторы).

Магнитное поле кругового тока в его центре

Рассмотрим круговой проводник, по которому течет постоянный ток $I$ (рис.1). Выделим на этом проводнике элемент $dl$, который можно считать прямолинейным. Если перейти к другому элементу этого же тока, затем к третьему и так далее, применить правило правого винта, то очевидно, что все магнитные поля, созданные этими элементами в центре, направлены вдоль одной прямой, перпендикуляру к плоскости кольца. Это означает, применяя принцип суперпозиции, мы векторное сложение заменим алгебраическим.

Запишем закон Био-Савара-Лапласа для модуля вектора индукции поля, создаваемого элементом d$l_1$:

$dB=frac{mu_{0}mu }{4pi }frac{Idl_{1}sin alpha }{r^{2}}left( 5right).$

Из рис.1 мы видим:

1. что расстояние от элементарного тока до центра витка равно его радиусу ($R$) и будет одинаковым для всех элементов на этом витке,
2. элемент $dl$ (как и все остальные элементы) будут нормальны к радиус-вектору $vec r$.

Учитывая сказанное выражение (5) представим в виде:

$dB=frac{mu_{0}mu }{4pi }frac{Idl_{1}}{R^{2}}left( 6 right)$.

Обезличивая витки с током, положим далее $dl_1=dl$.

Поскольку наш ток является непрерывным, то для нахождения полного поля в его центре, мы проинтегрируем (6), имеем:

$B=ointlimits_L {dB=} frac{mu_{0}mu }{4pi}frac{I}{R^{2}}ointlimits_L {dl} =frac{mu_{0}mu }{4pi}frac{I}{R^{2}}2pi Rto$

$B=mu_{0}mu frac{I}{2R}left( 7 right)$.

Индукция магнитного поля кругового тока на его оси

Найдем индукцию магнитного поля на оси кругового тока, если ток, текущий по нему равен $I$, радиус витка – $R$ (рис.2).

Как основу для выполнения поставленной задачи возьмем закон Био-Савара-Лапласа (1), где из рис.2 мы видим, что:

• $vec{r}=vec{R}+vec{h}$,

• $dvec{l}times vec{r}=dvec{l}times vec{R}+dvec{l}times vec{h}(9).$

Используя принцип суперпозиции закон (1) для нашего тока и формулы (8-9) запишем:

$vec{B}=ointlimits_L {dB=}$$frac{mu mu_{0}}{4pi }Iointlimits_L frac{dvec{l}timesvec{r}}{r^{3}} $
$=frac{mu mu_{0}}{4pi }frac{I}{r^{3}}left( ointlimits_L{dvec{l}times vec{R}+} ointlimits_L {dvec{l}times vec{h}}right)left( 10 right).$

В выражении (10) при записи интеграла, мы учли, что величина вектора $vec{r}$ не изменяется. Кроме этого вектор $vec h$, определяющий положение точки, в которой мы ищем поле, не изменяется при движении по нашему контуру, поэтому:

$ointlimits_L {dvec{l}times vec{h}} =(ointlimits_L {dvec{l})timesvec{h}} =0, left( 11 right),$

так как ( $ointlimits_L {dvec{l})=0.}$

Вычислим интеграл: $ointlimits_L {dvec{l}times vec{R}.}$ Введем единичный вектор ($vec n$), нормальный к плоскости витка с током.

$ointlimits_L {dvec{l}times vec{R}=ointlimits_L {vec{n}Rdl=vec{n}R}} ointlimits_L {dl=vec{n}R} 2pi R=2pi R^{2}vec{n}left( 12 right)$.

Подставляем результаты интегрирования из (12) в (10), имеем:

$vec{B}=frac{mu mu_{0}}{4pi }frac{I}{r^{3}}2pi R^{2}vec{n}=frac{mumu_{0}I}{2}frac{R^{2}}{left( R^{2}+h^{2}right)^{frac{3}{2}}}vec{n}left( 13 right)$

где при записи окончательного результата мы учли, что:

$r^{3}=left( R^{2}+h^{2} right)^{frac{3}{2}}$.

Кольца Гельмгольца

Кольцами Гельмгольца считают пару проводников в виде колец одного радиуса, расположенных в параллельных плоскостях (рис.3) на одной оси. Расстояние между плоскостями колец равно их радиусу.

Рассмотрим магнитное поле на оси этих колец.

Декартову систему координат разместим так, что ее начало совпадает с центром нижнего кольца с током. Ось Z нашей системы будет направлена по оси колец (рис.3).

Запишем индукцию магнитного поля в точке с координатой $z$ на оси колец. Используем формулу (13):

$B_{z}=frac{mu mu_{0}I}{2}R^{2}left[ frac{1}{left( R^{2}+z^{2}right)^{frac{3}{2}}}+frac{1}{left[ left( z-d right)^{2}+R^{2}right]^{frac{3}{2}}} right]left( 14right)$.

Исследуем полученное поле. Считается, что магнитное поле на оси колец Гельмгольца на посередине между ними является однородным.

Неоднородность в первом приближении характеризуют первой производной:

$frac{partial B_{z}}{partial z}=frac{3mu mu_{0}I}{2}R^{2}left[frac{-z}{left( R^{2}+z^{2} right)^{frac{5}{2}}}+frac{z-d}{left[ left(z-d right)^{2}+R^{2} right]^{frac{5}{2}}} right]left( 15 right)$.

Если $z=frac{d}{2}quad$ , подставим в (15), имеем:

$frac{partial B_{z}}{partial z}=0.$

Найдем $frac{partial^{2}B_{z}}{partial z^{2}}:$

$frac{partial^{2}B_{z}}{partial z^{2}}=frac{3mu mu_{0}I}{2}R^{2}left( frac{5z^{2}}{left( R^{2}+z^{2}right)^{frac{7}{2}}}-frac{1}{left( R^{2}+z^{2}right)^{frac{5}{2}}}+frac{5left( z-d right)^{2}}{left[ left( z-d right)^{2}+R^{2} right]^{frac{7}{2}}}-frac{1}{left[ left( z-dright)^{2}+R^{2} right]^{frac{5}{2}}} right)left( 16 right)$

По условию для колец Гельмгольца, имеем:
$d=R.$

На середине их общей оси ($z=frac{d}{2})$, получаем:

$frac{partial^{2}B_{z}}{partial z^{2}}=0, left( 17 right)$.

Равенство нулю второй производной от $B_z$ по координате $z$, показывает, что в на середине оси колец магнитное поле является однородным с высокой степенью точности.

В школьной физике в качестве источников магнитного поля рассматриваются постоянные магниты и проводники с током. Если постоянные магниты мы уже рассмотрели, то с проводниками давайте разберёмся в данном разделе. Простейшие формы проводников для расчёта магнитных полей:

• бесконечный прямолинейный проводник с током
• круговой виток с током (проводник в форме окружности)

Для каждого из этих проводников можно рассчитать напряжённость магнитного поля в точке.

Итак, движущийся заряд создаёт вокруг себя магнитное поле. Самый простой тип движущегося заряда — это обычный электрический ток. Вопрос только в том, как согнуть проводник:

• бесконечный прямолинейный проводник с током

Итак, возьмём бесконечный прямолинейный проводник с током. Слово «бесконечный» в данном случае небольшое приближение. Так для любой точки, находящейся непосредственно вблизи любого линейного проводника, сам проводник «кажется» бесконечным. Пусть по нашему проводнику течёт ток  (рис. 1). Прямолинейный проводник с током создаёт вихревое (круговое) магнитное поле вокруг себя. Направление вектора магнитной индукции задаётся правилом буравчика (правилом правой руки). Исходя из этого правила, найдём направление вектора (рис. 2).

Для подсчёта модуля вектора магнитной индукции поля вне прямолинейного бесконечного проводника с током можно использовать соотношение (рис. 3):

(1)

• где

3D модели рисунков достаточно сложны для рассмотрения, поэтому введены условные обозначения для направлений векторов/токов в трёхмерном пространстве (рис. 4).

Тогда перерисуем рисунок 3, в случае, если мы смотрим сверху провода (рис. 5.1). В этом случае ток течёт на нас, т.е. из рисунка. И в случае, когда мы смотрим на провод снизу вверх (рис. 5.2). В этом случае ток течёт от нас, т.е. внутрь рисунка.

На рисунке 5 точечной линией обозначено магнитное поле прямолинейного тока (оно круговое). Направление вектора магнитной индукции () определяется правилом буравчика (правилом правой руки).

Правило буравчика для прямолинейного тока: правой рукой обхватываем проводник с током, отогнутый большой палец сонаправляем с током, тогда согнутые 4 пальца показывают направление вектора магнитной индукции.

• круговой виток с током (проводник в форме окружности)

Второй вариант системы, в которой достаточно просто рассчитать модуль вектора магнитной индукции, — это круговой виток с током. Т.е. сам проводник с током представляет собой окружность. По данному проводнику ток может течь как по часовой стрелке (рис. 6.1), так и против часовой (рис. 6.2).

В целом, магнитное поле такого проводника достаточно сложное, однако для центра витка нахождение модуля вектора магнитной индукции не представляет проблем:

(2)

• где

Немного о  — относительной магнитной проницаемости среды. Это параметр, который описывает насколько сама среда воспринимает магнитное поле источника. В целом, это табличная величина.

Правило буравчика для кругового тока: обнимаем правой рукой провод, большой отогнутый палец правой руки направляем по току, тогда загнутые 4 пальца будут указывать направление вектора магнитной индукции.

Важно: для наших систем можно запомнить, что прямолинейный ток создаёт круговое магнитное поле (рис.5), а круговой ток создаёт прямолинейное магнитное поле (рис.6).

Вывод: для поиска модуля вектора магнитной индукции достаточно проанализировать систему в задаче и описать её через модель бесконечного прямолинейного или кругового проводника с током.