Как найти силу ТОКА? если известно: индукция, длина, сила проводника. (по формуле)
Adriano Celentano
Ученик
(117),
на голосовании
5 лет назад
Дополнен 5 лет назад
ТЕМА: Индукция магнитного поля
Голосование за лучший ответ
李西青
Просветленный
(42606)
5 лет назад
скажу, если ты объяснишь что такое “сила проводника”
Adriano CelentanoУченик (117)
5 лет назад
сила ампера
李西青
Просветленный
(42606)
ну дык берёшь выражение для силы Ампера
F=B * I * L* sin α
и выржаешь из него ток
I = F/ (B * L* sin α)
угол у тебя наверно 90 градусов, так что sin α = 1
I = F/ (B * L)
Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
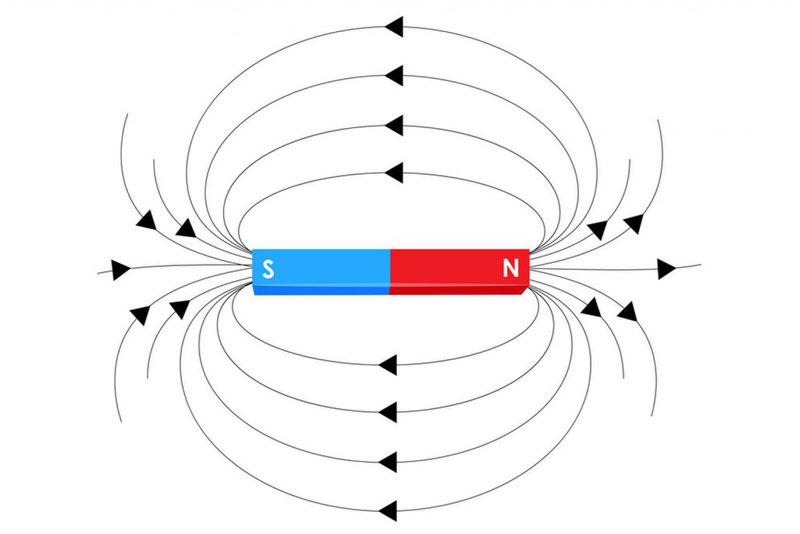
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
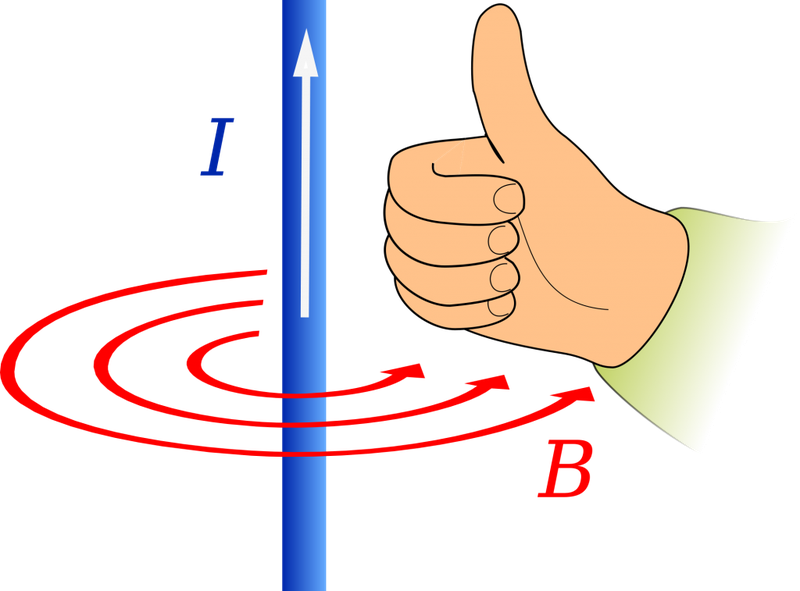
Сила Ампера
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
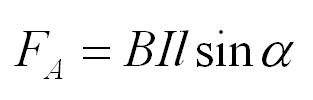
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
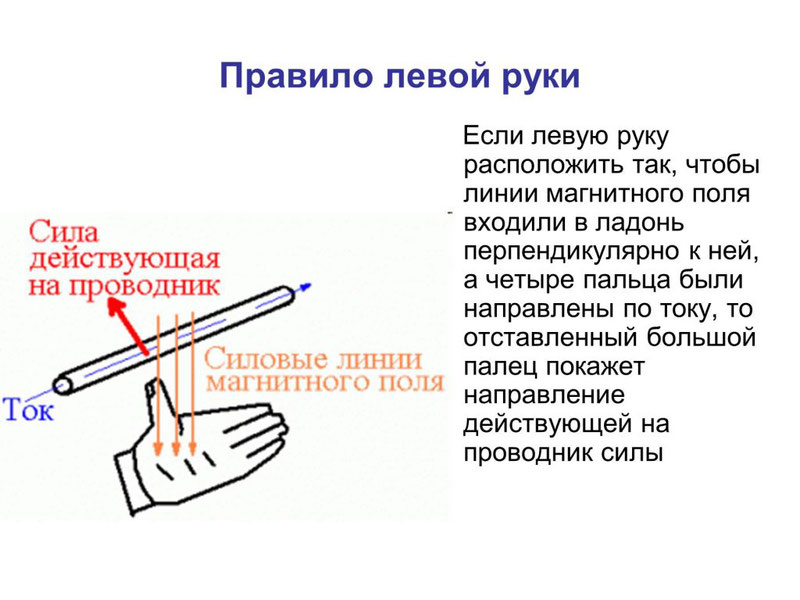
Сила Лоренца
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
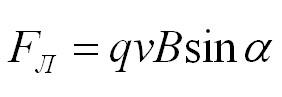
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
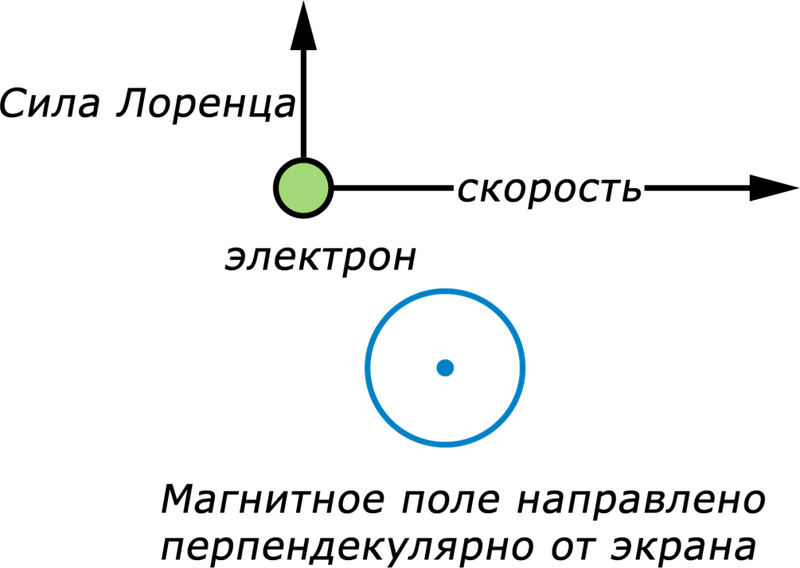
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
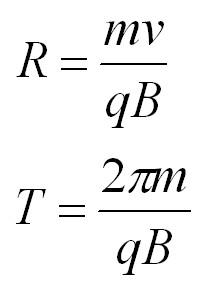
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
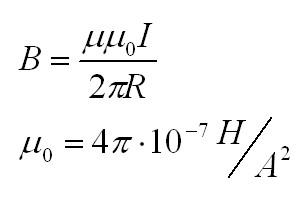
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
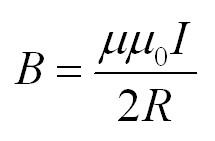
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
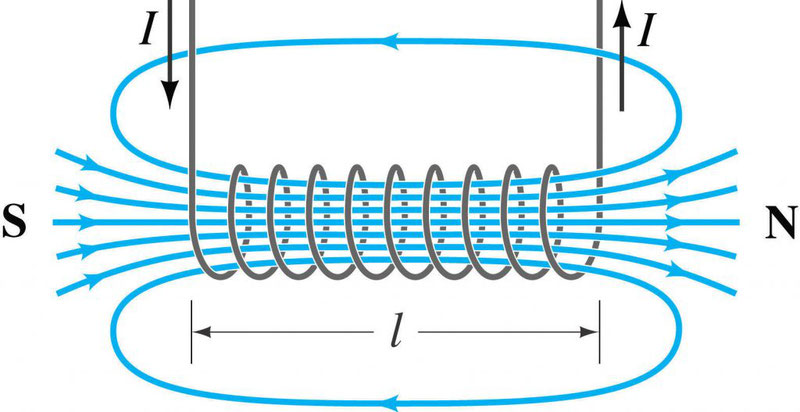
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
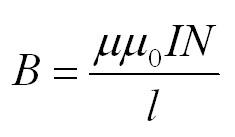
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Магнитный поток и ЭДС
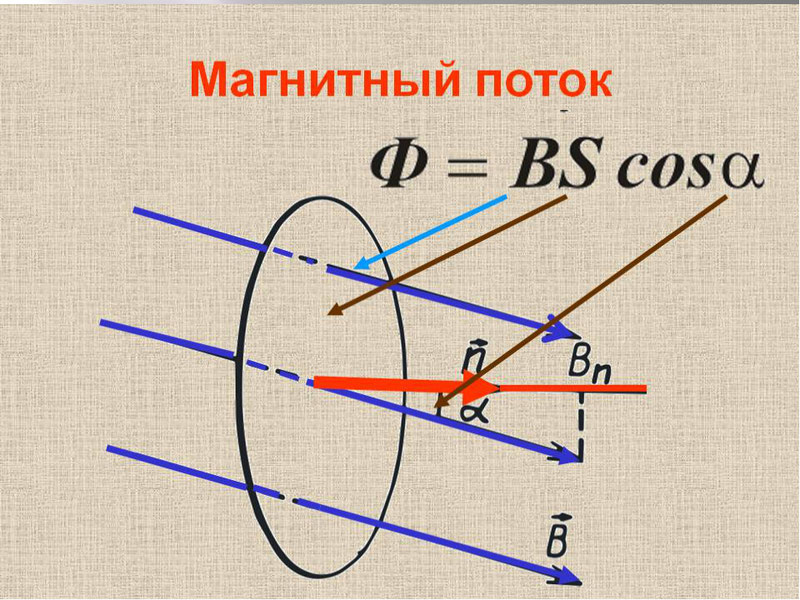
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
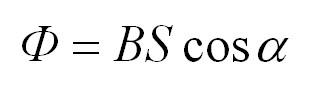
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.
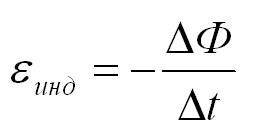
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
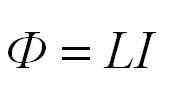
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
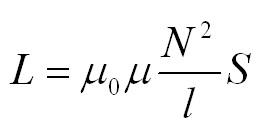
Формула для ЭДС самоиндукции:
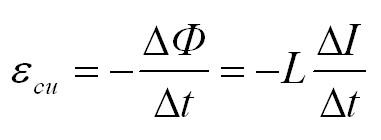
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
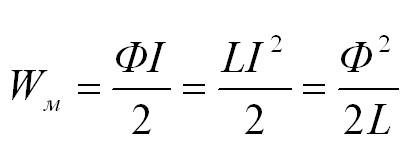
Объемная плотность энергии поля:
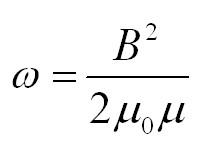
Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.
Электромагнитная индукция
-
Темы кодификатора ЕГЭ: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.
-
Магнитный поток
-
ЭДС индукции
-
Закон электромагнитной индукции Фарадея
-
Правило Ленца
-
Взаимодействие магнита с контуром
-
Закон Фарадея + Правило Ленца = Снятие модуля
-
Вихревое электрическое поле
-
ЭДС индукции в движущемся проводнике
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.
Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток.
Иными словами, пусть в магнитном поле находится замкнутый проводник; не будет ли в этом проводнике возникать электрический ток под действием магнитного поля?
Через десять лет поисков и экспериментов Фарадею наконец удалось этот эффект обнаружить. В 1831 году он поставил следующие опыты.
1. На одну и ту же деревянную основу были намотаны две катушки; витки второй катушки были проложены между витками первой и изолированы. Выводы первой катушки подключались к источнику тока, выводы второй катушки — к гальванометру (гальванометр — чувствительный прибор для измерения малых токов). Таким образом, получались два контура: «источник тока — первая катушка» и «вторая катушка — гальванометр».
Электрического контакта между контурами не было, только лишь магнитное поле первой катушки пронизывало вторую катушку.
При замыкании цепи первой катушки гальванометр регистрировал короткий и слабый импульс тока во второй катушке.
Когда по первой катушке протекал постоянный ток, никакого тока во второй катушке не возникало.
При размыкании цепи первой катушки снова возникал короткий и слабый импульс тока во второй катушке, но на сей раз в обратном направлении по сравнению с током при замыкании цепи.
Вывод.
Меняющееся во времени магнитное поле первой катушки порождает (или, как говорят, индуцирует) электрический ток во второй катушке. Этот ток называется индукционным током.
Если магнитное поле первой катушки увеличивается (в момент нарастания тока при замыкании цепи), то индукционный ток во второй катушке течёт в одном направлении.
Если магнитное поле первой катушки уменьшается (в момент убывания тока при размыкании цепи), то индукционный ток во второй катушке течёт в другом направлении.
Если магнитное поле первой катушки не меняется (постоянный ток через неё), то индукционного тока во второй катушке нет.
Обнаруженное явление Фарадей назвал электромагнитной индукцией (т. е. «наведение электричества магнетизмом»).
2. Для подтверждения догадки о том, что индукционный ток порождается переменным магнитным полем, Фарадей перемещал катушки друг относительно друга. Цепь первой катушки всё время оставалась замкнутой, по ней протекал постоянный ток, но за счёт перемещения (сближения или удаления) вторая катушка оказывалась в переменном магнитном поле первой катушки.
Гальванометр снова фиксировал ток во второй катушке. Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки.
3. Первая катушка была заменена постоянным магнитом. При внесении магнита внутрь второй катушки возникал индукционный ток. При выдвигании магнита снова появлялся ток, но в другом направлении. И опять-таки сила индукционного тока была тем больше, чем быстрее двигался магнит.
Эти и последующие опыты показали, что индукционный ток в проводящем контуре возникает во всех тех случаях, когда меняется «количество линий» магнитного поля, пронизывающих контур. Сила индукционного тока оказывается тем больше, чем быстрее меняется это количество линий. Направление тока будет одним при увеличении количества линий сквозь контур, и другим — при их уменьшении.
Замечательно, что для величины силы тока в данном контуре важна лишь скорость изменения количества линий. Что конкретно при этом происходит, роли не играет — меняется ли само поле, пронизывающее неподвижный контур, или же контур перемещается из области с одной густотой линий в область с другой густотой.
Такова суть закона электромагнитной индукции. Но, чтобы написать формулу и производить расчёты, нужно чётко формализовать расплывчатое понятие «количество линий поля сквозь контур».
к оглавлению ▴
Магнитный поток
Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.
Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади , находящийся в магнитном поле с индукцией
.
Пусть сначала магнитное поле перпендикулярно плоскости контура (рис. 1).

Рис. 1.
В этом случае магнитный поток определяется очень просто — как произведение индукции магнитного поля на площадь контура:
(1)
Теперь рассмотрим общий случай, когда вектор образует угол
с нормалью к плоскости контура (рис. 2).

Рис. 2.
Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая вектора магнитной индукции
(а та составляющая, которая параллельна контуру, не «течёт» сквозь него). Поэтому, согласно формуле (1), имеем
. Но
, поэтому
(2)
Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор параллелен плоскости контура (то есть
), то магнитный поток становится равным нулю.
А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2), а затем все эти магнитные потоки суммируем.
Единицей измерения магнитного потока является вебер (Вб). Как видим,
Вб = Тл · м = В · с. (3)
Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной — ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как
). Но множители
и
как раз и образуют магнитный поток!
Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.
Электромагнитная индукция — это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур.
к оглавлению ▴
ЭДС индукции
Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы, вызывающие движение зарядов.
Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС): . В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции и обозначается
.
Итак, ЭДС индукции — это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура.
Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.
к оглавлению ▴
Закон электромагнитной индукции Фарадея
Сила индукционного тока в опытах Фарадея оказывалась тем больше, чем быстрее менялся магнитный поток через контур.
Если за малое время изменение магнитного потока равно
, то скорость изменения магнитного потока — это дробь
(или, что тоже самое, производная
магнитного потока по времени).
Опыты показали, что сила индукционного тока прямо пропорциональна модулю скорости изменения магнитного потока:
Модуль поставлен для того, чтобы не связываться пока с отрицательными величинами (ведь при убывании магнитного потока будет ). Впоследствии мы это модуль снимем.
Из закона Ома для полной цепи мы в то же время имеем: . Поэтому ЭДС индукции прямо пропорциональна скорости изменения магнитного потока:
(4)
ЭДС измеряется в вольтах. Но и скорость изменения магнитного потока также измеряется в вольтах! Действительно, из (3) мы видим, что Вб/с = В. Стало быть, единицы измерения обеих частей пропорциональности (4) совпадают, поэтому коэффициент пропорциональности — величина безразмерная. В системе СИ она полагается равной единице, и мы получаем:
(5)
Это и есть закон электромагнитной индукции или закон Фарадея. Дадим его словесную формулировку.
Закон электромагнитной индукции Фарадея. При изменении магнитного потока, пронизывающего контур, в этом контуре возникает ЭДС индукции, равная модулю скорости изменения магнитного потока.
к оглавлению ▴
Правило Ленца
Магнитный поток, изменение которого приводит к появлению индукционного тока в контуре, мы будем называть внешним магнитным потоком. А само магнитное поле, которое создаёт этот магнитный поток, мы будем называть внешним магнитным полем.
Зачем нам эти термины? Дело в том, что индукционный ток, возникающий в контуре, создаёт своё собственное магнитное поле, которое по принципу суперпозиции складывается с внешним магнитным полем.
Соответственно, наряду с внешним магнитным потоком через контур будет проходить собственный магнитный поток, создаваемый магнитным полем индукционного тока.
Оказывается, эти два магнитных потока — собственный и внешний — связаны между собой строго определённым образом.
Правило Ленца . Индукционный ток всегда имеет такое направление, что собственный магнитный поток препятствует изменению внешнего магнитного потока .
Правило Ленца позволяет находить направление индукционного тока в любой ситуации.
Рассмотрим некоторые примеры применения правила Ленца.
Предположим, что контур пронизывается магнитным полем, которое возрастает со временем (рис. (3)). Например, мы приближаем снизу к контуру магнит, северный полюс которого направлен в данном случае вверх, к контуру.
Магнитный поток через контур увеличивается. Индукционный ток будет иметь такое направление, чтобы создаваемый им магнитный поток препятствовал увеличению внешнего магнитного потока. Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против внешнего магнитного поля.
Индукционный ток течёт против часовой стрелки, если смотреть со стороны создаваемого им магнитного поля. В данном случае ток будет направлен по часовой стрелке, если смотреть сверху, со стороны внешнего магнитного поля, как и показано на (рис. (3)).

Рис. 3. Магнитный поток возрастает
Теперь предположим, что магнитное поле, пронизывающее контур, уменьшается со временем (рис. 4). Например, мы удаляем магнит вниз от контура, а северный полюс магнита направлен на контур.

Рис. 4. Магнитный поток убывает
Магнитный поток через контур уменьшается. Индукционный ток будет иметь такое направление, чтобы его собственный магнитный поток поддерживал внешний магнитный поток, препятствуя его убыванию. Для этого магнитное поле индукционного тока должно быть направлено в ту же сторону , что и внешнее магнитное поле.
В этом случае индукционный ток потечёт против часовой стрелки, если смотреть сверху, со стороны обоих магнитных полей.
к оглавлению ▴
Взаимодействие магнита с контуром
Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?
Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.
1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.
Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.
Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .
Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1
Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.
Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.
Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .
Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.
к оглавлению ▴
Закон Фарадея + Правило Ленца = Снятие модуля
Выше мы обещали снять модуль в законе Фарадея (5). Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции — ведь без модуля, стоящего в правой части (5), величина ЭДС может получаться как положительной, так и отрицательной.
Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным . Противоположное направление обхода контура называется, соответственно, отрицательным . Какое именно направление обхода мы берём в качестве положительного, роли не играет — важно лишь сделать этот выбор.
Магнитный поток через контур считается положительным , если магнитное поле, пронизывающее контур, направлено туда, глядя откуда обход контура в положительном направлении совершается против часовой стрелки. Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным
.
ЭДС индукции считается положительной , если индукционный ток течёт в положительном направлении. В этом случае направление сторонних сил, возникающих в контуре при изменении магнитного потока через него, совпадает с положительным направлением обхода контура.
Наоборот, ЭДС индукции считается отрицательной , если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.
Итак, пусть контур находится в магнитном поле . Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен:
.
Предположим, далее, что магнитный поток увеличивается . Согласно правилу Ленца индукционный ток потечёт в отрицательном направлении (рис. 5).

Рис. 5. Магнитный поток возрастает
Стало быть, в данном случае имеем . Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.
А именно, предположим теперь, что магнитный поток убывает . По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть,
(рис. 6).

Рис. 6. Магнитный поток возрастает
Таков в действительности общий факт: при нашей договорённости о знаках правило Ленца всегда приводит к тому, что знак ЭДС индукции противоположен знаку скорости изменения магнитного потока :
(6)
Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.
к оглавлению ▴
Вихревое электрическое поле
Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое . Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.
Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем . Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.
Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора . Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.
Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора , (рис. 7).

Рис. 7. Вихревое электрическое поле при увеличении магнитного поля
Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис. 8).

Рис. 8. Вихревое электрическое поле при уменьшении магнитного поля
Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.
Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.
1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.
Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура .
Пусть, например, контур является кольцом радиуса и пронизывается однородным переменным магнитным полем. Тогда напряжённость
вихревого электрического поля одинакова во всех точках кольца. Работа
силы
, с которой вихревое поле действует на заряд
, равна:
Следовательно, для ЭДС индукции получаем:
к оглавлению ▴
ЭДС индукции в движущемся проводнике
Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает — ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.
Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости расположены параллельные рельсы, расстояние между которыми равно . Рельсы находятся в вертикальном однородном магнитном поле
. По рельсам движется тонкий проводящий стержень
со скоростью
; он всё время остаётся перпендикулярным рельсам (рис. 9).

Рис. 9. Движение проводника в магнитном поле
Возьмём внутри стержня положительный свободный заряд . Вследствие движения этого заряда вместе со стержнем со скоростью
на заряд будет действовать сила Лоренца:
Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами — не забывайте правило часовой стрелки или левой руки!).
Сила Лоренца играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда
от точки
к точке
наша сторонняя сила совершит работу:
(Длину стержня мы также считаем равной .) Стало быть, ЭДС индукции в стержне окажется равной:
(7)
Таким образом, стержень аналогичен источнику тока с положительной клеммой
и отрицательной клеммой
. Внутри стержня за счёт действия сторонней силы Лоренца происходит разделение зарядов: положительные заряды двигаются к точке
, отрицательные — к точке
.
Допустим сначала,что рельсы непроводят ток.Тогда движение зарядов в стержне постепенно прекратится. Ведь по мере накопления положительных зарядов на торце и отрицательных зарядов на торце
будет возрастать кулоновская сила, с которой положительный свободный заряд
отталкивается от
и притягивается к
— и в какой-то момент эта кулоновская сила уравновесит силу Лоренца. Между концами стержня установится разность потенциалов, равная ЭДС индукции (7).
Теперь предположим, что рельсы и перемычка являются проводящими. Тогда в цепи возникнет индукционный ток; он пойдёт в направлении
(от «плюса источника»
к «минусу» N). Предположим, что сопротивление стержня равно
(это аналог внутреннего сопротивления источника тока), а сопротивление участка
равно
(сопротивление внешней цепи). Тогда сила индукционного тока найдётся по закону Ома для полной цепи:
Замечательно, что выражение (7) для ЭДС индукции можно получить также с помощью закона Фарадея. Сделаем это.
За время наш стержень
проходит путь
и занимает положение
(рис. 9). Площадь контура возрастает на величину площади прямоугольника
:
Магнитный поток через контур увеличивается. Приращение магнитного потока равно:
Скорость изменения магнитного потока положительна и равна ЭДС индукции:
Мы получили тот же самый результат, что и в (7). Направление индукционного тока, заметим, подчиняется правилу Ленца. Действительно, раз ток течёт в направлении , то его магнитное поле направлено противоположно внешнему полю
и, стало быть, препятствует возрастанию магнитного потока через контур.
На этом примере мы видим, что в ситуациях, когда проводник движется в магнитном поле, можно действовать двояко: либо с привлечением силы Лоренца как сторонней силы, либо с помощью закона Фарадея. Результаты будут получаться одинаковые.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Электромагнитная индукция» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Содержание:
Электромагнитная индукция:
Неоценимая заслуга в изучении явления электромагнитной индукции принадлежит известному английскому физику М. Фарадею – непревзойденному мастеру проведения физического эксперимента.
 |
Фарадей Майкл (1791-1867) – выдающийся английский физик, основоположник учения об электромагнитном поле, один из основателей электрохимии, исследователь взаимодействия вещества и магнитного поля. |
Обнаружение в 1820 г. датским физиком X. Эрстедом связи магнитного поля с электрическим током положило начало фундаментальным исследованиям открытого явления. Обладая широким научным кругозором, выдающийся физик и исследователь М. Фарадей предусмотрел возможность обратной связи магнитного поля и электрического тока, когда появление магнитного поля приводит к возникновению электрического тока. В результате длительных научных поисков он в 1821 г. получил первые положительные результаты: добился того, что в замкнутых проводниках, находящихся в переменном магнитном поле, возникал электрический ток. Явление получило название электромагнитной индукции, а ток, возникающий в проводниках, назвали индукционным.
Явление возникновения электрического тока в замкнутом проводнике, который расположен в переменном магнитов ном поле, называется электромагнитной индукцией.
Опишем основные опыты М. Фарадея, которые можно повторить и на школьном оборудовании.
C клеммами гальванометра соединим длинный проводник, пасть которого укреплена в штативе.
Постоянный подковообразный магнит сначала будем приближать к проводнику, а потом удалять от него (рис. 2.26). При этом увидим, что стрелка гальванометра будет отклоняться сначала в одну сторону, потом в противоположную.
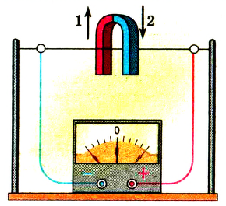
Изменим условия опыта. Укрепим теперь подковообразный магнит в лапках штатива, а проводник, присоединенный к клеммам гальванометра, будем вводить в между полюсное пространство и выводить из него (рис. 2.27). Стрелка гальванометра также будет отклоняться сначала в одну, а потом в противоположную сторону.
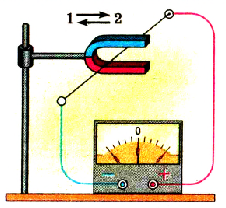
Pиc. 227. Опыт с движущимся проводником
Видоизменим опыт. Одну из катушек присоединим к клеммам гальванометра, а вторую включим в электрическую цепь, состоящую из источника постоянного тока и выключатели. Замкнув цепь второй катушки, будем приближать ее к первой катушке (рис. 2.28). Отклонение стрелки гальванометра засвидетельствует появление тока в цепи первой катушки. Направление этого тока изменится, если вторую катушку удалять от первой. При неподвижных катушках ток будет отсутствовать.
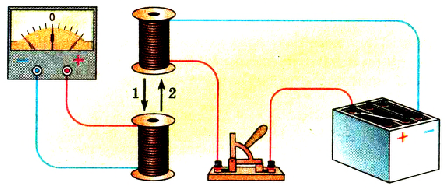
Рис. 228. Опыт с движущейся катушкой с током
Разместив вторую катушку неподвижно на первой, начнем замыкать и размыкать цепь второй катушки (рис. 2.29). Когда цепь будет замыкаться, стрелка гальванометра отклонится в одну сторону. При размыкании стрелка отклонится в противоположную сторону.
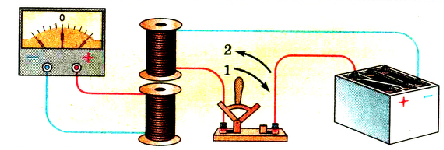
Pиc. 229. Замыкание и размыкание цепи второй катушки
Изменим условия последнего опыта. Включим в цепь второй катушки реостат и снова замкнем цепь. Когда стрелка остановится на нулевом делении, начнем изменять силу тока, перемещая ползунок реостата (рис. 2.30).
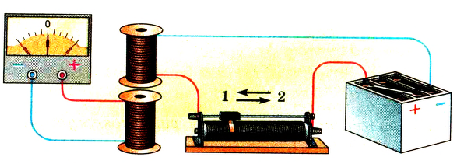
Рис. 230. Сила тока в катушке изменяется с помощью реостата
При увеличении силы тока в цепи первой катушки стрелка гальванометра будет отклоняться в одну сторону. При уменьшении силы тока отклонение стрелки будет противоположным.
После этого, не изменяя положения катушек и не разрывая цепи второй катушки, введем в катушки стальной стержень (рис. 2.31). Стрелка и в этом случае отклонится от положения равновесия и возвратится в начальное положение. Во время вынимания стержня из катушки заметим, что стрелка гальванометра отклоняется в противоположную сторону.
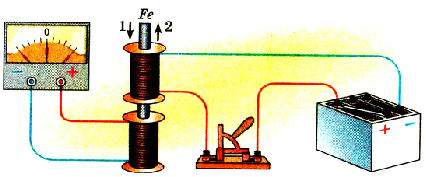
Pиc. 231. Опыт, когда движется стальной стержень
Электрический ток, возникающий в замкнутом проводнике в изменяющемся магнитном поле, называют индукционным.
Результаты всех опытов свидетельствуют, что при любом изменении магнитного поля или движении замкнутого проводника в магнитном поле возникает электрический ток. Его направление зависит от характера изменения магнитного поля: при увеличении магнитной индукции ток имеет одно направление, при уменьшении – противоположное.
На практике направление тока в проводнике, который возникает вследствие электромагнитной индукции, определяют по правилу правой руки (рис. 2.32): если правую руку разместить в поле так, чтобы линии магнитной индукции входили в ладонь, а отставленный большой палец показывал направление движения проводника, то вытянутые пальцы руки покажут направление тока в проводнике.
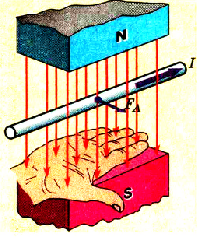
Рис. 2.32 Правило правой руки
Чтобы ток в проводниках протекал длительное время, необходимо, чтобы все это время существовала разность потенциалов. А это возможно при непрерывном движении проводника. При этом будет происходить разделе ние в проводнике положительно и отрицательно заряженных частиц под действием силы Лоренца, которая имеет неэлектростатическое происхождение. Это приводит к возникновению ЭДС индукции.
Определим способ рассчета ЭДС, для случая, когда прямой проводник, который является частью электрической цепи, равномерно движется в магнитном поле. Вызванное силой Лоренца движение заряженных частиц образует электрический ток, а в это время на него в магнитном поле будет действовать сила Ампера (рис. 2.33):
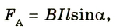
где В — модуль вектора магнитной индукции; I — сила тока в проводнике; l длина проводника; 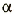 – угол между направлением тока в проводнике и вектором магнитной индукции.
– угол между направлением тока в проводнике и вектором магнитной индукции.
Возникающий ток в проводнике всегда будет иметь направление, при котором сила Ампера «тормозит» движение проводника. Чтобы проводник двигался равномерно (условие существования электрического тока), к нему нужно приложить силу, которая по модулю равна силе Ампера, а по направлению противоположна:
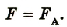
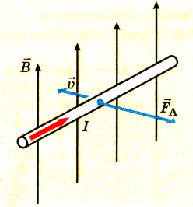
Рис. 2.33. К объяснению ЭДС индукции
Если за определенное время △t проводник сместится па △s, то работа будет равна
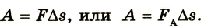
Таким образом,
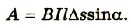
Приняв во внимание, что по определению сила тока равна 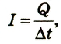 а ЭДС равна
а ЭДС равна 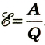 . И произведя определенные математические преобразования, получим
. И произведя определенные математические преобразования, получим
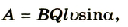
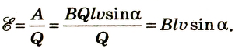
Таким образом, для случая, когда проводник движется равномерно в однородном магнитном поле, значение ЭДС индукции зависит от магнитной индукции поля, длины
прямого проводника и скорости его движения в магнитном поле, учитывая значение угла между  и
и  .
.
Правило Ленца
Правило установлено известным русским физиком Э.Х. Ленцем как обобщение многочисленных опытов по определению направления индукционного тока. C этой целью Э.Х. Ленц исследовал взаимодействие замкнутого проводника и переменного магнитного поля, которое вызвало индукционный ток в этом проводнике.
Чтобы лучше понять сущность этого правила, рассмотрим опыт.
На легком горизонтальном рычаге, который имеет вертикальную ось вращения, находятся два легких металлических кольца, одно из которых сплошное, я второе разрезано (рис. 2.35). Рычаг посажен на тонкое стальное острие так, чтобы трение было минимальным.
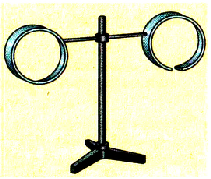
Pиc. 235. Прибор для демонстрации правила Ленца
Введем в сплошное кольцо катушку с ферромагнитным сердечником (электромагнитом), включенным в электрическую цепь из источника тока и выключателя (рис. 2.36).
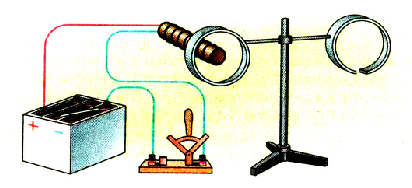
Рис. 236. К правилу Ленца
В момент .замыкания цепи кольцо, как бы отталкиваясь от катушки, сместится на определенное расстояние и развернет рычаг на некоторый угол.
В момент появления тока в электромагните электропроводное кольцо, находящееся возле полюса электромагнита, всегда — притягивается к нему.
Если опыт повторить, изменив направление тока в катушке, то будем наблюдать тот же эффект. Таким образом, определяющим в данном случае является не направление магнитной индукции, а характер изменения магнитной индукции.
Если опыт попытаться пронести с разрезанным кольцом, то подобного эффекта наблюдать не сможем. Это свидетельствует, что отталкивание кольца связано с индукционным током, который возникает в сплошном кольце.
При размыкании цепи питания электромагнита проводящее кольцо будет двигаться от него.
Чтобы разобраться в дальнейших рассуждениях, необходимо вспомнить, что параллельные проводники, в которых ток проходит в одном направлении, притягиваются, а в противоположных отталкиваются. Таким образом, если кольцо отталкивается от катушки, то в нем индуцируется ток, противоположный току в катушке по направлению.
Взаимно противоположными будут и магнитные индукции полей этих токов.
Обобщив результаты опытов, можно сделать выводы, к которым пришел Э.Х. Ленц: магнитное поле индукционного тока всегда противодействует изменениям, которые вызвали этот так.
Правило Ленца: индукционный ток в замкнутом проводнике имеет такое направление, что его магнитное поле компенсирует изменение магнитного поля, которое вызвало этот ток.
Магнитный поток
Электромагнитную индукцию можно наблюдать в двух случаях: когда проводник движется в однородном магнитном поле или неподвижный проводник находится и магнитном поле, магнитная индукция которого изменяется со временем. Нa практике, как правило, случается так, что одновременно изменяется магнитная индукция и положение проводника в магнитном поле. Примером может быть движение проводника в неоднородном магнитном поле. Так как в этом случае расчеты сложнее» для их упрощения ввели физическую величину, которая одновременно зависит и от индукции магнитного поля, и от параметров движения проводника. Эта величина получила название магнитного потока.
Представим себе проводник в виде замкнутого кольца, которое находится в магнитном поле (рис. 2.38-а). Приведем кольцо в движение так, чтобы оно двигалось в плоскости, перпендикулярной к линиям магнитного поля. При этом количество линий индукции магнитного поля, которые проходят через него, будет уменьшаться, и в кольце возникнет индукционный ток (рис. 2.38-б).
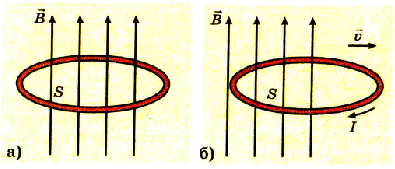
Pис. 238. Движение кольца в магнитом поле
Если теперь кольцо проводника поместить в магнитное поле, индукция которого изменяется, то количество линий магнитной индукции, которые проходят через контур, также будет изменяться и в проводнике возникнет индукционный ток (рис. 2.39).
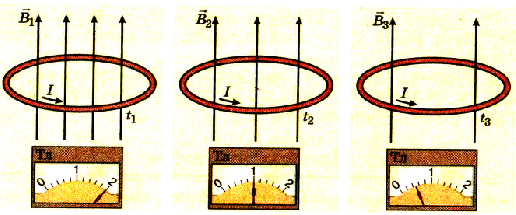
Pиc. 239. Изменение магнитного потока через кольцо
Оба описанных случая можно объяснить проще, если для каждого их них учитывать произведение площади кольца на значение магнитной индукции магнитного поля. Именно это произведение изменялось в обоих случаях. Фактически это произведение характеризовало поток линий магнитной индукции, которые пронизывают контур определенной площади, или просто — магнитный поток.
Магнитный поток Ф зависит не только от модуля магнитной индукции и площади контура, но и от угла, который образуют нормаль с плоскостью контура и вектором магнитной индукции поля (рис. 2.40). Поэтому в общем виде значении магнитного потока записывается как
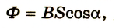
где Ф – магнитный поток; В – модуль магнитной индукции поля; 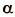 – угол между нормалью к плоскости контура и вектором магнитной индукции.
– угол между нормалью к плоскости контура и вектором магнитной индукции.
Величина, которая описывает магнитное поле и равна произведению магнитной индукции на площадь замкнутого контура и косинус угла (между вектором магнитной индукции и нормалью к контуру), называется магнитным потоком, или потоком магнитной индукции.
Анализ формулы показывает, что минимальное значение магнитного потока (Ф = 0) будет тогда, когда 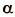 = 90º, т. е. плоскость контура параллельна линиям магнитного поля. Если
= 90º, т. е. плоскость контура параллельна линиям магнитного поля. Если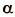 = 0, то магнитный поток при всех равных условиях будет максимальным (Ф = BS).
= 0, то магнитный поток при всех равных условиях будет максимальным (Ф = BS).
Магнитный поток – скалярная величина. В СИ магнитный поток измеряется в веберах (Вб), на честь известного немецкого физика В. Вебера.
Если магнитная индукция магнитного поля 1 Тл, а площадь контура, сквозь который проходит магнитный поток, 1 м2, то магнитный поток равен 1 веберу (1 Вб):
1 Вб = 1 Тл • 1 м2.
Любые изменения магнитного поля или площади контура вызывают явление электромагнитной индукции.
 |
Вебер Вильгельм Эдуард (1804-1881) – немецкий физик, основные работы посвящены электромагнетизму, работал также над проблемами акустики, теплоты, молекулярной физики, земного магнетизма. |
Таким образом, любое изменение магнитного потока обусловливает возникновение электрического тока в замкнутом проводящем контуре. C учетом закона Ома для полной цепи последний вывод можно записать так: любое, изменение. магнитного потока приводит к возникновению ЭДС индукции.
Закон электромагнитной индукции
Проанализировав результаты экспериментальных исследований электромагнитной индукции, можно найти общую формулу для выражения особенностей этого явления, которые отражают сущность закона электромагнитной индукции: при изменении магнитного потоки в замкнутых проводниках возникает электрический ток, вызванный ЭДС индукции, которая пропорциональна скорости изменения магнитного потока:
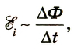 или
или 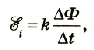
где 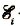 электродвижущая сила индукции;
электродвижущая сила индукции; 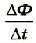 -скорость изменения магнитного потока Ф; k – коэффициент пропорциональности.
-скорость изменения магнитного потока Ф; k – коэффициент пропорциональности.
Закон электромагнитной индукции: электродвижущая сила индукции пропорциональна скорости изменения магнитного потока.
При использовании единиц СИ коэффициент k = 1. Приняв во внимание, что индукционный ток противодействует изменению магнитного потока (правило Ленца), окончательно имеем:
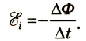
Так как согласно закону Ома 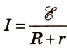 то можно записать его для случая электромагнитной индукции в виде
то можно записать его для случая электромагнитной индукции в виде 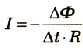 , где
, где 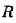 – сопротивление контура, а r=0.
– сопротивление контура, а r=0.
Заряд, который проходит в контуре вследствие электромагнитной индукции: Q = I∆t.
Учитывая, что заряд скалярная величина, а знак минус можно опустить, получим:
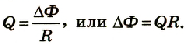
Пример решения задачи №1
Магнитный поток, пронизывающий катушку, которая состоит из 75 витков, равен 4,8 ∙ 10-3 Вб. На протяжении какого времени исчезнет этот поток, если в катушке индуцируется ЭДС индукции 0,74 В?
|
Дано: |
Решение ЭДС индукции возникает в катушке потому, что магнитный поток, пронизывающий ее, изменяется на △Φ = Φ2 – Φl. В каждом витке катушки при этом будет возникать ЭДС индукции в соответствии с законом ΔΦ электромагнитной индeкции: 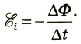 |
| ∆t – ? |
Общая ЭДС будет в N раз больше: 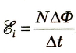 . Отсюда:
. Отсюда: 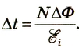 .
.
Подставив значения физических величин, получим
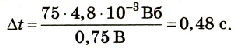
Ответ: ток исчезнет через 0,48 с.
Электродинамический микрофон
Одним из примеров практического применения явления электромагнитной индукции является электродинамический микрофон. C помощью этого прибора звуковые колебания превращаются в колебания электрического тока, которые усиливаются при помощи специальных электронных усилителей и используются в быту, научных исследованиях, производстве.
Микрофоны превращают звуковые колебания в электрические.
Обязательной частью электродинамического микрофона является постоянный магнит, изготовленный в виде кольца (рис. 2.41).
К одному из полюсов магнита приклеен цилиндрический стержень 1 из мягкого ферромагнетика (железа). К другому – ферромагнитная пластина 2 из такого же ферромагнетика. В центре этой пластины находится круглое отверстие, которое охватывает стержень. Диаметр отверстия несколько больше диаметра стержня, поэтому между стержнем и пластиной образуется узкая щель 5, в которой сосредоточен весь магнитный поток магнита.
На стержне находится мембрана 3, которая колеблется под действием звуковых волн. К нижней части мембраны приклеена небольшая катушка 4 с некоторым количеством витков изолированного провода. Катушка помещена в кольцевую щель
между полюсами постоянного магнита.
В электродинамическом микрофоне катушка находится в магнитном поле.
Концы катушки соединены гибкими проводниками со специальными клеммами. Если на мембрану микрофона попадают звуковые волны, то она начинает колебаться вместе с катушкой. При колебании катушки магнитный поток, пронизывающий ее, изменяется и в ней индуцируется ЭДС индукции.
В движущейся катушке, находящейся в магнитном поле, возникает ЭДС индукции.
Если катушка включена в цепь электронного усилителя, то электрические колебания усиливаются и могут быть или записаны на магнитный либо оптический диск, или сразу
воспроизведены громкоговорителем.
Принцип действия электродинамического микрофона используется в различных датчиках для изучения и контроля колебательных процессов.
Самоиндукция
Каждый проводник, в котором существует электрический ток, создает «собственное» магнитное поле. Это поле образуется сразу же, как только в проводнике начинает про ходить электрический ток. Если индукция магнитного поля перед замыканием цепи была равна нулю, то через некоторое время после замыкания она будет иметь максимальное значение B, соответствующее силе тока в проводнике. Таким образом, момент возникновения электрического тока можно читать моментом начала изменения магнитного потока. А любое изменение магнитного потока, по закону электромагнитной индукции, порождает вихревое электрическое поле, способствующее появлению ЭДС индукции во всех проводниках,находящихся в магнитном поле.
Явление самоиндукции выявил Д. Генри в 1832 г.
Не может быть исключения и для проводника, который является «источником» этого поля. Вихревое поле создает и в нем ЭДС индукции 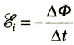 , которую назвали ЭДС самоиндукции.
, которую назвали ЭДС самоиндукции.
Наличие ЭДС самоиндукции можно подтвердить опытом. Для этого составим электрическую цепь из источника тока, выключателя и электрической лампочки (рис. 2.43). При
замыкании цепи лампочка зажигается практически мгновенно. Если же в цепь включить катушку с железным сердечником, то максимальная яркость свечения лампочки устанавливается постепенно (рис. 2.44).
Это является свидетельством того, что ток в цепи увеличивается во мгновенно, а на протяжении некоторого времени. Посмотрев на графики рисунков 2.45 и 2.46, можно сказать, что в цепи, где находится катушка из 100 витков, ток нарастает быстрее, чем в цепи, в которой находится катушка из 1000 витков. На прохождение тока н цепи существенно влияет также ферромагнитный сердечник в катушке (рис. 2.47).
Поскольку ЭДC самоиндукции противодействует ЭДС источники тока, то можно сделать вывод, что ЭДС самоиндукции зависит от характеристик катушки или проводника, включенного в электрическую цепь.
А магнитный поток, создаваемый катушкой или проводником, будет пропорционален силе тока в них: Ф ~ I. Если внести коэффициент пропорциональности, то можно получить более точное соотношение и новую формулу: Ф = L ∙ I. Здесь коэффициент пропорциональности L учитывает электромагнитные свойства катушки (проводника) и называется индуктивностью. Индуктивность определяется формой и размерами проводника, а также магнитными свойствами среды.
Физическую величину, которая характеризует электромагнитные свойства катушки или проводника, называют индуктивностью.
Если при изменении силы тока в проводнике на 1 А за 1 с в нем индуцируется ЭДС самоиндукции 1 В, то этот проводник имеет индуктивность 1 Гн.
В СИ индуктивность измеряют в генри (Гн) в честь известного американского физика Д. Генри.
Единица 1 генри имеет довольно большой размер, поэтому применяют, как правило, долевые единицы:
- 1 миллигенри = 1 мГн = 10-3 Гн;
- 1 микрогенри = 1 мкГн = 10-6 Гн.
Если в любом проводнике изменяется электрический ток, то это приводит к изменению магнитного потока ΔΦ — LΔI, которое вызывает ЭДС самоиндукции:
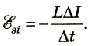
Явление самоиндукции наблюдается также при размыкании цепи c током. Составим цепь из источника тока, выключателя, катушки и лампочки. Лампу накаливания, сопротивление которой значительно меньше сопротивления катушки, включим параллельно катушке (рис. 2.48). Если замкнуть цепь, то накаливание волоска лампочки будет происходить постепенно, как
бы с задержкой. Если после полного загорания лампы разомкнуть ключ, то она ярко вспыхнет. Это будет проявлением самоиндукции. В результате размыкания цепи возникнет ЭДС самоиндукции, которая поддержит ток в цепи лампочки и катушки.
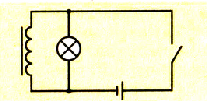
Рис. 2.48. Схема электрической цепи для наблюдения явления самоиндукции при размыкании
Пример решения задачи №2
Определить индуктивность катушки, если сила тока в ней изменяется на 50 А за 1 с и при этом появляется ЭДС самоиндукции 0,08 В.
|
Дано: |
Решение По закону ЭДС самоиндукции 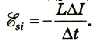 Отсюда 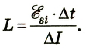 Подставив значения физических величин, получим 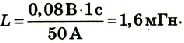 |
| L– ? |
Ответ: индуктивность катушки 1,6 мГн.
Энергия магнитного поля
Самоиндукция подтверждает действие закона сохранения и превращения энергии в электромагнитных явлениях.
Как известно, вследствие явления самоиндукции при замыкании цепи возникает ЭДС самоиндукции 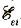 . Если же сила тока не изменяется, ЭДС самоиндукции не возникает. Такое положение в электрической цепи обусловлено тем, что за счет энергии источника тока выполняется работа по компенсации ЭДС самоиндукции. Это аналогично случаю, когда для сообщения скорости неподвижному телу необходимо выполнить определенную работу по преодолению инерции.
. Если же сила тока не изменяется, ЭДС самоиндукции не возникает. Такое положение в электрической цепи обусловлено тем, что за счет энергии источника тока выполняется работа по компенсации ЭДС самоиндукции. Это аналогично случаю, когда для сообщения скорости неподвижному телу необходимо выполнить определенную работу по преодолению инерции.
Любые изменения силы тока в катушке вызовут появление ЭДС индукции и приведут к выполнению работы источником тока для компенсации ее действия. Эта работа равна энергии магнитного поля катушки или проводника.
Для компенсации ЭДС самоиндукции источник тока выполнит работу по перемещению заряженных частиц, общий заряд которых равен Q. Приняв во внимание, что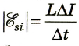 , и то, что ,
, и то, что , 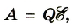 получим значение выполненной работы для явления самоиндукции:
получим значение выполненной работы для явления самоиндукции:
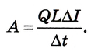
ЭДС самоиндукции зависит от индуктивности проводника и скорости изменения силы тока в нем.
При этом сила тока в цепи изменяется от пуля до Imax которое равно I0. По определению Q=IΔt.
Поскольку при замыкании цепи сила тока не имеет постоянного значения, то для упрощения расчетов будем считать,что сила тока линейно изменяется на протяжении всего времени. Тогда сила тока 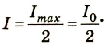
Таким образом,
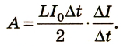
Изменение силы тока ΔI за интервал времени Δt равно I0.
Работа, выполненная источником тока, равна энергии магнитного поля катушки с током:
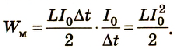
Энергия магнитного поля катушки с током пропорциональна индуктивности катушки и квадрату силы тока в ней.
- Магнитные свойства вещества
- Явление самоиндукции
- Закон электромагнитной индукции
- ЭДС индукции в движущемся проводнике
- Катушка индуктивности в цепях переменного тока
- Конденсатор в цепях переменного тока
- Электрический ток в различных средах
- Электромагнитная индукция в физике
Магнитный поток, проходящий через площадь S равен:
Ф = BScosα;
где:
Ф ― величина магнитного потока [Вб],
S ― площадь контура [м2],
B ― индукция магнитного поля [Тл],
α ― угол между нормалью $overrightarrow{n}$ к площади контура и вектором индукции магнитного поля $overrightarrow{B}$.
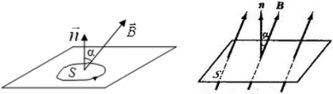
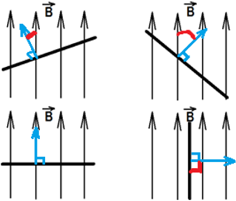
Если вектор индукции магнитного поля $overrightarrow{B}$ перпендикулярен площади контура, то магнитный поток равен:
Ф = BScos90° = BS;
Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором $overrightarrow{B}$ и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.
Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.
ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.
Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:
$varepsilon_i = -frac{Delta text{Ф}}{Delta t}$
где:
$varepsilon_i $ ― ЭДС электромагнитной индукции [B],
$frac{Delta text{Ф}}{Delta t}$ ― скорость изменения магнитного потока [Вб/с],
∆Ф ― изменение магнитного потока [Вб],
∆t ― время, за которое происходит это изменение [c].
Кроме того, ЭДС индукции равна производной магнитного потока по времени:
$varepsilon_i = -text{Ф}_t’$
где:
- ― ЭДС электромагнитной индукции [B],
- ― производная магнитного потока по времени [Вб/с].
Задача 1
Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?
Решение:
Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.
Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.
По закону электромагнитной индукции $varepsilon_i = -frac{Delta text{Ф}}{Delta t}$
ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text{Ф}_t’$
И это очень важный момент, без которого мы не сможем решить такого рода задачу.
Теперь посчитаем ЭДС индукции.
Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.
ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.
Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса
$text{Ф} underset{text{множитель}}{underbrace{aS}} ;; cdot ;; underset{text{сложная функция}}{underbrace{cos(bt)}}$.
Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text{Ф}_t’$
Подставив сюда значение производной, получим $varepsilon_i = -text{Ф}_t’$ = abS · sin (bt).
Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.
По закону Ома $I = frac{varepsilon}{R}$ , подставив сюда значение ЭДС, получаем $I = frac{abScdot sin(bt)}{R}$.
Мы получили зависимость силы тока от времени.
Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.
В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.
Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_{max} = frac{abS}{R}$.
Отсюда можно легко выразить площадь контура $S = frac{I_{max}R}{ab}$, подставив сюда все значения, получим $S = frac{I_{max}R}{ab} = frac{35cdot 10^{-3} Acdot 1,2text{Ом}}{6cdot 10^{-3}text{Тл} cdot 35000c^{-1}} = 0,002text{м}^2$
Ответ: 0,002
Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:
- увеличением или уменьшением модуля индукции магнитного поля (т. е. величины $frac{Delta B}{Delta t}$);
- изменением направления вектора магнитного поля (т. е. изменением угла α);
- деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины $frac{Delta S}{Delta t}$ );
- изменением нескольких из этих величин одновременно.
Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.
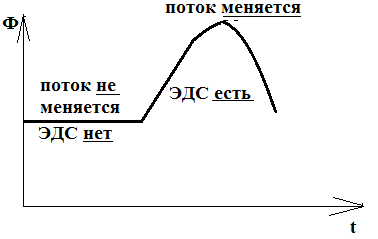
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.

Либо так, тогда будет меняться поток и возникать ЭДС:
Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.
Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.
Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.
Задача 2
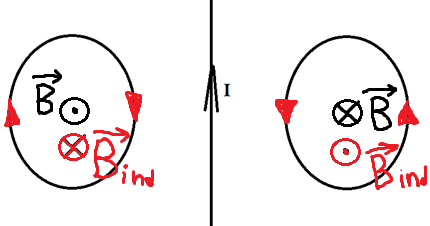
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?
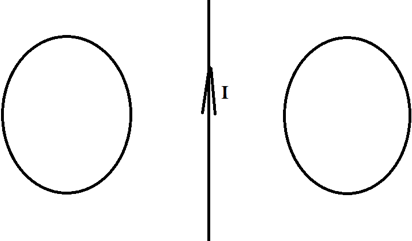
Решение:
Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?
Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.
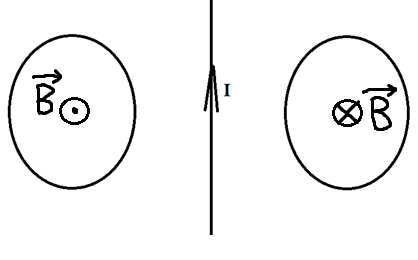
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?
Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.
Движение проводников
Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).
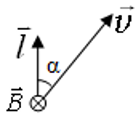
Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;
где:
$varepsilon_i$― ЭДС электромагнитной индукции [B],
B ― индукция магнитного поля [Тл],
l ― длина проводника [м],
v ― скорость движения проводника [м/с],
α ― угол между направлением вектора скорости $overrightarrow{v}$ и длиной проводника $overrightarrow{l}$ , если вектор индукции магнитного поля $overrightarrow{B}$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow{B} perp overrightarrow{v}, overrightarrow{B} perp overrightarrow{l}$
Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.
В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.
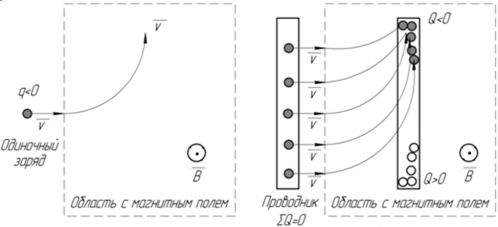
На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.
В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.
В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;
где:
U — разность потенциалов [В],
l — длина проводника [м],
v — скорость движения проводника $big[ frac{text{м}}{c} big]$
B — индукция магнитного поля [Тл],
α — угол между направлением скорости и длиной проводника.
В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.
В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = – frac{Delta text{Ф}}{Delta t}$
В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.
Задача 3
В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?
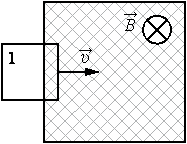
Решение:
Составим цепочку.
Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.
Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.
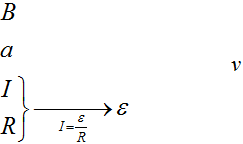
А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.
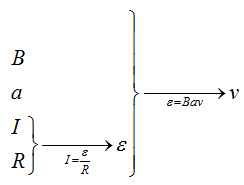
Пройдёмся вдоль этой цепочки.
Запишем закон Ома $I = frac{varepsilon}{R}$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac{varepsilon}{R} = frac{Bav}{R}$отсюда выразим скорость, и, подставив все величины, получим $v = frac{IR}{Ba} = frac{1cdot 10^{-3} Acdot 10text{Ом}}{0,1 text{Тл} cdot 0,1 text{м}} = 1 frac{text{м}}{c}$
Ответ: 1
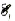 = 0,74 В.
= 0,74 В.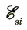 = 0,08 В.
= 0,08 В.