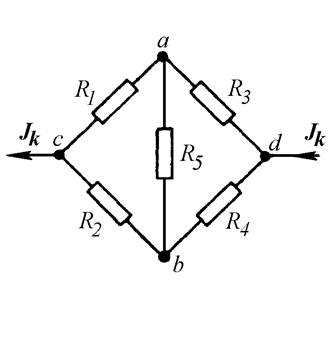
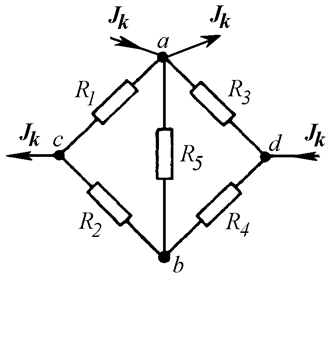
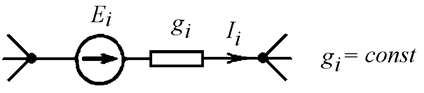
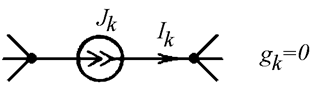
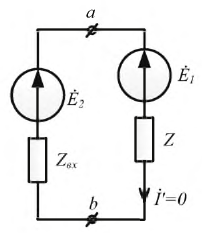
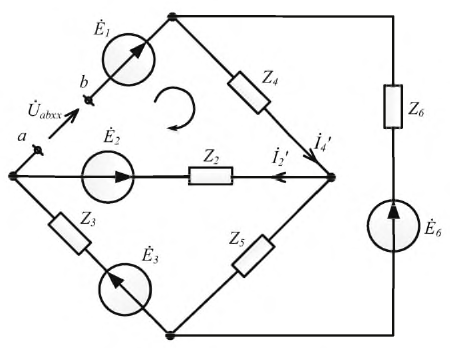
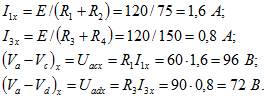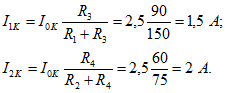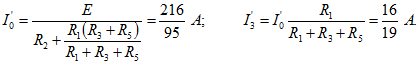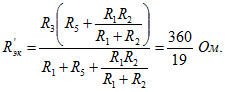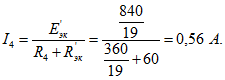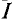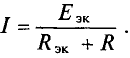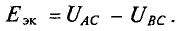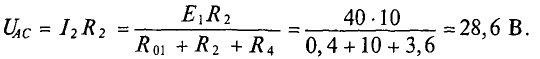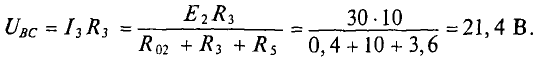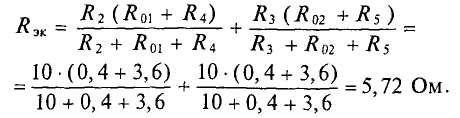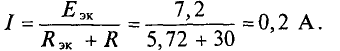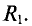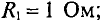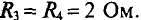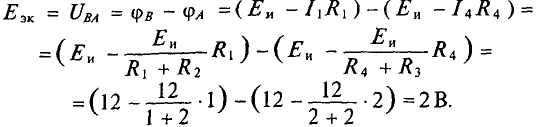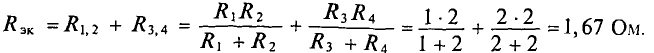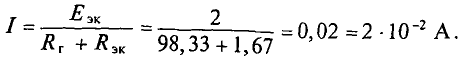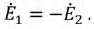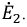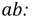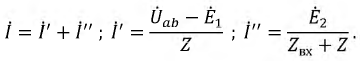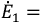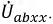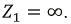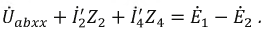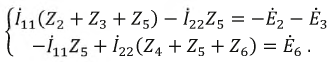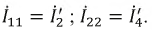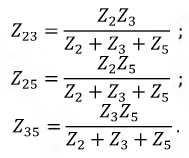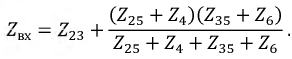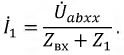Возьмем два участка цепи a–bи c–d (см.
рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на
рис. 1 положительных направлений напряжений
и токов.


Объединяя оба случая, получим
 |
(1) |
или для постоянного тока
| (2) |
Формулы (1) и (2) являются аналитическим выражением закона Ома для участка
цепи с источником ЭДС, согласно которому ток на участке цепи с источником
ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной
на сопротивление участка. В случае переменного тока все указанные величины суть
комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление
совпадает с выбранным направлением тока, и со знаком “-”, если их направление
противоположно направлению тока.
Основы символического метода расчета цепей
синусоидального тока
Расчет цепей переменного синусоидального тока может производиться не только
путем построения векторных диаграмм, но и аналитически – путем операций с комплексами,
символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством
векторных диаграмм является их наглядность, недостатком – малая точность графических
построений. Применение символического метода позволяет производить расчеты цепей
с большой степенью точности.
Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа
и законе Ома в комплексной форме.
Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно
такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только
токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных
величин.
1.
Первый закон Кирхгофа в комплексной форме:
| (3) |
2.
Второй закон Кирхгофа в комплексной форме:
| (4) |
или применительно к схемам замещения с источниками
ЭДС
| (5) |
3.
Соответственно матричная запись законов Кирхгофа в комплексной
форме имеет вид:
§
первый закон Кирхгофа:
| . |
(6) |
§
второй закон Кирхгофа
| (7) |
Пример.
Дано:
Рис. 2
Решение:
1.
.
2.

3.
.
4.
Принимая начальную фазу напряжения за нуль, запишем:
.
Тогда

5.
Поскольку ток распределяется обратно пропорционально сопротивлению
ветвей (это вытекает из закона Ома), то

6.
.
7.
Аналогичный результат можно получить, составив для данной схемы
уравнения по законам Кирхгофа в комплексной форме
или после подстановки численных значений параметров
схемы
Специальные методы расчета
Режим работы любой цепи полностью характеризуется уравнениями, составленными
на основании законов Кирхгофа. При этом необходимо составить и решить систему
с n неизвестными, что может оказаться
весьма трудоемкой задачей при большом числе n ветвей схемы. Однако, число уравнений, подлежащих решению, может
быть сокращено, если воспользоваться специальными методами расчета, к
которым относятся методы контурных токов и узловых потенциалов.
Метод контурных токов
Идея метода контурных токов: уравнения составляются только по второму закону
Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих
по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей
связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи
графа . Первый закон Кирхгофа выполняется автоматически.
Контуры можно выбирать произвольно, лишь бы их число было равно и чтобы каждый новый контур содержал хотя
бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми.
Их выбор облегчает использование топологических понятий дерева и ветвей связи.
Направления истинных и контурных токов выбираются произвольно. Выбор положительных
направлений перед началом расчета может не определять действительные направления
токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании
уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его
истинное направление противоположно.
Пусть имеем схему по рис. 3.
Выразим токи ветвей через контурные токи:
;
;
;
;
.
Обойдя контур aeda, по второму закону Кирхгофа
имеем
.
Поскольку ,
то
.
Таким образом, получили уравнение для первого контура относительно контурных
токов. Аналогично можно составить уравнения для второго, третьего и четвертого
контуров:

совместно с первым решить их относительно контурных токов и затем по уравнениям,
связывающим контурные токи и токи ветвей, найти последние.
Однако данная система уравнений может быть составлена формальным путем:

При составлении уравнений необходимо помнить следующее:
– сумма сопротивлений, входящих в
i–й контур;
– сумма сопротивлений, общих для i–го и k–го контуров, причем
;
члены на главной диагонали всегда пишутся со знаком “+”;
знак “+” перед остальными членами ставится в случае, если через общее сопротивление
i–й и k–
й контурные токи проходят в одном направлении, в противном случае ставится знак
“-”;
если i–й и k– й контуры не имеют общих сопротивлений, то ;
в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в
контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением
контурного тока, и “-”, если не совпадает.
В нашем случае, для первого уравнения системы, имеем:
Следует обратить внимание на то, что, поскольку , коэффициенты контурных уравнений всегда
симметричны относительно главной диагонали.
Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются
в левых частях уравнений как известные контурные токи: k– й контурный ток, проходящий через ветвь с k–
м источником тока равен этому току .
Метод узловых потенциалов
Данный метод вытекает из первого закона Кирхгофа.
В качестве неизвестных принимаются потенциалы узлов, по найденным значениям
которых с помощью закона Ома для участка цепи с источником ЭДС затем находят
токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного
из узлов (любого) принимается равным нулю. Таким образом, число неизвестных
потенциалов, а следовательно, и число уравнений равно , т.е. числу ветвей дерева
.
Пусть имеем схему по рис. 4, в которой примем
.
Допустим, что и
известны. Тогда значения токов на основании
закона Ома для участка цепи с источником ЭДС

Запишем уравнение по первому закону Кирхгофа для
узла а:
и подставим значения входящих
в него токов, определенных выше:
.
Сгруппировав соответствующие члены, получим:
.
Аналогично можно записать для узла b:
.
Как и по методу контурных токов, система уравнений
по методу узловых потенциалов может быть составлена формальным путем. При этом
необходимо руководствоваться следующими правилами:
1. В
левой части i–го
уравнения записывается со знаком “+”потенциал i–го узла, для которого составляется данное
i–е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i–му узлу, и со знаком “-”потенциал
соседних узлов, каждый из которых умножен
на сумму проводимостей ветвей, присоединенных к i–му
и k–му узлам.
Из сказанного следует, что все члены
, стоящие на главной диагонали в левой части
системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”,
причем . Последнее равенство по аналогии с методом
контурных токов обеспечивает симметрию коэффициентов уравнений относительно
главной диагонали.
2. В
правой части i–го
уравнения записывается так называемый узловой ток , равный сумме произведений ЭДС ветвей, подходящих
к i–му узлу, и проводимостей этих ветвей. При этом член суммы записывается
со знаком “+”, если соответствующая ЭДС направлена к i–му узлу, в противном случае ставится знак “-”. Если в подходящих
к i–му узлу ветвях содержатся источники тока,
то знаки токов источников токов, входящих в узловой ток простыми слагаемыми,
определяются аналогично.
В заключение отметим,
что выбор того или иного из рассмотренных методов определяется тем, что следует
найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений.
При расчете токов при одинаковом числе уравнений предпочтительнее использовать
метод контурных токов, так как он не требует дополнительных вычислений с использованием
закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных
цепей, но не удобен при расчете цепей со взаимной индуктивностью.
Литература
1.
Основы теории
цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е
изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2.
Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с
.
Контрольные вопросы и задачи
1. В
ветви на рис. 1
. Определить ток
.
Ответ: .
2. В
чем заключается сущность символического метода расчета цепей синусоидального
тока?
3. В
чем состоит сущность метода контурных токов?
4. В
чем состоит сущность метода узловых потенциалов?
5.
В цепи на рис. 5 ;
;
;
. Методом контурных токов определить комплексы
действующих значений токов ветвей.
Ответ: ;
;
.
6. В
цепи на рис. 6
. Рассчитать токи в ветвях, используя метод
узловых потенциалов.
Ответ: ;
;
;
;
;
;
.

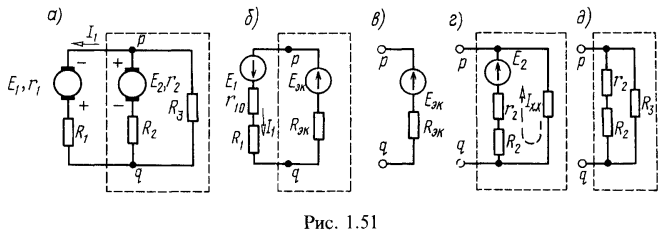
1. Для схемы цепи рис. 1.51, а методом эквивалентного источника ЭДС найти ток в ветви резистора, сопротивление которого , если
Решение:
Обозначим положительное направление искомого тока на исходной схеме (рис. 1.51, а). Рассмотрим часть схемы, подключенную к исследуемой первой ветви (обведенную штриховой линией), в качестве эквивалентного источника ЭДС и сопротивлением
. Нарисуем эквивалентную электрическую схему с эквивалентным источником напряжения (рис. 1.51, б).
На схеме выбрано произвольно положительное направление ЭДС эквивалентного источника к точке р. Это позволяет записать, для режима холостого хода эквивалентного источника с отключенной первой ветвью (рис. 1.51, в):
Развернутая схема эквивалентного источника в режиме холостого хода показана на рис. 1.51, г. Во внутренних ветвях источника ток
Напряжение холостого хода определяет ЭДС источника:
Найдем сопротивление эквивалентного источника.
Для подсчета сопротивления источника преобразуем его схему (см. рис. 1.51, г), заменив источник напряжения короткозамкнутым участком (рис. 1.51, д). Входное сопротивление последней схемы является сопротивлением эквивалентного источника
Возвращаясь к схеме рис. 1.51, б, найдем искомый ток по закону Ома:
2. Методами эквивалентного источника ЭДС и эквивалентного источника тока найти ток в ветви , если
(рис. 1.52, а).
Решение:
1. Рассчитаем методом эквивалентного источника ЭДС. Отключим ветвь с (рис. 1.52, б) и найдем его параметры с ЭДС
(т. е. напряжение
холостого хода между точками а и b) и
— сопротивление схемы рис. 1.52, в между точками а и b в режиме холостого хода при закороченных ЭДС
. Схема эквивалентного источника ЭДС приведена на рис. 1.52, г. ЭДС эквивалентного источника и его сопротивление равны:
Искомый ток согласно формуле (0.1.24)
2. При расчете методом эквивалентного источника тока ветвь закорачиваем (рис. 1.52, д). Ток
, проходящий но закороченной ветви ab, является током эквивалентного источника тока
. Найдем его. Это можно сделать, рассчитав двухузловую схему (рис. 1.52, д) методом узловых напряжений. Приняв потенциал точек а и b равным нулю
, найдем
Для определения тока вычисляем
и по первому закону Кирхгофа вычисляем
Сопротивление эквивалентного источника тока равно сопротивлению эквивалентного источника напряжения; однако его можно найти по (0.1.25):
.
Из схемы эквивалентного источника тока (рис. 1.52, е) по формуле (0.1.26) находим искомый ток
Получили тот же результат, что и по методу эквивалентного источника ЭДС.
В заключение рассмотрим вопрос о мощностях, доставляемых источниками при их преобразовании. Из теории известно, что при преобразованиях источников токи в ветвях, не подвергшихся преобразованию, остаются неизменными, а мощности, доставляемые источниками, изменяются. Так, для схем (рис. 1.52, г и е) ток в ветви , не подвергшейся преобразованию, в обоих случаях одинаков:
. Мощности же в цепях схем (рис. 1.52, г, е) различны:
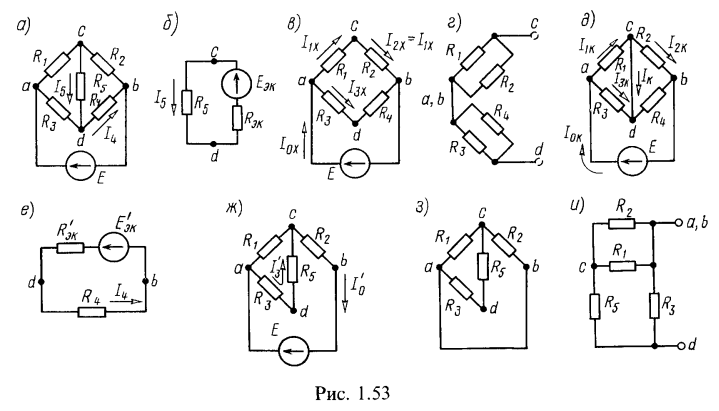
3. Методом эквивалентного источника ЭДС найти ток (рис. 1.53, а), проходящий через резистор, сопротивление которого
, если
.
Тем же методом определить ток в сопротивлении .
Решение:
На схеме рис. 1.53, а обозначим произвольное положительное направление искомого тока . Часть схемы (внешнюю к исследуемой ветви
) рассмотрим в виде некоторого источника ЭДС
. Стрелку ЭДС
произвольно направим к точке с (рис. 1.53, б). Таким образом, ЭДС источника определился напряжением холостого хода:
.
На развернутой схеме источника в режиме холостого хода (рис. 1.53, в) обозначим токи в ветвях .
По закону Ома,
Таким образом, ЭДС эквивалентного источника напряжения:
Найдем сопротивление эквивалентного источника ЭДС двумя методами:
1) путем непосредственного расчета по схеме: для этого в схеме рис. 1.53, в источник напряжения заменим короткозамкнутым участком; после этого схему рис. 1.53, в нарисуем в виде рис. 1.53, г.
Сопротивление источника равно сопротивлению цепи между точками с и d:
2) путем вычисления отношения ЭДС эквивалентного источника к току короткого замыкания; для этого в схеме рис. 1.53, в надо замкнуть точки с и d накоротко, вычислить ток , протекающий через короткозамкнутый участок (рис. 1.53. д), и найти сопротивление короткого замыкания по формуле (0.1.25). Источник ЭДС Е в короткозамкиутой схеме рис. 1.53, д нагружаем на эквивалентное сопротивление
Ток источника напряжения
Токи в ветвях
Отсюда
Сопротивление источника
Значения сопротивления источника, полученные этими методами одинаковы.
Возвращаясь к рис. 1.53, б, по закону Ома находим искомый ток
Таким образом, ток в сопротивлении направлен от точки d к точке с и равен 0,4 А.
Расчет тока резистора, сопротивление которого , метолом эквивалентного источника ЭДС проводится аналогично. Заменяем часть схемы, подключенную к точкам d и b ветви с сопротивлением
, эквивалентным источником
(рис. 1.53, е). ЭДС источника совпадает с напряжением в режиме холостого хода:
.
Для определения этого напряжения рассчитаем вначале токи в развернутой схеме источника в режиме холостого хода (рис. 1.53, ж):
Отсюда находим ЭДС источника
Для определения сопротивления источника ЭДС рассмотрим соответствующую пассивную схему (в схеме источник ЭДС заменен короткозамкнутым отрезком), показанную на рис. 1.53, з. Для ясности эта схема показана в виде рис. 1.53, и.
Сопротивление источника, равное входному сопротивлению последней схемы, относительно зажимов d и b:
Находим искомый ток по схеме эквивалентного источника ЭДС (рис. 1.53, е):
. (11.4)
Подставим
уравнения (11.2-11.4) в (11.1):
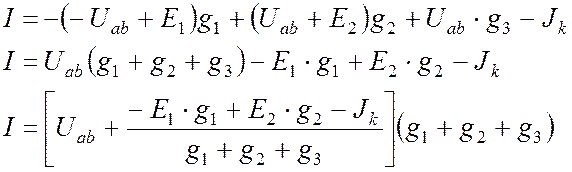
Теперь запишем
уравнение по закону Ома для эквивалентной ветви (Рис. 11.1 б):
. (11.6)
Из сравнения
(11.6) и (11.5) очевидны соотношения для параметров эквивалентной цепи:
, (11.7)
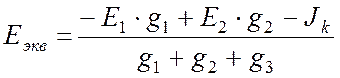
Обобщим
формулы (11.7) и (11.8) на произвольное количество параллельных ветвей.
Итак,
параллельные ветви с источниками энергии можно заменить одной эквивалентной
ветвью, содержащей последовательно включенные сопротивление и ЭДС. При этом
проводимость эквивалентной ветви равна арифметической сумме проводимостей всех
ветвей:
. (11.9)
Эквивалентная
ЭДС равна дроби, в знаменателе которой – сумма проводимостей всех ветвей (как
активных, так и пассивных). В числителе – алгебраическая сумма источников тока
плюс алгебраическая сумма произведений ЭДС на проводимость своей ветви:
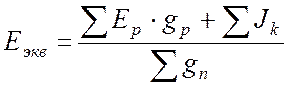
где p
– число ветвей с ЭДС;
k
– число ветвей с источниками тока;
n
– число всех ветвей.
В выражении
(11.10) с плюсом берутся те ЭДС и источники тока, которые совпадают по
направлению с эквивалентной ЭДС, с минусом – противоположные.
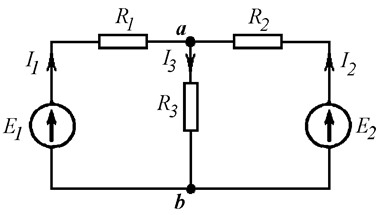
Пример
11.1: Найти ток I3 (Рис. 11.2).
Рис. 11.2
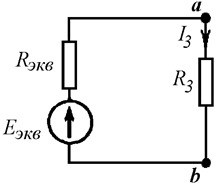
Исходную цепь
преобразуем, свернув две активные ветви в одну эквивалентную. При этом ветвь с
током I3 преобразованию не
подвергнется, а значит, не изменится ток в ней (Рис. 11.3):
Рис. 11.3
Параметры
эквивалентной ветви:
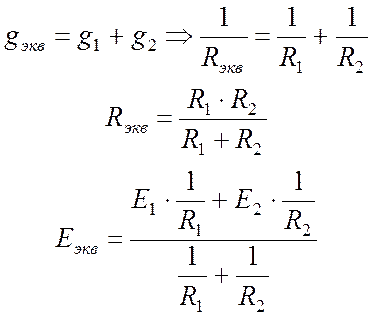
Очевидно, что
в преобразованной схеме (Рис. 11.3) ток I3
легко определяется по закону Ома:
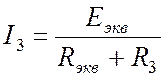
12. ВЫНЕСЕНИЕ ЭДС
И ИСТОЧНИКА ТОКА ИЗ ВЕТВИ
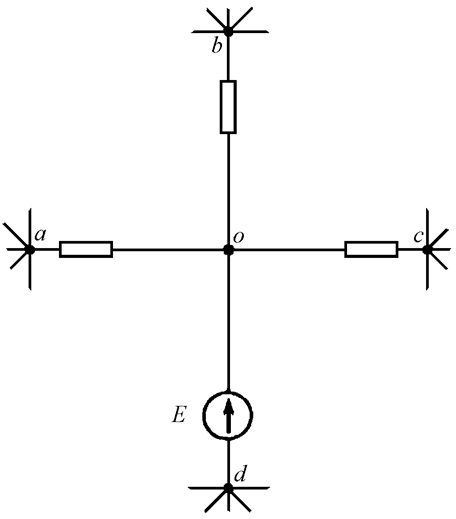
В сложной цепи
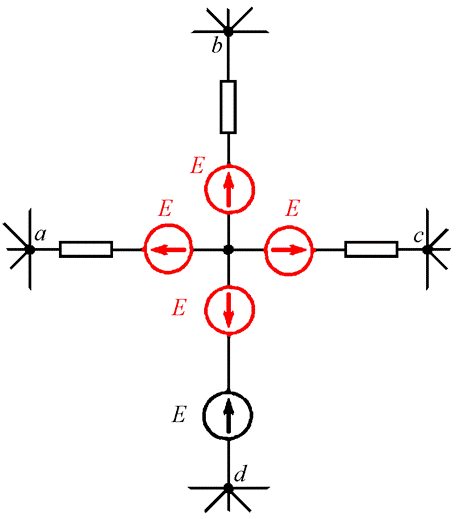
имеется ветвь с нулевым сопротивлением и идеальной ЭДС (Рис. 12.1).
Рис. 12.1
Требуется
преобразовать цепь таким образом, чтобы в ней не было ветви с нулевым сопротивлением.
Сделать это можно, удалив ЭДС E
из ветви. Тогда потенциалы узлов d и o будут равны, эти узлы можно будет объединить и ветвь с
нулевым сопротивлением исчезнет.
Идеальная ЭДС E располагается между узлами d
и o. Добавим во все ветви, примыкающие к узлу o, такие же ЭДС E, но
направленные не к узлу, а от узла (Рис. 12.2). Очевидно, что при
этом изменится потенциал узла o, но потенциалы
узлов a, b, c и d останутся
неизменными.
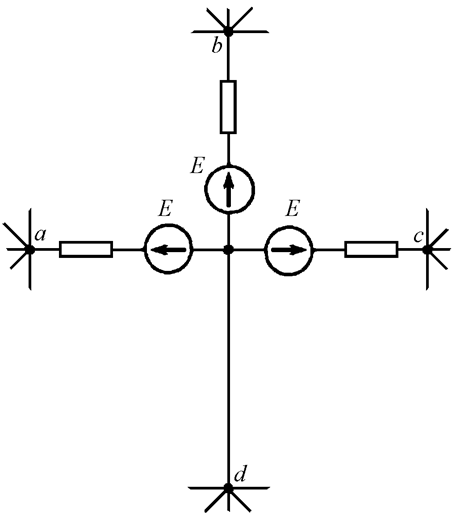
Рис. 12.2
Теперь в ветви
с нулевым сопротивлением имеются две равные и противоположно направленные ЭДС.
Они компенсируют друг друга, и их можно удалить из ветви (Рис. 12.3).
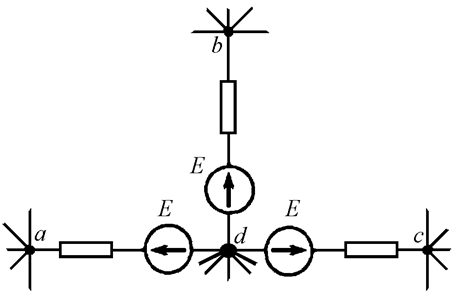
Рис. 12.3
Узлы, соединенные
ветвью с нулевым сопротивлением, не содержащей ЭДС, можно объединить. Новый
узел будет иметь тот же потенциал, что и у узла d
до преобразования. Таким образом, из схемы исключена ветвь с нулевым
сопротивлением и узел o (Рис. 12.4).
Рис. 12.4
Такая операция
называется вынесением ЭДС из ветви за узел. При вынесении ЭДС из ветви за узел
вместо исходной ЭДС появляются точно такие же ЭДС в остальных ветвях,
примыкающих к узлу, но ориентированные противоположно (если исходная ЭДС была
направлена к узлу, то ЭДС в эквивалентной схеме направлены от узла, и
наоборот).
Заметим, что
вынесение ЭДС из ветви за узел применимо к любым ветвям, а не только к ветвям с
нулевым сопротивлением.
Для вынесения
источника тока из ветви достаточно включить точно такие же источники тока
параллельно другим ветвям, но так, чтобы не изменилось токораспределение в
схеме.
Пример
12.1:
Вынести из
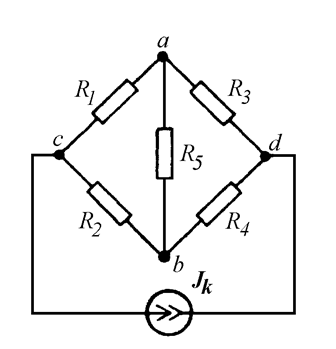
ветви источник тока (Рис. 12.5).
Рис. 12.5
Ток источника Jk вытекает из узла c и втекает в узел d.
Значит, и в преобразованной схеме ток Jk
должен вытекать из узла c и втекать в узел d (Рис. 12.6).
Рис. 12.6
Но если,
например, в узел a будет втекать ток Jk и одновременно вытекать ток Jk (Рис. 12.7), распределение
токов в схеме не изменится.
Рис. 12.7
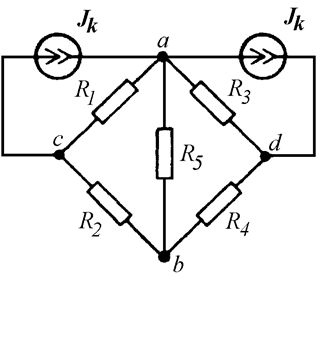
Вышеприведенные
рассуждения позволяют нам включить два источника тока параллельно ветвям с
резисторами R1 и R3
(Рис. 12.8).
Рис. 12.8
13. МЕТОД УЗЛОВЫХ
ПОТЕНЦИАЛОВ
Для расчета
токов в электрической цепи достаточно знать потенциалы всех узлов. Тогда с
помощью закона Ома можно найти токи.
Рис. 13.1
Электрическая
цепь – это система ветвей, соединенных друг с другом узлами. Каждая ветвь
упирается своими концами в два узла. Справедливо и обратное утверждение: любые
два узла цепи соединяются друг с другом ветвью. Это утверждение поможет нам
разработать алгоритм определения потенциалов узлов.
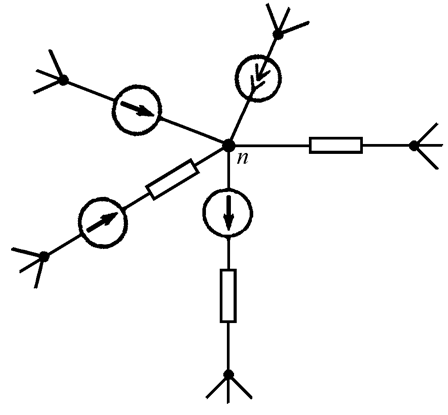
Представим
задачу в наиболее общем виде. Пусть в узле n
соединяется множество ветвей. При этом каждая ветвь на своем противоположном
конце также заканчивается узлом (Рис. 13.1).
Все ветви цепи
можно условно разбить на три группы.
Первая –
ветви, содержащие ЭДС и обладающие конечной проводимостью. Заметим, что к этой
же группе можно отнести ветви с конечной проводимостью без ЭДС. Такие ветви
будем обозначать индексом i (Рис. 13.2 а).
а)
б)
Рис. 13.2
Вторая –
ветви, содержащие источники тока. Проводимость этих ветвей равна нулю. Такие
ветви будем обозначать индексом k (Рис. 13.2 б).
Третья – ветви
с ЭДС и нулевым сопротивлением. Проводимость этих ветвей бесконечно велика. Как
было показано выше, такие ветви всегда можно устранить из схемы путем вынесения
ЭДС из ветви за узел. Поэтому в дальнейшем будем рассматривать цепь, в которой
нет ветвей с ЭДС и нулевым сопротивлением.
Пусть в узле n соединяются i‑ые и k‑ые ветви. Обозначим узлы, противоположные узлу n, индексами i и k (Рис. 13.3). Само
собой разумеется, количество i‑ых и k‑ых ветвей может быть каким угодно.
Метод эквивалентного генератора:
Метод эквивалентного генератора рационально применять в случае необходимости определения тока (напряжения, мощностн и др.) только одной ветви сложной электрической цепи.
Для этой цели разбивают сложную электрическую цепь на две части — на сопротивление R, ток которого
Активным этот двухполюсник называют потому, что в нем имеется источник ЭДС. Этот активный двухполюсник обладает определенной ЭДС
Ток в резисторе с сопротивлением R определяют по закону Ома
Таким образом, определение тока 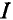
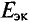
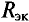
Величина ЭДС 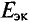
Внутреннее сопротивление эквивалентного генератора 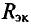
Практически для определения внутреннего сопротивления эквивалентного генератора измеряют амперметром ток между точки А и В работающего двухполюсника при коротком замыкании так как сопротивление амперметра настолько мало, что им можно пренебречь. Тогда
где 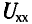
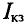
Такой метод практического определения внутреннего сопротивления эквивалентного генератора 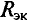
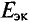
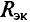
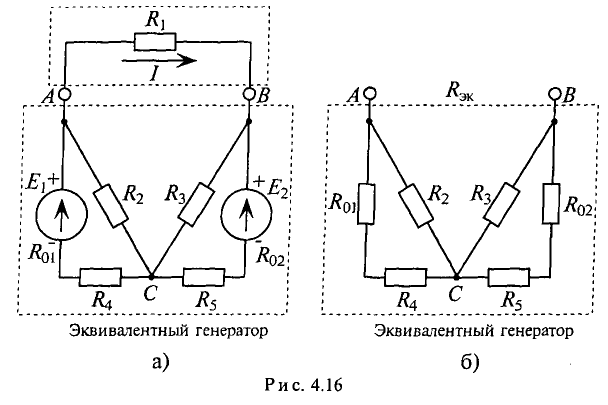
Пример 4.12
Определить ток в сопротивлении 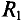
Решение
Для определения тока 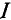
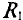
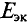
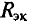
Знак «минус» обусловлен тем, что источники в схеме включены встречно и потенциал в точке А больше потенциала в точке В, так как 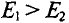
Напряжение
Напряжение
Следовательно, 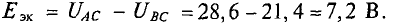
Искомый ток
Такой же ток получен в примере 4.6 на сопротивлении
Пример 4.13
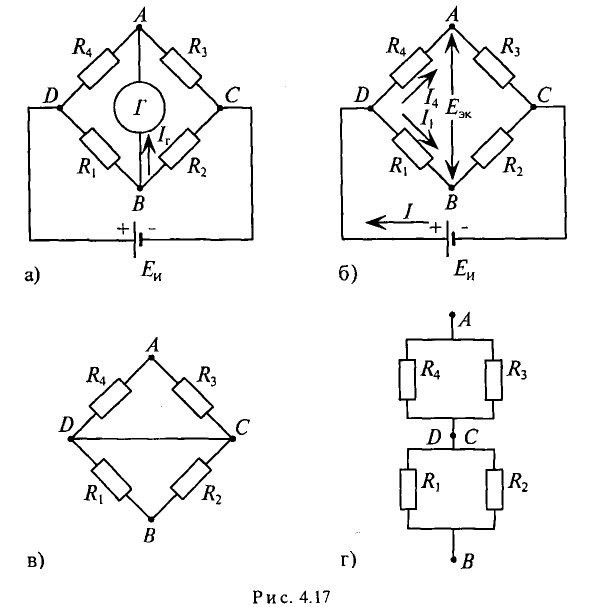
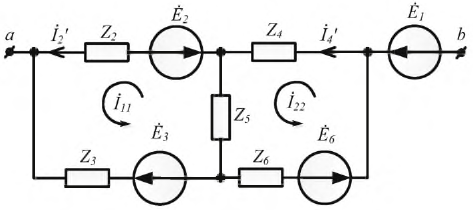
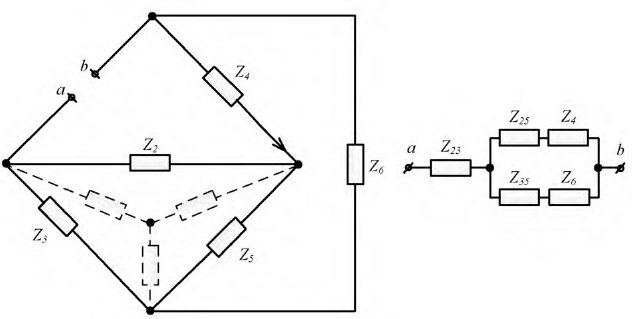
В схеме рис. 4.17а сопротивления плеч моста равны
Сопротивление гальванометра Rr = 98,33 Ом, ЭДС источника 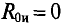
Решение
Для определения тока в цепи гальванометра 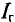
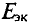
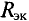
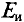
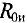
Для определения ЭДС эквивалентного генератора 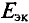
Тогда
При замене источника ЭДС 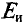
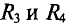
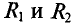
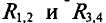
Тогда ток в ветви с гальванометром, который направлен из точки В в точку А, т. е. из точки с большим потенциалом в точку с наименьшим потенциалом (рис. 4.17а), будет равен
Метод эквивалентного генератора (активного двухполюсника)
Все методы, рассмотренные ранее, предполагали расчет токов одновременно во всех ветвях цепи. Однако в ряде случаев бывает необходимым контролировать ток в одной отдельно взятой ветви. В этом случае применяют для расчета метод эквивалентного генератора.
Пусть дана некоторая электрическая цепь, которую заменим активным двухполюсником (рис. 3.10), оставив только ветвь 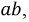
Сначала, введем в ветвь 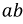
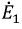
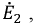
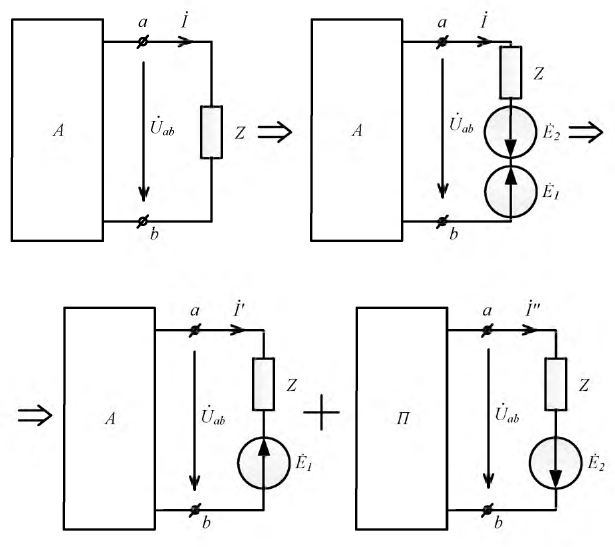
Затем, используя принцип наложения, данную цепь представим суммой двух цепей. В первой оставим все источники активного двухполюсника и источник ЭДС 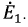
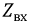
Рис. 3.10. Преобразование исходного двухполюсника в сумму двух цепей
На основании принципа наложения ток ветви
Поскольку 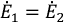
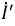
Напряжение на зажимах источника в режиме холостого хода численно равно его ЭДС. Тогда активный двухполюсник с источником 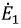
Рис. 3.11. Схема замещения активного двухполюсника
В этой схеме ЭДС 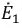
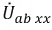
Таким образом, ток в ветви
Пусть дана цепь (рис. 3.12), в которой необходимо рассчитать ток 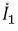
Рис. 3.12. Исходная цепь
Последовательность расчета:
1. Разомкнем ветвь с сопротивлением 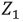
2. Зададим положительное направление 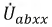
3. Токи 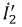
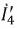
Тогда
4. Определим эквивалентное сопротивление пассивного двухполюсника. Для этого мысленно закоротим все источники ЭДС исходной цепи, оставляя в схеме для реальных источников их внутренние сопротивления.
В образовавшейся схеме пассивного двухполюсника невозможно определить эквивалентное сопротивление относительно зажимов 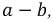
Преобразуем, например, «треугольник» сопротивлений 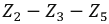
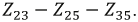
Рис. 3.14. Схема пассивного двухполюсника
Сопротивления этой схемы будут:
Входное сопротивление цепи 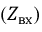
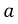
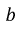
Окончательно имеем:
- Теоремы теории цепей
- Теорема обратимости (или взаимности)
- Теорема компенсации
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
- Метод свертывания электрической цепи
- Метод преобразования схем электрических цепей
- Параллельное соединение генераторов
- Метод узловых и контурных уравнений
Для расчета электрической цепи применяют два закона Кирхгофа. (Скорее их можно отнести не к законам, а к правилам. Но в большинстве учебников пишут именно о “законах” Кирхгофа. Поэтому и здесь будем обращаться к законам).
Первый закон Кирхгофа
Первый закон Кирхгофа применяют к узлам электрической цепи и выражают баланс токов в них. Первый закон Кирхгофа гласит:
Алгебраическая сумма токов сходящихся в узле электрической цепи равна 0.
Под словом “алгебраическая” имеется в виду, что учитывается знак перед током: “плюс” или “минус”.
В общем виде первый закон Кирхгофа можно записать как:
Для примера возьмем узел, в котором протекают токи, указанные стрелками (далее рассмотрим это все на конкретных схемах).
Токи, втекающие и вытекающие из узла, берутся с противоположными знаками. Втекающие в узел токи берутся со знаком, например, “+”, а вытекающие с “-“ (можно вытекающие брать с “+”, а втекающие с “-“). Главное, чтобы втекающие и вытекающие токи отличались по знаку.
Будем считать токи положительными, если они втекают в узел, а вытекающие из узла – отрицательными. Тогда первый закон Кирхгофа для узла, представленного на рисунке 2, запишется:
I1-I2+I3+I4=0
Это выражение можно записать и в следующем виде:
I2=I1+I3+I4;
Ток I2 мы перенесли за знак равенства, его знак поменялся на противоположный (был с “минусом”, стал с “плюсом”).
Остальные токи мы не переносим, поэтому их знаки не меняются.
Согласно последнему выражению, первый закон Кирхгофа можно сформулировать по-другому:
Сумма токов, втекающих (подходящих) в узел, равна сумме токов, вытекающих (отходящих) из узла.
Все это говорит о том, что в узле эти токи не остаются и заряд в узле не накапливается.
Для более полного понимания, представим электрическую цепь (схему электрической цепи), для которой запишем первый закон Кирхгофа.
Запишем для этой цепи первый закон Кирхгофа для узла “a” (о том, как определить количество уравнений по первому и второму законам Кирхгофа, рассмотрим в конце ).
I1+I2-I3=0 или I3=I1+I2.
Второй закон Кирхгофа
Этот закон применяется к контурам электрической цепи и выражает баланс напряжений в них. Второй закон Кирхгофа звучит так:
Алгебраическая сумма ЭДС в замкнутом контуре (с учетом направления обхода контура) равна алгебраической (учитывается знак “+” или “-“) сумме падений напряжений на всех сопротивлениях (элементах) этого контура.
Для того, чтобы правильно составить уравнения по второму закону Кирхгофа, нужно пользоваться следующим правилом:
ЭДС берется со знаком “+”, если ее действие совпадает с направлением обхода контура. Напряжение на элементе контура берется со знаком “+”, если направление тока через данный элемент совпадает с направлением обхода контура. Если не совпадает направление обхода контура с направлением тока через элемент, то напряжение этого элемента берется со знаком “-“.
Запишем второй закон Кирхгофа для цепи, представленной ниже:
Выбираем направление обхода контура по часовой стрелке. В данном случае направление тока и направление обхода контура совпадают, поэтому I·R1 и I·R2 взяли со знаком “+”. А также совпадает направление обхода контура и действие ЭДС, поэтому ЭДС также записали со знаком “+”.
Возьмем еще один пример.
Запишем для этой цепи второй закон Кирхгофа. Обход выбираем по часовой стрелке (указали обход контура на схеме круговой стрелкой внутри контура). Как видим, направление обхода контура и направление тока I1 совпадают, а ток I2 направлен напротив обхода контура.
Следовательно, падение напряжения на резисторе R1 запишется со знаком “+”, т. е. +I1·R1. А падение напряжения на R2 запишется со знаком “-“, т. е. –I2·R2.
Направление действия ЭДС совпадает с обходом контура, поэтому ЭДС E берем со знаком “+”.
Запишем второй закон Кирхгофа для этой цепи:
I1·R1-I2·R2=E
Ну и напоследок рассмотрим сложную электрическую цепь, состоящую из нескольких источников и резисторов.
Введем произвольно направление токов в ветвях, а также укажем на схеме в виде круговых стрелок направление обхода контуров.
Токи в ветвях направили произвольно, обход контура выбрали по часовой стрелке, а также узлы в этой схеме обозначили буквами a и b. Для того, чтобы понять, как и сколько уравнений по первому и второму законам Кирхгофа нужно составить для данной цепи, необходимо посчитать количество ветвей, узлов и независимых контуров.
Подробно вышесказанные понятия электрической цепи мы рассмотрим в следующих статьях. А пока вкратце.
Узел – это место соединения трех и более ветвей в электрической цепи (в данном случае таких узлов два. Это узлы “a” и “b”.
Ветвь – это участок электрической цепи, который образуется одним или несколькими последовательно соединенными элементами и через все эти элементы протекает один и тот же ток.
Контур – это любой замкнутый путь электрической цепи, проходящий по двум или нескольким ветвям.
Так же есть такое понятие как независимый контур.
Независимый контур должен включать в себя хотя бы одну ветвь, не входящую в другие контуры.
На рисунке 9 будет три контура, два из которых независимые. Если контур 1 независимый, контур 2 независимый(таким образом все три ветви этой схемы цепи вошли в эти независимые контуры). Тогда контур 3 уже независимым не будет, поскольку все ветви “заняты” остальными двумя контурами.
Или если контур 1 независимый (он включает в себя ветви с элементами E и R1). Контур 3 независимый (он включает в себя ветви с элементом E и ветвь с элементом R3. Элемент R3 ранее не входил в первый независимый контур), поэтому контур 3 считается независимым.
Получается, что все ветви “заняты”. Тогда контур 2 независимым уже не будет, поскольку в него не входят ветви или ветвь ранее не входящую в другие контура. Все ветви вошли в ранее независимые контуры 1 и 3.
В цепи на рисунке 9, в общем случае, три ветви, два узла и два независимых контура. Общее количество уравнений по законам(правилам) Кирхгофа составляется столько, сколько ветвей в схеме цепи за вычетом количества ветвей, где есть источник тока (именно источник тока, а не ЭДС). В нашей схеме нет источников тока, следовательно, составляются три уравнения по законам Кирхгофа. Теперь осталось определить, сколько уравнений нужно составить по первому и второму законам Кирхгофа. Общее количество уравнений будет три. Формула для определения количества уравнений по первому закону Кирхгофа следующая:
N1з.к.=Ny-1, где Ny – количество узлов.
Ny=2, тогда
N1.з.к.=Ny-1=2-1=1
Т. е. по первому закону Кирхгофа составляется одно уравнение для данной цепи, а общее количество уравнений – три. Таким образом, мы получаем, что по второму закону Кирхгофа нужно составить два уравнения. Или для определения количества уравнений по второму закону Кирхгофа есть формула:
N2.з.к.=Nв-(Ny-1), где Nв – количество ветвей
Nв=3, тогда:
N2.з.к.=3-(2-1)=2
По второму закону Кирхгофа составляется два уравнения. Составим систему, состоящую из трех уравнений. Одно уравнение по первому закону Кирхгофа (это уравнение составляется для любого узла a или b) и двух уравнений по второму закону Кирхгофа для двух любых независимых контуров, например, составим для контуров 1 и 2.
Неизвестными в данной системе являются токи I1, I2 и I3. Решая данную систему, находят эти неизвестные.
О том, как решаются задачи с более сложными цепями, мы поговорим в следующих статьях.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток – простыми словами;