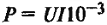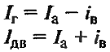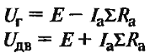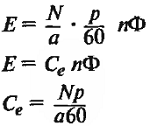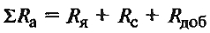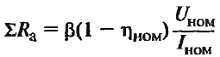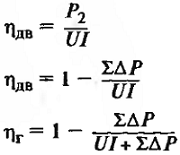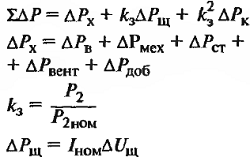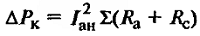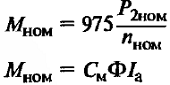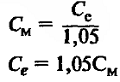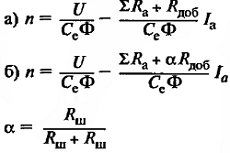Число
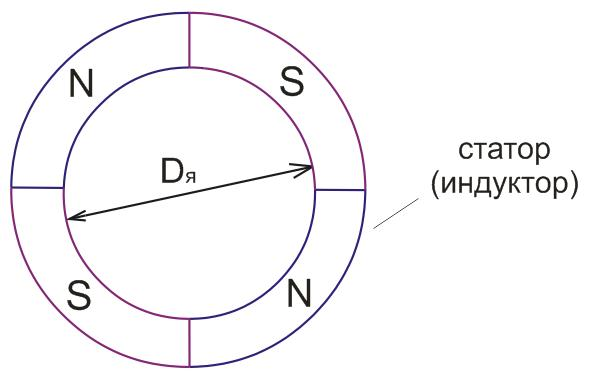
полюсов индуктора равно четырем. Вводится
р – число пар полюсов. Для этого статора
р = 2, а 2р = 4;
|
Рис. |
Рис. |
Индукция
магнитного поля ![]() , (17.1)
, (17.1)
где
Ф
– магнитный поток одного полюса; S
– площадь поверхности одного полюса.
![]() ; (17.2)
; (17.2)
![]() . (17.3)
. (17.3)
Найдем ЭДС якоря:
![]() ;
;
(17.4)
![]() , (17.5)
, (17.5)
где
![]() – конструктивная постоянная электрической
– конструктивная постоянная электрической
машины.
Электромагнитный момент, развиваемый в двигателе постоянного тока

Рис.
17.3. Якорь
Так
как проводники якоря находятся в
магнитном поле, и по ним течет ток, то
по закону Ампера на них действует сила.
Таким образом, на каждый проводник якоря
будет действовать вращающий момент:
![]() ; (17.6)
; (17.6)
![]() ; (17.7)
; (17.7)
![]() , (17.8)
, (17.8)
где
![]() – магнитная индукция.
– магнитная индукция.
![]() –электромагнитный
–электромагнитный
момент якоря. (17.9)
Назначение пускового сопротивления в схеме двигателе постоянного тока независимого возбуждения
Схема
двигателя постоянного тока независимого
возбуждения (ДПТ НВ) изображена на рис.
17.4.
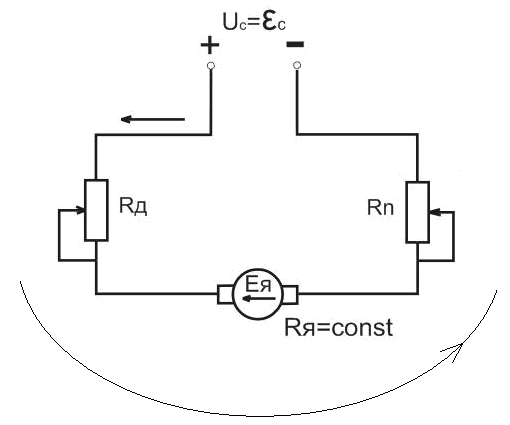
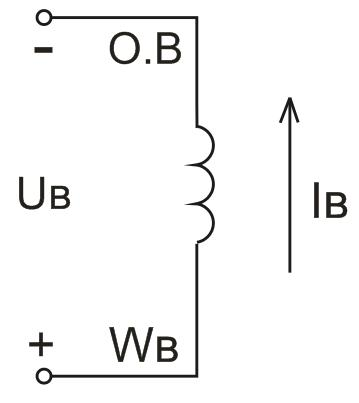
Рис.
17.4. Схема двигателя постоянного тока
независимого возбуждения:
Wв
– число
витков обмотки возбуждения.
По
второму закону Кирхгофа для цепи якоря
можем записать:
Uс
– Eя
= RД·Iя
+ Rя·IД
+
Rп·Iя.
(17.12)
Предположим,
что
![]() ,
,
тогда
![]() , (17.13)
, (17.13)
В
момент пуска ω = 0, т.е. Ея
= 0;
![]() –пусковой
–пусковой
ток. (17.14)
Пусть
![]() ;
;![]() ;
;
А)
![]() ,
,![]() ;
;
В)
![]() ,
,![]() – приемлемый для эксплуатации ток.
– приемлемый для эксплуатации ток.
Вывод.
Если не принять специальных мер (введение
пускового сопротивления в момент пуска),
обмотка якоря сгорит, то есть RП
используется для ограничения тока в
момент пуска.
При
увеличении скорости якоря от ω = 0 до ω
= ωном
ЭДС якоря Ея
увеличивается от 0 до Ея=Uс
и необходимость в Rп
пропадает, поэтому Rп
рассчитано
на кратковременный режим работы – на
период пуска. При достижении
ω = ωном
Rп
выводится
из работы.
Лекция 19. Основные уравнения дпт независимого возбуждения Регулирование скорости двигателя постоянного тока
-
Уравнение
баланса напряжений в цепи якоря (см.
(17.10) имеет вид
Ея
= Uс
– Iя(Rд
+ Rп
+ Rя), (18.1)
При
работе (Rп=
0) уравнение
баланса напряжений в цепи якоря будет
иметь вид
Ея
= Uс–
Iя(Rд+
Rя). (18.2)
-
Уравнение
электромагнитного момента имеет вид
Мя=
сФIя. (18.3) -
Уравнение
ЭДС в обмотке якоря имеет вид
Е=сФω. (18.4) -
Закон
Ома для магнитной цепи выражается
формулой
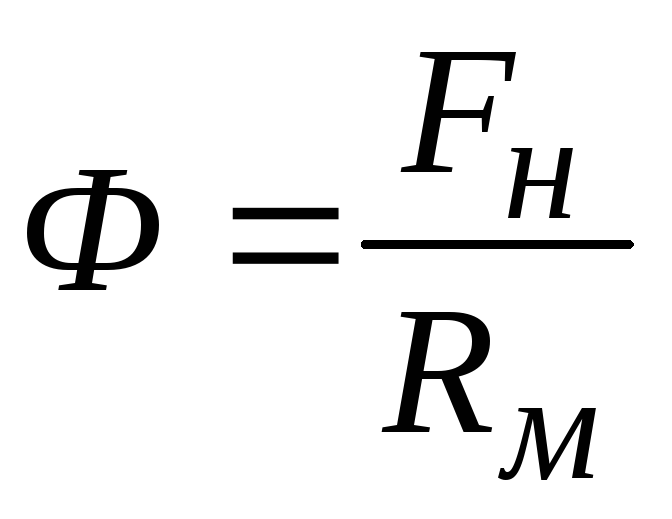 ,
,
(18.5)
где
Fн=
WвIв
(намагничивающая сила обмотки возбуждения);
Rм
– магнитное сопротивление участка
магнитной цепи, по которому замыкается
магнитный поток Ф.
![]() . (18.6)
. (18.6)
Из
выражения (18.4) получим
![]() . (18.7)
. (18.7)
Обозначим
![]() ;
;![]() ; (18.8–18.9)
; (18.8–18.9)
![]() ; (18.10)
; (18.10)
![]() , (18.11)
, (18.11)
где
![]() иIя
иIя
– являются
переменными; А
и В –
коэффициенты.
Следовательно,
уравнение
![]() ,
,
то есть зависимость![]() является прямой линией (рис. 18.1).
является прямой линией (рис. 18.1).

Рис.18.1.
График функции
![]()
В
точке В скорость
![]() =
=
0,
![]() .
.
В
точке А ток Iя=
0,
![]() .
.
Зависимость
(18.11) и рис. (18.1) представляют собой
электромеханическую характеристику
двигателя постоянного тока независимого
возбуждения, т.к.
![]() – механическая величина, аIЯ
– механическая величина, аIЯ
– электрическая величина.
Из
уравнения (18.10) видно, что скорость ДПТ
можно изменять:
1)
путем изменения UС,
такое регулирование скорости называется
якорным регулированием.
2)
путем изменения магнитного потока Ф,
такое регулирование скорости называется
полюсное регулирование.
3)
путем изменения добавочного сопротивления
RД
– реостатное регулирование.
Рассмотрим подробнее
эти способы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.
В результате взаимодействия Iя тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.
Противо ЭДС двигателя Eя
При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС Eя направленная навстречу Iя. Поэтому эта ЭДС называется противо ЭДС и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.
Eя = Се * Ф * n (1)
Ce — постоянный коэффициент определяемой конструкцией двигателя.
Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.
U = Eя + Iя * ∑R (2)
где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :
- обмотки якоря
- добавочных полюсов
- обмотки возбуждения (для двигателей с последовательным возбуждением)
Ток якоря Iя
Выразим из формулы 2 ток якоря.
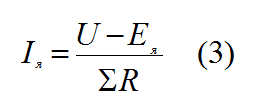
Частота вращения якоря
Из формул 1 и 2 выведем формулу для частоты вращения якоря.

Электромагнитная мощность двигателя
Pэм = Ея Iя (5)
Электромагнитный момент

где: ω = 2*π*f — угловая скорость вращения якоря, Cм — постоянный коэффициент двигателя (включает в себя конструктивные особенности данного двигателя)

Момент на валу двигателя, т.е. полезный момент, где М0 момент холостого хода;
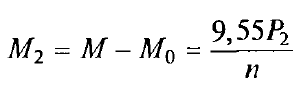
Р2 — полезная мощность двигателя
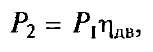
Расчетные формулы параметров машин постоянного тока
В таблице 1 представлены расчетные формулы для определения основных параметров машин постоянного тока.
В данной таблице собраны все формулы, которые касаются расчета параметров машин постоянного тока.
Таблица 1 — Расчетные формулы для определения основных параметров машин постоянного тока
| Наименование величин | Формулы | Принятые обозначения |
|---|---|---|
| Мощность, кВт |
|
I – ток машины, А; U – внешнее напряжение, В; |
| Ток генератора и двигателя, А |
|
Iа – ток якоря; Iв – ток параллельной обмотки возбуждения, А; |
| Внешнее напряжение, В |
|
∑Ra – сумма сопротивлений якорной цепи, Ом; Е – ЭДС машины, В; |
| ЭДС, В |
|
N – число проводников обмотки якоря; а – число пар параллельных ветвей в обмотке якоря; р – число пар полюсов; n – скорость вращения, об/мин. |
| Сопротивление якорной цепи, Ом |
|
Ф – магнитный поток пары полюсов, вебер; Rя, Rс, Rдоб. – сопротивления обмотки якоря, последовательной обмотки возбуждения и добавочных полюсов, Ом |
| Ориентировочной значение сопротивления цепи якоря, Ом |
|
Значение коэффициента β двигателей различного типа возбуждения: для независимого и параллельного возбуждения β=0,5; для смешанного β=0,6; для последовательного β=0,75; |
| КПД двигателя и генератора |
|
∑∆Р – суммарные потери в машине, кВт; |
| Суммарные потери, кВт |
|
∆Рх – потери холостого хода машины или постоянные потер, кВт; ∆Рв – потери на возбуждение, кВт; ∆Рмех. – механические потери на трение в подшипниках и о коллектор, кВт; ∆Рст. – магнитные потери в стали якоря, кВт; ∆Рвент. – вентиляционные потери, кВт; ∆Рдоб. – добавочные потери. В некомпенсированных машинах ∆Рдоб. = 1%Рном, в компенсированных 0,5%, кВт; kз – коэффициент загрузки; ∆Uщ = 2 В для графитных щеток; ∆Uщ = 0,6 В для металлографитных; |
| Переменные потери |
|
|
| Номинальный вращающий момент, кГм |
|
См – конструктивная постоянная момента; Ф – магнитный поток, вебер; |
| Расчетные коэффициенты для двигателя параллельного возбуждения |
|
|
| Скоростная характеристика двигателя |
|
|
| Искусственные скоростные характеристики |
|
а) искусственная скоростная характеристика при введении добавочного сопротивления Rдоб. последовательно в цепь якоря; б) искусственная скоростная характеристика двигателя при шунтировании якоря двигателя сопротивлением Rш; α – коэффициент шунтирования. |
Литература:
1. Справочная книга электрика. В.И. Григорьева, 2004 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
КПД генератора, параметры машин постоянного тока, ток генератора, ЭДС
Благодарность:
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding» и «PayPal».
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.
Двигатели постоянного тока с независимым возбуждением при якорном управлении
На практике скоростью двигателя, меняя ток якоря при неизменном потоке возбуждения, управляют двумя способами. Первый способ связан с изменением сопротивления добавочного резистора (реостата), включаемого последовательно в якорную цепь. Источник напряжения, питающего якорную цепь, имеет фиксированное значение. Этот способ довольно широко распространен для управления скоростью двигателей большой мощности (например, в электрическом транспорте). Второй способ связан с использованием регулируемого источника напряжения, питающего якорную цепь. Этот способ в основном используется для управления микромашинами автоматических систем.
Рассмотрение обоих способов начнем с описания динамики двигателя постоянного тока при якорном управлении, схема которого показана на
Рис. 3.14. Схема двигателя с независимым возбуждением
Необходимо найти математическое описание работы двигателя как
функционального элемента системы управления. При этом выходной величиной должна являться угловая скорость вращения вала двигателя со, а вхо- дыми величинами — напряжение управления (прикладывается к якорной цени) 11я и момент сопротивления нагрузки на валу двигателя Мн. Обмотка возбуждения ОВ подключена к источнику постоянного тока Uc. Считается известным общий момент инерции J, определяемый моментом инерции самого ротора двигателя и нагрузкой на его валу. Обмотка ротора характеризуется активным сопротивлением гя и индуктивностью Ья.
Рассмотрим систему уравнений (3.8), описывающих динамику двигателя:
Первое уравнение динамики двигателя — это закон Кирхгофа для якорной цепи двигателя. В данном уравнении слагаемое ссо — это иротивоЭДС, которая генерируется вращающимся ротором двигателя как генератором. Второе уравнение динамики — момент, развиваемый двигателем. Третье уравнение динамики — баланс моментов на валу двигателя.
В третьем уравнении первое слагаемое — динамический момент,
второе слагаемое (Ма) — собственный момент потерь из-за трения в коллекторном узле и подшипниках, третье — момент нагрузки (Ми). Более полно динамический момент можно определить с использованием понятия «кинетическая энергия вращающегося тела». Это понятие позволяет определить динамический момент как момент, связанный с ускоренным вращением тела. В самом деле, кинетическая энергия вращающегося тела –
Производная этой энергии определяет динамическую мощность
На практике в системах управления изменяющийся момент инерции нагрузки J встречается не так часто, поэтому в дальнейшем для сокращения записей динамический момент будем записывать в виде
Момент нагрузки на валу двигателя Мн — статический, разной природы (в том числе и момент сил сухого трения, вязкого трения и т.д.). При неизменном знаке скорости вращения ротора двигателя со этот момент в большинстве случаев удается описать аналитически.
Уравнения статики для двигателя получаются из системы (3.8) путем приравнивания нулю слагаемых с производными переменных:
Используя формулы (3.9), получаем статическую зависимость между входными параметрами двигателя и частотой вращения его ротора:
Полученное соотношение (3.10) позволяет построить механические (нагрузочные) и регулировочные статические характеристики двигателя, показанные на рис. 3.15.
Рис. 3.15. Статические характеристики двигателя:
а — механическая (нагрузочная); 6 — регулировочная
На этих характеристиках t/H0M — номинальное напряжение на якоре двигателя, скорость холостого хода сохх = K.lRUllOM – KXiMa, пусковой момент MIIVCK =
Линейность статических характеристик является основным достоинством двигателя постоянного тока с независимым возбуждением и с управлением по якорной цени.
Управление частотой вращения ротора двигателя путем введения в якорную цепь добавочных резисторов или реостата широко используется в электрическом транспорте. Такое управление базируется на увеличении крутизны наклона механической характеристики с увеличением сопротивления в цепи якоря. На рис. 3.16 приведена схема двигателя с тремя добавочными резисторами. В положении 1 верхнего переключателя в цени якоря будет максимальное значения сопротивления в виде суммы сопротивлений трех добавочных резисторов, в положении 4 все добавочные резисторы закорочены.
Рис. 3.16. Схема двигателя с тремя добавочными резисторами:
Rgi — добавочный резистор
Рассмотрим пусковой режим двигателя. Для плавного включения (запуска) двигателя и ограничения пускового тока применяют реостатное включение (реостатный пуск). Согласно формулам (3.9) пусковой ток /1IVCK при наличии добавочных резисторов и со = 0 оценивается как
Пусковой режим двигателя показан на рис. 3.17. Здесь представлены четыре механические характеристики двигателя для разных положений переключателя на схеме рис. 3.16. В положении 1 все дополнительные резисто-
Рис. 3.17. Пусковой режим двигателя
ры введены, и разгон идет по прямой 1 до скорости со,. При этом пусковой ток и момент не превышают заданных величин.
Далее переключатель переводят в положение 2. При этом шунтируется добавочный резистор с номером 3. Происходит увеличение скорости до значения со., (по статической характеристике 2).
Затем переключатель переводят в положение 3. Разгоняют двигатель до скорости со3 и т.д., пока не будут зашунтированы все добавочные резисторы. При этом ток в цепи якоря не превысит предельно допустимого значения
При управлении скоростью двигателя путем изменения величины сопротивления якорной цепи определяют тормозной режим как режим ограничения скорости при различных действующих моментах нагрузки и их знаках. Выделяют следующие тормозные режимы:
- 1) рекуперативное торможение;
- 2) торможение противовключением;
- 3) динамическое торможение.
Рекуперативное торможение поясняется рис. 3.18. Здесь изменение величины и знака момента нагрузки с Мщ на МН2 не приводит к неограниченному росту скорости, так как двигатель переходит в генераторный режим и начинает отдавать энергию в сеть. При этом появляется новая точка равновесия при содв = со2.
Рис. 3.18. Режим рекуперативного торможения
В уравнении якорной цепи напряжение противоЭДС становится больше напряжения, подводимого к якорю, и ток якоря поменяет свое направление, так как
В режиме «противовключения» изменение величины и знака скорости с со, на со2 при фиксированном внешнем моменте происходит за счет введения в цепь якоря добавочного резистора, как показано на рис. 3.19.
Режим динамического торможения поясняется рис. 3.20.
Рис. 3.19. Режим «противовключения»
Рис. 3.20. Режим динамического торможения:
а — электрическая схема; б — механические характеристики
В положении 1 переключателя, показанного на рис. 3.20, осуществляется нормальный режим работы двигателя от источника ?/>1. В соответствии с механической характеристикой, определяемой соотношением 11я = r>lI + coo, скорость вращения ротора будет cov В положении 2 переключателя осуществляется режим динамического торможения (цепь якоря закорачивается). В этом случае 0 = rj + ссо, и ротор двигателя будет вращаться в противоположную сторону со скоростью со2.
Основные уравнения двигателя постоянного тока (ДПТ)
В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.
В результате взаимодействия Iя тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.
Противо ЭДС двигателя Eя
При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС Eя направленная навстречу Iя. Поэтому эта ЭДС называется противо ЭДС и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.
Ce — постоянный коэффициент определяемой конструкцией двигателя.
Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.
где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :
- обмотки якоря
- добавочных полюсов
- обмотки возбуждения (для двигателей с последовательным возбуждением)
Ток якоря Iя
Выразим из формулы 2 ток якоря.
Частота вращения якоря
Из формул 1 и 2 выведем формулу для частоты вращения якоря.
Электромагнитная мощность двигателя
Электромагнитный момент
где: ω = 2*π*f — угловая скорость вращения якоря, Cм — постоянный коэффициент двигателя (включает в себя конструктивные особенности данного двигателя)
Момент на валу двигателя, т.е. полезный момент, где М0 момент холостого хода;
Электроника для всех
Блог о электронике
Двигатель постоянного тока. Характеристики и регулирование
После предыдущего поста о мотор-редукторе мне пришло несколько вопросов по регулированию двигателя постоянного тока. Так что пора написать очередной пост 🙂
Двигатель постоянного тока (ДПТ) это один из самых привычных и понятных электродвигателей, он изучается даже в школе, на физике. Он используется практически везде, где нужен малогабаритный моторчик, а также не спешит сдавать своих позиций и там, где мощность измеряется десятками киловатт. О нем и поговорим.
▌Конструктив и базовый принцип
Не буду тут особо распинаться, покажу картинку из википедии и укажу ряд основных узлов. Все остальное вы и так знаете и трогали своими руками.
1. Статор состоит из источника магнитного поля. Далеко не всегда это постоянный магнит, более того, постоянный магнит это скорей исключение, чем правило. Обычно все же это обмотка возбуждения. По крайней мере на всем, что больше кулака по размерам.
Работает все очень и очень просто. Обмотка якоря отталкивается от магнитного поля статора силой Ампера и совершает пол оборота, стремясь вывести эту силу на ноль и таки вывела бы если бы не коллектор, который ловко всех обламывает переключает полярность катушки и сила вновь становится максимальной. И так по кругу. Т.е. коллектор служит механическим инвертором напряжения в якоре. Запомните этот момент, он нам еще пригодится 🙂
Обычно в мелких моторчиках всего два полюса обмотки возбуждения (одна пара) и трехзубцовый якорь. Три зуба это минимум для запуска из любого положения, но чем больше зубцов тем более эффективно используется обмотка, меньше токи и более плавный момент, т.к сила является проекцией на угол, а активный участок обмотки проворачивается на меньший угол
▌Происходящие в двигателе процессы
Думаю многие из вас кто баловался с движками могли заметить, что у них есть ярко выраженный пусковой ток, когда мотор на старте может рвануть стрелку амперметра, например, до ампера, а после разгона ток падает до каких-нибудь 200мА.
Почему это происходит? Это работает противоэдс. Когда двигатель стоит, то ток который через него может пройти зависит только лишь от двух параметров — напряжения питания и сопротивления якорной обмотки. Так что предельный ток который может развить движок и на который следует рассчитывать схему узнать несложно. Достаточно замерить сопротивление обмотки двигателя и поделить на это значение напряжение питания. Просто по закону Ома. Это и будет максимальный ток, пусковой.
Но по мере разгона начинается забавная вещь, обмотка якоря движется поперек магнитного поля статора и в ней наводится ЭДС, как в генераторе, но направлена она встречно той, что вращает двигатель. И в результате, ток через якорь резко снижается, тем больше, чем выше скорость.
А если движок дополнительно еще подкручивать по ходу, то противоэдс будет выше питания и движок начнет вкачивать энергию в систему, став генератором.
▌Немного формул
Не буду грузить никого выводами, их найдете сами если захотите. Чтобы было поменьше матана рекомендую найти учебник по электроприводу для средних учебных заведений и годом выпуска подревней. От 50х-60х годов самое то 🙂 Там и картинки винтажные и расписано для вчерашнего выпускника сельской семилетки. Много букв и никакого грузилова, все четко и по делу.
Самая главная формула коллекторного двигателя постоянного тока:
- U — напряжение подаваемое на якорь
- Rя — сопротивление якорной цепи. Обычно за этот символ считают только сопротивление обмотки, хотя можно снаружи навесить резистор какой и он к ней приплюсуется. Тогда пишут как (Rя+Rд)
- Iя — ток в якорной цепи. Тот самый который замеряется амперметром при попытке измерять потребление движка 🙂
- Е — это противоэдс или ЭДС генератора, в генераторном режиме. Она зависит от конструкции двигателя, оборотов и описывается вот такой вот простой формулой
- Ce — одна из конструктивных констант. Они зависят от конструкции двигателя, числа полюсов, количества витков, толщин зазоров между якорем и статором. Нам она не особо нужна, при желании ее можно вычислить экспериментально. Главное, что она константа и на форму кривых не влияет 🙂
- Ф — поток возбуждения. Т.е. сила магнитного поля статора. В мелких моторчиках, где оно задается постоянным магнитом это тоже константа. Но бывает под возбуждение выведена отдельная обмотка и тогда мы можем ее менять.
- n — обороты якоря.
Ну и зависимость момента от тока и потока:
См — конструктивная констатнта.
Вот тут стоит обратить внимание, что зависимость момента от тока совершенно прямая. Т.е. просто замеряя ток, при неизменном потоке возбуждения, мы можем совершенно точно узнать величину момента. Это может быть важно, например, чтобы не сломать привод, когда двигло может развить такое усилие, что легко поломает то, что оно там вращает. Особенно с редуктором.
Ну и из этого же следует, что момент у машины постоянного тока зависит только от способности источника снабжать его током. Так что идеальный нерушимый сверхпроводящий движок вам на раз лом в узел завяжет, пусть даже он сам с ноготок будет. Только энергию подавай.
А теперь смешаем все это в кучу и получим зависимость оборотов от момента — механическую характеристику двигателя.
Если ее построить, то будет нечто следующее:
n0 — это обороты идеального холостого хода сферического двигателя в вакууме. Т.е. когда наш движок ну ваще халявит, момент равен нулю. Ток потребления тоже, естественно, ноль. Т.к. противоэдс равна напряжению. Чисто теоретический вариант. А вторая точка строится уже с каким-либо моментом на валу. Получается прямая зависимость оборотов от момента. А наклон характеристики определяется сопротивлением якорной цепи. Если никаких добавочных резисторов там нет, то это зовут естественной характеристикой.
Обороты идеального холостого хода зависят от напряжения и потока. Больше ни от чего. А если поток константа (постоянный магнит), то только от напряжения. Снижая напряжение вся наша характеристика параллельно смещается вниз. Уменьшили напряжение в два раза — скорость упала в два раза.
Если есть возможность менять поток возбуждения, то можно поднимать скорость выше номинальной. Тут зависимость обратная. Ослабляем поток — двигатель разгоняется, но либо падает момент, либо ему надо жрать больше тока.
Иной двигатель со снятием возбуждения может и в разнос пойти. Помнится сдавал я затянувшийся курсач по электроприводу, уже хрен знает спустя сколько времени после сессии. Вломы мне его делать было, ага 🙂 Ну и сидел в лаборатории, ждал препода. А там какие то балбесы, на курс ниже, лабу делали. Крутили движок вхолостую, а возбуждение к стенду приверчено было на соплях и слетело с клеммы. Движок в разнос пошел. У нас в лаборатории ЭПА ЮУРГУ все серьезно было, машины стояли нешуточные, по десятку киловатт и под сотню другую кг каждый. Все на суровом напряжении в 380 вольт.
В общем, когда эта дура взревела как монстр и стала рваться с креплений, я только и успел крикнуть, что все нахер от машины, вырубай к черту. Не успели, двигло сорвало с креплений, обмотка повылетала с пазов и движку пришел кирдык. Ладно никого не покалечило.
Впрочем, лабы привода это то еще развлечение было. У нас там и горело и взрывалось. Там я приобрел замечательные навыки чинить что угодно, чем угодно в сжатые сроки. В среднем, каждый успел по разу убить стенд наглухо, а лаба часто начиналась с починки паяльника, которым чинили осциллограф с помощью которого реанимировали убитый стенд.
Добавляя резисторы в якорную цепь мы можем увеличить наклон, т.е. чем больше грузим тем больше падает скорость.
Метод плох тем, что резисторы в цепи якоря должны быть расчитаны на ток двигателя, т.е. быть мощными и будут греться зря. Ну и момент резко падает, что плохо.
Есть еще двигатели не независимого, а последовательного возбуждения. Это когда обмотка статора включена последовательно якорю. Не каждый двигатель так можно включить, обмотка возбуждения должна выдерживать ток якоря. Но у них возникает одно интересное свойство. При пуске возникает большой пусковой ток и этот пусковой ток является же током возбуждения, обеспечивая огромный пусковой момент. Механическая характеристика напоминает гиперболу с максимумом в районе нулевых оборотов.
А дальше, по мере разгона, момент падает, а обороты наоборот растут. И если нагрузку убрать с вала, то движок сразу же уходит в разнос. Такие движки ставят на тягловый привод в основном. По крайней мере ставили раньше, до развития силовой электроники. С места эта хрень рвет так, что все стритсракеры нервно закуривают.
▌Режимы работы двигателя постоянного тока
Направление вращения движка зависит от направления тока якоря или направления потока возбуждения. Так что если взять коллекторный двигатель и подключить обмотку возбуждения параллельно якорю, то он будет прекрасно вращаться и на переменном токе (универсальные двигатели, их в кухонную технику часто ставят). Т.к. ток будет одновременно меняться и в якоре и в возбуждении. Момент правда будет пульсирующим, но это мелочи. А для реверса там надо будет поменять полярность включения якоря или возбуждения.
Если нарисовать механическую характеристику в четырех квадрантах, то у нас будет нечто похожее на это:
Вот, например, характеристика 1 на I участке у нас машина работает как двигатель. Нагрузка растет и в определенный момент двигатель останавливается и начинает вращаться в обратную сторону, т.е. нагрузка обращает его вспять. Это тормозной режим, противовключение. Режим очень тяжелый, двигло греется просто зверски, но для торможения очень эффективный. Если же момент на валу сменит направление и пойдет вращать навстречу движку, то мотор сразу же выйдет на генерацию (IV участок).
Характеристика 2 это то же самое, только с обратной полярностью питающего напряжения двигателя.
А характеристика 3 это динамическое торможение. Оно же реостатное. Т.е. когда мы берем и просто коротим наш двигатель на резистор или сам на себя. Можете сами проверить, возьмите любой моторчик и покрутите его, а потом закоротите ему якорь и покрутите снова. На валу будет ощутимое усилие, тем больше, чем качественнее движок.
Кстати, драйвера двигателей вроде L293 или L297 имеют возможность включить реостатное торможение, подачей обоих ключей вверх или вниз. При этом якорь коротится через драйвер на шину земли или питания.
▌Бесколлекторные двигатели постоянного тока
Коллекторный движок он очень хорош. Он чертовски легко и гибко регулируется. Можно повышать обороты, понижать, механическая характеристика жесткая, момент он держит на ура. Зависимость прямая. Ну сказка, а не мотор. Если бы не одна ложка говна во всей этой вкусняшке — коллектор.
Это сложный, дорогой и очень ненадежный узел. Он искрит, создает помехи, забивается проводящей пылью от щеток. А при большой нагрузке может полыхнуть, образовав круговой огонь и тогда все, капец движку. Закоротит все дугой наглухо.
Но что такое коллектор вообще? Нафига он нужен? Выше я говорил, что коллектор это механический инвертор. Его задача переключать напряжение якоря туда сюда, подставляя обмотку под поток.
А на дворе то уже 21 век и дешевые и мощные полупроводники сейчас на каждом шагу. Так зачем нам нужен механический инвертор если мы можем сделать его электронным? Правильно, незачем! Так что берем и заменяем коллектор силовыми ключами, а еще добавляем датчики положения ротора, чтобы знать в какой момент переключать обмотки.
А для пущего удобства выворачиваем двигатель наизнанку — гораздо проще вращать магнит или простенькую обмотку возбуждения, чем якорь со всей этой тряхомудией на борту. В качестве ротора тут выступает либо мощный постоянный магнит, либо обмотка питаемая с контактных колец. Что хоть и смахивает на коллектор, но не в пример надежней его.
И получаем что? Правильно! Бесщеточный двигатель постоянного тока aka BLDC. Все те же няшные и удобные характеристики ДПТ, но без этого мерзкого коллектора. И не надо путать BLDC с синхронными двигателями. Это совсем разные машины и разным принципом действия и управления, хотя конструктивно они ОЧЕНЬ схожи и тот же синхронник вполне может работать как BLDC, добавить ему только датчиков да систему управления. Но это уже совсем другая история.
Спасибо. Вы потрясающие! Всего за месяц мы собрали нужную сумму в 500000 на хоккейную коробку для детского дома Аистенок. Из которых 125000+ было от вас, читателей EasyElectronics. Были даже переводы на 25000+ и просто поток платежей на 251 рубль. Это невероятно круто. Сейчас идет заключение договора и подготовка к строительству!
А я встрял на три года, как минимум, ежемесячной пахоты над статьями :)))))))))))) Спасибо вам за такой мощный пинок.
106 thoughts on “Двигатель постоянного тока. Характеристики и регулирование”
Я очень ждал статей про двигатели. Специалист по электроприводу научил нас как работать с AVR, а про моторчики нифига не написал. Еще будут статьи на эту тему?
Мне порвала шаблон обратная зависимость между магнитным потоком возбуждения и скоростью вращения. По формуле я вижу, что это так, но понять не могу. Особенно удивил уход вразнос при отключении обмотки возбуждения. Если нет магнитного потока статора, то от чего «отталкивается» ротор? Как двигатель может вообще работать в таком режиме?
Отталкивается от остаточного возбуждения. Намагниченности полюсов. Но ты обрати внимание, что момент там тоже уходит в ноль. Так что либо отталкиваться бешеным током, либо снижать момент до нуля.
Да, про момент я заметил. Понятно, что разгон будет происходить только без нагрузки и только, если источник питания способен выдать нужный ток.
Статьи может быть будут еще, не скажу. Я, на самом деле, за 7 лет изрядно эту тему подзабыл за неиспользованием. Особенно касаемо всякого продвинутого регулирования и динамики привода. Так что не такой я уж специалист по приводу 🙂
Можно и без продвинутого регулирования для начала. Меня совсем базовые вещи интересуют. Типа, какие бывают способы управления и, соответственно, какие драйверы их реализуют, чем отличаются, плюсы, минусы, подводные камни. Для коллекторных и бесколлекторных двигателей постоянного тока. На что следует обратить внимание при разработке схем с электродвигателями, чтобы не сжечь все нафиг. В общем, такая статья в раздел «Начинающим». Но и более емкие статьи я бы с удовольствием прочитал.
Ну базовые вещи я уже описал 🙂 А дальше додумываешь сам. Напряжение можно рулить ШИМом. Можно обратную связь по току-моменту замутить. Обращаться с ними также как с любой индуктивностью, о чем я тоже уже писал. Не расписывал только H-мосты самодельные. Но тут тема такая, на всех не угодишь, слишком они разные бывают.
Он используется практически везде, где нужен малогабаритный моторчик
То-то все авиамодели, квадкоптеры и прочая летучая нечисть — на бесколлекторниках, кроме совсем позорного Китая за $100.
Я БУДУ ЧИТАТЬ ДО КОНЦА, ПРЕЖДЕ ЧЕМ КОММЕНТИРОВАТЬ. Я БУДУ ЧИТАТЬ ДО КОНЦА, ПРЕЖДЕ ЧЕМ КОММЕНТИРОВАТЬ. Я БУДУ ЧИТАТЬ ДО КОНЦА, ПРЕЖДЕ ЧЕМ КОММЕНТИРОВАТЬ. Я БУДУ ЧИТАТЬ ДО КОНЦА, ПРЕЖДЕ ЧЕМ КОММЕНТИРОВАТЬ. Я БУДУ ЧИТАТЬ ДО КОНЦА, ПРЕЖДЕ ЧЕМ КОММЕНТИРОВАТЬ.
Модели — не игрушки. Совсем другие требования, и другие цены.
А в дешевых игрушках, — как правило, дешевые коллекторные движки с проволочными щетками. Да и в самых дешевых моделях вертолета с соосными винтами (по сути, те же игрушки) — тоже коллекторные.
Имеется двигатель постоянного тока мощностью 60Вт, напряжение питания 48В. Как его можно переделать чтобы питать от 12В не потеряв в мощности?
[spoiler title=”источники:”]
http://electrikam.com/osnovnye-uravneniya-dvigatelya-postoyannogo-toka-dpt/
[/spoiler]
ЭЛЕКТРОДВИЖУЩАЯ СИЛА ОБМОТКИ ЯКОРЯ
 При вращении якоря генератора или двигателя в магнитном поле в его обмотке будет наводиться э. д. с.
При вращении якоря генератора или двигателя в магнитном поле в его обмотке будет наводиться э. д. с.
Магнитная индукция в различных точках на окружности якоря имеет разные значения, следовательно, различны и э. д. с, наводимые в отдельных проводах обмотки якоря. Электродвижущая сила машины, равная сумме э. д. с, наводимых в проводах любой из параллельных ветвей обмотки якоря, может быть определена через среднее значение э. д. с. провода, умноженное на число проводов ветви.
Если магнитный поток одного полюса — Ф, то при числе полюсов машины 2р и поверхности якоря Sсреднее значение магнитной индукции на поверхности якоря
Вср = (Ф • 2р)/S = (Ф • 2р)/πdl
где d — диаметр якоря, а l — его длина.
Среднее значение э. д. с. в каждом из проводов при
скорости вращения якоря п об/мин
Eср = Всрlυ((Ф • 2р)/πdl) l ((πdn)/ 60) = Ф2р(n/60)
Обозначим число проводов обмотки якоря N, а число параллельных ветвей ее — 2a. Тогда в каждой параллельной ветви обмотки якоря будет N/a последовательно соединенных проводов. Электродвижущая сила, наведенная в каждое параллельной ветви обмотки якоря, а следовательно, н э. д. с. машины
E = Ecp = 2p(n/60)(N/2a)Ф = (p/a)(n/60)NФ
Обозначив постоянную для данной машины величину N(p/(a•60)) через сЕ , получим :
Е = сЕФп.
Таким образом, э. д. с. машины пропорциональна магнитному потоку и скорости вращения ее якоря.
Рис. 8-12. Поперечная реакция якоря. Рис. 8-13. Перераспределение магнитной индукции от реакция якоря.
МОМЕНТ НА ВАЛУ МАШИНЫ
Независимо от того, в каком режиме работает машина — генератором или электродвигателем, на каждый провод якоря действует электромагнитная сила
Fпр = BcplI = (Ф2р/πdl)lI
где Bcp — среднее значение магнитное индукции; d и I — диаметр и длина якоря; Ф2р — полный поток многополюсной машины;
I=Iя/2а — ток одной параллельной ветви, т. е. одного провода.
Полная сила, действующая на N проводов якоря по касательной к окружности якоря.
Если машина работает генератором, момент будет тормозной (Мт); при работе ее электродвигателем момент будет вращающим (М в). Момент равен произведению тока якоря и потока машины.
МЕХАНИЧЕСКАЯ МОЩНОСТЬ МАШИНЫ ПОСТОЯННОГО ТОКА
Электрическая машина преобразует механическую энергию в электрическую или электрическую в механическую. При этом механическая мощность
Рм = Fυ
Так как F = 2M/d, a υ = ω(d/2) то
Рм = (2M/d)ω(d/2) = Mω
Подставляя сюда выражение для момента, получаем:
Рм = EIя
Таким образом, , развиваемая якорем машины механическая мощность равна ее электрической мощности, т.е. произведению электродвижущей силы и тока якоря. При работе машины генератором мощность EIя больше, чем мощность UIя, отдаваемая потребителю, так как Е > U. Когда машина работает электродвигателем и, значит, Е < U, тогда мощность EIя меньше мощности UIя, подаваемой из сети. Эта разница мощностей численно равна мощности тепловых потерь I2rя в обмотке якоря.
РЕАКЦИЯ ЯКОРЯ
Когда машина работает генератором вхолостую, т. е. при Iя = 0, магнитный поток возбуждения ФB, создаваем мый н. с. FB, существует один и проходит от северного полюса к южному через якорь (рис. 8-12). В этом случае индукция Вδ в воздушном зазоре, в пределах полюсного наконечника, остается практически постоянной.
Если генератор нагружен, т. е. по обмотке якоря проходит ток, якорь сам становится электромагнитом п его и. с. Fя создает второй поток — поперечный поток
якоря Фя. Он замыкается через воздушный зазор машины и поперек ее полюсов, уменьшая индукцию в воздушном зазоре Вδ под одним краем полюса (левым у северного и правым у южного и увеличивая Вδпод другим краем (правым у северного и левым у южного) (рис. 8-13). По отношению направлению вращения якоря можно сказать, что набегающий край полюса размагничивается, а сбегающий — намагничивается.
Суммарный поток машины Ф смещен в направлении вращения якоря; в ту же сторону смещена нейтраль машины, называемая в данном случае физической нейтралью (рис. 8-13). В результате поток Ф при нагрузке несколько уменьшается, так как вследствие насыщения стати размагничивание на набегающем краю полюса оказывается большим, чем намагничивание на сбегающем. Влияние н. с. якоря на величину магнитного потока машины при нагрузке называется реакцией якоря.
В современных машинах постоянного тока, нормального исполнения уменьшение магнитного потока под влиянием реакции якоря незначительно.
Главная опасность этого явления, как будет показано ниже, заключается в том, что магнитная индукция в воз-душном зазоре под краем полюса может сильно возрастать.
Если машина работает электродвигателем, то при направления тока в якоре, указанном на рис. 8-12, якорь будет вращаться в обратную сторону. Следовательно, реакция якоря будет сдвигать поток Фи физическую нейтраль против хода якоря.
Статья на тему Электродвижущая сила обмотки якоря