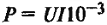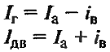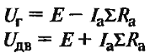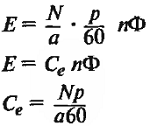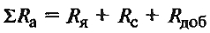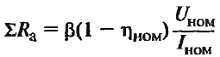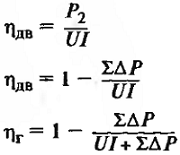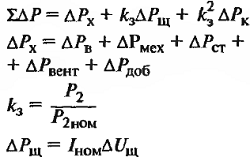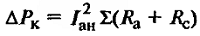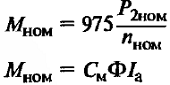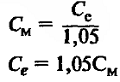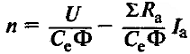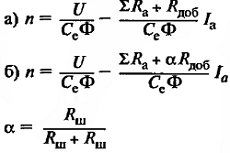В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.
В результате взаимодействия Iя тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.
Противо ЭДС двигателя Eя
При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС Eя направленная навстречу Iя. Поэтому эта ЭДС называется противо ЭДС и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.
Eя = Се * Ф * n (1)
Ce — постоянный коэффициент определяемой конструкцией двигателя.
Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.
U = Eя + Iя * ∑R (2)
где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :
- обмотки якоря
- добавочных полюсов
- обмотки возбуждения (для двигателей с последовательным возбуждением)
Ток якоря Iя
Выразим из формулы 2 ток якоря.
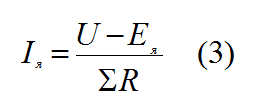
Частота вращения якоря
Из формул 1 и 2 выведем формулу для частоты вращения якоря.

Электромагнитная мощность двигателя
Pэм = Ея Iя (5)
Электромагнитный момент

где: ω = 2*π*f — угловая скорость вращения якоря, Cм — постоянный коэффициент двигателя (включает в себя конструктивные особенности данного двигателя)

Момент на валу двигателя, т.е. полезный момент, где М0 момент холостого хода;
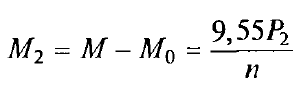
Р2 — полезная мощность двигателя
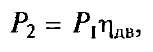
Рассмотрим
двигатель независимого (параллельного)
возбуждения с управлением за счет
изменения напряжения на якоре. Для того,
чтобы получить передаточную функцию
необходимо составить дифференциальное
уравнение, описывающее электрическую
цепь двигателя в переходном процессе
и дифференциальное уравнение движения
вала двигателя (механика процесса). В
переходном процессе обмотка якоря имеет
две составляющие сопротивления: активную
(обозначим ее здесь Rя)
и реактивную, которая будет определяться
величиной индуктивности обмотки Lя.
Подводимое напряжение U
уравновешивается ЭДС самоиндукции
якоря (![]()
), падением напряжения на активном
сопротивлении якоря (iяRя)
и противо–эдс
eя,
возникающей
в якоре при вращении, тогда будет
справедливо выражение вида
![]() , (6.1)
, (6.1)
где
Lя
– индуктивность якорной обмотки.
Для противо-эдс с большой степенью точности можно записать
ея=kэм. (6.2)
где
kэм=сеФ
– электромагнитный коэффициент
Дифференциальное
уравнение движения вала двигателя имеет
вид
![]() , (6.3)
, (6.3)
где
J
момент
инерции вращающихся частей, приведенный
к валу двигателя,
Мс
статический момент или момент сопротивления
(в общем случае равен сумме нагрузочного
момента и момента трения двигателя).
На
первом этапе будем считать , что
статическим моментом можно пренебречь
(т.е. пусть Мс=0),
тогда получим
![]() , (6.4)
, (6.4)
где
kэм=смФ
– электромагнитный коэффициент.
Величина тока якоря тогда, находится по формуле
![]() . (6.5)
. (6.5)
Подставим
выражения 5.3 и 5.6 в исходное дифференциальное
уравнение электрической цепи и получим
![]() . (6.6)
. (6.6)
Теперь
обе части уравнения 5.7 разделим на kэм,
а коэффициент
при второй производной разделим и
умножим на Rя.
Уравнение примет вид
 . (6.7)
. (6.7)
Введем
следующие обозначения:
![]() –
–
электромеханическая постоянная времени
двигателя,
![]() –
–
электромагнитная постоянная времени
якоря двигателя.
Теперь,
с учетом принятых обозначений можем
записать
![]() . (6.8)
. (6.8)
Для
получения передаточной функции нужно
данное уравнение записать относительно
изображений по Лапласу входного
напряжения и угловой скорости на выходе
двигателя
![]() . (6.9)
. (6.9)
Так
как передаточная функция представляет
собой отношение изображений выходной
и входной величин, то можно записать
![]() , (6.10)
, (6.10)
где
kдв=1/kэм
– коэффициент
передачи двигателя.
В
зависимости от соотношения величин
постоянных времени двигателя, вид его
передаточной функции можно изменять.
Так, если 4Тя>Тм,
что встречается
достаточно редко, двигатель описывается
колебательным звеном. Чаще всего 4Тя<Тм
и передаточную функцию можно представить
в виде
![]() . (6.11)
. (6.11)
При
анализе систем автоматического управления
с двигателем постоянного тока часто
пренебрегают электромагнитной постоянной,
ввиду ее малости (Тя0),
по сравнению с другими постоянными
времени системы, и используют передаточную
функцию вида
![]() . (6.12)
. (6.12)
Кроме
того, если выходной величиной является
не угловая скорость, а угол поворота
вала двигателя, которые, как известно,
связаны соотношением![]() ,
,
где(p)-
изображение
угла поворота вала двигателя, передаточная
функция принимает вид
![]() . (6.13)
. (6.13)
При
решении многих технических задач
оказывается возможным пренебречь
временем разгона (переходным процессом)
по сравнению с полным временем вращения
вала, и тогда двигатель может быть описан
идеальным интегрирующим звеном
![]() . (6.14)
. (6.14)
Приведенные
передаточные функции получены при
условии равенства нулю статического
момента. Можно показать, что они
справедливы для М=const,
если характеристики двигателя считать
линейными. Величина Мс
не влияет
на постоянные времени и коэффициент
передачи.
Для
практических расчетов параметров
передаточной функции двигателя, например,
при синтезе систем управления, могут
быть полезны следующие формулы:
![]() (6.15)
(6.15)
где
Uном
номинальное напряжение на якоре,
nном
номинальная частота вращения
[обороты/мин](задается в паспорте),
Iяном–
номинальный
ток якоря,
сх
– эмпирический
коэффициент(0,4 – для машин без
компенсационной обмотки, 0,1
с компенсационной обмоткой).

(6.16)
или
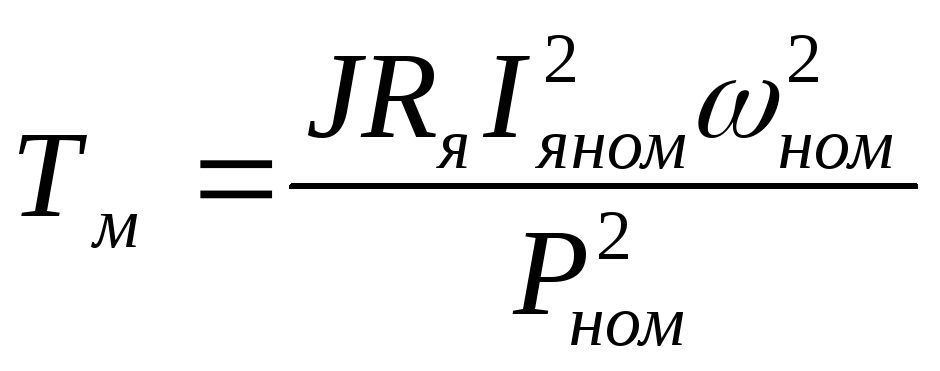 . (6.17)
. (6.17)
Необходимо
также учитывать, что при введении
добавочного сопротивления в цепь якоря
постоянные времени изменяются, причем
Тя
– уменьшается, а Тм
– растет.
Если двигатель рассматривается совместно
с механической нагрузкой и редуктором
на его валу, то при расчетах Тм
нужно
учитывать момент инерции редуктора и
нагрузки приведенный к валу двигателя.
Для
того, чтобы учесть влияние статического
момента нагрузки Мс,
удобнее воспользоваться методом
структурного моделирования, используя
те же базовые выражения 5.1 и 5.3. Считаем,
что Мс=const,
и его можно определить из выражения
![]() , (6.18)
, (6.18)
где
iс
– ток якоря соответствующий статической
нагрузке.
Уравнения
5.1 и 5.3 представим в форме:
![]() , (6.19)
, (6.19)
![]() , (6.20)
, (6.20)
где
kэм=смФ.
Тогда уравнение 5.19
можно записать относительно величины
падения напряжения в якорной цепи
![]() . (6.21)
. (6.21)
В
структурной схеме это может быть отражено
с помощью апериодического звена первого
порядка, на вход которого поступает
разность между напряжением и ЭДС
двигателя, а на выходе имеем падение
напряжения в цепи якоря (Рисунок5.4).Уравнение
5.19 запишем в виде ![]() ,
,
а так как![]() ,
,
то можно его записать относительно ЭДС
в виде
![]() . (6.22)
. (6.22)
На
структурной схеме данное уравнение
будет представлено интегрирующим звеном
с коэффициентом передачи
![]() ,
,
на выходе которого будем иметь напряжение
равное противо-ЭДС двигателя ея,
а на входе разность падения напряжения
на якоре и падения напряжения, определяемого
током статической нагрузки (Рисунок5.4).
Так как на выходе системы нужно иметь
скорость вращения двигателя, то
последовательно подключим безынерционное
звено с коэффициентом передачи
![]() ,
,
гдеkэм=сеФ.
А статический
момент вводится как возмущающее
воздействие через безынерционное звено
с коэффициентом
![]() .
.

![]()
Для составления
математических моделей двигателей
смешанного и тем более последовательного
возбуждения, которые обладают существенно
нелинейными характеристиками, используют
приближенные методы исследований,
которые рассматриваются в теории
автоматического управления, или
специально разработанные в теории
электропривода графоаналитические
методы.
Соседние файлы в папке лекции
- #
- #
- #
- #
- #
- #
- #
Глава девятая
МАШИНЫ ПОСТОЯННОГО ТОКА
Соотношение между напряжением, ЭДС и падением напряжения в сопротивлениях цепи якоря определяется на основании второго закона Кирхгофа, согласно которому (см. рис. 9.22)
(9,18)
U = E + Iя(rя + r) = kеФn + Iя(rя + r).
Будем считать, что у двигателей последовательного и смешанного возбуждения сопротивление rя включает в себя также и сопротивление последовательной обмотки.
Из (9.18)
(9.19)
| I = | U – E | = | U – kеФn | ; |
| rя + r | rя + r |
Как видно, ток якоря зависит не только от напряжения сети и сопротивлений цепи якоря, но и от ЭДС, индуктируемой в обмотке якоря. При работе двигателя вхолостую М = Мс = 0 и, как было показано ранее, Iя = 0. Из (9.19) следует, что ток Iя может быть равен нулю лишь в том случае, когда Е = U. При увеличении нагрузки двигателя ток Iя возрастает, что можно объяснить только уменьшением ЭДС Е. Поскольку у двигателя параллельного возбуждения при увеличении нагрузки магнитный поток не изменяется, а у двигателей последовательного и смешанного возбуждения он увеличивается, уменьшение ЭДС может происходить лишь вследствие снижения частоты вращения двигателей.
Расчетные формулы параметров машин постоянного тока
В таблице 1 представлены расчетные формулы для определения основных параметров машин постоянного тока.
В данной таблице собраны все формулы, которые касаются расчета параметров машин постоянного тока.
Таблица 1 — Расчетные формулы для определения основных параметров машин постоянного тока
| Наименование величин | Формулы | Принятые обозначения |
|---|---|---|
| Мощность, кВт |
|
I – ток машины, А; U – внешнее напряжение, В; |
| Ток генератора и двигателя, А |
|
Iа – ток якоря; Iв – ток параллельной обмотки возбуждения, А; |
| Внешнее напряжение, В |
|
∑Ra – сумма сопротивлений якорной цепи, Ом; Е – ЭДС машины, В; |
| ЭДС, В |
|
N – число проводников обмотки якоря; а – число пар параллельных ветвей в обмотке якоря; р – число пар полюсов; n – скорость вращения, об/мин. |
| Сопротивление якорной цепи, Ом |
|
Ф – магнитный поток пары полюсов, вебер; Rя, Rс, Rдоб. – сопротивления обмотки якоря, последовательной обмотки возбуждения и добавочных полюсов, Ом |
| Ориентировочной значение сопротивления цепи якоря, Ом |
|
Значение коэффициента β двигателей различного типа возбуждения: для независимого и параллельного возбуждения β=0,5; для смешанного β=0,6; для последовательного β=0,75; |
| КПД двигателя и генератора |
|
∑∆Р – суммарные потери в машине, кВт; |
| Суммарные потери, кВт |
|
∆Рх – потери холостого хода машины или постоянные потер, кВт; ∆Рв – потери на возбуждение, кВт; ∆Рмех. – механические потери на трение в подшипниках и о коллектор, кВт; ∆Рст. – магнитные потери в стали якоря, кВт; ∆Рвент. – вентиляционные потери, кВт; ∆Рдоб. – добавочные потери. В некомпенсированных машинах ∆Рдоб. = 1%Рном, в компенсированных 0,5%, кВт; kз – коэффициент загрузки; ∆Uщ = 2 В для графитных щеток; ∆Uщ = 0,6 В для металлографитных; |
| Переменные потери |
|
|
| Номинальный вращающий момент, кГм |
|
См – конструктивная постоянная момента; Ф – магнитный поток, вебер; |
| Расчетные коэффициенты для двигателя параллельного возбуждения |
|
|
| Скоростная характеристика двигателя |
|
|
| Искусственные скоростные характеристики |
|
а) искусственная скоростная характеристика при введении добавочного сопротивления Rдоб. последовательно в цепь якоря; б) искусственная скоростная характеристика двигателя при шунтировании якоря двигателя сопротивлением Rш; α – коэффициент шунтирования. |
Литература:
1. Справочная книга электрика. В.И. Григорьева, 2004 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
КПД генератора, параметры машин постоянного тока, ток генератора, ЭДС
Благодарность:
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding» и «PayPal».
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.
Основные уравнения двигателя постоянного тока (ДПТ)

В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.
В результате взаимодействия Iя тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.
Противо ЭДС двигателя Eя
При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС Eя направленная навстречу Iя. Поэтому эта ЭДС называется противо ЭДС и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.
Ce — постоянный коэффициент определяемой конструкцией двигателя.
Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.
где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :
- обмотки якоря
- добавочных полюсов
- обмотки возбуждения (для двигателей с последовательным возбуждением)
Ток якоря Iя
Выразим из формулы 2 ток якоря.
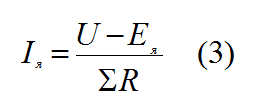
Частота вращения якоря
Из формул 1 и 2 выведем формулу для частоты вращения якоря.

Электромагнитная мощность двигателя
Электромагнитный момент

где: ω = 2*π*f — угловая скорость вращения якоря, Cм — постоянный коэффициент двигателя (включает в себя конструктивные особенности данного двигателя)

Момент на валу двигателя, т.е. полезный момент, где М0 момент холостого хода;
Электрический двигатель постоянного тока
Эра электродвигателей берёт своё начало с 30-х годов XIX века, когда Фарадей на опытах доказал способность вращения проводника, по которому проходит ток, вокруг постоянного магнита. На этом принципе Томасом Девенпортом был сконструирован и испытан первый электродвигатель постоянного тока. Изобретатель установил своё устройство на действующую модель поезда, доказав тем самым работоспособность электромотора.
Практическое применение ДПТ нашёл Б. С. Якоби, установив его на лодке для вращения лопастей. Источником тока учёному послужили 320 гальванических элементов. Несмотря на громоздкость оборудования, лодка могла плыть против течения, транспортируя 12 пассажиров на борту.
Лишь в конце XIX столетия синхронными электродвигателями начали оснащать промышленные машины. Этому способствовало осознание принципа преобразования электродвигателем постоянного тока механической энергии в электричество. То есть, используя электродвигатель в режиме генератора, удалось получать электроэнергию, производство которой оказалось существенно дешевле от затрат на выпуск гальванических элементов. С тех пор электродвигатели совершенствовались и стали завоёвывать прочные позиции во всех сферах нашей жизнедеятельности.
Устройство и описание ДПТ
Конструктивно электродвигатель постоянного тока устроен по принципу взаимодействия магнитных полей.
Самый простой ДПТ состоит из следующих основных узлов:
- Двух обмоток с сердечниками, соединенных последовательно. Данная конструкция расположена на валу и образует узел, называемый ротором или якорем.
- Двух постоянных магнитов, повёрнутых разными полюсами к обмоткам. Они выполняют задачу неподвижного статора.
- Коллектора – двух полукруглых, изолированных пластин, расположенных на валу ДПТ.
- Двух неподвижных контактных элементов (щёток), предназначенных для передачи электротока через коллектор до обмоток возбуждения.
 Рисунок 1. Схематическое изображение простейшего электродвигателя постоянного тока.
Рисунок 1. Схематическое изображение простейшего электродвигателя постоянного тока.
Рассмотренный выше пример – это скорее рабочая модель коллекторного электродвигателя. На практике такие устройства не применяются. Дело в том, что у такого моторчика слишком маленькая мощность. Он работает рывками, особенно при подключении механической нагрузки.
Статор (индуктор)
В моделях мощных современных двигателях постоянного тока используются статоры, они же индукторы, в виде катушек, намотанных на сердечники. При замыкании электрической цепи происходит образование линий магнитного поля, под действием возникающей электромагнитной индукции.
Для запитывания обмоток индуктора ДПТ могут использоваться различные схемы подключения:
- с независимым возбуждением обмоток;
- соединение параллельно обмоткам якоря;
- варианты с последовательным возбуждением катушек ротора и статора;
- смешанное подсоединение.
Схемы подключения наглядно видно на рисунке 2.
 Рисунок 2. Схемы подключения обмоток статора ДПТ
Рисунок 2. Схемы подключения обмоток статора ДПТ
У каждого способа есть свои преимущества и недостатки. Часто способ подключения диктуется условиями, в которых предстоит эксплуатация электродвигателя постоянного тока. В частности, если требуется уменьшить искрения коллектора, то применяют параллельное соединение. Для увеличения крутящего момента лучше использовать схемы с последовательным подключением обмоток. Наличие высоких пусковых токов создаёт повышенную электрическую мощность в момент запуска мотора. Данный способ подходит для двигателя постоянного тока, интенсивно работающего в кратковременном режиме, например для стартера. В таком режиме работы детали электродвигателя не успевают перегреться, поэтому износ их незначителен.
Ротор (якорь)
В рассмотренном выше примере примитивного электромотора ротор состоит из двухзубцового якоря на одной обмотке, с чётко выраженными полюсами. Конструкция обеспечивает вращение вала электромотора.
В описанном устройстве есть существенный недостаток: при остановке вращения якоря, его обмотки занимают устойчивое. Для повторного запуска электродвигателя требуется сообщить валу некий крутящий момент.
Этого серьёзного недостатка лишён якорь с тремя и большим количеством обмоток. На рисунке 3 показано изображение трёхобмоточного ротора, а на рис. 4 – якорь с большим количеством обмоток.
 Рисунок 3. Ротор с тремя обмотками
Рисунок 3. Ротор с тремя обмотками  Рисунок 4. Якорь со многими обмотками
Рисунок 4. Якорь со многими обмотками
Подобные роторы довольно часто встречаются в небольших маломощных электродвигателях.
Для построения мощных тяговых электродвигателей и с целью повышения стабильности частоты вращения используют якоря с большим количеством обмоток. Схема такого двигателя показана на рисунке 5.
 Рисунок 5. Схема электромотора с многообмоточным якорем
Рисунок 5. Схема электромотора с многообмоточным якорем
Коллектор
Если на выводы обмоток ротора подключить источник постоянного тока, якорь сделает пол-оборота и остановится. Для продолжения процесса вращения необходимо поменять полярность подводимого тока. Устройство, выполняющее функции переключения тока с целью изменения полярности на выводах обмоток, называется коллектором.
Самый простой коллектор состоит из двух, изолированных полукруглых пластин. Каждая из них в определённый момент контактирует со щёткой, с которой снимается напряжение. Одна ламель всегда подсоединена к плюсу, а вторая – к минусу. При повороте вала на 180º пластины коллектора меняются местами, вследствие чего происходит новая коммутация со сменой полярности.
Такой же принцип коммутации питания обмоток используются во всех коллекторах, в т. ч. и в устройствах с большим количеством ламелей (по паре на каждую обмотку). Таким образом, коллектор обеспечивает коммутацию, необходимую для непрерывного вращения ротора.
В современных конструкциях коллектора ламели расположены по кругу таким образом, что каждая пластина соответствующей пары находится на диаметрально противоположной стороне. Цепь якоря коммутируется в результате изменения положения вала.
Принцип работы
Ещё со школьной скамьи мы помним, что на провод под напряжением, расположенный между полюсами магнита, действует выталкивающая сила. Происходит это потому, что вокруг проволоки образуется магнитное поле по всей его длине. В результате взаимодействия магнитных полей возникает результирующая «Амперова» сила:
F=B×I×L, где B означает величину магнитной индукции поля, I – сила тока, L – длина провода.
Вектор «Амперовой» всегда перпендикулярен до линий магнитных потоков между полюсами. Схематически принцип работы изображён на рис. 6.
 Рис. 6. Принцип работы ДПТ
Рис. 6. Принцип работы ДПТ
Если вместо прямого проводника возьмём контурную рамку и подсоединим её к источнику тока, то она повернётся на 180º и остановится в в таком положении, в котором результирующая сила окажется равной 0. Попробуем подтолкнуть рамку. Она возвращается в исходное положение.
Поменяем полярность тока и повторим попытку: рамка сделала ещё пол-оборота. Логично припустить, что необходимо менять направление тока каждый раз, когда соответствующие витки обмоток проходят точки смены полюсов магнитов. Именно для этой цели и создан коллектор.
Схематически можно представить себе каждую якорную обмотку в виде отдельной контурной рамки. Если обмоток несколько, то в каждый момент времени одна из них подходит к магниту статора и оказывается под действием выталкивающей силы. Таким образом, поддерживается непрерывное вращение якоря.
Типы ДПТ
Существующие электродвигатели постоянного тока можно классифицировать по двум основным признакам: по наличию или отсутствию в конструкции мотора щеточно-коллекторного узла и по типу магнитной системы статора.
Рассмотрим основные отличия.
По наличию щеточно-коллекторного узла
Двигатели постоянного тока для коммутации обмоток, которых используются щёточно-коллекторные узлы, называются коллекторными. Они охватывают большой спектр линейки моделей электромоторов. Существуют двигатели, в конструкции которых применяется до 8 щёточно-коллекторных узлов.
Функции ротора может выполнять постоянный магнит, а ток от электрической сети подаётся непосредственно на обмотки статора. В таком варианте отпадает надобность в коллекторе, а проблемы, связанные с коммутацией, решаются с помощью электроники.
В таких бесколлекторных двигателях устранён один из недостатков –искрение, приводящее к интенсивному износу пластин коллектора и щёток. Кроме того, они проще в обслуживании и сохраняют все полезные характеристики ДПТ: простота в управлении связанном с регулировкой оборотов, высокие показатели КПД и другие. Бесколлекторные моторы носят название вентильных электродвигателей.
По виду конструкции магнитной системы статора
В конструкциях синхронных двигателей существуют модели с постоянными магнитами и ДПТ с обмотками возбуждения. Электродвигатели серий, в которых применяются статоры с потоком возбуждения от обмоток, довольно распространены. Они обеспечивают стабильную скорость вращения валов, высокую номинальную механическую мощность.
О способах подключения статорных обмоток шла речь выше. Ещё раз подчеркнём, что от выбора схемы подключения зависят электрические и тяговые характеристики двигателей постоянного тока. Они разные в последовательных обмотках и в катушках с параллельным возбуждением.
Управление
Не трудно понять, что если изменить полярность напряжения, то направление вращения якоря также изменится. Это позволяет легко управлять электромотором, манипулируя полярностью щеток.
Механическая характеристика
Рассмотрим график зависимости частоты от момента силы на валу. Мы видим прямую с отрицательным наклоном. Эта прямая выражает механическую характеристику электродвигателя постоянного тока. Для её построения выбирают определённое фиксированное напряжение, подведённое для питания обмоток ротора.
 Примеры механических характеристик ДПТ независимого возбуждения
Примеры механических характеристик ДПТ независимого возбуждения
Регулировочная характеристика
Такая же прямая, но идущая с положительным наклоном, является графиком зависимости частоты вращения якоря от напряжения питания. Это и есть регулировочная характеристика синхронного двигателя.
Построение указанного графика осуществляется при определённом моменте развиваемом ДПТ.
 Пример регулировочных характеристик двигателя с якорным управлением
Пример регулировочных характеристик двигателя с якорным управлением
Благодаря линейности характеристик упрощается управление электродвигателями постоянного тока. Поскольку сила F пропорциональна току, то изменяя его величину, например переменным сопротивлением, можно регулировать параметры работы электродвигателя.
Регулирование частоты вращения ротора легко осуществляется путём изменения напряжения. В коллекторных двигателях с помощью пусковых реостатов добиваются плавности увеличения оборотов, что особенно важно для тяговых двигателей. Это также один из эффективных способов торможения. Мало того, в режиме торможения синхронный электродвигатель вырабатывает электрическую энергию, которую можно возвращать в энергосеть.
Области применения
Перечислять все области применения электродвигателей можно бесконечно долго. Для примера назовём лишь несколько из них:
- бытовые и промышленные электроинструменты;
- автомобилестроение – стеклоподъёмники, вентиляторы и другая автоматика;
- трамваи, троллейбусы, электрокары, подъёмные краны и другие механизмы, для которых важны высокие параметры тяговых характеристик.
Преимущества и недостатки
К достоинствам относится:
- Линейная зависимость характеристик электродвигателей постоянного тока (прямые линии) упрощающие управление;
- Легко регулируемая частота вращения;
- хорошие пусковые характеристики;
- компактные размеры.
У асинхронных электродвигателей, являющихся двигателями переменного тока очень трудно достичь таких характеристик.
Недостатки:
- ограниченный ресурс коллектора и щёток;
- дополнительная трата времени на профилактическое обслуживание, связанное с поддержанием коллекторно-щёточных узлов;
- ввиду того, что мы пользуемся сетями с переменным напряжением, возникает необходимость выпрямления тока;
- дороговизна в изготовлении якорей.
По перечисленным параметрам из недостатков в выигрыше оказываются модели асинхронных двигателей. Однако во многих случаях применение электродвигателя постоянного тока является единственно возможным вариантом, не требующим усложнения электрической схемы.
Основные теоретические положения
Важное свойство ДПТ с независимым возбуждением от постоянных магнитов состоит в том, что результирующий момент сил от всех проводников якоря, называемый электромагнитным моментом двигателя M, пропорционален току якоря Iя, потребляемому двигателем от источника питания:
,
где k m – коэффициент пропорциональности, называемый постоянной момента двигателя. Его размерность [Нм/А]. По законам электромагнитной индукции в проводнике, движущемся в магнитном поле, возникает электродвижущая сила. Суммарная ЭДС катушек якоря E через коллектор и щетки прикладывается к внешним выводам двигателя. В двигательном режиме работы эта ЭДС направлена против внешнего напряжения U я, подведенного к якорю от источника питания. Поэтому ЭДС двигателя часто называется противоЭДС. Она прямо пропорциональна угловой скорости вращения вала двигателя w дв[рад/с]:
,
где k ω – коэффициент пропорциональности, называемый постоянной ЭДС двигателя. Его размерность [Вс/рад].
Природа электромагнитных явлений в ДПТ такова, что если используется система единиц СИ, то значения коэффициентов k ω и km численно равны.
Уравнения, описывающие электрические процессы в ДПТ
В электрической якорной цепи двигателя протекает ток I я под действием напряжения постоянного тока Ua источника питания и противоЭДС двигателя.
Рис. 1
Эта цепь характеризуется параметрами: активным сопротивлением R я [Ом] и индуктивностью L я [Гн] якорной обмотки. Вращающийся ротор, обладающий моментом инерции Ja [Нм с 2 /рад] , приводится в движение одновременным действием электромагнитного момента двигателя M дв и момента внешних сил M вн, приложенного к валу двигателя.
Исходные дифференциальные уравнения ДПТ составляются на основании законов физики. Для электрической цепи используется второй закон Кирхгофа, согласно которому можно записать уравнение
,
где член R я I я характеризует падение напряжения на активном сопротивлении якорной цепи в соответствии с законом Ома, а член L я ( dI я/ dt ) отражает наличие ЭДС самоиндукции, возникающей в обмотке при изменении тока якоря. В представленном уравнении не учитывается падение напряжения на щетках, зависящее нелинейно от тока якоря, но имеющее, как правило, относительно небольшое значение по сравнению с напряжением U я .
Дифференциальное уравнение, характеризующее процессы в механической части двигателя, составляется на основании второго закона Ньютона:
,
где M вн – момент внешних сил, действующий относительно оси вращения вала двигателя. В этом уравнении не учитывается действие сил трения, возникающих при вращении ротора, но оказывающих относительно слабое действие на ускорение вала ДПТ.
Используя вышеприведенные формулы и приводя дифференциальные уравнения к нормальной форме Коши, получим описание ДПТ в форме:
Для исследования процессов с помощью ЭВМ удобно использовать структурное представление математической модели ДПТ. Для этого преобразуем полученную систему линейных дифференциальных уравнений по Лапласу при нулевых начальных условиях. В результате получим систему алгебраических уравнений:
в которых s – переменная Лапласа, а величины I я( s ), w дв( s ), U я( s ), M вн( s ) – изображения по Лапласу переменных I я , w дв, U я, M вн соответственно. После эквивалентных преобразований эти уравнения могут быть представлены в форме:
где Тэ = L я / R я – электромагнитная постоянная времени якорной цепи двигателя.
По уравнениям с помощью системы SIMULINK может быть сформирована структурная схема ДПТ для его математического моделирования (рис.1).
Важным параметром ДПТ, определяющим его динамические свойства, является электромеханическая постоянная времени двигателя:
.
Зависимость между электромагнитным моментом двигателя и частотой вращения ротора в установившемся режиме при постоянных U я и M вн называется механической характеристикой двигателя. Уравнение механической характеристики имеет вид:
.
При пуске двигателя, когда скорость равна нулю, развивается пусковой момент
.
Частота вращения вала двигателя при отсутствии сопротивления называется частотой вращения холостого хода
.
[spoiler title=”источники:”]
http://www.asutpp.ru/elektrodvigatel-postoyannogo-toka.html
http://imed.narod.ru/el_mech/motor_dc.htm
[/spoiler]