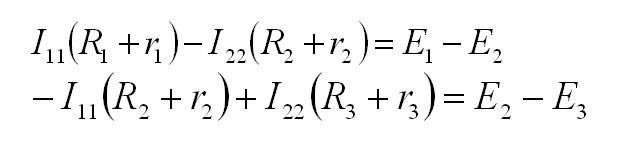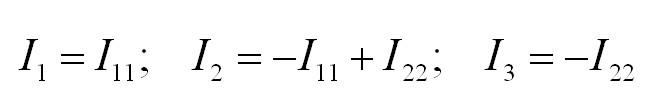Как найти токи исходной цепи

Метод наложения применяется для цепей
со смешанным соединением приемников,
имеющих несколько источников энергии.
Он основан на принципе суперпозиции,
который применительно к электрической
цепи гласит:

если в цепи
действует несколько источников энергии,
то токи в ее ветвях можно рассматривать
как алгебраическую сумму токов от
действия каждого источника в отдельности.

При расчете цепей по методу наложения
поочередно исключают все источники ЭДС
кроме одного и определяют токи в ветвях,
эти токи называются частичными или
парциальными.

E₂

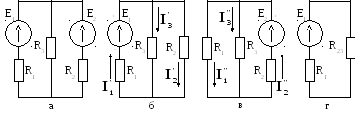
Рис. 1.12. Схемы цепи для определения токов
по методу наложения: (а) – исходная, (б)
– от ЭДС Е₁, (в) – от ЭДС Е₂,
(г) – для определения эквивалентного
сопротивления цепи

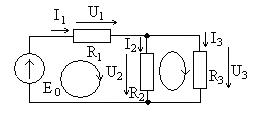
Для цепи, представленной на рис. 1.12а
исключаем ЭДС Е₂, тогда цепь
принимает вид, представленный на рис.
1.12б. Направления парциальных токов,ипредставлены в соответствии с направлением
ЭДС Е₁. Парциальные токи находим
по методу эквивалентного преобразования.
Приемники R₂и R₃ включены
параллельно, их можно заменить одним
эквивалентным с сопротивлением

.

После замены цепь принимает вид,
представленный на рис. 1.12г, ее элементы
включены последовательно и ток I₁’
можно определить по закону Ома

.

Напряжение на участке R₂₃можно
найти по закону Ома для участка цепи

.

Зная напряжение U₂₃легко определить
токии

.

Парциальные токи от действия источника
Е₂находятся аналогично, пользуясь
схемой 1.12 в.

Токи в ветвях исходной цепи находятся
алгебраическим суммированием
соответствующих парциальных токов:

и ,

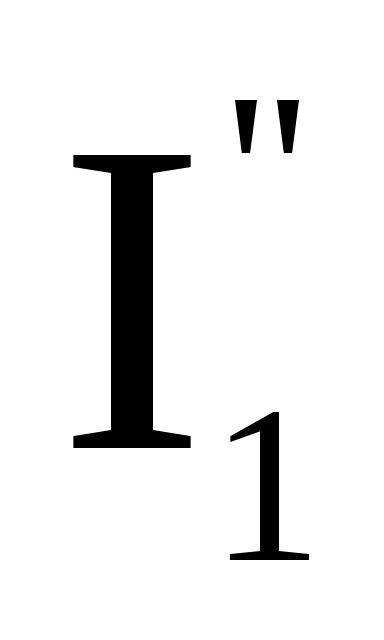
и ,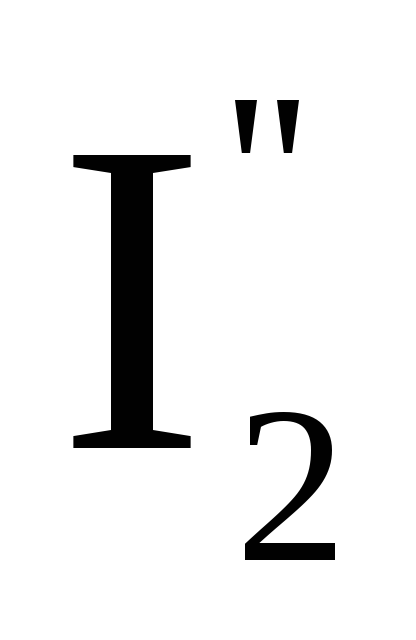

и .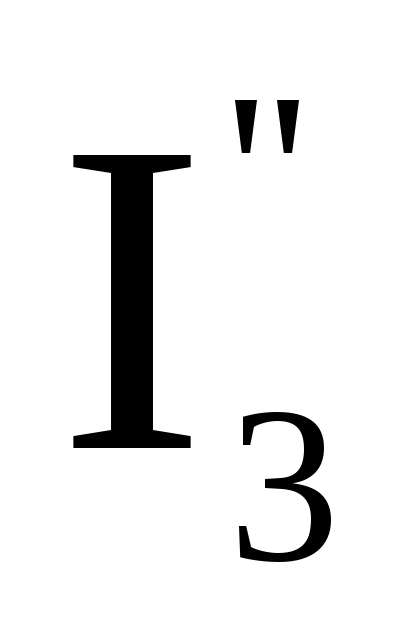

Пусть парциальные токи имеют следующие
значения:

= 17A,= 7A,= 10A,= 2A,= 6A,= 4A.

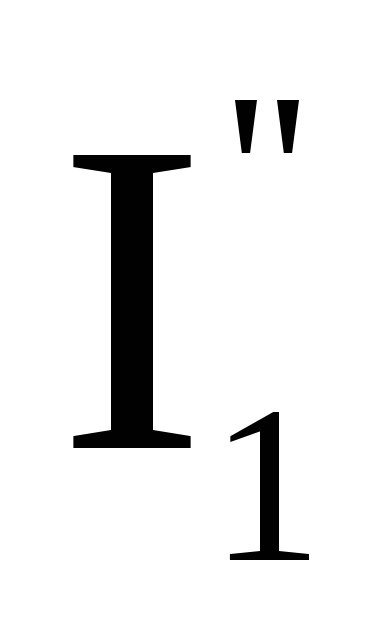
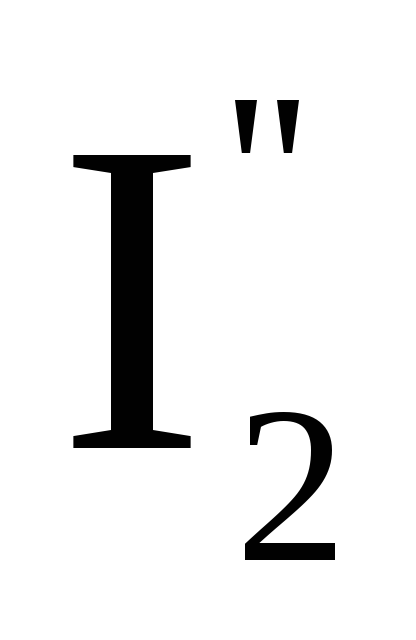
Ток
,
образованный первым источником Е₁течет по схеме снизу вверх, а ток,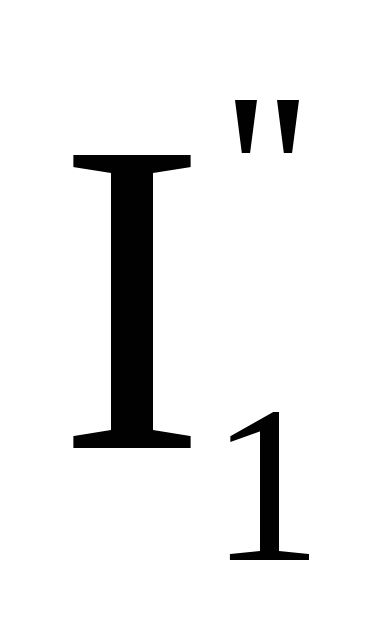
образованный вторым источником Е₂,
течет по схеме сверху вниз, рис. 1.12б и
рис. 1.12в. Причем>,
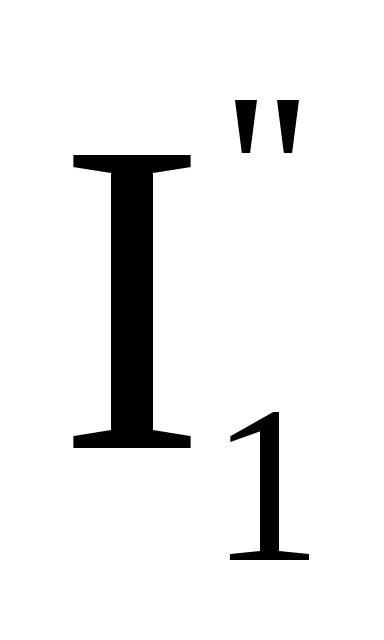
следовательно

I₁=–= 17 – 2= 15 A

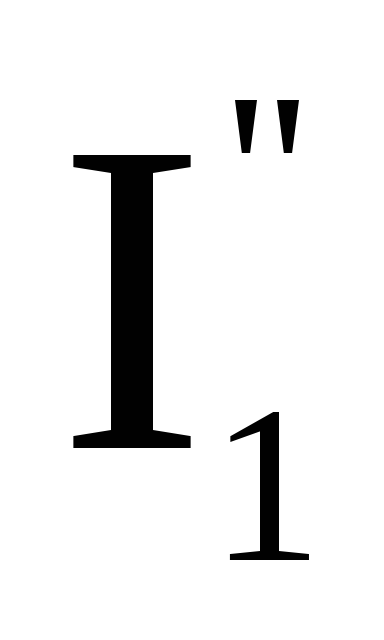
и имеет
направление большего тока
,
т.е. по схеме снизу вверх. Аналогично
находятся токи I₂и I₃

I₂=–= 7 – 6 = 1 A,

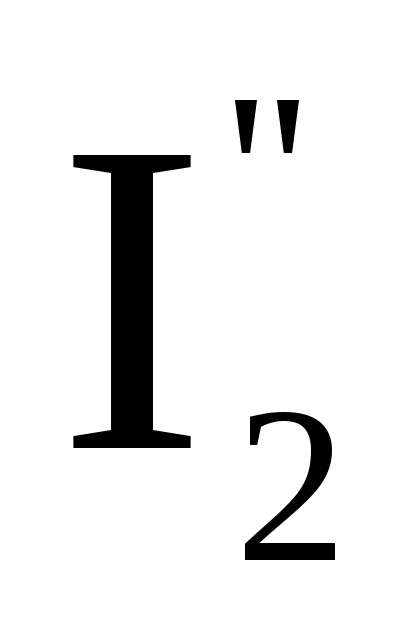
I₃=+= 10 + 4 =14 A.

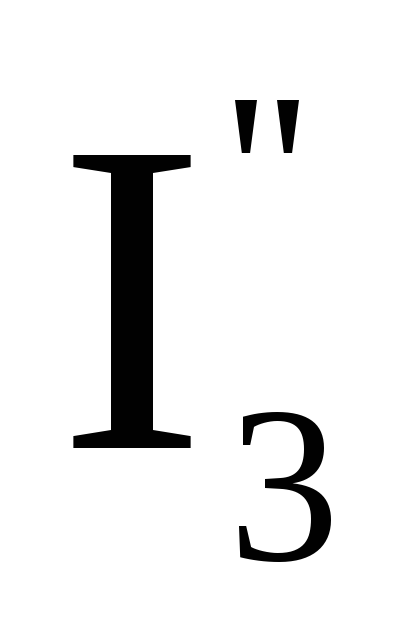
1.11. Понятие о балансе мощностей.

Независимо от того, каким методом
проводился расчет цепи, для проверки
правильности расчета составляется
баланс мощностей.

Согласно закону сохранения энергии
сумма мощностей, развиваемых всеми
источниками энергии, включенных в цепь,
равна сумме мощностей отдаваемых
приемником и мощностей потерь внутри
источника.

,

(1.17)

где i – номер
ветви цепи,

n – число
ветвей

Произведение EiIi
берется со знаком “+” если направления
ЭДС источника Е и тока I в i – ветви цепи
совпадают, если не совпадают, то
произведение EiIi
берется со знаком “–“. Физически знак
“–“ означает, что данный источник
энергии работает приемником. При
правильно рассчитанных токах баланс
мощностей должен сходиться с точностью
до 2%.

1.12 Потенциальная диаграмма.

П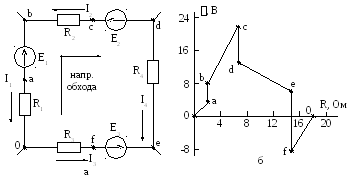отенциальная
диаграмма – это график распределения
потенциала вдоль какого-либо замкнутого
контура цепи. Потенциальная диаграмма
строится в прямоугольной системе
координат, в которой по горизонтальной
оси откладываются значения сопротивлений
между i-точкой контура и произвольно
выбранной точкой, потенциал которой
принят равным нулю.

Рис. 1.13. Контур сложной электрической
цепи (а) и его потенциальная диаграмма
(б)

По вертикальной оси откладываются
значения потенциалов всех точек контура,
в которых соединены два любых его
элемента, рассчитанные относительно
нулевой точки. При расчете потенциалов
следует помнить, что в пассивном элементе
стрелка тока указывает направление
уменьшения потенциала. Поэтому при
переходе через пассивный элемент,
например резистор, потенциал понижается
на величину падения напряжения в нем,
если направление тока в нем совпадает
с направлением обхода контура. Если это
условие не выполняется, потенциал
повышается на величину падения напряжения.
Стрелка ЭДС, наоборот, указывает
направление увеличения потенциала.
Поэтому при переходе через источник
энергии с ЭДС Еi и внутренним сопротивлением
r_i= 0 потенциал скачком увеличивается
на величину ЭДС источника Еi, если
направление ЭДС совпадает с направлением
обхода контура. Если это условие не
выполняется, потенциал скачком уменьшается
на величину ЭДС источника Ei. Рассмотрим
расчет потенциалов и построение диаграммы
на примере контура, представленного на
рис. 1.13 а.

Пусть E₁= 5 В, Е₂= 10 В, Е₃= 15 В, R₁= 2 Ом, R₂= 5 Ом, R₃= 3 Ом, R₄= 8 Ом. Расчетные значения
токов I₁= 1,5 А, I₂= 2,8 А, I₃= 2,8 А, I₄= 0,7 А.

Потенциал точки 0 примем равным нулю
₀= 0 R= 0. Потенциал
точки “а” выше потенциала точки “0”
на величину I₁R₁,
т.к. направление обхода не совпадает с
направлением тока I₁, т.е..
Сопротивление между точкой “0” и точкой
“а” R_0аравно сопротивлению
резистора R₁, т.е. R_0а= 2 Ом.

Потенциал точки “b” выше потенциала
точки “а” на величину ЭДС Е₁, т.к.
направление обхода совпадает с
направлением ЭДС Е₁, т.е..
Сопротивление между точкой “0” и точкой
“b” R_0bпо-прежнему R₁, т.е.
R_0b= 2Ом.

Потенциал точки “c”
рассчитывается аналогично:,
а сопротивление между точками “0” и
“с” R_0скак видно из рис. 1.13а R_0с=
R₁+ R₂= 2 + 5 =7 Ом.

Расчет потенциалов и сопротивлений для
других точек контура проводится
аналогично и дает:
_d= 12 В, R_0d= 7 Ом;
_e= 6,5 В, R_0e= 15 Ом;
_f
= – 8,5 В, R_0f= 15 Ом.

Заканчивается расчет вычислением
потенциала точки “0” относительно
предыдущей точки f:

₀=
_f
+ I₃R₃= – 8,5 +2,830

R₀₀= R₁+ R₂+ R₃+R₄= 2 + 5 + 3 + 8 = 18
Ом

При правильно рассчитанных токах
потенциальная диаграмма начинается в
точке с
=0
и заканчивается также в точке с
=
0, т.к. работа по переносу заряда не
зависит от формы пути, а зависит от
координат начальной и конечной точек.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Метод наложения токов. Пример решения

Наряду с методом контурных токов для анализа электрических цепей используется другой метод – метод наложения. Этот метод основан на  принципе наложения, который применяется только к линейным системам.

Метод наложения относительно прост, и в основном применяется для не сложных электрических цепей.

Его суть заключается в том, что токи в ветвях определяются как алгебраическая сумма их составляющих от каждого источника. То есть каждый источник тока вносит свою часть в каждый ток в цепи, а чтобы найти эти токи, нужно найти и сложить все составляющие. Таким образом, мы сводим решение одной сложной цепи к нескольким простым (с одним источником).

Порядок расчета 

1 – Составление частных схем, с одним источником ЭДС, остальные источники исключаются, от них остаются только их внутренние сопротивления.

2 – Определение частичных токов в частных схемах, обычно это несложно, так как цепь получается простой.

3 – Алгебраическое суммирование всех частичных токов, для нахождения токов в исходной цепи.

Пример решения методом наложения 

1. Для начала произвольно выберем направление токов, если в итоге какой либо ток получится со знаком минус, значит нужно изменить направление данного тока на противоположное.

 

2. Составим частную схему с первым источником ЭДС и рассчитаем частные токи в ней, убрав второй источник. Для удобства частичные токи будем обозначать штрихами. 

Свернем схему к одному контуру, с сопротивлением источника и эквивалентным сопротивлением цепи для нахождения тока источника I₁. Для тех, у кого возникают затруднения с нахождением эквивалентного сопротивления рекомендуем прочесть статью виды соединения проводников.

 

Найдем ток по закону Ома для полной цепи

Найдем напряжение на R₂₃₄₅

Тогда ток I₃ равен

А ток I₄

Определим напряжение на R₂₅ 

Найдем токи I₂ и I₅

3. Составим частную схему со вторым источником ЭДС 

Аналогичным образом вычислим все частичные токи от второй ЭДС 

4. Найдем токи в исходной цепи, для этого просуммируем частичные токи, учитывая их направление. Если направление частичного тока совпадает с направлением исходного тока, то берем со знаком плюс, в противном случае со знаком минус.

 

5. Проверим с правильность решения с помощью баланса мощностей. 

Небольшая погрешность связана с округлениями промежуточных значений в ходе выполнения вычислений.

Читайте также – Метод узловых потенциалов

Просмотров: 91965

Эта статья для тех, кто только начинает изучать теорию электрических цепей. Как всегда не будем лезть в дебри формул, но попытаемся объяснить основные понятия и суть вещей, важные для понимания. Итак, добро пожаловать в мир электрических цепей!

Хотите больше полезной информации и свежих новостей каждый день? Присоединяйтесь к нам в телеграм.

Электрические цепи

Электрическая цепь – это совокупность устройств, по которым течет электрический ток.

Рассмотрим самую простую электрическую цепь.  Из чего она состоит? В ней есть генератор – источник тока, приемник (например, лампочка или электродвигатель), а также система передачи (провода). Чтобы цепь стала именно цепью, а не набором проводов и батареек, ее элементы должны быть соединены между собой проводниками. Ток может течь только по замкнутой цепи. Дадим еще одно определение:

Электрическая цепь – это соединенные между собой источник тока, линии передачи и приемник.

Конечно, источник, приемник и провода – самый простой вариант для элементарной электрической цепи. В реальности в разные цепи входит еще множество элементов и вспомогательного оборудования: резисторы, конденсаторы, рубильники, амперметры, вольтметры, выключатели, контактные соединения, трансформаторы и прочее.

Кстати, о том, что такое трансформатор, читайте в отдельном материале нашего блога.

По какому фундаментальному признаку можно разделить все цепи электрического тока? По тому же, что и ток! Есть цепи постоянного тока, а есть – переменного. В цепи постоянного тока он не меняет своего направления, полярность источника постоянна. Переменный же ток периодически изменяется во времени как по направлению, так и по величине.

Сейчас переменный ток используется повсеместно. О том, что для этого сделал Никола Тесла, читайте в нашей статье.

Элементы электрических цепей

Все элементы электрических цепей можно разделить на активные и пассивные. Активные элементы цепи – это те элементы, которые индуцируют ЭДС. К ним относятся источники тока, аккумуляторы, электродвигатели. Пассивные элементы – соединительные провода и электроприемники.

Приемники и источники тока, с точки зрения топологии цепей, являются двухполюсными элементами (двухполюсниками). Для их работы необходимо два полюса, через которые они передают или принимают электрическую энергию. Устройства, по которым ток идет от источника к приемнику, являются четырехполюсниками. Чтобы передать энергию от одного двухполюсника к другому им необходимо минимум 4 контакта, соответственно для приема и передачи.

Резисторы – элементы электрической цепи, которые обладают сопротивлением. Вообще, все элементы реальных цепей, вплоть до самого маленького соединительного провода, имеют сопротивление. Однако в большинстве случаев этим можно пренебречь и при расчете считать элементы электрической цепи идеальными.

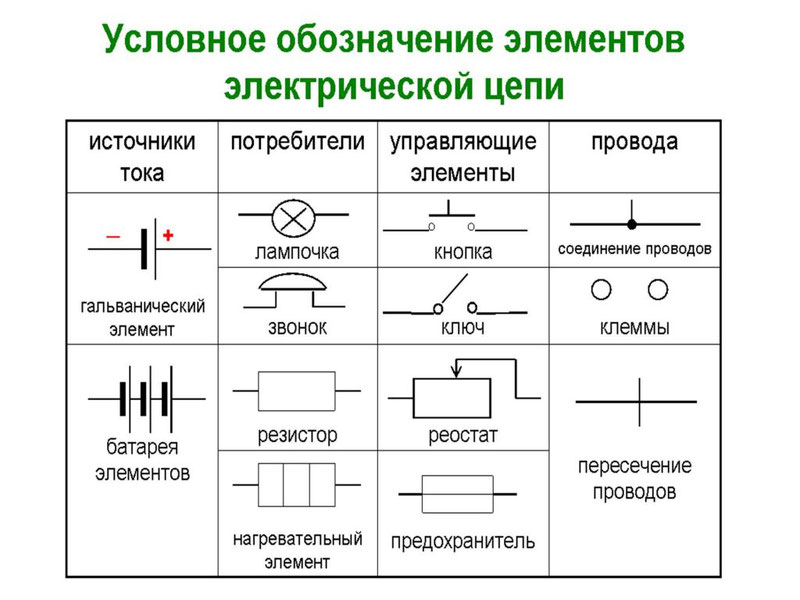
Существуют условные обозначения для изображения элементов цепи на схемах.

Кстати, подробнее про силу тока, напряжение, сопротивление и закон Ома для элементов электрической цепи читайте в отдельной статье.

Вольт-амперная характеристика – фундаментальная характеристика элементов цепи. Это зависимость напряжения на зажимах элемента от тока, который проходит через него. Если вольт-амперная характеристика представляет собой прямую линию, то говорят, что элемент линейный. Цепь, состоящая из линейных элементов – линейная электрическая цепь. Нелинейная электрическая цепь – такая цепь, сопротивление участков которой зависит от значений и направления токов.

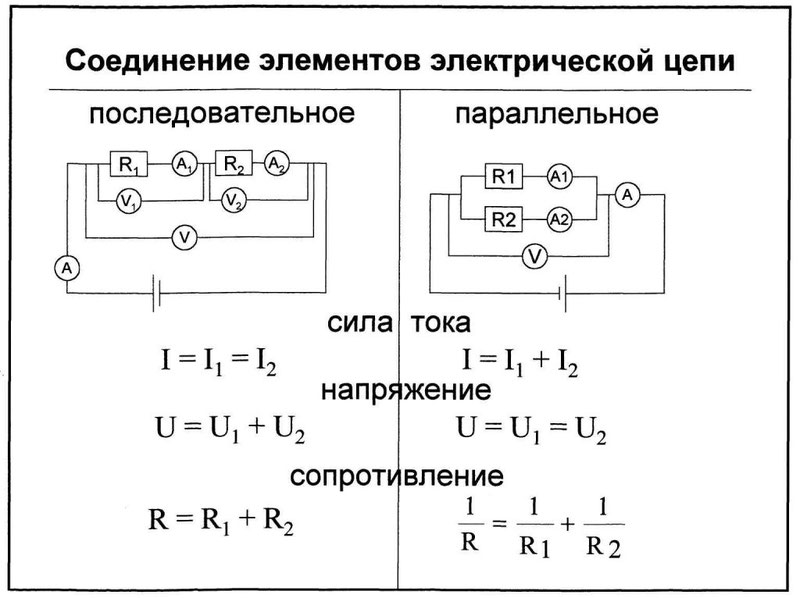
Какие есть способы соединения элементов электрической цепи? Какой бы сложной ни была схема, элементы в ней соединены либо последовательно, либо параллельно.

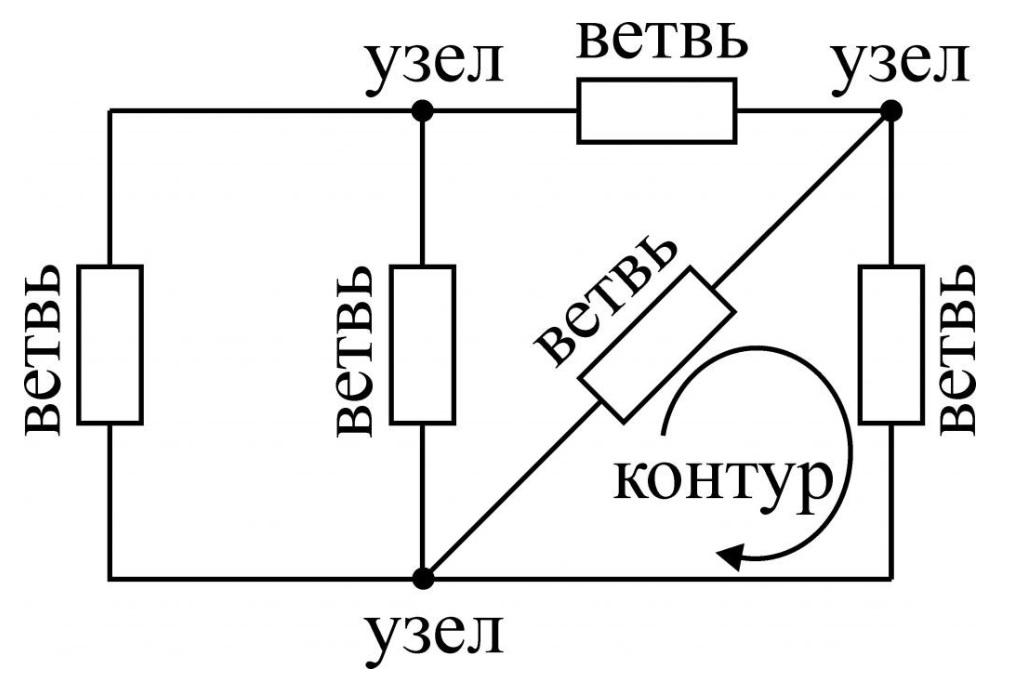
При решении задач и анализе схем используют следующие понятия:

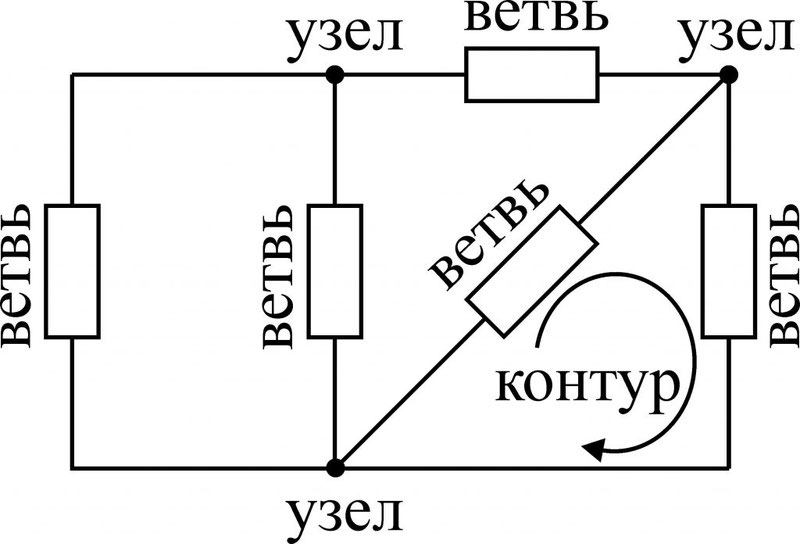
• Ветвь – такой участок цепи, вдоль которого течет один и тот же ток;
• Узел – соединение ветвей цепи;
• Контур – последовательность ветвей, которая образует замкнутый путь. При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.

Чтобы понять, что есть что, взглянем на рисунок:

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Классификация электрических цепей

По назначению электрические цепи бывают:

• Силовые электрические цепи;
• Электрические цепи управления;
• Электрические цепи измерения;

Силовые цепи предназначены для передачи и распределения электрической энергии. Именно силовые цепи ведут ток к потребителю.

Также цепи разделяют по силе тока в них. Например, если ток в цепи превышает 5 ампер, то цепь силовая. Когда вы щелкаете чайник, включенный в розетку, Вы замыкаете силовую электрическую цепь.

Электрические цепи управления не являются силовыми и предназначены для приведения в действие или изменения параметров работы электрических устройств и оборудования. Пример цепи управления – аппаратура контроля, управления и сигнализации.

Электрические цепи измерения предназначены для фиксации изменений параметров работы электрического оборудования.

Расчет электрических цепей

Рассчитать цепь – значит найти все токи в ней. Существуют разные методы расчета электрических цепей: законы Кирхгофа, метод контурных токов, метод узловых потенциалов и другие. Рассмотрим применение метода контурных токов на примере конкретной цепи.

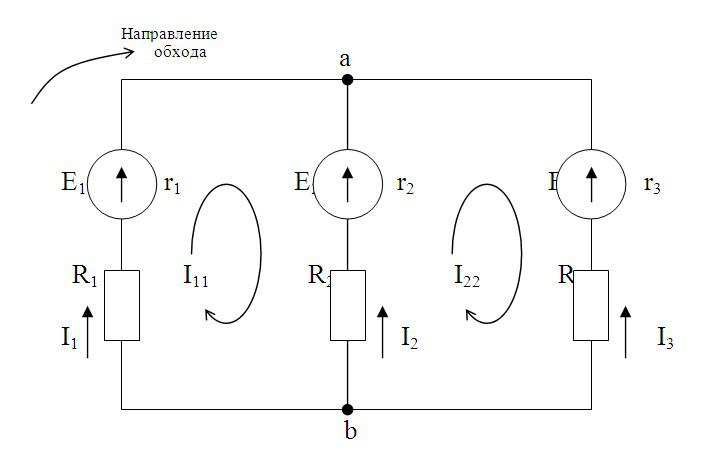
Сначала выделим контуры и обозначим ток в них. Направление тока можно выбирать произвольно. В нашем случае – по часовой стрелке. Затем для каждого контура составим уравнения по 2 закону Кирхгофа. Уравнения составляются так: Ток контура умножается на сопротивление контура, к полученному выражению добавляются произведения тока других контуров и общих сопротивлений этих контуров. Для нашей схемы:

Полученная система решается с подставкой исходных данных задачи. Токи в ветвях исходной цепи находим как алгебраическую сумму контурных токов

Какую бы цепь Вам ни понадобилось рассчитать, наши специалисты всегда помогут справится с заданиями. Мы найдем все токи по правилу Кирхгофа и решим любой пример на переходные процессы в электрических цепях. Получайте удовольствие от учебы вместе с нами!

Расчет электрической цепи методом наложения

Расчет электрических цепей

Для вычисления рабочих параметров радиотехнических устройств и отдельных схем применяют специальные методики. После изучения соответствующих технологий результат можно узнать быстро, без сложных практических экспериментов. Корректный расчет электрических цепей пригодится на стадии проектирования и для выполнения ремонтных работ.

Категории элементов и устройств электрической цепи

Для условного изображения определенной цепи применяют специальную схему. Кроме отдельных физических компонентов, она содержит сведения о направлении (силе) токов, уровнях напряжения и другую информацию. Качественная модель показывает реальные процессы с высокой точностью.

Компоненты электрической цепи:

• источник постоянного или переменного тока (Е) – аккумулятор или генератор, соответственно;
• пассивные элементы (R) – резисторы;
• компоненты с индуктивными (L) и емкостными (С) характеристиками;
• соединительные провода.

На рисунке обозначены:

• ветви – участки цепи с одним током;
• узлы – точки соединения нескольких ветвей;
• контур – замкнутый путь прохождения тока.

При решении практических задач выясняют, как узнать силу тока в отдельных ветвях. Полученные значения используют для анализа электрических параметров. В частности, можно определять падение напряжения на резисторе, мощность потребления подключенной нагрузки. При расчете цепей переменного тока приходится учитывать переходные энергетические процессы, влияние частоты.

Метод расчета по законам Ома и Кирхгофа

До изучения технологий вычислений необходимо уточнить особенности типовых элементов при подключении к разным источникам питания. При постоянном токе сопротивлением индуктивности можно пренебречь. Конденсатор эквивалентен разрыву цепи. Также следует учитывать следующие различия разных видов соединений резисторов:

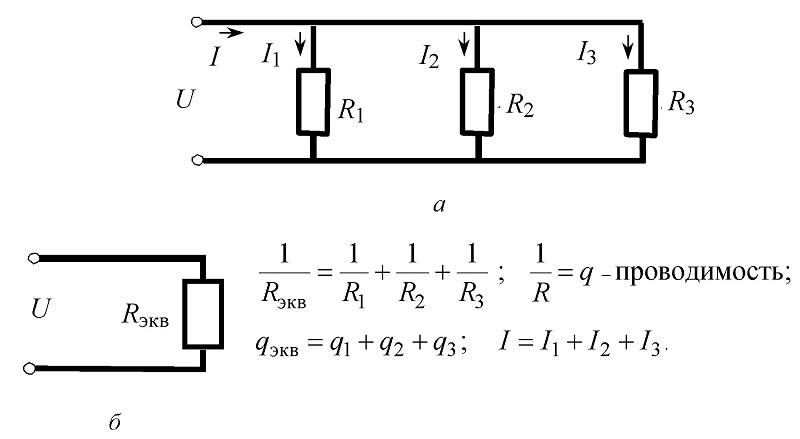
• последовательное – увеличивает общее сопротивление;
• параллельное – распределяет токи по нескольким ветвям, что улучшает проводимость.

Закон Ома для участка цепи

Типовая аккумуляторная батарея легкового автомобиля вырабатывает напряжение U = 12 V. Бортовой или внешний амперметр покажет соответствующее значение при измерении. Соединение клемм проводом недопустимо, так как это провоцирует короткое замыкание. Если жила тонкая (

К сведению. Результат показанного расчета пригодится для поиска подходящего резистора. Следует делать запас в сторону увеличения. По стандарту серийных изделий подойдет элемент с паспортной номинальной мощностью 5 Вт.

На практике приходится решать более сложные задачи. Так, при значительной длине линии нужно учесть влияние соединительных ветвей цепи. Через стальной проводник ток будет протекать хуже, по сравнению с медным аналогом. Следовательно, надо в расчете учитывать удельное сопротивление материала. Короткий провод можно исключить из расчета. Однако в нагрузке может быть два элемента. В любом случае общий показатель эквивалентен определенному сопротивлению цепи. При последовательном соединении Rэкв = R1 + R2 +…+ Rn. Данный метод пригоден, если применяется постоянный ток.

Закон Ома для полной цепи

Для вычисления такой схемы следует добавить внутреннее сопротивление (Rвн) источника. Как найти ток, показывает следующая формула:

Вместо напряжения (U) при расчетах часто используют типовое обозначение электродвижущей силы (ЭДС) – E.

Первый закон Кирхгофа

По классической формулировке этого постулата алгебраическая сумма токов, которые входят и выходят из одного узла, равна нулю:

I1 + I2 + … + In = 0.

Это правило действительно для любой точки соединения ветвей электрической схемы. Следует подчеркнуть, что в данном случае не учитывают характеристики отдельных элементов (пассивные, реактивные). Можно не обращать внимания на полярность источников питания, включенных в отдельные контуры.

Чтобы исключить путаницу при работе с крупными схемами, предполагается следующее использование знаков отдельных токов:

• входящие – положительные (+I);
• выходящие – отрицательные (-I).

Второй закон Кирхгофа

Этим правилом установлено суммарное равенство источников тока (ЭДС), которые включены в рассматриваемый контур. Для наглядности можно посмотреть, как происходит распределение контрольных параметров при последовательном подключении двух резисторов (R1 = 50 Ом, R2 = 10 Ом) к аккумуляторной батарее (Uакб = 12 V). Для проверки измеряют разницу потенциалов на выводах пассивных элементов:

• UR1 = 10 V;
• UR1 = 2 V;
• Uакб = 12 V = UR1 + UR2 = 10 + 2;
• ток в цепи определяют по закону Ома: I = 12/(50+10) = 0,2 А;
• при необходимости вычисляют мощность: P = I2 *R = 0,04 * (50+10) = 2,4 Вт.

Второе правило Кирхгофа действительно для любых комбинаций пассивных компонентов в отдельных ветвях. Его часто применяют для итоговой проверки. Чтобы уточнить корректность выполненных действий, складывают падения напряжений на отдельных элементах. Следует не забывать о том, что дополнительные источники ЭДС делают результат отличным от нуля.

Метод преобразования электрической цепи

Как определить силу тока в отдельных контурах сложных схем? Для решения практических задач не всегда нужно уточнение электрических параметров на каждом элементе. Чтобы упростить вычисления, используют специальные методики преобразования.

Расчет цепи с одним источником питания

Для последовательного соединения пользуются рассмотренным в примере суммированием электрических сопротивлений:

Rэкв = R1 + R2 + … + Rn.

Контурный ток – одинаковый в любой точке цепи. Проверять его можно в разрыве контрольного участка мультиметром. Однако на каждом отдельном элементе (при отличающихся номиналах) прибор покажет разное напряжение. По второму закону Кирхгофа можно уточнить результат вычислений:

E = Ur1 + Ur2 + Urn.

В этом варианте в полном соответствии с первым постулатом Кирхгофа токи разделяются и соединяются во входных и выходных узлах. Показанное на схеме направление выбрано с учетом полярности подключенного аккумулятора. По рассмотренным выше принципам сохраняется базовое определение равенства напряжений на отдельных компонентах схемы.

Как найти ток в отдельных ветвях, демонстрирует следующий пример. Для расчета приняты следующие исходные значения:

• R1 = 10 Ом;
• R2 = 20 Ом;
• R3= 15 Ом;
• U = 12 V.

По следующему алгоритму будут определяться характеристики цепи:

• базовая формула для трех элементов:

Rобщ = R1*R2*R3/(R1*R2 + R2*R3 + R1*R3.

• подставив данные, вычисляют Rобщ = 10 * 20 * 15 / (10*20 + 20*15 +10*15) = 3000 /(200+300+150) = 4,615 Ом;
• I = 12/ 4,615 ≈ 2,6 А;
• I1 = 12/ 10 = 1,2 А;
• I2 = 12/20 = 0,6 А;
• I3 = 12/15 = 0,8 А.

Как и в предыдущем примере, рекомендуется проверить результат вычислений. При параллельном соединении компонентов должно соблюдаться равенство токов на входе и суммарного значения:

I = 1,2 + 0,6 + 0,8 = 2,6 А.

Если применяется синусоидальный сигнал источника, вычисления усложняются. При включении в однофазную розетку 220V трансформатора придется учитывать потери (утечку) в режиме холостого хода. В этом случае существенное значение имеют индуктивные характеристики обмоток и коэффициент связи (трансформации). Электрическое сопротивление (ХL) зависит от следующих параметров:

• частоты сигнала (f);
• индуктивности (L).

Вычисляют ХL по формуле:

Чтобы находить сопротивление емкостной нагрузки, подойдет выражение:

Следует не забывать о том, что в цепях с реактивными компонентами сдвигаются фазы тока и напряжения.

Расчет разветвленной электрической цепи с несколькими источниками питания

Пользуясь рассмотренными принципами, вычисляют характеристики сложных схем. Ниже показано, как найти ток в цепи при наличии двух источников:

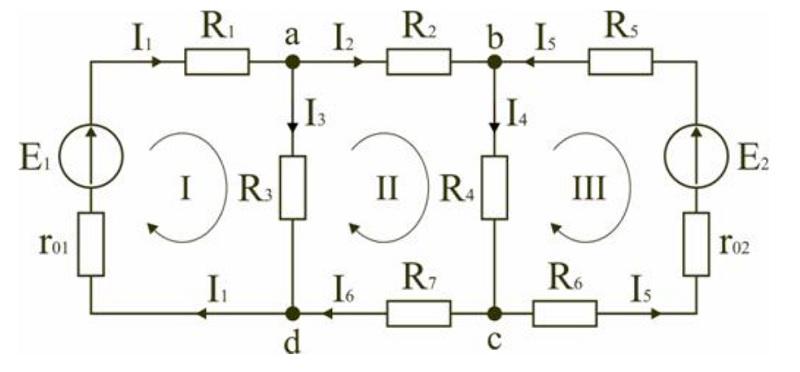
• обозначают компоненты и базовые параметры во всех контурах;
• составляют уравнения для отдельных узлов: a) I1-I2-I3=0, b) I2-I4+I5=0, c) I4-I5+I6=0;
• в соответствии со вторым постулатом Кирхгофа, можно записать следующие выражения для контуров: I) E1=R1 (R01+R1)+I3*R3, II) 0=I2*R2+I4*R4+I6*R7+I3*R3, III) -E2=-I5*(R02+R5+R6)-I4*R4;
• проверка: d) I3+I6-I1=0, внешний контур E1-E2=I1*(r01+R1)+I2*R2-I5*(R02+R5+R6)+I6*R7.

Дополнительные методы расчета цепей

В зависимости от сложности устройства (электрической схемы), выбирают оптимальную технологию вычислений.

Метод узлового напряжения

Основные принципы этого способа базируются на законе Ома и постулатах Кирхгофа. На первом этапе определяют потенциалы в каждом узле. Далее вычисляют токи в отдельных ветвях с учетом соответствующих электрических сопротивлений (отдельных компонентов или эквивалентных значений). Проверку делают по рассмотренным правилам.

Метод эквивалентного генератора

Эта технология подходит для быстрого расчета тока в одной или нескольких контрольных ветвях.

В данной методике общую цепь представляют в виде источника тока с определенным напряжением и внутренним сопротивлением. Далее выполняют вычисления по контрольной ветви с применением стандартного алгоритма.

Видео

Источник

РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

2015-04-01
17963

Цепь постоянного тока

В цепи постоянного тока действуют постоянные напряжения, протекают постоянные токи и присутствуют только резистивные элементы (сопротивления).

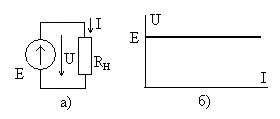
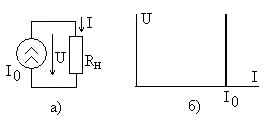
Идеальным источником напряжения называют источник, напряжение на зажимах которого, создаваемое внутренней электродвижущей силой (ЭДС ), на зависит от формируемого им в нагрузке тока (рис. 6.1а). При этом имеет место равенство . Вольтамперная характеристика идеального источника напряжения показана на рис. 6.1б.

Идеальным источником тока называют источник, который отдает в нагрузку ток, не зависящий от напряжения на зажимах источника, Рис. 6.2а. Его вольтамперная характеристика показана на рис. 6.2б.

В сопротивлении связь между напряжением и током определяется законом Ома в виде

Пример электрической цепи показан на рис. 6.3. В ней выделяются ветви, состоящие из последовательного соединения нескольких элементов (источника E и сопротивления ) или одного элемента ( и ) и узлы – точки соединения трех и более ветвей, отмеченные жирными точками. В рассмотренном примере имеется ветви и узла.

Кроме того, в цепи выделяются независимые замкнутые контуры, не содержащие идеальные источники тока. Их число равно . В примере на рис. 6.3 их число , например, контуры с ветвями E и , показанные на рис. 6.3 овалами со стрелками, указывающими положительное направление обхода контура.

Связь токов и напряжений в цепи определяется законами Кирхгофа.

Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле электрической цепи, равна нулю,

Втекающие в узел токи имеют знак плюс, а вытекающие минус.

Второй закон Кирхгофа: алгебраическая сумма напряжений на элементах замкнутого независимого контура равна алгебраической сумме ЭДС идеальных источников напряжения, включенных в этом контуре,

Напряжения и ЭДС берутся со знаком плюс, если их положительные направления совпадают с направлением обхода контура, в противном случае используется знак минус.

Для приведенного на рис. 6.3 примера по закону Ома получим подсистему компонентных уравнений

По законам Кирхгофа подсистема топологических уравнений цепи имеет вид

Расчет на основе закона Ома

Этот метод удобен для расчета сравнительно простых цепей с одним источником сигнала . Он предполагает вычисление сопротивлений участков цепи, для которых известна вели-

чина тока (или напряжения), с последующим определением неизвестного напряжения (или тока). Рассмотрим пример расчета цепи, схема которой приведена на рис. 6.4, при токе идеального источника А и сопротивлениях Ом, Ом, Ом. Необходимо определить токи ветвей и , а также напряжения на сопротивлениях , и .

Известен ток источника , тогда можно вычислить сопротивление цепи относительно зажимов источника тока (параллельного соединения сопротивления и последовательно соединен-

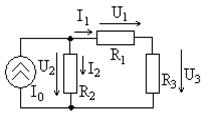
Рис. 6.4 ных сопротивлений и ),

Напряжение на источнике тока (на сопротивлении ) равно

Затем можно найти токи ветвей

Полученные результаты можно проверить с помощью первого закона Кирхгофа в виде . Подставляя вычисленные значения, получим А, что совпадает с величиной тока источника.

Зная токи ветвей, нетрудно найти напряжения на сопротивлениях (величина уже найдена)

По второму закону Кирхгофа . Складывая полученные результаты, убеждаемся в его выполнении.

Расчет цепи по уравнениям Кирхгофа

Проведем расчет токов и напряжений в цепи, показанной на рис. 6.3 при и . Цепь описывается системой уравнений (6.4) и (6.5), из которой для токов ветвей получим

Из первого уравнения выразим , а из третьего

Тогда из второго уравнения получим

Из уравнений закона Ома запишем

Нетрудно убедиться, что выполняется второй закон Кирхгофа

Подставляя численные значения, получим

Эти же результаты можно получить, используя только закон Ома.

Мощность в цепи постоянного тока

Действующие в цепи идеальные источники тока и (или) напряжения отдают мощность в подключенную к ним цепь (нагрузку). Для цепи на рис. 6.1а отдаваемая идеальным источником напряжения мощность равна

а в цепи на рис. 6.2а идеальный источник тока отдает в нагрузку мощность

Подключенная к источнику внешняя резистивная цепь потребляет от него мощность, преобразуя ее в другте виды энергии, чаще всего в тепло.

Если через сопротивление протекает ток , а приложенное к нему напряжение равно , то для потребляемой сопротивлением мощности получим

С учетом уравнений закона Ома (6.1) можно записать

Если в цепи несколько сопротивлений, то сумма потребляемых ими мощностей равна суммарной мощности, отдаваемой в цепь всеми действующими в ней источниками. Это условие баланса мощностей.

Например, для цепи на рис. 6.3 в общем виде получим

Подставляя в левую часть равенства (6.11) полученные ранее выражения для токов, получим

что соответствует правой части выражения (6.11).

Аналогичные расчеты можно проделать и для цепи на рис. 6.4.

Условие баланса мощностей позволяет дополнительно контролировать правильность расчетов.

Источник

1.2 Метод наложения

1.2 Метод наложения

Метод наложения основан на свойстве линейности электрических цепей. Метод наложения справедлив только для линейных цепей. Метод наложения применяется для определения токов в ветвях схемы с несколькими источниками.

Алгоритм метода наложения:

1) выбирают положительные направления токов в ветвях цепи;

2) находят частичные токи в ветвях, вызванные каждым источником по отдельности (схему рассчитывают столько раз, сколько источников действует в схеме);

3) токи в ветвях по методу наложения находят как алгебраическую сумму частичных токов (знак частичного тока при суммировании определяется по положительному направлению тока ветви).

Решение задач методом наложения

Задача 1.2.1 . В электрической цепи рис. 1.2.1 с тремя источниками энергии определить все токи в ветвях, воспользовавшись методом наложения.

1. Выполним расчет цепи при воздействии источника ЭДС E₁, полагая E₃ = 0, J = 0. Источники считаем идеальными, поэтому внутренние сопротивления ЭДС равны нулю, а источника тока – бесконечности. С учетом этого изобразим расчетную схему (рис. 1.2.2).

Определение токов в полученной схеме будем вести, пользуясь методом эквивалентных преобразований:

R ′ Э = R 5 + R 2 ⋅ ( R 3 + R 4 ) R 2 + ( R 3 + R 4 ) = 15 + 30 ⋅ ( 10 + 5 ) 30 + ( 10 + 5 ) = 25 О м ; I ′ 1 = E 1 R ′ Э = 150 25 = 6 A ; I ′ 5 = I ′ 1 = 6 A ; I ′ 2 = I ′ 1 ⋅ R 3 + R 4 R 2 + ( R 3 + R 4 ) = 6 ⋅ 10 + 5 30 + ( 10 + 5 ) = 6 A ; I ′ 3 = I ′ 1 ⋅ R 2 R 2 + ( R 3 + R 4 ) = 6 ⋅ 30 30 + ( 10 + 5 ) = 4 A ; I ′ 3 = I ′ 4 = 4 A .

2. Расчет электрической цепи при воздействии ЭДС источника Е₃ выполним, полагая Е₁ = 0, J = 0 (рис. 1.2.3).

В соответствии с рис. 1.2.3 имеем:

R ″ Э = R 3 + R 4 + R 2 ⋅ R 5 R 2 + R 5 = 10 + 5 + 30 ⋅ 15 30 + 15 = 25 О м ; I ″ 3 = E 3 R ″ Э = 50 25 = 2 A ; I ″ 4 = I ″ 3 = 2 A ; I ″ 2 = I ″ 4 ⋅ R 5 R 2 + R 5 = 2 ⋅ 15 15 + 30 = 0,66 A ; I ″ 5 = I ″ 4 ⋅ R 2 R 2 + R 5 = 2 ⋅ 30 15 + 30 = 1,33 A ; I ″ 1 = I ″ 5 = 1,33 A .

3. Расчет электрической цепи при действии источника тока выполним, полагая E₁ = 0, Е₂ = 0 (рис. 12.4).

В соответствии с рис. 1.2.4 имеем:

R ? Э = R 4 + R 2 ⋅ R 5 R 2 + R 5 = 5 + 30 ⋅ 15 30 + 15 = 15 О м .

Находим токи в параллельных ветвях:

I ? 3 = J ⋅ R ? Э R ? Э + R 3 = 15 ⋅ 15 15 + 10 = 9 A ; I ? 4 = J ⋅ R 3 R ? Э + R 3 = 15 ⋅ 10 15 + 10 = 6 A ; I ? 2 = I ? 4 ⋅ R 5 R 2 + R 5 = 6 ⋅ 15 15 + 30 = 2 A ; I ? 5 = I ? 4 ⋅ R 2 R 2 + R 5 = 6 ⋅ 30 15 + 30 = 4 A .

Ток I ? рассчитываем по первому закону Кирхгофа:

I ? 1 + I ? 5 − J = 0 ; I ? 1 = J − I ? 5 = 15 − 4 = 11 A .

4. В соответствии с принятыми направлениями токов в исходной схеме определим их значения по методу наложения как алгебраическую сумму частичных токов всех промежуточных расчетных схем:

I 1 = I ′ 1 + I ″ 1 − I ? 1 = 6 + 1,33 − 11 = − 3,67 A ; I 2 = I ′ 2 − I ″ 2 − I ? 2 = 2 − 0,66 − 2 = − 0,66 A ; I 3 = − I ′ 3 − I ″ 3 + I ? 3 = − 4 − 2 + 9 = 3 A ; I 4 = I ′ 4 + I ″ 4 + I ? 4 = 4 + 2 + 6 = 12 A ; I 5 = I ′ 5 + I ″ 5 + I ? 5 = 6 + 1,33 + 4 = 11,33 A .

Правильность решения задачи проверяем по первому закону Кирхгофа:

− J + I 3 + I 4 = 0 ; − 15 + 3 + 12 = 0 ; − I 2 − I 4 + I 5 = 0 ; − ( − 0,66 ) − 12 + 11,33 = 0.

Токи I₁ и I₂ получились отрицательными, т.е. их истинное направление в схеме противоположно принятому положительному направлению.

Источник

Помощь студентам в учёбе

Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.

Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.

У меня конфиденциальность и безопасность высокого уровня. Никто не увидит Ваше задание, кроме меня и моих преподавателей, потому что WhatsApp и Gmail — это закрытые от индексирования системы , в отличие от других онлайн-сервисов (бирж и агрегаторов), в которые Вы загружаете своё задание, и поисковые системы Yandex и Google индексируют всё содержимое файлов, и любой пользователь сможет найти историю Вашего заказа, а значит, преподаватели смогут узнать всю историю заказа. Когда Вы заказываете у меня — Вы получаете максимальную конфиденциальность и безопасность.

Моё видео:

Как вы работаете?

Вам нужно написать сообщение в WhatsApp (Контакты ➞ тут) . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.

Сколько может стоить заказ?

Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.

Какой срок выполнения заказа?

Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Как оплатить заказ?

Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Какие гарантии и вы исправляете ошибки?

В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.

Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.

Теперь напишите мне в Whatsapp или почту (Контакты ➞ тут) и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.

Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.

После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.

of your page —>

Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.

В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!

Жду ваших заказов!

С уважением

Изучу , оценю , оплатите , через 2-3 дня всё будет на «4» или «5» !

Откройте сайт на смартфоне, нажмите на кнопку «написать в чат» и чат в whatsapp запустится автоматически.

f9219603113@gmail.com

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.9219603113.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник