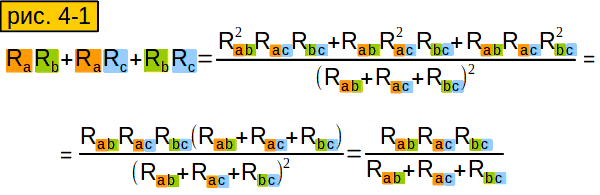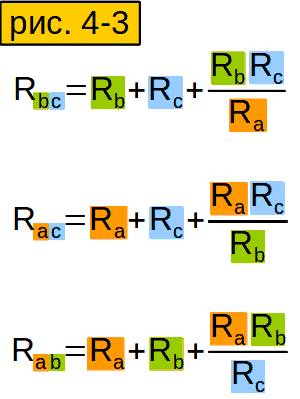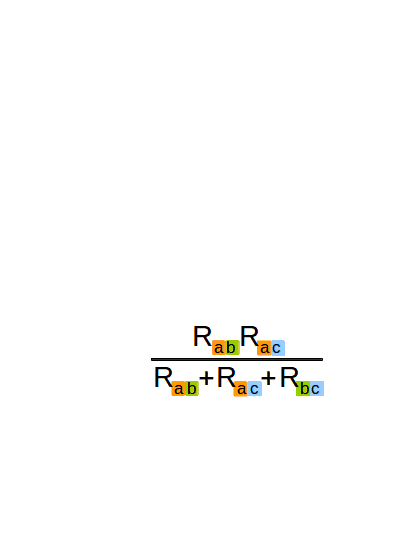П
Рис. 3. 11. 3.12.
ри соединении треугольником (рис.
4.11.) каждая фаза приемника подключена
к двум линейным проводам, поэтому каждое
фазное напряжение равно соответствующему
линейному напряжению.
Таким образом,
соединение треугольником следует
применять тогда, когда каждая фаза
трехфазного приемника рассчитана на
напряжение, равное номинальному линейному
напряжению сети.
Рис. 4.11.
Фазные токи
,
,
в общем случае не равны линейным токам
,
,
и могут быть найдены по следующим
соотношениям:
,
,
.
Линейные токи
,
,
могут быть определены через значения
фазных токов. Из первого закона Кирхгофа
запишем:
,
,
.
Использую указанные
соотношения и имея векторы фазных токов,
можно построить векторную диаграмму
линейных токов (рис. 4.12.).
При симметричной
нагрузке соединением «треугольник»
равны в отдельности активные и полные
реактивные сопротивления всех фаз
,
Однако, как правило,
однофазные приемники подключаются не
одновременно. Нагрузку можно считать
симметричной лишь тогда, когда включены
все приемники. Для каждой фазы могут
быть использованы все методы расчета,
рассмотренные ранее применительно к
однофазной цепи с одним источником.
Зная, например, фазные напряжения и
сопротивления, можно по закону Ома найти
фазные токи по формулам
,
,
При симметричной
нагрузке,
,
-фазные токи равны друг другу и сдвинуты
по фазе относительно соответствующих
фазных напряжений на одинаковые углы.
В
Рис. 3. 13.
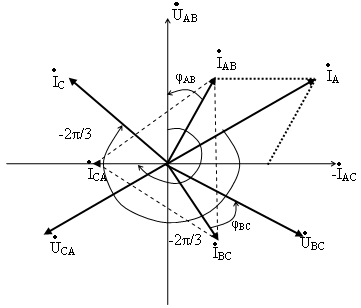
екторная диаграмма фазных напряжений
и токов на рис. 4.13. показывает, что при
симметричной нагрузке векторы фазных
токов равны по величине и сдвинуты по
фазе относительно друг друга на угол.
Векторы линейных
токов
изображают результирующими векторов
фазных токов, как показано на рис. 4.13.
Из векторной диаграммы следует, что.
Рис. 4.13.
Такое же соотношение
существует между любыми другими фазными
и линейными токами. Поэтому можно
написать, что при симметричной нагрузке
.
Зная фазные
напряжения, токи и углы сдвига фаз между
ними, либо токи и сопротивления, можно
найти фазные мощности. Например, мощности
фазы АВ будут равны
Таким же путем
находим мощности фаз ВС и СА. В силу
равенства напряжений, токов, углов
сдвига фаз и сопротивлений при симметричной
нагрузке
,
,
.
При симметричной
нагрузке активная Р,
реактивная Q
и полная S
мощности трехфазного приемника
,
,
.
В качестве
номинальных напряжений и токов трехфазных
приемников указываются обычно линейные
напряжения и токи. Учитывая это, мощности
трехфазных приемников желательно также
выражать через линейные напряжения и
токи
,
,
.
4.6. Несимметричные нагрузки при соединении треугольником
Несимметричной
нагрузкой считают такую, при которой
активное или реактивное сопротивление
хотя бы одной из фаз не равно сопротивлениям
других фаз (рис. 4.14.) rAB
= rBC
= rC;
XAB=XBC≠X
CA.
В таком
случае при несимметричной нагрузке ZAB
≠ ZBC
≠ ZCA.
Фазные токи, углы
сдвига фаз между фазными напряжениями
и токами, а также мощности могут быть
определены по формулам
,
,
Так как,
а при несимметричной нагрузкеZAB
≠ ZBC
≠ ZCA,
то.
Рис. 4.14.
Углы сдвига фаз
между фазными токами и напряжениями
зависят от величины и характера
сопротивлений фаз и могут быть определены
следующим образом
;
;
.
Т.о., при несимметричной
нагрузке фазные токи, углы сдвига фаз
и фазные мощности в общем случае
различные.
Зная фазные
напряжения, токи и углы сдвига фаз между
ними, либо токи и сопротивления, можно
найти фазные мощности. Например, мощности
фазы AB
Активные и реактивные
мощности приемника
;
.
Векторная диаграмма
при несимметричной нагрузке для случая,
когда в фазе AB
имеется активное сопротивление, в фазе
BC
– активное и индуктивное сопротивления,
фазе CA
– активное и емкостное сопротивления,
приведена на рис. 4.15. Построение векторов
линейных токов произведено в соответствии
с выражениями
,
,
.
Е
кроме фазных токов, требуется определить
линейные токи, то их можно так же
определить по векторной диаграмме, не
прибегая к решению задачи в комплексной
форме.
Рис. 4.15.
О
Рис. 3. 15.
тключение нагрузки одной из фаз
можно считать частным случаем
несимметричной нагрузки, при которой
сопротивление отключенной фазы равно
бесконечности. Так при отключении фазыCA
сопротивление Z
CA
= ∞. При этом, ток
;
фазные токи,
а также углыφAB,
φ BC
не изменятся, а линейные токи
уменьшатся и будут равны
,
.
Как провести преобразование треугольника в звезду и обратно
Содержание
- 1 Общие положения
- 2 Типы соединений в электрических схемах
- 3 От треугольника к звезде
- 4 Если звёзды преобразовывают, то это кому-нибудь нужно
- 5 Заключение
- 6 Видео по теме
Расчёты электрических цепей, проводимые на стадии проектирования или при выполнении ремонтных работ, позволяют определить значения напряжений и величины токов на любых участках цепи. Существует несколько расчётных методов, опирающихся на закон Ома (ЗО) и правила Кирхгофа (ПК). Для упрощения вычислений на отдельных участках схем, имеющих структуру соединений отличную от параллельных или последовательных, часто применяется преобразование из «треугольника» в «звезду» и обратно.
Общие положения
Основным физическим законом, на котором базируются расчёты цепей различного типа сложности, является ЗО. Он был открыт немецким учёным Г. Омом (1789–1854) в 1827 г.
Математическое представление закона Ома
На основании открытия Ома и закона сохранения электрического заряда немецкий исследователь Г. К. Кирхгоф (1824–1887) сформулировал два полезных правила, которым часто присваивают статус законов, хотя это не вполне корректно, так как они являются следствием более фундаментальных явлений. Иногда эти правила называют уравнениями соединений.
Правила Кирхгофа
На основании ПК для любой электрической схемы может быть составлена система математических уравнений, где в качестве неизвестных будут выступать токи I, в ветвях электрической цепи. Предполагается, что сопротивления (нагрузки) R и напряжение источника тока E известны.
Типы соединений в электрических схемах
Основные типы соединений элементов (потребителей) электрических цепей следующие:
- Последовательное.
- Параллельное.
- Смешанное.
Первые два типа представлены на рисунке ниже.
Формулы для токов и напряжений при последовательном и параллельном соединениях
Понятно, что смешанный тип соединения представляет собой комбинацию параллельных и последовательных участков.
Примеры смешанных соединений
Алгоритм расчёта токов на основе ЗО и ПК хорошо работает, когда вся электрическая схема состоит из участков смешанных соединений с разным количеством нагрузок (сопротивлений). Формулы для фрагментов схем, изображённых на рисунках 03 и 04, просты и удобны для анализа схем. Однако, некоторые схемные решения не всегда имеют такой вид. К таковым относятся, например, участки схем в виде треугольника и звезды.
Соединения треугольник и звезда
Видно, что в этих конфигурациях при подключении компонентов не наблюдаются исключительно параллельные или последовательные цепочки. В англоязычной литературе вместо треугольника используется термин «дельта» и обозначение соответствующей греческой буквой Δ, а звезда обозначается английской буквой Y. В таких случаях очень удобным оказывается метод преобразования «электрического» треугольника в звезду (Δ в Y). Соответственно, возможно и обратное преобразование из звезды в эквивалентный ей треугольник (Y в Δ).
От треугольника к звезде
Чаще возникает потребность в преобразовании Δ в Y. Суть замены состоит в том, что потенциалы трёх точек А, В, С и токи, втекающие или вытекающие из них, должны остаться изначальными. Поэтому окружающая цепь не «почувствует» никаких изменений.
Уравнения для преобразований
На рисунке выше приведены формулы, с помощью которых можно осуществить корректный переход (замену) треугольника сопротивлений в эквивалентную звезду (Δ в Y) или обратно Y в Δ. Для вывода формул составляется система уравнений на основе ПК, где в качестве неизвестных выступают сопротивления RA, RB, RC (случай Δ в Y). Решением системы уравнений будут значения сопротивлений звезды RA, RB, RC, выраженные через значения сопротивлений в треугольнике RAВ, RBС, RАС.
Если звёзды преобразовывают, то это кому-нибудь нужно
В качестве примера применения метода на рисунке ниже приведена мостовая схема с набором сопротивлений R1, R2, R3, R4, R5.
Исходная схема
Для сопротивлений А, В, С можно применить, рассматриваемый метод, то есть, преобразование треугольника в эквивалентную звезду (Δ в Y).
Выбор треугольника АВС
С помощью формул вычисляются сопротивления звезды RA, RB, RC.
Вычисление сопротивлений звезды
Таким образом, трансформировав треугольник в звезду, получим схему, изображённую на рисунке ниже.
Схема после преобразования
После подстановки вместо RA, RB, RC их числовых значений, рассчитанных ранее, получается простая, эквивалентная схема, содержащая только последовательные и параллельные цепочки.
Окончательный результат
Заключение
Преобразование треугольник-звезда представляет собой математический алгоритм по замене отдельных участков цепей с помощью эквивалентных сопротивлений с целью упрощения схемы для проведения расчётов с последовательными и/или параллельными комбинациями резисторов. Этот метод, конечно, не является единственно возможным при анализе подобных электрических схем. Задача может решаться «в лоб» с помощью ПК или с привлечением методов контурных токов или узловых потенциалов.
Рассмотренные преобразования часто используют для расчётов мостовых схем, которые находят своё применение при измерении не только сопротивлений, но и ёмкостей и индуктивностей.
Видео по теме


Методы расчета резисторных схем постоянного тока
3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»
Рассматриваемый метод основан на том, что сложную схему, имеющую три вывода (узла), можно заменить другой, с тем же числом выводов (узлов). Замену следует произвести так, чтобы сопротивление участка между двумя любыми выводами новой схемы было таким же, как у прежней. В результате получится цепь, сопротивление которой эквивалентно сопротивлению данной по условию. Общее сопротивление обеих цепей будет одинаковым. Однако, поскольку в результате такого преобразования изменяются токи внутри цепи, такую замену можно проводить только в тех случаях, когда не надо находить распределение токов.
Подобные преобразования широко известны для случая двух выводов. Так, например, два резистора сопротивлениями R1 и R2, включенные последовательно, можно заменить одним резистором сопротивлением R1 + R2. Если резисторы включены параллельно, то их можно заменить одним резистором сопротивлением
$frac{R_1R_2}{R_1 + R_2}$
И в этих случаях распределение токов в цепи (или в части цепи) претерпевает изменения. Рассмотрим более сложное преобразование схем, имеющих три вывода (трехполюсников). Иначе это называется преобразованием «звезды» (рис. а) в «треугольник» (рис. б), и наоборот.
Сопротивления резисторов в схеме «звезда» обозначаются с индексом точки, с которой соединен этот резистор, например, резистор r1 соединен с точкой 1. В «треугольнике» индексы резисторов соответствуют точкам, между которыми они включены, например, резистор R13 подключен к точкам 1 и 3. Как отмечено выше, чтобы заменить одну из этих схем другой, нужно получить такие соотношения между их сопротивлениями, чтобы эквивалентные сопротивления между любыми точками были одинаковы для обеих схем (при условии сохранения числа этих точек). Так, в «звезде» сопротивление между точками 1 и 2 равно r1 + r2, в «треугольнике»
$frac{R_{12}(R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}$,
следовательно, для того чтобы сопротивления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы выполнялось следующее равенство:
$r_1 + r_2 = frac{R_{12}(R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}$.
Аналогично для точек 2 и 3 и для точек 1 и 3:
$r_2 + r_3 = frac{R_{23}(R_{12} + R_{13})}{R_{12} + R_{13} + R_{23}}$,
$r_1 + r_3 = frac{R_{13}(R_{12} + R_{23})}{R_{12} + R_{13} + R_{23}}$.
Сложим все эти уравнения и, поделив обе части на 2, получим:
$r_1 + r_2 + r_3 = frac{R_{12}R_{13} + R_{12}R_{23} + R_{13}R_{23}}{R_{12} + R_{13} + R_{23}}$.
Вычитая из этого уравнения поочередно предыдущие, получим:
$r_1 = frac{R_{12}R_{13}}{R_{12} + R_{13} + R_{23}}$,
$r_2 = frac{R_{12}R_{23}}{R_{12} + R_{13} + R_{23}}$,
$r_3 = frac{R_{13}R_{23}}{R_{12} + R_{13} + R_{23}}$.
Эти выражения легко запомнить:
знаменатель в каждой формуле есть сумма сопротивлений всех резисторов «треугольника», а в числителе дважды повторяется индекс, стоящий слева:
$r_1 rightarrow R_{12}R_{13}, r_2 rightarrow R_{12}R_{23}, r_3 rightarrow R_{13}R_{23}$.
Аналогично получают и формулы обратного преобразования:
$R_{12} = frac{r_1r_2 + r_1r_3 + r_2r_3}{r_3}$,
$R_{13} = frac{r_1r_2 + r_1r_3 + r_2r_3}{r_2}$,
$R_{23} = frac{r_1r_2 + r_1r_3 + r_2r_3}{r_1}$.
Последние выражения также легко запомнить и проверить:
числитель у всех уравнений один и тот же, а в знаменателе стоит сопротивление резистора с индексом, которого не достает в левой части выражения.
Этот метод представляет собой наиболее универсальный подход к решению практически всех типов задач на разветвленные цепи.
Задача 27. Определите сопротивление цепи АВ (рис.), если R1 = R5 = 1 Ом, R2 = R6 = 2 Ом, R3 = R7 = 3 Ом, R4 = R8 = 4 Ом.
Решение. Преобразуем «треугольники» R1R2R8 и R4R5R6 в эквивалентные «звезды». Схема примет иной вид (рис.).
Сопротивления $r_1, r_2, …, r_6$ найдем по формулам:
$r_1 = frac{R_1R_8}{R_1 + R_2 + R_8} = frac{4}{7}$ Ом;
$r_2 = frac{R_1R_2}{R_1 + R_2 + R_8} = frac{2}{7}$ Ом;
$r_3 = frac{R_2R_8}{R_1 + R_2 + R_8} = frac{8}{7}$ Ом;
$r_4 = frac{R_4R_6}{R_4 + R_5 + R_6} = frac{8}{7}$ Ом;
$r_5 = frac{R_5R_6}{R_4 + R_5 + R_6} = frac{2}{7}$ Ом;
$r_6 = frac{R_4R_5}{R_4 + R_5 + R_6} = frac{4}{7}$ Ом.
Теперь нет никаких препятствий для расчета схемы, которая состоит из последовательно и параллельно соединенных резисторов (рис.). После простых расчетов получим
$R_{AB} = frac{47}{14}$ Ом
1.1. Шаговый (рекуррентный) метод
1.2. Метод преобразования
1.3. Метод равнопотенциальных узлов
1.3.1. Метод исключения «пассивных» участков цепи
1.3.2. Метод объединения равнопотенциальных узлов
1.3.3. Метод разделения узлов
1.3.4. Метод расщепления ветвей
1.4.1 Расчет эквивалентных сопротивлений линейных бесконечных цепей
1.4.2. Расчет эквивалентных сопротивлений плоскостных бесконечных цепей
1.4.3. Расчет эквивалентных сопротивлений объемных бесконечных цепей
2. Расчет цепей по правилам Кирхгофа
3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»

4 инструмента крутого Кирхгофщика
Внимание! Чтобы увидеть ответы на вопросы, кликните по ним. Кликать надо по тексту, а не по пустому месту. Чтобы сменить картинку, кликните по кнопке. Если ответ на вопрос вам не ясен, советую хорошо подумать, прежде чем смотреть ответ.
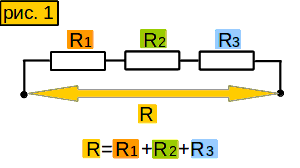
Инструмент 1. Вычисление сопротивления цепи из нескольких последовательно соединённых сопротивлений
Просто, как ….. Сложил все эти сопротивления и получил сопротивление цепи.
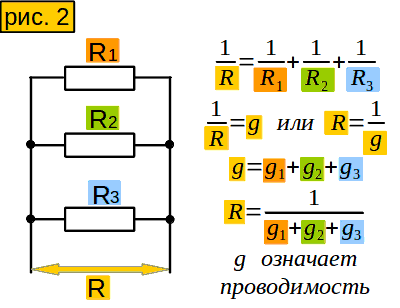
Инструмент 2. Вычисление сопротивления участка из нескольких параллельно соединённых сопротивлений
Рассмотрим участок с двумя параллельными одинаковыми сопротивлениями. Сопротивление его в два раза меньше, чем каждого сопротивления. Если сопротивлений три, сопротивление участка будет в три раза меньше.
Какую тут можно провести аналогию?
Несколько одинаковых дырок. Через них протечёт воды в столько раз больше, чем через одну дырку, сколько дырок имеется.
А как быть, если сопротивления не одинаковые? Есть такое понятие – проводимость. Оно означает величину, обратную сопротивлению. (рисунок 2)
Так если сопротивление больше, то проводимость что?
меньше
Чтобы вычислить проводимость нашего участка, надо сложить проводимости сопротивлений. Потом можно легко найти сопротивление участка.
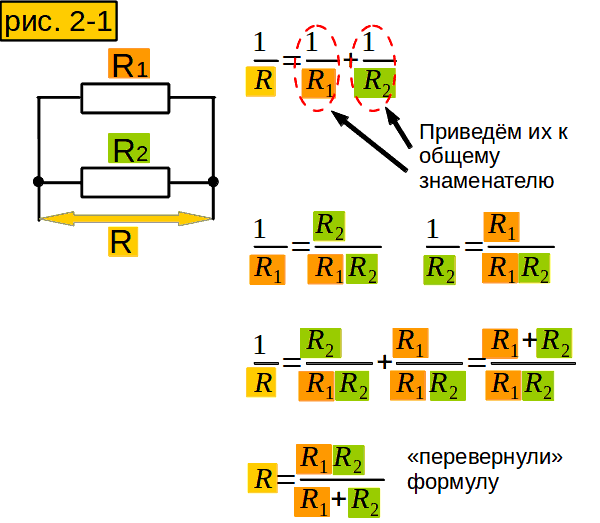
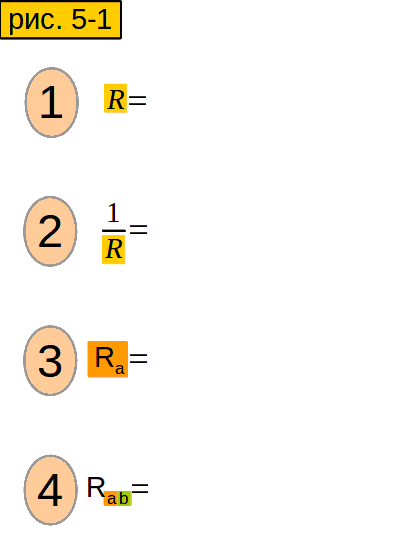
А нельзя ли вычислить сопротивление участка, не преобразуя сопротивления в проводимости, а потом обратно? Можно. Пусть у нас участок из двух параллельно соединённых сопротивлений (рис. 2-1). Проводимость его равна сумме проводимостей сопротивлений (1 строчка). Приведём проводимости сопротивлений к общему знаменателю (2 строчка). Сложим их и получим суммарную проводимость (3 строчка). “Переворачиваем” формулу (4 строчка) и получаем формулу для участка из двух параллельно соединённых сопротивлений. А если сопротивлений не два, а больше?
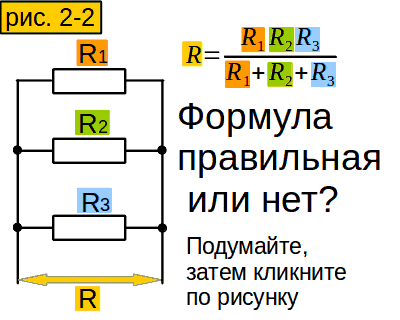

Сформулируйте своими словами формулу сопротивления участка из нескольких параллельных сопротивлений, чтобы лучше её запомнить.
Надо умножить все сопротивления, и разделить на сумму произведений этих сопротивлений, но в каждом этом произведнии одного сопротивления не хватает. Вы, может быть, и получше сформулируете.
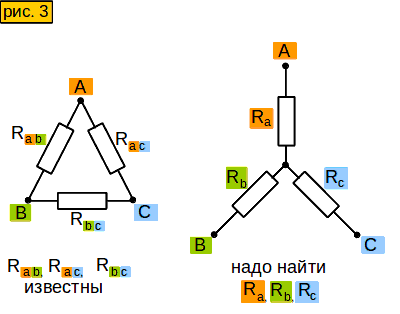
Инструмент 3. Преобразование “треугольника” в “звезду”
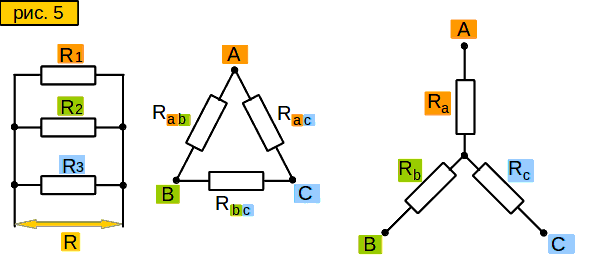
Пусть у нас в схеме есть вот такой участок цепи – “треугольник” (рис. 3, слева). Нам надо заменить его участком вот такого вида – “звездой” (рис. 3, справа), но чтобы сопротивления между сторонами “звезды” были такими же, как между соответствующими лучами “треугольника”. Зачем это нужно? Позже узнаете.
Смотрим на “звезду” на рис. 3. Допустим, мы знаем сопротивления между точками
A и B, то есть (Ra+Rb);
A и C, то есть (Ra+Rc);
B и C, то есть (Rb+Rc).
Чему будут равны сопротивления Ra, Rb, Rc ?
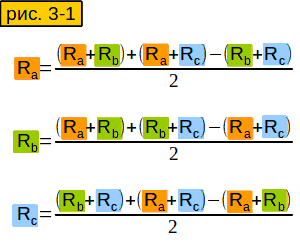
Зная все сопротивления между концами лучей “звезды”, мы можем вычислить сопротивление каждого отдельного луча.
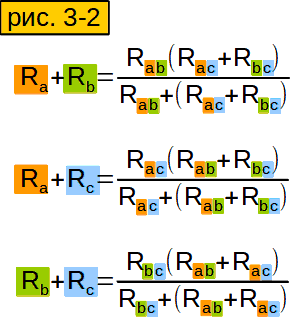
Теперь будем вычислять сопротивления между точками A, B, и C (звезды) через сопротивления треугольника, которые нам известны (рис. 3-2). Для начала вычислим сопротивление между точками A и B звезды (рис. 3-2 верхняя строчка). В нашем треугольнике мы имеем два параллельно включённых сопротивления – Rab и (Rac+Rbc). Вычислять их общее сопротивление мы умеем (ответы на вопросы 3 и 4). Вычисляем сопротивления между точками A и C, B и C (2 и 3 строчки). Обратите внимание, что во всех формулах знаменатель одинаковый.
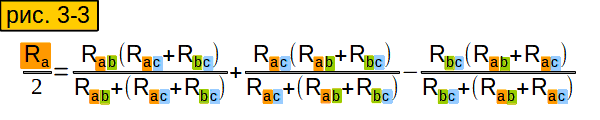
Теперь можно вычислить сопротивление отдельного луча (рис. 3-3). Формула получилась очень громоздкая, но мы её хорошенько подсократим.
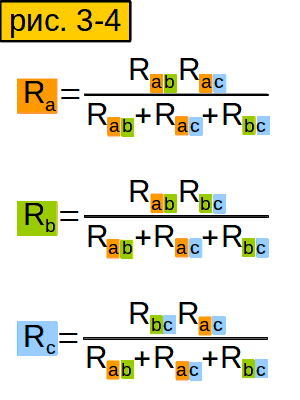
И получим вот такую стройную и изящную формулу (рис. 3-4, верхняя строчка). Аналогично вычисляем сопротивления других лучей звезды.
Сформулируйте своими словами формулу из рисунка 3-4, чтобы лучше её запомнить.
Чтобы найти сопротивление луча “звезды”, надо умножить сопротивления сторон “треугольника”, которые “прилегают” (“имеют ту же букву”), и разделить на сумму сопротивлений всех сторон “треугольника”.
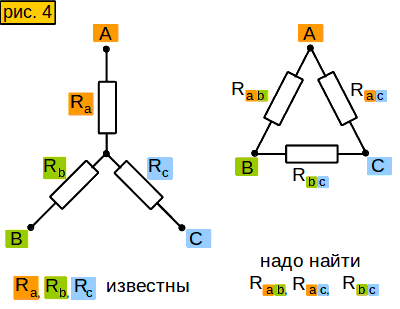
Инструмент 4. Преобразование “звезды” в “треугольник”
Иногда полезно делать обратное преобразование – “звезды” в “треугольник”. Нельзя ли вычислить сопротивление стороны “треугольника” через сопротивления эквивалентной “звезды”, используя формулы, которые мы уже вывели? Можно. Смотрим рисунок 3-4. Проделаем с формулами этого рисунка следующий трюк: попарно их перемножим и результаты сложим (смотрим рис. 4-1).
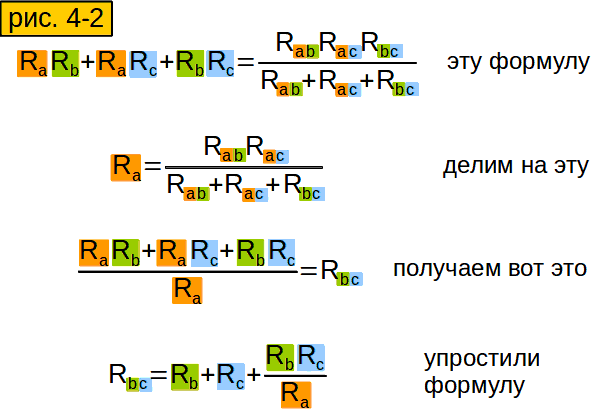
Затем результат разделим на верхнюю формулу рисунка 3-4. Получится у нас вот что: рисунок 4-2, третья сверху формула. Маленько её подсократим и получим нижнюю формулу.
Как раз то, что нам надо!
Сопротивления других сторон “треугольника” выводятся аналогично (рисунок 4-3).
Сформулируйте своими словами формулу из рисунка 4-3, чтобы лучше её запомнить.
Чтобы найти сопротивление стороны “треугольника”, надо сложить сопротивления соответствующих сторон “звезды” (у которых “те же буквы”), и ещё прибавить произведение тех же сторон “звезды”, делёное на оставшуюся сторону.
Зубрилка
об ошибках сообщайте по адресу obuchmat@mail.ru
Продолжение следует
На домашнюю страницу
Из векторной диаграммы цепи с последовательным соединением имеем треугольник напряжений:
,
где cos j – коэффициент мощности, .
Согласно закону Ома ;
;
.
Делим каждую сторону треугольника напряжений на ток и получаем треугольник сопротивлений:
;
;
;
.
Умножаем каждую сторону треугольника напряжений на ток, и получаем треугольник мощностей:
;
;
;
,
здесь P – активная мощность [Вт]; S – полная мощность, вырабатываемая источником [ВА]; Q – реактивная мощность [ВАр].
Коэффициент мощности показывает, насколько эффективно и рационально используется энергия. Р характеризует ту часть энергетического процесса, в которой электрическая энергия потребляется приемником и преобразуется в другие виды энергии, т.е. в полезные дела. Q характеризует ту часть энергетического процесса, которая связана с изменением энергии электрического поля емкости или магнитного поля индуктивности. Реактивная мощность не совершает полезной работы, т.к. электрическая энергия не преобразуется в другие виды энергии.