Методы расчета линейных электрических цепей
 Закон
Закон
Ома
– падение напряжения на элементе равно
произведению величины сопротивления
этого элемента на величину тока,
протекающего через него.
Первый
закон Кирхгофа
–
сумма токов, втекающих в узел, равна
сумме токов, вытекающих из узла.
Второй
закон Кирхгофа
– в замкнутом контуре алгебраическая
сумма напряжений источников электрической
энергии равна алгебраической сумме
падений напряжений на элементах контура.
При обходе контура в произвольно
выбранном направлении значения
напряжений берутся с плюсом, если
направление обхода контура и направления
напряжений совпадают и берутся с
минусом, если этого совпадения нет.
Расчет методом эквивалентного преобразования
Этот
метод применяется для не очень сложных
пассивных электрических цепей, такие
цепи встречаются довольно часто, и
поэтому этот метод находит широкое
применение. Основная идея метода состоит
в том, что электрическая цепь
последовательно преобразуется
(“сворачивается”) до одного
эквивалентного элемента, как это
показано на рис. 1.13, и определяется
входной ток. Затем осуществляется
постепенное возвращение к исходной
схеме (“разворачивание”) с
последовательным определением токов
и напряжений.
Последовательность
расчёта:
1.
Расставляются условно–положительные
направления токов и напряжений.
2.
Поэтапно эквивалентно преобразуются
участки цепи. При этом на каждом этапе
во вновь полученной после преобразования
схеме расставляются токи и напряжения
в соответствии с п. 1.
3.
В результате эквивалентного преобразования
определяется величина эквивалентного
сопротивления цепи.
4.
Определяется входной ток цепи с помощью
закона Ома.
5.
Поэтапно возвращаясь к исходной схеме,
последовательно находятся все токи и
напряжения.
Рассмотрим
этот метод на примере (рис. 1.15). В
исходной схеме расставляем
условно–положительные направления
токов в ветвях и напряжений на элементах.
Нетрудно согласиться, что под действием
источника E
с указанной полярностью направление
токов и напряжений такое, какое показано
стрелками. Для удобства дальнейшего
пояснения метода, обозначим на схеме
узлы а и б. При обычном расчете это можно
не делать.
Далее
осуществляем последовательно
эквивалентное преобразование схемы.
Вначале объединяем параллельно
соединенные элементы, и находим
(рис. 1.15, б):
![]()
Затем,
объединяя все последовательно соединенные
элементы, завершаем эквивалентное
преобразование схемы (рис. 1.15, в):
![]()
В
последней схеме (рис. 1.15, в) находим
ток I1:
![]()
Теперь
возвращаемся к предыдущей схеме
(рис. 1.15, б). Видим, что найдCенный
ток I1
протекает через R1,
R2,3,
R4
и создает на них падение напряжения.
Найдем эти напряжения:
![]() .
.![]() Возвращаясь
Возвращаясь
к исходной схеме (рис. 1.15, а), видим,
что найденное напряжениеUаб
прикладывается к элементам R2
и R3.
Значит,
можем записать, что![]() U2
U2
= U3
= Uа,б
Токи
в этих элементах находят из совершенно
очевидных соотношений:
Итак,
схема рассчитана.
расчет
с помощью законов кирхгофа
Этот
метод наиболее универсален и применяется
для расчета любых цепей. при расчете
этим методом первоначально определяются
токи в ветвях, а затем напряжения на
всех элементах. токи находятся из
уравнений, полученных с помощью законов
кирхгофа. так как в каждой ветви цепи
протекает свой ток, то число исходных
уравнений должно равняться числу ветвей
цепи. число ветвей принято обозначать
через n.
часть этих уравнений записываются по
первому закону кирхгофа, а часть – по
второму закону кирхгофа. все полученные
уравнения должны быть независимыми.
это значит, чтобы не было таких уравнений,
которые могут быть получены путем
перестановок членов в уже имеющемся
уравнении или путем арифметических
действий между исходными уравнениями.
при составлении уравнений используются
понятия независимых и зависимых узлов
и контуров. рассмотрим эти понятия.
независимым
узлом
называется узел, в который входит хотя
бы одна ветвь, не входящая в другие
узлы. если число узлов обозначим через
к,
то число независимых узлов равно (к–1).
на схеме (рис. 1.16) из двух узлов только
один независим.
независимым
контуром
называется контур, который отличается
от других контуров хотя бы одной ветвью,
не входящей в другие контура. в противном
случае такой контур называется зависимым.
если
число ветвей цепи равно n,
то число независимых контуров равно
[n
–
(к–1)].
в
схеме (рис. 1.16) всего три контура, но
только два независимых контура, а третий
– зависим. выделять независимые контура
можно произвольно, т. е. в качестве
независимых контуров можно выбрать
при первом расчете одни, а при втором
расчете (повторном) – другие, которые
раньше были зависимыми. результаты
расчета будут одинаковыми.
если
по первому закону кирхгофа составить
уравнения для (к–1)
независимых узлов, а по второму закону
кирхгофа составить уравнения для [n
–
(к–1)]
независимых контуров, то общее число
уравнений будет равно:
(K–1)
+ [n
–
(K–1)]
= n.
Это
означает, что для расчёта имеется
необходимое число уравнений.
Последовательность
расчёта:
1.
Расставляем условно – положительные
направления токов и напряжений.
2.
Определяем число неизвестных токов,
которое равно числу ветвей (n).
3.
Выбираем независимые узлы и независимые
контура.
4 .
.
С помощью первого закона Кирхгофа
составляем (К–1)
уравнений для независимых узлов.
5.
С помощью второго закона Кирхгофа
составляем [n
–
(К–1)]
уравнений для независимых контуров.
При этом напряжения на элементах
выражаются через токи, протекающие
через них.
6.
Решаем составленную систему уравнений
и определяем токи в ветвях. При получении
отрицательных значений для некоторых
токов, необходимо их направления в
схеме изменить на противоположные,
которые и являются истинными.
7.
Определяем падения напряжений на всех
элементах схемы.
Рассмотрим
последовательность расчета на примере
схемы, приведенной на рис. 1.16. Учитывая
направление источника E,
расставляем условно–положительные
направления токов и напряжений. В схеме
три ветви, поэтому нам необходимо
составить три уравнения. В схеме два
узла, следовательно, из них только один
независимый. В качестве независимого
узла выберем узел 1. Для него запишем
уравнение по первому закону Кирхгофа:
I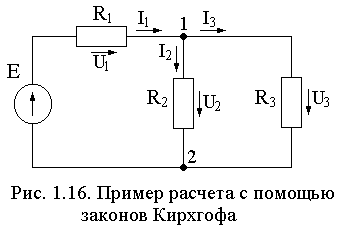 1
1
= I2
+ I3.
Далее
необходимо составить два уравнения по
второму закону Кирхгофа. В схеме всего
три контура, но независимых только два.
В качестве независимых контуров выберем
контур из элементов E–R1–R2
и контур из элементов R2–
R3.
Обходя эти два контура по направлению
движения часовой стрелки, записываем
следующие два уравнения:
E
= I1,R1
+
I2R2
,
0
= – I2R2
+ I3R3
.
Решаем
полученные три уравнения и определяем
токи в ветвях. Затем через найденные
токи по закону Ома определяем падения
напряжений на всех элементах цепи.
расчет
методом контурных токов
Сложные
схемы характеризуются наличием
значительного числа ветвей. В случае
применения предыдущего метода это
приводит к необходимости решать систему
из значительного числа уравнений.
Метод
контурных токов позволяет заметно
уменьшить число исходных уравнений.
При расчёте методом контурных токов
используются понятия независимого
контура и зависимого контура, которые
нам уже известны. Кроме них в этом методе
используются ещё следующие понятия:
– собственный
элемент контура
– элемент, относящийся только к одному
контуру;
– общий
элемент контура
– элемент, относящийся к двум и более
контурам цепи.
Обозначаем,
как и раньше, через К
число узлов, а через n
число ветвей цепи. Тогда число независимых
контуров цепи определяется по уже
известной формуле [n
–
(К–1)].
Метод
основывается на предположении, что в
каждом независимом контуре течёт
собственный контурный ток (рис. 1.17),
и вначале находят контурные токи в
независимых контурах. Токи в ветвях
цепи определяют через контурные токи.
При этом исходят из того, что в собственных
элементах контура токи совпадают с
контурным током данного контура, а в
общих элементах ток равен алгебраической
сумме контурных токов тех контуров, к
которым принадлежит данный элемент.
Последовательность
расчёта:
1.
Определяется число ветвей (n)
и число узлов (К)
цепи. Находится число независимых
контуров [n
–
(К–1)].
2.
Выбирается [n
–
(К–1)]
не зависимых контура.
3.
Выбирается условно–положительное
направление контурных токов в каждом
из независимых контуров (обычно
показывается стрелкой).
4.
Для каждого из независимых контуров
составляется уравнение по второму
закону Кирхгофа. При этом падение
напряжения на собственных элементах
определяется как произведение контурного
тока на величину сопротивления, а на
общих элементах – как произведение
алгебраической суммы всех контурных
токов, протекающих через данный элемент,
на величину его сопротивления. Обход
контура производится, как правило, в
направлении собственного контурного
тока.
5.
Решается система из [n
–
(К–1)]
уравнений и находятся контурные токи.
6.
Токи в ветвях схемы находятся следующим
образом:
– в
собственных элементах контура ток
равен контурному току;
– в
общих элементах контура ток равен
алгебраической сумме токов, протекающих
через данный элемент.
Рассмотрим
в общем виде применение этого метода
для расчёта схемы, приведенной на
рис. 1.17.
В
этой схеме три ветви и два узла,
следовательно, в ней только два
независимых контура. Выбираем эти
контура и показываем в них направления
(произвольно) контурных токов Iк1
и
Iк2.
Составляем два уравнения по второму
закону Кирхгофа:
 .
.
Решив
эту систему уравнений, находим контурные
токи Iк1
и Iк2.
Затем определяем токи в ветвях:
I1
= Iк1
, I3
= Iк2
, I2
= Iк1
– Iк2
.
РАСЧЕТ
МЕТОДОМ НАЛОЖЕНИЯ
Метод
применяется для расчета цепей, содержащих
несколько (два и более) источников
электрической энергии. Подчеркнем, что
этот метод применим для расчета только
линейных цепей. Метод основывается на
том положении, что в каждой ветви цепи
ток равен алгебраической сумме токов,
создаваемых каждым источником.
Следовательно, необходимо определить
токи, создаваемые каждым источником в
отдельности, а затем их просуммировать
с учетом направлений.
Последовательность
расчета:
1.
В электрической цепи оставляют только
один источник ЭДС. Вместо исключенного
источника ЭДС ставится или резистор,
величина которого равна величине
внутреннего сопротивления источника
ЭДС, или перемычка, если внутреннее
сопротивление источника равно нулю.
2.
Определяются токи во всех ветвях,
создаваемые этим источником ЭДС.
3.
Оставляется в цепи следующий источник
ЭДС, а с остальными поступают аналогично
тому, как сказано в п. 1.
4.
Определяются токи в цепи, создаваемые
вторым источником ЭДС.
5.
Аналогично поступают с оставшимися
источниками.
6.
Истинные токи в ветвях цепи определяются
как алгебраическая сумма токов в этих
ветвях, созданных каждым из источников.
Рассчитаем
цепь, изображенную на рис. 1.18, методом
наложения. Будем считать, что внутренние
сопротивления источников ЭДС равны
нулю.
В
начале оставляем источник E1,
а источник E2
убирается
и в место него ставится перемычка
(рис. 1.18, б). В полученной схеме
находим токи методом эквивалентного
преобразования:
![]()


![]()
![]()
Затем
оставляем только источник E2,
а вместо E1
ставится перемычка (рис. 1.18, в). В
полученной схеме определяем токи в
ветвях также методом эквивалентного
преобразования:
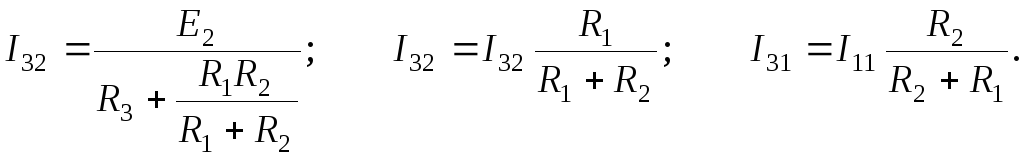
Находим
действительные токи в исходной схеме
(рис. 1.18, а) алгебраическим
суммированием найденных токов.
Ток
I1
равен разности тока I11
и тока I12:
I1
= I11
– I12.
Ток
I2
равен сумме токов I21
и I22,
т. к. они совпадают по направлению:
I2
= I21
+ I22.
Ток
I3
равен разности тока I32
и тока I31:
I3
= I32
– I31.
Соседние файлы в папке шпоргалка
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Расчет электрических цепей постоянного тока:
Основная цель расчета электрической цепи заключается в определении токов в ее ветвях. Зная токи, нетрудно найти напряжения и мощности ветвей и отдельных элементов цепи.
Величины токов, напряжений, мощностей дают возможность оценить условия и эффективность работы электротехнического оборудования и приборов во всех участках электрической цепи.
Связь между э.д.с., напряжениями и токами линейных электрических цепей выражается линейными уравнениями, т. е. уравнениями первой степени, поэтому для расчета их применяются аналитические методы с обычными алгебраическими преобразованиями.
Законы Кирхгофа
Для расчета электрических цепей наряду с законом Ома применяются два закона Кирхгофа, являющиеся следствиями закона сохранения энергии.
Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлам электрических цепей:
в ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю:

В эту сумму токи входят с разными знаками в зависимости от направления их по отношению к узлу. На основании первого закона Кирхгофа для каждого узла можно составить уравнение токов. Например, для точки 3 схемы рис. 3.16 такое уравнение имеет вид
I1 + I2 — I4 — I7 = 0.
В этом уравнении токи, направленные к узлу, условно взяты положительными, а токи, направленные от узла, — отрицательными:
I1 + I2 = I4 + I7. (4.2)
Уравнение (4.2) позволяет дать другую формулировку первого закона Кирхгофа:
сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла.
Этот закон следует из принципа непрерывности тока. Если допустить преобладание в узле токов одного направления, то заряд одного знака должен накапливаться, а потенциал узловой точки непрерывно изменяться, что в реальных цепях не наблюдается.
Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам электрических цепей:
в контуре электрической цепи алгебраическая сумма напряжений на его ветвях равна нулю:

Для доказательства второго закона Кирхгофа обойдем контур 1-2-3-4-5-6-1 в схеме рис. 3.16 по часовой стрелке и запишем выражения потенциалов точек контура при указанных направлениях токов в ветвях (выбраны произвольно). Обход начнем от точки 1, потенциал которой V1. Потенциал каждой последующей точки выразим относительно точки предыдущей: V2 = V1 + Е1; V3 = V2 — I1R1; V4 = V3 — I4R4; V5 = V4 — E3; V6 = V5 + I6R6; V1 = V6 — I3R3.
Изменение потенциала по выбранному контуру должно быть равно нулю, так как оно выражает работу, затраченную на перемещение частиц, обладающих вместе единицей заряда, по замкнутому пути в электрических полях источников и приемников энергии. Таким образом, в замкнутом контуре
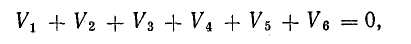
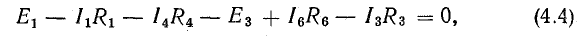
или
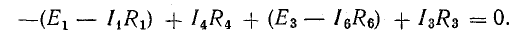
В этом уравнении напряжения ветвей
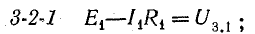
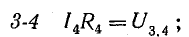
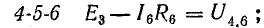
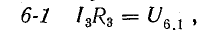
поэтому 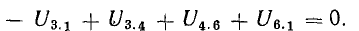
В уравнении (4.4) напряжения, направленные по обходу контура, считаются положительными, а направленные против обхода — отрицательными.
Уравнение (4.4) перепишем в следующем виде:
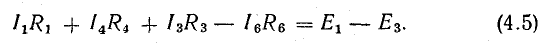
Уравнение (4.5) позволяет дать другую формулировку второго закона Кирхгофа:
в контуре электрической цепи алгебраическая сумма падений напряжения на пассивных элементах равна алгебраической сумме э. д. с. этого контура:

Другим контурам соответствуют другие уравнения, которые нетрудно написать, не прибегая к выражениям потенциалов точек контура.
Для этого можно пользоваться следующим правилом. В левую часть уравнения следует записать алгебраическую сумму падений напряжения в пассивных элементах контура, а в правую—алгебраическую сумму э.д.с., встречающихся при обходе контура.
При этом положительными считаются токи и э. д. с., направление которых совпадает с направлением обхода.
Согласно этому правилу, запишем уравнения для двух других контуров схемы, представленной на рис. 3.16:
для 1-2-3-6-1
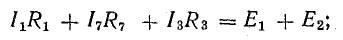
для 3-4-6-3
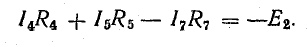
Неразветвленная электрическая цепь
Элементы неразветвленной электрической цепи соединены между собой последовательно.
Отличительной особенностью последовательного соединения является то, что электрический ток во всех участках цепи один и тот же.
Общий случай последовательного соединения
Рассмотрим общий случай последовательного соединения источников и приемников электрической энергии (рис. 4.1), пренебрегая внутренними сопротивлениями источников. Составим уравнение по второму закону Кирхгофа, произвольно задавшись направлением тока в цепи и направлением обхода контура (например, по часовой стрелке):
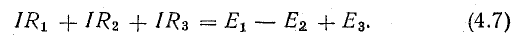
Ток в цепи

При обходе контура видно, что относительно направления обхода э. д. с. Е1 и Е3 направлены одинаково, т. е. согласно, а э. д. с. Е2 — им навстречу.
Ток в цепи определяется действием всех трех э.д.с., и при заданных направлениях э. д. с. и тока нетрудно установить, что элементы с э. д. с. E1 и Е3 вырабатывают электрическую энергию, а элемент с э. д. с. Е2 ее потребляет. Если в качестве источников э. д. с. в данном случае предположить аккумуляторы, то источники Е1 и Е3 разряжаются, а источник Е2 заряжается.
В элементах цепи, характеризующихся сопротивлениями R1, R2 и R3, электрическая энергия преобразуется в тепловую. Рассматривая в качестве примера схему рис. 4.1, нетрудно убедиться в том, что второй закон Кирхгофа является следствием закона сохранения энергии в применении его к контуру электрической цепи.
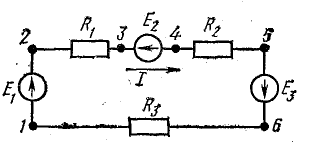
Рис. 4.1. Схема неразветвленной электрической цепи
Для этого достаточно умножить уравнение (4.7) на I, перенеся предварительно Е2 в левую часть:
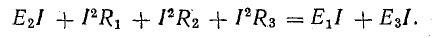
Получим уравнение баланса мощности – для рассматриваемой цепи: сумма мощностей источников электрической энергии равна сумме мощностей приемников.
Ток в цепи с последовательным соединением элементов (рис. 4.1) не изменится и баланс мощностей сохранится, если произвести перестановку элементов цепи, сгруппировав э. д. с. и сопротивления, как показано на рис. 4.2, а.
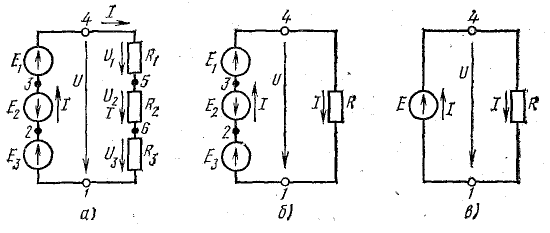
Рис. 4.2. Преобразование схемы неразветвленной электрической цепи
Последовательное соединение пассивных элементов
Участок цепи 4-5-6-1 представляет собой последовательное соединение резисторов. На рассматриваемом участке действует напряжение U, равное алгебраической сумме э. д. с. левой части схемы [см. правую часть уравнения (4.7)]. Это напряжение равно также сумме падений напряжения в правой части схемы [см. левую часть уравнения (4.7)].
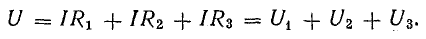
Вынеся I за скобку, получим
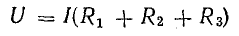
или
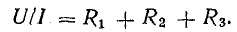
Отношение U/I = R есть некоторое сопротивление, эквивалентное по своему действию всем трем сопротивлениям:
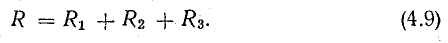
Это равенство позволяет на участке 4-5-6-1 три сопротивления заменить одним (эквивалентным) и получить более простую схему (рис. 4.2, б) при условии неизменности тока в цепи и сохранении того же баланса мощностей. Этот вывод можно распространить на любое число последовательно включенных пассивных элементов:

т. е. общее сопротивление неразветвленной цепи равно сумме сопротивлений ее участков.
Последовательное соединение источников э.д.с.
Участок 1-2-3-4 цепи на рис. 4.2, а представляет собой последовательное соединение источников э. д. с. Напряжение между точками 4-1 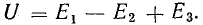
Последнее равенство позволяет на участке 1-2-3-4 три э. д. с. заменить одной (эквивалентной)

и получить более простую схему (рис. 4.2, в), в которой только одна (эквивалентная) э. д. с. Е.
Этот вывод можно распространить на любое число последовательно включенных источников. Если э. д. с. всех источников равны и направлены согласно, как это имеет место при включении аккумуляторных элементов в батарее, то общая э. д. с. может быть определена по формуле

где Еn — э. д. с. одного элемента; n — число элементов в батарее.
Согласно составленной эквивалентной схеме (рис. 4.2, в),
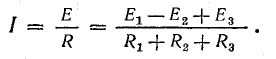
Потенциальная диаграмма
В схеме, представленной на рис. 4.1, при переходе от точки 1 к точке 2 потенциал повышается на величину Е1, а при переходе от точки 2 к точке 3 — снижается на величину U2.3 = IR1. При переходе от точки 3 к точке 4 потенциал понижается на величину U3.4 = —E2.
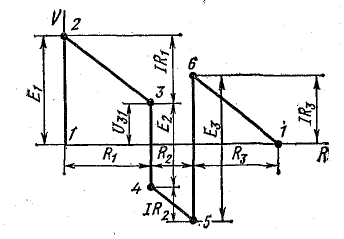
Рис. 4.3. Потенциальная диаграмма электрической цепи
Изменение потенциалов в электрической цепи можно наглядно изобразить графически в виде потенциальной диаграммы.
Потенциальная диаграмма представляет собой график изменения потенциала при обходе цепи, построенный в прямоугольной системе координат, в которой по оси абсцисс откладываются в определенном масштабе сопротивления участков цепи, а по оси ординат — потенциалы соответствующих точек. Потенциальная диаграмма цепи, изображенной на рис. 4.1, показана на рис. 4.3.
Потенциалы точек цепи найдены согласно равенствам
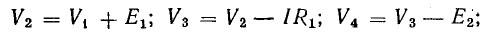
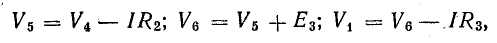
причем потенциал точки 1 принят равным нулю.
Поскольку внутренние сопротивления источников э. д. с. приняты равными нулю, при переходе через эти элементы потенциалы изменяются скачком.
Задача 4.3.
Генератор постоянного тока, аккумуляторная батарея и два резистора с постоянным сопротивлением составляют неразветвленную цепь Э. д. с. генератора Eг = 120 В; внутреннее сопротивление rг = 1,0 Ом, э. д. с. батареи Еа = 72 В, внутреннее сопротивление rа = 3 Ом, R1 = 16 Ом, R2 = 12 Ом.
Определить ток в цепи, составить баланс мощностей и построить потенциальную диаграмму цепи.
Решение. По условию задачи составлена схема (рис 4.4), из которой видно, что генератор и аккумуляторная батарея включены согласно: относительно произвольно выбранного направления обхода цепи обе э. д. с. направлены одинаково.
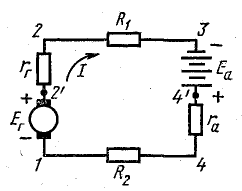
Рис. 4.4. К задаче 4.3
Эквивалентная э. д. с. цепи
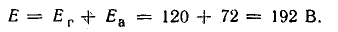
Эквивалентное внутреннее сопротивление
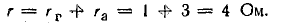
Эквивалентное сопротивление нагрузки
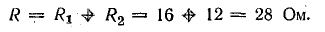
Ток в цепи
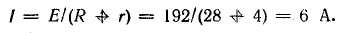
Для составления баланса мощностей найдем мощность каждого элемента цепи:
генератора
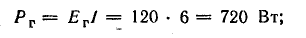
аккумуляторной батареи
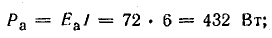
потерь внутри генератора
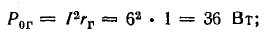
потерь внутри аккумуляторной батареи
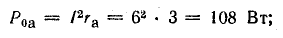
потребления в резисторе R1
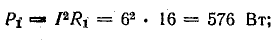
потребления в резисторе R2
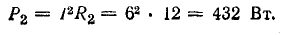
Баланс мощностей (общая мощность источников энергии равна суммарной мощности потребления)

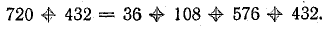
Для построения потенциальной диаграммы найдем потенциалы точек цепи, полагая потенциал точки 1 V1 = 0:
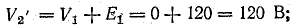
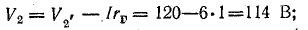
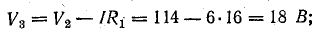
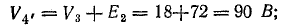
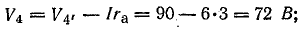
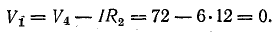
Потенциальная диаграмма показана на рис. 4.5.
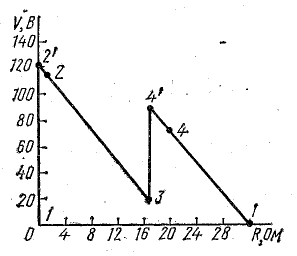
Рис. 4.5. Потенциальная диаграмма.
Разветвленная электрическая цепь с двумя узлами
Разветвленная электрическая цепь, как видно из названия, состоит из нескольких ветвей.
Ветви, присоединенные к одной паре узлов, включены параллельно (рис. 4.7, а). Отличительной особенностью параллельного соединения является то, что ко всем ветвям приложено одно и то же напряжение.
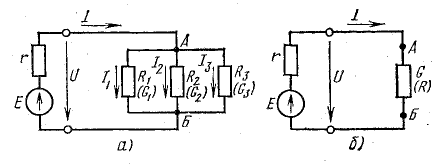
Рис. 4.7. Преобразование схемы с параллельным соединением приемников
Параллельное соединение пассивных элементов
Приемники электрической энергии, представленные на схеме рис.4. 7, а сопротивлениями R1, R2, R3 и источник электрической энергии Е с внутренним сопротивлением r подключены к одной паре узлов (точки А и Б). Составим уравнение токов для узла А в соответствии с первым законом Кирхгофа: 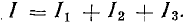
Токи приемников можно выразить, используя напряжение между узлами и проводимости ветвей:
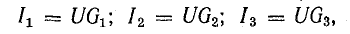
где
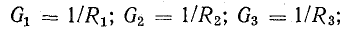
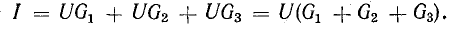
Разделим это уравнение на U:
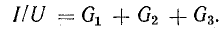
Отношение UU есть проводимость G, соответствующая общему току цепи и общему напряжению:

Этот вывод можно распространить на любое число n параллельно соединенных приемников:

При параллельном соединении пассивных ветвей общая проводимость между двумя узлами равна сумме проводимостей всех ветвей.
Исходя из формул (4.13) и (4.14), можно заменить три проводимости (в общем случае n проводимостей) одной (эквивалентной) проводимостью GО и получить более простую схему (рис. 4.7, б).
Эквивалентное сопротивление при параллельном соединении нескольких ветвей определяется из равенства
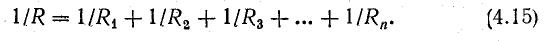
Очень часто встречается параллельное соединение двух ветвей. В этом случае эквивалентное сопротивление определяется по формуле
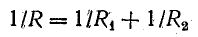
или

Схема на рис. 4.7, б, полученная после замены трех проводимостей одной (эквивалентной), представляет собой простейшую схему электрической цепи.
Ток в этой схеме, равный току в неразветвленной части (рис. 4.7,а), определяется по формуле 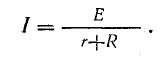
Целью расчета электрической цепи является не только определение общего тока, но и тока в каждой ветви.
Если заданы э.д.с. и все сопротивления, то после определения общего тока по формуле (3.15) нужно определить напряжение между узловыми точками и токи в ветвях по закону Ома:
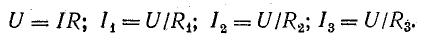
Параллельное соединение источников энергии
В практике часто встречаются случаи параллельного включения источников электрической энергии, работающих совместно на один или несколько приемников (рис. 4.8).
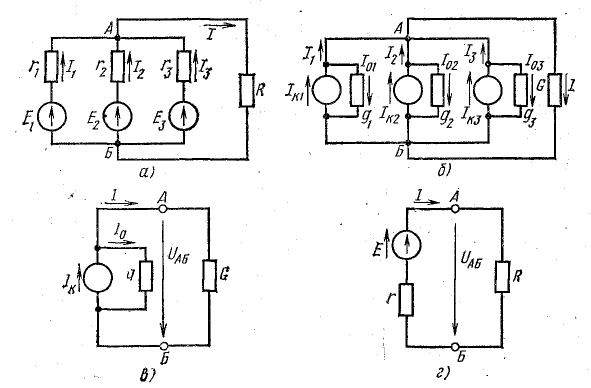
Рис. 4.8. Преобразование схемы с параллельным соединением источников
В таких случаях определением токов в источниках решается важная задача распределения нагрузки между ними.
Представим источники энергии в схеме рис. 4.8, а эквивалентными схемами источников тока, а сопротивление приемника заменим проводимостью G (рис. 4.8, б):

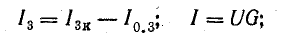


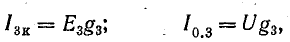
где U = Uаб — напряжение между узловыми точками А и Б.
По первому закону Кирхгофа, для узла А
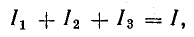
или
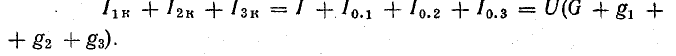
Это равенство дает основание три источника тока заменить одним (эквивалентным), а схему рис. 4.8, б заменить более простой (рис. 4.8, в). Эквивалентный источник тока характеризуется током короткого замыкания
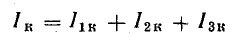
и внутренней проводимостью
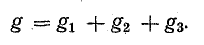
Для схемы рис. 4.8, в
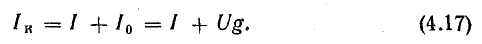
Напряжение между узлами
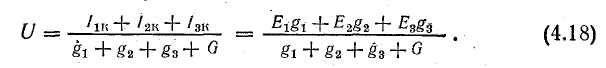
Токи в ветвях можно определить по следующим формулам:
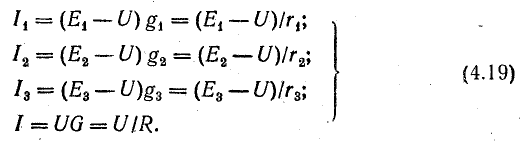
Из этих выражений следует, что источники с относительно большей э. д. с. и меньшим внутренним сопротивлением имеют больший ток, т. е. принимают на себя большую нагрузку. Если э. д. с. и внутренние сопротивления источников одинаковы, нагрузка между ними распределяется поровну.
Общий ток в этом случае определяется произведением тока одного источника In на число параллельно включенных источников:

Величина тока каждого источника ограничена его номинальным значением Iном, сверх которого нагружать источник нельзя. Параллельное соединение источников применяется для увеличения общего тока, благодаря чему достигается увеличение мощности потребления энергии без изменения напряжения.
От схемы с эквивалентным источником тока можно перейти к схеме с эквивалентным источником э. д. с. (рис. 4.8, г), разделив уравнение (4.17) на g:
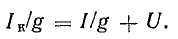
Так как l/g = r — внутреннее сопротивление эквивалентного источника э. д. с., то Iкr = Ir + U.
Но Iкr — Е — э. д. с. эквивалентного источника; Ir — падение напряжения во внутреннем сопротивлении, поэтому Е = U + Ir.
Рассматривается метод расчета разветвленных электрических цепей, предусматривающий замену всех источников э.д.с. одним (эквивалентным), который принято называть эквивалентным генератором.
Общий случай параллельного соединения источников и приемников электрической энергии
Выводы и формулы, полученные ранее, могут быть применены для расчета электрических цепей с двумя узловыми точками, между которыми содержится любое число параллельных ветвей с источниками и приемниками энергии, в том числе и такие ветви, которые имеют несколько элементов, соединенных последовательно (например, схема рис. 4.9).
Порядок расчета таких цепей, предусматривающий предварительное определение напряжения между узловыми точками, называется методом узлового напряжения.
Для применения этого метода должны быть заданы э.д.с. источников и проводимости ветвей (последние можно определить, если заданы сопротивления элементов каждой ветви).
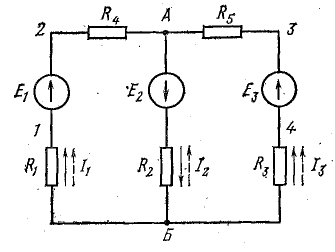
Рис. 4.9. Схема с двумя узлами
В общем случае токи в ветвях и э. д. с. могут иметь различное направление, поэтому при определении узлового напряжения нужно взять алгебраическую сумму произведений ЕG и формула (4.18) примет вид

Знак э. д. с. устанавливается в соответствии с положительным направлением токов в ветвях, которое выбирается произвольно, но одинаково для всех ветвей (например, от Б к А).
Э. д. с. ветви считается положительной, если ее направление совпадает с положительным направлением тока. В противном случае э. д. с. подставляют со знаком минус в формулу (4.21) и также при определении токов по формулам (4.19).
Задача 4.8.
Для схемы, изображенной на рис. 4.7, а, известны: Е = 130 В, r = 0,5 Ом, R1 = 30 Ом, R2 = 20 Ом, R3 = 12 Ом. Определить токи в схеме, мощность передачи энергии приемникам и к. п. д. источника.
Решение. Вначале определим эквивалентное сопротивление между точками А и Б:
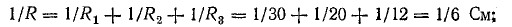
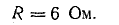
Ток в неразветвленной части цепи
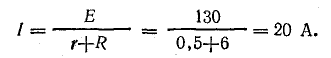
Для определения токов в параллельных ветвях между узловыми точками определим напряжение на зажимах источника, которое в данном случае равно напряжению на приемниках:
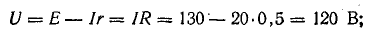
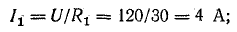
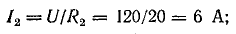
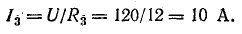
Проверим правильность определения токов по уравнению (4.1):
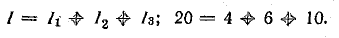
Мощность передачи энергии приемникам
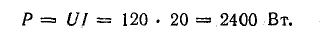
К. п. д. источника
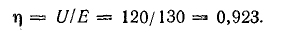
Задача 4.10.
Для схемы, изображенной на рис. 4.7, а, известны: R1 = 10 Ом; R2 = 15 Ом; R3 = 6 Ом, r = 0,5 Ом, l3 = 10 А. Определить токи в схеме, мощность и к. п. д. источника.
Решение. Используя данные условия, относящиеся к третьей ветви, определим напряжение между узлами А и Б по закону Ома:
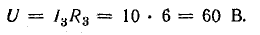
Напряжение U является общим для всех ветвей, присоединенных к точкам А и Б. Это дает возможность использовать ту же формулу для определения токов в двух ветвях:
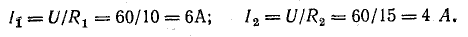
Ток в неразветвленной части цепи
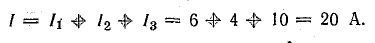
Э. д. с. источника
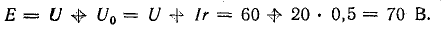
Мощность источника
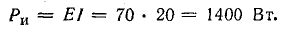
Мощность потребления энергии приемниками
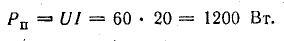
К. п. д. источника
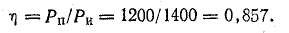
Задача 4.12.
Определить токи и составить баланс мощностей для схемы, изображенной на рис. 4.9, если известны: E1 = 120 В; E2 = 80 В; E3 = 60 В; r1 = 0,5 Ом; r2 = 0,4 Ом; r3 = 0,2 Ом; R1 = 2 Ом; R2 = 15,6 Ом; R3 = 12,4 Ом; R4 = 7,5 Ом; R5 = 7,4 Ом.
Решение. Применяя метод узлового напряжения, найдем UАБ по формуле (4.21). Предварительно зададим положительное направление токов от Б к А и подсчитаем проводимости ветвей:
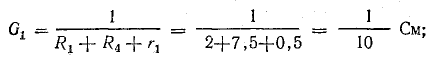
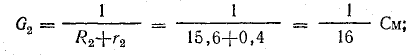
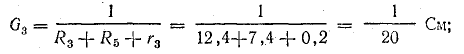
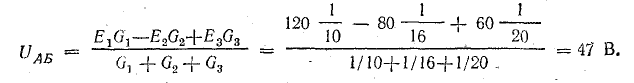
Токи в ветвях:
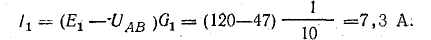
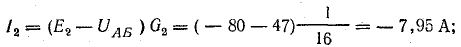
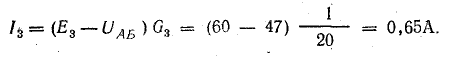
Токи l1 и l3 положительны. Их направление совпадает с выбранным ранее условно-положительным направлением от узла Б к узлу А. Направление тока l2 противоположно положительному направлению; в результате расчета этот ток получился отрицательным. На схеме рис. 4.9 пунктиром показано положительное направление токов в ветвях, а сплошной стрелкой — их действительное направление.
Для составления баланса мощностей необходимо подсчитать мощность каждого элемента схемы, в том числе и мощность потерь внутри источников. Заметим, что направления э. д. с. и токов во всех ветвях совпадают — источники Э. д. с. являются источниками энергии.
Мощности источников: P1.1 = E1I1 = 120 • 7,3 = 876 Вт; P1.2 = Е2I2 = 80 • 7,95 = 636 Вт; Р1.3 = E3I3 = 60 • 0,65 = 39 Вт.
Общая мощность источников 1551 Вт.
При определении мощности источников можно не задумываться над тем, в каком режиме работает тот или другой источник. Ответ на этот вопрос дает знак полученной мощности, если токи и э. д. с. подставлять с теми знаками, какие были приняты или получены в расчете. Например, мощность второго источника положительна: P1.2 = —80 • (—7,95) = 636 Вт. Это указывает на то, что в данной ветви работает источник энергии. Раньше Е2 и I2 сразу были взяты положительными, так как отмечено совпадение направлений напряжения и тока.
Мощность потерь внутри источников: 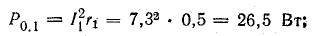
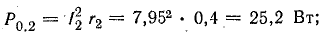
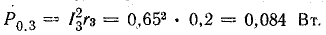
Общая мощность потерь внутри источников приблизительно 52 Вт. Мощность приемников:
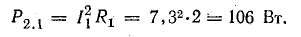
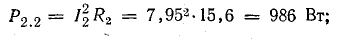
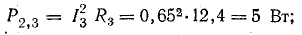
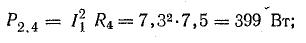
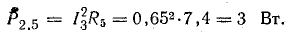
Общая мощность приемников 1499 Вт.
Баланс мощностей (мощность источников равна мощности приемников плюс мощность потерь внутри источников) 1551 Вт = 1499 + 52 Вт.
Расчет электрических цепей методом эквивалентных сопротивлений (метод «свертывания» цепи)
Метод эквивалентных сопротивлений применяется для расчета таких электрических цепей, в которых имеются пассивные элементы, включенные между собой последовательно, параллельно или по смешанной схеме.
Определение эквивалентных сопротивлений
На схеме рис. 4.10, а сопротивления R3 и R4 включены последовательно: между ними (в точке 3) нет ответвления с током, поэтому I3 = I4. Эти два сопротивления можно заменить одним (эквивалентным), определив его как сумму 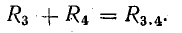
После такой замены получается более простая схема (рис. 4.10, б). Сопротивления R2 и R3.4 соединены параллельно, их можно заменить одним (эквивалентным), определив его по формуле (4.16):
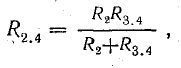
и получить более простую схему (рис. 4.10, в).
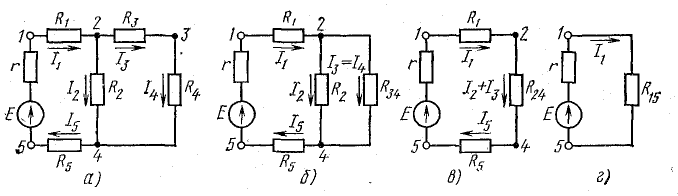
Рис. 4.10. К методу эквивалентных сопротивлений
В схеме рис. 4.10, в сопротивления R1, К2.4, К5 соединены последовательно. Заменив эти сопротивления одним (эквивалентным) сопротивлением между точками 1 и 5, получим простейшую схему (рис. 4.10, г).
Подобными преобразованиями схему смешанного соединения пассивных элементов с одним источником энергии в большинстве случаев можно привести к простейшей схеме. В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает расчет.
Определение токов
В простейшей схеме (рис. 4.10, г) ток I определяется по закону Ома с использованием формулы (3.15). Токи в других ветвях первоначальной схемы определяют, переходя от схемы к схеме в обратном порядке.
Из схемы рис. 4.10, в видно, что
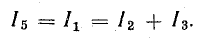
Кроме того, напряжение между точками 2 и 4
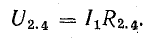
Зная это напряжение, легко определить токи I2 и I3 = I4:
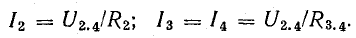
После определения токов I1 и I5 напряжение U2.4 можно найти как разность потенциалов между точками 2 и 4. Для этого положим V4 известным (например, равным нулю), а V2 найдем так же, как при построении потенциальной диаграммы, обойдя от точки 4 неразветвленный участок цепи с током I1 =I5:
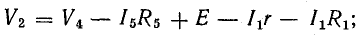
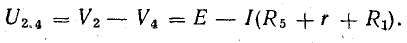
Метод преобразования треугольника и звезды сопротивлений
Пассивные элементы в электрических цепях соединяются не только последовательно или параллельно. Во многих схемах можно выделить группы из трех элементов, образующих треугольник или звезду сопротивлений.
При расчете подобных цепей упрощение схем выполняют известным методом эквивалентных сопротивлений, но предварительно проводят преобразование треугольника сопротивлений в эквивалентную звезду или наоборот.
Треугольник и звезда сопротивлений
Рассмотрим в качестве примера схему рис. 4 .11, а, которая применяется для измерения сопротивлений (схема моста Уитстона).
В этой схеме нет элементов, соединенных последовательно или параллельно, но имеются замкнутые контуры из трех сопротивлений (треугольники сопротивлений), причем точки, разделяющие каждую пару смежных сопротивлений, являются узловыми.
К узловым точкам a, b, c присоединен треугольник сопротивлений Rab, Rbc, Rca. Его можно заменить эквивалентной трехлучевой звездой сопротивлений Ra, Rb, Rc (на рисунке изображены штриховыми линиями), присоединенных с одной стороны к тем же точкам a, b, c, а с другой — в общей (узловой) точке e.
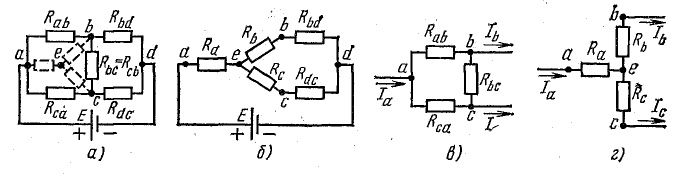
Рис. 4.11. Преобразование треугольника сопротивлений в эквивалентную звезду
Смысл замены становится понятным при рассмотрении эквивалентной схемы 4.11, б, где сопротивления Rb и Rbd соединены между собой последовательно, так же как b сопротивления Rc и Rdc.
Две ветви между узловыми точками e и d с этими парами сопротивлений соединены параллельно. Соответствующими преобразованиями схему можно привести к простейшему виду.
Преобразование треугольника сопротивлений в эквивалентную звезду
Замена треугольника сопротивлений эквивалентной звездой и наоборот осуществляется при условии, что такая замена не изменяет потенциалов узловых точек a, b, c, являющихся вершинами треугольника и эквивалентной звезды.
Одновременно предполагают, что в остальной части схемы, не затронутой преобразованием, режим работы не изменяется (не меняются токи, напряжения, мощности). Для доказательства возможности перехода от треугольника к звезде и наоборот рассмотрим схемы рис. 4.11, в, г.
Эти схемы остаются эквивалентными для всех режимов, в том числе и для режима, при котором Ia = 0, что соответствует обрыву общего провода, ведущего к точке а. В этом случае в схеме треугольника между точками b и c включены параллельно две ветви с сопротивлениями Rbc и Rab + Rca
Общее сопротивление между этими точками
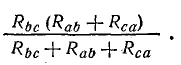
В схеме звезды между точками b и c включены последовательно сопротивления Rb и Rc. Общее сопротивление между этими точками Rb + Rc.
По условиям эквивалентности напряжение между точками b и c и токи Ib и Ic в обеих схемах должны быть одинаковыми. Следовательно, и сопротивления между точками b и c в обеих схемах одинаковы, т. е.
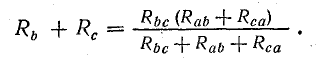
Полагая Ib =0, а затем Ic = 0, получим:
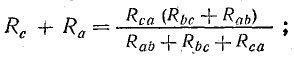
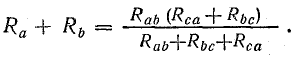
Совместное решение трех полученных уравнений приводит к следующим выражениям, которые служат для определения сопротивлений трехлучевой звезды по известным сопротивлениям эквивалентного треугольника:
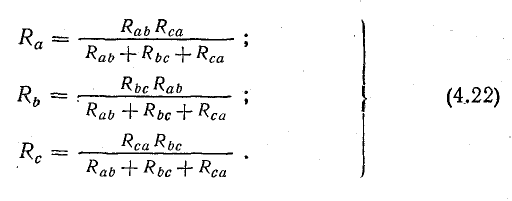
Преобразование звезды сопротивлений в эквивалентный треугольник
Для расчета некоторых схем применяется преобразование трехлучевой звезды в эквивалентный треугольник, которое показано на рис. 4.12, а, где схема взята такой же, как на рис. 4.11, а.
При этом для определения параметров треугольника по заданным параметрам звезды пользуются формулами, которые записаны применительно к схемам рис. 4.12, а, б:
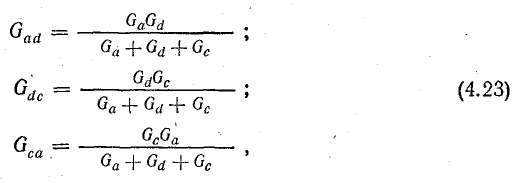
где Gad; Gdc; Gca — проводимости сторон треугольника; Ga; Gd; Gc — проводимости лучей звезды.
Зная проводимости, нетрудно определить сопротивления треугольника, если это необходимо.
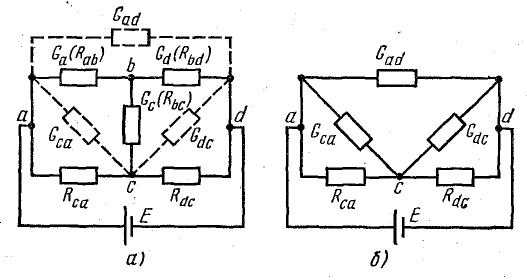
Рис. 4.12. Преобразование трехлучевой звезды в эквивалентный треугольник
- Методы анализа сложных электрических цепей
- Метод узловых напряжений
- Метод узловых потенциалов
- Принцип и метод наложения
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Электрическая цепь
- Электрический ток
Закон Ома
Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).
Онлайн калькулятор
Найти силу тока
Напряжение: U = В
Сопротивление: R = Ом

Формула
Пример
Если напряжение на концах участка цепи U = 12 В, а его электрическое сопротивление R = 2 Ом, то:
Сила тока на этом участке I = 12 /2= 6 А
Найти напряжение
Сила тока: I = A
Сопротивление: R = Ом

Формула
Пример
Если сила тока на участке цепи I = 6 А, а электрическое сопротивление этого участка R = 2 Ом, то:
Напряжение на этом участке U = 6⋅2 = 12 В
Найти сопротивление
Напряжение: U = В
Сила тока: I = A
Формула
Пример
Если напряжение на концах участка цепи U = 12 В, а сила тока на участке цепи I = 6 А, то:
Электрическое сопротивление на этом участке R = 12 /6 = 2 Ом
Закон Ома для полной цепи
Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.
Онлайн калькулятор
Найти силу тока
ЭДС: ε = В
Сопротивление всех внешних элементов цепи: R = Ом
Внутреннее сопротивление источника напряжения: r = Ом
Формула
Пример
Если ЭДС источника напряжения ε = 12 В, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
Сила тока I = 12 /4+2 = 2 А
Найти ЭДС
Сила тока: I = А
Сопротивление всех внешних элементов цепи: R = Ом
Внутреннее сопротивление источника напряжения: r = Ом
Формула
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
ЭДС ε = 2 ⋅ (4+2) = 12 В
Найти внутреннее сопротивление источника напряжения
Сила тока: I = А
ЭДС: ε = В
Сопротивление всех внешних элементов цепи: R = Ом
Внутреннее сопротивление источника напряжения: r =
Формула
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а ЭДС источника напряжения ε = 12 В, то:
Внутреннее сопротивление источника напряжения r = 12/2 — 4 = 2 Ом
Найти сопротивление всех внешних элементов цепи
Сила тока: I = А
ЭДС: ε = В
Внутреннее сопротивление источника напряжения: r = Ом
Сопротивление всех внешних элементов цепи: R =
Формула
Пример
Если сила тока в цепи I = 2A, внутреннее сопротивление источника напряжения r = 2 Ом, а ЭДС источника напряжения ε = 12 В, то:
Закон Ома для участка цепи. Закон Джоуля — Ленца. Работа и мощность электрического тока. Виды соединения проводников.
В электрической цепи происходит преобразование энергии упорядоченного движения заряженных частиц в тепловую. Согласно з-ну сохранения энергии работа тока равна количеству выделившегося тепла.
Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток:
Работа и мощность электрического тока.
Работа электрического тока:
Мощность электрического тока (работа в единицу времени):
В электричестве иногда применяется внесистемная единица работы — кВт . ч (киловатт-час).
1 кВт . ч = 3,6 . 10 6 Дж.
Виды соединения проводников.
Последовательное соединение.

1. Сила тока во всех последовательно соединенных участках цепи одинакова:
I1=I2=I3=. =In=.
2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке:
U=U1+U2+. +Un+.
3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка:
R=R1+R2+. +Rn+.
Если все сопротивления в цепи одинаковы, то:
R=R1 . N
При последовательном соединении общее сопротивление увеличивается (больше большего).
Параллельное соединение.
1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках.
2. Напряжение на всех параллельно соединенных участках цепи одинаково:
U1=U2=U3=. =Un=.
3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению):
Если все сопротивления в цепи одинаковы, то:
При параллельном соединении общее сопротивление уменьшается (меньше меньшего).
4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках:
5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках:
P=P1+P2+. +Pn+.
6. Т.к. силы тока во всех участках одинаковы, то: U1:U2. Un. = R1:R2. Rn.
Для двух резисторов: — чем больше сопротивление, тем больше напряжение.
4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках:
A=A1+A2+. +An+.
5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках:
P=P1+P2+. +Pn+.
6. Т.к. напряжения на всех участках одинаковы, то:
Для двух резисторов: ![]() — чем больше сопротивление, тем меньше сила тока.
— чем больше сопротивление, тем меньше сила тока.
Закон Ома

Физика — наука эмпирическая. Ее основные законы вытекают из практического опыта и частенько много лет не имеют теоретических обоснований. Именно так обстоит дело с главным законом электротехники, который открыл в 1826 году выдающийся немецкий ученый Георг Симон Ом.
Электрические явления люди наблюдали сотни лет. Но никак не связывали между собой заряженность потертого янтаря и молнию. Только на исходе XVIII столетия электричество стали внимательно исследовать. В 1795 году Алессандро Вольта изобрел «вольтов столб», химическую батарею, и обнаружил появление тока в проводнике, соединяющем ее полюса. Сферы применения электричества стремительно множились, и появилась острая необходимость в расчетных формулах для инженеров. Эту задачу решали многие ученые, но первым сформулировал главную формулу электротехники именно Георг Ом. Он ввел в обиход понятие сопротивления и опытным путем установил зависимость между основными характеристиками электрической цепи.
Расчет электрических цепей
Для вычисления рабочих параметров радиотехнических устройств и отдельных схем применяют специальные методики. После изучения соответствующих технологий результат можно узнать быстро, без сложных практических экспериментов. Корректный расчет электрических цепей пригодится на стадии проектирования и для выполнения ремонтных работ.

Категории элементов и устройств электрической цепи
Для условного изображения определенной цепи применяют специальную схему. Кроме отдельных физических компонентов, она содержит сведения о направлении (силе) токов, уровнях напряжения и другую информацию. Качественная модель показывает реальные процессы с высокой точностью.
Компоненты электрической цепи:
- источник постоянного или переменного тока (Е) – аккумулятор или генератор, соответственно;
- пассивные элементы (R) – резисторы;
- компоненты с индуктивными (L) и емкостными (С) характеристиками;
- соединительные провода.

На рисунке обозначены:
- ветви – участки цепи с одним током;
- узлы – точки соединения нескольких ветвей;
- контур – замкнутый путь прохождения тока.
При решении практических задач выясняют, как узнать силу тока в отдельных ветвях. Полученные значения используют для анализа электрических параметров. В частности, можно определять падение напряжения на резисторе, мощность потребления подключенной нагрузки. При расчете цепей переменного тока приходится учитывать переходные энергетические процессы, влияние частоты.
Метод расчета по законам Ома и Кирхгофа
До изучения технологий вычислений необходимо уточнить особенности типовых элементов при подключении к разным источникам питания. При постоянном токе сопротивлением индуктивности можно пренебречь. Конденсатор эквивалентен разрыву цепи. Также следует учитывать следующие различия разных видов соединений резисторов:
- последовательное – увеличивает общее сопротивление;
- параллельное – распределяет токи по нескольким ветвям, что улучшает проводимость.
Закон Ома для участка цепи
Типовая аккумуляторная батарея легкового автомобиля вырабатывает напряжение U = 12 V. Бортовой или внешний амперметр покажет соответствующее значение при измерении. Соединение клемм проводом недопустимо, так как это провоцирует короткое замыкание. Если жила тонкая (
К сведению. Результат показанного расчета пригодится для поиска подходящего резистора. Следует делать запас в сторону увеличения. По стандарту серийных изделий подойдет элемент с паспортной номинальной мощностью 5 Вт.
На практике приходится решать более сложные задачи. Так, при значительной длине линии нужно учесть влияние соединительных ветвей цепи. Через стальной проводник ток будет протекать хуже, по сравнению с медным аналогом. Следовательно, надо в расчете учитывать удельное сопротивление материала. Короткий провод можно исключить из расчета. Однако в нагрузке может быть два элемента. В любом случае общий показатель эквивалентен определенному сопротивлению цепи. При последовательном соединении Rэкв = R1 + R2 +…+ Rn. Данный метод пригоден, если применяется постоянный ток.
Закон Ома для полной цепи
Для вычисления такой схемы следует добавить внутреннее сопротивление (Rвн) источника. Как найти ток, показывает следующая формула:
Вместо напряжения (U) при расчетах часто используют типовое обозначение электродвижущей силы (ЭДС) – E.
Первый закон Кирхгофа
По классической формулировке этого постулата алгебраическая сумма токов, которые входят и выходят из одного узла, равна нулю:
I1 + I2 + … + In = 0.
Это правило действительно для любой точки соединения ветвей электрической схемы. Следует подчеркнуть, что в данном случае не учитывают характеристики отдельных элементов (пассивные, реактивные). Можно не обращать внимания на полярность источников питания, включенных в отдельные контуры.
Чтобы исключить путаницу при работе с крупными схемами, предполагается следующее использование знаков отдельных токов:
- входящие – положительные (+I);
- выходящие – отрицательные (-I).
Второй закон Кирхгофа
Этим правилом установлено суммарное равенство источников тока (ЭДС), которые включены в рассматриваемый контур. Для наглядности можно посмотреть, как происходит распределение контрольных параметров при последовательном подключении двух резисторов (R1 = 50 Ом, R2 = 10 Ом) к аккумуляторной батарее (Uакб = 12 V). Для проверки измеряют разницу потенциалов на выводах пассивных элементов:
- UR1 = 10 V;
- UR1 = 2 V;
- Uакб = 12 V = UR1 + UR2 = 10 + 2;
- ток в цепи определяют по закону Ома: I = 12/(50+10) = 0,2 А;
- при необходимости вычисляют мощность: P = I2 *R = 0,04 * (50+10) = 2,4 Вт.
Второе правило Кирхгофа действительно для любых комбинаций пассивных компонентов в отдельных ветвях. Его часто применяют для итоговой проверки. Чтобы уточнить корректность выполненных действий, складывают падения напряжений на отдельных элементах. Следует не забывать о том, что дополнительные источники ЭДС делают результат отличным от нуля.
Метод преобразования электрической цепи
Как определить силу тока в отдельных контурах сложных схем? Для решения практических задач не всегда нужно уточнение электрических параметров на каждом элементе. Чтобы упростить вычисления, используют специальные методики преобразования.
Расчет цепи с одним источником питания
Для последовательного соединения пользуются рассмотренным в примере суммированием электрических сопротивлений:
Rэкв = R1 + R2 + … + Rn.
Контурный ток – одинаковый в любой точке цепи. Проверять его можно в разрыве контрольного участка мультиметром. Однако на каждом отдельном элементе (при отличающихся номиналах) прибор покажет разное напряжение. По второму закону Кирхгофа можно уточнить результат вычислений:
E = Ur1 + Ur2 + Urn.

В этом варианте в полном соответствии с первым постулатом Кирхгофа токи разделяются и соединяются во входных и выходных узлах. Показанное на схеме направление выбрано с учетом полярности подключенного аккумулятора. По рассмотренным выше принципам сохраняется базовое определение равенства напряжений на отдельных компонентах схемы.
Как найти ток в отдельных ветвях, демонстрирует следующий пример. Для расчета приняты следующие исходные значения:
По следующему алгоритму будут определяться характеристики цепи:
- базовая формула для трех элементов:
Rобщ = R1*R2*R3/(R1*R2 + R2*R3 + R1*R3.
- подставив данные, вычисляют Rобщ = 10 * 20 * 15 / (10*20 + 20*15 +10*15) = 3000 /(200+300+150) = 4,615 Ом;
- I = 12/ 4,615 ≈ 2,6 А;
- I1 = 12/ 10 = 1,2 А;
- I2 = 12/20 = 0,6 А;
- I3 = 12/15 = 0,8 А.
Как и в предыдущем примере, рекомендуется проверить результат вычислений. При параллельном соединении компонентов должно соблюдаться равенство токов на входе и суммарного значения:
I = 1,2 + 0,6 + 0,8 = 2,6 А.
Если применяется синусоидальный сигнал источника, вычисления усложняются. При включении в однофазную розетку 220V трансформатора придется учитывать потери (утечку) в режиме холостого хода. В этом случае существенное значение имеют индуктивные характеристики обмоток и коэффициент связи (трансформации). Электрическое сопротивление (ХL) зависит от следующих параметров:
Вычисляют ХL по формуле:
Чтобы находить сопротивление емкостной нагрузки, подойдет выражение:
Следует не забывать о том, что в цепях с реактивными компонентами сдвигаются фазы тока и напряжения.
Расчет разветвленной электрической цепи с несколькими источниками питания
Пользуясь рассмотренными принципами, вычисляют характеристики сложных схем. Ниже показано, как найти ток в цепи при наличии двух источников:
- обозначают компоненты и базовые параметры во всех контурах;
- составляют уравнения для отдельных узлов: a) I1-I2-I3=0, b) I2-I4+I5=0, c) I4-I5+I6=0;
- в соответствии со вторым постулатом Кирхгофа, можно записать следующие выражения для контуров: I) E1=R1 (R01+R1)+I3*R3, II) 0=I2*R2+I4*R4+I6*R7+I3*R3, III) -E2=-I5*(R02+R5+R6)-I4*R4;
- проверка: d) I3+I6-I1=0, внешний контур E1-E2=I1*(r01+R1)+I2*R2-I5*(R02+R5+R6)+I6*R7.

Дополнительные методы расчета цепей
В зависимости от сложности устройства (электрической схемы), выбирают оптимальную технологию вычислений.
Метод узлового напряжения
Основные принципы этого способа базируются на законе Ома и постулатах Кирхгофа. На первом этапе определяют потенциалы в каждом узле. Далее вычисляют токи в отдельных ветвях с учетом соответствующих электрических сопротивлений (отдельных компонентов или эквивалентных значений). Проверку делают по рассмотренным правилам.
Метод эквивалентного генератора
Эта технология подходит для быстрого расчета тока в одной или нескольких контрольных ветвях.

В данной методике общую цепь представляют в виде источника тока с определенным напряжением и внутренним сопротивлением. Далее выполняют вычисления по контрольной ветви с применением стандартного алгоритма.
Видео
Расчет электрической цепи по закону Кирхгофа
Содержание:
Законы Кирхгофа
Уравнения, описывающие поведение электрической цепи, составляют на основе законов Кирхгофа. Они определяют связь между токами и напряжениями элементов, образующих цепь. Уравнения, составленные согласно этим законам, называют уравнениями Кирхгофа.
Первый закон Кирхгофа определяет баланс токов в узлах электрической цепи.
Он формулируется следующим образом:
Алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:
 В уравнении (3.1) токи, направленные от узла, записывают с положительным знаком. Токи, направленные к узлу, записывают со знаком минус.
В уравнении (3.1) токи, направленные от узла, записывают с положительным знаком. Токи, направленные к узлу, записывают со знаком минус.
Система уравнений по первому закону Кирхгофа, записанная для всех узлов цепи, линейно зависима. В этом легко убедиться, сложив все уравнения. Поскольку ток каждой ветви входит в два уравнения с разными знаками, сумма тождественно равна нулю. Поэтому число независимых уравнений по первому закону Кирхгофа равно  , где
, где  – число узлов цепи.
– число узлов цепи.
Второй закон Кирхгофа устанавливает баланс напряжений в контуре цепи:
Алгебраическая сумма напряжений ветвей в контуре равна нулю:

Если напряжение ветви совпадает с направлением обхода контура, то напряжению приписывают знак плюс, если же нет – знак минус. Перенесем напряжения источников напряжения, равные ЭДС этих источников, в правую часть. Уравнение (3.2) примет вид

В соответствии с последним равенством алгебраическая сумма напряжений ветвей в контуре электрической цепи равна алгебраической сумме ЭДС источников.
Число независимых уравнений, записанных по второму закону Кирхгофа, равно числу независимых контуров. Число таких контуров определяется формулой  , где
, где  – число ветвей.
– число ветвей.
Возможно вам будут полезны данные страницы:
Порядок составления уравнений но законам Кирхгофа
1. Необходимо сначала выбрать положительные направления токов и напряжений ветвей. Положительное направление тока показывают стрелкой на выводе элемента. Положительное направление напряжения показывают стрелкой, расположенной рядом с элементом. Полярности напряжений резисторов выбирают согласованными с направлениями токов. Направления токов источников напряжения выбирают совпадающими с направлениями ЭДС.
2. Записываем уравнения по первому закону Кирхгофа для  узлов.
узлов.
3. Выбираем направления обхода контуров и записываем уравнения по законам Кирхгофа. Сопротивление проводника, соединяющего элементы, очень мало по сравнению с сопротивлением резистора и игнорируется. Ячейки внутренней цепи удобно выбирать в качестве независимых цепей. Можно воспользоваться и другим способом: выбрать по порядку контуры, так, чтобы каждый следующий контур содержал, по меньшей мере, одну ветвь, не входящую в предыдущие контуры.
4. Решаем полученную систему уравнений и определяем токи и напряжения цепи.
5. После определения токов и напряжений необходимо выполнить проверку. Для этого вычисленные значения переменных подставляют в одно из уравнений, составленных по законам Кирхгофа.
При составлении уравнений в качестве неизвестных рассматривают либо токи, либо напряжения резистивных элементов.
В первом случае уравнения цепи составляют относительно неизвестных токов резистивных элементов и напряжений на источниках тока. Напряжения на резистивных элементах, входящие в уравнения по второму закону Кирхгофа, выражают через токи по закону Ома. Такой способ составления уравнений называют токов ветвей.
Число совместно решаемых уравнений в методе токов ветвей можно сократить, если контуры выбирать так, чтобы они не включали источники тока. В этом случае неизвестными будут только токи резистивных элементов, и по второму закону Кирхгофа достаточно составить  уравнений, где
уравнений, где  – количество источников тока.
– количество источников тока.
Во втором случае уравнения цепи составляются относительно напряжений резистивных элементов и токов источников напряжения. Токи резисторов представляют произведением проводимости на напряжение на резисторе. Этот способ составления уравнений называют методом напряжений ветвей.
В дальнейшем для решения задач мы будем использовать в основном метод токов ветвей.
Пример 3.1. Записать уравнения Кирхгофа для цепи, показанной на рис. 3.1.
Решение. Сначала выберем направления токов резистивных элементов и пронумеруем узлы. Неизвестными являются токи резистивных элементов  . Поэтому необходимо составить пять уравнений. Цепь содержит четыре узла; это означает, что по первому закону Кирхгофа можно составить три уравнения. Число уравнений по второму закону Кирхгофа равно двум.
. Поэтому необходимо составить пять уравнений. Цепь содержит четыре узла; это означает, что по первому закону Кирхгофа можно составить три уравнения. Число уравнений по второму закону Кирхгофа равно двум.
 Запишем уравнения по первому закону Кирхгофа для узлов 1, 2, 3. Контуры I и II выберем так, чтобы они не включали источник тока, иначе в системе уравнений появится дополнительная переменная – напряжение источника тока. Направления обхода контуров выберем совпадающими с направлением движения часовой стрелки. В результате получим систему из пяти уравнений с пятью неизвестными токами:
Запишем уравнения по первому закону Кирхгофа для узлов 1, 2, 3. Контуры I и II выберем так, чтобы они не включали источник тока, иначе в системе уравнений появится дополнительная переменная – напряжение источника тока. Направления обхода контуров выберем совпадающими с направлением движения часовой стрелки. В результате получим систему из пяти уравнений с пятью неизвестными токами:
Узел 1:  ;
;
Узел 2:  ;
;
Узел З:  ;
;
Контур I: 
Контур II: 
Для решения системы уравнений целесообразно использовать математические пакеты, например MathCAD или Matlab.
Напряжение на зажимах источника тока можно затем найти, записав уравнения для контуров, включающих  или
или 
Пример задачи с решением 3.2.
Рассчитать токи в цепи, изображенной на рис. 3.2. Номиналы элементов:  ,
, 

Решение. Сначала выберем направления токов резистивных элементов и пронумеруем узлы. В рассматриваемой схеме шесть неизвестных токов  , следовательно, необходимо составить шесть независимых уравнений. Цепь содержит четыре узла; это означает, что по первому закону Кирхгофа можно составить три уравнения. Еще три уравнения составим по второму закону Кирхгофа. Наличие источника тока учитывалось при определении числа уравнений по второму закону Кирхгофа.
, следовательно, необходимо составить шесть независимых уравнений. Цепь содержит четыре узла; это означает, что по первому закону Кирхгофа можно составить три уравнения. Еще три уравнения составим по второму закону Кирхгофа. Наличие источника тока учитывалось при определении числа уравнений по второму закону Кирхгофа.
Составим уравнения по первому закону Кирхгофа для узлов 1, 2 и 3. Уравнения по второму закону Кирхгофа запишем для контуров I, II, III. Направление обхода контуров выбираем по часовой стрелке.
В результате получим систему из шести уравнений с шестью неизвестными токами:
 В матричной форме записи:
В матричной форме записи:
 Решением системы уравнений являются следующие значения токов:
Решением системы уравнений являются следующие значения токов: 
Знак минус в численных значениях токов означает, что направление токов при заданных условиях выбрано навстречу истинному.
На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).
Услуги:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Электрические цепи постоянного тока
Содержание:
Расчет электрических цепей постоянного тока:
Основная цель расчета электрической цепи заключается в определении токов в ее ветвях. Зная токи, нетрудно найти напряжения и мощности ветвей и отдельных элементов цепи.
Величины токов, напряжений, мощностей дают возможность оценить условия и эффективность работы электротехнического оборудования и приборов во всех участках электрической цепи.
Связь между э.д.с., напряжениями и токами линейных электрических цепей выражается линейными уравнениями, т. е. уравнениями первой степени, поэтому для расчета их применяются аналитические методы с обычными алгебраическими преобразованиями.
Законы Кирхгофа
Для расчета электрических цепей наряду с законом Ома применяются два закона Кирхгофа, являющиеся следствиями закона сохранения энергии.
Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлам электрических цепей:
в ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю: 
В эту сумму токи входят с разными знаками в зависимости от направления их по отношению к узлу. На основании первого закона Кирхгофа для каждого узла можно составить уравнение токов. Например, для точки 3 схемы рис. 3.16 такое уравнение имеет вид
I1 + I2 — I4 — I7 = 0.
В этом уравнении токи, направленные к узлу, условно взяты положительными, а токи, направленные от узла, — отрицательными:
I1 + I2 = I4 + I7. (4.2)
Уравнение (4.2) позволяет дать другую формулировку первого закона Кирхгофа:
сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла.
Этот закон следует из принципа непрерывности тока. Если допустить преобладание в узле токов одного направления, то заряд одного знака должен накапливаться, а потенциал узловой точки непрерывно изменяться, что в реальных цепях не наблюдается.
Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам электрических цепей:
в контуре электрической цепи алгебраическая сумма напряжений на его ветвях равна нулю: 
Для доказательства второго закона Кирхгофа обойдем контур 1-2-3-4-5-6-1 в схеме рис. 3.16 по часовой стрелке и запишем выражения потенциалов точек контура при указанных направлениях токов в ветвях (выбраны произвольно). Обход начнем от точки 1, потенциал которой V1. Потенциал каждой последующей точки выразим относительно точки предыдущей: V2 = V1 + Е1; V3 = V2 — I1R1; V4 = V3 — I4R4; V5 = V4 — E3; V6 = V5 + I6R6; V1 = V6 — I3R3.
Изменение потенциала по выбранному контуру должно быть равно нулю, так как оно выражает работу, затраченную на перемещение частиц, обладающих вместе единицей заряда, по замкнутому пути в электрических полях источников и приемников энергии. Таким образом, в замкнутом контуре 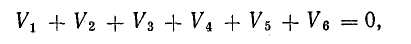
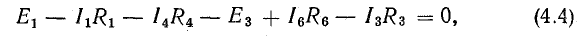
или 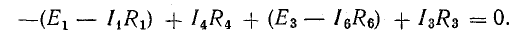
В этом уравнении напряжения ветвей 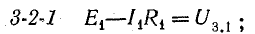
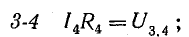
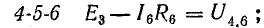
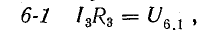
поэтому 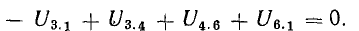
В уравнении (4.4) напряжения, направленные по обходу контура, считаются положительными, а направленные против обхода — отрицательными.
Уравнение (4.4) перепишем в следующем виде: 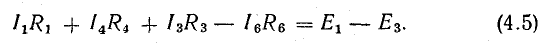
Уравнение (4.5) позволяет дать другую формулировку второго закона Кирхгофа:
в контуре электрической цепи алгебраическая сумма падений напряжения на пассивных элементах равна алгебраической сумме э. д. с. этого контура: 
Другим контурам соответствуют другие уравнения, которые нетрудно написать, не прибегая к выражениям потенциалов точек контура.
Для этого можно пользоваться следующим правилом. В левую часть уравнения следует записать алгебраическую сумму падений напряжения в пассивных элементах контура, а в правую—алгебраическую сумму э.д.с., встречающихся при обходе контура.
При этом положительными считаются токи и э. д. с., направление которых совпадает с направлением обхода.
Согласно этому правилу, запишем уравнения для двух других контуров схемы, представленной на рис. 3.16:
для 1-2-3-6-1 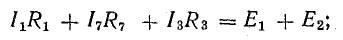
для 3-4-6-3 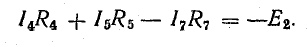
Неразветвленная электрическая цепь
Элементы неразветвленной электрической цепи соединены между собой последовательно.
Отличительной особенностью последовательного соединения является то, что электрический ток во всех участках цепи один и тот же.
Общий случай последовательного соединения
Рассмотрим общий случай последовательного соединения источников и приемников электрической энергии (рис. 4.1), пренебрегая внутренними сопротивлениями источников. Составим уравнение по второму закону Кирхгофа, произвольно задавшись направлением тока в цепи и направлением обхода контура (например, по часовой стрелке):
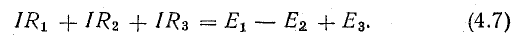
Ток в цепи 
При обходе контура видно, что относительно направления обхода э. д. с. Е1 и Е3 направлены одинаково, т. е. согласно, а э. д. с. Е2 — им навстречу.
Ток в цепи определяется действием всех трех э.д.с., и при заданных направлениях э. д. с. и тока нетрудно установить, что элементы с э. д. с. E1 и Е3 вырабатывают электрическую энергию, а элемент с э. д. с. Е2 ее потребляет. Если в качестве источников э. д. с. в данном случае предположить аккумуляторы, то источники Е1 и Е3 разряжаются, а источник Е2 заряжается.
В элементах цепи, характеризующихся сопротивлениями R1, R2 и R3, электрическая энергия преобразуется в тепловую. Рассматривая в качестве примера схему рис. 4.1, нетрудно убедиться в том, что второй закон Кирхгофа является следствием закона сохранения энергии в применении его к контуру электрической цепи.

Рис. 4.1. Схема неразветвленной электрической цепи
Для этого достаточно умножить уравнение (4.7) на I, перенеся предварительно Е2 в левую часть: 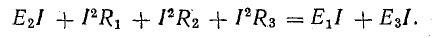
Получим уравнение баланса мощности – для рассматриваемой цепи: сумма мощностей источников электрической энергии равна сумме мощностей приемников.
Ток в цепи с последовательным соединением элементов (рис. 4.1) не изменится и баланс мощностей сохранится, если произвести перестановку элементов цепи, сгруппировав э. д. с. и сопротивления, как показано на рис. 4.2, а. 
Рис. 4.2. Преобразование схемы неразветвленной электрической цепи
Последовательное соединение пассивных элементов
Участок цепи 4-5-6-1 представляет собой последовательное соединение резисторов. На рассматриваемом участке действует напряжение U, равное алгебраической сумме э. д. с. левой части схемы [см. правую часть уравнения (4.7)]. Это напряжение равно также сумме падений напряжения в правой части схемы [см. левую часть уравнения (4.7)]. 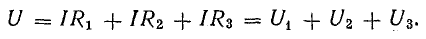
Вынеся I за скобку, получим 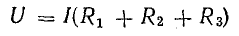
или 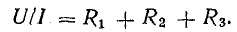
Отношение U/I = R есть некоторое сопротивление, эквивалентное по своему действию всем трем сопротивлениям: 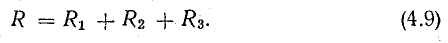
Это равенство позволяет на участке 4-5-6-1 три сопротивления заменить одним (эквивалентным) и получить более простую схему (рис. 4.2, б) при условии неизменности тока в цепи и сохранении того же баланса мощностей. Этот вывод можно распространить на любое число последовательно включенных пассивных элементов: 
т. е. общее сопротивление неразветвленной цепи равно сумме сопротивлений ее участков.
Последовательное соединение источников э.д.с.
Участок 1-2-3-4 цепи на рис. 4.2, а представляет собой последовательное соединение источников э. д. с. Напряжение между точками 4-1 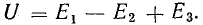
Последнее равенство позволяет на участке 1-2-3-4 три э. д. с. заменить одной (эквивалентной) 
и получить более простую схему (рис. 4.2, в), в которой только одна (эквивалентная) э. д. с. Е.
Этот вывод можно распространить на любое число последовательно включенных источников. Если э. д. с. всех источников равны и направлены согласно, как это имеет место при включении аккумуляторных элементов в батарее, то общая э. д. с. может быть определена по формуле 
где Еn — э. д. с. одного элемента; n — число элементов в батарее.
Согласно составленной эквивалентной схеме (рис. 4.2, в), 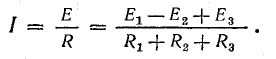
Потенциальная диаграмма
В схеме, представленной на рис. 4.1, при переходе от точки 1 к точке 2 потенциал повышается на величину Е1, а при переходе от точки 2 к точке 3 — снижается на величину U2.3 = IR1. При переходе от точки 3 к точке 4 потенциал понижается на величину U3.4 = —E2. 
Рис. 4.3. Потенциальная диаграмма электрической цепи
Изменение потенциалов в электрической цепи можно наглядно изобразить графически в виде потенциальной диаграммы.
Потенциальная диаграмма представляет собой график изменения потенциала при обходе цепи, построенный в прямоугольной системе координат, в которой по оси абсцисс откладываются в определенном масштабе сопротивления участков цепи, а по оси ординат — потенциалы соответствующих точек. Потенциальная диаграмма цепи, изображенной на рис. 4.1, показана на рис. 4.3.
Потенциалы точек цепи найдены согласно равенствам
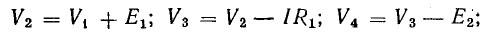
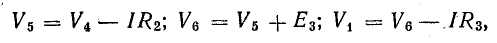
причем потенциал точки 1 принят равным нулю.
Поскольку внутренние сопротивления источников э. д. с. приняты равными нулю, при переходе через эти элементы потенциалы изменяются скачком.
Задача 4.3.
Генератор постоянного тока, аккумуляторная батарея и два резистора с постоянным сопротивлением составляют неразветвленную цепь Э. д. с. генератора Eг = 120 В; внутреннее сопротивление rг = 1,0 Ом, э. д. с. батареи Еа = 72 В, внутреннее сопротивление rа = 3 Ом, R1 = 16 Ом, R2 = 12 Ом.
Определить ток в цепи, составить баланс мощностей и построить потенциальную диаграмму цепи.
Решение. По условию задачи составлена схема (рис 4.4), из которой видно, что генератор и аккумуляторная батарея включены согласно: относительно произвольно выбранного направления обхода цепи обе э. д. с. направлены одинаково. 
Рис. 4.4. К задаче 4.3
Эквивалентная э. д. с. цепи 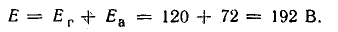
Эквивалентное внутреннее сопротивление 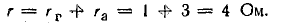
Эквивалентное сопротивление нагрузки 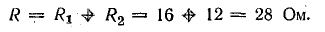
Ток в цепи 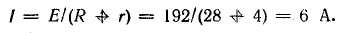
Для составления баланса мощностей найдем мощность каждого элемента цепи:
генератора 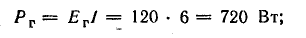
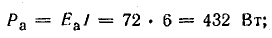
потерь внутри генератора
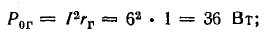
потерь внутри аккумуляторной батареи
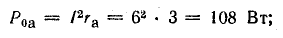
потребления в резисторе R1
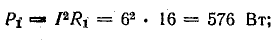
потребления в резисторе R2
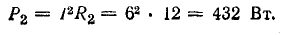
Баланс мощностей (общая мощность источников энергии равна суммарной мощности потребления) 
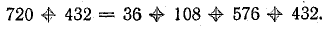
Для построения потенциальной диаграммы найдем потенциалы точек цепи, полагая потенциал точки 1 V1 = 0:
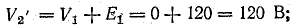
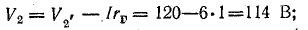
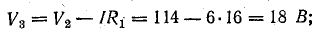
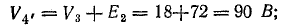
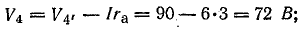
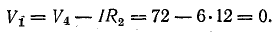
Потенциальная диаграмма показана на рис. 4.5.

Рис. 4.5. Потенциальная диаграмма.
Разветвленная электрическая цепь с двумя узлами
Разветвленная электрическая цепь, как видно из названия, состоит из нескольких ветвей.
Ветви, присоединенные к одной паре узлов, включены параллельно (рис. 4.7, а). Отличительной особенностью параллельного соединения является то, что ко всем ветвям приложено одно и то же напряжение.

Рис. 4.7. Преобразование схемы с параллельным соединением приемников
Параллельное соединение пассивных элементов
Приемники электрической энергии, представленные на схеме рис.4. 7, а сопротивлениями R1, R2, R3 и источник электрической энергии Е с внутренним сопротивлением r подключены к одной паре узлов (точки А и Б). Составим уравнение токов для узла А в соответствии с первым законом Кирхгофа: 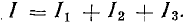
Токи приемников можно выразить, используя напряжение между узлами и проводимости ветвей: 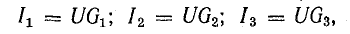
где 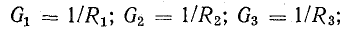
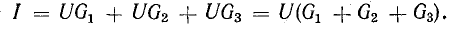
Разделим это уравнение на U: 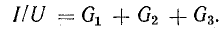
Отношение UU есть проводимость G, соответствующая общему току цепи и общему напряжению: 
Этот вывод можно распространить на любое число n параллельно соединенных приемников: 
При параллельном соединении пассивных ветвей общая проводимость между двумя узлами равна сумме проводимостей всех ветвей.
Исходя из формул (4.13) и (4.14), можно заменить три проводимости (в общем случае n проводимостей) одной (эквивалентной) проводимостью GО и получить более простую схему (рис. 4.7, б).
Эквивалентное сопротивление при параллельном соединении нескольких ветвей определяется из равенства
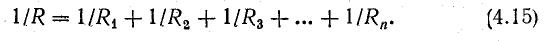
Очень часто встречается параллельное соединение двух ветвей. В этом случае эквивалентное сопротивление определяется по формуле 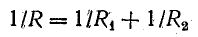

Схема на рис. 4.7, б, полученная после замены трех проводимостей одной (эквивалентной), представляет собой простейшую схему электрической цепи.
Ток в этой схеме, равный току в неразветвленной части (рис. 4.7,а), определяется по формуле 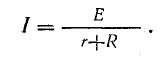
Целью расчета электрической цепи является не только определение общего тока, но и тока в каждой ветви.
Если заданы э.д.с. и все сопротивления, то после определения общего тока по формуле (3.15) нужно определить напряжение между узловыми точками и токи в ветвях по закону Ома: 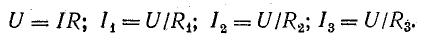
Параллельное соединение источников энергии
В практике часто встречаются случаи параллельного включения источников электрической энергии, работающих совместно на один или несколько приемников (рис. 4.8).

Рис. 4.8. Преобразование схемы с параллельным соединением источников
В таких случаях определением токов в источниках решается важная задача распределения нагрузки между ними.
Представим источники энергии в схеме рис. 4.8, а эквивалентными схемами источников тока, а сопротивление приемника заменим проводимостью G (рис. 4.8, б):

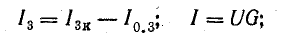


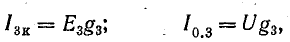
где U = Uаб — напряжение между узловыми точками А и Б.
По первому закону Кирхгофа, для узла А 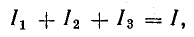
или 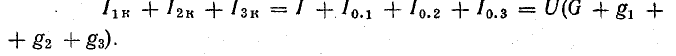
Это равенство дает основание три источника тока заменить одним (эквивалентным), а схему рис. 4.8, б заменить более простой (рис. 4.8, в). Эквивалентный источник тока характеризуется током короткого замыкания
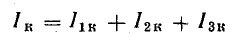
и внутренней проводимостью 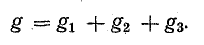
Для схемы рис. 4.8, в 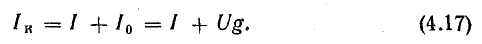
Напряжение между узлами 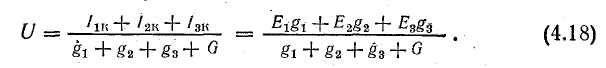
Токи в ветвях можно определить по следующим формулам:
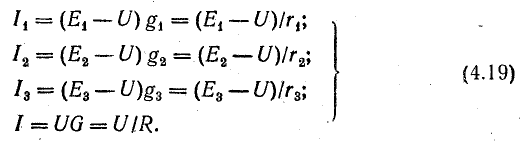
Из этих выражений следует, что источники с относительно большей э. д. с. и меньшим внутренним сопротивлением имеют больший ток, т. е. принимают на себя большую нагрузку. Если э. д. с. и внутренние сопротивления источников одинаковы, нагрузка между ними распределяется поровну.
Общий ток в этом случае определяется произведением тока одного источника In на число параллельно включенных источников: 
Величина тока каждого источника ограничена его номинальным значением Iном, сверх которого нагружать источник нельзя. Параллельное соединение источников применяется для увеличения общего тока, благодаря чему достигается увеличение мощности потребления энергии без изменения напряжения.
От схемы с эквивалентным источником тока можно перейти к схеме с эквивалентным источником э. д. с. (рис. 4.8, г), разделив уравнение (4.17) на g: 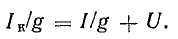
Так как l/g = r — внутреннее сопротивление эквивалентного источника э. д. с., то Iкr = Ir + U.
Но Iкr — Е — э. д. с. эквивалентного источника; Ir — падение напряжения во внутреннем сопротивлении, поэтому Е = U + Ir.
Рассматривается метод расчета разветвленных электрических цепей, предусматривающий замену всех источников э.д.с. одним (эквивалентным), который принято называть эквивалентным генератором.
Общий случай параллельного соединения источников и приемников электрической энергии
Выводы и формулы, полученные ранее, могут быть применены для расчета электрических цепей с двумя узловыми точками, между которыми содержится любое число параллельных ветвей с источниками и приемниками энергии, в том числе и такие ветви, которые имеют несколько элементов, соединенных последовательно (например, схема рис. 4.9).
Порядок расчета таких цепей, предусматривающий предварительное определение напряжения между узловыми точками, называется методом узлового напряжения.
Для применения этого метода должны быть заданы э.д.с. источников и проводимости ветвей (последние можно определить, если заданы сопротивления элементов каждой ветви). 
Рис. 4.9. Схема с двумя узлами
В общем случае токи в ветвях и э. д. с. могут иметь различное направление, поэтому при определении узлового напряжения нужно взять алгебраическую сумму произведений ЕG и формула (4.18) примет вид 
Знак э. д. с. устанавливается в соответствии с положительным направлением токов в ветвях, которое выбирается произвольно, но одинаково для всех ветвей (например, от Б к А).
Э. д. с. ветви считается положительной, если ее направление совпадает с положительным направлением тока. В противном случае э. д. с. подставляют со знаком минус в формулу (4.21) и также при определении токов по формулам (4.19).
Задача 4.8.
Для схемы, изображенной на рис. 4.7, а, известны: Е = 130 В, r = 0,5 Ом, R1 = 30 Ом, R2 = 20 Ом, R3 = 12 Ом. Определить токи в схеме, мощность передачи энергии приемникам и к. п. д. источника.
Решение. Вначале определим эквивалентное сопротивление между точками А и Б: 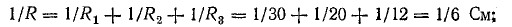
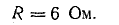
Ток в неразветвленной части цепи 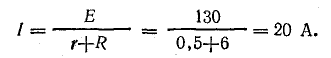
Для определения токов в параллельных ветвях между узловыми точками определим напряжение на зажимах источника, которое в данном случае равно напряжению на приемниках: 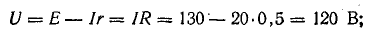
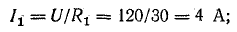
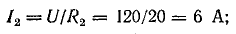
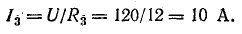
Проверим правильность определения токов по уравнению (4.1):
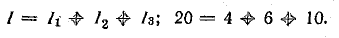
Мощность передачи энергии приемникам 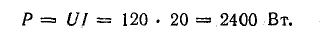
К. п. д. источника 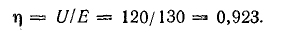
Задача 4.10.
Для схемы, изображенной на рис. 4.7, а, известны: R1 = 10 Ом; R2 = 15 Ом; R3 = 6 Ом, r = 0,5 Ом, l3 = 10 А. Определить токи в схеме, мощность и к. п. д. источника.
Решение. Используя данные условия, относящиеся к третьей ветви, определим напряжение между узлами А и Б по закону Ома: 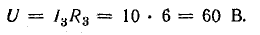
Напряжение U является общим для всех ветвей, присоединенных к точкам А и Б. Это дает возможность использовать ту же формулу для определения токов в двух ветвях: 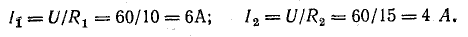
Ток в неразветвленной части цепи 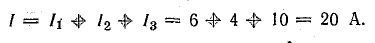
Э. д. с. источника 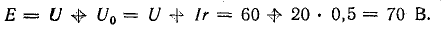
Мощность источника 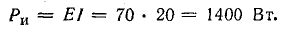
Мощность потребления энергии приемниками
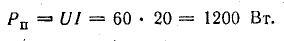
К. п. д. источника 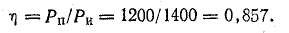
Задача 4.12.
Определить токи и составить баланс мощностей для схемы, изображенной на рис. 4.9, если известны: E1 = 120 В; E2 = 80 В; E3 = 60 В; r1 = 0,5 Ом; r2 = 0,4 Ом; r3 = 0,2 Ом; R1 = 2 Ом; R2 = 15,6 Ом; R3 = 12,4 Ом; R4 = 7,5 Ом; R5 = 7,4 Ом.
Решение. Применяя метод узлового напряжения, найдем UАБ по формуле (4.21). Предварительно зададим положительное направление токов от Б к А и подсчитаем проводимости ветвей: 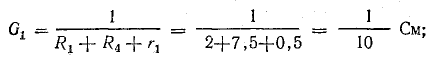
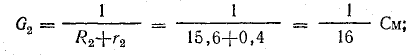
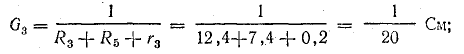
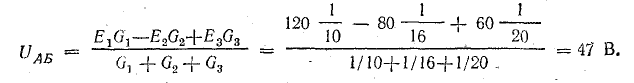
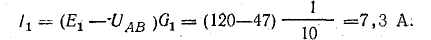
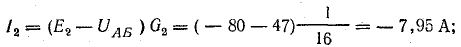
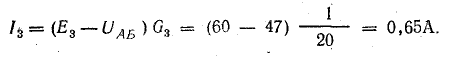
Токи l1 и l3 положительны. Их направление совпадает с выбранным ранее условно-положительным направлением от узла Б к узлу А. Направление тока l2 противоположно положительному направлению; в результате расчета этот ток получился отрицательным. На схеме рис. 4.9 пунктиром показано положительное направление токов в ветвях, а сплошной стрелкой — их действительное направление.
Для составления баланса мощностей необходимо подсчитать мощность каждого элемента схемы, в том числе и мощность потерь внутри источников. Заметим, что направления э. д. с. и токов во всех ветвях совпадают — источники Э. д. с. являются источниками энергии.
Мощности источников: P1.1 = E1I1 = 120 • 7,3 = 876 Вт; P1.2 = Е2I2 = 80 • 7,95 = 636 Вт; Р1.3 = E3I3 = 60 • 0,65 = 39 Вт.
Общая мощность источников 1551 Вт.
При определении мощности источников можно не задумываться над тем, в каком режиме работает тот или другой источник. Ответ на этот вопрос дает знак полученной мощности, если токи и э. д. с. подставлять с теми знаками, какие были приняты или получены в расчете. Например, мощность второго источника положительна: P1.2 = —80 • (—7,95) = 636 Вт. Это указывает на то, что в данной ветви работает источник энергии. Раньше Е2 и I2 сразу были взяты положительными, так как отмечено совпадение направлений напряжения и тока.
Мощность потерь внутри источников: 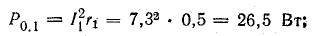
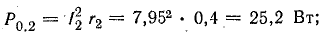
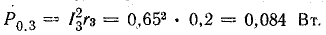
Общая мощность потерь внутри источников приблизительно 52 Вт. Мощность приемников: 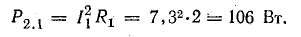
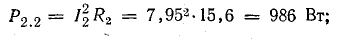
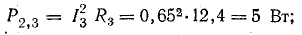
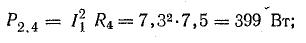
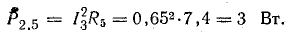
Общая мощность приемников 1499 Вт.
Баланс мощностей (мощность источников равна мощности приемников плюс мощность потерь внутри источников) 1551 Вт = 1499 + 52 Вт.
Расчет электрических цепей методом эквивалентных сопротивлений (метод «свертывания» цепи)
Метод эквивалентных сопротивлений применяется для расчета таких электрических цепей, в которых имеются пассивные элементы, включенные между собой последовательно, параллельно или по смешанной схеме.
Определение эквивалентных сопротивлений
На схеме рис. 4.10, а сопротивления R3 и R4 включены последовательно: между ними (в точке 3) нет ответвления с током, поэтому I3 = I4. Эти два сопротивления можно заменить одним (эквивалентным), определив его как сумму 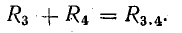
После такой замены получается более простая схема (рис. 4.10, б). Сопротивления R2 и R3.4 соединены параллельно, их можно заменить одним (эквивалентным), определив его по формуле (4.16):
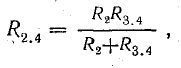
и получить более простую схему (рис. 4.10, в).

Рис. 4.10. К методу эквивалентных сопротивлений
В схеме рис. 4.10, в сопротивления R1, К2.4, К5 соединены последовательно. Заменив эти сопротивления одним (эквивалентным) сопротивлением между точками 1 и 5, получим простейшую схему (рис. 4.10, г).
Подобными преобразованиями схему смешанного соединения пассивных элементов с одним источником энергии в большинстве случаев можно привести к простейшей схеме. В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает расчет.
Определение токов
В простейшей схеме (рис. 4.10, г) ток I определяется по закону Ома с использованием формулы (3.15). Токи в других ветвях первоначальной схемы определяют, переходя от схемы к схеме в обратном порядке.
Из схемы рис. 4.10, в видно, что 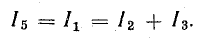
Кроме того, напряжение между точками 2 и 4 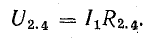
Зная это напряжение, легко определить токи I2 и I3 = I4:
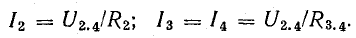
После определения токов I1 и I5 напряжение U2.4 можно найти как разность потенциалов между точками 2 и 4. Для этого положим V4 известным (например, равным нулю), а V2 найдем так же, как при построении потенциальной диаграммы, обойдя от точки 4 неразветвленный участок цепи с током I1 =I5: 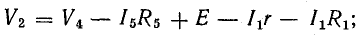
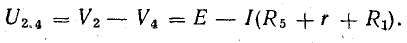
Метод преобразования треугольника и звезды сопротивлений
Пассивные элементы в электрических цепях соединяются не только последовательно или параллельно. Во многих схемах можно выделить группы из трех элементов, образующих треугольник или звезду сопротивлений.
При расчете подобных цепей упрощение схем выполняют известным методом эквивалентных сопротивлений, но предварительно проводят преобразование треугольника сопротивлений в эквивалентную звезду или наоборот.
Треугольник и звезда сопротивлений
Рассмотрим в качестве примера схему рис. 4 .11, а, которая применяется для измерения сопротивлений (схема моста Уитстона).
В этой схеме нет элементов, соединенных последовательно или параллельно, но имеются замкнутые контуры из трех сопротивлений (треугольники сопротивлений), причем точки, разделяющие каждую пару смежных сопротивлений, являются узловыми.
К узловым точкам a, b, c присоединен треугольник сопротивлений Rab, Rbc, Rca. Его можно заменить эквивалентной трехлучевой звездой сопротивлений Ra, Rb, Rc (на рисунке изображены штриховыми линиями), присоединенных с одной стороны к тем же точкам a, b, c, а с другой — в общей (узловой) точке e.

Рис. 4.11. Преобразование треугольника сопротивлений в эквивалентную звезду
Смысл замены становится понятным при рассмотрении эквивалентной схемы 4.11, б, где сопротивления Rb и Rbd соединены между собой последовательно, так же как b сопротивления Rc и Rdc.
Две ветви между узловыми точками e и d с этими парами сопротивлений соединены параллельно. Соответствующими преобразованиями схему можно привести к простейшему виду.
Преобразование треугольника сопротивлений в эквивалентную звезду
Замена треугольника сопротивлений эквивалентной звездой и наоборот осуществляется при условии, что такая замена не изменяет потенциалов узловых точек a, b, c, являющихся вершинами треугольника и эквивалентной звезды.
Одновременно предполагают, что в остальной части схемы, не затронутой преобразованием, режим работы не изменяется (не меняются токи, напряжения, мощности). Для доказательства возможности перехода от треугольника к звезде и наоборот рассмотрим схемы рис. 4.11, в, г.
Эти схемы остаются эквивалентными для всех режимов, в том числе и для режима, при котором Ia = 0, что соответствует обрыву общего провода, ведущего к точке а. В этом случае в схеме треугольника между точками b и c включены параллельно две ветви с сопротивлениями Rbc и Rab + Rca
Общее сопротивление между этими точками 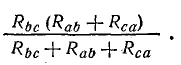
В схеме звезды между точками b и c включены последовательно сопротивления Rb и Rc. Общее сопротивление между этими точками Rb + Rc.
По условиям эквивалентности напряжение между точками b и c и токи Ib и Ic в обеих схемах должны быть одинаковыми. Следовательно, и сопротивления между точками b и c в обеих схемах одинаковы, т. е. 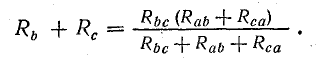
Полагая Ib =0, а затем Ic = 0, получим: 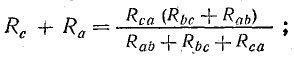
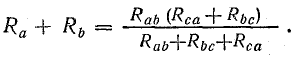
Совместное решение трех полученных уравнений приводит к следующим выражениям, которые служат для определения сопротивлений трехлучевой звезды по известным сопротивлениям эквивалентного треугольника: 
Преобразование звезды сопротивлений в эквивалентный треугольник
Для расчета некоторых схем применяется преобразование трехлучевой звезды в эквивалентный треугольник, которое показано на рис. 4.12, а, где схема взята такой же, как на рис. 4.11, а.
При этом для определения параметров треугольника по заданным параметрам звезды пользуются формулами, которые записаны применительно к схемам рис. 4.12, а, б: 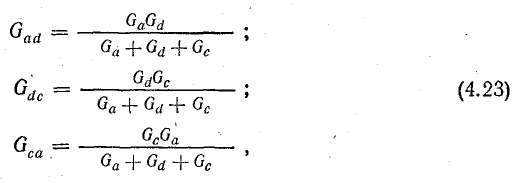
где Gad; Gdc; Gca — проводимости сторон треугольника; Ga; Gd; Gc — проводимости лучей звезды.
Зная проводимости, нетрудно определить сопротивления треугольника, если это необходимо.

Рис. 4.12. Преобразование трехлучевой звезды в эквивалентный треугольник
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Методы анализа сложных электрических цепей
- Метод узловых напряжений
- Метод узловых потенциалов
- Принцип и метод наложения
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Электрическая цепь
- Электрический ток
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://natalibrilenova.ru/raschet-elektricheskoj-tsepi-po-zakonu-kirhgofa/
http://www.evkova.org/elektricheskie-tsepi-postoyannogo-toka
[/spoiler]
Всем доброго времени суток. В прошлой статье я рассматривал типы соединений приемников энергии в электрических цепях, а так же законы Кирхгофа, которые определяют основные соотношения токов и напряжений в этих цепях. Но кроме знания основных законов электротехники необходимо уметь рассчитывать неизвестные параметры электрических цепей по заданным известным параметрам. Так, например, по известным напряжениям, ЭДС и сопротивлениям необходимо знать какую мощность будет потреблять тот или иной приемник энергии, а так же вся цепь в целом. Этим мы и займёмся в данной статье.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Расчёт электрических цепей с помощью законов Кирхгофа
Существует несколько методов расчёта электрических цепей, которые различаются между собой параметрами, которые необходимо найти, а так же количеством необходимых расчётов.
Вначале я расскажу, как произвести расчёт цепи в общем виде, но в результате размеры вычислений будут неоправданно большими. Данный метод расчёта основан на законах Ома и Кирхгофа и используется при расчётах небольших цепей с малым количеством контуров. Для этого составляют систему уравнений из (q — 1) уравнений для узлов цепи и n уравнений для независимых контуров. Независимые контуры характеризуются тем, что при составлении уравнений для каждого нового контура входит хотя бы одна новая ветвь, не вошедшая в предыдущий контур. Таким образом, количество уравнений в системе уравнений по данному методу расчёта цепи будет определяться следующим выражением
![]()
В качестве примера рассчитаем электрическую цепь, приведённую на рисунке ниже
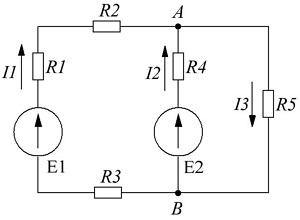
Пример электрической цепи для расчёта по законам Ома и Кирхгофа.
В качестве примера возьмём следующие параметры схемы: E1 = 50 B, E2 = 30 B, R1 = R3 = 10 Ом, R2 = R5 = 20 Ом, R4 = 25 Ом.
- Составим уравнение по первому закону Кирхгофа. Так как узла у нас два, то выберем узел А и составим для него уравнение. Я выбрал условно, что токи I1 и I2 втекают в узел, а I3 – вытекает, тогда уравнение будет иметь вид
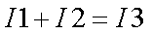
- Составим недостающие уравнения по второму закону Кирхгофа. В схеме у нас два независимых контура: E1R1R2R4E2R3 и E2R4R5, поэтому выбирая произвольное направление контуров составим недостающие два уравнения. Я выбрал обход по ходу часовой стрелке, поэтому уравнения имеют вид
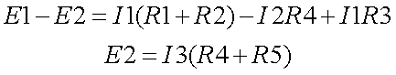
Таким образом, получившаяся система уравнений будет иметь следующий вид
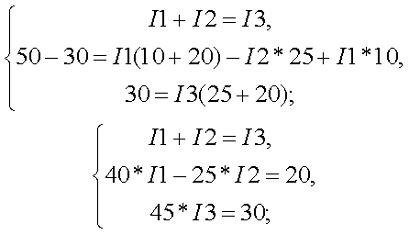
Решив данную систему, получим следующие результаты: I1 ≈ 0,564 А, I2 ≈ 0,103 А, I2 ≈ 0,667 А.
В результате решения системы уравнений по данному методу может оказаться, что токи получились отрицательными. Это значит, что действительное направление токов противоположно по направлению выбранному.
Метод контурных токов
Рассмотренный выше метод расчета электрических цепей при анализе больших и разветвленных цепей приводит к неоправданно трудоемким расчетам, поэтому редко применяется. Более широко используется метод контурных токов, позволяющий значительно сократить количество уравнений. При этом вместо токов в ветвях электрической цепи определяются так называемые контурные токи при помощи второго закона Кирхгофа. Таким образом, количество требуемых уравнений будет равняться числу независимых контуров. В качестве примера рассчитаем цепь изображённую на рисунке ниже
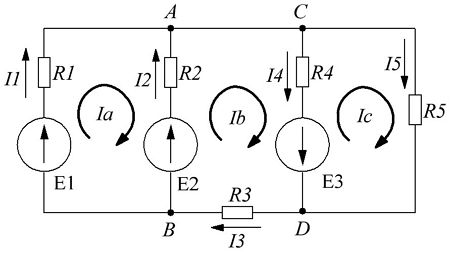
Расчет цепи методом контурных токов.
Если бы мы вели расчёт цепи по методу законов Ома и Кирхгофа, то необходимо было бы решить систему из пяти уравнений. Для расчёта по методу контурных токов необходимо всего три уравнения.
В начале расчёта выделяют независимые контуры, в нашем случае это: E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем контурам присваивают произвольно направленный контурный ток, который имеет одинаковое направление для всех участков выбранного контура, в нашем случае для первого контура контурный ток будет Ia, для второго – Ib, для третьего – Ic. Как видно из рисунка некоторые контурные токи соответствуют токам в ветвях
![]()
Остальные же токи можно найти как разность двух контурных токов
![]()
В результате выбора контурных токов можно составить систему уравнений по второму закону Кирхгофа
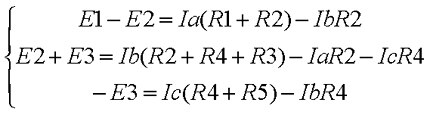
Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений
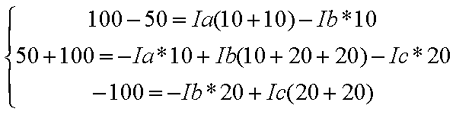
В результате решения системы получим Ia = I1 = 4,286 А, Ib = I3 = 3,571 А, Ic = I5 = -0,714 А, I2 = -0,715 А, I4 = 4,285 А. Так же как и в предыдущем случае если токи получаются отрицательными, значит действительное направление противоположно принятому. Таким образом, токи I2 и I5 имеют направление противоположное изображённым на рисунке.
Метод узловых напряжений
Кроме метода контурных токов, для уменьшения трудоемкости расчётов, применяют метод узловых напряжений, при этом возможно еще меньшее число уравнений, так как при этом методе их число достигает
![]()
где q – количество узлов в электрической цепи.
Принцип расчёта электрической цепи заключается в следующем:
- Принимаем один из узлов цепи за базисный и присваиваем ему потенциал равный нулю;
- Для оставшихся узлов составляем уравнения по первому закону Кирхгофа, заменяя токи в ветвях по закону Ома через напряжение и сопротивление;
- После решения получившейся системы уравнений вычисляем токи в ветвях по обобщенному закону Ома.
В качестве примера возьмём предыдущую цепь и составим систему уравнений
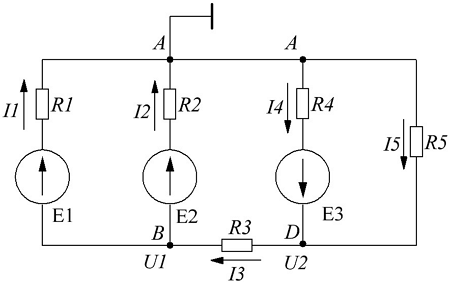
Схема для решения уравнений методом узловых потенциалов.
В качестве базисного возьмём узел А и заземлим его, для остальных узлов B и D составим уравнения по первому закону Кирхгофа
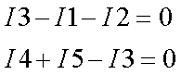
Примем потенциалы узлов В = U1 и D = U2, тогда токи в ветвях выразятся через обобщённый закон Ома
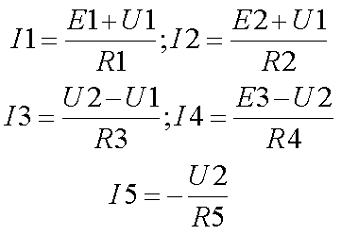
В результате получившаяся система будет иметь следующий вид
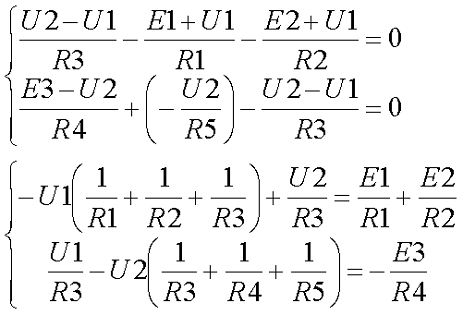
Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений
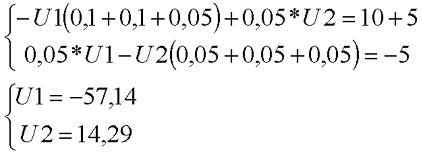
В результате решения системы уравнений мы пришли к следующим результатам: потенциал в узле В – U1 = -57,14 В, а в узле D – U2 = 14,29 В. Теперь нетрудно посчитать, что токи в ветвях будут равны
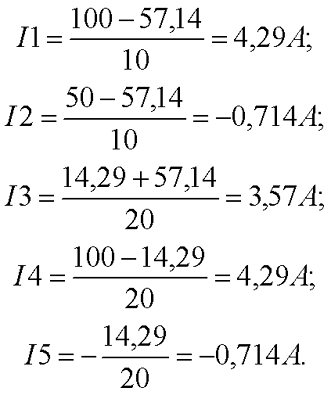
Результат решения для токов I2 и I5 получился отрицательным, так как действительное направление токов противоположно направлению, изображённому на рисунке. Данные результаты совпадают с результатами, полученными для этой же схемы при расчёте по методу контурных токов.
