Как найти толщину пластинки в опыте юнга

40

Министерство
образования и науки РФ

Государственное
образовательное учреждение

высшего
профессионального образования

Тульский
государственный университет

Кафедра физики

Муравлева Л.В.

Семин В.А.

Скотникова О.И.

МЕТОДИЧЕСКИЕ
УКАЗАНИЯ

к
практическии занятиям

по дисциплине

ФИЗИКА

Тула
2010

1. Опыт Юнга

Д

Рис.1

ва источника когерентного света S₁
и S₂,
находящиеся в некоторой среде с
показателем преломления n,
и расстояние между которыми равно 2d,
освещают экран, находящийся на расстоянии

,
светом с длиной волны 
(см. рис.1). На экране возникает
интерференционная картина в виде
чередующихся светлых полос.

Координату
светлой
полосы
(координату точки максимальной
освещенности) с номером m
можно определить по формуле

. (1.1)

Координату
темной
полосы
(координату точки минимальной освещенности)
с номером m
можно определить по формуле

. (1.2)

Ширина
полосы (или расстояние между соседними
светлыми или темными полосами с номерами
m
и
m
+
1) находится по формуле

. (1.3)

Задача 1

Рис.2

В опыте Юнга (см.рис.2) на пути каждого
интерферирующего луча, идущего в воздухе,
перпендикулярно им поместили тонкие
стеклянные пластинки толщиной h₁
= 1 мкм и h₂
=2 мкм и показателем преломления n
=1,5. При
этом центральная светлая полоса
сместилась на m
= 2 полосы.
Найти длину волны светового луча 
(в мкм).

Решение:

Рассмотрим
точку на экране, в которой наблюдается
максимум второго порядка. При этом
разность хода двух лучей, на пути которых
еще не поставили стеклянные пластинки,
равна

. (1.4)

Если
на пути первого луча поставить пластинку
толщины h₁
и показателем преломления n,
то ход первого луча станет равным

. (1.5)

Аналогично,
ход второго луча станет равным

. (1.6)

При
этом в точке, где наблюдался максимум
второго порядка, теперь наблюдается
центральный максимум, сместившийся из
своего положения на две полосы. Условием
нахождения центрального максимума
служит равенство нулю разности хода
лучей (1.6) и (1.5):

(1.7)

Подставляя
в (1.7) выражение (1.4), получим:

м.

Ответ:
0,25 мкм

1-1.
В опыте Юнга расстояние между отверстиями
d,
а расстояние от отверстий до экрана l.
Определить положение m-ой
а) светлой полосы, б) темной полосы, если
отверстия освещены монохроматическим
светом с длиной волны .

l
= 1 м; d
=
1 мм; m
= 1; 
= 0,6 мкм.

Ответы:
а) 0,6 мм; б) 0,9 мм.

1-2.
В опыте Юнга расстояние между отверстиями
d
= 1 мм, а расстояние от отверстий до экрана
l.
Отверстия освещены монохроматическим
светом с длиной волны .
Ширина интерференционной полосы x.

а)
Определить расстояние от отверстия до
экрана. x
= 1 мм; 
= 0,5 мкм; d
= 1 мм.

б)
Определить ширину интерференционной
полосы. l
= 1 м; 
= 0,6 мкм; d
= 1 мм.

в)
Определить расстояние между отверстиями.
l
=
1 м; x
= 1 мм; 
= 0,6 мкм.

г)
Определить 
(в нм).
l
= 2 м; d
= 1 мм; x
= 1 мм.

Ответы:
а) 2м; б) 0,6 мм; в) 0,6 мм; г) 500 нм.

1-3.
Во сколько раз увеличится расстояние
между соседними интерферен­цион­ны­ми
полосами на экране в опыте Юнга, если
зеленый светофильтр (₁
= 500 нм) заменить красным (₂
= 650 нм)?

Ответ:
в 1,3 раза

1-4.
Во сколько раз увеличится расстояние
между соседними интерференцион­ны­ми
полосами на экране в опыте Юнга, если
экран переместить с расстояния

на расстояние

?

= 1 м;

= 2 м.

Ответ:
2

1-5.
Во сколько раз уменьшится расстояние
между соседними интерференцион­ны­ми
полосами на экране в опыте Юнга, если
расстояние между отверстиями увеличить
от

до

?

= 1 мм;

= 2 мм.

Ответ:
2

1-6.
В опыте Юнга на пути одного из
интерферирующих лучей перпендикулярно
к нему поместили тонкую стеклянную
пластинку с показателем преломления n
=
1,5. При этом центральная светлая полоса
сместилась на m
полос. Длина волны .

а)
Найти оптическую разность хода лучей
(в мкм)? m
= 2; 
= 0,5 мкм.

б)
Найти толщину пластинки (в мкм). m
= 2; 
= 0,5 мкм.

в)
На сколько полос сместится центральная
светлая полоса?

h
= 2 мкм; 
= 0,5 мкм.

Ответы:
а) 1 мкм; б) 2 мкм; в) на 2 полосы

1-7.
В опыте Юнга на пути каждого интерферирующего
луча перпендикулярно поместили тонкие
стеклянные пластинки толщиной

и

и показателем преломления n.
При этом центральная светлая полоса
сместилась на m
полос.
Длина волны равна .

а)
Найти показатель преломления n.

= 1 мкм;

= 3 мкм; 
= 0,5 мкм; m
= 2.

б)
На сколько полос сместилась центральная
светлая полоса.

= 1 мкм;

= 3 мкм; 
= 0,5 мкм; n
=
1,5.

в)
Найти толщину пластины

(в мкм).

= 3 мкм; m
= 2; 
= 0,5 мкм; n
=
1,5.

Ответы:
а) 1,5; б) на 2 полосы; в) 1 мкм.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь  похожее условие и решить свою по аналогии.   Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.

Опыт Юнга состоит в интерференции света от двух  источников на экране. Когерентные источники в данном опыте получают путем разведения лучей от обычного источника света – сначала свет проходит через узкую щель S, дающую источник достаточно малого размера, затем он попадает на две узкие щели, расположенные симметрично, достаточно близко друг от друга – получаем когерентные источники S’ и S”.  В области перекрывания волн от этих источников размещается экран, на котором наблюдается результат интерференции – чередование темных и светлых полос, то есть областей максимума и минимума интенсивностей света.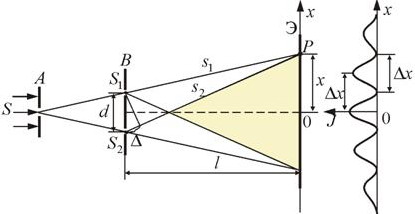

В опыте Юнга когерентные источники образованы отражением в зеркале источника, находящегося на расстоянии h  от зеркала. Расстояние до экрана равно 1м. Первоначально ширина полос на экране равна 0,3 мм, после отодвигания источника от зеркала на  дополнительное расстояние 0,6 мм ширина полос стала равной 0,2 мм. Найти длину волны света.

В опыте Юнга расстояние между щелями 0,1 мм, длина волны 0,6 мкм, ширина полос на экране 1 см. Найти расстояние от источников до экрана. 

В опыте Юнга длина волны меняется с 500 нм на 650 нм. Во сколько раз изменилась ширина полос на экране?

В опыте Юнга расстояние между источника 1 мм, расстояние от источников до экрана 3м, ширина полос на экране 1,5 мм. Найти длину волн света.

В опыте Юнга расстояние между щелями 0,5 мм, длина волны 600 нм, расстояние от источников до экрана 3м.  Найти ширину полос на экране. 

В опыте Юнга расстояние между щелями 0,1 мм, длина волны 500 нм, расстояние от источников до экрана 1,2м.  Найти ширину полос на экране. 

В опыте Юнга расстояние между источника 0,5 мм, расстояние от источников до экрана 5м, ширина полос на экране 5 мм. Найти длину волн света.

В опыте Юнга расстояние между источника 0,7 мм, расстояние от источников до экрана 4м. Сколько светлых полос поместится на ширине экрана 2 см?

В опыте Юнга на ширине экрана 1 см размещается 10 темных полос. Расстояние до экрана 1 м. Найти расстояние между источниками. 

Найти расстояние между красной и фиолетовой полосами второго порядка на экране  в опыте Юнга.

В опыте Юнга на пути лучей от источников помещают две пластинки разной толщины. В какую сторону и на сколько сместятся полосы на экране?

Ниже вы можете посмотреть видеоролик, объясняющий смысл опыта Юнга.

Формула для интерференционных максимумов в присутствии стеклянной пластинки примет вид:

где h- толщина пластинки, n-показатель преломления.
У меня есть такие данные НМ
n=1,5
Картинка, где часть слева эта интерференционная картина без пластины , а часть справа с пластиной.
Также есть величина расстояния между соседними максимумами для интерференционной картины без пластины и она равна 6.23.
Мне кажется не хватает каких-то данных, может кто-то направить, что надо сделать? Мне нужно найти толщину пластины.

Страница 1 из 4

16.1. При фотографировании спектра Солнца было найдено, что желтая спектральная линия (λ = 589нм) в спектрах, полученных от левого и правого краев Солнца, была смещена на Δλ = 0,008 нм. Найти скорость v вращения солнечного диска.

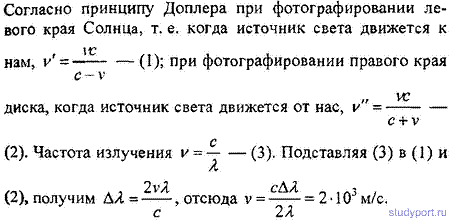
16.2. Какая разность потенциалов U была приложена между электродами гелиевой разрядной трубки, если при наблюдении вдоль пучка α-частиц максимальное доплеровское смещение линии гелия (λ = 492,2 нм) получилось равным Δλ = 0,8 нм?

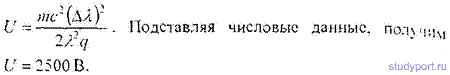
16.3. При фотографировании спектра звезды Андромеды было найдено, что линия титана (λ = 495,4им) смещена к фиолетовому концу спектра на Δλ = 0,17 нм. Как движется звезда относительно Земли?

16.4. Во сколько раз увеличится расстояние между соседними интерференционными полосами на экране в опыте Юнга, если зеленый светофильтр (λ₁=500нм) заменить красным (λ₂ = 650 нм)?

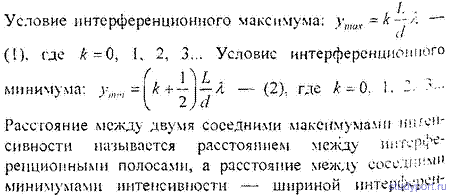
16.5. В опыте Юнга отверстия освещались монохроматическим светом (λ = 600нм). Расстояние между отверстиями d = 1мм, расстояние от отверстий до экрана L = 3m. Найти .положение трех первых светлых полос.

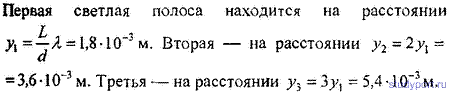
16.6. В опыте с зеркалами Френеля расстояние между мнимыми изображениями источника света d = 0,5 мм, расстояние до экрана L = 5 м. В зеленом свете получились интерференционные полосы, расположенные на расстоянии l = 5 мм друг от друга. Найти длину волны X зеленого света.

16.7. В опыте Юнга па пути одного из интерферирующих помещалась тонкая стеклянная пластинка, вследствие чего центральная светлая полоса смещалась в положение, первоначально занятое пятой светлой полосой (не считая центральной). Луч падает перпендикулярно к поверхности пластинки. Показатель преломления пластинки п = 1,5. Длина волны λ = 600 нм. Какова толщина h пластинки?

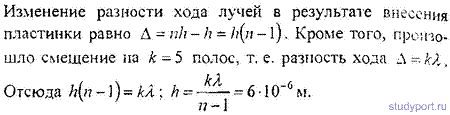
16.8. В опыте Юнга стеклянная пластинка толщиной h = 12см помещается на пути одного из интерферирующих лучей перпендикулярно к лучу. На сколько могут отличаться друг от друга показатели преломления в различных местах пластинки, чтобы изменение разности хода от этой неоднородности не превышало Δ = 1 мкм?

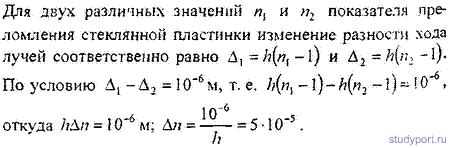
16.9. На мыльную пленку падает белый свет под углом i = 45° к поверхности пленки. При какой наименьшей толщине пленки отраженные лучи будут окрашены в желтый цвет (λ = 600 нм)? Показатель преломления мыльной воды п = 1,33.

16.10. Мыльная пленка, расположенная вертикально, образует клин вследствие стекания жидкости. При наблюдении интерференционных полос в отраженном свете ртутной дуги (λ = 546,1 нм) оказалось, что расстояние между пятью полосами l = 2 см. Найти угол γклина. Свет падает перпендикулярно к поверхности пленки. Показатель преломления мыльной воды n = 1,33.

16.11. Мыльная пленка, расположенная вертикально, образует клин вследствие стекания жидкости. Интерференция наблюдается в отраженном свете через красное стекло (λ₁ = 631 нм). Расстояние между соседними красными полосами при этом l₁ = 3 мм. Затем эта же пленка наблюдается через синее стекло (λ₂ = 400нм). Найти расстояние l₂ между соседними синими полосами. Считать, что за время измерений форма пленки не изменится и свет падает перпендикулярно к поверхности пленки.

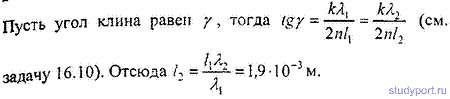
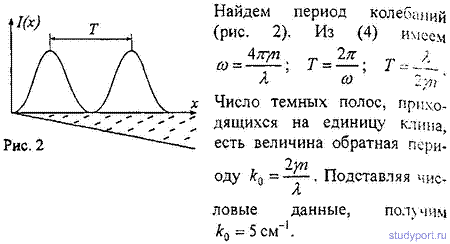
16.12. Пучок света (λ = 582 нм) падает перпендикулярно к поверхности стеклянного клина. Угол клина γ = 20°. Какое число k₀темных интерференционных полос приходится на единицу длины клина? Показатель преломления стекла n = 1,5.

16.13. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Наблюдение ведется в отраженном свете. Радиусы двух соседних темных колец равны r_k = 4,0мм и r_k+1 = 4,38 мм. Радиус кривизны линзы R = 6,4м. Найти порядковые номера колец и длину волны λ падающего света.

16.14. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Радиус кривизны линзы R=8,6. Наблюдение ведется в отраженном свете. Измерениями установлено, что радиус четвертого темного кольца (считая центральное темное пятно за нулевое) r₄= 4,5 мм. Найти длину волны λпадающего света.

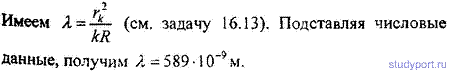
16.15. Установка для получения колец Ньютона освещается белым светом, падающим по нормали к поверхности пластинки. Радиус кривизны линзы R = 5 м. Наблюдение ведется в проходящем свете. Найти рад1гусы г_с и г_кр четвертого синего коль-^ (Я_с = 400 нм) и третьего красного кольца (Я_кр = 630 нм).

16.16. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Радиус кривизны линзы R = 15 м. Наблюдение ведется в отраженном свете. Расстояние между пятым и двадцать пятым светлыми кольцами Ньютона l = 9 мм. Найти длину волны λ монохроматического света.

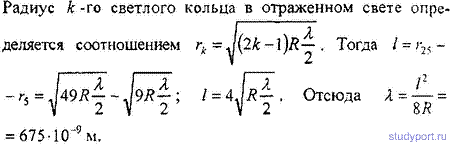
16.17. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Наблюдение идет в отраженном свете. Расстояние между вторым и двадцатым темными кольцами l₁ = 4,8 мм. Найти расстояние 1₂ между третьим и шестнадцатым темными кольцами Ньютона.

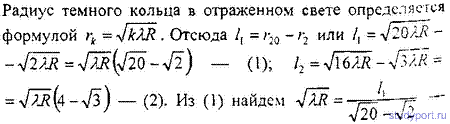
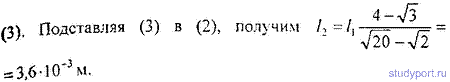
16.18. Установка для получения колец Ньютона освещается светом от ртутной дуги, падающим по нормали к поверхности пластинки. Наблюдение ведется в проходящем свете. Какое по порядку светлое кольцо, соответствующее линии λ₁ = 579,1 нм, совпадает со следующим светлым кольцом, соответствующим линии λ₂= 577 нм?

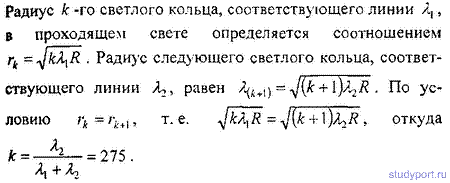
16.19. Установка для получения колец Ньютона освещается светом с длиной волны λ= 589 нм, падающим по нормали к поверхности пластинки. Радиус кривизны линзы R = 10м. Пространство между линзой и стеклянной пластинкой заполнено жидкостью. Найти показатель преломления жидкости, если радиус третьего светлого кольца в проходящем свете r₃ = 3,65 мм.

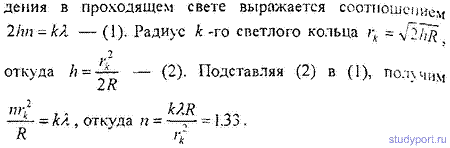
16.20. Установка для получения колец Ньютона освещается монохроматическим светом с длиной волны λ = 600нм, падающим по нормали к поверхности пластинки. Найти толщину h воздушного слоя между линзой и стеклянной пластинкой в том месте, где наблюдается четвертое темное кольцо в отраженном свете.