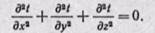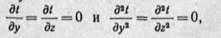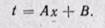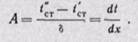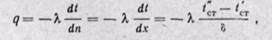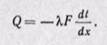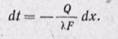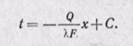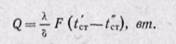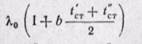14
1.1. Теплопроводность плоской стенки
1.1.1. Однослойная стенка (Рис. 1.1)
Рассматривается
однородная плоская стенка. Материал
стенки однородный, температурное поле
стационарное, одномерное. Толщина стенки
δ, остальные размеры неограниченно
велики. Коэффициент теплопроводности
известенλ = const.
Температуры на поверхности стенкиТ1иТ2.
Рис.
1.1. Теплопроводность плоской однослойной
стенки
Плотность
теплового потока, Вт/м2:
.
(1.1)
Здесь:
λ/δ,
Вт/(м2·К)– тепловая
(термическая) проводимость;
δ/λ– тепловое (термическое) сопротивление;
(Т1
–Т2)– температурный
напор.
Температура
в стенке изменяется линейно.
1.1.2.
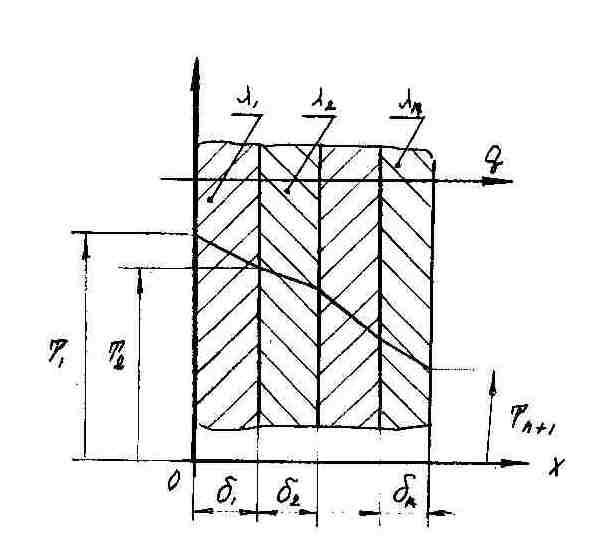
Многослойная плоская стенка (Рис. 1.2)
Рассматривается
многослойная плоская стенка. Количество
слоев n. Слои идеально плотно прилегают
друг к другу, материал в пределах каждого
слоя однородный. Толщины слоев стенкиδi. Коэффициенты
теплопроводности слоевλi
. Температуры на поверхности стенкиТ1иТn+1.
Рис.
1.2. Теплопроводность многослойной
плоской стенки
Плотность
теплового потока, Вт/м2:
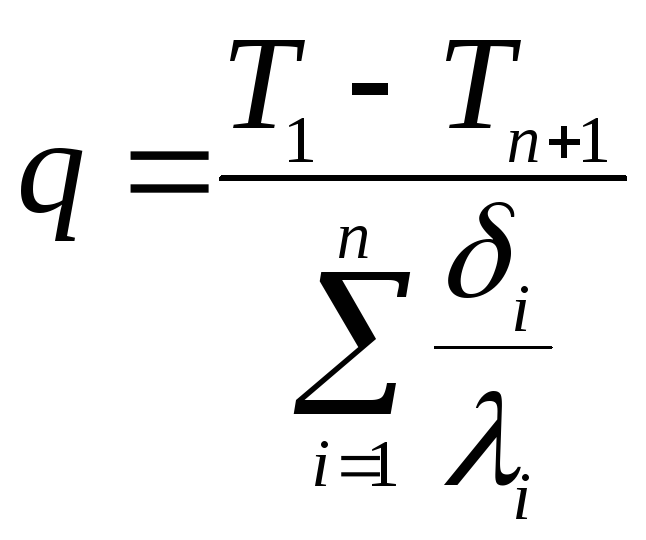
Значения
температур на соприкасающихся
поверхностях:
, (1.3)
В
пределах каждого слоя температура
изменяется линейно, в целом же температурное
поле изображается ломаной линией.
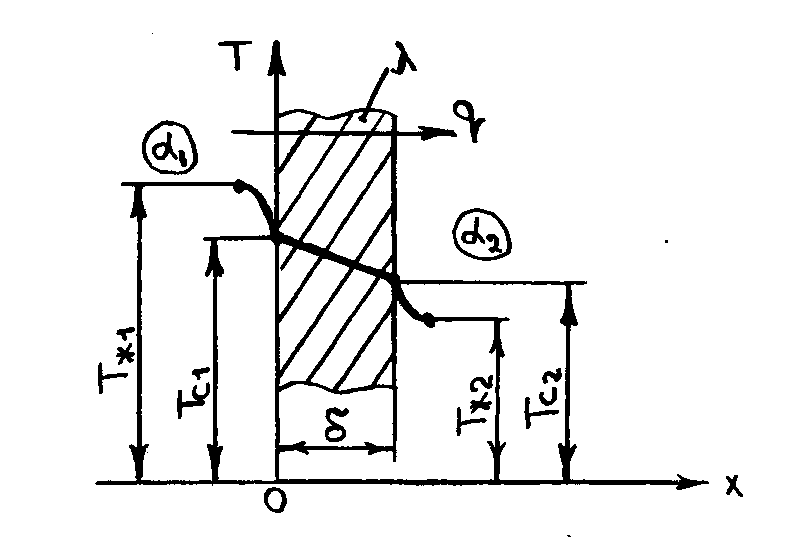
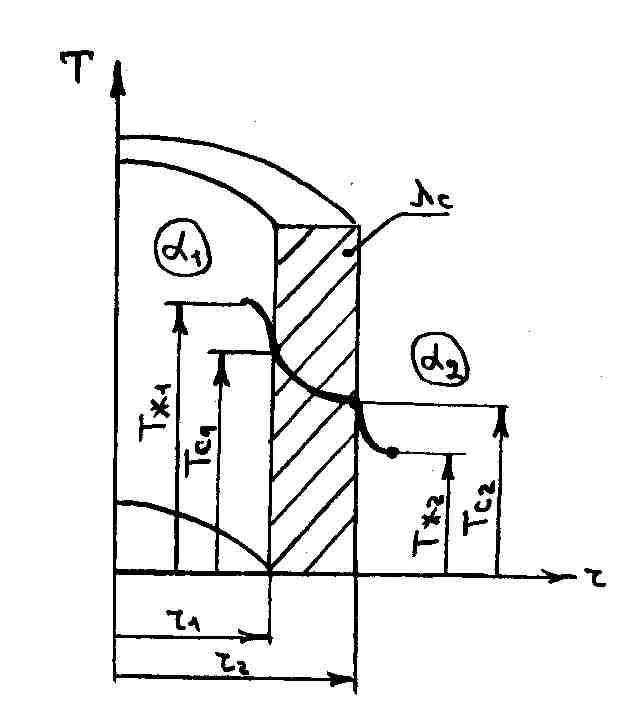
1.1.3. Теплопередача через плоскую стенку
(Рис. 1.3)
Рис.
1.3. Теплопередача через плоскую стенку
Стенка
разделяет две жидкости с различной
температурой: Тж1иТж2;Тж1>Тж2.
Известны коэффициенты теплоотдачи от
нагретой жидкости к стенкеα1и от стенки к холодной жидкостиα2.
Величиныλ, α1, α2,
Тж1, Тж2являются
постоянными во времени и не изменяются
вдоль поверхности стенки.
Плотность
теплового потока, проходящего через
однослойную стенку:

где К
– коэффициент теплопередачи, Вт/(м2К):

Величину
обратную коэффициенту теплопередачи
называют тепловым (термическим)
сопротивлением теплопередачи Rт:
. (1.6)
Для
случая теплопередачи через многослойную
плоскую стенку:
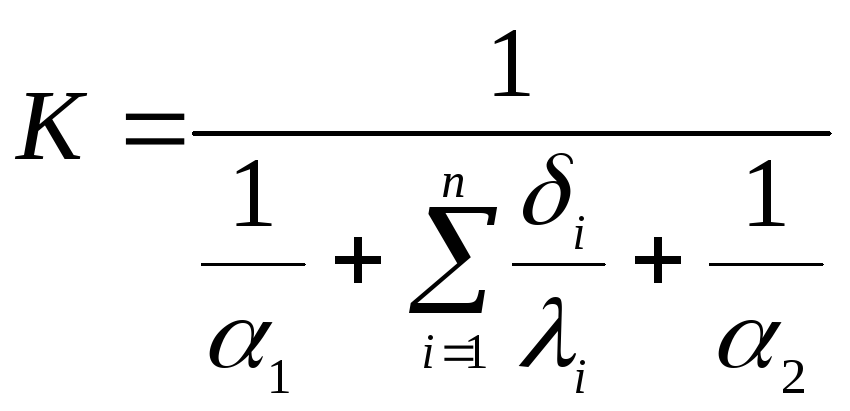
, (1.8)
где δí
– толщина отдельных слоев стенки;λí – – коэффициент
теплопроводности каждого изnслоев.
Значения
температуры на внешних поверхностях
стенки Тс1иТс2:
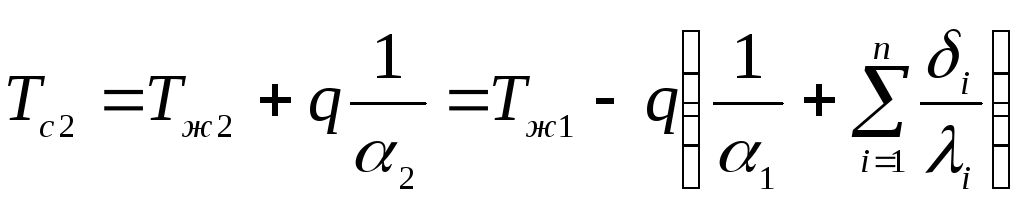
1.2. Теплопроводность цилиндрической стенки
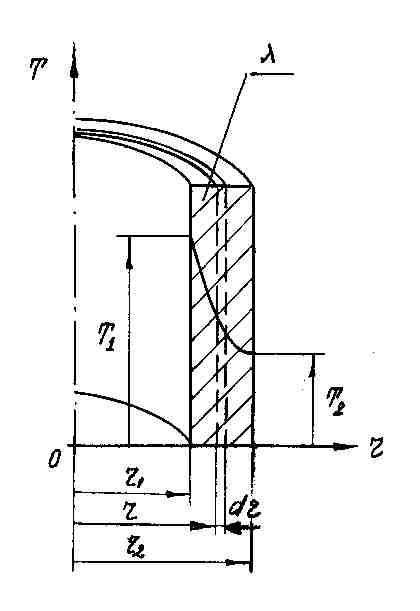
1.2.1.
однослойная стенка (Рис. 1.4)
Рис.
1.4. Теплопроводность однослойной
цилиндрической стенки
Величина
теплового потока, Вт:
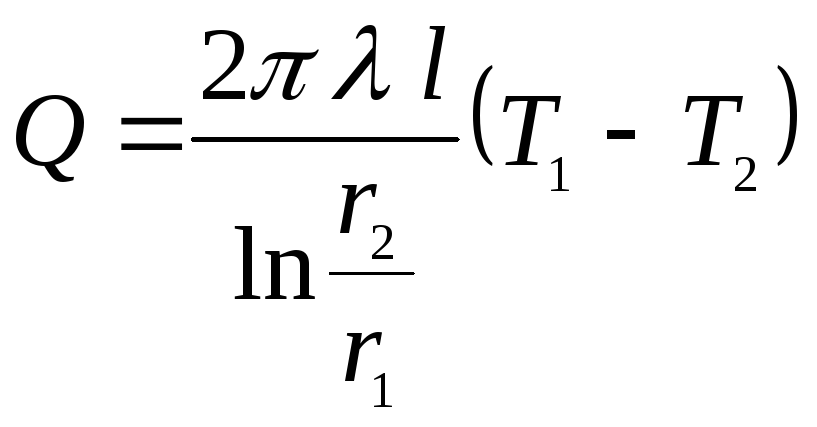
ℓ –
длина цилиндра, м;
r1
, r2 –
внутренний и наружный радиус трубы
соответственно,м.
Линейная
плотность теплового потока, Вт/м:
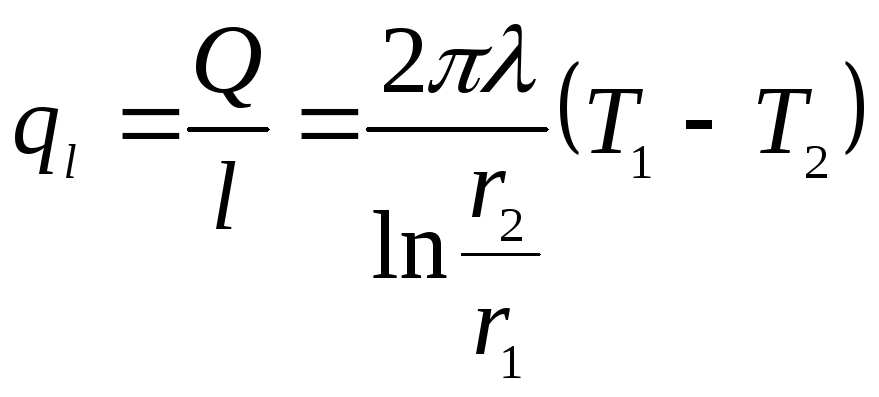
Температура
изменяется по логарифмическому закону.
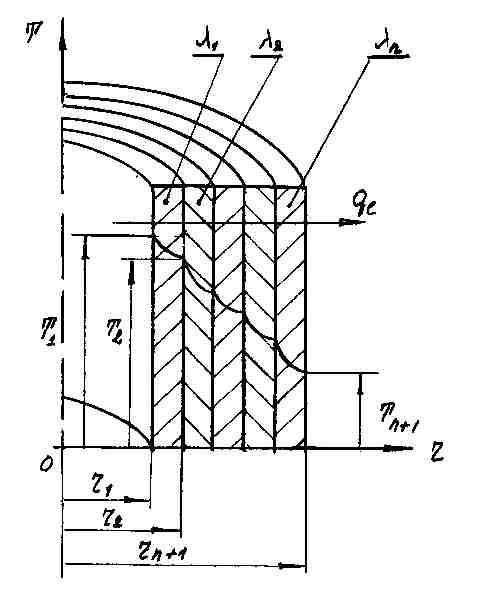
1.2.2.
Многослойная цилиндрическая стенка
(Рис. 1.5)
Рис.
1.5. Теплопроводность многослойной
цилиндрической стенки
Величина
теплового потока, Вт:
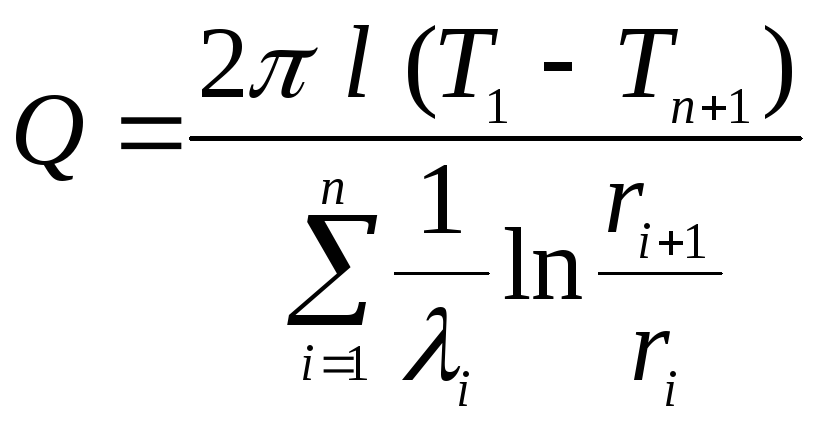
Линейная
плотность теплового потока через стенку,
Вт/м:
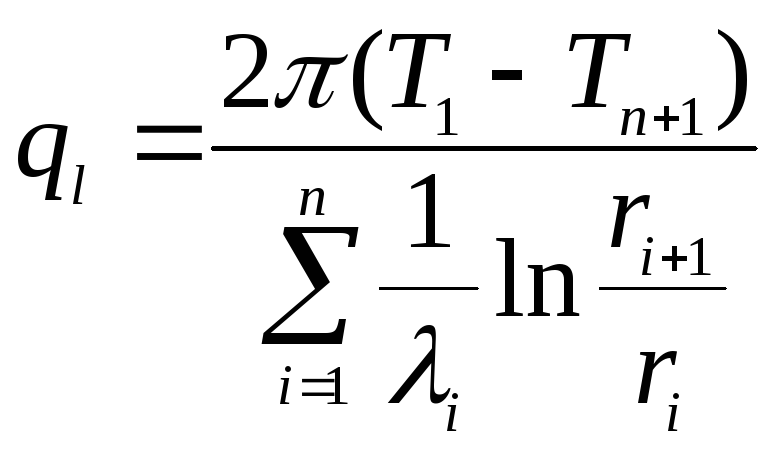
Температура
на поверхностях соприкосновения слоев:
. (1.14),
где n– номер поверхности по порядку.
В
пределах каждого слоя температура
изменяется по логарифмическому закону.
Температурное поле стенки в целом
представляет собой ломаную кривую.
1.2.3.
Теплопередача через цилиндрическую
стенку (Рис. 1.6)
Рис.
1.6. Теплопередача через цилиндрическую
стенку
Линейная
плотность теплового потока, Вт/м:
, (1.15)
где:
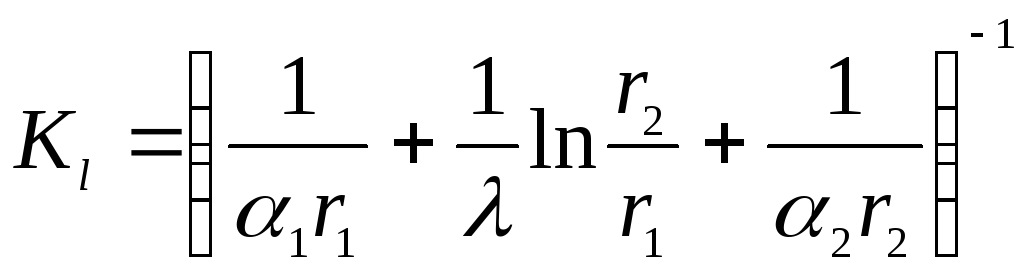
–
линейный коэффициент теплопередачи,
Вт/(м2К):
(1.17)
–
линейное тепловое сопротивление, Вт/(м
К);
Тж1– температура жидкости, протекающей
внутри трубы;
Тж2– температура жидкости обтекающей трубу;
α1– коэффициент теплоотдачи от горячей
жидкости к стенке, Вт/(м2
К);
α2– коэффициент теплоотдачи от стенки к
холодной жидкости, Вт/(м2
К);
Для
многослойной стенки:
, (1.18)
где n
– число слоев.
Температуры
внутренней и наружной стенок:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ТЕПЛОМАССООБМЕН Задачи. Теплопередача. Сложный теплообмен № 2 2016 год
План • 1. Теплопроводность через плоскую стенку. • 2. Теплопроводность стенку. через цилиндрическую
1. Теплопроводность через плоскую стенку Целью расчета передачи тепла теплопроводностью в стационарном тепловом режиме (температурное поле не меняется во времени) является либо определение величины плотности теплового потока, либо нахождение распределения температуры по толщине стенки.
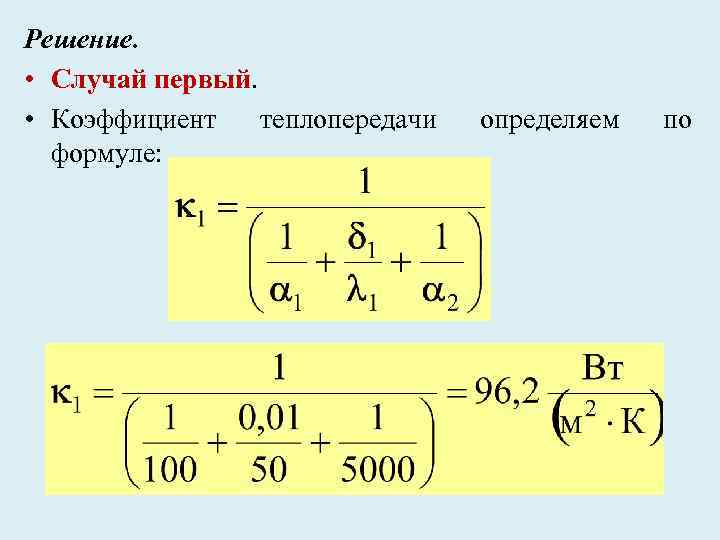
• Пример № 1. Определить плотность теплового потока, проходящего через плоскую стальную стенку толщиной δ 1= 10 мм с λ 1=50 Вт/(м·К), и коэффициенты теплопередачи для двух случаев. В первом случае: температура газов t 1 = 1127 ºC, температура кипящей воды t 2 = 227ºC, коэффициент теплоотдачи от газов к стенке α 1=100 Вт/(м 2·К) и от стенки к кипящей воде α 2=5000 Вт/(м 2·К). Во втором случае в процессе эксплуатации поверхность нагрева со стороны газов покрылась слоем сажи толщиной δ 2= 10 мм с λ 2=0, 09 Вт/(м·К). Температура газов и воды остается без изменения. • Вычислить температуры поверхностей между слоями, а также определить во сколько раз уменьшится коэффициент теплопередачи с появлением слоя сажи. Как изменится плотность теплового потока и температура поверхности стенки, если со стороны воды появится накипь толщиной 10 и 30 мм с λ 3=2, 0 Вт/(м·К)? Со стороны газа поверхность стенки чистая.
Решение. • Случай первый. • Коэффициент теплопередачи формуле: определяем по
• Плотность теплового потока находим по уравнению: • Температуру стенки со стороны газов определяем по формуле: • Температуру стенки со стороны воды определяем по формуле:
• Второй случай. • Коэффициент теплопередачи через многослойную плоскую стенку определяем по формуле:
• Плотность теплового потока находим по уравнению: • Температура наружного слоя сажи • Температура внутреннего слоя сажи
• Температура внутренней поверхности стенки (со стороны воды) • Вывод. Слой сажи в 2 мм уменьшает коэффициент теплопередачи от газов к воде в 3, 13 раза.
• Третий случай (А). • Коэффициент теплопередачи при накипи толщиной 10 мм
• Плотность теплового потока находим по уравнению: • Температура стальной стены со стороны газов • Температура внутреннего слоя между стеной и накипью
• Температура внутренней поверхности накипи (со стороны воды)
• Третий случай (Б). • Коэффициент теплопередачи при накипи толщиной 30 мм • Плотность теплового потока в этом случае
• Плотность теплового потока в этом случае • Температура стальной стены со стороны газов • Температура внутреннего слоя между стеной и накипью
• Температура внутренней поверхности накипи (со стороны воды) • Выводы: • Приведенные расчеты показывают, что появление накипи на поверхности нагрева уменьшает теплопередачу: Ø слой 10 мм – на 32, 4%; Ø слой 30 мм – на 59%
• Расчеты показали, что температура стальной стенки с появлением накипи резко возрастает и при толщине в 30 мм достигает 771 °С, что абсолютно недопустимо. • Появление большого слоя накипи может привести к взрыву котла.
• Пример № 2. Определить потерю тепла через стенку печи при стационарном режиме, если температура внутренней поверхности кладки tкл = tп = 1300°C, температура окружающей среды tо = 0°C. Толщина шамотной кладки стенки δш = 0, 46 м; толщина изоляционной кладки из диатомитового кирпича δд = 0, 115 м и толщина изоляции из вермикулитовых плит δв = 0, 05 м. Определить температуры на границах слоев. • Литература: • 1. Теория, конструкции и расчеты металлургических печей: Учебник для техникумов. В 2 -х томах. 2 -е изд. перераб. и доп. • Т. 2. Мастрюков Б. С. Расчеты металлургических печей. – М. : Металлургия, 1986. 376 с.
Решение. Согласно приложению XI в [1, стр. 366– 368] коэффициент теплопроводности: • для шамотного кирпича λш = 0, 88 + 0, 00023 tср. ш; • для диатомитового кирпича λд = 0, 163 + 0, 00043 tср. д; • для вермикулитовых плит λв = 0, 081 + 0, 00023 tср. в. • Пологая температуру на наружной поверхности кладки tн = 100 °C и принимая в первом приближении распределение температуры по толщине кладки линейным, из геометрических соотношений найдем температуры на границах раздела слоев.
Определим средние температуры по толщине слоев материалов, • для шамотного кирпича: • λш = 0, 88 + 0, 00023· 858, 4=1, 078 Вт/(м·К). • для диатомитового кирпича • λд = 0, 163 + 0, 00043· 306, 4=0, 29 Вт/(м·К).
• для вермикулит вой плиты: • λв = 0, 081 + 0, 00023· 148=0, 115 Вт/(м·К). • Согласно формуле Плотность теплового потока через трехслойную стенку равна
Коэффициент теплоотдачи конвекцией от наружной поверхности печи (футеровки) в окружающую среду определяем по формуле для приближенных расчетов: • Найдем уточненные значения температур раздела слоев футеровки по формулам:
• Определим уточненные значения средних температур слоев и коэффициентов теплопроводности: • для шамотного кирпича: • λш = 0, 88 + 0, 00023· 1102, 5=1, 13 Вт/(м·К). • для диатомитового кирпича • λд = 0, 163 + 0, 00043· 721, 5=0, 47 Вт/(м·К). • для вермикулит вой плиты: • λв = 0, 081 + 0, 00023· 298=0, 152 Вт/(м·К).
Найдем уточненное значение плотность теплового потока через трехслойную стенку
• Теперь найдем уточненные значения температур на границах раздела слоев, средние температуры слоев и коэффициенты теплопроводности:
• для шамотного кирпича: • λш = 0, 88 + 0, 00023· 1051, 9=1, 12 Вт/(м·К). • для диатомитового кирпича • λд = 0, 163 + 0, 00043· 654, 75=0, 44 Вт/(м·К). • для вермикулит вой плиты: • λв = 0, 081 + 0, 00023· 298, 05=0, 148 Вт/(м·К).
Найдем снова уточненное значение плотность теплового потока через стенку
• Поскольку расхождение между двумя последними значениями плотности теплового потока через стенку менее 5% • то последнее значение плотности теплового потока • считаем окончательным, а распределение температур по толщине стенки будет
2. Теплопроводность через цилиндрическую стенку
• Пример № 1. • Стальной паропровод диаметром d 1/d 2=180/200 мм с теплопроводностью λ 1 = 50 Вт/(м·К) покрыт слоем жароупорной изоляции толщиной δ 2=50 мм, λ 2 = 0, 18 Вт/(м·К). Сверх этой изоляции лежит слой пробки δ 3=50 мм, λ 3 = 0, 06 Вт/(м·К). Температура протекающего внутри пара равна t 1=427ºC, температура наружного воздуха t 2 =27 ºC. Коэффициент теплоотдачи от пара к трубе α 1=200 Вт/(м 2·К), коэффициент теплоотдачи от поверхности пробковой изоляции воздуху α 2=10 Вт/(м 2·К). Определить потери теплоты на 1 м трубопровода, а также температуры поверхностей отдельных слоев.
Решение. • Из условия задачи следует, что dвн=d 1=0, 18 м, d 2=0, 20 м, d 3=0, 30 м, и dнар=d 4=0, 40 м. • Коэффициент теплопередачи многослойной цилиндрической стенки определяем по уравнению:
• Плотность теплового потока на 1 м трубы • Температуру внутренней поверхности трубы определяем по уравнению: • Термическим сопротивлением трубы можно пренебречь наружную температуру поверхности трубы считать равной
• Температуру наружной поверхности жароупорной изоляции определяем по уравнению: • Температуру наружной пробковой изоляции определяем по уравнению: • Из приведенных расчетов видно, что слой жароупорной изоляции слишком тонок и не предохраняет пробку от самовозгорания, так как максимально допустимая температура для пробки составляет 80 ºC, следовательно, слой жароупорной изоляции надо увеличить.
• Пример № 2. • Футеровка секционной печи имеет цилиндрическую форму и состоит из слоя магнезита толщиной δм=0, 23 м и слоя шамота толщиной δш=0, 23 м. Диаметр рабочего пространства печи d 1=1 м, температура печи tп=t 1=1500ºC. Температура воздуха в цехе tок=t 2=30 °C. Какова должна быть толщина слоя диатомитовой изоляции, чтобы тепловые потери через стенку печи не превышали q=10 к. Вт/м? Определить температуру наружной поверхности изоляционного слоя. Коэффициент теплопроводности λм = 5, 5 Вт/(м·К); шамота λш = 0, 8 Вт/(м·К); диатомита λд = 0, 17 Вт/(м·К); коэффициент теплоотдачи конвекцией в окружающую среду α 2=11, 63 Вт/(м 2·К).
Решение. • Для решения поставленной задачи воспользуемся формулой • где • Применительно к сформулированным условиям
• или • Полученное уравнение можно решить методом последовательного приближения. Принимаем d 4=2 м. Тогда • Принимаем d 4=2, 1 м. Тогда
• Т. о. толщина изоляции • будет достаточной для выполнения сформулированных условий. Поскольку стандартная ширина кирпича равна 115 мм. Примем δд=0, 115 м и • В этом случае
• Температуру наружной поверхности футеровки найдем по формуле:
Теплопроводность через стенку
Под теплопередачей через стенку понимают процесс передачи теплоты между двумя средами через непроницаемую стенку любой геометрической формы в стационарном и нестационарном режимах теплообмена. Стенка может быть многослойной.
Рассмотрим стационарный режим теплопередачи через плоскую, цилиндрическую и сферическую стенки при котором теплопередача – величина постоянная и температурное поле не изменяется во времени и зависит только от координаты. В этом случае при условии постоянства теплофизических свойств тела температура в плоской стенке изменяется линейно, а в цилиндрической – по логарифмическому закону, т.е.
Q = const и T = f(x) – линейная (при плоской стенке) или логарифмическая функция (при круглой стенке).
Согласно второму закону термодинамики процесс теплопередачи идет от среды с большей температурой к среде с меньшей температурой.
Теплопередача через непроницаемую стенку включает в себя следующие процессы:
- теплоотдачу от горячей среды к стенке;
- теплопроводность внутри стенки;
- теплоотдачу от стенки к холодной среде.
Теплопередача через плоскую стенку (граничные условия первого рода)
Теплопроводность – первое элементарное тепловое явление переноса теплоты посредством теплового движения микрочастиц в сплошной среде, обусловленное неоднородным распределением температуры.
Совокупность значений температуры для всех точек пространства в данный момент времени называется температурным полем.
Если температурное поле не изменяется во времени, то мы имеем дело со стационарным тепловым режимом.
Тепловой поток Q [Вт] – это количество теплоты, передаваемой в единицу времени (1 Дж/с=1 Вт).
Поверхностная плотность теплового потока рассчитывается по формуле:
где Q – тепловой поток [Вт]; F – площадь стенки [м 2 ].
На основании закона Фурье q=-λdT/dx, значение плотности теплового потока для однослойной стенки будет определяться по формуле:
где δ = dx – толщина стенки, λ
λ/δ; [Вт/м 2 *К] – коэфициент тепловой проводности стенки.
а обратная величина –
R = δ/λ; [м 2. К/Вт] – термическое сопротивление стенки.
Для теплового потока формулу так же можно представить в виде:
Общее количество теплоты проходящее через площадь стены S за время t можно представить как:
Распределение температуры в плоской стенке
Рассмотрим изменение температуры в нашей стене. Так как у нас тепловой поток постоянный, то dT/dx = const=C1; T=C1х+С2 (1). Определим С1 и С2 через граничные условия.
При х=0 T=T1, подставим в уравнение (1) и получим T1=С2.
При х=δ T=T2, подставим в уравнение (1) и получим T2=С1*δ+С2, T2=С1*δ+T1, получим: С1=(Т2-T1)/δ. Теперь подставим в уравнение (1) найденные С1 и С2, получим следующее распределение температуры в нашей стене:
Если нам нужно узнать на какой глубине стены Т=То, то формула преобразуется в следующий вид:
Теплопроводность через многослойную стенку
Если у нас есть стенка из нескольких (n) слоев с разными коэффициентами теплопроводности λi и разной толщиной δi.
Термическое сопротивление стенки считается так:
Для теплового потока формула будет иметь вид:
Температура на границе слоя вычисляется по следующей формуле:
Например, если нужно вычислить температуру между 3-м и 4-м слоем, формула будет такая:
Эквивалентная теплопроводность многослойной стенки:
Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)
Теплопередача – это более сложный процесс теплообмена между жидкими и газообразными средами, разделенными твердой стенкой. Теплопередача включает в себя и процесс теплопроводности, и процесс теплоотдачи.
Коэффициент теплоотдачи α, Вт/(м 2 ·К) – это количество теплоты, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и окружающей средой, равной одному градусу.
Коэффициент теплопередачи k, Вт/(м 2 ·К), характеризует тепловой поток, проходящий через единицу площади поверхности стенки при разности температуры сред, равной одному градусу:
q = k * (Tвозд.внутри – Tвозд.снаружи); Вт/м 2
Коэффициент теплопередачи для n слойной стенки:
Термические сопротивления теплоотдаче на внешних поверхностях стенки будут равны:
Тогда общее термическое сопротивление теплопередаче будет равно:
Температуры на поверхности стенки можно определить по формулам:
Теплопроводность через цилиндрическую стенку (граничные условия первого рода)
Теплообменные аппараты в большинстве случаев имеют не плоские, а цилиндрические поверхности, например рекуператоры типа “труба в трубе”, кожухотрубные водонагреватели и т.д. Поэтому возникает необходимость рассмотрения основных принципов расчета цилиндрических поверхностей.
Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно:
Подставим значения граничные значение и вспомним, что разность логарифмов равна логарифму отношению аргументов, получим:
Распределение температур внутри однородной цилиндрической стенки подчиняется логарифмическому закону, и уравнение температурной кривой имеет вид:
Количество теплоты, проходящее через стенку трубы, может быть отнесено либо к единице длины трубы L, либо к единице внутренней F1 или внешней F2 поверхности трубы. При этом расчетные формулы принимают следующий вид:
Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.
Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.
Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.
Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.
Теплопроводность через однослойную плоскую стенку
Дифференциальное уравнение теплопроводности позволяет определить температуру в зависимости от времени и координат в любой точке поля.
Для любого конкретного случая к нему надо присоединить необходимые краевые условия.
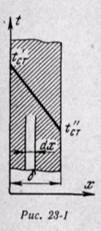
Но при принятых условиях первые и вторые производные от ( по y иz также равны нулю:
поэтому уравнение теплопроводности можно написать в следующем виде:
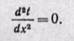
Интегрируя уравнение (23-1), находим
После вторичного интегрирования получаем
При постоянном коэффициенте теплопроводности это уравнение прямой линии. Следовательно, закон изменения температуры при прохождении теплоты через плоскую стенку будет линейным.
Найдем постоянные интегрирования А и В.
При х = 0 температура t = t’cr — B; при х = δ температура t = t”cr — Аδ +tст, откуда
Плотность теплового потока найдем из уравнения Фурье (22-7)
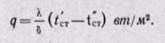
Зная удельный тепловой поток, можно вычислить общее количество теплоты, которое передается через поверхность стенки F за время τ:
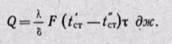
Количество теплоты, которое передается теплопроводностью через плоскую стенку, прямо пропорционально коэффициенту теплопроводности стенки К, ее площади F, промежутку времени т, разности температур на наружных поверхностях стенки (t’ст — t”ст) и обратно пропорционально толщине стенки δ. Тепловой поток зависит не от абсолютного значения температур, а от их разности
t’ст — t”ст = Δt наtзываемой температурным напором.
Полученное уравнение (23-2) является справедливым для случая, когда коэффициент теплопроводности является постоянной величиной. В действительности коэффициент теплопроводности реальных тел зависит от температуры и закон изменения температур будет выражаться кривой линией. Если коэффициент теплопроводности зависит от температуры в незначительной степени, то на практике закон изменения температур считают линейным.
Уравнение (23-2) можно получить непосредственно из закона Фурье (22-6), считая, что температура изменяется только в направлении оси х:
Разделив переменные, получаем
Интегрируя последнее уравнение при условии Q = const, находим
Постоянную интегрирования С найдем из граничных условий:
при х = 0 температура
при х = δ температура 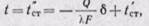
Введем в уравнение (23-2) поправки па зависимость λ от t, считая эту зависимость линейной:

В этом случае, подставив в уравнение Фурье вместо К его значение из формулы (а), получаем

Разделив переменные и интегрируя в пределах от х = 0 до x = δ и в интервале температур от t’ст до t”ст, получаем
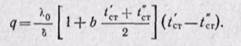
Полученное уравнение (23-4) позволяет определить плотность теплового потока при переменном коэффициенте теплопроводности. В этом уравнении множитель
является среднеинтегралыюй величиной коэффициента теплопроводности.
В уравнении (23-2) было принято λ,=const и равным среднему значению λср. Поэтому, сравнивая уравнения (23-2) и (23-4), получаем

Следовательно, если λср определяется при среднеинтегральной температуре то формулы (23-2) и (23-4) равнозначны.
При этом плотность теплового потока может определяться из уравнения
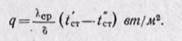
Интегрируя уравнение (б) в пределах от х — О до любой текущей координаты х и в интервале температур от t’ст ДО tx, получим уравнение температурного поля
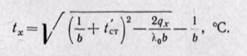
Из этого уравнения следует, что температура внутри стенки изменяется по кривой. Если коэффициент b отрицателен, то кривая будет направлена выпуклостью вниз; если b положителен, то выпуклостью вверх.
Теплопроводность плоской однослойной стенки
Теплопроводность плоской однослойной стенки
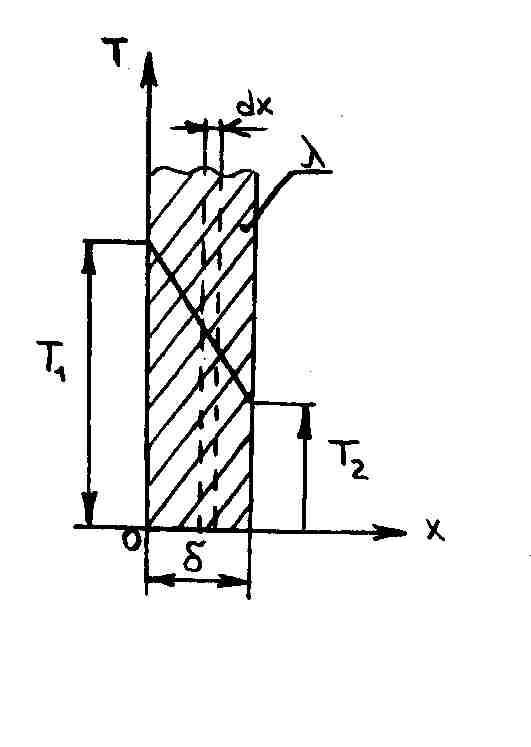
- Рис. 11. 3. Плоские стены. Рассмотрим однородную стенку толщиной b, выполненную из материала, теплопроводность которого l не зависит от температуры. Поверхность левой стороны стены поддерживается при постоянной постоянной температуре l, по высоте стены, а правой-низкой, но при постоянной температуре 1 г.
Давление р определяется отношением суммы нормальных к поверхности составляющих сил образующихся вследствие ударов о стенку хаотически движущихся микрочастиц рабочего тела, к площади поверхности А. Людмила Фирмаль
Температура стены изменяется только по ее толщине, направлению оси x рис. 11. 3. То есть температурное поле является 1-мерным, а температурный градиент равен d1 dx. Найти плотность теплового потока через заданную стенку и установить характер изменения температуры вдоль толщины стенки.
- Уравнение Фурье одномерного температурного поля. Чтобы интегрировать это уравнение, разделите переменные 11 — х- После интеграции 11. 2 Чтобы найти интегральную постоянную, используйте известные температуры x-0, −6 и x-1 2. Таким образом, c f таким образом, уравнение k. 2 будет иметь следующий формат АГ.
Термодинамической системой называется совокупность макроскопических тел, которые могут взаимодействовать между собой и с другими телами, составляющими внешнюю среду, в виде обмена энергией или веществом. Людмила Фирмаль
Когда вы решаете уравнение Хорошо О Плотность теплового потока плоской стенки прямо пропорциональна теплопроводности, перепаду температур и обратно пропорциональна толщине стенки. Изменение температуры по отношению к толщине стенки выражается формулой 11. 2.

Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
[spoiler title=”источники:”]
http://helpiks.org/3-16578.html
http://lfirmal.com/teploprovodnost-ploskoj-odnoslojnoj-stenki/
[/spoiler]
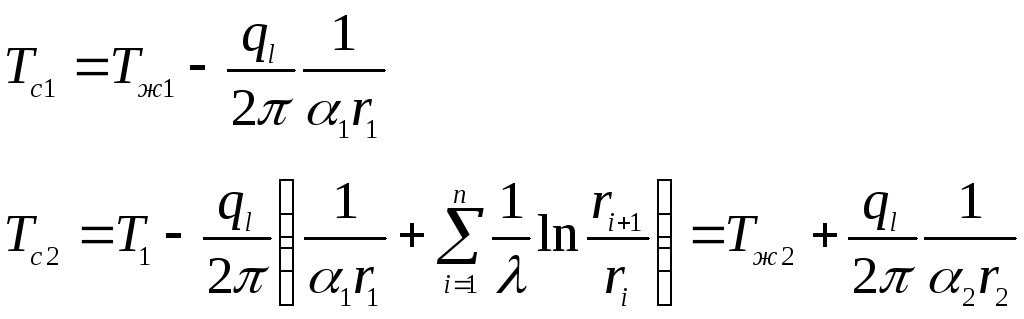
















![Решение. Согласно приложению XI в [1, стр. 366– 368] коэффициент теплопроводности: • для шамотного Решение. Согласно приложению XI в [1, стр. 366– 368] коэффициент теплопроводности: • для шамотного](https://present5.com/presentation/138047442_454994745/image-18.jpg)