ускорение. по какой формуле найти ускорение при торможении?
Рома
Ученик
(84),
закрыт
7 месяцев назад
Дополнен 11 лет назад
а если известно только длина торможения и начальная скорость?
Дополнен 11 лет назад
а если известно только длина торможения и начальная скорость?
Перейти к содержимому
Задача №34. Ускорение при торможении и длина пути торможения автомобиля
Определить ускорение автомобиля при торможении и длину пути торможения, если автомобиль за время торможения равное 5 секундам снизил скорость с 10 метров в секунду до 5 метров в секунду.
Дано: v0=10 м/с; v1=5 м/с; t=5 с
Найти: a — ?; L — ?
Решение:
Ускорение при торможении определяем по формуле
 м/с2
м/с2
Путь при торможении определяем по формуле
 м
м
Ответ: ускорение автомобиля при торможении составило -1 метр в секунду в квадрате, путь при торможении равен 37,5 метрам
Unit Converter
Enter the velocity before braking and the total stopping distance into the calculator to determine the Braking Acceleration.
- All Acceleration Calculators
- Braking Force Calculator
- Stopping Distance Calculator
- Brake Caliper Clamping Force Calculator
Braking Acceleration Formula
The following equation is used to calculate the Braking Acceleration.
Ab = V^2 / (2*SD)
- Where Ab is the Braking Acceleration (m/s^2)
- V is the velocity before braking (m/s)
- SD is the total stopping distance (m)
Braking acceleration is also often referred to as braking deceleration.
What are the units for Braking Acceleration?
The most common units for Braking Acceleration are m/s^2.
How to Calculate Braking Acceleration?
Example Problem:
The following example problem outlines the steps and information needed to calculate the Braking Acceleration.
First, determine the velocity before braking. In this example, the velocity before braking is determined to be 150 (m/s).
Next, determine the total stopping distance. For this problem, the total stopping distance is measured to be 10 (m).
Finally, calculate the Braking Acceleration using the formula above:
Ab = V^2 / (2*SD)
Inserting the values from above and solving the equation with the imputed values gives:
Ab = 150^2 / (2*10) = 1125 (m/s^2)
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Ускорение тела, возникающее вследствие силы трения
Известно, что сила трения скольжения направлена в сторону, противоположную направлению относительной скорости движения трущихся тел.
Отсюда следует, что ускорение, которое такая сила сообщает движущемуся телу, тоже направлено против относительной скорости. А это значит, что действие силы трения приводит к уменьшению абсолютного значения скорости тела относительно того тела, по которому оно скользит.
Если на тело, которое скользит по неподвижной поверхности, никакие силы, кроме силы трения не действуют, то оно, в конце концов, останавливается. Рассмотри этот часто встречающийся случай.
Представим себе, что перед движущимся поездом неожиданно появилось некоторое препятствие и машинист отключил двигатель и включил тормоз. Начиная с это момента, на поезд действует только сила трения, так как сила тяжести скомпенсирована реакцией рельсов, а сила сопротивления воздуха мала. Через некоторое время $t$ поезд, пройдя расстояние $l$ – тормозной путь, остановится. Найдем время $t$, нужное для остановки, и расстояние $l$, которое поезд пройдет за это время.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Под действием сила трения $overline{F}_{mp} $поезд будет двигаться с ускорением, равным:
Выберем координатную ось $x$ так, чтобы ее положительное направление совпадало с направлением скорости движения поезда.

Рисунок 1.
Так как сила трения $overline{F}_{mp} $направлена в противоположном направлении, ее проекция на ось х отрицательна. Отрицательна и проекция вектора ускорения на ось $x$. Поэтому если абсолютное значение силы трения равно $left|overline{F}_{mp} right|$, то:
Но ускорение определяется также формулой:
где $v_{0} $- скорость поезда до начала торможения.
Время торможения при движении тела под действием силы трения
Так как нас интересует промежуток времени $t$ от начала торможения до остановки поезда, то конечная скорость $v=0$. Тогда:
«Движение тела под действием силы трения» 👇
Таким образом:
Получим выражения для времени торможения:
Нахождение пути, пройденного телом под действием силы трения
А теперь найдем тормозной путь $l$. Для этого воспользуемся формулой:
Так как $v=0$, то:
Так как $overline{a}=-frac{left|overline{F}_{mp} right|}{m} $, получим:
Из этой формулы видно, что пройденный до остановки путь пропорционален квадрату скорости. Если увеличить скорость вдвое, то потребуется вчетверо больший путь для остановки.
Пример 1
С какой скоростью двигался автомобиль, если после выключения двигателя он прошел до остановки путь равный $80$ м? Коэффициент трения принять равным $0,25$.
Дано: $l=80$м, $mu =0,25$.
Найти: $v$-?
Решение:
Воспользуемся раннее выведенными формулами для нахождения тормозного пути:
$l=frac{mv_{0}^{2} }{2overline{left|F_{mp} right|}} $. (1)
Так как $F_{mp} =mu mg$, подставим в формулу (1) и получим:
$l=frac{mv_{0}^{2} }{2mu mg} $. (2)
Выразив из формулы (2) $v_{0} $найдем величину искомой скорости:
$v_{0} =sqrt{2mu gl} =20$м/с
Ответ: Скорость автомобиля до выключения двигателя $v_{0} =20$ м/с.
Пример 2
Сноубордист массой $80$ кг, имеющий в конце спуска скорость $20$ м/с, останавливается через $40$ с после окончания спуска. Определите силу трения и коэффициент трения.
Дано: $m=80$кг, $v_{0} =20$м/с, $t=40$с.
Найти: $F_{mp} $, $mu $-?
Решение:
Уравнение движения сноубордиста будет иметь вид:
[ma=F_{mp} .]
Используя выражения для нахождения ускорения (конечная скорость $v=0$), получим:
[a=-frac{v_{0} }{t} .]
Тогда:
$F_{mp} =ma=-mfrac{v_{0} }{t} =40H$.
Так как сила трения $overline{F}_{mp} $равна $F_{mp} =mu Bg$, находим коэффициент трения $mu $:
[mu =frac{F_{mp} }{mg} =0,05.]
Ответ: $F_{mp} =40H$, $mu =0,05$.
Пример 3
Сани массой $16$ кг перемещают по горизонтальной плоскости под действием силы $180 H$, направленной под углом $30^circ$ к горизонтали. Коэффициент терния саней о плоскость $0,5$. Определить ускорения, с которым движутся сани.
Дано: $m=16$кг, $F=180 H$, $alpha =30^circ$, $mu =0,5$.
Найти: $a$-?
Решение:
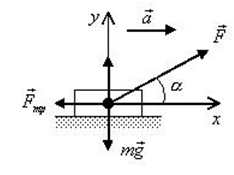
Рисунок 2.
Уравнение движения тела:
[moverline{a}=moverline{g}+overline{N}+overline{F}+overline{F}_{mp} .]
Выберем направление осей $x$ и $y$ и спроецируем на них силы и ускорение:
[begin{array}{l} {ma=Fcos alpha -F_{mp} } \ {0=-Bg+N+Fsin alpha } end{array}]
Поскольку $F_{mp} =mu N$, а из второго уравнения $N=mg-Fsin alpha $, то $F_{mp} =mu (mg-Fsin alpha )$. Тогда из первого уравнения ускорение:
$a=frac{1}{m} [Fcos alpha -mu (mg-Fsin alpha )]approx 7,6м/с^2$
Ответ: $a$=$7,6м/с^2$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

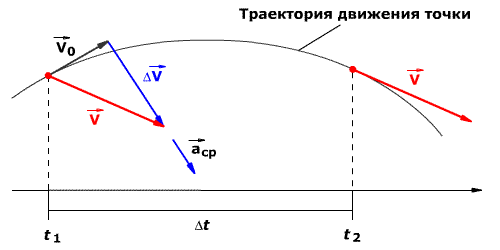 Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
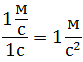
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:


При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
а направление вектора ускорения совпадает с вектором скорости 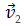
Если скорость тела по модулю уменьшается, то есть
то направление вектора ускорения противоположно направлению вектора скорости 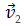 Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а
Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а 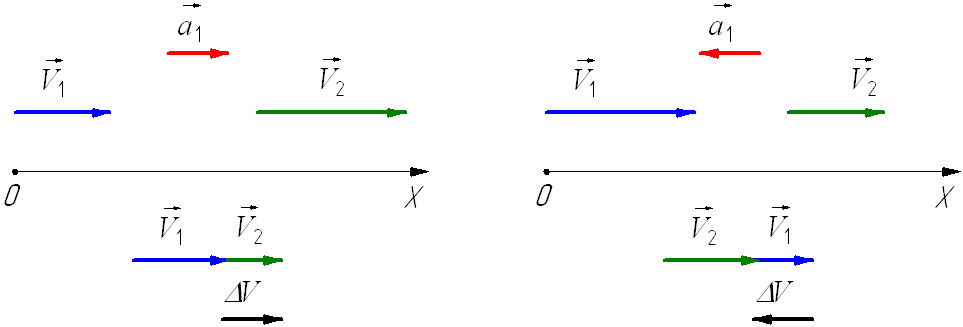
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
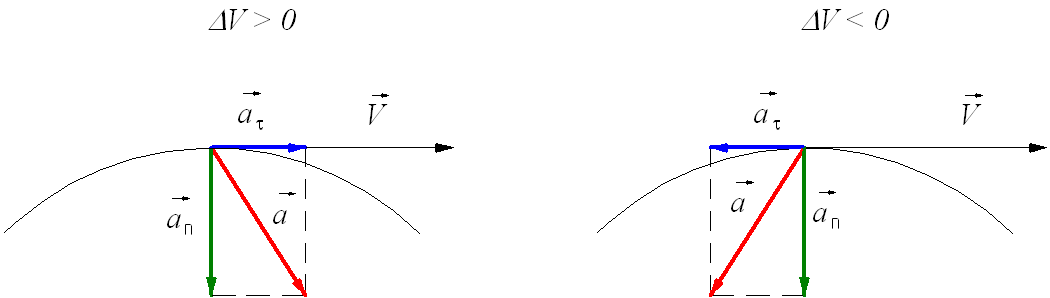
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения 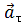 (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
(см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 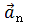 Вектор нормального ускорения направлен по радиусу кривизны траектории.
Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
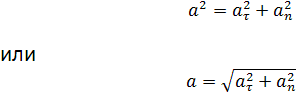
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
Источник
Перемещение и путь при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:
Подставляем известные данные в формулу:
Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
Когда тело тормозит, через некоторое время t1оно останавливается. Поэтому скорость в момент времени t1 равна 0:
При торможении перемещение s1 равно:

Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
При разгоне перемещение s2 равно:

При этом модуль перемещения в течение всего времени движения равен:
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:

Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:
Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

 Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).
Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).
Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Теперь мы можем выделить кинематические характеристики движения тела:
Перемещение тела определяется формулой:
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
Кинетическая энергия тела определяется формулой:
Скорость при прямолинейном равноускоренном движении равна:
v = v 0 + a t = 5 − 6 t
Поэтому кинетическая энергия тела равна:
Следовательно, правильная последовательность цифр в ответе будет: 34.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
pазбирался: Алиса Никитина | обсудить разбор | оценить
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Весь график можно поделить на 3 участка:
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s1и s2, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить
Источник
Ускорение при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

vx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Запишем исходные данные:
Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить
Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с? 
Алгоритм решения
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:
Подставляем данные формулу и вычисляем модуль ускорения:

pазбирался: Алиса Никитина | обсудить разбор | оценить
Источник

