доказать тождество
a+b2a−b−a−b2a+b=ba−b−b2−aba2−b2
.
Решение. Здесь лучше использовать третий способ.
Преобразуем выражение в левой части:
a+ba+b2a−b−a−ba−b2a+b=a+b2−a−b22a−ba+b=a2+2ab+b2−a2−2ab+b22a−ba+b==a2+2ab+b2−a2+2ab−b22a−ba+b=4ab2a2−b2=4⋅a⋅b2⋅a2−b2=2aba2−b2.
Преобразуем выражение в правой части:
ba−b−b2−aba2−b2=ba+ba−b−b2−aba−ba+b=ba+ba−ba+b−b2−aba−ba+b==ba+b−b2−aba−ba+b=ab+b2−b2+aba−ba+b=2aba2−b2.
Получили одинаковые выражения в левой и правой частях:
Тождество доказано.
В доказательстве были применены формулы сокращённого умножения:
a2−b2=a−ba+b;a+b2=a2+2ab+b2;a−b2=a2−2ab+b2.
- Альфашкола
- Уроки по математике
- Выражения
- Тождественное равенство рациональных выражений
Тождественное равенство рациональных выражений – онлайн урок
К сожалению, информация по данному уроку пока отсутствует.
Тождественное равенство рациональных выражений
Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.
Алгебраическая дробь – это дробь, числитель и знаменатель которой являются многочленами. Другими словами, алгебраическая дробь – это деление двух многочленов, записанное с помощью дробной черты.
Рациональным выражением называют выражение, в котором несколько алгебраических дробей соединены знаками арифметических действий.
Чтобы привести алгебраические дроби к общему знаменателю, нужно:
1) найти общий знаменатель для данных дробей;
2) найти дополнительный множитель для каждой дроби;
3) умножить числитель каждой дроби на ее дополнительный множитель;
4) записать дроби с найденными новыми числителями и общим знаменателем.
Для того, чтобы сложить (вычесть) две или более дроби с одинаковым знаменателем, нужно сложить (вычесть) их числители, а знаменатель оставить прежним.
Чтобы умножить дробь на натуральное число, нужно ее числитель умножить на это число, а знаменатель оставить без изменений.
Произведением дробей называется такая дробь, числитель которой равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей.
Формулы сокращенного умножения.
Теперь установи соответствие между картинками и определениями, которые мы только что повторили.
Прежде чем мы начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:
1. Равенство рациональных выражений;
2. Тождество;
3. Решение задач на доказательство тождеств.
Для продолжения урока кликните на кнопку ниже:
Отзывы:
Гоша с удовольствием занимается с Вами. Спасибо!
Самый лучший учитель. Вот бы у нас в школе были такие учителя. Спасибо
Огромное спасибо за интересный урок!
Похожие уроки
Содержание:
Вы уже знакомы с целыми рациональными выражениями, то есть с выражениями, которые не содержат деления на выражение с переменной, например:
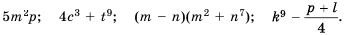
Любое целое выражение можно представить в виде многочлена стандартного вида, например:
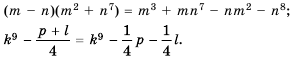
В отличие от целых выражений, выражения
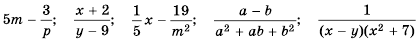
содержат деление на выражение с переменной. Такие выражения называют дробными рациональными выражениями. Целые рациональные и дробные рациональные выражения называют рациональными выражениями.
Рациональные выражения — это математические выражения, содержащие действии сложения, вычитания, умножения, деления и возведения в степень с целым показателем.
Определение рациональной дроби
Рациональное выражение вида 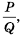 , где
, где 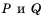 – выражения, содержащие числа или переменные, называют дробью. Выражение
– выражения, содержащие числа или переменные, называют дробью. Выражение 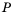 – ее числитель, a
– ее числитель, a 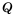 – знаменатель. Если
– знаменатель. Если 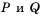 в дроби – многочлены, то дробь называют рациональной дробью.
в дроби – многочлены, то дробь называют рациональной дробью.
Целое рациональное выражение имеет смысл при любых значениях входящих в него переменных, так как при нахождении его значения выполняют действия сложения, вычитания, умножения и деления на число, отличное от нуля, что всегда выполнимо.
Рассмотрим дробное рациональное выражение — 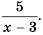 . Его значение можно найти для любого
. Его значение можно найти для любого 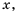 кроме
кроме 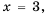 так как при
так как при 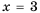 знаменатель дроби обращается в нуль. В этом случае говорят, что выражение
знаменатель дроби обращается в нуль. В этом случае говорят, что выражение 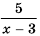 имеет смысл при всех значениях переменной
имеет смысл при всех значениях переменной 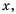 кроме
кроме 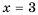 (или же при
(или же при 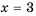 не имеет смысла).
не имеет смысла).
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных в выражении.
Эти значения образуют область определения выражения, или область допустимых значений переменных в выражении.
Пример:
Найдите допустимые значения переменной в выражении:
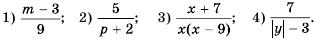
Решение:
1) Выражение имеет смысл при любых значениях переменной 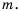 2) Допустимые значения переменной
2) Допустимые значения переменной 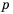 – все числа, кроме числа
– все числа, кроме числа 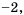 так как это число обращает знаменатель дроби в нуль. 3) Знаменатель дроби
так как это число обращает знаменатель дроби в нуль. 3) Знаменатель дроби 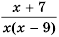 обращается в нуль при
обращается в нуль при 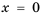 или
или 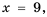 поэтому допустимые значения переменной
поэтому допустимые значения переменной 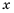 – все числа, кроме чисел 0 и 9. 4) Допустимые значения переменной
– все числа, кроме чисел 0 и 9. 4) Допустимые значения переменной 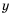 – все числа, кроме 3 и -3.
– все числа, кроме 3 и -3.
Кратко ответы можно записать следующим образом: 1) 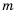 – любое число;
– любое число; 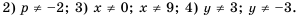
Рассмотрим условие равенства дроби нулю. Так как 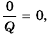 если
если 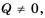 то можно сделать вывод, что дробь
то можно сделать вывод, что дробь 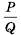 равна нулю тогда и только тогда, когда числитель
равна нулю тогда и только тогда, когда числитель 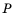 равен нулю, а знаменатель
равен нулю, а знаменатель 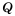 не равен нулю, то есть
не равен нулю, то есть 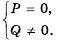
Пример:
При каких значениях переменной равно нулю значение дроби:
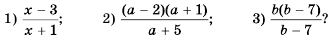
Решение:
1) Числитель дроби равен нулю при 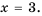 Это значение переменной не обращает знаменатель в нуль, поэтому число 3 является значением переменной, при котором данная дробь равна нулю. 2) Числитель дроби равен нулю при
Это значение переменной не обращает знаменатель в нуль, поэтому число 3 является значением переменной, при котором данная дробь равна нулю. 2) Числитель дроби равен нулю при 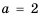 или
или  Для каждого из этих значений знаменатель дроби нулю не равен. Поэтому числа 2 и -1 – те значения переменной, при которых данная дробь равна нулю. 3) Числитель дроби равен нулю, если
Для каждого из этих значений знаменатель дроби нулю не равен. Поэтому числа 2 и -1 – те значения переменной, при которых данная дробь равна нулю. 3) Числитель дроби равен нулю, если 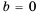 или
или 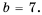 При
При 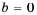 знаменатель дроби нулю не равен, а при
знаменатель дроби нулю не равен, а при 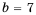 знаменатель дроби обращается в нуль, то есть такой дроби не существует. Следовательно, данная дробь равна нулю только при
знаменатель дроби обращается в нуль, то есть такой дроби не существует. Следовательно, данная дробь равна нулю только при 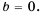
Ответ. 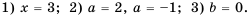
А еще раньше
Древнегреческий математик Диофант (прибл.  в. н. э.) рассмотрел рациональные дроби и действия с ними в своей работе «Арифметика». В частности, на страницах этой книги можно встретить доказательство тождеств
в. н. э.) рассмотрел рациональные дроби и действия с ними в своей работе «Арифметика». В частности, на страницах этой книги можно встретить доказательство тождеств
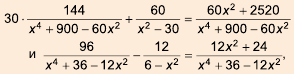
записанных символикой того времени.
Выдающийся английский ученый Исаак Ньютон (1643-1727) в своей монографии «Универсальная арифметика» (1707 г.) определяет дробь следующим образом: «Запись одной из двух величин под другой, ниже которой между ними проведена черта, означает часть или же величину, возникающую при делении верхней величины на нижнюю». В этой работе Ньютон рассматривает не топько обычные дроби, но и рациональные.
Определение: Дробь, числитель и знаменатель которой — многочлены, называется рациональной дробью.
Например, выражения 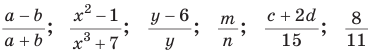
являются рациональными дробями.
Рациональная дробь является рациональным выражением. Выражения, составленные из чисел, переменных с помощью действий сложения, вычитания, умножения, деления, возведения в натуральную степень, называют рациональными выражениями.
Если рациональное выражение не содержит деления на выражение с переменными, то оно называется целым рациональным выражением.
Рассмотрим задачу: Туристы в первый день проплыли на лодке по течению реки 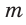 км, а во второй — на 6 км больше. Сколько времени продолжалось все путешествие, если собственная скорость лодки равна
км, а во второй — на 6 км больше. Сколько времени продолжалось все путешествие, если собственная скорость лодки равна 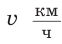 , а скорость течения реки —
, а скорость течения реки — 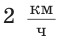 ?
?
Решение:
Так как за два дня туристы преодолели 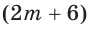 км по течению реки, а скорость движения лодки по течению реки равна
км по течению реки, а скорость движения лодки по течению реки равна 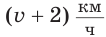 , то время, затраченное на весь путь, ч равно
, то время, затраченное на весь путь, ч равно 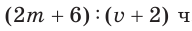 . Частное
. Частное 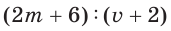 можно записать в виде дроби
можно записать в виде дроби 
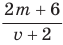 .
.
Ответ: 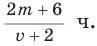
При решении этой задачи получили дробь, в числителе и знаменателе которой записаны многочлены. Такая дробь называется рациональной.
Целые рациональные выражения
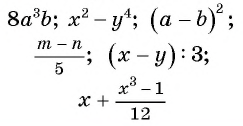
Например, выражения 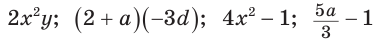 являются целыми рациональными выражениями.
являются целыми рациональными выражениями.
Рациональное выражение, содержащее деление на выражение с переменными, называют дробным рациональным выражением.
Дробные рациональные выражения
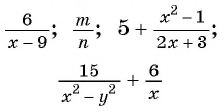
Например, выражения 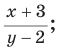
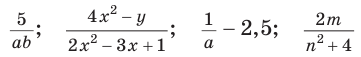 являются дробными рациональными выражениями, поскольку содержат (кроме действий сложения, вычитания, умножения) деление на выражение с переменными.
являются дробными рациональными выражениями, поскольку содержат (кроме действий сложения, вычитания, умножения) деление на выражение с переменными.
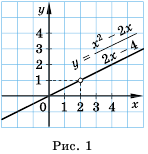
Связь между понятиями «рациональная дробь», «целое рациональное выражение» и «дробное рациональное выражение» иллюстрирует рисунок 1.
Целые рациональные выражения имеют смысл при любых значениях входящих в них переменных.
Например, областью определения выражения 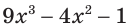 является множество всех действительных чисел.
является множество всех действительных чисел.
Рациональные выражения:
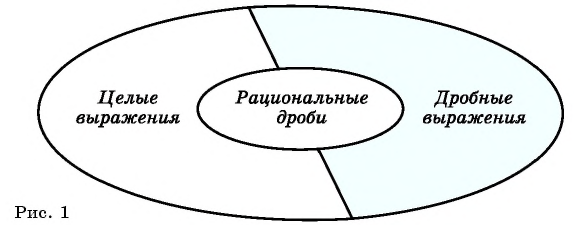
Дробные рациональные выражения имеют смысл при всех значениях переменных, кроме тех, которые обращают знаменатели дробей в нуль.
Например, выражение 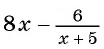 при
при 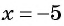 не имеет смысла, так как при
не имеет смысла, так как при 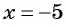 знаменатель дроби
знаменатель дроби 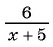 обращается в нуль. Значит, данное выражение имеет смысл при всех значениях переменной, кроме
обращается в нуль. Значит, данное выражение имеет смысл при всех значениях переменной, кроме 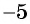 .
.
Рациональная дробь  имеет смысл при любых значениях переменной, кроме чисел
имеет смысл при любых значениях переменной, кроме чисел 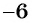 и
и 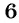 , так как при
, так как при 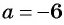 и при
и при 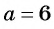 знаменатель дроби обращается в нуль.
знаменатель дроби обращается в нуль.
Областью определения рациональной дроби является множество всех значений входящих в нее переменных, кроме тех, которые обращают ее знаменатель в нуль.
Пример №1
Найдите область определения рациональной дроби:
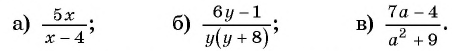
Решение:
а) Областью определения рациональной дроби 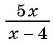 является множество всех действительных чисел, кроме числа
является множество всех действительных чисел, кроме числа 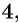 так как при
так как при 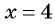 знаменатель дроби обращается в нуль. Можно записать:
знаменатель дроби обращается в нуль. Можно записать: 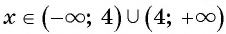 .
.
б) Найдем, при каких значениях переменной знаменатель дроби 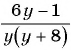 обращается в нуль. Для этого решим уравнение
обращается в нуль. Для этого решим уравнение 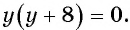 Корнями данного уравнения являются числа
Корнями данного уравнения являются числа 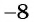 и
и 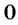 . Значит, областью определения дроби
. Значит, областью определения дроби 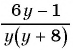 является множество всех действительных чисел, кроме чисел
является множество всех действительных чисел, кроме чисел 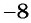 и
и 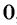 , т. е.
, т. е. 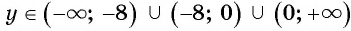 .
.
в) Поскольку выражение 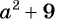 является положительным числом при любых значениях переменной, то нет таких значении переменной, при которых знаменатель дроби
является положительным числом при любых значениях переменной, то нет таких значении переменной, при которых знаменатель дроби 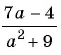 был бы равен нулю. Значит, рациональная дробь имеет смысл при любых значениях переменной, т. е. областью определения дроби является множество всех действительных чисел,
был бы равен нулю. Значит, рациональная дробь имеет смысл при любых значениях переменной, т. е. областью определения дроби является множество всех действительных чисел, 
Рациональные выражения:
Пример №2
Какие из следующих выражений:
а) 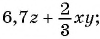
б) 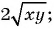
в) 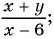
г) 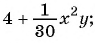
д) 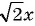 — являются рациональными?
— являются рациональными?
Решение:
Выражения а), в), г) и д) являются рациональными, так как составлены из чисел, переменных и содержат действия сложения, вычитания, умножения и деления. Выражение б) не является рациональным, так как содержит действие извлечения корня из выражения с переменными.
Пример №3
Какие из следующих выражений:
а) 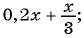
б) 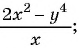
в) 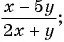
г) 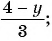
д) 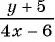 — являются дробными рациональными?
— являются дробными рациональными?
Решение:
Выражения б), в), д) являются дробными рациональными, так как составлены из чисел, переменных, натуральных степеней переменных с помощью действий сложения, вычитания, умножения и содержат действие деления на рациональное выражение с переменными.
Пример №4
Какие из следующих выражений:
а) 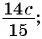
б) 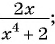
в) 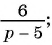
г) 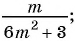
д) 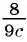 являются рациональными дробями?
являются рациональными дробями?
Решение:
Выражения а) — д) являются рациональными дробями, так как каждое из них представляет собой дробь, числитель и знаменатель которой являются многочленами.
Пример №5
Найдите значение выражения:
а) 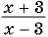 при
при 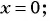
б) 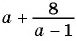 при
при 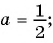
в) 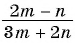 при
при 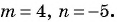
Решение:
а) Подставим 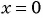 в выражение
в выражение 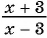 , и получим:
, и получим: 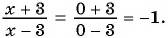
б) При 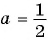 имеем:
имеем:
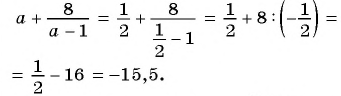
в) Если 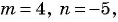 то
то 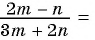
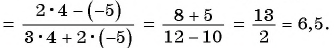
Область определения рациональной дроби
Пример №6
Найдите область определения рациональной дроби:
а) 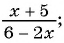
б) 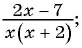
в) 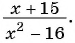
Решение:
а) Найдем, при каком значении переменной знаменатель дроби обращается в нуль. Для этого решим уравнение 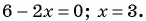 Областью определения данной дроби является множество всех действительных чисел, кроме числа 3, т. е.
Областью определения данной дроби является множество всех действительных чисел, кроме числа 3, т. е. 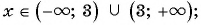
б) 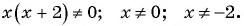 Областью определения данной дроби является множество всех действительных чисел, кроме чисел
Областью определения данной дроби является множество всех действительных чисел, кроме чисел 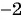 и
и 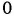 , т. е.
, т. е. 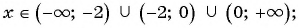
в) 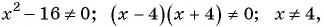
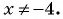 Областью определения данной дроби является множество всех действительных чисел, кроме чисел
Областью определения данной дроби является множество всех действительных чисел, кроме чисел 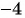 и
и 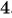 . Значит,
. Значит, 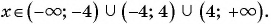
Пример №7
Найдите область определения рационального выражения:
а) 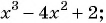
б) 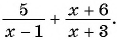
Решение:
а) Выражение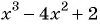 является целым рациональным, его областью определения является множество всех действительных чисел, т. е.
является целым рациональным, его областью определения является множество всех действительных чисел, т. е. 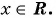
б) Знаменатель первой дроби обращается в нуль при 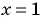 , а знаменатель второй дроби равен нулю при
, а знаменатель второй дроби равен нулю при 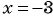 . Значит, областью определения данного выражения является множество всех действительных чисел, кроме чисел
. Значит, областью определения данного выражения является множество всех действительных чисел, кроме чисел 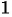 и
и 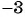 . Таким образом,
. Таким образом, 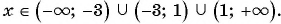
Основное свойство рациональной дроби
Действия с рациональными дробями выполняются по тем же правилам, что с обыкновенными дробями. Так, согласно основному свойству обыкновенных дробей, если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.
Например, 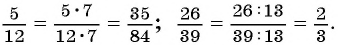
Аналогичное свойство можно сформулировать для рациональных дробей.
Если числитель и знаменатель дроби умножить или разделить на одно и то же выражение, не равное нулю, то получится дробь, тождественно равная данной.
Это свойство называют основным свойством дроби.
Для любой рациональной дроби 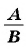 справедливо тождество
справедливо тождество 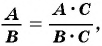 где
где 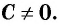
Умножим числитель и знаменатель дроби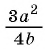 на одночлен
на одночлен 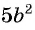 и получим:
и получим: 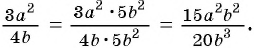 В этом случае говорят, что дробь
В этом случае говорят, что дробь 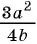 привели к новому знаменателю
привели к новому знаменателю 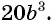
Пример №8
Приведите дробь:
а) 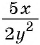 к знаменателю
к знаменателю 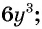
б) 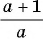 к знаменателю
к знаменателю 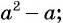
в) 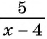 к знаменателю
к знаменателю 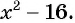
Решение:
а) 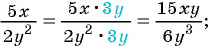
б) 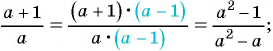
в) 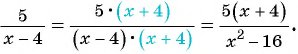
Если основное свойство дроби записать справа налево, то получится равенство
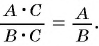
Это равенство позволяет дробь 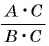 заменить на тождественно равную ей дробь
заменить на тождественно равную ей дробь 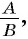 разделив числитель и знаменатель дроби
разделив числитель и знаменатель дроби 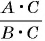 на множитель
на множитель 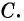
Например, разделим числитель и знаменатель дроби 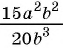 на одночлен
на одночлен 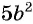 и получим:
и получим: 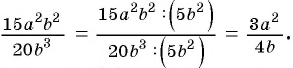 В этом случае говорят, что дробь
В этом случае говорят, что дробь 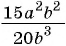 сократили на множитель
сократили на множитель 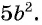 .
.
Сократить рациональную дробь — это значит числитель и знаменатель дроби разделить на их общий множитель.
Например, сократим дробь 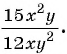 Для этого нужно найти множитель, на который можно разделить числитель и знаменатель дроби. Одночлены
Для этого нужно найти множитель, на который можно разделить числитель и знаменатель дроби. Одночлены 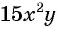 и
и 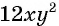 имеют общий множитель
имеют общий множитель 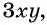 на который можно сократить данную дробь:
на который можно сократить данную дробь:
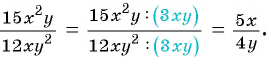
Чтобы сократить рациональную дробь, нужно:
- Разложить (если возможно) числитель и знаменатель дроби на множители.
- Определить общий множитель числителя и знаменателя дроби.
- Разделить числитель и знаменатель данной дроби на общий множитель.
Сократите дробь 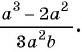
(1) 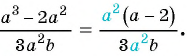
(2) 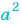 — общий множитель числителя и знаменателя дроби.
— общий множитель числителя и знаменателя дроби.
(3) 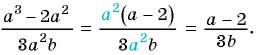
Пример №9
Сократите дробь:
а) 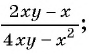
б) 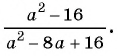
Решение:
а)
- (1) Разложим числитель и знаменатель дроби на множители:
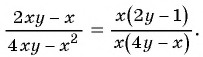
- (2) Числитель и знаменатель дроби имеют общий множитель
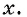
- (3) Разделим числитель и знаменатель данной дроби на общий множитель, т. е. сократим дробь:
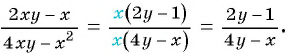
б)
Из основного свойства дроби следует, что 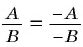 и
и 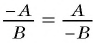 (и в том и в другом случае вторая дробь получена из первой умножением числителя и знаменателя на
(и в том и в другом случае вторая дробь получена из первой умножением числителя и знаменателя на 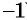 ).
).
Пример №10
Приведите дробь 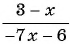 к знаменателю
к знаменателю 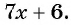
Решение:
Воспользуемся равенством 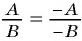 и получим:
и получим: 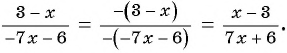
Пример №11
Сократите дробь:
а) 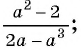
б) 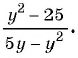
Решение:
а) Разложим знаменатель дроби на множители и получим:
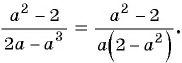
Выражения 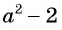 и
и 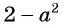 отличаются только знаками. Чтобы сократить дробь, поменяем знаки одного из множителей
отличаются только знаками. Чтобы сократить дробь, поменяем знаки одного из множителей 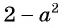 или
или 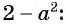
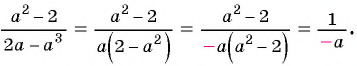
Полученный ответ можно записать в виде 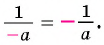 В этом случае говорят, что знак «минус» поставили перед дробью.
В этом случае говорят, что знак «минус» поставили перед дробью.
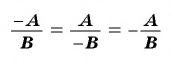
б) Разложим числитель и знаменатель дроби на множители и получим:
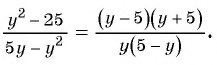
Поменяем знаки одного из множителей 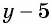 или
или 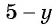 и поставим знак «минус» перед дробью:
и поставим знак «минус» перед дробью:
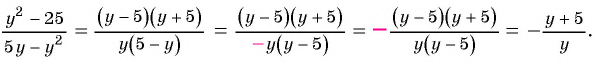
Пример №12
Приведите дробь 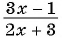 к знаменателю:
к знаменателю:
а) 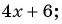
б) 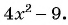
Решение:
а) Умножим числитель и знаменатель дроби на 2 и получим:
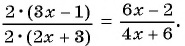
б) Умножим числитель и знаменатель дроби на 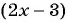 и получим:
и получим: 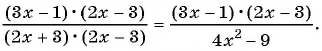
Разберём лекцию подробно:
Вспомним основное свойство обыкновенной дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получим дробь, равную данной. Иначе говоря, для любых натуральных чисел 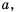
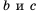 справедливо равенство:
справедливо равенство:
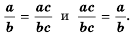
Докажем, что эти равенства являются верными не только для натуральных значений 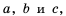 но и для любых других значений при условии
но и для любых других значений при условии 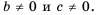
Докажем сначала, что 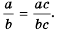
Пусть 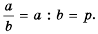 Тогда по определению частного
Тогда по определению частного 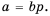 Умножим обе части этого равенства на
Умножим обе части этого равенства на 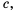 получим:
получим: 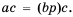 Используя переставное и сочетательное свойства умножения, приходим к равенству:
Используя переставное и сочетательное свойства умножения, приходим к равенству: 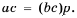 Так как
Так как 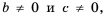 то и
то и 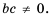 Из последнего равенства (по определению частного) имеем:
Из последнего равенства (по определению частного) имеем: 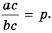 Поскольку
Поскольку 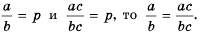
Это равенство является тождеством, следовательно, можем поменять в нем левую и правую части местами:
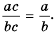
Это тождество дает возможность заменить дробь 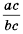 на дробь
на дробь 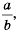 , то есть сократить дробь
, то есть сократить дробь 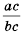 на общий множитель
на общий множитель 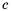 числителя и знаменателя.
числителя и знаменателя.
Свойство дроби, выраженное равенствами 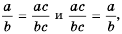 называют основным свойством рациональной дроби.
называют основным свойством рациональной дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля выражение, то получим дробь, равную данной.
Рассмотрим примеры применения этого свойства для дробей на их области допустимых значений переменной.
Пример №13
Сократите дробь 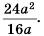
Решение:
Представим числитель и знаменатель этой дроби в виде произведений, содержащих одинаковый (общий) множитель 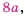 и сократим дробь на это выражение:
и сократим дробь на это выражение:
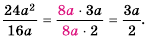
Ответ: 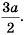
Пример №14
Сократите дробь 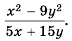
Решение:
Разложим на множители числитель и знаменатель дроби: 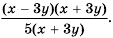 Сократим дробь на
Сократим дробь на 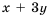 – общий множитель числителя и знаменателя:
– общий множитель числителя и знаменателя: 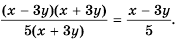
Ответ: 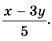
Таким образом, чтобы сократить дробь, нужно:
- разложить на множители числитель и знаменатель дроби, если это необходимо;
- выполнить деление числителя и знаменателя на их общий множитель и записать ответ.
Тождество 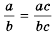 дает возможность приводить дроби к заданному другому (новому) знаменателю.
дает возможность приводить дроби к заданному другому (новому) знаменателю.
Пример №15
Приведите дробь 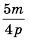 к знаменателю
к знаменателю 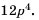
Решение:
Поскольку 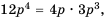 то, умножив числитель и знаменатель дроби
то, умножив числитель и знаменатель дроби 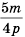 на
на 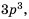 получим дробь со знаменателем
получим дробь со знаменателем 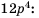
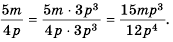
Множитель 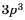 называют дополнительным множителем числителя и знаменателя дроби
называют дополнительным множителем числителя и знаменателя дроби 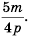
Ответ: 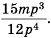
Пример №16
Приведите дробь 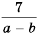 к знаменателю
к знаменателю 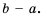
Решение:
Поскольку 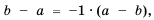 то, умножив числитель и знаменатель дроби
то, умножив числитель и знаменатель дроби 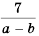 на -1, получим дробь со знаменателем
на -1, получим дробь со знаменателем 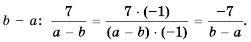
Дробь 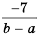 можно заменить тождественно равным ему выражением
можно заменить тождественно равным ему выражением 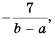 так как изменение знака перед дробью приводит к изменению знака в числителе или знаменателе.
так как изменение знака перед дробью приводит к изменению знака в числителе или знаменателе.
Поэтому 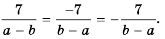
Ответ. 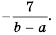
Аналогично, например, 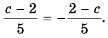 Следовательно,
Следовательно,
- если изменить знак в числителе (или знаменателе) дроби одновременно со знаком перед дробью, то получим дробь, тождественно равную данной.
Это правило можно записать с помощью тождества:
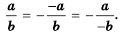
Пример №17
Найдите область определения функции 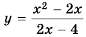 и постройте ее график.
и постройте ее график.
Решение:
Область определения функции – все числа, кроме тех, которые обращают знаменатель 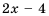 в нуль. Так как
в нуль. Так как 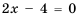 при
при 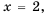 то область определения функции все числа, кроме числа 2. Упростим дробь
то область определения функции все числа, кроме числа 2. Упростим дробь 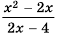 путем сокращения:
путем сокращения: 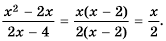 Следовательно, функция
Следовательно, функция 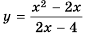 имеет вид
имеет вид 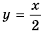 при условии
при условии 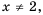 а ее графиком является прямая
а ее графиком является прямая 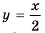 точки с абсциссой 2, то есть без точки (2; 1). Такую точку называют «выколотой» и обязательно исключают ее из графика, изображая «пустой».
точки с абсциссой 2, то есть без точки (2; 1). Такую точку называют «выколотой» и обязательно исключают ее из графика, изображая «пустой».
График функции 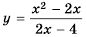 представлен на рисунке 1.
представлен на рисунке 1.
Сокращение рациональных дробей
Пример №18
Сократите дробь 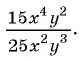
Решение:
Дробь можно сократить на 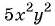 — общий множитель числителя и знаменателя дроби:
— общий множитель числителя и знаменателя дроби:
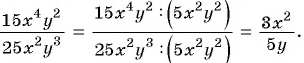
Пример №19
Сократите дробь:
а) 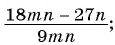
б) 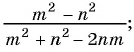
в) 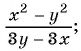
г) 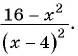
Решение:
а) Разложим на множители числитель дроби и сократим дробь:
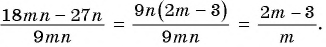
б) С помощью формул сокращенного умножения разложим на множители числитель и знаменатель дроби и получим:
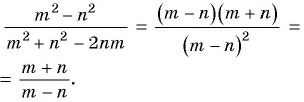
в) Разложим на множители числитель и знаменатель дроби:
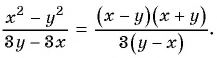
Множители 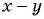 и
и 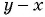 отличаются только знаками. Поменяем знаки одного из множителей
отличаются только знаками. Поменяем знаки одного из множителей 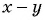 или
или 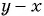 и поставим знак «минус» перед дробью:
и поставим знак «минус» перед дробью:
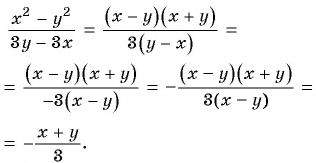
г) После разложения на множители числителя дроби имеем:
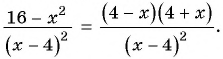
Воспользуемся тем, что 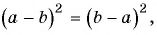 т. е.
т. е. 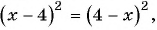 и получим:
и получим:
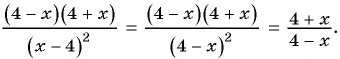
Пример №20
Сократите дробь:
а) 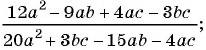
б) 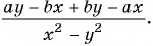
Решение:
а) С помощью способа группировки разложим числитель и знаменатель дроби на множители и сократим дробь:
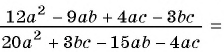
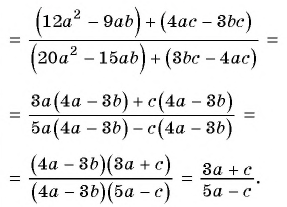
б) 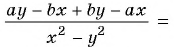
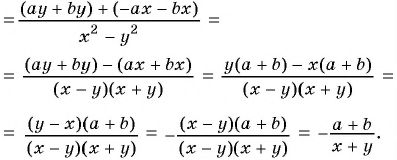
Пример №21
Сократите дробь:
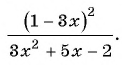
Решение:
Для разложения на множители знаменателя дроби воспользуемся формулой разложения квадратного трехчлена на множители: 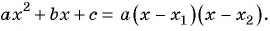 Найдем корни квадратного трехчлена
Найдем корни квадратного трехчлена 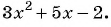 Для этого решим квадратное уравнение
Для этого решим квадратное уравнение 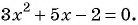
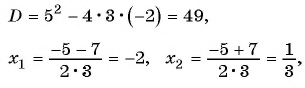
тогда 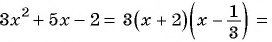
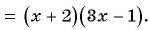
Сократим дробь:
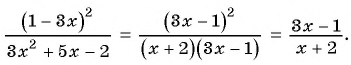
Пример №22
Упростите выражение 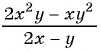 и найдите его значение при
и найдите его значение при 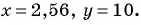
Решение:
Упростим выражение, сократив дробь:
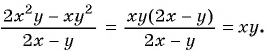
Подставим 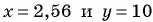 в выражение
в выражение 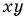 и получим
и получим 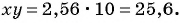
Пример №23
Из данных рациональных дробей выберите дробь, тождественно равную дроби 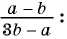
а) 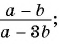
б) 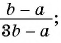
в) 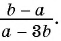
Решение:
Выполним преобразования:
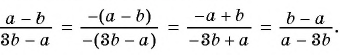
Дроби 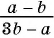 тождественно равна дробь в).
тождественно равна дробь в).
Пример №24
Приведите дробь:
а) 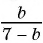 к знаменателю
к знаменателю 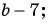
б) 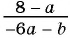 к знаменателю
к знаменателю 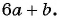
Решение:
Умножим числитель и знаменатель дроби на 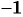 и получим:
и получим:
а) 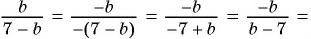
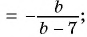
б) 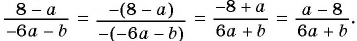
Пример №25
Постройте график функции 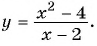
Решение:
Областью определения данной функции является множество всех действительных чисел, кроме числа 2.
Сократим дробь 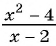 и получим:
и получим:
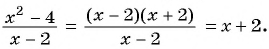
Необходимо построить график функции 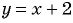 при
при 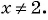 Графиком данной функции является прямая
Графиком данной функции является прямая 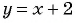 без точки (2; 4).
без точки (2; 4).
Сложение и вычитание рациональных дробей
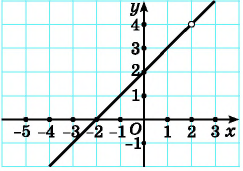
Вспомним, как складывают и вычитают обыкновенные дроби. Например:
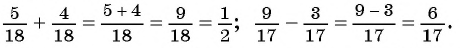
Сложение и вычитание рациональных дробей выполняются по таким же правилам, что сложение и вычитание обыкновенных дробей.
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.
Затем, если возможно, следует сократить полученную дробь.
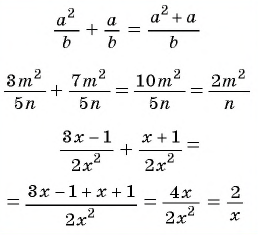
Пример №26
Найдите сумму рациональных дробей:
а) 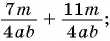
б) 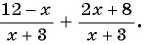
Решение:
а) 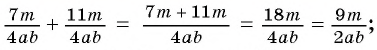
б) 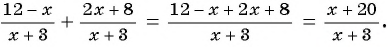
Чтобы вычесть дроби с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тем же. Затем, если возможно, следует сократить полученную дробь.
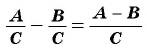
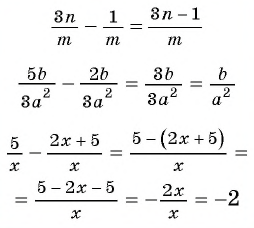
Пример №27
Найдите разность рациональных дробей:
а) 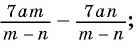
б) 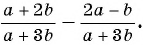
Решение:
а) 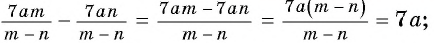
б) 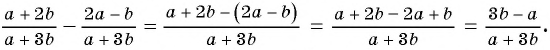
При сложении и вычитании обыкновенных дробей с разными знаменателями их приводят к общему знаменателю (например, 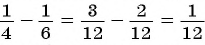 ).
).
Для того чтобы выполнить сложение или вычитание рациональных дробей с разными знаменателями, их также нужно привести к общему знаменателю.
Чтобы привести рациональные дроби к общему знаменателю, нужно:
- Разложить знаменатель каждой дроби на множители (если это необходимо) и определить общий знаменатель дробей.
- Умножить числитель и знаменатель каждой дроби на недостающие множители из общего знаменателя дробей.
Приведите к общему знаменателю рациональные дроби 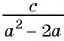 и
и 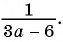
(1) 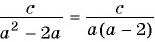 и
и 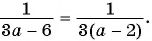
Общий знаменатель 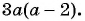
(2) 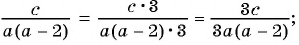
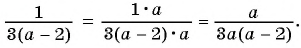
Пример №28
Приведите к общему знаменателю дроби: а) 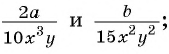
б) 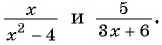
Решение:
а) Общим знаменателем данных дробей является одночлен 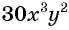 , поскольку НОК (10, 15) = 30 и переменные
, поскольку НОК (10, 15) = 30 и переменные 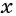 и
и 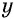 взяты с наибольшим показателем степени.
взяты с наибольшим показателем степени.
Умножим числитель и знаменатель первой дроби на 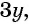 а числитель и знаменатель второй дроби на
а числитель и знаменатель второй дроби на 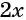 и приведем дроби к общему знаменателю:
и приведем дроби к общему знаменателю:
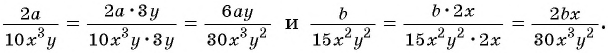
б) Разложим на множители знаменатель каждой дроби и получим:
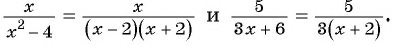
Умножим числитель и знаменатель первой дроби на 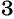 , а числитель и знаменатель второй дроби на
, а числитель и знаменатель второй дроби на 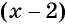 и приведем дроби к общему знаменателю:
и приведем дроби к общему знаменателю:
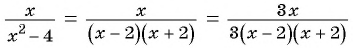
и
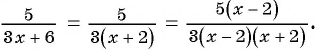
Чтобы выполнить сложение (вычитание) рациональных дробей с разными знаменателями, нужно:
- Привести дроби к общему знаменателю.
- Применить правила сложения (вычитания) дробей с одинаковыми знаменателями.
Найдите сумму рациональных дробей 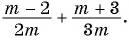
(1) 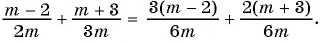
(2) 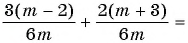
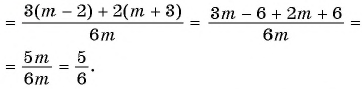
Пример №29
Найдите разность рациональных дробей
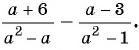
Решение:
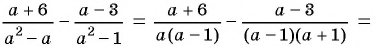
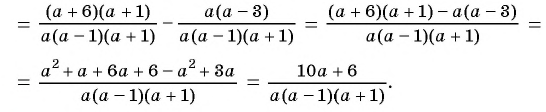
Сложение и вычитание дробей с одинаковыми знаменателями
Вспомним, как сложить дроби с одинаковыми знаменателями. Нужно сложить их числители, а знаменатель оставить тот же. Например:
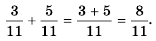
Запишем это правило в виде формулы:
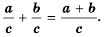
Это равенство справедливо для любых дробей. Докажем его (при условии 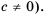
Пусть 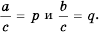 Тогда по определению частного
Тогда по определению частного 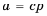
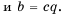 Имеем:
Имеем: 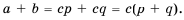 Поскольку
Поскольку 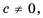 то по определению частного
то по определению частного 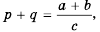
следовательно, 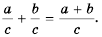
Сформулируем правило сложения дробей с одинаковыми знаменателями:
чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Пример №30
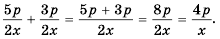
Аналогично можно доказать тождество
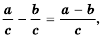
при помощи которого записывают правило вычитания дробей с одинаковыми знаменателями.
Сформулируем правило вычитания дробей с одинаковыми знаменателями:
чтобы вычесть дроби с одинаковыми знаменателями, нужно от числителя уменьшаемого отнять числитель вычитаемого, а знаменатель оставить тот же.
Пример №31
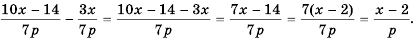
Рассмотрим еще несколько примеров.
Пример №32
Найдите сумму и разность дробей
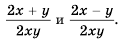
Решение:
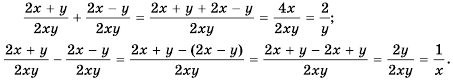
Ответ.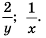
Пример №33
Упростите выражение
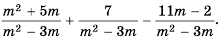
Решение:
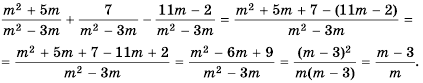
Ответ: 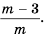
Пример №34
Найдите сумму 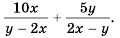
Решение:
Так как 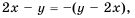 то второе слагаемое можно записать с тем же знаменателем, что и в первом слагаемом:
то второе слагаемое можно записать с тем же знаменателем, что и в первом слагаемом:
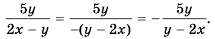
Тогда
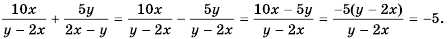
Ответ: 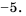
Если в тождествах 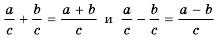 поменять местами левые и правые части, то получим тождества:
поменять местами левые и правые части, то получим тождества:
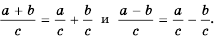
С помощью этих тождеств дробь, числитель которой является суммой или разностью нескольких выражений, можно записать в виде суммы или разности нескольких дробей.
Пример №35
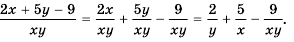
Пример №36
Запишите дробь в виде суммы или разности целого выражения и дроби: 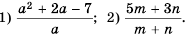
Решение:
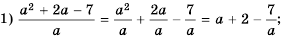
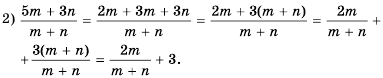
Ответ. 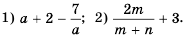
Пример №37
Выполните сложение рациональных дробей:
а) 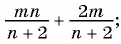
б) 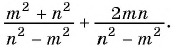
Решение:
а) 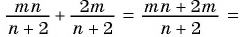
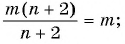
б) 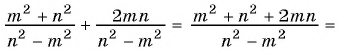
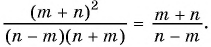
Пример №38
Найдите разность рациональных дробей:
а) 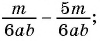
б) 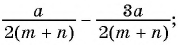
в) 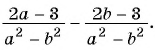
Решение:
а) 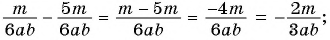
б) 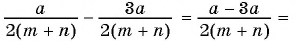
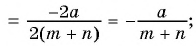
в) 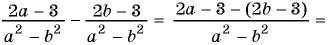
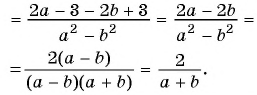
Пример №39
Выполните действия:
а) 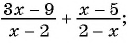
б) 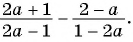
Решение:
а) Знаменатели дробей отличаются только знаком. Поменяем знак в знаменателе второй дроби и перед этой дробью и получим:
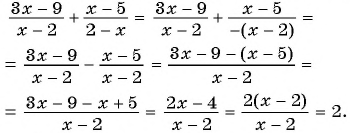
б) 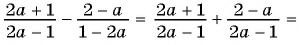
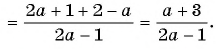
Пример №40
Выполните действия:
а) 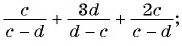
б) 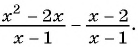
Решение:
а) 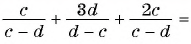
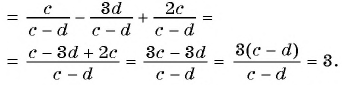
б) 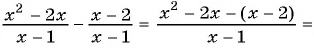
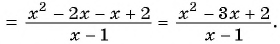
Разложим на множители квадратный трехчлен в числителе дроби и сократим дробь:
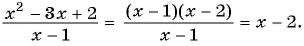
Сложение и вычитание дробей с разными знаменателями
Если дроби имеют разные знаменатели, то их, как и обычные дроби, сначала приводят к общему знаменателю, а потом складывают или вычитают по правилу сложения или вычитания дробей с одинаковыми знаменателями.
Рассмотрим, как прибавить дроби 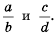 Приведем эти дроби к их общему знаменателю
Приведем эти дроби к их общему знаменателю 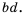 Для этого числитель и знаменатель дроби
Для этого числитель и знаменатель дроби 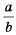 умножим на
умножим на 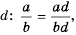 числитель и знаменатель дроби
числитель и знаменатель дроби 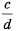 умножим на
умножим на 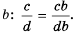 Дроби
Дроби 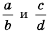 привели к общему знаменателю
привели к общему знаменателю 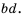 Напомним, что
Напомним, что 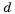 называют дополнительным множителем числителя и знаменателя дроби —
называют дополнительным множителем числителя и знаменателя дроби — 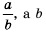 дополнительным множителем числителя и знаменателя дроби
дополнительным множителем числителя и знаменателя дроби 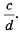
Описанную последовательность действий для сложения дробей с разными знаменателями можно записать так:
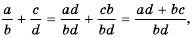
или сокращенно:
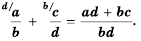
Аналогично выполняют и вычитание дробей с разными знаменателями:
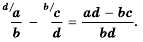
Пример №41
Выполните действие: 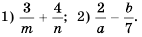
Решение:
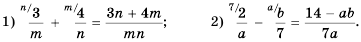
Общим знаменателем двух или более дробей может быть не только произведение их знаменателей. Вообще у дробей есть бесконечно много общих знаменателей. Часто при сложении и вычитании дробей с разными знаменателями удается найти более простой общий знаменатель, чем произведение знаменателей этих дробей. В таком случае говорят о простейшем общем знаменателе (аналогично наименьшему общему знаменателю числовых дробей).
Рассмотрим пример, где знаменатели дробей – одночлены.
Пример №42
Выполните сложение 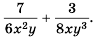
Решение. Общим знаменателем данных дробей можно считать одночлен 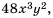 который является произведением знаменателей дробей, но в данном случае он не будет простейшим общим знаменателем. Попробуем найти простейший общий знаменатель, что для дробей, знаменатели которых являются одночленами, будет также одночленом. Коэффициент этого одночлена должен делиться и на 6, и на 8. Наименьшим из таких чисел будет 24. В общий знаменатель каждая из переменных должна входить с наибольшим из показателей степени, которые содержат знаменатели дробей. Таким образом, простейшим знаменателем будет одночлен
который является произведением знаменателей дробей, но в данном случае он не будет простейшим общим знаменателем. Попробуем найти простейший общий знаменатель, что для дробей, знаменатели которых являются одночленами, будет также одночленом. Коэффициент этого одночлена должен делиться и на 6, и на 8. Наименьшим из таких чисел будет 24. В общий знаменатель каждая из переменных должна входить с наибольшим из показателей степени, которые содержат знаменатели дробей. Таким образом, простейшим знаменателем будет одночлен 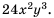 Тогда дополнительным множителем для первой дроби станет выражение
Тогда дополнительным множителем для первой дроби станет выражение 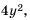 так как
так как 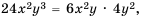 а для второй – выражение
а для второй – выражение 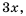 так как
так как 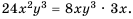 Следовательно, имеем:
Следовательно, имеем:
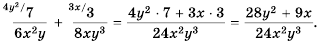
Ответ: 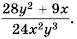
Обратите внимание, что в примере 2 при приведении дробей к общему знаменателю дополнительные множители 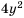 и
и 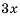 не содержали ни одного общего множителя, отличного от единицы. Это означает, что мы нашли простейший общий знаменатель дробей.
не содержали ни одного общего множителя, отличного от единицы. Это означает, что мы нашли простейший общий знаменатель дробей.
Рассмотрим пример, в котором знаменателями дробей являются многочлены.
Пример №43
Выполните вычитание
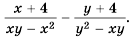
Решение:
Чтобы найти общий знаменатель, разложим знаменатели на множители:
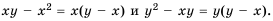
Простейшим общим знаменателем дробей будет выражение 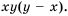 Тогда дополнительным множителем для первой дроби станет
Тогда дополнительным множителем для первой дроби станет 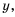 а для второй –
а для второй – 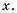 Выполним вычитание:
Выполним вычитание:
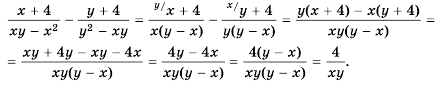
Ответ. 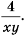
Таким образом, чтобы выполнить сложение или вычитание дробей с разными знаменателями, нужно:
- разложить на множители знаменатели дробей, если это необходимо;
- найти общий знаменатель, лучше простейший;
- записать дополнительные множители;
- найти дробь, которая является суммой или разницей данных дробей;
- упростить эту дробь и получить ответ.
Аналогично выполняют сложение и вычитание целого выражения и дроби.
Пример №44
Упростите выражение 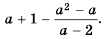
Решение:
Запишем выражение 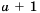 в виде дроби со знаменателем 1 и выполним вычитание:
в виде дроби со знаменателем 1 и выполним вычитание:
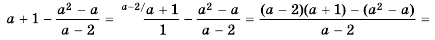
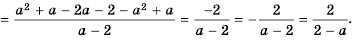
Ответ: 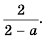
Пример №45
Выполните сложение рациональных дробей:
а) 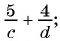
б) 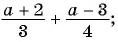
в) 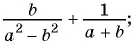
г) 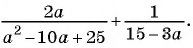
Решение:
а) 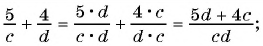
б) 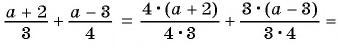
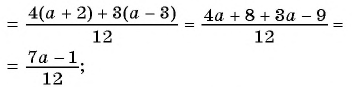
в) 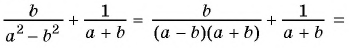
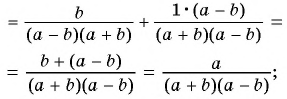
г) 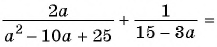
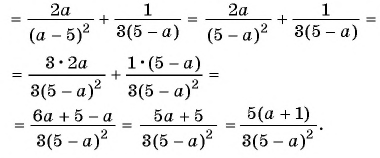
Пример №46
Выполните вычитание:
а) 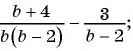
б) 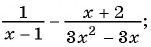
в) 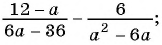
г) 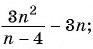
д) 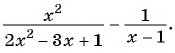
Решение:
а) 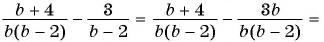
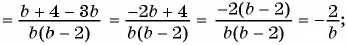
б) 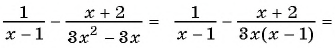
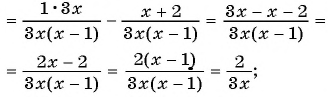
в) 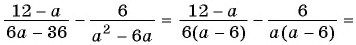
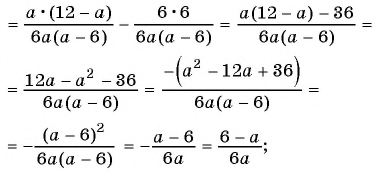
г) 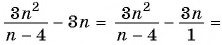
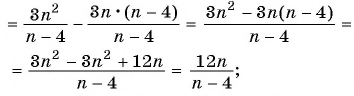
д) Разложим на множители квадратный трехчлен в знаменателе первой дроби и получим:
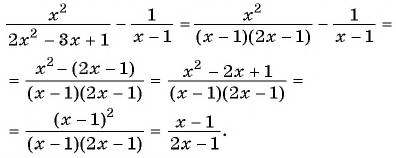
Пример №47
Представьте в виде дроби выражение
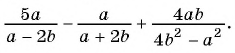
Решение:
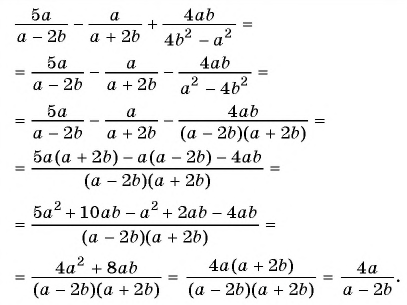
Умножение и деление рациональных дробей
Вспомним, как умножают и делят обыкновенные дроби.
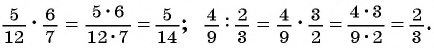
Правила умножения и деления рациональных дробей аналогичны правилам умножения и деления обыкновенных дробей.
Произведение рациональных дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель равен произведению знаменателей данных дробей. 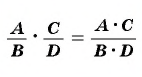
Чтобы найти произведение рациональных дробей, нужно:
- Произведение числителей данных дробей записать в числителе новой дроби, а произведение знаменателей данных дробей записать в знаменателе новой дроби.
- Сократить полученную дробь, если это возможно.
Найдите произведение рациональных дробей 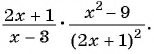
(1) 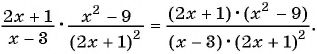
(2) 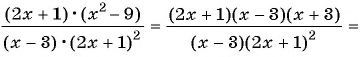
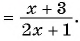
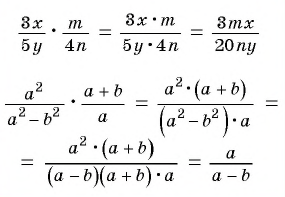
Пример №48
Найдите произведение рациональных дробей:
а) 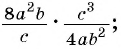
б) 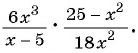
Решение:
а) 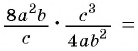
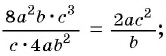
б) 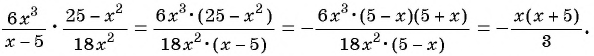
Правило умножения рациональных дробей можно использовать при возведении рациональной дроби в степень. Например:
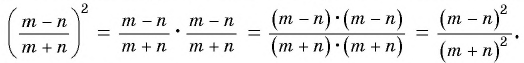
Обобщим этот прием и получим правило:
Чтобы возвести рациональную дробь в степень, нужно возвести в эту степень числитель дроби и полученный результат записать в числителе новой дроби, возвести в эту степень знаменатель дроби и полученный результат записать в знаменателе новой дроби.
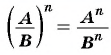
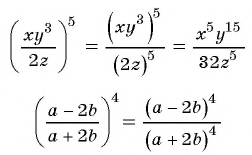
Пример №49
Возведите в степень дробь:
а) 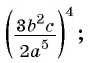
б) 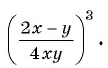
Решение:
а) 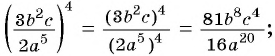
б) 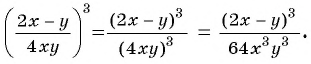
Чтобы разделить одну рациональную дробь на другую, нужно делимое умножить на дробь, обратную делителю.
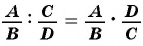
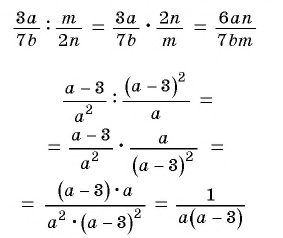
Пример №50
Найдите частное:
а) 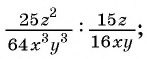
б) 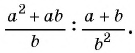
Решение:
а) 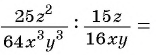
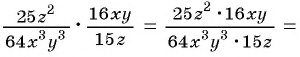
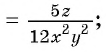
б) 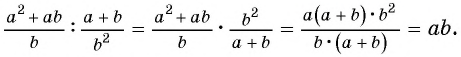
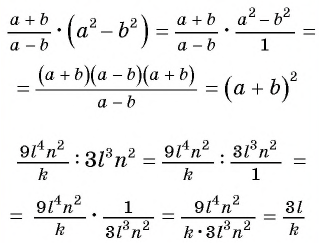
Пример №51
Представьте в виде дроби рациональное выражение:
а) 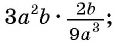
б) 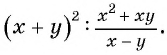
Решение:
а) Представим множитель 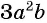 в виде рациональной дроби:
в виде рациональной дроби: 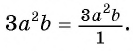
Выполним умножение дробей:
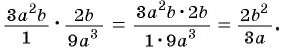
б) Представим выражение 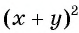 в виде рациональной дроби
в виде рациональной дроби 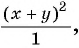 получим:
получим: 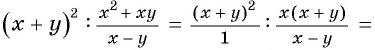
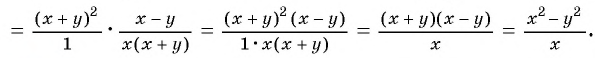
Пример №52
Выполните умножение рациональных дробей:
а) 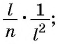
б) 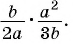
Решение:
а) 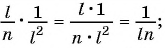
б) 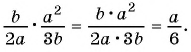
Пример №53
Представьте в виде рациональной дроби произведение:
а) 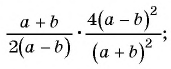
б) 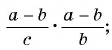
в) 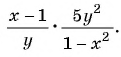
Решение:
а) 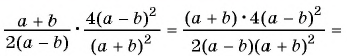
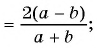
б) 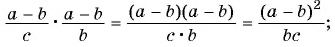
в) 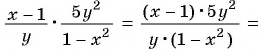
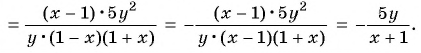
Пример №54
Представьте в виде рациональной дроби выражение:
а) 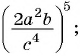
б) 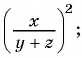
в) 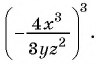
Решение:
а) 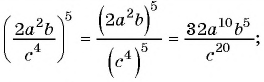
б) 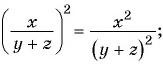
в) 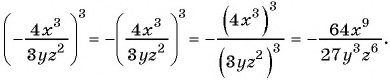
Пример №55
Представьте в виде степени рациональную дробь:
а) 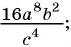
б) 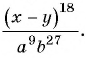
Решение:
а) 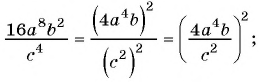
б) 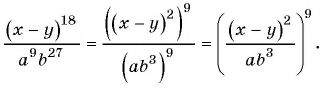
Пример №56
Выполните деление рациональных дробей:
а) 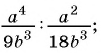
б) 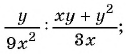
в) 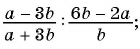
г) 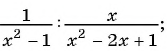
д) 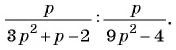
Решение:
а) 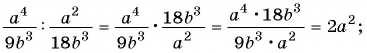
б) 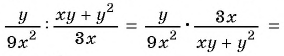
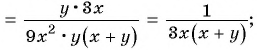
в) 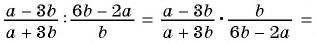
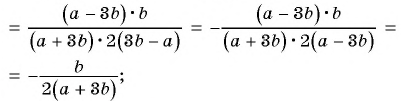
г) 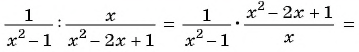
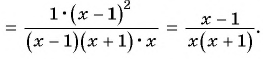
д) Воспользуемся формулой разложения квадратного трехчлена на множители и получим: 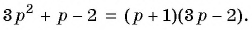
Тогда
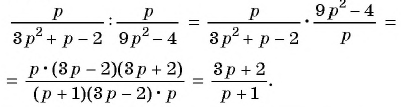
Пример №57
Выполните действия:
а) 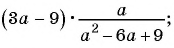
б) 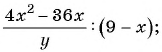
в) 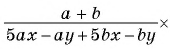
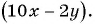
Решение:
а) 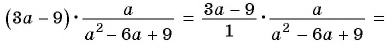
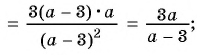
б) 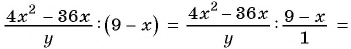
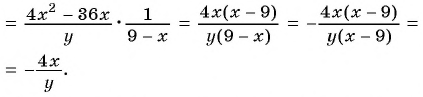
в) Разложим на множители многочлен, применив способ группировки:
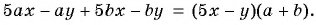
Тогда 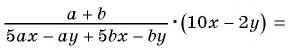
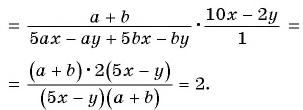
Пример №58
Найдите значение выражения
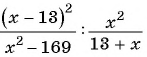
при 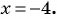
Решение:
Выполним деление:
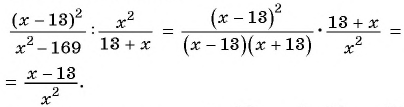
При 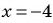 получим:
получим: 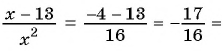
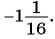
Пример №59
Найдите значение выражения 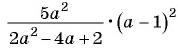
при 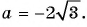
Решение:
Выполним умножение:
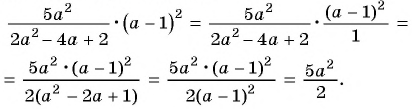
При 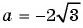 имеем:
имеем:
Умножение дробей
Напомним, что произведением двух обыкновенных дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей данных дробей:
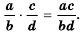
Докажем, что это равенство является тождеством для любых значений 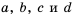 при условии, что
при условии, что 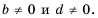
Пусть 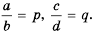 Тогда по определению частного
Тогда по определению частного 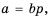
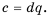 Поэтому
Поэтому 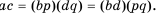 Так как
Так как 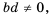 то, снова учитывая определение частного, получим:
то, снова учитывая определение частного, получим: 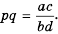 следовательно, если
следовательно, если 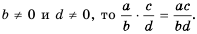
Сформулируем правило умножения дробей.
Чтобы умножить дробь на дробь, нужно перемножить отдельно числители и отдельно знаменатели сомножителей и записать первый результат в числителе, а второй – в знаменателе произведения дробей.
Пример №60
Выполните умножение 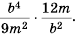
Решение:
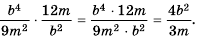
Ответ: 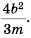
Пример №61
Найдите произведение
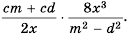
Решение.
Используем правило умножения дробей и разложим на множители числитель первой дроби и знаменатель второй:
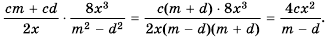
Ответ.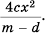
Обратите внимание, что в примерах 1 и 2 при умножении дробей мы не находили сразу же результат умножения числителей и знаменателей. Сначала мы записали произведения в числителе и в знаменателе по правилу умножения дробей, потом сократили полученную дробь, так как она оказалась сократимой, а уже затем выполнили умножение в числителе и в знаменателе и записали ответ. Целесообразно это учитывать и в дальнейшем.
Пример №62
Умножить дробь 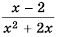 на многочлен
на многочлен 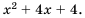
Решение:
учитывая, что 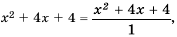 имеем:
имеем:
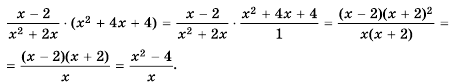
Ответ. 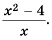
Правило умножения дробей можно распространить на произведение трех и более множителей.
Пример №63
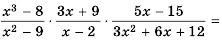
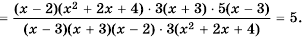
Возведение дроби в степень
Рассмотрим возведение дроби 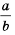 в степень
в степень 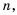 где
где 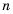 – натуральное число.
– натуральное число.
По определению степени и правилу умножения дробей имеем:
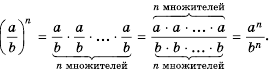
Следовательно:
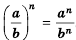
Сформулируем правило возведения дроби в степень.
Чтобы возвести дробь в степень, нужно возвести в эту степень числитель и знаменатель и первый результат записать в числитель, а второй – в знаменатель дроби.
Пример №64
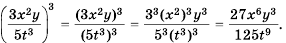
Пример №65
Представьте выражение 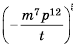 в виде дроби.
в виде дроби.
Решение:
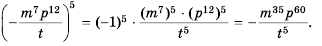
Ответ: 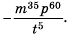
Деление дробей
Напомним, чтобы найти частное двух обыкновенных дробей, нужно делимое умножить на дробь, обратную делителю:
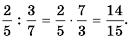
Формулой это можно записать так:
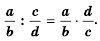
Докажем, что это равенство является тождеством для любых значений 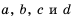 при условии, что
при условии, что 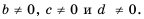
Так как: 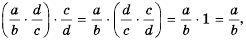
то по определению частного имеем: 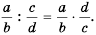
Следовательно, если 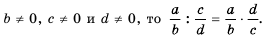
Дробь 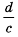 называют обратной дроби
называют обратной дроби 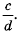
Сформулируем правило деления дробей.
Чтобы разделить одну дробь на другую, нужно первую дробь у множить на дробь, обратную второй.
Пример №66
Разделите дробь 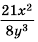 на дробь
на дробь 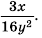
Решение:
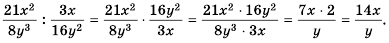
Ответ. 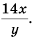
Пример №67
Выполните деление 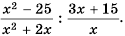
Решение:
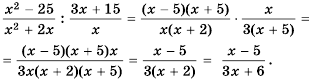
Ответ: 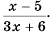
Пример №68
Упростите выражение: 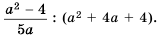
Решение:
Так как 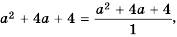 то:
то:
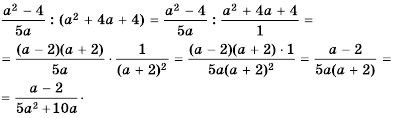
Ответ: 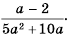
Преобразования рациональных выражений
При решении многих задач требуется упрощать рациональные выражения, приводя их к рациональным дробям. Для этого выполняют преобразования рациональных выражений.
Чтобы преобразовать рациональное выражение, нужно:
- Установить порядок действий в выражении.
- Выполнить действия по порядку, используя правила сложения, вычитания, умножения и деления рациональных дробей.
Упростите выражение:
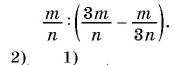
(1) 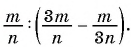
(2) 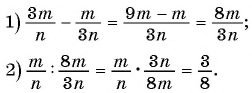
Пример №69
Представьте выражение 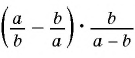 в виде рациональной дроби.
в виде рациональной дроби.
Решение:
(1) Сначала необходимо выполнить вычитание выражений, стоящих в скобках, а затем выполнить умножение.
(2) 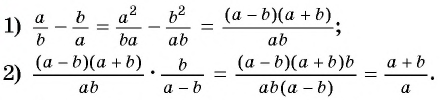
Преобразование рационального выражения можно выполнить не по действиям, а “цепочкой”. В данном случае получим:
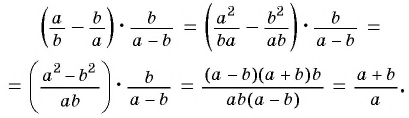
Пример №70
Найдите значение выражения
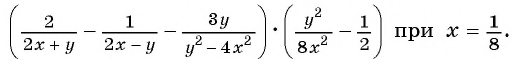
Решение:
Упростим выражение, выполнив действия по порядку:
1) 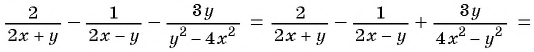
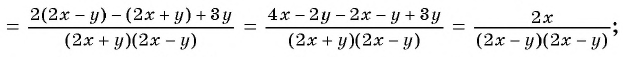
2) 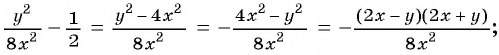
3) 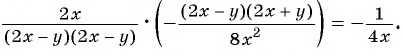
При 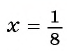 получим:
получим: 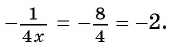
Преобразования рациональных выражений можно выполнять наряду с другими, ранее изученными преобразованиями.
Пример №71
Упростите выражение 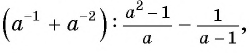 приведя его к рациональной дроби.
приведя его к рациональной дроби.
Решение:
1) 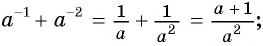
2) 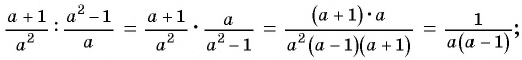
3) 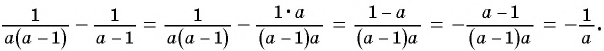
Правила преобразования рациональных выражений можно использовать и для преобразования выражений, содержащих корни.
Пример №72
Сократите дробь:
а) 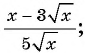
б) 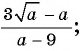
в) 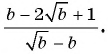
Решение:
а) 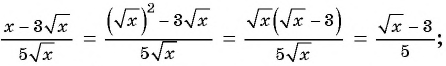
б) 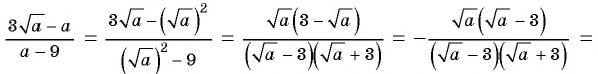
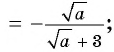
в) 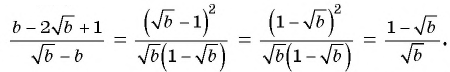
Пример №73
Упростите выражение 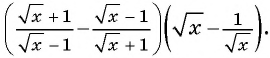
Решение:
1) 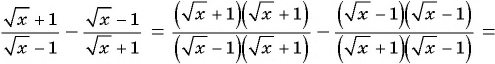
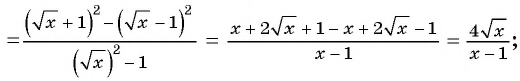
2) 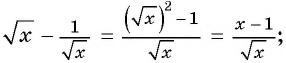
3) 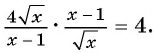
Пример №74
Представьте выражение 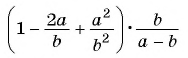 в виде дроби.
в виде дроби.
Решение:
1) 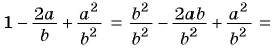
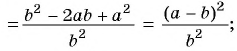
2) 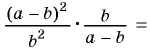
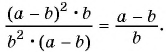
Пример №75
Найдите значение выражения 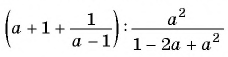 при
при 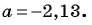
Решение:
Преобразуем данное выражение “цепочкой”:
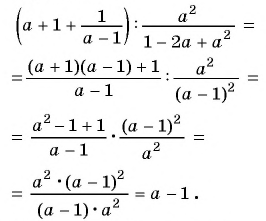
При 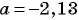 получим:
получим: 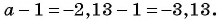
Пример №76
Упростите выражение
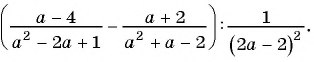
Решение:
1) Корнями квадратного трехчлена 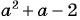 являются числа
являются числа 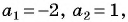 значит,
значит, 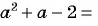
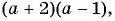 тогда:
тогда:
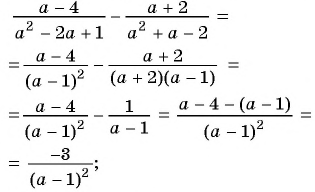
2) 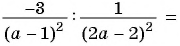
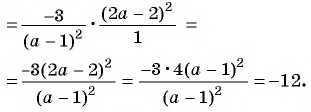
Пример №77
Докажите, что значение выражения
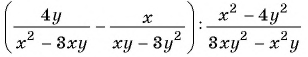
не зависит от значений переменных.
Решение:
Значение выражения при различных значениях переменных из области его определения можно найти, предварительно упростить его:
1) 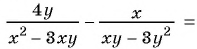
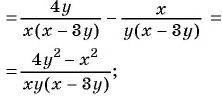
2) 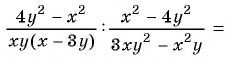
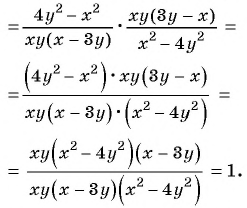
Получили, что результат упрощения равен числу 1, значит при любых значениях переменных из области определения значение данного выражения равно 1, т. е. не зависит от значений переменных.
Пример №78
Упростите выражение
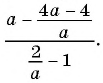
Решение:
Запишем дробь в виде частного и получим: 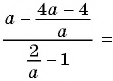
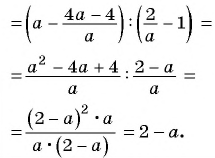
Пример №79
Упростите выражение
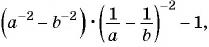 приведя его к несократимой дроби.
приведя его к несократимой дроби.
Решение:
1) 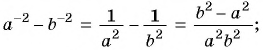
2) 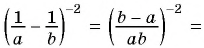
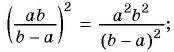
3) 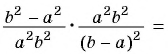
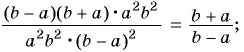
4) 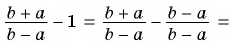
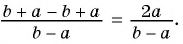
Пример №80
Примените к выражению алгоритм сокращения рациональной дроби:
а) 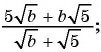
б) 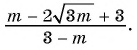
Решение:
а) 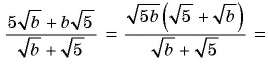
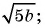
б) 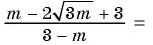
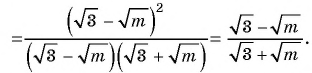
Пример №81
Упростите выражение
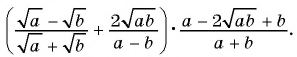
Решение:
1) 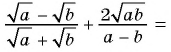
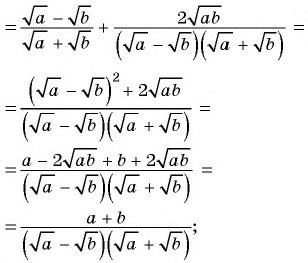
2) 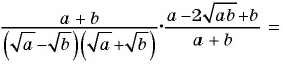
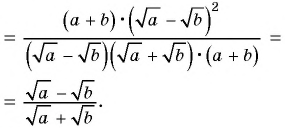
Пример №82
Найдите значение выражения 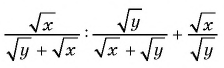 при
при 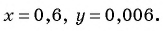
Решение:
Упростим данное выражение:
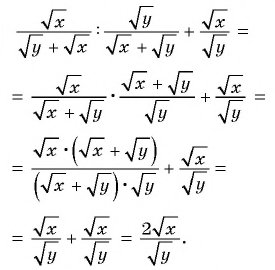
При 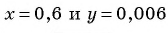 получим:
получим:
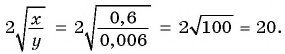
- Заказать решение задач по высшей математике
Тождественные преобразования рациональных выражений
Рассмотрим примеры преобразований рациональных выражений.
Пример №83
Докажите тождество 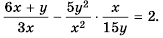
Решение:
Упростим левую часть равенства:
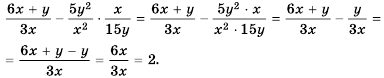
С помощью тождественных преобразований мы привели левую часть равенства к правой. Следовательно, равенство является тождеством.
Пример №84
Упростите выражение
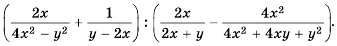
Решение:
Сначала выполним действие в каждой из скобок, а потом – действие деления:
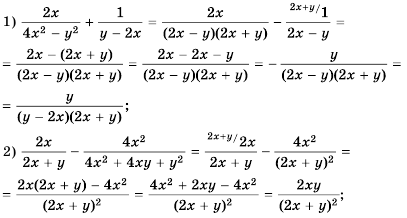
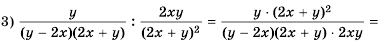
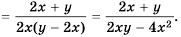
Ответ: 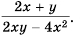
Решение можно было записать и в виде «цепочки»:
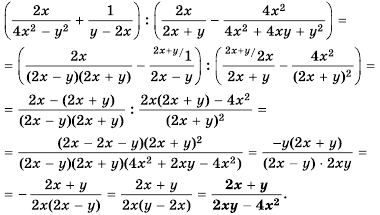
Каждое выражение, содержащее сумму, разность, произведение и частное рациональных дробей, можно представить в виде рациональной дроби.
Пример №85
Докажите, что при всех допустимых значениях переменных значение дроби 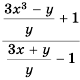 неотрицательно.
неотрицательно.
Решение:
Можно представить эту дробь в виде частного 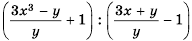 и далее преобразовать ее, как предложено в примере 2.
и далее преобразовать ее, как предложено в примере 2.
А можно, используя основное свойство дроби, умножить числитель и знаменатель данной дроби на их общий знаменатель, то есть на 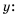
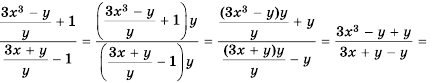
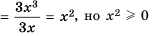 при любом значении
при любом значении 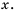
- Функция в математике
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Система показательных уравнений
- Непрерывные функции и их свойства
- Правило Лопиталя
- Вычисления в Mathematica с примерами
План урока:
Понятие рационального выражения
Сокращение рациональных выражений
Представление дроби в виде суммы дробей
Преобразование рациональных выражений
Понятие рационального выражения
В 5 и 6 классе мы уже изучали дроби и действия над ними. В 7 классе рассматривались рациональные числа, которые, по сути, и являются дробями. Однако до этого мы изучали только так называемые числовые дроби, у которых в числителе и знаменателе стоят какие-то числа либо выражения с числами, но не переменные величины.

Следующие дроби являются числовыми:

Однако нередко в алгебре приходится иметь дело и с дробями, которые содержат переменные. В качестве примера подобных выражений можно привести:

Так как деление на ноль является недопустимой операцией в алгебре, то некоторые дроби могут не иметь смысла. Так, дробь

бессмысленна, так как ее знаменатель 21 – 3•7 равен нулю.
Если дробь содержит переменные величины, то ее значение зависит от этих переменных. Так, дробь

при у = 4 принимает значение, равное 9. Если же у = 3, то эта дробь окажется бессмысленной.
Значения переменных величин, при которых дробь сохраняет свой смысл, называют допустимыми значениями переменных.
Пример. Укажите множество допустимых значений величин х и у для дроби

Решение. Недопустим только случай, при котором в знаменателе находится ноль, то есть когда выполняется равенство
х – у = 0
или равносильное ему равенство
х = у
Следовательно, допустимыми значениями являются все такие пары (х; у), что х ≠ у.
Пример. Каковы допустимые значения величин а и b в дроби

Решение. В данной записи есть три дробных черты, а значит, и три знаменателя:

Ни один из знаменателей не должен равняться нулю, поэтому

Перенесем в последнем неравенстве 2-ое слагаемое вправо, изменив знак (правила преобразований выражений со знаком ≠ точно такие же, как и у равенств):

По свойству пропорции имеем:
1•а ≠ 1•b
а ≠b
Итак, допустимыми являются все значения a и b, при которых а ≠ 0, b≠ 0, a≠b.
Пример. Найдите множество допустимых значений х для дроби

Решение.
Ясно, что знаменатель должен отличаться от нуля:
х2 – 25 ≠ 0
Чтобы найти, при каких значениях неизвестной величины знаменатель обращается в ноль, надо решить уравнение
х2 – 25 = 0
Представим полином в левой части как произведение, применив формулу квадрата разности:
х2 – 52= 0
(х – 5)(х + 5) = 0
х = 5 или х = – 5
Получаем, что исходная дробь сохраняет смысл при любых х, отличных от – 5 и 5.
Порою дроби, содержащие переменные, могут встречаться в тождествах.
Пример. Докажите тождество

Решение. У дроби в левой части знаменатель всегда положителен, поэтому все допустимыми являются все значения c. Согласно свойству операции деления, делимое равно произведению делителя и частного, поэтому для доказательства тождества надо лишь показать справедливость равенства
(с3 – 2с2 + с – 2) = (с – 2)(с2 + 1)
Раскроем скобки в правой части:
(с – 2)(с2 + 1) = с3 – 2с2 + с – 2
Получили одинаковое выражение и для левой, и для правой части тождества, следовательно, оно верное.
Теперь сформулируем понятие рационального выражения.

Среди рациональных выражений выделяют целые и дробные выражения.


Приведем примеры целых рациональных выражений:

А вот несколько примеров дробных рациональных выражений:

Стоит заметить, что дробь и дробное выражение – это два разных понятия. Для иллюстрации приведем два примера:
 – это дробь, но целое, а не дробное выражение;
– это дробь, но целое, а не дробное выражение;- (х + 7):t – это дробное выражение, но не дробь.
Отдельно отметим, что дробь равна нулю тогда, когда ее числитель равен нулю, а знаменатель нет. Если же и знаменатель равен нулю, то получается недопустимое действие – деление на ноль, поэтому дробь не будет иметь смысла.
Пример. Найдите все корни уравнения

Решение. На первый взгляд уравнение кажется сложным, особенно из-за знаменателя. Однако он здесь почти не играет роли. В левой части находится дробь, значит, нулю равен ее знаменатель:
(х – 1)(х + 2) = 0
х – 1 = 0 или х + 2 = 0
х = 1 или х = – 2
Получили два корня. Осталось убедиться, что при этих значениях х дробь не становится бессмысленной, то есть ее знаменатель не обращается в ноль. При х = 1 имеем знаменатель
2•14 – 3•13 + 5•1 – 4 = 2 – 3 + 5 – 4 = 0
поэтому число 1 НЕ является корнем уравнения. Теперь проверим знаменатель при х = – 2:
2•(– 2)4 – 3•( – 2)3 + 5•( – 2) – 4 =
= 32 + 24 – 10 – 4 = 42
Получается, что единственное корень уравнения – это ( – 2).
Ответ: – 2
Сокращение рациональных выражений
Узнав, какие выражения являются рациональными, мы приступим к изучению их преобразований. Напомним главное свойство дроби:

Оно означает, что числитель и знаменатель можно умножить на произвольное число (кроме нуля), то значение дроби останется прежним:

Это правило остается верным и в том случае, когда вместо чисел используются переменные величины.

Например, возможны такие преобразования рациональных выражений:


Например, пусть надо привести дробь

к знаменателю 6а2b2.
На что именно надо умножитель знаменатель, что получился одночлен 6а2b2? Очевидно, что
6а2b2 = 2а2b•3b
Поэтому выражения над и под дробной чертой надо умножить на 3b:

Использованный нами множитель 3b называют дополнительным множителем.
Обратная операция, при которой из знаменателя и числителя убирают совпадающие множители, называется сокращением дроби:

Это тождество означает, что дроби можно сокращать, убирая общий множитель, например:

Аналогичные действия можно совершать не только с числовыми дробями, но и с дробными выражениями:

В последнем примере мы вынесли общие множители за скобки (2х и 7у), чтобы над и под чертой появилась одинаковая сумма х + 3у, которую можно сократить.
Однако при сокращении дробей важно учитывать область ее допустимых значений, ведь из-за изменения знаменателя она может измениться. Например, пусть требуется построить график функции

В числителе стоит разность квадратов, которую можно разложить на множители:

Казалось бы, мы получили линейную функцию
y = x + 2
чей график нам известен – это прямая. Но она определена при всех возможных х, в то время как исходная дробь бессмысленна при х = 2, ведь тогда знаменатель становится равен нулю. Поэтому график функции будет выглядеть как прямая, однако одна из ее точек, с координатами (2; 4), будет «выколотой» точкой, и исключенной:

Данный рисунок означает, что графиком функции – прямая линия, кроме точки (2; 4)

Выколотая точка на графике изображается маленьким незакрашенным кружочком.
Следующее важное свойство дроби связано со знаком минус. Знак, стоящий перед дробью, можно перенести либо в знаменатель, либо в числитель:

Также напомним, что можно поменять местами уменьшаемое и вычитаемое в скобках, если изменить перед ней знак:
(а – b) = – (b– а)
Применение этих правил позволяет упрощать некоторые дроби, например:

Более сложный пример:

Рассмотрим такое понятие, как однородный многочлен. Так называют тот полином, у которого все одночлены имеют одинаковую степень.

Подробнее о степени одночлена можно узнать в этом уроке. Если коротко, то степень одночлена – эта сумма степеней у всех переменных, входящих в его буквенную часть. Например, у следующих мономов степень равна 4:
- 3х4 (у единственной переменной степень равна 4);
- 8х3у (степень у х равна 3, а степень у равна 1, 3 + 1 = 4);
- 5х2у2 (степени у обеих переменных равны 2, 2 + 2 = 4);
- 10у4 (в буквенной части только переменная у, чья степень равна 4).
Соответственно, многочлен 3х4 + 8х3у + 5х2у2 + 10у4, составленный из всех этих мономов, будет однородным. Примерами однородных полиномов также являются:
- z6 + v6 – 2z2v4 (здесь степени мономов равны 6);
- a2 – ab (степень одночленов равна 2).
В отношении однородных полиномов, состоящих из двух переменных, можно применять особый прием. Достаточно поделить его на одну из переменных в степени полинома, и получится выражение, зависящее только от одной дроби. Поясним это на примере. Пусть надо вычислить значение отношения

если известно другое отношение:

В исходной дроби представляет собой отношение двух однородных полиномов третьей степени. Поэтому поделим их на y3 (можно было делить и на х3). При этом значение дроби не изменится, ведь мы делим числитель и знаменатель на одинаковый моном:

Получили выражение, которое зависит только от отношения

Попытаемся найти эту величину из условия

Отсюда следует, что

Теперь подставим найденное отношение в формулу(1):

До этого мы рассматривали примеры дробных выражений, состоящие из полиномов с целыми коэффициентами. Если же используются дробные числа, то от них всегда можно избавиться, домножив дробь на какое-нибудь число.
Например, дана дробь

Коэффициенты при у и у2 дробные. Избавимся от них. Для этого используем дополнительный множитель 12:

Далее рассмотрим сложение и вычитание дробных выражений. Проще всего эту операцию проводить в том случае, когда у дробей совпадают знаменатели. В такой ситуации используются уже нам известные правила:



Сложим две величины:

В их знаменателе стоит одинаковый полином, а потому операция будет выглядеть так:

Здесь мы в числителе использовали формулу квадрата разности.
Теперь вычтем из выражения

дробь

У них совпадают знаменатели, поэтому проблем с вычитанием не возникает:

Заметим, что обычно у дробных выражения стараются сокращать до тех пор, пока не получится несократимая дробь.
Если у дробей различные знаменатели, то приводят к общему знаменателю, домножая их на какой-нибудь дополнительный множитель.
Рассмотрим следующий пример:

Знаменатели дробей разные, однако, обе дроби можно привести к знаменателю 24х2у3. Почему именно к нему? Дело в том, у коэффициентов мономов 6х2у и 8ху3 наименьшим общим кратным (НОК) является число 24 (о НОК можно узнать из этого урока). Добавим к этому коэффициенту переменные из одночленов с наибольшими показателями (х2 и у3) и получим моном 24х2у3. Итак,домножим первую дробь на 4у2, а вторую – на 3х:

Есть и более простой способ найти общий знаменатель, для этого достаточно просто перемножить знаменатели дробей-слагаемых. Однако дальнейшие преобразования будут более долгими. Решим таким путем тот же пример:

В числителе возможно вынесение общего множителя 2ху за скобки:

Видно, что конечный результат операции не изменился.
Если в знаменателях складываемых дробей стоят многочлены, то стоит попробовать разложить их на множители. За счет этого порою удается найти более простой общий знаменатель.
Пусть надо сложить выражения

Вынесем в знаменателях за скобки множители х и у:

В знаменателях есть похожие множители, (3х – у) и (у – 3х). Чтобы они оказались одинаковыми, надо поменять местами вычитаемое и уменьшаемое в одних скобках. Для этого перед ними надо добавить знак «минус»:

Общим множителем этих дробей является произведение ху(3х – у):

Осталось разложить числитель, где стоит разность квадратов:

Следующий важный навык, который может потребоваться при работе с рациональными выражениями – это выделение целой части из дроби.
Продемонстрируем эту операцию на примере

Перепишем дробь, поменяв порядок слагаемых в числителе:

И в знаменателе, и в числителе есть сумма х2 + 1. Теперь можно произвести выделение целой части:

В справедливости данного преобразования можно убедиться, выполнив его «в обратную сторону»:

Любой многочлен можно сделать дробью, если приписать ему числитель, равный 1. Пусть надо упростить формулу

Заменим 2х – 1 на дробь и произведем вычитание:


Упростить далее эту дробь довольно сложно, но всё же возможно. Для этого надо заменить одночлен (– 3х2) на разность (– х2 – 2х2), а 14х на сумму (6х+8х). Посмотрим, что получится в результате:

Складывать можно и более двух дробей. Пусть надо упростить сумму

Будем складывать слагаемые последовательно, то есть сначала сложим два первых слагаемых, потом к результату добавим третье, а далее и 4-ое слагаемое:


Представление дроби в виде суммы дробей
Сумму двух дробей можно представить в виде несократимой дроби единственным образом, например:

Однако у обратной задачи, разложения одной дроби на сумму нескольких других, есть бесконечной множество решений:

То же самое верно в отношении дробных выражений. Например,

можно разложить так:

С другой стороны, это же выражение можно представить в следующем виде:

Для раскладывания дроби на сумму дробей можно воспользоваться методом неопределенных коэффициентов, предложенным Рене Декартом в 1637 году. Покажем, как его использовать, на примере. Пусть надо представить в виде суммы двух дробей отношение

Заметим, что знаменатель х2 – 4 можно записать как произведение полиномов первой степени (х – 2)(х + 2):

Это означает, что исходное выражение можно представить как сумму дробей со знаменателями (х – 2) и (х + 2). Обозначим числители в этих дробях как неизвестные величины aи b (они и носят название неопределенных коэффициентов). Тогда можно записать, что

Задача сводится к тому, чтобы найти a и b. Для этого преобразуем сумму дробей:

Полученная дробь должна равняться исходной дроби:

У правой и левой части равны знаменатели, а значит, должны равняться и числители:
(a + b)x + (2a– 2b) = 2x + 6
Это тождество может быть верным только тогда, когда справа и слева равны коэффициенты перед переменной х, а также свободные члены, поэтому можно записать систему:

Решив эту систему, мы сможем найти значения a и b. Используем метод подстановки, выразив а из первого уравнения:
а + b = 2
а = 2 – b
Подставим эту формулу во второе уравнение:
2а – 2b = 6
2 (2 – b) – 2b = 6
4 – 4b = 6
– 4b = 10
b = – 2,5
Далее находим a:
а = 2 – b = 2 – (– 2,5) = 2 + 2,5 = 4,5
Итак, получили, что a = 4,5 и b = – 2,5. Это значит, исходную дробь можно разложить следующим образом:


Теперь рассмотрим, как производится умножение и деление дробных выражений. Эти действия аналогичны операциям с обычными числами, которые уже изучались в 5 классе. Напомним две основные формулы:



Пусть требуется перемножить величины

Эта операция осуществляется так:

Теперь посмотрим, как выполняется деление:

Деление заменяется умножением на дробь, обратную делителю:

Для упрощения выражений часто используют формулы сокращенного умножения:

При возведении дроби в степень надо отдельно возводить в степени знаменатель и числитель:

Вообще для любого натурального числа nбудет верным тождество:

Пусть надо возвести в 4-ую степень дробь

Выглядеть это будет так:

Преобразование рациональных выражений
Если у дроби в знаменателе и числителе записаны полиномы, то ее называют рациональной дробью. В виде рациональной дроби можно записать любое рациональное выражение.
Пусть надо записать в виде рациональной дроби выражение

Сначала выполним вычитание в скобках, а потом и деление:

Обратим внимание, что выражение
(2а + 1)2 – (2а – 1)2
представляет собой не что иное, как разность квадратов, для которой можно применить формулу сокращенного умножения:
(2а + 1)2 – (2а – 1)2 = (2а + 1 + 2а – 1)( 2а + 1 – (2а – 1)) =
= (2а + 1 + 2а – 1)( 2а + 1 – 2а + 1).
Используя это, продолжим работать с дробью:

Однако иногда удобнее не производить вычисления в скобках, а использовать распределительный закон умножения:
(а + b)с = ас + bc
Пусть требуется упростить произведение:

Сначала раскроем скобки:


Часто проблемы возникают с так называемыми «многоэтажными» дробями. Так называют дроби, у которых в числителе и знаменателе стоят другие дробные выражения. Выглядят они внушительно, однако правила работы с ними такие же, как и с другими выражениями. Каждая дробная черта просто означает операцию деления.
Пусть требуется выполнить преобразование дробного рационального выражения

Сначала представим эту дробь как операцию деления:

Теперь в каждой из скобок произведем сложение:

Осталось заменить деление на умножение:

