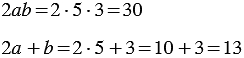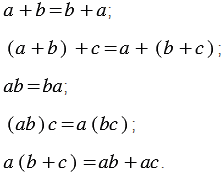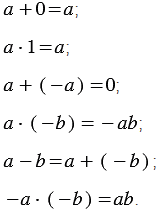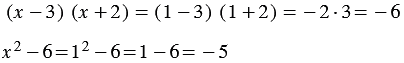После того, как мы разобрались с понятием тождеств, можно переходить к изучению тождественно равных выражений. Цель данной статьи – объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равными другим.
Тождественно равные выражения: определение
Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Приведем основное определение, взятое из одного учебника:
Тождественно равными друг другу будут такие выражения, значения которых будут одинаковы при любых возможных значениях переменных, входящих в их состав.
Также тождественно равными считаются такие числовые выражения, которым будут отвечать одни и те же значения.
Это достаточно широкое определение, которое будет верным для всех целых выражений, смысл которых при изменении значений переменных не меняется. Однако позже возникает необходимость уточнения данного определения, поскольку помимо целых существуют и другие виды выражений, которые не будут иметь смысла при определенных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определять область допустимых значений. Сформулируем уточненное определение.
Тождественно равные выражения – это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равными друг другу при условии одинаковых значений.
Фраза «при любых допустимых значениях переменных» указывает на все те значения переменных, при которых оба выражения будут иметь смысл. Это положение мы объясним позже, когда будем приводить примеры тождественно равных выражений.
Можно указать еще и такое определение:
Тождественно равными выражениями называются выражения, расположенные в одном тождестве с левой и правой стороны.
Примеры выражений, тождественно равных друг другу
Используя определения, данные выше, рассмотрим несколько примеров таких выражений.
Для начала возьмем числовые выражения.
Так, 2+4 и 4+2 будут тождественно равными друг другу, поскольку их результаты будут равны (6 и 6).
Точно так же тождественно равны выражения 3 и 30:10, (22)3 и 26(для вычисления значения последнего выражений нужно знать свойства степени).
А вот выражения 4-2 и 9-1 равными не будут, поскольку их значения разные.
Перейдем к примерам буквенных выражений. Тождественно равными будут a+b и b+a, причем от значений переменных это не зависит (равенство выражений в данном случае определяется переместительным свойством сложения).
Например, если a будет равно 4, а b – 5, то результаты все равно будут одинаковы.
Еще один пример тождественно равных выражений с буквами – 0·x·y·z и 0. Какими бы ни были значения переменных в этом случае, будучи умноженными на 0, они дадут 0. Неравные выражения – 6·x и 8·x, поскольку они не будут равны при любом x.
В том случае, если области допустимых значений переменных будут совпадать, например, в выражениях a+6 и 6+a или a·b·0 и 0, или x4 и x, и значения самих выражений будут равны при любых переменных, то такие выражения считаются тождественно равными. Так, a+8=8+a при любом значении a, и a·b·0=0 тоже, поскольку умножение на 0 любого числа дает в итоге 0. Выражения x4 и x будут тождественно равными при любых x из промежутка [0, +∞).
Но область допустимого значения в одном выражении может отличаться от области другого.
Например, возьмем два выражения: x−1 и x-1·xx. Для первого из них областью допустимых значений x будет все множество действительных чисел, а для второго – множество всех действующих чисел, за исключением нуля, ведь тогда мы получим 0 в знаменателе, а такое деление не определено. У этих двух выражений есть общая область значений, образованная пересечением двух отдельных областей. Можно сделать вывод, что оба выражения x-1·xx и x−1 будут иметь смысл при любых действительных значениях переменных, за исключением 0.
Основное свойство дроби также позволяет нам заключить, что x-1·xx и x−1 будут равными при любом x, которое не является 0. Значит, на общей области допустимых значений эти выражения будут тождественно равны друг другу, а при любом действительном x говорить о тождественном равенстве нельзя.
Если мы заменяем одно выражение на другое, которое является тождественно равным ему, то этот процесс называется тождественным преобразованием. Это понятие очень важно, и подробно о нем мы поговорим в отдельном материале.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
доказать тождество:
2t−(17−(t−7))=3(t−8)
.
Решение:
выпишем отдельно левую часть равенства и преобразуем, т. е. попытаемся доказать, что она равна правой части.
При раскрытии скобок (обеих) знаки поменяем, т. к. перед скобками стоит знак минус.
2t−(17−(t−7))=2t−17+(t−7)==2t¯−17+t¯−7=3t−24=3(t−8).
.
Получили, что левая часть исходного равенства равна правой.
Значит, исходное равенство — тождество.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Алгебра
- Тождественно равные выражения. Тождества
Два выражения, значения которых равны при любых значениях переменных, называют тождественно равными.
Рассмотрим две пары выражений:
|
1) Найдем их значения при Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных |
2) Найдем их значения при Мы получили один и тот же результат. Однако, можно указать такие значения Мы получили разные результаты. |
Следовательно, выражения 
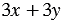
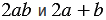
Равенство, верное при любых значениях переменных, называется тождеством.
Равенство 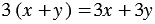
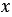
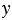
Также к тождествам можно отнести равенства, выражающие свойства сложения и умножения чисел:
Можно привести и другие примеры тождеств:
Тождествами считают и верные числовые равенства.
Очень часто при вычислении значений выражений, легче сначала упростить имеющееся выражение, а затем выполнять вычисления.
Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения.
К тождественным преобразованиям можно отнести приведение подобных слагаемых и раскрытие скобок.
Примеры:
1) 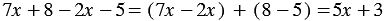
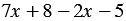
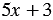
2) 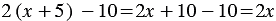
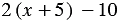
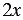
Для того, чтобы доказать, что данное равенство является тождеством (или доказать тождество), используют следующие методы:
1) тождественно преобразуют одну из частей данного равенства, получая другую часть;
2) тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение;
3) доказывают, что разность левой и правой частей данного равенства тождественно равна нулю.
Также, чтобы доказать, что равенство не является тождеством, достаточно привести контрпример, т.е. указать такое значение переменной (или переменных, если их несколько), при котором данное равенство не выполняется.
Пример: Докажите, что равенство 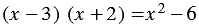
Решение: Приведем контрпример. Если 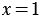
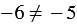
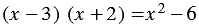
Советуем посмотреть:
Введение в алгебру
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Степень с натуральным показателем
Свойства степени с натуральным показателем
Одночлены
Многочлены
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Функции
Системы линейных уравнений с двумя переменными
Алгебра
Правило встречается в следующих упражнениях:
7 класс
Номер 136,
Мерзляк, Полонский, Якир, Учебник
Номер 139,
Мерзляк, Полонский, Якир, Учебник
Номер 314,
Мерзляк, Полонский, Якир, Учебник
Номер 317,
Мерзляк, Полонский, Якир, Учебник
Номер 363,
Мерзляк, Полонский, Якир, Учебник
Номер 535,
Мерзляк, Полонский, Якир, Учебник
Номер 567,
Мерзляк, Полонский, Якир, Учебник
Номер 1202,
Мерзляк, Полонский, Якир, Учебник
Номер 1235,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 23,
Мерзляк, Полонский, Якир, Учебник
Номер 25,
Мерзляк, Полонский, Якир, Учебник
Номер 27,
Мерзляк, Полонский, Якир, Учебник
Номер 28,
Мерзляк, Полонский, Якир, Учебник
Номер 93,
Мерзляк, Полонский, Якир, Учебник
Номер 120,
Мерзляк, Полонский, Якир, Учебник
Номер 168,
Мерзляк, Полонский, Якир, Учебник
Номер 419,
Мерзляк, Полонский, Якир, Учебник
Номер 434,
Мерзляк, Полонский, Якир, Учебник
Номер 487,
Мерзляк, Полонский, Якир, Учебник
Докажем тождество:
$frac{a^2+b^2}{ab} (frac{6a+b}{a^2 – b^2} : frac{6a^3 + b^3 + a^2b + 6ab^2}{2ab^2 – 2a^2 b} + frac{a+b}{a^2 + b^2}) = frac{a^2 + b^2}{ab(a+b)}$
Упростим левую часть тождества:
Найдём условия, при которых выражения $a^2 – b^2$, $2ab^2 – 2a^2b$,
$6a^3 + b^3 + a^2 b + 6ab^2$, $ab$ не обращаются в 0.
$a^2 – b^2 neq 0$ при $a neq b$, $a neq -b$
$2ab^2 – 2a^2b neq 0$ при $a neq b$, $a neq 0$, $b neq 0$
$6a^3 + b^3 + a^2b + 6ab^2 neq 0$ при $a neq -frac{b}{6}$
$ab neq 0$ при $a neq 0$, $b neq 0$,
- $frac{6a+b}{a^2-b^2}:frac{6a^3+b^3+a^2 b+6ab^2}{2ab^2 – 2a^2b} = frac{6a+b}{a^2-b^2}cdotfrac{2ab^2-2a^2 b}{6a^3+b^3+a^2b+6ab^2}=frac{6a+b}{a^2-b^2} cdot frac{-2ab(a-b)}{(a^2+b^2)(6a+b)} = frac{-2ab}{(a^2+b^2)(6a+b)}$
- $frac{-2ab}{(a^2+b^2)(6a+b)} + frac{a+b}{a^2+b^2} = frac{-2ab+(a+b)^2}{(a^2+b^2)(a+b)} = frac{-2ab+a^2+2ab+b^2}{(a^2+b^2)(a+b)} = frac{a^2+b^2}{(a^2+b^2)(a+b)} = frac{1}{a+b}$
- $frac{a^2+b^2}{ab} cdot frac{1}{a+b} = frac{a^2+b^2}{ab(a+b)}$
Итак, $frac{a^2+b^2}{ab(a+b)} = frac{a^2+b^2}{ab(a+b)}$, ч. т. д.
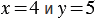
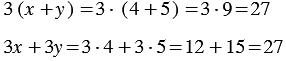
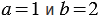
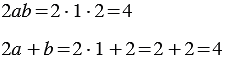
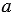 и
и 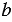 , при которых значения этих выражений не будут иметь равные значения. Например, если
, при которых значения этих выражений не будут иметь равные значения. Например, если 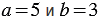 , то
, то