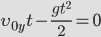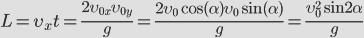Как найти траекторию движения параболы

I. Механика

Тестирование онлайн

Движение тела, брошенного горизонтально

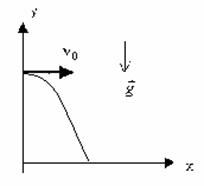
Рассмотрим движение тела, брошенного в горизонтальном направлении с некоторой высоты h и начальной скоростью v₀. Траектория такого движения имеет вид спадающей ветви параболы.

Для описания движения тела необходимо задать координатные оси. Ось Оy направим вертикально вверх, горизонтальную ось Оx – вдоль полета. Такое движение по криволинейной траектории рассматривают как сумму двух движений, протекающих независимо друг от друга – движение с ускорением свободного падения вдоль оси Оy и равномерного прямолинейного движения вдоль оси Оx.

Движение вдоль горизонтальной оси Оx равномерное.

Движение вдоль вертикальной оси ОУ – свободное падение тела с некоторой высоты h (на графике y₀).

Реальная скорость тела в некоторый момент времени – это векторная сумма горизонтальной составляющей скорости v_x и вертикальной скорости v_y.

Движение тела, брошенного под углом к горизонту

Угол броска определяет траекторию движения, дальность полета, максимальную высоту подъема тела.

Аналогично движению тела, брошенного горизонтально, это движение рассматривают как сумму независимых движений: равномерного движения вдоль горизонтальной оси ОХ и свободного падения тела вдоль вертикальной оси ОУ.

Движение вдоль горизонтальной оси ОХ равномерное.

Движение вдоль вертикальной оси ОУ – свободное падение тела, брошенного вертикально вверх с некоторой начальной скоростью v_0y. Тело поднимается на максимальную высоту h, затем возвращается вниз.

Действительная скорость, с которой движется тело.

Упражнения

При каком угле бросания достигается максимальная дальность полета?

При угле бросания 45 0 , так как можно вывести формулу для дальности полета . Максимальная дальность полета будет при

Движение тела, брошенного горизонтально или под углом к горизонту.

Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли ( g ) – вдоль вертикальной оси ( y ), вдоль оси х движение равномерное и прямолинейное.

Движение тела, брошенного горизонтально.

Выразим проекции скорости и координаты через модули векторов.

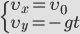
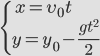
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:

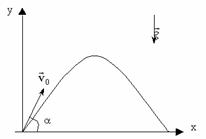
Движение тела, брошенного под углом к горизонту.

Порядок решения задачи аналогичен предыдущей.

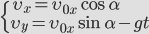
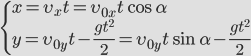
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):

.

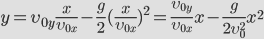Мы получили квадратичную зависимость между координатами. Значит траектория – парабола.

Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.

Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело .
Время, за которое тело долетит до середины, равно: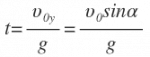

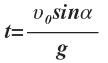
Тогда: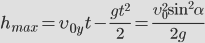

Максимальная высота:

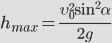
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна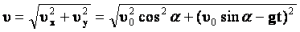

Угол, под которым направлен вектор скорости в любой момент времени:

Траектория движения

Определение и основные понятия траектории движения

Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.

Линию, которую описывает частица при своем движении, называется траекторией движения.

В зависимости от формы траектории механическое движение можно разделить на:

• прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
• и криволинейное перемещение (траектория – кривая линия).

Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.

При движении точки с постоянным ускорением, которое описывает уравнение:

Уравнение траектории движения

Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.

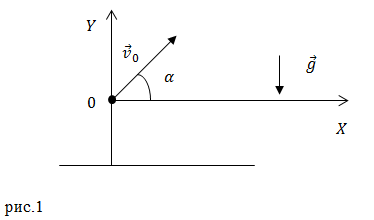
Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:

Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:

Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.

Вершина этой параболы находится в точке с координатами:

Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($frac$) от нее по $x$.

Обратимость движения

Из представления о траектории можно конкретизировать смысл обратимости механического движения.

Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.

Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.

Параметры траектории движения

Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:

• Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки – это значит указать эти функции: [x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]
• При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение: [overline=overlineleft(tright)left(7right).]
• Третьим способом описания движения является описание с помощью параметров траектории.

Путь – это скалярная величина, равная длине траектории.

Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:

Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:

где $s$ – путь точки по траектории; $t$ – время движения; $A$ – коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.

Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.

Примеры задач с решением

Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline=Aoverline+Bxoverline , $где $overline$, $overline$ – орты осей X и Y; $A$,B – постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit<>

Решение: Рассмотрим уравнение изменения скорости частицы:

Из этого уравнения следует, что:

Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):

Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:

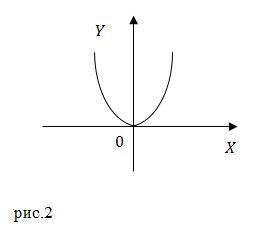
Задание: Движение материальной точки в плоскости описывает система уравнений: $left< begin x=At. \ y=At(1+Bt) end right.$, где $A$ и $B$ – положительные постоянные. Запишите уравнение траектории точки.

Решение: Рассмотрим систему уравнений, которая задана в условии задачи:

Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:

Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:

[spoiler title=”источники:”]

http://www.eduspb.com/node/1669

http://www.webmath.ru/poleznoe/fizika/fizika_95_traektorija_dvizhenija.php

[/spoiler]

Движение тела, брошенного горизонтально или под углом к горизонту.
Это движение в плоскости, поэтому для описания движения необходимо 2 координаты. Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
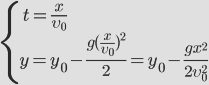	– между координатами квадратичная зависимость, траектория – парабола!
Следовательно, для решения этой задачи необходимо решить уравнение
Оно будет иметь решение при t=0 (начало движения) и
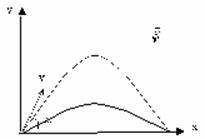
Зная время полета, найдем максимальное расстояние, которое пролетит тело: Дальность полета: Из этой формулы следует, что: – максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45 0 ; – на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.

Часть
1. «Координатный
способ задания движения точки»

Движение точки
задано уравнениями

(м),

(м).

Определить
и построить траекторию. Определить и
показать на чертеже положение точки в
начальный момент и в момент времени
.
Для указанных моментов времени найти
скорость и ускорение точки. Изобразить
на чертеже соответствующие векторы:
,

и
,
.

Решение. Для исключения времени выразим его первого из первого уравнения через координату x и подставим во второе уравнение: или .

Полученное
уравнение представляет собой уравнение
параболы (Рис.1) с вершиной в точке (4; 0).
Выясним, вся ли парабола является
траекторией точки, или только ее часть.
Для этого найдем начальное положение
точки
,
подставив в уравнения движения
:

,

(м).

Таким
образом, точка начинает свое движение
из вершины параболы
.

Установим
направление движения. Для этого, пользуясь
заданными уравнениями движения,
проанализируем, как изменяются координаты
точки при возрастании времени
.
В нашем случае очевидно, что с течением
времени координата

возрастает, а координата

убывает. Следовательно, точка движется
вправо.

Таким
образом, траекторией точки является
правая ветвь параболы (Рис.1).

Найдем
положение точки в момент времени
,
подставив в уравнения движения
:

(м),

(м).

Положение

точки показано на Рис.2.

Найдем как функции
времени проекции скорости на координатные
оси, а также ее модуль и направляющие
косинусы:

,

,

;

,

.

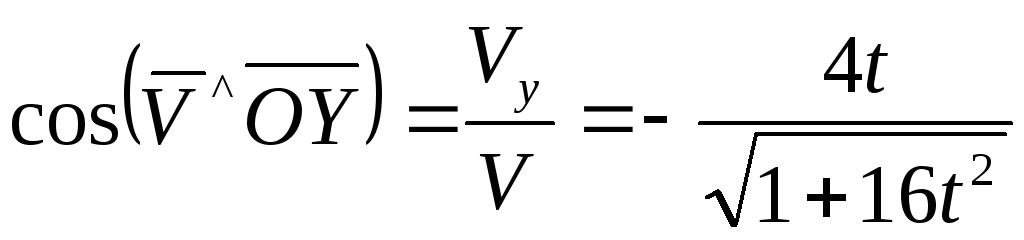В заданные моменты
времени получаем:

при

,

,

,

,

;

при

,

,

,

,

.

Найдем как функции
времени проекции ускорения на координатные
оси, а также его модуль и направляющие
косинусы:

,

,

;

,

.

Очевидно, что в рассматриваемом движении ни модуль, ни направление вектора ускорения не зависят от времени, поэтому найденные значения справедливы для любого момента времени: . Векторы скорости и ускорения в начальный момент времени и в момент времени показаны на Рис.2 (они могут быть построены либо через модуль и направляющие косинусы, либо через проекции).

Часть
2. «Естественный
способ задания движения точки»

Точка
М
движется по траектории, представляющей
собой половину окружности радиуса r,
согласно закону

(м). Начало отсчета криволинейной координаты (точка О) и направление ее положительного отсчета указаны на Рис.3.

Определить
как функции времени проекцию вектора
скорости на орт касательной
,
а также проекции вектора ускорения на
орт касательной

и на орт главной нормали
.
Построить графики зависимостей
,

,

и
.
Показать положение точки на траектории
в начальный момент и в момент времени

.
Найти и изобразить на чертеже векторы
скорости, касательного и нормального
ускорений, а также вектор полного
ускорения для указанных моментов
времени.

Решение.

Определим

,

и
:

;
(а)

;
(b)

.
(c)

Полученные
функции (a)
и (b),
а также заданный закон движения позволяют
построить графики
,

и

(Рис.4). Найдем положение точки М
в начальный момент и в момент времени

,
подставив в заданный закон движения

и
:

(м);


(м).

Покажем
соответствующие положения точки на
траектории. Поскольку длина полной
окружности равна
,
то

составляет 1/4 окружности. Откладывая
полученную величину в сторону
положительного отсчета криволинейной
координаты (т.к.
),
находим точку

(Рис.4). Криволинейная координата

отрицательна и по модулю в два раза
меньше
,
поэтому точка

отстоит от точки О
влево на 1/8 окружности.

Подставив
указанные моменты времени в уравнение
(а),
найдем

;

(м/с).

Таким
образом, начальная скорость точки равна
нулю. Покажем на чертеже вектор
.
Поскольку его проекция на касательную
ось
,
он направлен в сторону убывания дуговой
координаты (Рис.5). (Напомним, что
касательная ось всегда направлена в
сторону возрастания дуговой координаты).

Аналогичным
образом из (b)
и (c)
найдем:

(м/с²);


(м/с²).

;

(м/с²).

Векторы
нормального, касательного и полного
ускорений точки М
показаны на Рис.5. Отметим, что направление
касательного ускорения, так же как и
скорости, определяется знаком его
проекции на касательную ось. Нормальное
ускорение (если оно отлично от нуля)
всегда направлено в сторону вогнутости
траектории (его проекция на главную
нормаль не может быть отрицательной).

Поскольку

,
вектор полного ускорения в начальный
момент времени совпадает с касательным
ускорением. В момент времени

вектор

определяется
как векторная
сумма

и
.
Его модуль равен

(м/с²),

а
угол, составляемый с направлением
главной нормали, определим через тангенс:

.

Часть
3. «Переход
от координатного способа задания
движения точки к естественному»

Движение
точки задано уравнениями:

(м);

(м).

Найти
уравнение траектории и построить ее на
чертеже. показать
на ней начальное положение точки и найти
закон движения точки по траектории
,
приняв за начало отсчета дуговой
координаты начальное положение точки
и считая, что точка начинает свое движение
в сторону возрастания дуговой координаты.

Решение.

Чтобы
найти уравнение траектории точки
исключим время из уравнений движения.
Для этого из первого уравнения выразим

,
а из второго
,
затем возведём их в квадрат и сложим:

;

;

;

;

.

Очевидно,
что окружность радиуса

м
с
координатами центра

включает траекторию движения точки
(Рис.6). Необходимо только уточнить,
является ли вся окружность траекторией
или только её часть представляет эту
траекторию.

Для
определения начального положения точки
на траектории подставим в уравнения
движения значение времени
.
Находим, что точка в начальный момент
движения занимает положение
,
определяемое координатами
,

,
т.е.
.

Установим
направление движения точки по траектории
при возрастании времени от

до

с.
Подставив в уравнения движения

найдем, что при этом координаты движущейся
точки будут равны:
;

,
т.е.
.
Следовательно, точка

начинает своё движение по окружности
от точки

в направлении часовой стрелки.

Легко
убедится в том, что при

точка занимает положение
,
а при

точка приходит в
.
Из этого следует, что вся окружность
является траекторией движения точки.

Проекции
вектора скорости

на оси координат равны

Y S M0 V0 A M r Wn W V M3 M1 C W O X M2 V1 Рис. 6

, . Модуль этого вектора равен ; при с . Направляющие косинусы вектора являются функцией времени, т.е. направление этого вектора непрерывно изменяется:

при

:

Установим
закон движения точки вдоль траектории.
Начало отсчёта криволинейной координаты
(точку
)
совместим с начальным положением точки

.
В качестве положительного направления
отсчёта криволинейной координаты
выберем направление движения точки.
Поскольку точка движется в сторону
возрастания криволинейной координаты

,
то

,
()

После
интегрирования этого выражения найдем

.

При

,
поэтому

и закон движения точки вдоль траектории
будет следующим:

Соседние файлы в папке Примеры выполнения

• #
• #
• #

  03.03.20153.66 Кб2Содержание OneNote.onetoc2

I. Механика

Тестирование онлайн

Движение тела, брошенного горизонтально

Рассмотрим движение тела, брошенного в горизонтальном направлении с некоторой высоты h и начальной скоростью v₀. Траектория такого движения имеет вид спадающей ветви параболы.

Для описания движения тела необходимо задать координатные оси. Ось Оy направим вертикально вверх, горизонтальную ось Оx — вдоль полета. Такое движение по криволинейной траектории рассматривают как сумму двух движений, протекающих независимо друг от друга — движение с ускорением свободного падения вдоль оси Оy и равномерного прямолинейного движения вдоль оси Оx.

Движение вдоль горизонтальной оси Оx равномерное.

Движение вдоль вертикальной оси ОУ — свободное падение тела с некоторой высоты h (на графике y₀).

Реальная скорость тела в некоторый момент времени — это векторная сумма горизонтальной составляющей скорости v_x и вертикальной скорости v_y.

Движение тела, брошенного под углом к горизонту

Угол броска определяет траекторию движения, дальность полета, максимальную высоту подъема тела.

Аналогично движению тела, брошенного горизонтально, это движение рассматривают как сумму независимых движений: равномерного движения вдоль горизонтальной оси ОХ и свободного падения тела вдоль вертикальной оси ОУ.

Движение вдоль горизонтальной оси ОХ равномерное.

Движение вдоль вертикальной оси ОУ — свободное падение тела, брошенного вертикально вверх с некоторой начальной скоростью v_0y. Тело поднимается на максимальную высоту h, затем возвращается вниз.

Действительная скорость, с которой движется тело.

Упражнения

При каком угле бросания достигается максимальная дальность полета?

При угле бросания 45 0 , так как можно вывести формулу для дальности полета . Максимальная дальность полета будет при

Движение тела, брошенного горизонтально или под углом к горизонту.

Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли ( g ) – вдоль вертикальной оси ( y ), вдоль оси х движение равномерное и прямолинейное.

Движение тела, брошенного горизонтально.

Выразим проекции скорости и координаты через модули векторов.

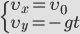
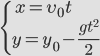
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:

Движение тела, брошенного под углом к горизонту.

Порядок решения задачи аналогичен предыдущей.

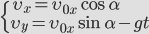
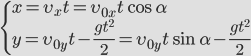
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):

.

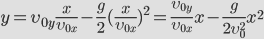Мы получили квадратичную зависимость между координатами. Значит траектория — парабола.

Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.

Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело .
Время, за которое тело долетит до середины, равно: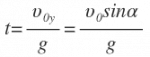

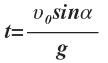
Тогда: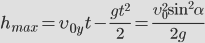

Максимальная высота:

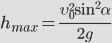
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна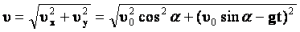

Угол, под которым направлен вектор скорости в любой момент времени:

Как определить a, b и c по графику параболы

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент (a) можно найти с помощью следующих фактов:

— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

Решаем систему.
Пример:

Вычтем из второго уравнения первое:

Подставим (9a) вместо (b):

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

Подставим в первое уравнение (a):

Получается квадратичная функция: (y=-x^2-9x-15).

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

Сложим 2 уравнения:

Подставим во второе уравнение:

Теперь найдем точки пересечения двух функций:

Теперь можно найти ординату второй точки пересечения:

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.

График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).

Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).

Движение тела, брошенного горизонтально или под углом к горизонту.
Это движение в плоскости, поэтому для описания движения необходимо 2 координаты. Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
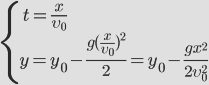	— между координатами квадратичная зависимость, траектория – парабола!
Следовательно, для решения этой задачи необходимо решить уравнение
Оно будет иметь решение при t=0 (начало движения) и
Зная время полета, найдем максимальное расстояние, которое пролетит тело: Дальность полета: Из этой формулы следует, что: — максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45 0 ; — на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)