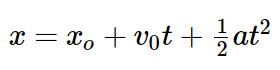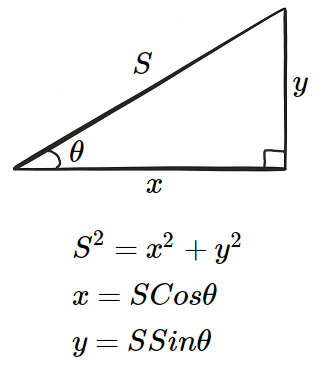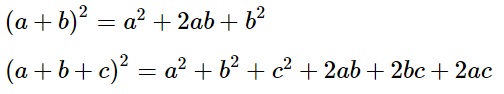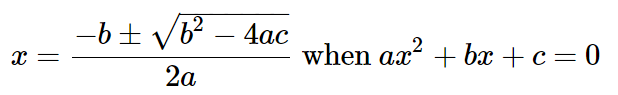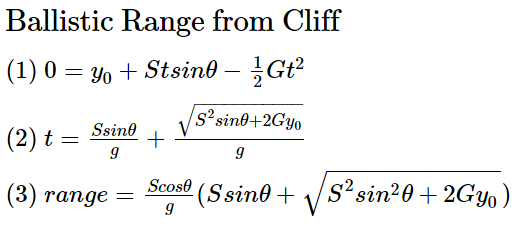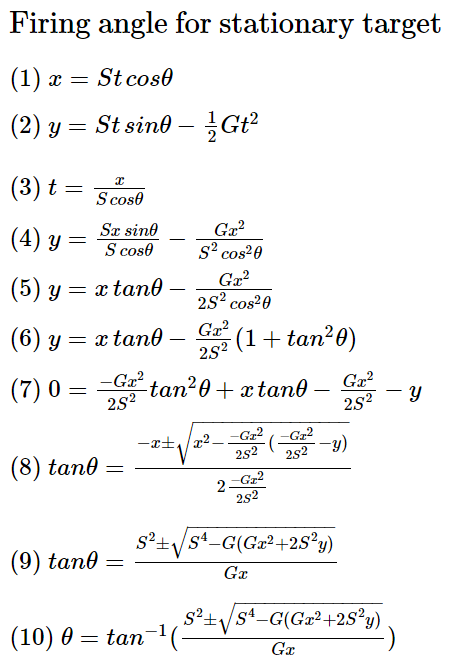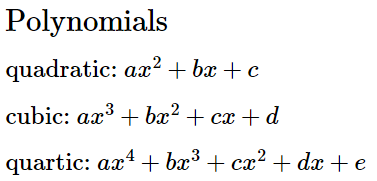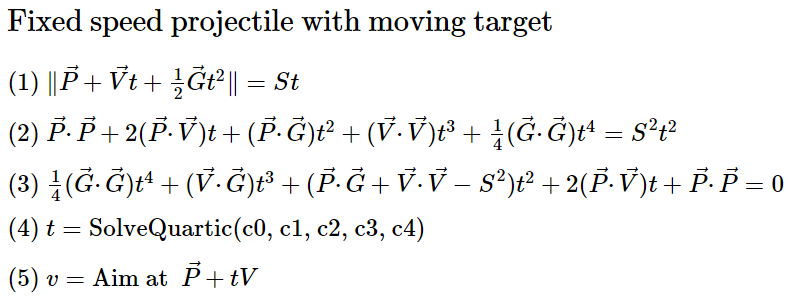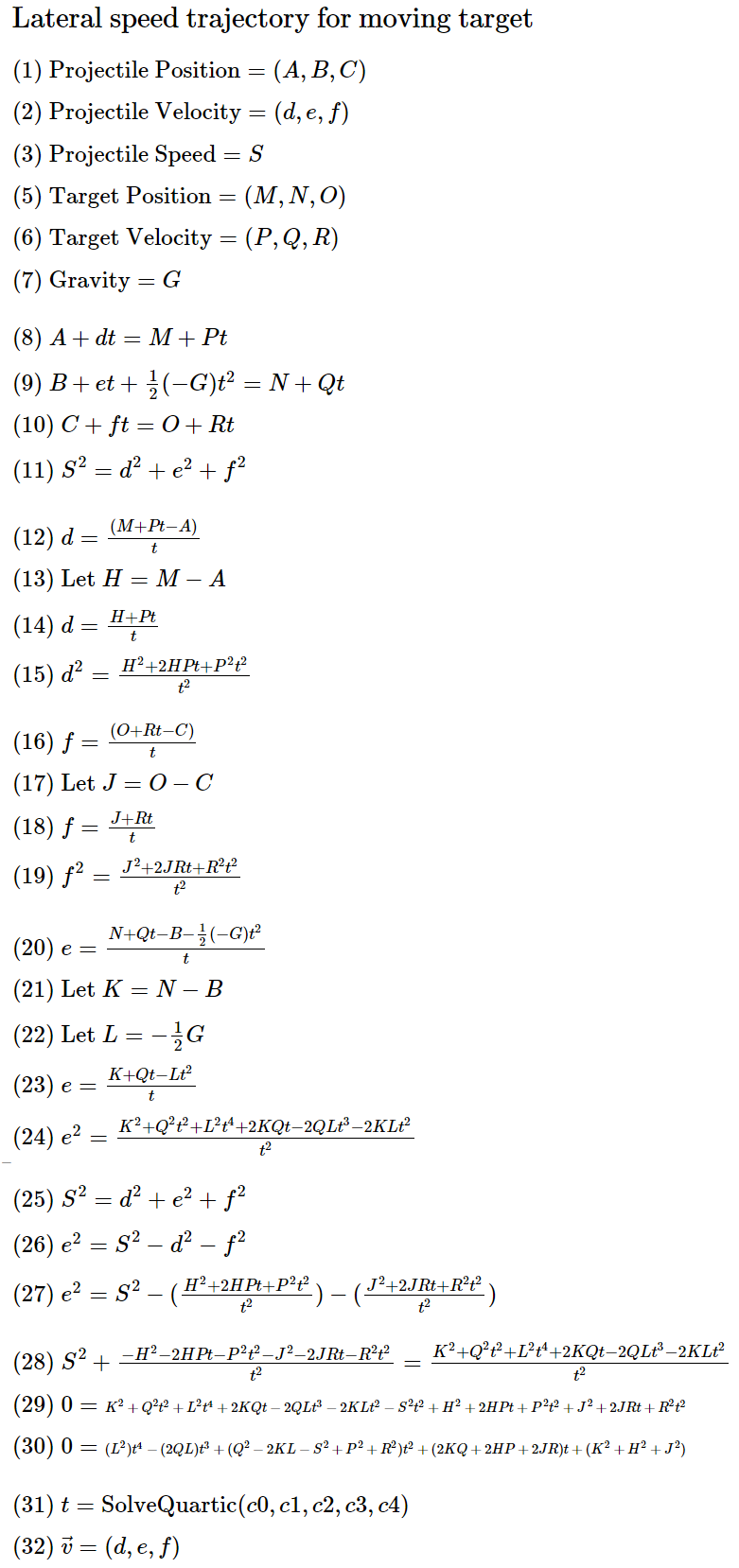Как найти траекторию движения снаряда

Вычисляем баллистические траектории в играх

При разработке видеоигр часто встречается задача вычисления угла выстрела для попадания в цель. Она настолько распространена, что я писал код для её решения в буквальном смысле для каждой игры, над которой работал.

Когда возникала эта проблема, я обычно брал ручку с блокнотом и решал её с нуля. Мне это надоело. Чтобы сэкономить себе из будущего немного времени, я выложу это решение в Интернет. Кроме того, я расскажу о необычной «фишке», которую предпочитаю использовать из соображений эстетики.

Уравнения движения

Задача всегда начинается одинаково. У нас есть стреляющий и цель: под каким углом нужно стрелять снарядом, чтобы он поразил цель?

Существует четыре основных уравнения движения. В статье мы воспользуемся только одним.

Если объяснять на словах, то конечная позиция РАВНА исходной позиции ПЛЮС скорость, умноженная на время ПЛЮС половина ускорения, умноженная на время в квадрате. Это простое уравнение, для его решения необходимо немного алгебры и несколько тригонометрических тождеств.

Освежим знания

Прежде чем начать, давайте вкратце освежим память.

Если дан снаряд с постоянной скоростью S и углом выстрела θ (theta), то мы можем вычислить компоненты скорости x и y. Или если есть S и мы каким-то образом найдём y, то можем вычислить θ и x.

Мы используем алгебру.

Мы часто будем пользоваться формулой корней квадратного уравнения.

Дальность

При разработке видеоигр нам, вероятно, нужно будет знать максимальную дальность полёта снаряда. Искусственный интеллект должен понимать, насколько близко нужно подойти, а игрокам нужны чёткие наглядные индикаторы опасных зон.

Существует очень простое уравнение максимальной дальности на плоской поверхности. Мы сразу же ринемся в омут с головой и начнём с обобщённого вида.

Если дан снаряд с постоянной скоростью (S) и гравитацией (G), то какой будет его максимальная дальность полёта?

1. Подставим известные нам переменные (y0, S, G) в основное уравнение движения.
2. Применим формулу корней квадратного уравнения. Отбросим меньшее значение.
3. Подставим t в x = S*cos θ*t и упростим.

Демо

Для тестирования и визуализации я создал демо на Unity. В нём используются чайники, стреляющие чайниками. Пиф-паф!

Демо: Unity-демо в WebGL

В демо есть несколько ползунков. В видео показан индикатор дальности стрельбы нашего чайника-турели. При увеличении скорости увеличивается дальность. При снижении гравитации дальность тоже растёт. Всё довольно просто.

Угол стрельбы для попадания по неподвижной мишени

Теперь начинается интересное.

Если снаряд имеет постоянную скорость (S), а гравитация равна (G), то под каким углом его нужно выстреливать, чтобы попасть в неподвижную мишень?

Бах. Теперь у нас есть два уравнения и два неизвестных. Давайте их проанализируем.

1. Первое уравнение, два неизвестных (t, θ)
2. Второе уравнение, два неизвестных (t, θ)
3. Вычислить t из (1)
4. Подставить (3) в (2)
5. Тригонометрическая подстановка: sin θ/cosθ = tanθ
6. Тригонометрическая подстановка: 1/(cos θ)^2 = 1 + (tan θ)^2
7. Развернём и преобразуем
8. Формула корней квадратного уравнения
9. Умножим верхнюю/нижнюю часть на -S^2/x. Перенесём S^4/x^2 под корень
10. Применим к каждой части арктангенс

Та-да! В результате мы получили два угла. Один высокий и один низкий. Вот как это выглядит на практике.

Визуальное несовершенство

Взгляните на показанный выше gif. Когда чайник начинает стрелять, всё выглядит довольно неплохо. Высокая дуга красива и радует глаз. Низкая дуга кажется чёткой и эффективной.

Однако при увеличении дальности всё становится не таким красивым. Низкая дуга почти плоская. Высокая дуга чрезмерно высока. В этом и заключается проблема снаряда с постоянной скоростью. Он выглядит красиво, только когда цель находится на границах его радиуса дальности.

Существует ли способ получше?

Скорость горизонтального перемещения

Я часто предпочитаю задавать горизонтальную скорость снаряда, только в плоскости земли. Тогда я могу явным образом задать высоту дуги. То есть переменной становится скорость и гравитация.

Такой подход имеет множество преимуществ. Во-первых, он всегда выглядит красиво!

Во-вторых, его дизайн более интуитивен. Дизайнеров не волнует абсолютная скорость. Им важно, что турель имеет дальность 20 метров и что для перемещения на это расстояние снарядам требуется 1 секунда. Они не обязаны пользоваться строящим графики калькулятором, чтобы менять значения баланса. А художественные изменения не должны влиять на геймплейные механики.

В-третьих, так проще попадать по движущейся мишени. Чуть позже я раскрою это подробнее.

Вот как это выглядит:

Вычисление скорости горизонтального перемещения

Если дан снаряд с горизонтальной скоростью (S) и пиковой высотой (y_peak), то какими должны быть скорость и гравитация для поражения неподвижной мишени?

1. Основное уравнение движения
2. Решаем (1), подставив 2
3. Зададим, что y_peak (пользовательская константа) снаряд достигает во время (1/2)t
4. Зададим, что y_end (высота цели) снаряд достигает во время t
5. Магия!
6. Ещё магия!
7. Вектор стрельбы равен (S, v.y) с гравитационным ускорением g

Вуаля! Хотя постойте-ка. Магия? Это жульничество! Да, но вполне оправданное.

Пункты (3) и (4) — это ещё два уравнения с двумя неизвестными. Я ленивый и не хочу их записывать. Плюс я запутаюсь и перепутаю знак, поэтому позволю компьютеру решить их за меня.

Точнее, я воспользовался Wolfram Alpha. Рекомендую каждому иметь Wolfram в своём инструментарии, он довольно полезен.

Если a+c == 2b, то y0, y_peak и y_end лежат на одной прямой. То есть мы стреляем по прямой.

Скорость горизонтального перемещения при подвижной мишени

Итак, у нас есть два разных вычисления траектории. Однако враги обычно не стоят на месте, они перемещаются. Нам нужно вычислять траекторию, чтобы поражать подвижную мишень.

Именно здесь проявляются все достоинства скорости горизонтального перемещения. Задав скорость в плоскости земли, очень просто выполнить вычисления для подвижной мишени.

1. Где X — позиция мишени, а V — её скорость
2. Возводим обе части в квадрат.
3. Преобразуем в квадратное уравнение
4. Применяем формулу корней квадратного уравнения

Пункты с 5 по 9 см. в предыдущем разделе.

Меня это очень радует. Пиу-пиу-пиу!

Постоянная скорость с подвижной мишенью

А что если нам нужно поразить подвижную мишень снарядом с постоянной скоростью? Ой-ёй. Это очень запутанная задача! Даже не знаю, как к ней подступиться.

За всю мою карьеру мне не доводилось её решать. Обычно в играх не нужна точная артиллерия. Это просто неинтересно! Вместо этого мы приблизительно вычисляем будущую позицию и целимся в случайную точку рядом с ней. Игроки воспринимают артиллерийский огонь как дождь из глупых снарядов, а не как гарантированную смерть с лазерным наведением.

В процессе написания этого поста я нашёл решение задачи снаряда с постоянной скоростью и движущейся мишени, которого не было в Интернете в готовом виде. Стоит заметить, что вам, вероятно, не понадобится реализовывать его в своей игре. Но я потратил на него много времени, поэтому не хочу, чтобы оно было потеряно впустую!

Уравнения четвёртой степени

Скорее всего, вы не захотите использовать его в своей игре именно из-за уравнений четвёртой степени. По сути, для решения требуется одно из таких уравнений.

Квадратные уравнения имеют простое и изящное решение в виде формулы корней квадратного уравнения. Кубические уравнения решаемы несколькими разными способами. Однако уравнения четвёртой степени — это настоящая головная боль.

Решение таких уравнений находится далеко за рамками этой статьи. Честно говоря, и за пределами моих математических способностей. К счастью для нас, в книге 1990 года Graphics Gems I есть код для решения уравнений четвёртого порядка. Я использовал этот код для своего демо. Не могу гарантировать его точности и численной устойчивости, используйте его крайне осмотрительно.

Способ первый

Итак, давайте его решим. Каким должен быть угол выстрела снарядом с постоянной скоростью по движущейся мишени? Этот способ взят из поста 2007 года Джеймса Макнейлла и дополнен информацией Райана Джакетта.

1. Где P — позиция мишени, а V — скорость мишени
2. Возводим обе части в квадрат
3. Преобразуем
4. Вычисляем коэффициенты уравнения четвёртого порядка и вставляем в SolveQuartic
5. Используем t для вычисления позиции мишени при вычислении траектории до неподвижной точки.

Способ работает. Все сложные задачи выполняет SolveQuartic. Затем мы используем решение для неподвижной мишени, изложенное выше.

Способ второй

Прежде чем я нашёл первый способ, я вывел решение другим способом. Оно состоит из гораздо большего количества шагов. Однако я нахожу конечный результат более изящным. Плюс я потратил примерно восемь листов бумаги и не хочу, чтобы эти деревья пожертвовали собой зазря.

Чёрт возьми. 32 шага!? Это хуже, чем кажется.

1–7 — объявляем переменные.

8–11 — объявляем систему уравнений. Четыре уравнения, четыре неизвестных — d, e, f, t.

12–15 — вычисляем по (8) величину d. Перемножаем d^2 на будущее.

16–19 — вычисляем по (10) величину f. Перемножаем f^2 на будущее.

20–24 — вычисляем по (9) величину e. Перемножаем e^2 на будущее.

25–27 — вычисляем по (11) величину e^2. Подставляем d^2 и f^2.

28–30 — приравниваем (27) к (24). Умножаем на t^2 и преобразуем в уравнение четвёртой степени.

31 — подставляем коэффициенты в SolveQuartic.

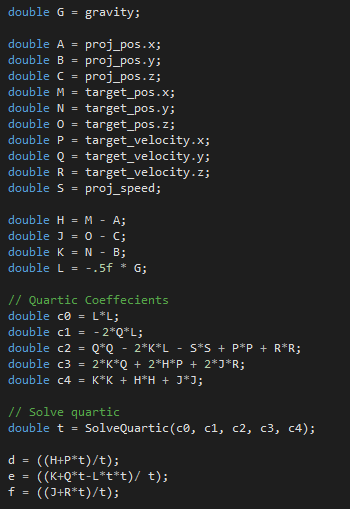
32 — подставляем положительные вещественные корни в (14), (18), (23) для d, e, f.

Код довольно короткий. Объявлению переменных отведено больше строк, чем самим вычислениям! Разумеется, кроме SolveQuartic.

Предупреждение

Код, написанный для этого теста, не проверен в бою, а пост никем не рецензировался. Вероятно, в нём есть несколько опечаток, ошибок и неучтённых пограничных случаев. Если найдёте подобные ошибки, пожалуйста, сообщите мне. Втайне, чтобы никто не узнал о моём позоре.

Рассматривайте этот код не как готовое решение, а как опорную точку.

Инструменты

При создании этого поста я использовал несколько инструментов. Многие из них были для меня новыми.

• Unity для создания демо.
• Paper, Affinity Designer и MSPaint для создания изображений.
• Arachnid Latex + MathJax для формул LaTeX.
• FFmpeg для преобразования последовательности скриншотов в анимацию.
• Gfycat для встраивания анимаций.
• Чайник из Юты. Пиу-пиу!

Синтаксис LaTeX ужасен, его сложно учить. Все формулы LaTeX можно найти здесь. Вот пример:

Заключение

Вот и всё. Я потратил на этот пост гораздо больше времени, чем ожидал. Я решил задачу, которую никогда не решал прежде и изучил несколько новых инструментов. И это того стоило.

В этом посте нет ничего нового или оригинального. Я пытался объяснять подробно, но чтобы не быть при этом слишком многословным. Мне очень нравится, что теперь полные описания можно найти в одном месте. Надеюсь, они окажутся полезными для людей.

Исходный код

Проект Unity

Unity-демо в WebGL

1) Задачи о движении снаряда.

Рассмотрим следующую задачу механики.

Снаряд пущен с Земли с начальной скоростью
v₀ = 30 м/с под углом 
= 45° к ее поверхности; требуется найти
траекторию его движения и расстояние
S между начальной и конечной точкой этой
траектории.

Пренебрегая размерами снаряда, будем
считать его материальной точкой. Введем
систему координат xOy, совместив ее начало
O с исходной точкой, из которой пущен
снаряд, ось x направим горизонтально, а
ось y — вертикально (рис. 1).

Рис. 1

Тогда, как это известно из школьного
курса физики, движение снаряда описывается
формулами:

где t — время, g = 10 м/с² —
ускорение свободного падения. Эти
формулы и дают математическую модель
поставленной задачи. Выражая t через x
из первого уравнения и подставляя во
второе, получим уравнение траектории
движения снаряда:

Эта кривая (парабола) пересекает ось x
в двух точках: x₁ = 0 (начало траектории)
и
(место
падения снаряда). Подставляя в полученные
формулы заданные значения v0 и a, получим

ответ: y = x – 90x², S = 90 м.

Отметим, что при построении этой модели
использован ряд предположений: например,
считается, что Земля плоская, а воздух
и вращение Земли не влияют на движение
снаряда.

 2) Задача о баке с наименьшей
площадью поверхности. 

Требуется найти высоту h₀ и радиус
r₀ жестяного бака объема V = 30 м³,
имеющего форму закрытого кругового
цилиндра, при которых площадь его
поверхности S минимальна (в этом случае
на его изготовление пойдет наименьшее
количество жести).

Запишем следующие формулы для объема
и площади поверхности цилиндра высоты
h и радиуса r:

V = r²h, S = 2r(r
+ h).

Выражая h через r и V из первой формулы и
подставляя полученное выражение во
вторую, получим:

Таким образом, с математической точки
зрения, задача сводится к определению
такого значения r, при котором достигает
своего минимума функция S(r). Найдем те
значения r₀, при которых производная

обращается в ноль:Можно
проверить, что вторая производная
функции S(r) меняет знак с минуса на плюс
при переходе аргумента r через точку
r₀. Следовательно, в точке r0 функция
S(r) имеет минимум. Соответствующее
значение h₀ = 2r₀. Подставляя
в выражение для r₀ и h₀ заданное
значение V, получим искомый радиус
и
высоту

3) Транспортная задача. 

В городе имеются два склада муки и два
хлебозавода. Ежедневно с первого склада
вывозят 50 т муки, а со второго —
70 т на заводы, причем на первый —
40 т, а на второй — 80 т.

Обозначим через a_ij стоимость
перевозки 1 т муки с i-го склада на j-й
завод (i, j = 1,2). Пусть

a₁₁ = 1,2 р., a₁₂ =
1,6 р., a₂₁ = 0,8 р., a₂₂
= 1 р.

Как нужно спланировать перевозки, чтобы
их стоимость была минимальной?

Придадим задаче математическую
формулировку. Обозначим через x₁
и x₂ количество муки, которое надо
перевезти с первого склада на первый и
второй заводы, а через x₃ и x₄ —
со второго склада на первый и второй
заводы соответственно. Тогда:

x₁ + x₂ = 50, x₃ + x₄ =
70, x₁ + x₃ = 40, x₂ + x₄
= 80.        (1)

Общая стоимость всех перевозок
определяется формулой

f = 1,2x₁ + 1,6x₂ + 0,8x₃ + x₄.

С математической точки зрения, задача
заключается в том, чтобы найти четыре
числа x₁, x₂, x₃ и x₄,
удовлетворяющие всем заданным условиям
и дающим минимум функции f. Решим систему
уравнений (1) относительно xi (i = 1, 2, 3, 4)
методом исключения неизвестных. Получим,
что

x₁ = x₄ – 30, x₂ = 80 – x₄,
x₃ = 70 – x₄,        
(2)

а x₄ не может быть определено
однозначно. Так как x_i 0
(i = 1, 2, 3, 4), то из уравнений (2) следует,
что 30x₄70.
Подставляя выражение для x₁, x₂,
x₃ в формулу для f, получим

f = 148 – 0,2x₄.

Легко видеть, что минимум этой функции
достигается при максимально возможном
значении x₄, то есть при x₄ =
70. Соответствующие значения других
неизвестных определяются по формулам
(2): x₁ = 40, x₂ = 10, x₃ = 0.

4) Задача о радиоактивном распаде.

Пусть N(0) — исходное количество атомов
радиоактивного вещества, а N(t) —
количество нераспавшихся атомов в
момент времени t. Экспериментально
установлено, что скорость изменения
количества этих атомов N'(t) пропорциональна
N(t), то есть N'(t)=–N(t),
>0 — константа
радиоактивности данного вещества. В
школьном курсе математического анализа
показано, что решение этого дифференциального
уравнения имеет вид N(t) = N(0)e^–t.
Время T, за которое число исходных атомов
уменьшилось вдвое, называется периодом
полураспада, и является важной
характеристикой радиоактивности
вещества. Для определения T надо положить
в формуле
Тогда
Например,
для радона  =
2,08410^–6,
и следовательно, T = 3,15 сут.

5) Задача о коммивояжере.

Коммивояжеру, живущему в городе A₁,
надо посетить города A₂, A₃ и
A₄, причем каждый город точно один
раз, и затем вернуться обратно в A₁.
Известно, что все города попарно соединены
между собой дорогами, причем длины дорог
b_ij между городами A_i и A_j
(i, j = 1, 2, 3, 4) таковы:

b₁₂ = 30, b₁₄ = 20, b₂₃ = 50, b₂₄
= 40, b₁₃ = 70, b₃₄ = 60.

Надо
определить порядок посещения городов,
при котором длина соответствующего
пути минимальна.

Изобразим каждый город точкой на
плоскости и пометим ее соответствующей
меткой Ai (i = 1, 2, 3, 4). Соединим эти точки
отрезками прямых: они будут изображать
дороги между городами. Для каждой
«дороги» укажем ее протяженность в
километрах (рис. 2). Получился граф —
математический объект, состоящий из
некоторого множества точек на плоскости
(называемых вершинами) и некоторого
множества линий, соединяющих эти точки
(называемых ребрами). Более того, этот
граф меченый, так как его вершинам и
ребрам приписаны некоторые метки —
числа (ребрам) или символы (вершинам).
Циклом на графе называется последовательность
вершин V₁, V₂, …, V_k, V₁
такая, что вершины V₁, …, V_k —
различны, а любая пара вершин V_i,
V_i+1 (i = 1, …, k – 1) и пара V₁, V_k
соединены ребром. Таким образом,
рассматриваемая задача заключается в
отыскании такого цикла на графе,
проходящего через все четыре вершины,
для которого сумма всех весов ребер
минимальна. Найдем перебором все
различные циклы, проходящие через четыре
вершины и начинающиеся в A₁:

1) A₁,
A₄,
A₃,
A₂,
A₁;
2) A₁,
A₃,
A₂,
A₄,
A₁;
3) A₁,
A₃,
A₄,
A₂,
A₁.

Найдем теперь длины этих циклов (в км):
L₁ = 160, L₂ = 180, L₃ = 200. Итак,
маршрут наименьшей длины — это
первый.

Заметим, что если в графе n вершин и все
вершины попарно соединены между собой
ребрами (такой граф называется полным),
то число циклов, проходящих через все
вершины, равно
Следовательно,
в нашем случае имеется ровно три цикла.

6) Задача о нахождении связи между
структурой и свойствами веществ.

Рассмотрим
несколько химических соединений,
называемых нормальными алканами. Они
состоят из n атомов углерода и n + 2 атомов
водорода (n = 1, 2 …), связанных между собой
так, как показано на рисунке 3 для n = 3.
Пусть известны экспериментальные
значения температур кипения этих
соединений:

y_э(3) = – 42°, y_э(4) = 0°, y_э(5)
= 28°, y_э(6) = 69°.

Требуется найти приближенную зависимость
между температурой кипения и числом n
для этих соединений. Предположим, что
эта зависимость имеет вид

y an + b,

где a, b — константы, подлежащие
определению. Для нахождения a и b
подставим в эту формулу последовательно
n = 3, 4, 5, 6 и соответствующие значения
температур кипения. Имеем:

– 42  3a + b, 0
 4a + b, 28 
5a + b, 69  6a
+ b.

Для определения наилучших a и b
существует много разных методов.
Воспользуемся наиболее простым из них.
Выразим b через a из этих уравнений:

b  – 42 – 3a,
b  – 4a, b 
28 – 5a, b  69 –
6a.

Возьмем в качестве искомого b среднее
арифметическое этих значений, то есть
положим b  16 – 4,5a.
Подставим в исходную систему уравнений
это значение b и, вычисляя a, получим
для a следующие значения: a37,
a28, a28,
a36. Возьмем в
качестве искомого a среднее значение
этих чисел, то есть положим a34.
Итак, искомое уравнение имеет вид

y  34n – 139.

Проверим точность модели на исходных
четырех соединениях, для чего вычислим
температуры кипения по полученной
формуле:

y_р(3) = – 37°, y_р(4) = – 3°,
y_р(5) = 31°, y_р(6) = 65°.

Таким образом, ошибка расчетов данного
свойства для этих соединений не превышает
5°. Используем полученное уравнение для
расчета температуры кипения соединения
с n = 7, не входящего в исходное множество,
для чего подставим в это уравнение n =
7: y_р(7) = 99°. Результат получился
довольно точный: известно, что
экспериментальное значение температуры
кипения y_э(7) = 98°.

7) Задача об определении надежности
электрической цепи.

Здесь мы рассмотрим пример вероятностной
модели. Сначала приведем некоторые
сведения из теории вероятностей —
математической дисциплины, изучающей
закономерности случайных явлений,
наблюдаемых при многократном повторении
опыта. Назовем случайным событием A
возможный исход некоторого опыта.
События A₁, …, A_k образуют
полную группу, если в результате опыта
обязательно происходит одно из них.
События называются несовместными, если
они не могут произойти одновременно в
одном опыте. Пусть при n-кратном повторении
опыта событие A произошло m раз. Частотой
события A называется число W = . Очевидно,
что значение W нельзя предсказать точно
до проведения серии из n опытов. Однако
природа случайных событий такова, что
на практике иногда наблюдается следующий
эффект: при увеличении числа опытов
значение
практически
перестает быть случайным и стабилизируется
около некоторого неслучайного числа
P(A), называемого вероятностью события
A. Для невозможного события (которое
никогда не происходит в опыте) P(A)=0, а
для достоверного события (которое всегда
происходит в опыте) P(A)=1. Если события
A₁, …, A_k образуют полную
группу несовместимых событий, то
P(A₁)+…+P(A_k)=1.

Пусть, например, опыт состоит в
подбрасывании игральной кости и
наблюдении числа выпавших очков X. Тогда
можно ввести следующие случайные события
A_i ={X = i}, i = 1, …, 6. Они образуют полную
группу несовместных равновероятных
событий, поэтому P(A_i) = (i = 1, …, 6).

Суммой событий A и B называется событие
A + B, состоящее в том, что в опыте происходит
хотя бы одно из них. Произведением
событий A и B называется событие AB,
состоящее в одновременном появлении
этих событий. Для независимых событий
A и B верны формулы

P(AB) = P(A)•P(B), P(A + B) = P(A) + P(B).

8) Рассмотрим теперь следующую задачу.
Предположим, что в электрическую цепь
последовательно включены три элемента,
работающие независимо друг от друга.
Вероятности отказов 1-го, 2-го и 3-го
элементов соответственно равны P₁
= 0,1, P₂ = 0,15, P₃ = 0,2. Будем считать
цепь надежной, если вероятность того,
что в цепи не будет тока, не более 0,4.
Требуется определить, является ли данная
цепь надежной.

Так как элементы включены последовательно,
то тока в цепи не будет (событие A), если
откажет хотя бы один из элементов. Пусть
A_i — событие, заключающееся в
том, что i-й элемент работает (i = 1, 2, 3).
Тогда P(A1) = 0,9, P(A2) = 0,85, P(A3) = 0,8. Очевидно,
что A₁A₂A₃ — событие,
заключающееся в том, что одновременно
работают все три элемента, и

P(A₁A₂A₃)
= P(A₁)•P(A₂)•P(A₃)
= 0,612.

Тогда P(A) + P(A₁A₂A₃)
= 1, поэтому P(A) = 0,388 < 0,4.
Следовательно, цепь является
надежной.

В заключение отметим, что приведенные
примеры математических моделей (среди
которых есть функциональные и структурные,
детерминистические и вероятностные)
носят иллюстративный характер и,
очевидно, не исчерпывают всего разнообразия
математических моделей, возникающих в
естественных и гуманитарных науках.

.

Как упадет брошенный предмет, по какой траектории полетит пуля и как рассчитать правильное направление для попадания в цель – всё это объясняется таким понятием как баллистическое движение и изучается соответствующей наукой.

Наверное каждый при просмотре фильмов о работе экспертов-криминалистов слышал выражение «аэробаллистическая экспертиза», и удивлялся тому, как лихо они определяют местоположение стрелка, и тип, а иногда и модель оружия, из которого был произведен, зачастую, фатальный выстрел.

Понятие баллистики

Определение баллистики звучит следующим образом – наука о движении тел, двигающихся в пространстве. Она изучает в первую очередь принципы движения всевозможных объектов, в частности пуль и снарядов, а также законы природы, влияющие на это движение и способность тела преодолевать возникшие на его пути преграды.

Физика и математика – вот основы, на которых базируется эта наука, они позволяют при должных знаниях рассчитывать траекторию полёта пули, исходя из воздействия на неё внешних сил, и её проникающую способность.

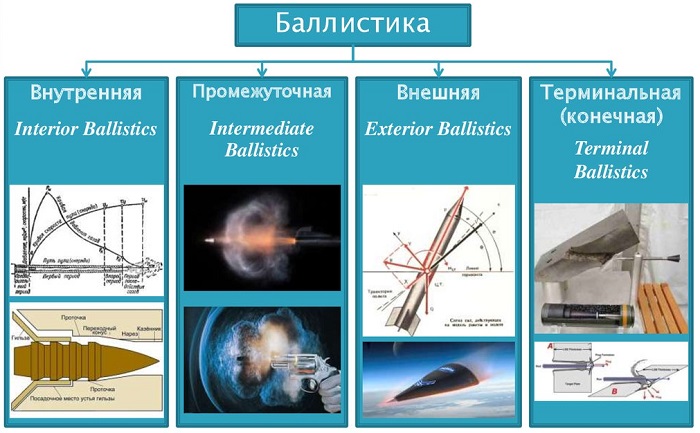
Сама же наука о законах полета снарядов делится на 4 направления:

1. Исследование движения пули или снаряда в канале ствола орудия изучает направление, которое называется внутренняя баллистика.

2. Поведение снаряда на выходе из канала ствола и в районе дульного среза исследуется промежуточной баллистикой и используется в разработке пламегасящих устройств и глушителей.

3. Вопросы движения снаряда в атмосфере и при воздействии внешних факторов изучаются внешней баллистикой. Основная область её применения – установление поправок на упреждение и влияние скорости ветра на траекторию.

4. Изучение проникающей способности снаряда – цель исследований баллистики под названием преградная (терминальная), которую изучают специалисты по вопросам бронезащиты.

История возникновения баллистики

Испокон веков основным занятием человека являлось уничтожение себе подобных. Сперва для этого использовались булыжники и палки, после чего человечество пришло к тому, что дистанционное оружие дает целый ряд преимуществ его владельцу. 

Так или иначе баллистика изучалась по мере развития человечества, параллельно с развитием механизмов для поражения противника на расстоянии.

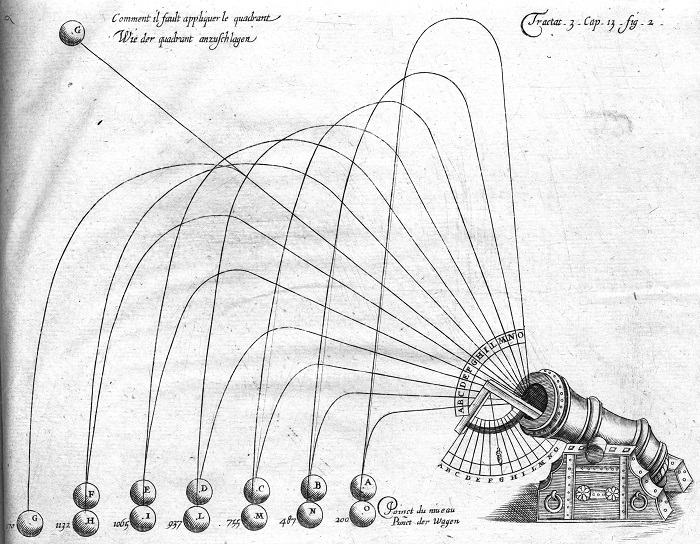
Метательные камни, ножи и дротики, ручные пращи, луки, арбалеты, а впоследствии – баллисты, катапульты, требушеты, толлеоны и, в конце концов, огнестрельное оружие и артиллерийские орудия – все эти средства толкали науку баллистики на протяжении всей своей истории.

Начало изучения траектории полета снаряда, как науки, было положено Николло Тарталья в 1537 году, начавшим исследование кривой движения этого тела. Продолжил изучение Галилей, сформулировав параболическую теорию.

Развивал данную тему и Ньютон, благодаря изучению законов воздушного сопротивления которого стало возможным доказать невозможность параболической кривой полета снаряда. Его дело продолжил Бенджамин Робинс, основное исследование которого – расчет начальной скорости ядра. 

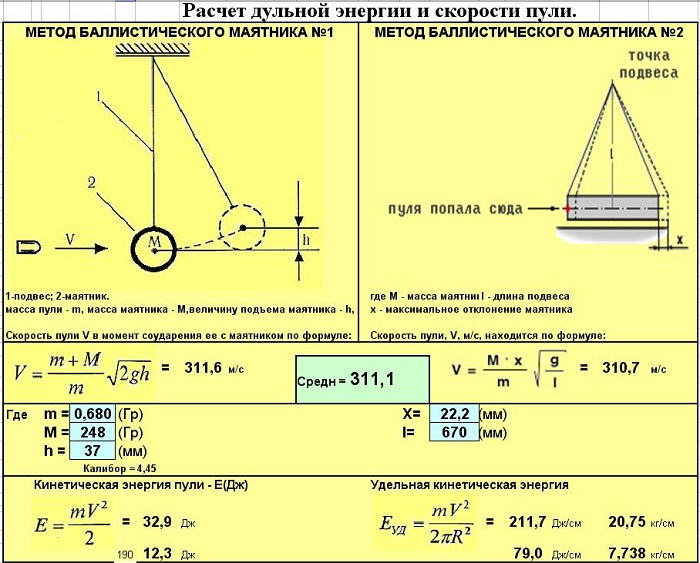
Он даже изобрел актуальный по сей день баллистический маятник. Прибор, с помощью которого определяют эффективность взрывчатых веществ, фиксируя при их подрыве угол отклонения маятника.

Далее баллистика развивалась семимильными шагами. Вошедшее в обиход в начале XIX века нарезное оружие, а также использование адаптированных под него снарядов и нового образца патрона, с пулей продолговатой формы, а точнее – необходимость изучения их эффективности и дальнейшей оптимизации, стали серьезным толчком в изучении данной науки, поскольку характеристики нового оружия были весьма высоки, что обуславливало широкую его популярность, и как следствие – высокий спрос.

Одним из ключевых витков истории баллистики стала разработка численного метода интегрирования дифференциальных уравнений, созданного Карлом Рунге и Мартином Кутта. Определенные элементы их метода позволяли с максимальной точностью вести расчеты траектории тел в пространстве. 

Появлялись всё новые виды вооружения, конструкторы отчаянно экспериментировали с длиной ствола, внутренними нарезами и наполнением патрона, двигая науку вперед.

Баллистическая траектория

Итак, что же в итоге представляет собой баллистическая траектория? Современная энциклопедия гласит: «Это траектория движения свободно брошенного тела под действием только силы тяжести». 

Например, межконтинентальные баллистические ракеты считаются таковыми, поскольку продолжают своё движение к цели после выключения двигателей, как раз-таки по траектории, которую называют баллистической. 

Здесь же – расчет ведения огня по настильной траектории, проще говоря – плавно опускающейся линии по ходу полета снаряда, и расчет возможности преодолевать возвышения по пути к конечной точке.

Фактически, таковым является движение любого тела в пространстве, при отсутствии какой-либо дополнительной тяги.

Основные формулы баллистического движения

При расчетах и изучении баллистического движения любого тела, стоит обратить внимание на огромное количество факторов – массу, скорость и обтекаемость тела, атмосферные условия и многое-многое другое. Но даже при учете этого, в баллистике есть свои основные формулы, применяемые в исследованиях.

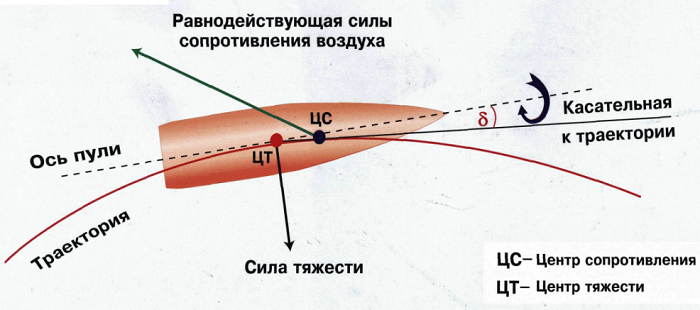
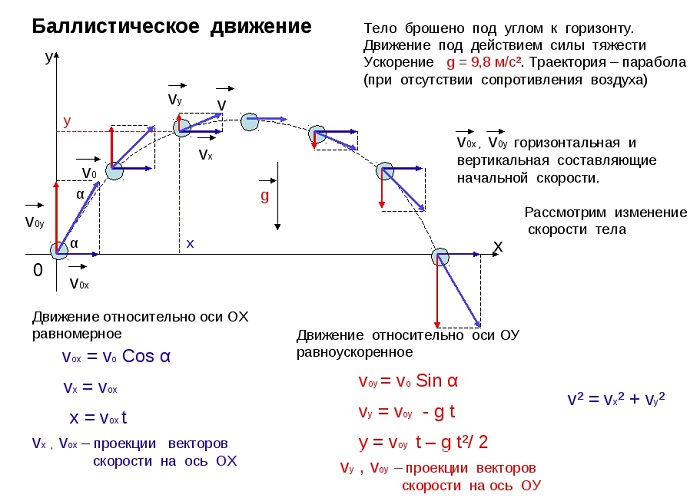
На брошенное под углом к горизонту тело в полете действует по меньшей мере – сила тяжести и сопротивление воздуха. Если исключить из этого силу сопротивления, то, согласно 2-го закону Ньютона, тело движется с ускорением, равным ускорению свободного падения; проекции ускорения на координатные оси равны ах = 0, ау = -g.

Проекции скорости тела, следовательно, изменяются со временем следующим образом:

V_x = V_x0 = V₀ * cos α;

V_y = V_y0 – g * t = V₀
* sin α – g * t,

где V₀ – начальная скорость, α – угол бросания.

Координаты тела, следовательно, изменяются так:

x = x₀ + V₀ * t * cos α;

y = y₀ + V₀ * t * sin α – 0,5 * g * t².

Если за точку отсчета берутся координаты х = у = 0, то:

x = V₀ * t * cos α;

y = V₀ * t * sin α – 0,5 * g * t².

Дальнейшие расчеты производятся при введении таких переменных как дальность полета и время, в итоге же получается финальное уравнение траектории движения. Выглядит оно следующим образом: 

y = x * tg α – g * x² / 2 * V₀² * cos²α.

Melnikov Peter Nikolaevich, candidate of technical science, leading researcher, peter@olvs.miee.ru, Russia, Moscow, Zelenograd, National Research University of Electronic Technology,

Sazonov Aleksey Alexadrovich, candidate of technical science, head of department, als@olvs.miee.ru, Russia, Moscow, Zelenograd, National Research University of Electronic Technology

УДК 623.55.025

РАСЧЕТЫ ТРАЕКТОРИИ ПОЛЕТА АРТИЛЛЕРИЙСКОГО

СНАРЯДА

П.Н. Мельников, М.А. Терпигорев

Приведена методика перехода от табличного способа расчета траектории полета артиллерийского снаряда к расчету траектории полета снаряда способом численного интегрирования системы дифференциальных уравнений задачи внешней баллистики.

Ключевые слова: артиллерийская зенитная стрельба, вычислительная система.

Одна из основных задач, решаемых вычислительной системой артиллерийского зенитного комплекса – это задача встречи снаряда с целью. В свою очередь, ядро задачи встречи составляет задача прогнозирования траектории полета снаряда на произвольный отрезок времени в будущем. В большинстве зенитных комплексов, принятых в настоящее время на вооружение, прогнозирование траектории полета снаряда решается табличным способом. Для каждого разрабатываемого образца вооружения составляются оригинальные таблицы стрельбы, которые состоят из баллистических и поправочных таблиц. Ниже будет рассматриваться конкретный вариант наполнения таблиц, что не повлияет на общность результатов работы, но придаст материалу статьи большую стройность изложения.

В состав баллистических таблиц входят три таблицы:

г = ГТ(Б, Е); а = Та(Ц Е); р= ЩБ, Е), (1)

где т – двумерная таблица полетного времени снаряда в зависимости от полной дальности полета и угла места цели; а – двумерная таблица угла превышения в зависимости от полной дальности полета и угла места цели (вертикальная плоскость); в – двумерная таблица угла деривации в зависимости от полной дальности полета и угла места цели (горизонтальная плоскость).

Размер таблицы зависит от калибра артиллерийского орудия (для калибра 30 мм размер таблицы составляет около 200 значений). В связи с

компактностью таблиц их размещение в памяти вычислительной системы не вызывает трудностей. Выборка из двумерной таблицы, как правило, сопровождается линейной интерполяцией значений для произвольных аргументов дальности D и угла места E. Практическая реализация задачи встречи с использованием табличного прогнозирования траектории полета снаряда возможна, если производительность вычислительной системы превышает миллион операций в секунду. Для настоящего уровня развития вычислительной техники указанное требование по производительности вычислений является довольно скромным (например, микроконтроллер фирмы Atmel AT91R40807 производительностью 30 миллионов операций в секунду снят с производства как морально устаревший).

Альтернативой табличному способу расчета траектории полета снаряда является способ численного интегрирования системы дифференциальных уравнений, описывающих траекторию полета снаряда в атмосфере Земли. Задача построения системы дифференциальных уравнений, в основе которой лежит изучение влияния действия внешних сил и моментов сил на снаряд с момента прохождения его среза дула ствола орудия, называется основной задачей внешней баллистики. Этой задачей занимались довольно давно, теория вопроса достаточно проработана [1, 2]. В этой литературе представлена расчетная модель для вычисления кинематических элементов траектории полета снарядов, которая позволяет учесть форму и вращение Земли, возмущение атмосферы, принудительное вращение снаряда, колебания снаряда относительно центра масс. Практическая реализация задачи встречи с использованием метода численного интегрирования системы дифференциальных уравнений траектории полета снаряда возможна, если производительность вычислительной системы превышает 15 миллионов операций в секунду. Такая производительность вычислений вполне доступна на практике (например, микроконтроллер фирмы Atmel AT91R40008 производительностью 60 миллионов операций в секунду, AT91SAM9 – 200 миллионов операций в секунду, процессоры фирмы Texas Instruments TMS320C64x+ – 1000 миллионов операций в секунду). Таким образом, в настоящее время не существует объективных препятствий в практической реализации метода численного решения задачи внешней баллистики в вычислительной системе зенитного комплекса.

Хотя метод численного интегрирования по сравнению с табличным является более затратным, он превосходит последний в точности определения параметров траектории полета снаряда. Табличный метод представляет собой приближенное частное решение, в котором упрощенно учитывается взаимное влияние (иными словами, учитывается только главный член разложения) отдельных внешних факторов на результат решения задачи внешней баллистики снаряда. Это важно по той причине, что в табличном методе решение ищется в виде суммы: расчет траектории полета

снаряда в стандартных метеобаллистических условиях (баллистические таблицы) плюс изменения в траектории, вызванные отклонениями баллистических и метеорологических условий от принятых за стандартные (поправочные таблицы). Таким образом, точность табличного метода расчета ограничена учетом только линейных связей внешних факторов с результатом.

Система дифференциальных уравнений моделирует влияние физических процессов (имеющих место в атмосфере Земли) на формирование траектории полета снаряда. На вход задачи подаются не стандартные, а реальные метеобаллистические параметры, которые трансформируются в результат согласно алгоритму численного интегрирования, поэтому влияние внешних факторов на результат в этом методе учитывается наиболее полно. В дополнение к отмеченному, в системе дифференциальных уравнений учитывается влияние факторов, которых нет в табличном методе, например, влияние на параметры траектории снаряда вращения Земли вокруг своей оси. Фактор суточного вращения Земли приводит к учету изменения силы тяжести снаряда, учету зависимости силы тяжести от широты стояния орудия, к учету влияния ускорения Кориолиса на снаряд.

Опережающие темпы развития цифровой элементной базы по сравнению с темпами совершенствования материальной части артиллерийского вооружения создали условия повышения эффективности существующих зенитных комплексов за счет внедрения более совершенных алгоритмов управления, которые не удалось реализовать ранее из-за ограниченных возможностей вычислительной техники. В рамках предполагаемой модернизации предлагается заменить алгоритм табличного прогнозирования траектории полета снаряда на алгоритм численного интегрирования системы дифференциальных уравнений задачи внешней баллистики полета снаряда. Предметом настоящей работы являются исследование проблем, которые имеют место при реализации алгоритма интегрирования дифференциальных уравнений полета снаряда, при условии, что в качестве исходных данных принимаются известные баллистические таблицы артиллерийского орудия.

Исходная система дифференциальных уравнений траектории полета снаряда, в соответствии с [1, 2], представлена в фазовых координатах

{ V, О, ¥}, где V – производная земной скорости снаряда, О – производная

угла наклона траектории, ¥ – производная угла пути. Задача встречи снаряда с целью решается в земной прямоугольной системе координат ГОСТ 20058-80 [3](начало координат в точке орудия; ось ОбУб направлена вверх по местной вертикали; ось ОбХб параллельна линии топографической координатной сетки и направлена на север; ось Об/б дополняется до

получения правой системы координат). Для согласования систем координат предлагается преобразовать фазовые координаты { V, О, ХР} в фазовые координаты {&сх,&су,&сг} стартовой прямоугольной системы координат ГОСТ 20058-80 (начало координат и ось ОбУс совпадают с началом и осью земной системы координат; ось ОбХс находится в плоскости стрельбы и направлена в сторону цели; ось Об/с дополняется до получения правой системы координат). Численное интегрирование системы дифференциальных уравнений траектории полета снаряда выполняется в стартовой прямоугольной системе координат. В результате интегрирования получают траекторию снаряда в фазовых координатах { Хс, Ус, Zc}. Для приведения результатов к земной прямоугольной системе координат { Хб, Уб, Zs} достаточно развернуть стартовую систему координат на величину азимута орудия. Так как баллистические таблицы представлены в стартовой системе координат, то и задачу согласования табличного и численного методов предлагается решать в стартовой системе координат.

Суть задачи согласования рассматриваемых методов заключается в том, чтобы рассчитать величины согласующих коэффициентов для метода численного интегрирования, при которых оба метода расчета дают одинаковые результаты с точностью до заданной погрешности. Задача согласования решается для неподвижной цели, неподвижного орудия в нормальных метеобаллистических условиях без учета фактора вращения Земли.

Входными величинами численного метода являются угол возвышения орудия О о и время полета снаряда т0. Входными величинами табличного метода являются угол места цели Ео и полная дальность полета снаряда Б о . Таблицы коэффициентов для согласования методов {1Х, ¡у, 12}

предлагается рассчитывать для каждой координаты { Хс, Ус, Zc }, при этом в качестве значений аргументов принимаются наборы величин О о и Б о .В качестве задающих значений дальностей Б о предлагается набор известных табличных значений (например, 2оо, 4оо, боо м, …- баллистические таблицы представлены с шагом 200 м по дальности). В качестве задающих значений О о предлагается набор значений с фиксированным шагом (например, ©о = 0°,3°,6°,…). Значения коэффициентов согласования {1Х, 1у}

включаются в качестве множителей при расчете коэффициента сопротивления воздуха, а {} – коэффициента деривации.

Расчет коэффициентов согласования начинается с задания величин угла возвышения орудия О о и полной дальности полета снаряда Б о . Так

как угол возвышения О, угол места Е и угол превышения а связаны ме-

92

жду собой соотношением

0 = Е + а, (2)

то значение Е0 при известном значении 0 0 определяется из баллистической таблицы а = Та( £>0, Е). По рассчитанному значению Е0 и заданному значению В0 из баллистической таблицы т = Тт(£0, Е0) находится полетное время снаряда Т). По рассчитанному значению Е0 и заданному значению В0 из баллистической таблицы ¡ = Тр(£0,Е0) находится угол деривации ¡0. Таким образом, из данных баллистических таблиц следует, что снаряд, выпущенный под углом к горизонту 0 0, через время полета Т0 должен оказаться в точке { X0,У0, ^о}.

Х0 = В • Со5(Е0) • Со5(¡0); = В • Б1п(Е0);

70 = В0 • (Е0) • МД,)

В результате интегрирования системы дифференциальных уравнений полета снаряда, при тех же начальных условиях, получим точку с координатами { Хг, Уг, Т^г}. Значения коэффициентов согласования

{1Х, 1у, 1г} назначаются из множества допустимых значений [ 1п, 1т ], где 1п – минимальное допустимое значение коэффициента (например, 1 =0.5); 1т – максимальное допустимое значение коэффициента (например, 1 =1.9).

Расхождение результатов расчета траектории снаряда оценивается погрешностями

Ах = зЬб(Хг – X0); Ау = зЬб(Уг – У0); Az = зЬб(Zг – ). (4)

Фиксация величин коэффициентов согласования при условии минимума суммарной погрешности

А г = ^А* + Ау + А2) (5)

позволяет рассчитать их оптимальные значения {1°, 1°°, 1°}.

Контроль величин составляющих (4) и суммарной (5) погрешностей позволяет разработчику оценить степень соответствия табличного и численного способов расчета и обоснованно принять решение к дальнейшему использованию оптимальных коэффициентов согласования в решении задачи внешней баллистики способом численного интегрирования системы дифференциальных уравнений, описывающих траекторию полета артиллерийского снаряда в атмосфере Земли.

Список литературы

1. Дмитриевский А.А., Лысенко Л.Н. Внешняя баллистика: ечебник для студентов вузов. 4-е изд., перераб. и доп. М.: Машиностроение, 2005.

608 с.

2. Коновалов А. А., Николаев Ю.В. Внешняя баллистика. М.: ЦНИИ информации, 1979. 228 с.

3. ГОСТ 20058-80 Динамика летательных аппаратов в атмосфере. Термины, определения и обозначения.

Мельников Петр Николаевич, канд. техн. наук, вед. науч. сотр., peter@olvs.miee.ru, Россия, Москва, Зеленоград, Национальный исследовательский университет «МИЭТ»

Терпигорев Михаил Александрович, канд. техн. наук, ст. науч. сотр., terpm@olvs.miee.ги, Россия, Москва, Зеленоград, Национальный исследовательский университет «МИЭТ»

CALCULATIONS OF THE TRAJECTORY OF AN ARTILLERY PROJECTILE

P.N.Melnikov, M.A. Terpigorev

In the article the method of transition from the tabular method of calculating the trajectory of an artillery shell to the calculation of the trajectory of the projectile by the method of numerical integration of differential equations of tasks external ballistics.

Key words: artillery fire, calculating system.

Melnikov Peter Nikolaevich, candidate of technical science, leading researcher, peter@olvs.miee.ru, Russia, Moscow, Zelenograd, National Research University of Electronic Technology,

Terpigorev Micle Alexandrovich, candidate of technical science, senior researcher, terpm@olvs.miee.ru, Russia, Moscow, Zelenograd, National Research University of Electronic Technology

УДК 551.508.54

ОДНОПЛОСКОСТНОЙ ДАТЧИК СКОРОСТИ ВОЗДУШНОГО ПОТОКА

А.П. Панов, А.Н. Серов, И.Н. Мочегов

Рассмотрены основные методы измерения скорости ветра и предложена структурная схема одноплоскостного датчика скорости воздушного потока. Объяснены принципы функционирования датчика ветра. Приведены требования, предъявляемые к форме обтекателя. Представлены результаты моделирования и натурного испытания разработанного устройства.

Ключевые слова: дифференциальный датчик давления, анемометр, тензомо-

дуль.

На точность работы системы управления объектом специального назначения оказывает влияние множество факторов [1]. Одним из основ-