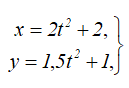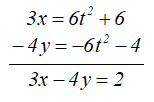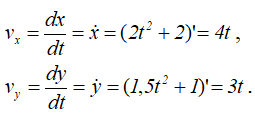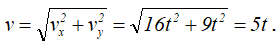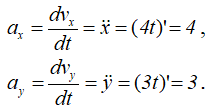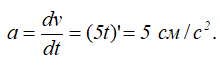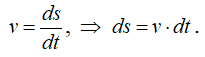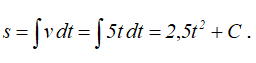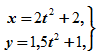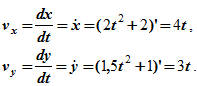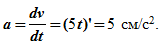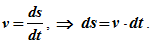Пример решения задачи по определению траектории равноускоренного движения точки, заданного уравнениями, скорости и ускорения в некоторые моменты времени, координаты начального положения точки, а также путь, пройденный точкой за время t.
Задача
Движение точки A задано уравнениями:
где x и y – в см, а t – в с. Определить траекторию движения точки, скорость и ускорение в моменты времени t0=0 с, t1=1 с и t2=5 с, а также путь, пройденный точкой за 5 с.
Другие примеры решений >
Помощь с решением задач >
Решение
Расчет траектории
Определяем траекторию точки. Умножаем первое заданное уравнение на 3, второе – на (-4), а затем складываем их левые и правые части:
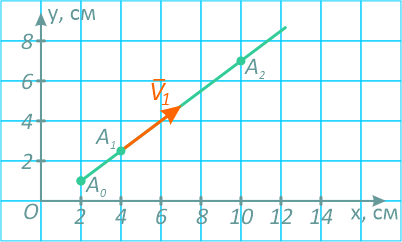
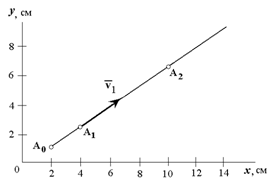
Получилось уравнение первой степени – уравнение прямой линии, значит движение точки – прямолинейное (рисунок 1.5).
Другие видео
Для того, чтобы определить координаты начального положения точки A0, подставим в заданные уравнения значения t0=0; из первого уравнения получим x0=2 см, из второго y0=1 см.
Рисунок 1.5
При любом другом значении t координаты x и y движущейся точки только возрастают, поэтому траекторией точки служит полупрямая 3x-4y=2 с началом в точке A0 (2; 1).
Расчет скорости
Определяем скорость движения точки, найдя сначала ее проекции на оси координат:
тогда
При t0=0с скорость точки v0=0, при t1=1с – v1=5 см/с, при t2=5с – v2=25см/с.
Расчет ускорения
Определяем ускорение точки. Его проекции на оси координат:
Проекции ускорения не зависят от времени движения,
т.е. движение точки равноускоренное, векторы скорости и ускорения совпадают с траекторией точки и направлены вдоль нее.
С другой стороны, поскольку движение точки прямолинейное, то модуль ускорения можно определить путем непосредственного дифференцирования уравнения скорости:
Определение пути
Определяем путь, пройденный точкой за первые 5с движения. Выразим путь как функцию времени:
Проинтегрируем последнее выражение:
Если t=t0=0, то C=s0; в данном случае s0=0, поэтому s=2,5t2. Находим, что за 5с точка проходит расстояние s|t=5с=2,5∙52=62,5 см.
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Траектория движения в физике, теория и онлайн калькуляторы
Траектория движения
Определение и основные понятия траектории движения
Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.
Определение
Линию, которую описывает частица при своем движении, называется траекторией движения.
В зависимости от формы траектории механическое движение можно разделить на:
- прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
- и криволинейное перемещение (траектория – кривая линия).
Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.
При движении точки с постоянным ускорением, которое описывает уравнение:
[overline{r}left(tright)={overline{r}}_0+{overline{v}}_0t+frac{overline{a}t^2}{2}left(1right),]
(где $overline{r}left(tright)$ – радиус-вектор точки в момент времени $t$; ${overline{v}}_0$ – начальная скорость движения точки; $overline{a}$ – ускорение точки,) траектория движения представляет собой плоскую кривую, что означает все точки этой кривой находятся в одной плоскости. Положение этой плоскости в пространстве задают векторы ускорения и начальной скорости. Ориентацию координатных осей чаще всего выбирают так, чтобы плоскость движения совпадала с одной из координатных плоскостей. В этом случае векторное уравнение (1) можно свести к двум скалярным уравнениям.
Уравнение траектории движения
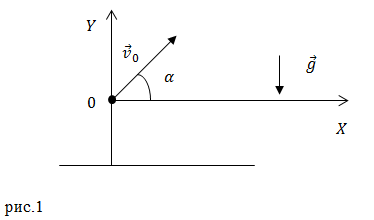
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.
Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:
[left{ begin{array}{c}
x=v_0t{cos alpha left(2right), } \
y=v_0t{sin alpha }-frac{gt^2}{2}left(3right). end{array}
right.]
Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:
[t=frac{x}{v_0{cos alpha }}; y=v_0frac{x}{v_0{cos alpha }}{sin alpha }-frac{g}{2}{left(frac{x}{v_0{cos alpha }}right)}^2to y=x tg alpha -frac{gx^2}{2v^2_0{cos}^2alpha }left(4right).]
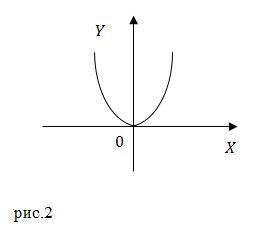
Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.
Вершина этой параболы находится в точке с координатами:
[left{ begin{array}{c}
x=frac{v^2_0{sin alpha {cos alpha } }}{g} \
y=frac{v^2_0{sin}^2alpha }{2g} end{array}
right.left(5right).]
Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($frac{dy}{dx}$) от нее по $x$.
Обратимость движения
Из представления о траектории можно конкретизировать смысл обратимости механического движения.
Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.
Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.
Параметры траектории движения
Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:
- Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки – это значит указать эти функции:
- При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline{r}$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline{r}$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение:
- Третьим способом описания движения является описание с помощью параметров траектории.
[x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]
[overline{r}=overline{r}left(tright)left(7right).]
Путь – это скалярная величина, равная длине траектории.
Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:
[s=sleft(tright)left(8right).]
Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:
[s=Atleft(9right),]
где $s$ – путь точки по траектории; $t$ – время движения; $A$ – коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.
Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.
Примеры задач с решением
Пример 1
Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline{v}=Aoverline{i}+Bxoverline{j} , $где $overline{i}$, $overline{j}$ – орты осей X и Y; $A$,B – постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit{}
Решение: Рассмотрим уравнение изменения скорости частицы:
[overline{v}=Aoverline{i}+Bxoverline{j} left(1.1right).]
Из этого уравнения следует, что:
[left{ begin{array}{c}
v_x=A, \
v_y=Bx end{array}
right.left(1.2right).]
Из (1.2) имеем:
[dx=v_xdt=Adtto dt=frac{dx}{A};;dy=v_ydt=Bxdtto dy=Bxfrac{dx}{A} left(1.3right).]
Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):
[y=intlimits^x_0{frac{B}{A}}xdx=frac{B}{2A}x^2.]
Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:
[left{ begin{array}{c}
x=0 \
y=0. end{array}
right.]
Пример 2
Задание: Движение материальной точки в плоскости описывает система уравнений: $left{ begin{array}{c}
x=At. \
y=At(1+Bt) end{array}
right.$, где $A$ и $B$ – положительные постоянные. Запишите уравнение траектории точки.
Решение: Рассмотрим систему уравнений, которая задана в условии задачи:
[left{ begin{array}{c}
x=At. \
y=Atleft(1+Btright) end{array}
right.left(2.1right).]
Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:
[t=frac{x}{A}left(2.2right).]
Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:
[y=Atleft(1+Btright)=At+ABt^2=Afrac{x}{A}+AB{(frac{x}{A})}^2=x+frac{B}{A}x^2.]
Ответ: $y=x+frac{B}{A}x^2$
Читать дальше: ускорение тела.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Кинематика. Задачи на движение с равномерным ускорением
Расчет параметров движения с равномерным ускорением по заданным.
Решил сделать универсальный решатель задач на движение с равномерным ускорением.
Думаю, среди школьников должно пользоваться популярностью.
В чем тут суть — как известно, движение с равномерным ускорением описывается следующими уравнениями:
Итого мы имеем пять параметров движения — начальную скорость, конечную скорость, ускорение, время движения и перемещение, и два уравнения. Очевидно, что для того, чтобы систему уравнений можно было решить, три параметра должны быть заданы, и два неизвестны.
Как подсказывает калькулятор Элементы комбинаторики. Перестановки, размещения, сочетания, разных условий задач, то есть сочетаний из пяти по три, всего десять. То есть всего вообще может быть только десять типов задач на движение с равномерным ускорением.
Вот эти десять типов задач и решает калькулятор ниже — как только вводится три любых параметра, остальные два рассчитываются по одному из десяти способов. Чтобы указать неизвестный параметр — ставим прочерк.
iSopromat.ru
Пример решения задачи по определению траектории равноускоренного движения точки, заданного уравнениями, скорости и ускорения в некоторые моменты времени, координаты начального положения точки, а также путь, пройденный точкой за время t.
Задача
где x и y – в см, а t – в с. Определить траекторию движения точки, скорость и ускорение в моменты времени t0=0 с, t1=1 с и t2=5 с, а также путь, пройденный точкой за 5 с.
Решение
Расчет траектории
Определяем траекторию точки. Умножаем первое заданное уравнение на 3, второе – на (-4), а затем складываем их левые и правые части:
Получилось уравнение первой степени – уравнение прямой линии, значит движение точки – прямолинейное (рисунок 1.5).
Для того, чтобы определить координаты начального положения точки A0, подставим в заданные уравнения значения t0=0; из первого уравнения получим x0=2 см, из второго y0=1 см. При любом другом значении t координаты x и y движущейся точки только возрастают, поэтому траекторией точки служит полупрямая 3x-4y=2 с началом в точке A0 (2; 1).
Расчет скорости
Расчет ускорения
Определяем ускорение точки. Его проекции на оси координат:
Проекции ускорения не зависят от времени движения,
т.е. движение точки равноускоренное, векторы скорости и ускорения совпадают с траекторией точки и направлены вдоль нее.
С другой стороны, поскольку движение точки прямолинейное, то модуль ускорения можно определить путем непосредственного дифференцирования уравнения скорости:
Определение пути
Определяем путь, пройденный точкой за первые 5с движения. Выразим путь как функцию времени:
Проинтегрируем последнее выражение:
Если t=t0=0, то C=s0; в данном случае s0=0, поэтому s=2,5t 2 . Находим, что за 5с точка проходит расстояние
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Траектория движения
Определение и основные понятия траектории движения
Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.
Линию, которую описывает частица при своем движении, называется траекторией движения.
В зависимости от формы траектории механическое движение можно разделить на:
- прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
- и криволинейное перемещение (траектория – кривая линия).
Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.
При движении точки с постоянным ускорением, которое описывает уравнение:
Уравнение траектории движения
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.
Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:
Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:
Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.
Вершина этой параболы находится в точке с координатами:
Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($frac$) от нее по $x$.
Обратимость движения
Из представления о траектории можно конкретизировать смысл обратимости механического движения.
Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.
Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.
Параметры траектории движения
Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:
- Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки – это значит указать эти функции: [x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]
- При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение: [overline=overlineleft(tright)left(7right).]
- Третьим способом описания движения является описание с помощью параметров траектории.
Путь – это скалярная величина, равная длине траектории.
Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:
Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:
где $s$ – путь точки по траектории; $t$ – время движения; $A$ – коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.
Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.
Примеры задач с решением
Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline=Aoverline+Bxoverline , $где $overline$, $overline$ – орты осей X и Y; $A$,B – постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit<>
Решение: Рассмотрим уравнение изменения скорости частицы:
Из этого уравнения следует, что:
Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):
Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:
Задание: Движение материальной точки в плоскости описывает система уравнений: $left< begin x=At. \ y=At(1+Bt) end right.$, где $A$ и $B$ – положительные постоянные. Запишите уравнение траектории точки.
Решение: Рассмотрим систему уравнений, которая задана в условии задачи:
Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:
Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/fizika/fizika_95_traektorija_dvizhenija.php
[/spoiler]
По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t1 (с) найти положение точки на траектории, ее скорость, полное, касательное и нормальнее ускорения, а также радиус кривизны траектории в соответствующей точке.
Необходимые для решения данные приведены в табл. 20.
| Решение | Формат | Размер | Наличие |
| Вариант 1 | doc / pdf | 777 КБ / 244 КБ | Готово |
| Вариант 2 | doc / pdf | 476 КБ / 246 КБ | Готово |
| Вариант 3 | doc / pdf | 531 КБ / 251 КБ | Готово |
| Вариант 4 | doc / pdf | 504 КБ / 245 КБ | Готово |
| Вариант 5 | doc / pdf | 507 КБ / 248 КБ | Готово |
| Вариант 6 | doc / pdf | 471 КБ / 238 КБ | Готово |
| Вариант 7 | doc / pdf | 508 КБ / 244 КБ | Готово |
| Вариант 8 | doc / pdf | 516 КБ / 247 КБ | Готово |
| Вариант 9 | doc / pdf | 469 КБ / 239 КБ | Готово |
| Вариант 10 | doc / pdf | 504 КБ / 247 КБ | Готово |
| Вариант 11 | doc / pdf | 469 КБ / 238 КБ | Готово |
| Вариант 12 | doc / pdf | 488 КБ / 248 КБ | Готово |
| Вариант 13 | doc / pdf | 509 КБ / 248 КБ | Готово |
| Вариант 14 | doc / pdf | 488 КБ / 243 КБ | Готово |
| Вариант 15 | doc / pdf | 519 КБ / 250 КБ | Готово |
| Вариант 16 | doc / pdf | 501 КБ / 242 КБ | Готово |
| Вариант 17 | doc / pdf | 489 КБ / 247 КБ | Готово |
| Вариант 18 | doc / pdf | 536 КБ / 251 КБ | Готово |
| Вариант 19 | doc / pdf | 512 КБ / 245 КБ | Готово |
| Вариант 20 | doc / pdf | 505 КБ / 245 КБ | Готово |
| Вариант 21 | doc / pdf | 509 КБ / 246 КБ | Готово |
| Вариант 22 | doc / pdf | 476 КБ / 238 КБ | Готово |
| Вариант 23 | doc / pdf | 491 КБ / 241 КБ | Готово |
| Вариант 24 | doc / pdf | 530 КБ / 251 КБ | Готово |
| Вариант 25 | doc / pdf | 477 КБ / 239 КБ | Готово |
| Вариант 26 | doc / pdf | 820 КБ / 251 КБ | Готово |
| Вариант 27 | doc / pdf | 854 КБ / 253 КБ | Готово |
| Вариант 28 | doc / pdf | 477 КБ / 197 КБ | Готово |
| Вариант 29 | doc / pdf | 481 КБ / 241 КБ | Готово |
| Вариант 30 | doc / pdf | 789 КБ / 268 КБ | Готово |
Уравнения
движения являются одновременно
уравнениями траектории точки в
параметрической форме. Для получения
уравнения траектории из уравнений
движения необходимо исключить параметр
t
:
sin
(t
) =
;
cos
(t
) =
. (1)
Если
обе части каждого равенства возвести
в квадрат и сложить, то получим уравнение
эллипса:
–
= 1. (2)
Горизонтальная
полуось эллипса =
2 м, вертикальная полуось эллипса b
= 4 м, а координаты его центра
= 3 м; =
0. Траекторию точки строим в масштабе
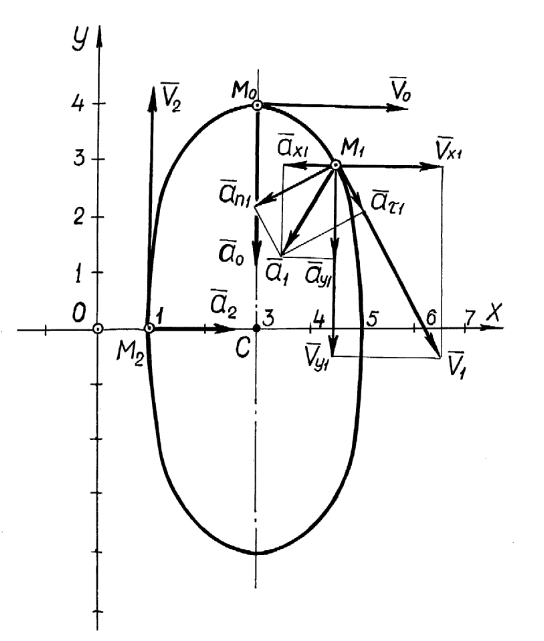
на рисунке (рисунок 3).
4.2.2 Определение положения точки на траектории
Для
определения положения точки на траектории
в уравнения ее координат подставляем
соответствующее время.
В
начальный момент времени при t
= 0 из этих уравнений получим:
=
3 м , =
4 м.
В
заданный момент времени при =
1 c:
=
2 sin
+ 3 = 4,4 м ;
=
4 cos
= 2,8 м.
По
вычисленным координатам показываем
положения точек ,
на
траектории (рисунок 3).
3.3.2.3 Определение скорости и ускорения точки
Скорость
и ускорение точки найдем по их проекциям
на оси координат
;
;
(3)
;
.
(4)
Тогда
начальный момент времени при t
= 0 получим:
м/с;
;
=
1,57 м/с .;
м/
;
.
Рисунок 3
В
заданный момент времени при
:
;
;
;
;
;
.
Выбираем
масштаб скорости и ускорения и строим
векторы скорости и ускорения и их
проекции для точек
(рисунок 46). Величину выбранного масштаба
необходимо указать на рисунке.
4.2.4 Определение касательного, нормального ускорения точки
и радиуса кривизны траектории
При
движении точки по криволинейной
траектории ускорение точки можно
выразить через проекции на естественные
оси: касательную и нормаль ,
где
– касательное ускорение точки
;
(5)
–
нормальное ускорение ;
(6)
где
–
радиус кривизны траектории.
Нормальное
ускорение можно вычислить, зная полное
ускорение точки и его касательную
составляющую
.
(7)
Подставляем
в формулы (3.17), (3.18), (3.19) значения величин,
найденных для соответствующих моментов
времени. В начальный момент времени при
:
;
;
.
В
заданный момент времени при :
;
;
.
В
выбранном масштабе ускорений показываем
проекции ускорения точек
на естественные оси координат (рисунок
46), что позволяет осуществить проверку
решения.
На
графике необходимо иметь соблюдение
условия:
.
-
Пример решения
задачи К2
Механизм
состоит из ступенчатых колес 1 и 2,
связанных между собой ременной передачей,
колеса 2 и 3 находятся в зацеплении,
колесо 1 находится в зацеплении с зубчатой
рейкой 4, груз 5 находится на конце нити,
намотанной на шкив 3 радиуса
(рисунок 4).
Определить
скорости точек В и С, ускорение груза
5, ускорение точки А и угловое ускорение
колеса 2 в момент времени t
= 2 c,
если заданы закон движения рейки
и
размеры колес
Решение
1. Рейка 4 совершает поступательное движение по закону
Определим
скорость движения рейки .
При
Ускорение
рейки найдем из соотношения .
Знак
ускорения не совпадает со знаком
скорости, следовательно, рейка движется
замедленно.
2.
Точка К, лежащая на ободе колеса ,
движется со скоростью,
равной скорости
рейки, находящейся в зацеплении с
колесом, т.е.
Учитывая,
что ,
определим угловую скорость колеса 1:
.
При
.
Определим
угловое ускорение колеса 1: 
Ускорение точки
А ступенчатого колеса 1найдем из
выражения :
,
Скорость точки С, лежащей на ободе
колеса 3 радиуса ,
находим по формуле: .
5.Ускорение
груза 5 равно касательному ускорению
точки N
колеса 3:
.
6.
Найденные параметры движения точек и
звеньев механизма изображаем на рисунке
(рисунок 4).
где
.
.
.
Рисунок 4
3.
Колеса радиусов
и
связаны бесконечным ремнем. При отсутствии
проскальзывания скорости всех точек
ремня одинаковы, т.е.
а
угловые скорости и угловые ускорения
валов 1 и 2 обратно пропорциональны
радиусам колес:
, тогда
;
Скорость точки В,
лежащей на ободе колеса 2, рассчитываем
по формуле
.
4.
Колеса радиусов
и
находятся в зацеплении друг с другом,
поэтому угловую скорость и угловое
ускорение колеса 3 найдем из соотношений:
;
.