Траектория движения в физике, теория и онлайн калькуляторы
Траектория движения
Определение и основные понятия траектории движения
Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.
Определение
Линию, которую описывает частица при своем движении, называется траекторией движения.
В зависимости от формы траектории механическое движение можно разделить на:
- прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
- и криволинейное перемещение (траектория – кривая линия).
Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.
При движении точки с постоянным ускорением, которое описывает уравнение:
[overline{r}left(tright)={overline{r}}_0+{overline{v}}_0t+frac{overline{a}t^2}{2}left(1right),]
(где $overline{r}left(tright)$ – радиус-вектор точки в момент времени $t$; ${overline{v}}_0$ – начальная скорость движения точки; $overline{a}$ – ускорение точки,) траектория движения представляет собой плоскую кривую, что означает все точки этой кривой находятся в одной плоскости. Положение этой плоскости в пространстве задают векторы ускорения и начальной скорости. Ориентацию координатных осей чаще всего выбирают так, чтобы плоскость движения совпадала с одной из координатных плоскостей. В этом случае векторное уравнение (1) можно свести к двум скалярным уравнениям.
Уравнение траектории движения
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.
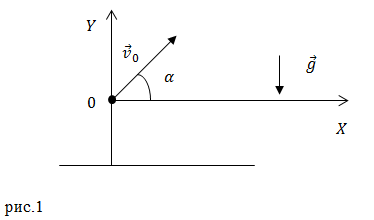
Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:
[left{ begin{array}{c}
x=v_0t{cos alpha left(2right), } \
y=v_0t{sin alpha }-frac{gt^2}{2}left(3right). end{array}
right.]
Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:
[t=frac{x}{v_0{cos alpha }}; y=v_0frac{x}{v_0{cos alpha }}{sin alpha }-frac{g}{2}{left(frac{x}{v_0{cos alpha }}right)}^2to y=x tg alpha -frac{gx^2}{2v^2_0{cos}^2alpha }left(4right).]
Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.
Вершина этой параболы находится в точке с координатами:
[left{ begin{array}{c}
x=frac{v^2_0{sin alpha {cos alpha } }}{g} \
y=frac{v^2_0{sin}^2alpha }{2g} end{array}
right.left(5right).]
Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($frac{dy}{dx}$) от нее по $x$.
Обратимость движения
Из представления о траектории можно конкретизировать смысл обратимости механического движения.
Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.
Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.
Параметры траектории движения
Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:
- Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки – это значит указать эти функции:
- При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline{r}$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline{r}$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение:
- Третьим способом описания движения является описание с помощью параметров траектории.
[x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]
[overline{r}=overline{r}left(tright)left(7right).]
Путь – это скалярная величина, равная длине траектории.
Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:
[s=sleft(tright)left(8right).]
Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:
[s=Atleft(9right),]
где $s$ – путь точки по траектории; $t$ – время движения; $A$ – коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.
Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.
Примеры задач с решением
Пример 1
Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline{v}=Aoverline{i}+Bxoverline{j} , $где $overline{i}$, $overline{j}$ – орты осей X и Y; $A$,B – постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit{}
Решение: Рассмотрим уравнение изменения скорости частицы:
[overline{v}=Aoverline{i}+Bxoverline{j} left(1.1right).]
Из этого уравнения следует, что:
[left{ begin{array}{c}
v_x=A, \
v_y=Bx end{array}
right.left(1.2right).]
Из (1.2) имеем:
[dx=v_xdt=Adtto dt=frac{dx}{A};;dy=v_ydt=Bxdtto dy=Bxfrac{dx}{A} left(1.3right).]
Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):
[y=intlimits^x_0{frac{B}{A}}xdx=frac{B}{2A}x^2.]
Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:
[left{ begin{array}{c}
x=0 \
y=0. end{array}
right.]
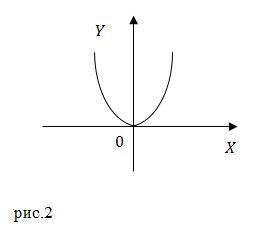
Пример 2
Задание: Движение материальной точки в плоскости описывает система уравнений: $left{ begin{array}{c}
x=At. \
y=At(1+Bt) end{array}
right.$, где $A$ и $B$ – положительные постоянные. Запишите уравнение траектории точки.
Решение: Рассмотрим систему уравнений, которая задана в условии задачи:
[left{ begin{array}{c}
x=At. \
y=Atleft(1+Btright) end{array}
right.left(2.1right).]
Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:
[t=frac{x}{A}left(2.2right).]
Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:
[y=Atleft(1+Btright)=At+ABt^2=Afrac{x}{A}+AB{(frac{x}{A})}^2=x+frac{B}{A}x^2.]
Ответ: $y=x+frac{B}{A}x^2$
Читать дальше: ускорение тела.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Траектория движения тела – это линия, которая была описана материальной точкой при перемещении из одной точки в другую с течением времени.
Виды движений тела
Существуют несколько видов движений и траекторий твердого тела:
- поступательное;
- вращательное, то есть движение по окружности;
- плоское, то есть перемещение по плоскости;
- сферическое, характеризующее движение по поверхности сферы;
- свободное, иначе говоря, произвольное.
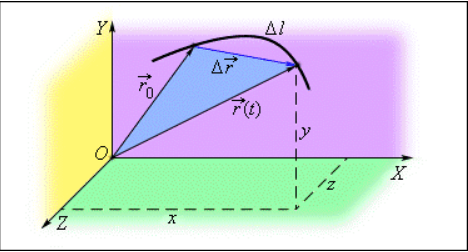
Рисунок 1. Определение точки при помощи координат x=x(t), y=y(t), z=z(t) и радиус-вектора r→(t), r0→ является радиус-вектором точки в начальный момент времени
Положение материальной точки в пространстве в любой момент времени может быть задано при помощи закона движения, определенный координатным способом, через зависимость координат от времени x=x(t), y=y(t), z=z(t) или от времени радиус-вектора r→=r→(t), проведенного из начала координат к заданной точке. Это показано на рисунке 1.
Перемещение тела
Перемещение тела s→=∆r12→=r2→-r1→ – направленный отрезок прямой, соединяющий начальную с конечной точкой траектории тела. Значение пройденного пути l равняется длине траектории, пройденной телом за определенный промежуток времени t.
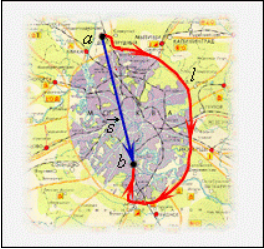
Рисунок 2. Пройденный путь l и вектор перемещения s→ при криволинейном движении тела, a и b – начальная и конечная точки пути, принятые в физике
По рисунку 2 видно, что при движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.
Перемещение принято считать векторной величиной. Этот отрезок имеет направление.
Путь – скалярная величина. Считается числом.
Сумма двух последовательных перемещений из точки 1 в точку 2 и из токи 2 в точку 3 является перемещением из точки 1 в точку 3, как показано на рисунке 3.
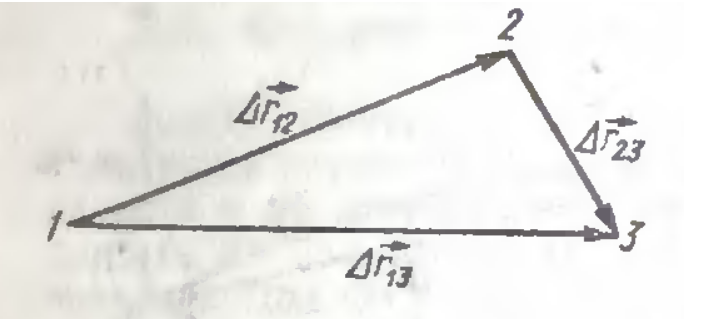
Рисунок 3. Сумма двух последовательных перемещений ∆r→13=∆r→12+∆r→23=r→2-r→1+r→3-r→2=r→3-r→1
Когда радиус-вектор материальной точки в определенный момент времени t является r→(t), в момент t+∆t есть r→(t+∆t), тогда ее перемещение ∆r→ за время ∆t равняется ∆r→=r→(t+∆t)-r→(t).
Перемещение ∆r→ считается функцией времени t: ∆r→=∆r→(t).
По условию дан движущийся самолет, представленный на рисунке 4. Определить вид траектории точки М.
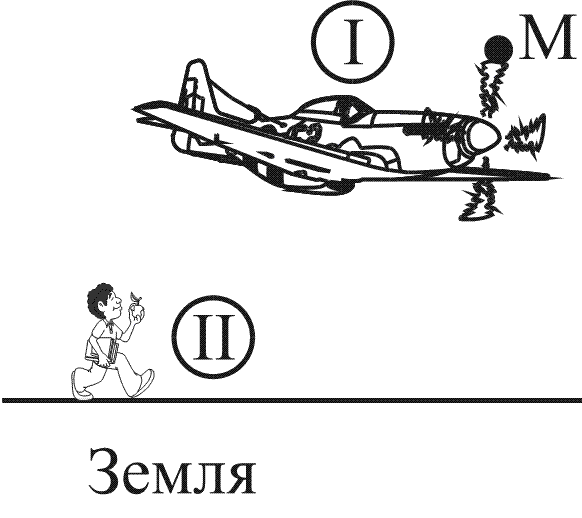
Рисунок 4
Решение
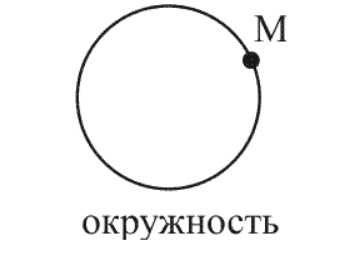
Необходимо рассмотреть систему отсчета I, называемую «Самолет» с траекторией движения точки М виде окружности.
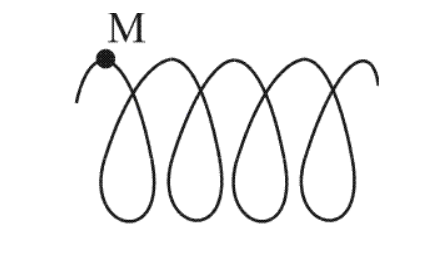
Будет задана система отсчета II «Земля» с траекторией движения имеющейся точки М по спирали.
Дана материальная точка, которая совершает движение из А в В. Значение радиуса окружности R=1 м. Произвести нахождение S, ∆r→.
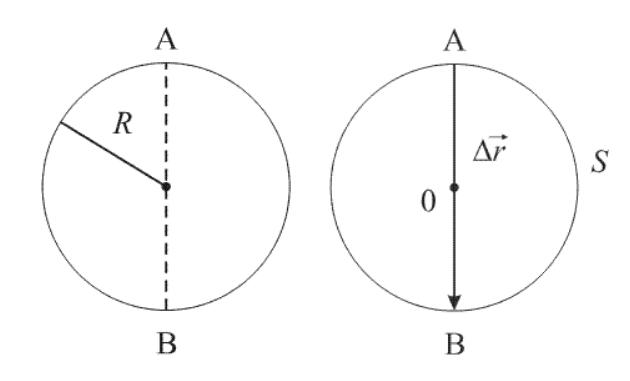
Решение
Во время движения из А в В точка проходит путь, который равен половине окружности, записываемой формулой:
S=πR.
Подставляем числовые значения и получаем:
S=3,14·1 м=3,14 м.
Перемещением ∆r→ в физике считается вектор, соединяющий начальное положение материальной точки с конечным, то есть А с В.
Подставив числовые значения, вычислим:
∆r→=2R=2·1=2 м.
Ответ: S=3,14 м; ∆r→=2 м.
Общие сведения
Под движением тела понимают процесс его перемещения из одной точки пространства в другую. Произошедшее действие исследуют относительно другого объекта или выбранных начальных координат. При этом положение вовсе не обязательно может изменяться сразу ко всем окружающим его телам. Например, стоящий человек на Земле находится в состоянии покоя по отношению к планете, но движется относительно Солнца.
В физике принято любое изменение определять в системе пространственных координат. За оси принимают перпендикулярные линии x, y, z. Совокупность данных, используемых для изучения движения, называют системой отсчёта.
Существует несколько видов механического перемещения (во времени) физической точки:
- равномерное и равноускоренно прямолинейное;
- по дуге;
- гармоническое колебание.
При движении тело проходит определённый путь. Описать его можно виртуальной линией, при этом она может быть как прямой, так и кривой. Именно она и называется траекторией движения. По сути, эта линия соединяет последовательно все положения точки в пространстве — от начальной до конечной. Длина отрезка является пройденным путём и считается векторной величиной.
Изменение радиус-вектора r (значения, задающего положение точки в пространстве относительно другого тела) описывает кинематический закон: r = r (t). В трёхмерных декартовых координатах его можно записать так: r = xe + ye + ze = (x, y, z). Вектор, построенный из начальной точки движущегося тела в расположение её в данный момент времени, то есть приращение радиус-вектора за определённый промежуток t, как раз и называют перемещением.
Результирующее движение же равно векторной сумме последовательных изменений положения. При прямолинейном перемещении вектор пути совпадает с соответствующим участком траектории, а модуль перестановки равняется пройденному расстоянию.
Время, за которое тело пройдёт по установленной траектории пути, называют скоростью. Фактически это быстрота изменения координаты. Физики, исследуя передвижение, изучают не только положение материальной точки в начальный и конечный момент времени, но и закон, по которому происходит перемещение. Другими словами, они определяют зависимость радиус-вектора от времени.
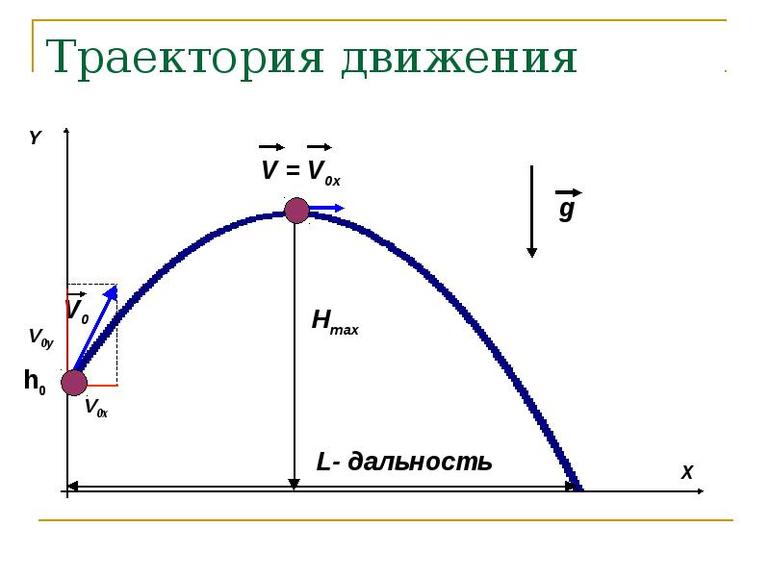
Горизонтальное перемещение
Пусть имеется тело, брошенное горизонтально поверхности. Высота падения равняется h, а начальная скорость V0. Здесь систему отсчёта удобно связать с Землёй. Объект будет передвигаться под действием силы тяжести. Остальными силами, например, сопротивлением воздуха, можно пренебречь. Тело перемещается в плоскости, содержащей вектора ускорения и свободного падения (g).
Таким образом, система начальных условий будет выглядеть так: x (t = 0) = 0; y (t = 0) = 0; v0x = v0; voy = 0. Вектор ускорения постоянный, поэтому a = g. Если тело представить как совокупность материальных точек, движущихся по одинаковому пути, то путь можно определить как сумму перемещений по прямым. Уравнение скорости примет вид: v (t) = v0 + gt. Об изменении положения можно сказать, что оно выполняется с постоянной скоростью и ускорением в горизонтальной плоскости, являясь равномерным. Значит, проекцию на оси ординаты и абсциссы можно записать как vx = v0; vy = -gt.

Скорость перемещения рассчитывают по формуле: V = √(V 2 x + V2 y). После подстановки полученных ранее выражений равенство примет вид: V = √(V 2 0 + g 2 t 2). Отсюда следует, что уравнение для вектора движения материальной точки будет: s (t) = s0 + V0t + (g t 2) / 2, где: s0 — смещение тела, соответствующее начальному моменту времени.
Так как s0 = y (t = 0) = h0, то скалярные выражения для координат изменяющей положение частицы можно представить в виде системы: x = V0t; y = h0 — (gt2 / 2). Перемещение происходит по прямой как отдельное движение в двух плоскостях, при этом из формулы следует, что изменение положения будет соответствовать правой половине направленной вниз параболы. Учитывая то, что время можно определить из отношения икса к начальной скорости (t = x /V0), можно записать окончательную формулу для вычисления траектории движения тела: y = h0 — (gx2) / (22V0) .
Можно сделать вывод, что уравнение траектории не записывается через время, поэтому частица будет и перемещаться обратно по той же самой траектории. Временные отрезки между точками пути будут одинаковы как при прямом, так и при обратном движении.
Каждому положению соответствует определённое значение скорости, которое не зависит от направления перемещения. Нужно отметить, что наибольшей величиной в горизонтальной траектории полёта будет начальная точка.
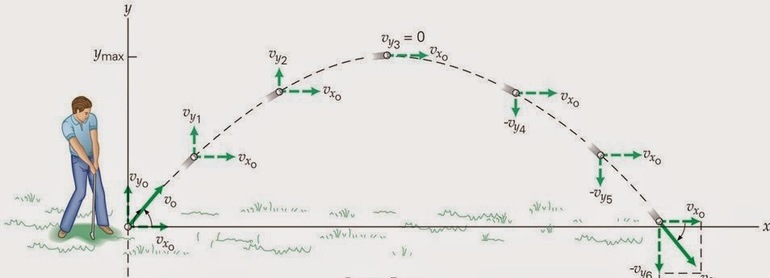
Движение тела под углом
Свободное падение является частным случаем равноускоренного, то есть на перемещаемый объект действует только сила притяжения. Если физическая точка перемещается, то кривая, которая описывается её радиус-вектором, обозначает пройденный путь. Эту траекторию можно описать некоторой математической функцией.
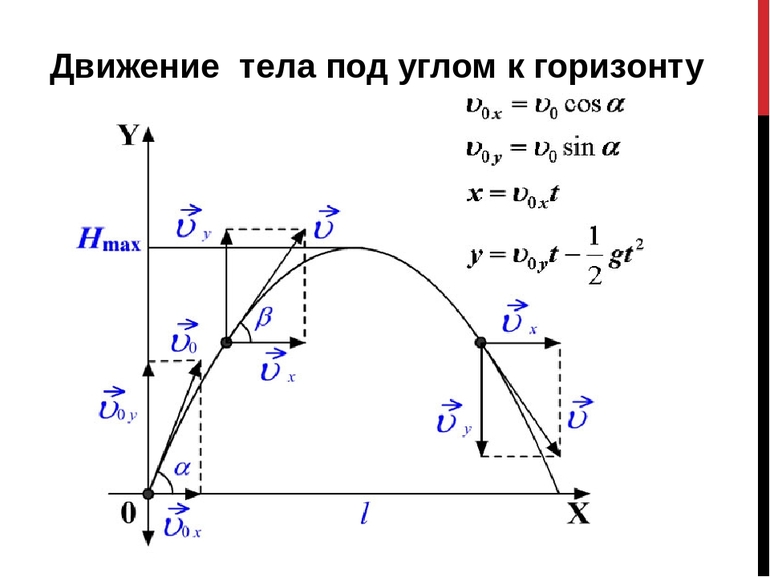
Итак, вектор скорости точки определяется как производная по времени: V = dr / dt = r. Ускорение же можно найти, продифференцировав скорость: a = dV / dt = d 2 r / dt. Если обозначить производную времени точкой, то формулу можно переписать так: a = V = r.
Для того чтобы вывести формулу, нужно воспользоваться основными выражениями, определяющими проекции:
- ускорения: ax = 0, ay = – g, az = 0;
- радиус-вектора: rx (t) = V0 * cosat, ry (t) = v * sin (at — (g * t2)/2)), rz (t) = 0;
- скорости: vx (t) = V0 * cosa, vy (t) = V0 * sin (a — gt), vz (t) = 0.
Чтобы запись зависимости вертикальной оси от горизонтальной была как можно более компактной, соответствующие координаты rx и ry можно обозначить через икс и игрек. Из уравнения, связывающего координатную ось X и время, можно определить t как функцию ординаты. Линейное выражение будет иметь вид: t = x / (Vo * cosa).
Если полученную формулу для времени подставить в уравнение для игрек координаты, то вместо временного параметра появится икс. То есть можно будет вывести зависимость абсциссы от ординаты: y = V 0 * sinat — (g * t2) / 2 = (tga) * x — (g / 2 * V0 * cos2a) * x2. Значение t нужно подставить в каждое слагаемое, но при этом учесть, что отношение синуса к косинусу называют тангенсом. Альфа в формуле — это угол между направлением начальной скорости и горизонтальным направлением (угол броска). После исключения времени из этих уравнений получим уравнение траектории.
В итоге останется два слагаемых. Первое будет линейно по иксу, а второе квадратично. Таким образом, зависимость игрека от икса в уравнении траектории — это парабола (справа стоит квадратичная функция). Она проходит через начало координат. Если верно равенство x = 0, то игрек тоже будет равняться нулю.
Следует обратить внимание на то, что в квадрате стоит отрицательный коэффициент. Известно, что если перед квадратичным слагаемым в уравнении параболы стоит отрицательное число, то концы кривой будут направлены вниз.
Решение задач
Решение практических заданий лучше всего помогает закрепить полученные знания. Существуют физические сборники, которые интересны тем, что включают в себя различные примеры, приближенные к реалистичным задачам. Прорешивая их самостоятельно, ученик не только лучше разберётся в теме, но и научится применять полученные знания на практике.
Вот два таких задания:

- Пусть имеется тело, движение которого описывается равенствами: x = Vx * t; y = y0 + Vy * t. Нужно определить траекторию его перемещения, учитывая, что Vx = 20 см/с, Vy = 2 м/с, Yo = 0,2 м. Для решения задачи нужно записать систему, определяемую исходными данными. Затем из первого равенства выразить время: t = x / Vx. Полученную формулу можно подставить в выражение нахождения координат абсциссы: y = y0 + (Vy * x) / Vx. Если теперь использовать исходные данные, то уравнение, описывающее траекторию, примет вид: y = 0.2 + 4x. Равенство напоминает собой формулу прямой: y = k * x + b. Исходя из этого можно утверждать, что траектория пути также будет представлять собой прямую линию. Действительно, в этом можно убедиться, если построить график движения. Для этого нужно взять несколько произвольных значений для икса, подставить их в формулу и найти вторую координату.
- Следующая задача довольно интересная. Нужно составить траекторию движения для тела, движущегося равномерно со скоростью два метра в секунду, при отклонении пути от оси икс на 60 градусов. За начало координат нужно принять точку (0, 0). Тогда начальный радиус-вектор тоже будет равен нулю: R = 0. Для успешного решения примера понадобится вспомнить скалярные уравнения для проекции при равномерном движении. Так как по условию вектор задан, то можно найти его проекцию на ось игрек: Vx = v * cos60 = 1; Vy = v * cos30 = √3. Отсюда: x = Vx * t = t; y = Vy * t = √3t.
Таким образом, чтобы успешно решать задачи, нужно знать несколько основных формул для определения местоположения тела, а также то, как выглядят уравнения параболы и прямой.
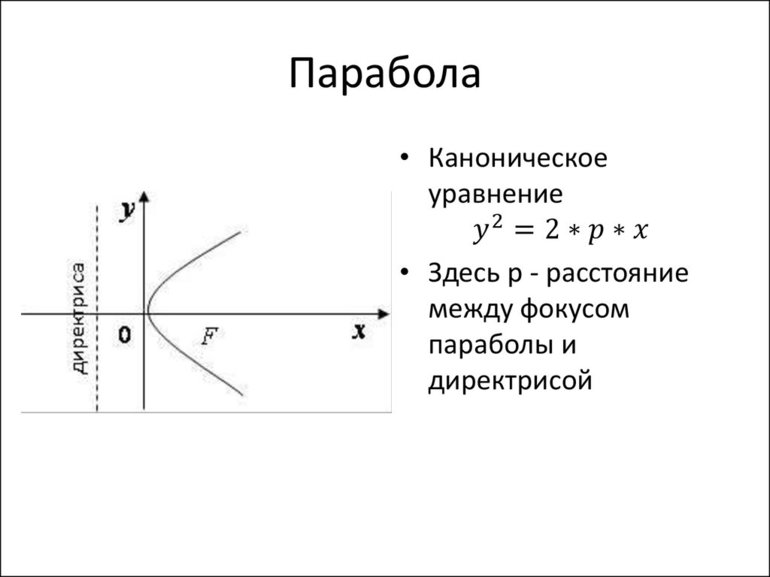
Стоит отметить, что существующие онлайн-калькуляторы не умеют вычислять формулы, описывающие траекторию пути. Но вместе с тем их можно использовать для выполнения расчётов или как справочники.

Траектории трёх объектов (угол запуска — 70°, Distance — расстояние, Height — высота), разное лобовое сопротивление
Траекто́рия материа́льной то́чки — линия в пространстве, являющаяся множеством геометрических точек, где можно найти материальную точку, в физической задаче[1]. Вид траектории свободной материальной точки зависит от действующих на точку сил, начальных условий движения и от выбора системы отсчёта, а несвободной — также от наложенных связей[2].
Понятие о траектории имеет смысл и в отрыве от какого-либо реального движения. Но траектория, изображаемая в некоторой системе координат, сама по себе не даёт информации о причинах движения тела по ней, пока не выполнен анализ конфигурации поля действующих на тело сил в той же координатной системе[3].
Способы задания траектории[править | править код]
Вид траектории не зависит от особенностей её прохождения материальной точкой, поэтому для задания траектории могут применяться не физические законы или модели, а средства дифференциальной геометрии.
Так, траектория иногда задаётся функцией/функциями, связывающ-ей/-ими координаты на линии движения точки:
в случае движения по прямой,
для плоского случая,
и
в объёмном случае.
Но здесь необходимы взаимная однозначность связи координат и отсутствие повторного прохождения материальной точкой каких-либо участков. Например, если тело двигалось по отрезку от 

В общем случае движение материальной точки в кинематике описывается зависимостью радиус-вектора от времени:
.
Такая зависимость представляет траекторию, давая избыток информации — кроме формы прочерчиваемой точкой геометрической линии, имея 

,
где 










В выбранной системе отсчета, кривая, описываемая концом радиус-вектора в пространстве, может быть представлена в виде сопряжённых дуг различной кривизны, находящихся в общем случае в пересекающихся плоскостях. При этом кривизна каждой дуги определяется её радиусом кривизны (не путать с радиус-вектором 
Траектория и смежные понятия[править | править код]
,
- где цифры 1 и 2 маркируют начальное и конечное положения точки, соответственно;
- Перемещение — вектор из начального положения точки в конечное
,
- при этом всегда
;
- Радиус кривизны — радиус дуги окружности, наилучшим образом аппроксимирующей траекторию в заданной точке.
Скорость материальной точки всегда направлена по касательной к дуге, используемой для описания траектории. При этом существует связь между величиной скорости 


.
Не всякое движение с известной скоростью по кривой известного радиуса и найденное по приведённой выше формуле нормальное (центростремительное) ускорение связано с проявлением силы, направленной по нормали к траектории (центростремительной силы). Так, найденное по данным фотографии суточного движения светил ускорение любой из звёзд отнюдь не говорит о существовании вызывающей это ускорение силы, притягивающей её к Полярной звезде как центру вращения.
Траектория и уравнения динамики[править | править код]
Представление траектории как следа, оставляемого движением материальной точки, связывает чисто кинематическое понятие о траектории, как геометрической проблеме, с динамикой движения материальной точки, то есть проблемой определения причин её движения. Фактически, решение уравнений Ньютона (при наличии полного набора исходных данных) даёт траекторию материальной точки.
Движение свободной материальной точки[править | править код]
В соответствии с первым законом Ньютона, иногда называемым законом инерции, должна существовать такая система, в которой свободное тело сохраняет (как вектор) свою скорость. Такая система отсчёта называется инерциальной. Траекторией такого движения является прямая линия, а само движение называется равномерным и прямолинейным.
Движение под действием внешних сил[править | править код]
- в инерциальной системе отсчёта
Если в инерциальной системе скорость 



,
где 


В общем случае тело не бывает свободно в своём движении, и на его положение, а в некоторых случаях и на скорость, налагаются ограничения — связи. Если связи накладывают ограничения только на координаты тела, то такие связи называются геометрическими. Если же они распространяются и на скорости, то они называются кинематическими. Если уравнение связи может быть проинтегрировано во времени, то такая связь называется голономной.
Действие связей на систему движущихся тел описывается силами, называемыми реакциями связей. В таком случае сила, входящая в левую часть выражения закона Ньютона, есть векторная сумма активных (внешних) сил и реакции связей.
Существенно, что в случае голономных связей становится возможным описать движение механических систем в обобщённых координатах, входящих в уравнения Лагранжа. Число этих уравнений зависит лишь от числа степеней свободы системы и не зависит от количества входящих в систему тел, положение которых необходимо определять для полного описания движения.
Если же связи, действующие в системе идеальны, то есть в них не происходит переход энергии движения в другие виды энергии, то при решении уравнений Лагранжа автоматически исключаются все неизвестные реакции связей.
Наконец, если действующие силы принадлежат к классу потенциальных, то при соответствующем обобщении понятий становится возможным использования уравнений Лагранжа не только в механике, но и других областях физики.[5]
Действующие на материальную точку силы в этом понимании однозначно определяют форму траектории её движения (при известных начальных условиях). Обратное утверждение в общем случае несправедливо, поскольку одна и та же траектория может иметь место при различных комбинациях активных сил и реакций связи.
- в неинерциальной системе отсчёта
Если система отсчёта неинерциальна (то есть движется с неким ускорением относительно инерциальной системы отсчёта), то в ней также возможно использование закона Ньютона, однако в левой части необходимо учесть так называемые силы инерции (в том числе, центробежную силу и силу Кориолиса, связанные с вращением неинерциальной системы отсчёта)[4].
Значимость выбора системы отсчёта[править | править код]

Суточное движение светил в системе отсчёта, связанной с фотоаппаратом в проекции на плоскость рисунка
Уточнение о «привязке» траектории к выбору координатной системы принципиально, так как форма траектории зависит от этого выбора[6]. Качественные и количественные различия траекторий возникают и между инерциальными системами, и если одна или обе системы неинерциальны.
Наблюдаемость траектории[править | править код]
Возможно наблюдение траектории при неподвижности объекта, но при движении системы отсчёта. Так, звёздное небо может послужить хорошей моделью инерциальной и неподвижной системы отсчёта. Однако при длительной экспозиции эти звёзды представляются движущимися по круговым траекториям.
Возможен и противоположный случай, когда тело явно движется, но траектория в проекции на плоскость наблюдения является одной неподвижной точкой. Это, например, случай летящей прямо в глаз наблюдателя пули или уходящего от него поезда.
Модификация формы траектории[править | править код]

Прямолинейное равномерно ускоряющееся движение в одной инерциальной системе в общем случае будет параболическим в другой равномерно двигающейся инерциальной системе отсчёта.
Нередко оказывается, что форма траектории зависит от системы отсчёта, избранной для описания движения материальной точки радикальным образом. Так, прямолинейное равноускоренное движение (скажем, свободое падение) в одной инерциальной системе в общем случае будет параболическим в другой равномерно двигающейся инерциальной системе отсчёта (см. рис.).
В соответствии с принципом относительности Галилея, существует бесконечное множество равноправных инерциальных систем (ИСО), движение которых одна относительно другой не может быть установлено никаким образом путём наблюдения любых процессов и явлений, происходящих только в этих системах. Прямая траектория равномерного движения объекта в одной системе будет выглядеть также прямой в любой другой инерциальной системе, хотя величина и направление скорости будут зависеть от выбора системы, то есть от величины и направления их относительной скорости.
Вместе с тем Принцип Галилея не утверждает, что одно и то же явление, наблюдаемое из двух разных ИСО, будут выглядеть одинаково. Поэтому рисунок предупреждает о двух типичных ошибках, связанных с забвением того, что:
1. Истинно, что любой вектор (в том числе вектор силы) может быть разложен по крайней мере на две составляющие. Но это разложение совершенно произвольно и не значит, что такие компоненты существуют в действительности. Для подтверждения их реальности должна привлекаться дополнительная информация, в любом случае не взятая из анализа формы траектории. Например, по рисунку 2 невозможно определить природу силы F, так же как невозможно утверждать, что она сама является или не является суммой сил разной природы. Можно лишь утверждать, что на изображённом участке она постоянна, и что для формирования наблюдаемой в данной СО криволинейности траектории служит вполне определённая в данной СО центростремительная часть этой силы. Зная лишь траекторию материальной точки в какой-либо инерциальной системе отсчёта и её скорость в каждый момент времени, нельзя определить природу сил, действовавших на неё.
2. Даже в случае наблюдения из ИСО, форма траектории ускоренно движущегося тела будет определяться не только действующими на него силами, но и выбором этой ИСО, никак на эти силы не влияющим. Центростремительная сила, показанная на рисунке 2, получена формально, и её величина непосредственно зависит от выбора ИСО.
Пример для вращающейся системы[править | править код]

Траектории одного и того же движения в неподвижной и вращающейся системах отсчёта. Вверху в инерциальной системе видно, что тело двигается по прямой. Внизу в неинерциальной видно, что тело повернуло в сторону от наблюдателя по кривой.
Представим себе работника театра, передвигающегося в колосниковом пространстве над сценой по отношению к зданию театра равномерно и прямолинейно и несущего над вращающейся сценой дырявое ведро с краской. Он будет оставлять на ней след от падающей краски в форме раскручивающейся спирали (если движется от центра вращения сцены) и закручивающейся — в противоположном случае. В это время его коллега, отвечающий за чистоту вращающейся сцены и на ней находящийся, будет поэтому вынужден нести под первым недырявое ведро, постоянно находясь под первым. И его движение по отношению к зданию также будет равномерным и прямолинейным, хотя по отношению к сцене, которая является неинерциальной системой, его движение будет искривлённым и неравномерным . Более того, для того, чтобы противодействовать сносу в направлении вращения, он должен мышечным усилием преодолевать действие силы Кориолиса, которое не испытывает его верхний коллега над сценой, хотя траектории обоих в инерциальной системе здания театра будут представлять прямые линии.
Но можно себе представить, что задачей рассматривающихся здесь коллег является именно нанесение прямой линии на вращающейся сцене. В этом случае нижний должен потребовать от верхнего движения по кривой, являющейся зеркальным отражением следа от ранее пролитой краски,оставаясь при этом над любой точкой прямой, проходящей в избранном радиальном направлении. Следовательно, прямолинейное движение в неинерциальной системе отсчёта не будет являться таковым для наблюдателя в инерциальной системе.
Более того, равномерное движение тела в одной системе, может быть неравномерным в другой. Так, две капли краски, упавшие в разные моменты времени из дырявого ведра, как в собственной системе отсчёта, так и в системе неподвижного по отношению к зданию нижнего коллеги (на уже прекратившей вращение сцене), будут двигаться по прямой (к центру Земли). Различие будет заключаться в том, что для нижнего наблюдателя это движение будет ускоренным, а для верхнего его коллеги, если он, оступившись, будет падать, двигаясь вместе с любой из капель, расстояние между каплями будет увеличиваться пропорционально первой степени времени, то есть взаимное движение капель и их наблюдателя в его ускоренной системе координат будет равномерным со скоростью 


Поэтому форма траектории и скорость движения по ней тела, рассматриваемая в некоторой системе отсчёта, о которой заранее ничего не известно, не даёт однозначного представления о силах, действующих на тело. Решить вопрос о том, является ли эта система в достаточной степени инерциальной, можно лишь на основе анализа причин возникновения действующих сил.
Таким образом, в неинерциальной системе, во-первых, кривизна траектории и/или непостоянство скорости являются недостаточным аргументом в пользу утверждения о том, что на движущееся по ней тело действуют внешние силы, которые в конечном случае могут быть объяснены гравитационными или электромагнитными полями, а во-вторых, прямолинейность траектории является недостаточным аргументом в пользу утверждения о том, что на движущееся по ней тело не действуют никакие силы.
Бестраекторное движение[править | править код]
Согласно квантовомеханическим представлениям, в отношении движения микрочастицы (электрона или другой) в ограниченном пространстве следует говорить не о траектории 




См. также[править | править код]
- Сложное движение
Примечания[править | править код]
- ↑ Понятие траектории достаточно наглядно может быть проиллюстрировано трассой бобслея (если по условиям задачи можно пренебречь её шириной). И именно трассой, а не самим бобом.
- ↑ Физический энциклопедический словарь, статья Траектория, стр. 764 / гл. ред. А. М. Прохоров — М.: Советская энциклопедия (1984).
- ↑ Так улица, в начале которой висит знак «кирпич» останется в принципе траекторией движения по ней. А поезда разной массы, движущиеся под различными тяговыми усилиями на сцепных крюках локомотивов и потому с разной скоростью, будут двигаться по одной и той же траектории, определяемой формой рельсового пути, налагающего на движение несвободного тела (поезда) конкретные связи, интенсивность которых будет в каждом случае различной
- ↑ 1 2 С. Э. Хайкин. Силы инерции и невесомость. М., 1967 г. Изд-во «Наука». Главная редакция физико-математической литературы.
- ↑ Физический энциклопедический словарь/ Гл. ред. А. М. Прохоров. Ред.кол. Д. М. Алексеев, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др. М.: Сов.энциклопедия, 1983. — 323 с.,ил, 2 л.цв.ил. страница 282.
- ↑ Так, Луна обращается вокруг Земли только в системе отсчёта, связанной с их общим центром гравитации (находится внутри Земного шар). В системе же отсчёта, началом которой является Солнце, Луна обращается вокруг него по той же эллиптической орбите, что и Земля, но с периодическими отклонениями от неё на величину расстояния от Луны до Земли. Никакого взаимного обращения этих небесных тел в этом случае просто нет.
Наличие земного притяжения для объяснения формы траектории Луны в системе координат, связанной с Солнцем, вообще не обязательно. Так, исчезни Земля, Луна могла бы продолжать двигаться, как самостоятельное небесное тело, по той же самой старой траектории, а её периодические возмущения можно было бы тогда в качестве гипотезы объяснить изменением силы тяготения, скажем, за счёт вариации массы Солнца по причине пульсации его светимости (что, кстати, и наблюдается в определённых пределах в действительности).
И обе упомянутые формы траектории истинны и оба объяснения их формы на основании правильно проведённого анализа действующих сил справедливы. Но они исключают друг друга, как исключается возможность одновременного рассмотрения при выборе той или иной системы координат.
- ↑ ВОЛНОВА́Я ФУ́НКЦИЯ : [арх. 10 августа 2022] / Д. В. Гальцов // Великий князь — Восходящий узел орбиты. — М. : Большая российская энциклопедия, 2006. — С. 641-642. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 5). — ISBN 5-85270-334-6.
В физике есть ещё одна формула измерения траектории (пути): s=4Atv, где A – амплитуда, t – время, v – частота колебаний
Литература[править | править код]
- Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
- Фриш С. А. и Тиморева А. В. Курс общей физики, Учебник для физико-математических и физико-технических факультетов государственных университетов, Том I. М.: ГИТТЛ, 1957
Ссылки[править | править код]
- Траектория и вектор перемещения, раздел учебника по физике[неавторитетный источник]
Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.
Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.
Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.
Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.
Путь
Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.
Вектор перемещения
Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.
Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.
Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).
Рис. 1.1. Вектор перемещения и пройденный путь.
На рис. 1.1:
![]()
Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.
Правило сложения векторов
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).
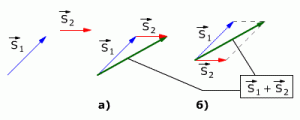
Рис. 1.2. Сложение векторов перемещений.
На рис 1.2 показаны правила сложения векторов S1 и S2:
а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма
Проекции вектора перемещения
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения ![]() (см.рис. 1.3).
(см.рис. 1.3).
Выберем ось ОХ так, чтобы вектор ![]() лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно Аx и Вx. Длина отрезка АxВx на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть
лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно Аx и Вx. Длина отрезка АxВx на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть
Sx = AxBx
ВАЖНО!
Напоминаю для тех, кто не очень хорошо знает математику: не путайте вектор ![]() с проекцией вектора на какую-либо ось (например, Sx). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.
с проекцией вектора на какую-либо ось (например, Sx). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.
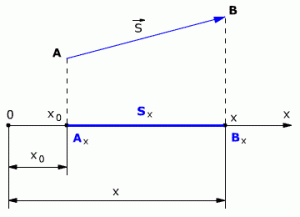
Рис. 1.3. Проекция вектора перемещения.
Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть
Sx = x – x0
Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:
Sy = y – y0 Sz = z – z0
Здесь x0, y0, z0 — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).
Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).
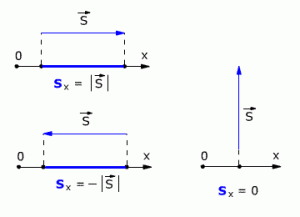
Рис. 1.4. Модули проекции вектора перемещения.
Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х0 и у0, то есть А(х0, у0). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.
Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).
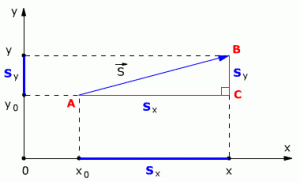
Рис. 1.5. Движение тела на плоскости.
Определим проекции вектора перемещения на осях ОХ и OY:
Sx = x – x0 Sy = y – y0
На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как
АС = sx CB = sy
По теореме Пифагора
S2 = Sx2 + Sy2
Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:
![]()
Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.
