Как найти траекторию пули

Внешняя
баллистика – это наука, изучающая
движение пули в воздухе (т.е. после
прекращения действия на нее пороховых
газов).

Вылетев из канала
ствола под действием пороховых газов,
пуля движется по инерции. Для того чтобы
определить, как же движется пуля
необходимо рассматривать траекторию
ее движения. Траекторией
называется кривая линия, описываемая
центром тяжести пули во время полета.

Пуля при полете в
воздухе подвергается действиям двух
сил: силы тяжести и силы сопротивления
воздуха. Сила тяжести заставляет
постепенно понижаться, а сила сопротивления
воздуха непрерывно замедляет движение
пули и стремится опрокинуть ее. В
результате действия этих сил скорость
полета пули постепенно уменьшается,
а ее траектория представляет собой по
форме неравномерно изогнутую кривую.

Сопротивление
воздуха полету пули вызывается тем, что
воздух представляет собой упругую
среду, поэтому в этой среде затрачивается
часть энергии пули,
что вызывается тремя основными причинами:

• трением воздуха;

• образованием
  завихрений;

• образованием
  баллистической волны.

Равнодействующая
этих сил составляет силу сопротивления
воздуха.

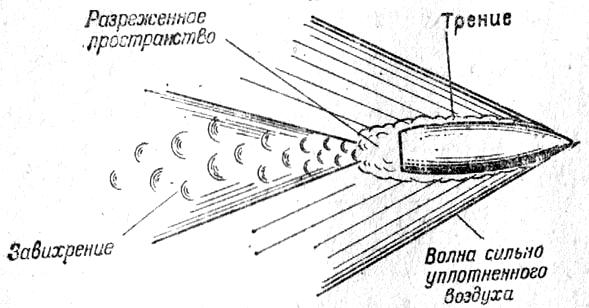
Рис. 2.
Образование
силы сопротивления воздуха.

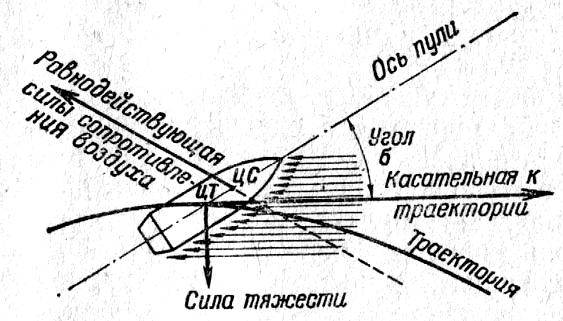
Рис. 3.
Действие
силы сопротивления воздуха на полет
пули:

ЦТ – центр тяжести;
ЦС – центр сопротивления воздуха.

Частицы воздуха,
соприкасающиеся с движущейся пулей
создают трение и уменьшают скорость
полета пули. Примыкающий к поверхности
пули слой воздуха, в котором движение
частиц изменяется в зависимости от
скорости называется пограничным слоем.
Этот слой воздуха, обтекая пулю, отрывается
от ее поверхности и не успевает сразу
же сомкнуться за донной частью.

За донной частью
пули образуется разряженное пространство,
вследствие чего появляется разность
давления на головную и донную части.
Эта разность создает силу, направленную
в сторону обратную движению пули, и
уменьшающую скорость ее полета. Частицы
воздуха, стремясь заполнить разрежение,
образовавшееся за пулей, создают
завихрение.

Пуля при полете
сталкивается с частицами воздуха и
заставляет их колебаться. Вследствие
этого перед пулей повышается плотность
воздуха и образуется звуковая волна.
Поэтому полет пули сопровождается
характерным звуком. При скорости полета
пули, меньшей скорости звука, образование
этих волн оказывает незначительное
влияние на ее полет, т.к. волны
распространяются быстрее скорости
полета пули. При скорости полета пули,
большей скорости звука, от набегания
звуковых волн друг на друга создается
волна сильно уплотненного воздуха
–
баллистическая волна, замедляющая
скорость полета пули, т.к. пуля тратит
часть своей энергии на создание этой
волны.

Действие силы
сопротивления воздуха на полет пули
очень велико: оно вызывает уменьшение
скорости и дальности полета. Например,
пуля при начальной скорости
800 м/с в
безвоздушном пространстве полетела бы
на дальность
32620 м;
дальность же полета этой пули при наличии
сопротивления воздуха равна лишь
3900 м.

Величина силы
сопротивления воздуха в основном зависит
от:

• скорости полета
  пули;

• формы и калибра
  пули;

• от поверхности
  пули;

• плотности воздуха

и возрастает с
увеличением скорости полета пули, ее
калибра и плотности воздуха.

При сверхзвуковых
скоростях полета пули, когда основной
причиной сопротивления воздуха является
образование уплотнения воздуха перед
головной частью (баллистической волны)
выгодны пули с удлиненной остроконечной
головной частью.

Таким образом,
сила сопротивления воздуха уменьшает
скорость движения пули и опрокидывает
её. В результате этого пуля начинает
«кувыркаться», возрастает сила
сопротивления воздуха, уменьшается
дальность полета и понижается её действие
по цели.

Стабилизация пули
в полете обеспечивается приданием пуле
быстрого вращательного движения вокруг
своей оси, а также – хвостовым оперением
гранаты. Скорость вращения при вылете
из нарезного оружия составляет: пуль
3000-3500 об/с, проворачивание оперенных
гранат 10-15 об/с. Вследствие вращательного
движения пули, воздействия силы
сопротивления воздуха и силы тяжести
происходит отклонение пули в правую
сторону от вертикальной плоскости,
проведенной через ось канала ствола, –
плоскости
стрельбы.
Отклонение пули от нее при полете в
сторону вращения называется деривацией.

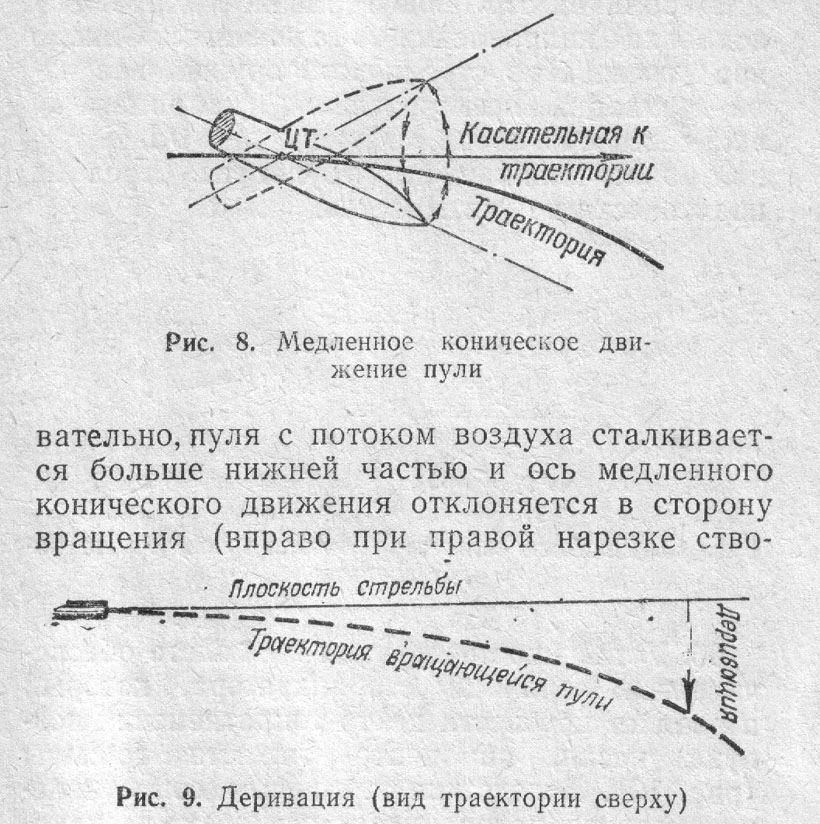
Рис. 4. Деривация
(вид траектории сверху).

В результате
действия этих сил пуля совершает полет
в пространстве по неравномерно изогнутой
кривой линии, называемой траекторией.

Продолжим
рассмотрение элементов и определений
траектории пули.

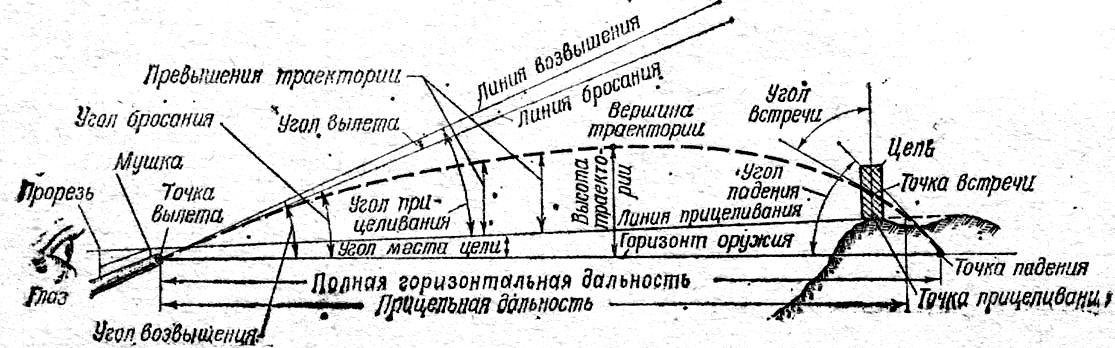
Рис. 5. Элементы
траектории.

Центр дульного
среза ствола называется точкой
вылета. Точка
вылета является началом траектории.

Горизонтальная
плоскость проходящая через точку вылета
называется горизонтом
оружия. На
чертежах, изображающих оружие и траекторию
сбоку, горизонт оружия имеет вид
горизонтальной линии. Траектория дважды
пересекает горизонт оружия: в точке
вылета и в точке падения.

Прямая линия,
являющаяся продолжением оси канала
ствола наведенного
оружия,
называется
линией возвышения.

Вертикальная
плоскость, проходящая через линию
возвышения называется
плоскостью стрельбы.

Угол, заключенный
между линией возвышения и горизонтом
оружия называется
углом возвышения.
Если этот угол отрицательный, то он
называется
углом склонения (снижения).

Прямая линия,
являющаяся продолжением оси канала
ствола в
момент вылета пули,
называется линией
бросания.

Угол, заключенный
между линией бросания и горизонтом
оружия, называется углом
бросания.

Угол, заключенный
между линией возвышения и линией
бросания, называется углом
вылета.

Точка пересечения
траектории с горизонтом оружия называется
точкой падения.

Угол, заключенный
между касательной к траектории в точке
падения и горизонтом оружия называется
углом падения.

Расстояние от
точки вылета до точки падения называется
полной
горизонтальной дальностью.

Скорость пули в
точке падения называется
окончательной скоростью.

Время движения
пули от точки вылета до точки падения
называется полным
временем полета.

Наивысшая точка
траектории называется
вершиной траектории.

Кратчайшее
расстояние от вершины траектории до
горизонта оружия называется
высотой траектории.

Часть траектории
от точки вылета до вершины называется
восходящей ветвью,
часть траектории от вершины до точки
падения называется нисходящей
ветвью траектории.

Точка на цели (или
вне её),
в которую наводится оружие, называется
точкой
прицеливания (ТП).

Прямая линия от
глаза стрелка до точки прицеливания
называется линией
прицеливания.

Расстояние от
точки вылета до пересечения траектории
с линией прицеливания, называется
прицельной дальностью.

Угол, заключенный
между линией возвышения и линией
прицеливания, называется
углом прицеливания.

Угол, заключенный
между линией прицеливания и горизонтом
оружия называется
углом места цели.

Прямая, соединяющая
точку вылета с целью, называется линией
цели.

Расстояние от
точки вылета до цели по линии цели
называется наклонной
дальностью.
При стрельбе
прямой наводкой линия цели практически
совпадает с линией прицеливания, а
наклонная дальность – с прицельной
дальностью.

Точка пересечения
траектории с поверхностью цели (земли,
преграды) называется точкой
встречи.

Угол, заключенный
между касательной к траектории и
касательной к поверхности цели (земли,
преграды) в точке встречи, называется
углом встречи.

Форма траектории
зависит от величины угла возвышения.
С увеличением угла возвышения высота
траектории и полная горизонтальная
дальность полета пули увеличивается.
Но это происходит до известного предела.
За этим пределом высота траектории
продолжает увеличиваться,
а полная горизонтальная дальность
начинает уменьшаться.

Угол возвышения,
при котором полная горизонтальная
дальность полета пули становится
наибольшей, называется углом
наибольшей дальности
(величина этого угла составляет около
35°).

Различают настильные
и навесные траектории:

1. Настильной
   – называется траектория, получаемая
   при углах возвышения меньших угла
   наибольшей дальности.

2. Навесной
   –
   называется траектория, получаемая при
   углах возвышения больших угла наибольшей
   дальности.

Настильная и
навесная траектории, получаемые при
стрельбе из одного и того же оружия при
одной и той же начальной скорости и
имеющие одинаковую полную горизонтальную
дальность, называются – сопряжёнными.

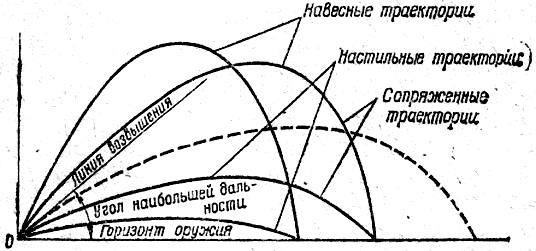
Рис. 6. Угол наибольшей
дальности,

настильные, навесные
и сопряжённые траектории.

Траектория более
настильна, если она меньше поднимается
над линией цели, и чем меньше угол
падения. Настильность траектории влияет
на величину дальности прямого выстрела,
а также на величину поражаемого и
мертвого пространства.

При стрельбе из
стрелкового оружия и гранатометов
используются только настильные
траектории. Чем настильнее траектория,
тем на большем протяжении местности
цель может быть поражена с одной
установкой прицела (тем меньшее влияние
на результаты стрельбы оказывает ошибка
в определении установки прицела): в этом
заключается практическое значение
траектории.

Прямой выстрел.
Поражаемое, прикрытое и мертвое
пространства

Прямой выстрел,
поражаемое, прикрытое и мертвое
пространства наиболее близко соприкасаются
с вопросами стрелковой практики.

Большинство целей
для танков, БМП, стрелкового оружия
имеют значительные размеры по высоте
и требуют для их поражения прямого
попадания. Получить прямое попадание
можно при прямом выстреле и в случае,
если траектория проходит через поражаемое
пространство цели. Настильность
траектории влияет на величину дальности
прямого выстрела.

При прямом
выстреле
траектория пули на всем своем протяжении
до цели не поднимается выше цели и не
опускается ниже ее основания. Он может
быть получен при различных установках
прицела, положениях цели (относительно
горизонта оружия) и точки прицеливания.

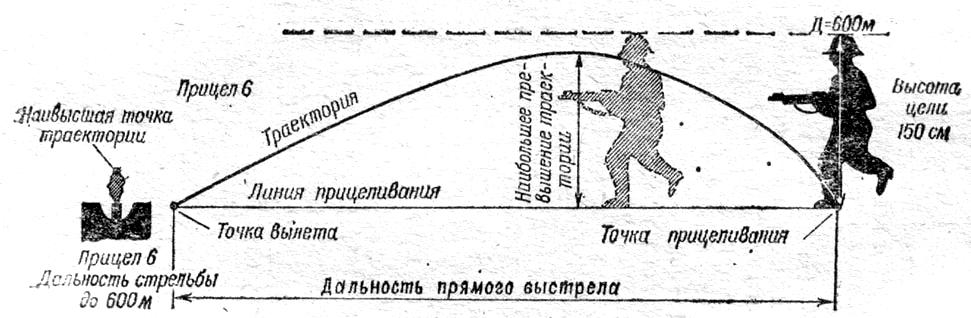
Рис. 7. Прямой
выстрел.

Если имеет место
прямой выстрел, то при правильном
направлении стрельбы пуля (траектория)
обязательно пройдет через цель и будет
получено прямое попадание.

Дальность прямого
выстрела – это такая дальность стрельбы,
при которой высота траектории равна
высоте цели.

Значение дальности
прямого выстрела состоит в том, что в
пределах этой дальности обеспечивается
высокая вероятность попадания в цель
с первого выстрела, а в случае промаха
при первом выстреле – возможность
попадания в нее при последующих выстрелах
с одной исходной установкой прицела.

В пределах дальности
прямого выстрела в напряженные моменты
боя стрельба может вестись без перестановки
прицела, при этом точка прицеливания
по высоте, как правило, выбирается на
нижнем краю цели.

Поражаемым
пространством
(глубиной
поражаемого пространства)
называется расстояние на местности, на
протяжении которого нисходящая ветвь
траектории не превышает высоты цели.

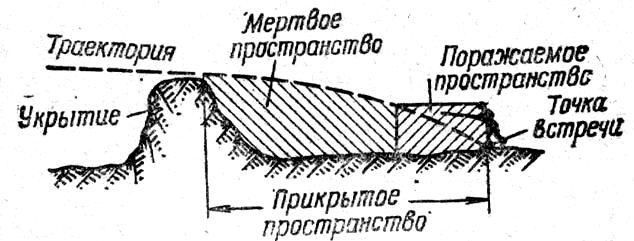
Рис. 8. Поражаемое,
прикрытое и мертвое пространства.

Глубина поражаемого
пространства зависит от:

• высоты
  цели (глубина будет тем больше, чем выше
  цель);

• настильности
  траектории (глубина будет тем больше,
  чем настильнее траектория);

• угла
  наклона местности (на переднем скате
  она уменьшается, на обратном скате
  увеличивается).

Пространство за
укрытием, не пробиваемым пулями, от его
гребня до точки встречи называется
прикрытым
пространством.

Часть прикрытого
пространства, на котором цель не может
быть поражена при данной траектории,
называется мертвым
пространством. Глубина
мертвого пространства равна разности
прикрытого и поражаемого пространства.

Таким образом,
необходимо отметить,
что движение пули представляет собой
сложный и динамичный процесс, требующий
тщательного изучения.

В отзывах к предыдущим выпускам нашего альманаха, товарищи отмечают, что, дескать, многовато теории и маловато Жизненных Примеров. Внемлю.

В сегодняшнем выпуске нашего альманаха мы узнаем всё, что нужно, и ещё немного, про высоту траектории пули. Для начала — теория, школьный курс физики за 7 класс, законы Ньютона, путь пройденный телом при постоянном ускорении.

D = g*t²/2

Пуля, летящая в цель, под действием силы притяжения земли с ускорением g, за время полёта t, снижается на расстояние D.
Сопротивлением воздуха можно пренебречь. Это уравнение в данном трактате появляется чисто из вредности, для собственно стрельбы его знать — совершенно лишнее.

Всё, конец теоретической части.

Практика, из этого следующая, однако, далеко не так проста, как может показаться поначалу.

Начнём с нестрашного, и поначалу дадим слово Капитану Очевидность. Если направить прицел туда же, куда и ствол, навести на цель, и выстрелить — пуля в цель не попадёт.

На самом деле ось прицела всегда находится под небольшим углом к оси ствола (на иллюстрации, для наглядности, угол преувеличен — в реальности он как правило не превышает 1º, и, естественно, задаётся не наклоном прицела как такового, а небольшим смещением проекции сетки внутри прицела).

Ноль прицела — дистанция, на которой траектория и линия прицеливания совпадают по высоте. Баллистические таблицы для разных дистанций приводят соответствующий угол прицеливания, который нужно ввести поправками прицела, чтобы перенести ноль на нужное нам расстояние. Нулей бывает два — ближний и дальний.

От знания первого, “ближнего” ноля практической пользы меньше, чем от дальнего. Пристрелка винтовки, к примеру, на 25 м, с ценой деления прицела 0.1 мрад, потребует определения средней точки попадания с точностью 1.25 мм, что на практике — мало реалистично. Ближний ноль иногда используется в армейских наставлениях для быстрой пристрелки, когда недоступно длинное стрельбище, или после установки нового прицела для “черновой” пристрелки (чтобы наверняка быть в мишени), при этом рекомендуется, при возможности, проверить и уточнить пристрелку во второй точке нуля траектории.

Для [второго, дальнего ноля] пристрелки как правило выбирается дистанция 100м. Как мы увидим в следующих выпусках нашего альманаха, влияние атмосферных условий на этом расстоянии ещё совсем невелико, но в то же время уже легко определить среднюю точу попадания с достаточной точностью.

До сих пор мы рассматривали прицел нормального человека. Рассмотрим прицел

курильщика

жирафа.

На иллюстрации выпукло выступает влияние высоты монтажа прицела на траекторию. Высота оси прицела по отношению к оси ствола — один из параметров, необходимых для просчёта траектории; не зная его, невозможно определить угол прицеливания, под которым (по отношению к линии прицеливания) пуля выходит из ствола. При одной и той же дистанции ноля траектории, чем выше над стволом установлен прицел — тем больше угол прицеливания.

Насколько важно знать точное расстояние между осью ствола и осью прицела, и как именно оно влияет на траекторию, проще всего будет объяснить на примере. Известный нам снайпер Гуня на днях прочёл в одной книге, что (а) ближнего нужно любить и (б) ближнего нужно любить как себя самого. Применив дедуктивный метод, Гуня решил, что прежде всего нужно раз в жизни как следует полюбить себя самого, разбил копилку, и купил к винтовке новый роскошный прицел. Линза объектива на новом прицеле оказалась больше, и новый прицел в старый монтаж не встал — упирался объективом в ствол. Пришлось сменить монтаж, отчего расстояние от оси прицела до оси ствола увеличилось с 52 до 62 мм.

Внимание, вопрос: что делать Гуне со старыми баллистическими таблицами, в составление и выверку которых вложено много времени и патронов.

Внимание, ответ: при пристрелке нового прицела на той же дистанции, что и старого, средняя точка попадания сместится ровно на разницу высоты линии прицеливания. В нашем случае, СТП будет выше на 1см. Поскольку Гуня сам себе не враг, барабанчики подстроек у него градуированы в миллирадианах. При цене клика 0.1 мрад, и пристрелке на 100м, разница угла прицеливания будет 1см на 100м = 1 клик. Итого: по сравнению со старым прицелом, на всех дистанциях нужно будет подстраивать на один клик меньше, чем прописано в старых баллистических таблицах (или после пристрелки открутить на один клик вниз, и использовать старые таблицы как есть) [1].

Дополнительный вывод: для измерения высоты прицела, вполне достаточно точности плюс-минус пара миллиметров — в пристрелке на 100м речь идёт о десятых долях клика.

Вопрос с баллистическими таблицами успешно разрешился, Гуня радовался дивному новому прицелу, как в последний раз радовался в детстве собственному велосипеду, но на этом дело не закончилось. Для комфортной вкладки с новой высотой монтажа, пришлось на приклад мастерить щёку. Проклиная собственную лень и невнимательность на давно забытых школьных уроках труда, Гуня утешал себя мыслью, цитирую, “зато теперь, с высоким прицелом, возрастёт дальность прямого выстрела (ДПВ)”, потому, что прочитал такое утверждение на каком-то форуме в Интернете.

Наглядный пример поможет нам понять как всё сложится с утешением, и о чём вообще речь. В часы досуга, снайпер Гуня охотится на Адских Телепузиков. Габаритный чертёж Адского Телепузика прилагается:

На охоте Гуня целится в середину цели — в Пузо. Дальность прямого выстрела определяется как дистанция, вплоть до которой высота траектории пули не выходит за габариты цели, без регулировки прицела[2]. Например, в случае старого доброго карабина K31 в калибре 7.5х55мм, пристрелянного на 100м, выглядит это так [3]:

Шкала — дистанция в метрах. Красная зона — габарит цели, т.е. плюс-минус 50 см траектории. Сплошная линия — траектория с высотой прицела 8 см. Пунктирная линия — траектория с высотой прицела 5 см. При очень серьёзной разнице высоты монтажа[4], разница в дальности прямого выстрела получается относительно скромная; 316-303=13 метров. Вывод: ДПВ в первую очередь определяется баллистикой калибра, высота прицельных роль играет сравнительно небольшую, и утешение Гуне выходит слабое.

Внимательный читатель отметит, что ДПВ зависит также от дистанции пристрелки. Как правило, когда говорят о ДПВ “вообще”, имеется в виду максимальная ДПВ, то есть с такой дистанцией пристрелки в ноль, при которой пик высоты траектории как раз соответствует верхней кромке мишени. В нашем случае такой ноль находится на 434 м, а прямой выстрел по метровой цели возможен аж до 511 м:

Естественно, ДПВ зависит и от размеров цели. По этой причине, к сравнительным цифрам “дальности прямого выстрела” из разных источников нужно относиться с осторожностью; в разных странах размеры стандартной мишени бывают разные. В большинстве случаев, стандартная мишень, соответствующая армейским реалиям, имеет в высоту от 40 до 60 см (“грудная фигура” из наставлений советской армии — 50 см). На этом принципе, ещё с конца 19в, основан так называемый “боевой ноль” оружия пехоты — положение прицела, обеспечивающее максимальную дальность прямого выстрела, которое используют когда нет возможности выставить точное значение прицела, соответствующее расстоянию до врага.

Исключительно в порядке добавления статье полемической ценности, рассмотрим походя “вечнозелёный” вопрос “АК против M16” с точки зрения ДПВ. АКМ стреляет патроном 57-Н-231, АК-74 заряжен 7Н6М, а M16 и М4 — SS109; Для “приведения к общему знаменателю”, во всех случаях используется высота прицела 7 см. Дистанция в метрах, высота траектории в сантиметрах.

Прицеливание по центру, высота цели 30 см:

На этой понятной картинке изображена траектория, соответствующая “боевому нулю” из наставления армии США (TM 9-1005-319-10, M16A2 / M4A1) — ноль на 300 м., до 350 метров — прямой выстрел по центру грудной клетки (30 см в высоту — зона, в которой примерно находятся жизненно-важные органы).

Прицеливание “под обрез” (по поясу), высота цели 50 см:

А на этой понятной картинке мы читаем наставления армии СССР для автоматов АКМ и АК-74 с секторным прицелом в положении “П” — “постоянный”. До ноля в 440 м для АК-74 (для АКМ — 350 м), при точке прицеливания на уровне пояса, прямой выстрел не выходит за габариты человеческого торса — 50 см в высоту.

Онтологические, политические и стрелковые выводы из приведённых графиков наверняка в изобилии сделают эксперты на Интернете. Мне же, при всём вышесказанном, остаётся пожелать, чтобы во всём Мире всегда царил Мир, все были друг к другу добры и отзывчивы, чтобы жадности-ненависти-злобности не было промеж людей, одним словом — чтобы конкретное знание “боевого ноля” оружия пехоты никому из нас никогда в жизни не понадобилось. При этом, в мирное время, понимание дистанции прямого выстрела может оказаться очень полезным для охотников. У охотника — гораздо более строгие рамки желаемого результата, нежели чем у пехотинца [5], но принципы остаются совершенно те же самые. Искомая зона попадания может быть совсем небольшой; вместо того, чтобы пристреливать прицел на 100м и в критический момент пытаться на глазок прикинуть расстояние и лихорадочно вспоминать высоту траектории, нужно, как в научно-фантастических утопиях 1960-х, где про светлое будущее, призвать на помощь роботов, чтобы те делали дурную работу, а человек же занимался исключительно полезными и важными делами.

Пример: опытный охотник Гуня опытным путём выясняет, что Адского Телепузика можно остановить только выстрелом в голову, 20 см в высоту. Гуня берёт на охоту верный ижевский карабин Тигор под аутентичный 7.62х54, высота прицела 8 см, барнаульский патрон HPBT с БК G1 = 0.530 [6], “смертельная зона” — 20 см. Скормив все эти знания хорошему баллистическому калькулятору, получаем максимальную ДПВ = 278м (с пристрелочным нулём на 238 м). Это значит, что до 278 метров дистанции о ней можно вообще не думать [7]. При этом, естественно, не обязательно замерять 238 метров для пристрелки, достаточно пристреляться на 100, и посмотреть в баллистическом калькуляторе сколько кликов нужно подкрутить (в нашем случае, например — 8 х 0.1 мрад) чтобы оказаться в нужном нуле.

Для сравнения, при обычной пристрелке на 100м, для цели высотой 20см, ДПВ была бы 197м; ценой нескольких кликов прицела покупается 278-197=81 метр беззаботности.

Некоторым, возможно 278 метров — достаточно, но Гуня, например, знает, что Адского Телепузика близко подпускать нельзя, не то сожрёт. Дальность прямого выстрела является частным случаем более общего понятия опасной зоны (ОЗ). При заданном ноле траектории, опасная зона — отрезок дистанций вокруг ноля, где траектория по высоте не выходит за габариты цели.

Например, для вышеупомянутого Тигора с барнаульским патроном [8], по цели высотой 20 см, на разных дистанциях стрельбы опасные зоны выглядят так:

На 200м — опасная зона, собственно, является прямым выстрелом; от нуля до 248м — мы в цели. На 400м траектория становится круче, ОЗ сужается до 420-377=43м. На 600м же — совсем строго, ОЗ=610-589=21м. Если на 400 м лазерный дальномер “зацепится” за куст в 15м от цели — ничего страшного, пуля недруга найдёт. На 600 же метров, с той же ошибкой определения дистанции, недруг только напугается (а потом отомстит!). К 1000м, для справки, диапазон “допустимой” ошибки в оценке дистанции для этого калибра сужается до ±4м (что, впрочем, далеко не самый существенный фактор, на фоне остальных трудностей попадания в цель 20 см на 1000 м из карабина Тигр).

Иными словами, вывод: чем больше дистанция стрельбы, тем точнее её нужно знать.

В мире лёгкого стрелкового оружия до изобретения компактных лазерных дальномеров определение точной дистанции стрельбы было искусством для посвящённых, требовавшим 30 лет медитации на вершине горы, ежедневных изнуряющих упражнений, и эзотерических ритуалов по вызову духа Людмилы Павличенко. Снайперские дистанции времён Великой Отечественной редко превышали 300-400 метров. С изобретением и распространением компактных лазерных дальномеров ситуация несравнимо улучшилась, но у дальномеров тоже есть свои ограничения (отражающие свойства поверхности и размеры цели, погодные условия, “засекаемость” в определённых диапазонах, etc.), к тому же, не всегда есть время дальномером воспользоваться. До сих пор вопрос точной дистанции до цели решён не до конца и не всегда убедительно.

Возможным ответом является избежание вопроса. По сей день одной из основных характеристик патрона является настильность траектории — чем настильнее, тем больше ОЗ, и тем меньше влияние ошибок в определении дистанции. Ни для чего другого настильность не нужна; если расстояние до цели точно известно, навесная траектория прекрасно справляется с задачей.

“Так за чем же дело стало”, — спросит внимательный читатель предыдущих выпусков нашего альманаха, — “взять пулю с высоким баллистическим коэффициентом, которая хорошо сохраняет скорость полёта, разогнать её как следует, и пожалуйста — настильность налицо.” На практике, однако, не всё так просто: требования “с высоким БК” и “разогнать её как следует” прямо друг другу противоречат. В рамках конкретного патрона, энергия ограничена максимальным давлением в гильзе на момент выстрела. При прочих равных, одна и та же энергия, сообщённая лёгкой пуле, задаст ей бо́льшую скорость, чем тяжёлой. Баллистический коэффициент, как мы помним из предыдущих выпусков — способность пули сохранять скорость вопреки сопротивлению воздуха — прямо пропорционален массе. Иными словами — чем тяжелее пуля, тем меньше она разгоняется, но зато потом меньше тормозится из-за сопротивления воздуха.

Для одного и того же калибра производители зачастую выпускают патроны с самыми разными пулями; уже по изобилию ассортимента можно догадаться, что каждая пуля — в чём-то компромисс, а универсального рецепта счастья не существует. Многие стрелки [9], однако, возводят высоту траектории в абсолют и религиозную догму, и примыкают к одной из двух враждующих сект — свидетели лёгкого-быстрого, и свидетели тяжёлого-медленного. В 2009 г., с изданием книги “Прикладная баллистика при стрельбе на дальние дистанции” Браяна Лица [10], религиозная война вспыхнула с новой силой. В своей книге гражданин Лиц сравнивает две абстрактные пули, немного в рекламном стиле (“а это — обычный стиральный порошок”), без упоминания конкретных моделей, веса, дульной скорости, etc., и приходит к выводу, что траектория тяжёлой пули с высоким БК становится настильнее лёгкой, начиная с 500-550 метров дистанции, что выглядит примерно так (высота траектории в сантиметрах, дистанция в метрах):

Настильность вблизи

и на средних и дальних дистанциях

В какой-то момент траектория тяжёлой пули становится настильнее лёгкой, и догоняет и перегоняет её по высоте, см. точку пересечения графиков.

Nota bene: здесь и далее сравниваются пули схожей конструкции и формы, иначе можно начать сравнивать самые разные более или менее аэродинамичные снаряды, и с одной и той же массой пули и дульной скоростью получить какие угодно результаты, доказывающие что попало куда ни попадя.

Справедливость заключений Лица в реальности поможет проверить наш виртуальный знакомый. Как-то раз, два товарища — снайпер Гуня и снайпер Кузя — собрались на охоту на Адского Телепузика. Взяли они совершенно одинаковые винтовки калибра .308 Winchester, и запаслись патронами Lapua Scenar, но разными. Гуня незадолго до того прочёл “Прикладную баллистику”, стал Большим Энтузиастом Большого БК, и выбрал 185 гран / 12 г, БК G7 = 0.242, 755 м/с дульной скорости. Кузя, давно стреляющий 167-грановым Сценаром, решил не менять привычек: 10.85 г., БК G7 = 0.219, 820 м/с дульной.

И вот что получилось (шкала — дистанция в метрах, график — высота траектории):

Как и ожидалось, на ближних дистанциях более лёгкая пуля обладает более настильной траекторией.

…но и на дальних дистанциях тоже. Гуня несколько раз перепроверил цифры; обещанного в книге пересечения высоты траекторий на средних дистанциях не наблюдалось. Более того, опасная зона для лёгкой пули оставалась больше (пусть ненамного), чем для тяжёлой — бо́льшая настильность траектории сохранялась вплоть до 1км.

То есть, конечно, из-за разницы БК, тяжёлая пуля рано или поздно догонит и перегонит лёгкую. В нашем случае это происходит около 890м дистанции — горизонтальные скорости становятся равны. Но чтобы долететь до этой дистанции, тяжёлая пуля затратила больше времени и, соответственно, из-за силы тяжести набрала бо́льшую скорость вертикального падения и, при той же самой горизонтальной скорости, продолжает падать быстрее. Настильность траектории — соотношение горизонтальной скорости к вертикальной — для двух пуль выравнивается только в 1300м от дульного среза, что в случае .308 — интересная, но абсолютно бесполезная информация.

“Подрыв основ, расшатывание скреп, кому теперь верить, нет я спрашиваю”, — горестно подумал Гуня, помотал головой, и решил, что дело, наверное, в конструкции конкретной пули Lapua Scenar, которая, может быть, лучше летает в лёгком весе. Друзья повторили эксперимент с патронами БПЗ “Кентавр” [11], Hornady [12], Sellier & Bellot [13] (и ещё некоторыми другими) — принципиальные результаты оставались теми же.

“Ладно”, — не сдавался Гуня, — “а может быть дело в калибре”. В самом деле, .308 Win известен в числе прочего тем, что не умеет разгонять до убедительных скоростей дальнобойные пули, тяжёлые для диаметра 7.62мм — в районе 14-15 г., а винтовки, соответственно, не умеют их стабилизировать. И началось: друзья перепробовали самые разные калибры и пули, от 5.56×45мм до .50 BMG, с заходами в .338LM и 6.5х55мм [14] — всякий раз [15] приходя к тем же заключениям. Во имя Науки, популяция Адских Телепузиков была поставлена на грань исчезновения, но жертвы были не напрасны, мы теперь знаем много нового.

Выводы:
(справедливые для пуль схожей конструкции и формы, в одном и том же калибре, с правильно подобранными навесками пороха)

1. На коротких дистанциях траектория лёгких и быстрых пуль — более настильная. Это, впрочем, и так было ясно.

2. Больший БК тяжёлых пуль компенсирует разницу в начальной скорости только далеко внизу траектории: настильность между тяжёлыми и лёгкими пулями выравнивается к 1300 м для калибров класса .308, а также для .338LM, и около 900-1000 м для шведского 6.5×55 или 6.5×47 Lapua.

3. До того, т.е. на всех практических средних и дальних дистанциях, траектория лёгких пуль — настильнее. (Разница, впрочем — невелика.)

Любитель тяжёлых пуль Гуня был посрамлён, а любитель лёгких пуль Кузя торжествовал, но торжество его было неполным, с гнильцой оказалось торжество. На средних и дальних дистанциях, несмотря на меньшую настильность траектории, на практике Гуня настрелял не в пример больше Адских Телепузиков. Отчасти это объяснялось сохранением энергии: возвращаясь к их первому опыту, энергия тяжёлой пули в .308 превосходит лёгкую уже начиная с 550м, а на дальних дистанциях лёгкие пули лишь отскакивали от чугунных лбов инфернальных созданий. Но дело было не только в терминальной баллистике (которая выходит за рамки нашего исследования); на дальних дистанциях тяжёлые пули попросту чаще попадали по цели. Почему так произошло — мы узнаем в следующем выпуске нашего альманаха.

______________________
[1] К слову, если между баллистическими таблицами и реальностью наблюдается одно и то же угловое расхождение на самых разных дистанциях, например 2 клика прицела на 300, 500 и 700 м — либо неправильно задана высота прицела, либо надо проверить пристрелку в ноль.

[2] “Прямой” выстрел, впрочем, не обязательно определяют с прицеливанием по центру мишени; иногда, например, речь идёт о прицеливании “под обрез”. Логика и принцип, впрочем, остаются те же самые — не выход траектории за габариты мишени.

[3] Здесь и далее для расчётов используется баллистический калькулятор JBM, замечательно умеющий подсчитывать опасные зоны и дальность прямого выстрела. Недостатков у калькулятора два — (1) писал его гражданин из США, а может Либерии, отчего программа по умолчанию всё считает в ярдах, дюймах и прочих фунтах (Monsieur знает толк в извращениях), всякий раз нужно переключать в метрическую систему, и (2) не понимает иных языков, кроме английского, “дикари-с”. Для справки, “target height” — высота цели, используется для расчётов “опасной зоны” (“danger space”). “Vital Zone Radius” — “радиус смертельной зоны”, используется для расчётов ДПВ.

[4] 2½-3 см примерно соответствуют разнице по высоте между “родными” прицельными АКМоидов и оптикой на высоком кроне, или целиком и оптикой СВД.

[5] Раненый враг на войне, как цинично это ни прозвучит — едва ли не предпочтительнее убитого, поскольку мобилизует гораздо больше ресурсов на эвакуацию, лечение, etc. Охотники себе не позволяют подобных вольностей, планка милосердия поставлена значительно выше.

[6] Если верить производителю. Я бы на всякий случай перепроверил (см. предыдущие выпуски нашего альманаха).

[7] Также лучше не думать о том, что поперечник рассеивания данного комплекса оружие-патрон на этой дистанции, при всех Гуниных стараниях, может быть больше 20 см, но речь, в данный момент, не об этом.

[8] Для других калибров и стволов опасные зоны легко определить с помощью JBM (см. комментарий [2]) введя в “target height” высоту цели, и отметив “Include Danger Space” в параметрах вывода — результат вычислений в колонке “Danger Space” содержит ОЗ для соответствующих дистанций. То же самое, впрочем, можно получить с любым баллистическим калькулятором, задав ноль на нужной дистанции и запросив данные на каждый метр траектории, чтобы можно было определить с точностью до метра где высота траектории выходит из габаритов цели.

[9] В особенности это относится к Интернет-стрелкам.

[10] Неоднократно упомянутый на страницах нашего альманаха, Браян Лиц — Учоный, автор очень неплохих книг по популярной баллистике, и конструктор пуль с Большим Баллистическим Коэффициентом в компании Berger Bullets.

[11] SPBT 10.7 г / БК G1 0.435 / 797 м/с против SPBT 11.7 г / БК G1 0.452 / 736 м/с (здесь и далее — по данным производителя)

[12] 155gr BTHP Match против 178gr BTHP Match

[13] Охотничьи SPCE 9.7 г / БК G1 0.280 / 850 м/с против SPCE 11.7 г / БК G1 0.316 / 765 м/с

[14] С момента изобретения баллистических калькуляторов, удовлетворение баллистического любопытства стоит гораздо дешевле, чем в былые времена. К тому же, нет опасности нарваться на неприятности с охотнадзором по причине использования 50-граммовых бронебойно-зажигательных пуль калибра 12.7мм по редким видам Адских Телепузиков.

[15] Единственное исключение — патроны Lapua Scenar LockBase калибра .308 весом 9.72 г. и 11 г., где тяжёлая пуля на средних дистанциях действительно обгоняет лёгкую. Объясняется это начальными скоростями: значительно выше (840 м/с) среднего для “тяжёлого” варианта, и немного ниже (850 м/с) среднего для “лёгкого”. Причины выбора таких навесок пороха контора Lapua не объясняет.

Вычисление траектории пули служит полезным введением в некоторые ключевые понятия классической физики, но также имеет много возможностей для включения более сложных факторов. На самом базовом уровне траектория пули работает так же, как траектория любого другого снаряда. Ключом является разделение компонентов скорости на оси (x) и (y) и использование постоянного ускорения под действием силы тяжести для определения того, как далеко пуля может пролететь до удара о землю. Тем не менее, вы также можете включить сопротивление и другие факторы, если вы хотите более точный ответ.

TL; DR (слишком долго; не читал)

Проигнорируйте сопротивление ветра, чтобы вычислить расстояние, пройденное пулей, используя простую формулу:

x = v _0x √2h ÷ g

Где (v _0x) – его начальная скорость, (h) – высота, с которой он выстрелил, и (g) – ускорение под действием силы тяжести.

Эта формула включает в себя сопротивление:

x = v _{x 0} т – CρAv ² т ² ÷ 2м

Здесь (C) – коэффициент сопротивления пули, (ρ) – плотность воздуха, (A) – площадь пули, (t) – время полета и (m) – масса пули.

Справочная информация: (х) и (у) компоненты скорости

Главное, что вам нужно понять при расчете траекторий, это то, что скорости, силы или любой другой «вектор» (который имеет направление, а также силу) можно разделить на «компоненты». Если что-то движется под углом 45 градусов к горизонтали, думайте об этом как о движении по горизонтали с определенной скоростью и по вертикали с определенной скоростью. Объединение этих двух скоростей и учет их различных направлений дает вам скорость объекта, включая как скорость, так и их результирующее направление.

Используйте функции cos и sin для разделения сил или скоростей на их компоненты. Если что-то движется со скоростью 10 метров в секунду под углом 30 градусов к горизонтали, x-составляющая скорости равна:

v _x = v cos (θ) = 10 м / с × cos (30 °) = 8, 66 м / с

Где (v) – это скорость (т. Е. 10 метров в секунду), и вы можете указать любой угол вместо (θ) в соответствии с вашей проблемой. Компонент (y) задается аналогичным выражением:

v _y = v sin (θ) = 10 м / с × sin (30 °) = 5 м / с

Эти два компонента составляют первоначальную скорость.

Основные траектории с уравнениями постоянного ускорения

Ключ к большинству проблем, связанных с траекториями, заключается в том, что снаряд перестает двигаться вперед, когда он падает на пол. Если пуля стреляет с 1 метра в воздухе, когда ускорение под действием силы тяжести уменьшает ее на 1 метр, она не может двигаться дальше. Это означает, что y-компонент – это самая важная вещь для рассмотрения.

Уравнение для смещения y-компонента:

y = v 0y t – 0.5gt ²

Индекс «0» означает начальную скорость в направлении (y), (t) означает время и (g) означает ускорение под действием силы тяжести, которое составляет 9, 8 м / с ². Мы можем упростить это, если пуля стреляет совершенно горизонтально, поэтому у нее нет скорости в направлении (y). Это оставляет:

у = -0, 5 гт ²

В этом уравнении (y) означает смещение от начальной позиции, и мы хотим знать, сколько времени требуется пуле, чтобы упасть с ее начальной высоты (h). Другими словами, мы хотим

у = -h = -0, 5 гт ²

Который вы реорганизуете в:

t = √2h ÷ g

Это время полета для пули. Его прямая скорость определяет расстояние, которое он проходит, и это определяется как:

х = v _0x т

Где скорость – это скорость, с которой он покидает пистолет. Это игнорирует эффекты перетаскивания, чтобы упростить математику. Используя уравнение для (t), найденное минуту назад, пройденное расстояние составляет:

x = v _0x √2h ÷ g

Для пули, которая стреляет со скоростью 400 м / с и стреляет с высоты 1 метра, это дает:

x_ _ = 400 м / с √

= 400 м / с × 0, 452 с = 180, 8 м

Таким образом, пуля проходит около 181 метра до удара по земле.

Включение Drag

Для более реалистичного ответа создайте перетаскивание в приведенные выше уравнения. Это немного усложняет ситуацию, но вы можете достаточно легко рассчитать ее, если найдете необходимые биты информации о вашей пуле, а также о температуре и давлении, где она стреляет. Уравнение для силы из-за сопротивления:

F _drag = −CρAv ² ÷ 2

Здесь (C) представляет коэффициент сопротивления пули (вы можете узнать для конкретной пули, или используйте C = 0, 295 в качестве общего показателя), ρ – плотность воздуха (около 1, 2 кг / кубический метр при нормальном давлении и температуре), (A) – площадь поперечного сечения пули (вы можете решить это для конкретной пули или просто использовать A = 4, 8 × 10 ^-5 м ², значение для калибра.308), а (v) – это скорость пули. Наконец, вы используете массу пули, чтобы превратить эту силу в ускорение для использования в уравнении, которое можно принять за m = 0, 016 кг, если вы не имеете в виду конкретную пулю.

Это дает более сложное выражение для пройденного расстояния в направлении (x):

x = v _{x 0} т – C ρ Av ² т ² ÷ 2м

Это сложно, потому что технически сопротивление уменьшает скорость, что, в свою очередь, уменьшает сопротивление, но вы можете упростить задачу, просто рассчитав сопротивление на основе начальной скорости 400 м / с. Используя время полета 0, 452 с (как и раньше), это дает:

x_ _ = 400 м / с × 0, 452 с – ÷ 2 × 0, 016 кг

= 180, 8 м – (0, 555 кг м ÷ 0, 032 кг)

= 180, 8 м – 17, 3 м = 163, 5 м

Таким образом, добавление сопротивления изменяет оценку примерно на 17 метров.

Внешняя баллистика изучает закономерности движения пули после выхода из ствола до встречи с целью. Наука это сложная, но кое-что из нее необходимо знать каждому охотнику.

Внешняя баллистика начинается c момента выхода пули из ствола и заканчивается, когда она достигает цели. Все это время пуля находится в свободном полете, и на нее влияют многие факторы. Внешняя баллистика именно это и изучает. Однако мы рассмотрим лишь те аспекты, которые особенно важны для охотников.

ЭЛЕМЕНТЫ БАЛЛИСТИКИ

Как только пуля покидает ствол, на нее сразу же начинают действовать три фактора:

• сила притяжения к земле;
• ветер начинает ее сносить в сторону;
• сопротивление воздуха становится труднопреодолимым препятствием.

Пуля противостоит этому благодаря:

• скорости (чтобы пролететь как можно больше до тех пор, пока сила тяжести не опустит ее на землю);
• весу (чтобы лучше сохранять эту скорость);
• оптимальной аэродинамической форме (чтобы легко рассекать воздух).

Мы рассмотрим эти важнейшие элементы.

ТРАЕКТОРИЯ

Во время свободного полета пуля движется по параболе, называемой траектория. (Это выражение не совсем верно. По параболе пуля могла бы двигаться, если бы ствол в момент выстрела был расположен горизонтально и не было бы сопротивления воздуха. — Прим. редакции).

Линия канала ствола — это строгая прямая, совпадающая с осью ствола и продленная по направлению полета. (В наших стрелковых наставлениях различают две похожие линии. Линию выстрела — продолжение оси канала ствола, наведенного на цель оружия и линию бросания, — продолжение оси канала ствола в момент выстрела. Угол между этими линиями называется углом вылета. Он образуется за счет отдачи. — Прим. редакции).

Линия прицеливания — это прямая, проходящая через центр оптического прицела. Эти две линии непараллельны. Линия канала ствола стремится слегка вверх и пересекает линию прицеливания примерно на 25 ярдах от дульного среза. Линия канала ствола направляет пулю под восходящим углом, что помогает ей сопротивляться силе гравитации. В противном случае пуля начала бы падать ниже линии прицеливания, как только она покидала ствол. Пуля набирает высоту, пересекает линию прицеливания, затем летит по высокой дуге, постепенно замедляясь из-за сопротивления воздуха. Потом сила притяжения становится сильнее движущей силы пули, и она начинает опускаться к земле. Она второй раз пересекает линию прицеливания (нулевая точка) и в конце концов падает на землю.

Таким образом, траектория может быть разделена на три части: восходящая ветвь, где пуля набирает высоту, максимальная ордината (наивысшая точка) и нисходящая ветвь.

Для охотника из этих трех частей наиболее важной является максимальная ордината — наивысшая точка траектории. В старых баллистических таблицах встречаются ссылки на высоту траектории (ВТ). Это та же максимальная ордината.

Сила гравитации — наиболее важный фактор. Мы заранее делаем поправку на силу притяжения, располагая винтовку так, чтобы ствол был слегка поднят вверх.

Любая пуля, выпущенная параллельно горизонту, теряет высоту с одинаковой скоростью, независимо от веса. Если за 1/10 секунды одна пуля пролетает 300 футов, а другая — только 200 футов, кажется, что первая лучше сопротивляется силе тяжести. На самом деле она не лучше сопротивляется, а просто дальше улетает.

Прицел на винтовке устанавливается так, чтобы линия прицеливания и линия канала ствола пересекались. Если линию прицеливания расположить горизонтально, то линия канала ствола будет направлена вверх. Точка, в которой нисходящая ветвь пересекает линию прицеливания, является точкой попадания (ноль). Если меняется угол между линией прицеливания и линией канала ствола, то изменяется и положение нулевой точки, и максимальной ординаты. Часто охотники хотят пристрелять свое оружие «в ноль» на большие дистанции, но сложность состоит в том, чтобы сохранить максимальную ординату не более 3-х дюймов выше линии прицеливания, чтобы при стрельбе на меньшие дистанции пули не проходили выше цели.

БАЛЛИСТИЧЕСКИЙ КОЭФФИЦИЕНТ — ХАРАКТЕРИСТИКА ФОРМЫ ПУЛИ

Поскольку скорость является главным параметром, противодействующим силе сопротивления воздуха, важно иметь начальную скорость как можно более высокой и сохранять ее как можно дольше. Однако у начальной скорости пули есть предел, связанный с современными техническими возможностями. Сохранение начальной скорости на траектории определяет форма пули. Количественно это характеризуется баллистическим коэффициентом (БК). Чем лучше обтекаемость и аэродинамика пули, тем выше ее БК. Мы не будем углубляться в происхождение и использование БК. Да, он слегка меняется от скорости пули, турбулентности воздуха и других факторов. Но вы можете использовать любые БК и компьютерные программы и графики — разница в результатах будет несущественной.

Чтобы начать серьезную работу с внешней баллистикой, необходимо знать две очень важные вещи:

• точные количественные данные скорости пуль;
• баллистический коэффициент вашей пули.

Единственный способ узнать реальную скорость пуль, выпущенных из вашего оружия, — это прохронографировать их. С помощью портативного хронографа Кеннета Ойлера можно получить надежные и точные данные о скорости каждой пули.

Для вычисления баллистического коэффициента нужно два хронографа, компьютер и математический склад ума. Если хотя бы одного из перечисленных компонентов нет, придется верить производителям патронов на слово. Но обычно нет большого несоответствия между опубликованными данными о величине БК и их измеренными значениями. Кроме того, несоответствие в несколько тысячных в БК не так важно для вычисления основных показателей, как значительное несоответствие начальной скорости, что бывает довольно часто.

КОМПЬЮТЕРНАЯ РЕВОЛЮЦИЯ

В середине 80-х появился персональный компьютер, а спустя некоторое время — баллистические компьютерные программы. Наряду со значениями скорости, получаемыми хронографами, появилась возможность вычисления «проседания» пули, потери скорости, количества движения, кинетической энергии, словом, всего, чего только захочешь. Самое главное, что мы можем представить, — точную траекторию пули, используя наши собственные данные о ее скорости.

Баллистические программы дают точные результаты благодаря функциям лобового сопротивления и различным формулам, используемым для вычисления математической модели траектории. Несмотря на то что во многих компаниях есть хорошие специалисты, несомненно, лучшие специалисты по баллистике работают в компании «Сьерре» (Sierra) и в исследовательской группе Ойлера. И те и другие издали баллистические программы. Это явно лучшие программы, и каждый стрелок должен иметь хотя бы одну из них.

«БАЛЛИСТИЧЕСКИЙ ИССЛЕДОВАТЕЛЬ» (ПРОГРАММА ЛАБОРАТОРИИ ОЙЛЕРА)

Эта компьютерная программа вычисляет траекторию и все ее параметры для любых патронов, зарядов пороха и разных пуль при различных скоростях и в разных условиях. В ней содержатся данные о выпускаемых боеприпасах и пулях. Она может высчитывать все необходимые данные о выстреле, основанные на этой информации, и некоторых дополнительных данных, которые может ввести стрелок. Результаты могут быть представлены в виде графика или таблиц.

«Данные о выстреле» включают в себя траекторию, скорость, энергию, понижение, дальность по горизонту и некоторые другие. Программа выполняет гораздо больше расчетов, которые подробно описаны в руководстве. Она производит вычисления, основанные на различных баллистических моделях, и может вычислить любые, в том числе и экзотические параметры, основываясь на введенных данных. На практике она берет ваш баллистический коэффициент и скорость и вычисляет траекторию. Если вы введете данные о направлении ветра и его скорости, то она вычислит и ветровой снос. Если вы добавите другие факторы, влияющие на траекторию, например температуру, барометрическое давление, высоту и угол стрельбы, программа их тоже обработает.

Каждый набор вычислений для данной скорости пули и ее БК называется трассированием. Программа может прорабатывать три трассировки одновременно и выводить их в одном графике для удобства сравнения.

Данные о боеприпасах и пулях из «Баллистического Исследователя» можно вызвать и использовать для вычислений, что позволит сравнить показатели вашего оружия с показателями завода — изготовителя патронов.

В общем, это очень полезная программа и совсем не сложная для тех, кто пользуется персональным компьютером.

ПРОГРАММА КОМПАНИИ «СЬЕРРА»

По сути, баллистическая программа компании «Сьерра» выполняет те же вещи, что и программа Ойлера, но у нее другой подход и, соответственно, она немного более гибкая.

Программа не совсем проста для пользователя, но как только вы начинаете в ней разбираться (особенно с терминологией), она предлагает несколько полезных функций. Например, у нее есть отдельная функция вычисления баллистического коэффициента с использованием данных, введенных пользователем.

Обе программы очень удобны для компьютерных баллистических вычислений.

БАЛЛИСТИЧЕСКИЕ ТОНКОСТИ, КОТОРЫЕ МОГУТ СБИТЬ С ТОЛКУ

К сожалению, многие статьи по внешней баллистике и баллистические компьютерные программы часто отклоняются от темы и больше уделяют внимания таким вопросам, как высота, барометрическое давление, влажность, температура, угол выстрела. (В наших наставлениях этот параметр называется «угол места цели». — Прим. редакции).

Эти факторы объективно влияют на траекторию, но для «среднего» охотника, стреляющего на дистанции до 300 метров, они не являются определяющими Кстати, с помощью любой баллистической программы, особенно программы Ойлера, можно проверить, насколько мало их влияние.

К примеру, охотник пристреливает свое ружье дома, на высоте 600 метров над уровнем моря, и хочет узнать, как изменится траектория пули при охоте на горных баранов на высоте 2000 метров. Компьютерная программа это рассчитает. Однако практическое значение эта поправка имеет только для бенчреста при стрельбе на 1000 ярдов (914,4 метра). Нормальное рассеяние при повторных выстрелах, как правило, больше, чем это влияние.

Исключение составляет стрельба по целям, находящимся значительно выше или ниже стрелка (когда угол места цели составляет 30 градусов и более). В этом случае требуется изменение угла прицеливания. Говоря практическим языком, пуля полетит гораздо выше над линией прицеливания — по сравнению со стрельбой на ровной местности. Компьютерные программы определяют точно, насколько выше точки прицеливания «прилетят» пули в зависимости от угла превышения (или понижения). Но эти тонкости при стрельбе на средние охотничьи дистанции не слишком важны. Вам достаточно знать, что при стрельбе вверх или вниз нужно прицеливаться на несколько дюймов ниже.

Полина ЗВЕРЕВА
Фото Антона ЖУРАВКОВА
Охота и рыбалка 4-2010