Как найти транспонированная союзная матрица

Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.

Матрица $A^{-1}$ называется обратной по отношению к квадратной матрице $A$, если выполнено условие $A^{-1}cdot A=Acdot A^{-1}=E$, где $E$ – единичная матрица, порядок которой равен порядку матрицы $A$.

Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой равен нулю определитель.

Обратная матрица $A^{-1}$ существует тогда и только тогда, когда матрица $A$ – невырожденная. Если обратная матрица $A^{-1}$ существует, то она единственная.

Есть несколько способов нахождения обратной матрицы, и мы рассмотрим два из них. На этой странице будет рассмотрен метод присоединённой матрицы, который полагается стандартным в большинстве курсов высшей математики. Второй способ нахождения обратной матрицы (метод элементарных преобразований), который предполагает использование метода Гаусса или метода Гаусса-Жордана, рассмотрен во второй части.

Метод присоединённой (союзной) матрицы

Пусть задана матрица $A_{ntimes n}$. Для того, чтобы найти обратную матрицу $A^{-1}$, требуется осуществить три шага:

1. Найти определитель матрицы $A$ и убедиться, что $Delta Aneq 0$, т.е. что матрица А – невырожденная.
2. Составить алгебраические дополнения $A_{ij}$ каждого элемента матрицы $A$ и записать матрицу $A_{ntimes n}^{*}=left(A_{ij} right)$ из найденных алгебраических дополнений.
3. Записать обратную матрицу с учетом формулы $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$.

Матрицу ${A^{*}}^T$ часто именуют присоединённой (взаимной, союзной) к матрице $A$.

Если решение происходит вручную, то первый способ хорош лишь для матриц сравнительно небольших порядков: второго (пример №2), третьего (пример №3), четвертого (пример №4). Чтобы найти обратную матрицу для матрицы высшего порядка, используются иные методы. Например, метод Гаусса, который рассмотрен во второй части.

Пример №1

Найти матрицу, обратную к матрице $A=left( begin{array} {cccc} 5 & -4 &1 & 0 \ 12 &-11 &4 & 0 \ -5 & 58 &4 & 0 \ 3 & -1 & -9 & 0 end{array} right)$.

Решение

Так как все элементы четвёртого столбца равны нулю, то $Delta A=0$ (т.е. матрица $A$ является вырожденной). Так как $Delta A=0$, то обратной матрицы к матрице $A$ не существует.

Ответ: матрицы $A^{-1}$ не существует.

Пример №2

Найти матрицу, обратную к матрице $A=left(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)$. Выполнить проверку.

Решение

Используем метод присоединённой матрицы. Сначала найдем определитель заданной матрицы $A$:

$$
Delta A=left| begin{array} {cc} -5 & 7\ 9 & 8 end{array}right|=-5cdot 8-7cdot 9=-103.
$$

Так как $Delta A neq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:

begin{aligned}
& A_{11}=(-1)^2cdot 8=8; ; A_{12}=(-1)^3cdot 9=-9;\
& A_{21}=(-1)^3cdot 7=-7; ; A_{22}=(-1)^4cdot (-5)=-5.\
end{aligned}

Составляем матрицу из алгебраических дополнений: $A^{*}=left( begin{array} {cc} 8 & -9\ -7 & -5 end{array}right)$.

Транспонируем полученную матрицу: ${A^{*}}^T=left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$ (полученная матрица часто именуется присоединённой или союзной матрицей к матрице $A$).
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, имеем:

$$
A^{-1}=frac{1}{-103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)

=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)
$$

Итак, обратная матрица найдена:

$$A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right).$$

Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $A^{-1}cdot A=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$, а в виде $-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$:

$$
A^{-1}cdot{A}
=-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)cdotleft(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)

=-frac{1}{103}cdotleft(begin{array} {cc} -103 & 0 \ 0 & -103 end{array}right)
=left(begin{array} {cc} 1 & 0 \ 0 & 1 end{array}right)
=E
$$

Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.

Ответ: $A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$.

Пример №3

Найти обратную матрицу для матрицы $A=left( begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right)$. Выполнить проверку.

Решение

Начнём с вычисления определителя матрицы $A$. Итак, определитель матрицы $A$ таков:

$$
Delta A=left| begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right| = 18-36+56-12=26.
$$

Так как $Delta Aneq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:

$$
begin{aligned}
& A_{11}=(-1)^{2}cdotleft|begin{array}{cc} 9 & 4\ 3 & 2end{array}right|=6;;
A_{12}=(-1)^{3}cdotleft|begin{array}{cc} -4 &4 \ 0 & 2end{array}right|=8;;
A_{13}=(-1)^{4}cdotleft|begin{array}{cc} -4 & 9\ 0 & 3end{array}right|=-12;\

& A_{21}=(-1)^{3}cdotleft|begin{array}{cc} 7 & 3\ 3 & 2end{array}right|=-5;;
A_{22}=(-1)^{4}cdotleft|begin{array}{cc} 1 & 3\ 0 & 2end{array}right|=2;;
A_{23}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 7\ 0 & 3end{array}right|=-3;\

& A_{31}=(-1)^{4}cdotleft|begin{array}{cc} 7 & 3\ 9 & 4end{array}right|=1;;
A_{32}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 3\ -4 & 4end{array}right|=-16;;
A_{33}=(-1)^{6}cdotleft|begin{array}{cc} 1 & 7\ -4 & 9end{array}right|=37.
end{aligned}
$$

Составляем матрицу из алгебраических дополнений и транспонируем её:

$$
A^*=left( begin{array} {ccc} 6 & 8 & -12 \ -5 & 2 & -3 \ 1 & -16 & 37end{array} right); ;
{A^*}^T=left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right).
$$

Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, получим:

$$
A^{-1}=frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)=
left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)
$$

Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $Acdot A^{-1}=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$, а в виде $frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)$:

$$
Acdot{A^{-1}}
=left( begin{array}{ccc}
1 & 7 & 3 \
-4 & 9 & 4\
0 & 3 & 2end{array} right)cdot
frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)

=frac{1}{26}cdotleft( begin{array} {ccc} 26 & 0 & 0 \ 0 & 26 & 0 \ 0 & 0 & 26end{array} right)

=left( begin{array} {ccc} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1end{array} right)

=E
$$

Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.

Ответ: $A^{-1}=left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$.

Пример №4

Найти матрицу, обратную матрице $A=left( begin{array} {cccc} 6 & -5 & 8 & 4\ 9 & 7 & 5 & 2 \ 7 & 5 & 3 & 7\ -4 & 8 & -8 & -3 end{array} right)$.

Решение

Для матрицы четвёртого порядка нахождение обратной матрицы с помощью алгебраических дополнений несколько затруднительно. Однако такие примеры в контрольных работах встречаются.

Чтобы найти обратную матрицу, для начала нужно вычислить определитель матрицы $A$. Лучше всего в данной ситуации это сделать с помощью разложения определителя по строке (столбцу). Выбираем любую строку или столбец и находим алгебраические дополнения каждого элемента избранной строки или столбца.

Например, для первой строки получим:

$$
A_{11}=left|begin{array}{ccc} 7 & 5 & 2\ 5 & 3 & 7\ 8 & -8 & -3 end{array}right|=556;;
A_{12}=-left|begin{array}{ccc} 9 & 5 & 2\ 7 & 3 & 7 \ -4 & -8 & -3 end{array}right|=-300;
$$

$$
A_{13}=left|begin{array}{ccc} 9 & 7 & 2\ 7 & 5 & 7\ -4 & 8 & -3 end{array}right|=-536;;
A_{14}=-left|begin{array}{ccc} 9 & 7 & 5\ 7 & 5 & 3\ -4 & 8 & -8 end{array}right|=-112.
$$

Определитель матрицы $A$ вычислим по следующей формуле:

$$
Delta{A}=a_{11}cdot A_{11}+a_{12}cdot A_{12}+a_{13}cdot A_{13}+a_{14}cdot A_{14}=6cdot 556+(-5)cdot(-300)+8cdot(-536)+4cdot(-112)=100.
$$

А далее продолжаем находить алгебраические дополнения:

$$
begin{aligned}
& A_{21}=-77;;A_{22}=50;;A_{23}=87;;A_{24}=4;\
& A_{31}=-93;;A_{32}=50;;A_{33}=83;;A_{34}=36;\
& A_{41}=473;;A_{42}=-250;;A_{43}=-463;;A_{44}=-96.
end{aligned}
$$

Матрица из алгебраических дополнений:

$$A^*=left(begin{array}{cccc} 556 & -300 & -536 & -112\ -77 & 50 & 87 & 4 \ -93 & 50 & 83 & 36\ 473 & -250 & -463 & -96end{array}right)$$

Присоединённая матрица:

$${A^*}^T=left(begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96end{array}right)$$

Обратная матрица:

$$
A^{-1}=frac{1}{100}cdot left( begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96 end{array} right)=
left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)
$$

Проверка, при желании, может быть произведена так же, как и в предыдущих примерах.

Ответ: $A^{-1}=left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)$.

Во второй части будет рассмотрен иной способ нахождения обратной матрицы, который предполагает использование преобразований метода Гаусса или метода Гаусса-Жордана.

Для того что бы найти обратную матрицу можно использовать два метода: с помощью алгебраических дополнений (метод присоединённой (союзной) матрицы) или элементарных преобразований (метод Жордано-Гаусса).
Рассмотрим как найти обратную матрицу с помощью алгебраических дополнений.

Обратной матрицей называется матрицы A^-1 при умножении на исходную матрицу A получается единичная матрица E.

A·A^-1 = A^-1 · A = E

Алгоритм нахождения обратной матрицы с помощью алгебраических дополнений:

1. Найти определитель (детерминант) матрицы A. Если определитель ≠ 0, то обратная матрица существует. Если определитель = 0, то обратная матрица не существует.
2. Найти матрицу миноров M.
3. Из матрицы M найти матрицу алгебраических дополнений C^*.
4. Транспонировать матрицу (поменяем местами строки со столбцами) C^*, получить матрицу C^*T.
5. По формуле найти обратную матрицу.
   

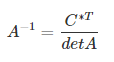
Пример

Рассмотрим данный метод на примере. Дана матрицы 3х3:

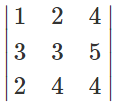
Найдем определитель (детерминант) матрицы, detA = 12 обратная матрица существует.

Найдем минор M₁₁ и алгебраическое дополнение A₁₁. В матрице А вычеркиваем строку 1 и столбец 1.

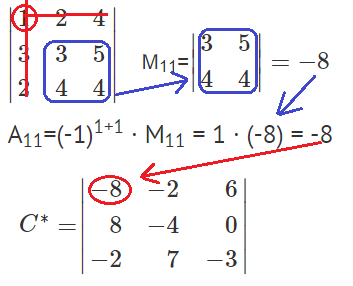
Найдем минор M₁₂ и алгебраическое дополнение A₁₂. В матрице А вычеркиваем строку 1 и столбец 2.

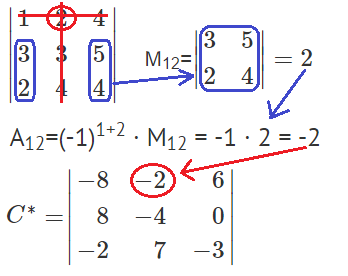
Остальные миноры и алгебраические дополнения находятся аналогично. В итоге получаем матрицу C^*.

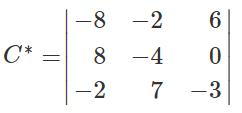
Найдем транспонированную союзную матрицу алгебраических дополнений C^*T.

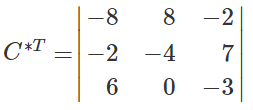
Найдем обратную матрицу. Ответ:

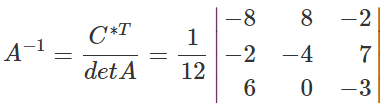
Многие считают, что тема «Транспонированные матрицы» довольно сложная, но это не так. В студенческом курсе математики транспонирование выполняется легко и без каких-либо усилий. Для того чтобы понимать, как именно осуществляется операция, необходимо знать, что такое матрица.

Онлайн-калькулятор

Что такое транспонированная матрица

Матрица, полученная из данной заменой каждой ее строки столбцом с этим же номером, называется матрицей транспонированной данной. Обозначается такая матрица ATA^{T} или A′A’.

При транспонировании матрицы AA размера m×nmtimes n получаем матрицу ATA^{T} размера n×mntimes m.

В общем виде транспонированная матрица для матрицы

Am×n=(a11a12…a1na21a22…a2n…………am1am2…amn)A_{mtimes n}=begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\a_{21}&a_{22}&…&a_{2n}\…&…&…&…\a_{m1}&a_{m2}&…&a_{mn}end{pmatrix}

выглядит следующим образом:

An×mT=(a11a21…am1a12a22…am2…………a1na2n…amn)A^{T}_{ntimes m}=begin{pmatrix}a_{11}&a_{21}&…&a_{m1}\a_{12}&a_{22}&…&a_{m2}\…&…&…&…\a_{1n}&a_{2n}&…&a_{mn}end{pmatrix}.

Элементы ii строки исходной матрицы становятся элементами ii столбца транспонированной матрицы. Таким образом, транспонирование матрицы заключается в том, что строки исходной матрицы AA записывают в новую матрицу по столбцам.

Пример 1

Транспонировать матрицы K=(15−2314−18)K=begin{pmatrix}15&-23&14&-18end{pmatrix} и L=(25−10118)L=begin{pmatrix}25\-10\11\8end{pmatrix}.

KT=(15−2314−18)K^{T}=begin{pmatrix}15\-23\14\-18end{pmatrix},

LT=(25−10118)L^{T}=begin{pmatrix}25&-10&11&8end{pmatrix}.

Пример 2

Транспонировать матрицу G=(5−311820514−86537−94)G=begin{pmatrix}5&-3&11&8\2&0&5&1\4&-8&6&5\3&7&-9&4end{pmatrix}.

GT=(5243−30−871156−98154)G^{T}=begin{pmatrix}5&2&4&3\-3&0&-8&7\11&5&6&-9\8&1&5&4end{pmatrix}.

Свойства транспонированных матриц

1. Дважды транспонированная матрица равна исходной матрице: ATT=(AT)T=AA^{TT}=(A^{T})^{T}=A.
2. Транспонированная матрица суммы равна сумме транспонированных матриц: (A+B)T=AT+BT(A+B)^{T}=A^{T}+B^{T}.
3. Транспонированная матрица произведения равна произведению транспонированных матриц: (A⋅B)T=AT⋅BT(Acdot B)^{T}=A^{T}cdot B^{T}.
4. При транспонировании можно выносить скаляр (число, на которое можно разделить все элементы матрицы): (k⋅A)T=k⋅AT(kcdot A)^{T}=kcdot A^{T}.
5. Определитель исходной матрицы и определитель транспонированной матрицы равны.

С понятием определителя матрицы мы познакомимся на следующем уроке.

Возникли сложности с матрицей? На нашем сервисе предусмотрена платная помощь с решением задач по алгебре от экспертов!

Тест по теме «Транспонирование матрицы»

Матрица и ее практическое применение

• Авторы
• Руководители
• Файлы работы
• Презентация
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Матрицы применяются в повседнейвной жизни и используются во всех отраслях деятельности. При решении различных практических задач в математике, биологии, физике, технике, химии, экономике, маркетинге, психологии и других областях науки используют матрицы. Матрицы внедрились в программные обеспечения, что является актуальным в современном мире.

Цель работы: Изучить матрицы, применение их в практических задачах, а также и в прикладных задачах, основанных на жизненных решениях проблем.

Для достижения цели можно выделить ряд задач исследования:

– изучение понятия матриц;

– определение видов матриц;

– вычисление опрделителей матриц;

– выполнение действий над матрицами;

– решение задач с применением матриц;

– использование задач из повседнейной жизни.

В математике матрица это прямоугольная таблица, состоящая из каких-либо элементов. Элементами матрицы могут быть различные данные о предметах, объектах, событиях, явлениях и т.д.

Матрицы бывают различных видов: квадратная, вектор-строка, вектор-столбец, диагональная, единичная, нулевая, транспонированная,

Над матрицами можно выполнять некоторые действия: сложение, вычистание, умножение на число, умножение матриц, деление матриц, возведение в степень и т.д. Матрицы также обладают различными свойствами: коммуникативность относительно сложения, ассоциативность сложения, ассоциативность умножения, дистрибутивность относительно сложения, дистрибутивность относительно умножения и т.д.

Определитель (детерминант) – это одна из основных численных характеристик квадратной матрицы, которую применяют при решении многих задач. Определитель матрицы чаще используют в решении систем линейных алгебраических уравнений (СЛАУ) и в нахождении обратной матрицы. Самое главное – определитель матрицы можно найти только для квадратной матрицы.

Благодаря теории детерминантов стало возможным ввести разные расчеты, связанные с матрицами. Например, открытие позволило вычислять определитель для квадратной матрицы и находить обратную матрицу.

Объект исследования: теория матриц, её применение

Гипотеза: зная свойства матриц и действия над ними, можно решать задачи широкого спектра, а применение её в различных сферах деятельности показывает и доказывает востребованность в познании мира матриц. [1]

1. Теоретические аспекты матрицы

1.1. История развития и применение матриц

В Древнем Китае матрицу называли «Волшебным квадратом». Магический квадрат 3 × 3 был известен около 2200 до н.э. и изображался на черепаховом панцере. Данный нормальный магический квадрат изобразил Ло Шу (рис.1). Позже они стали известны арабским математикам и в это же время стало известно о принципе сложения матриц.

Рис. 1 Изображение Ло Шу

В конце XVII века получило развитие теория определителей и тогда швейцарский математик Габриэль Крамер (1704-1752) приступил к разработке своей теории. В 1751 году он опубликовал «правило Крамера» и параллельно в это же время был опубликован «метод Гаусса». Эти две публикации раскрывали метод решения «систем линейных алгебраических уравнений», но для «правила Крамера» используется ненулевой определитель матрицы системы, а для «метода Гаусса» – последовательное исключение неизвестных.

Теория матриц начала активное развитие в середине XIX века. В это время уже были формулированы правила сложения и умножения матриц. Результаты теории матриц разработаны и отражены в работах ученых: ирландский математик и физик Уильям Гамильтон (1805-1865), английский математик Артур Кэли (1821-1895), немецкие математики Карл Вейерштрасс (1815-1897) и Фердинанд Георг Фробениус (1849-1917), французский математик Мари Энмон Камиль Жордан (1838-1922) и ввел термин «матрица» Джеймс Сильвестр (1814-1897) в 1850г.

В 1858году А.Кэли опубликовал «Мемуар по теории матриц», в котором дается первое абстрактное определение матрицы. У.Гамильтон и А.Кэли разработали теорию матриц: «любая квадратная матрица удовлетворяет своему характеристическому уравнению».

В 1878 году Ф.Г.Фробениус опубликовал работу «О линейных подстановках и алгебраических уравнениях», в которой доказывает результаты канонических матрицах. Он также доказал общую теорему матриц: «матрица удовлетворяет своему характеристическому уравнению». К.Вейерштрасс в своих лекциях использовал аксиоматическое определение определителя, а в 1903году после его смерти было опубликована статья «О теории детерминантов». Мари Энмон Камиль Жордан ввел нормальную (каноническую) форму матриц, которая имеет вид блочно-диагональной матрицы, по диагонали располагаются жордановы клетки.

Матрицы широко применяются в математике, физике, информатике, химии, биологии, экономике, технике, статистике и т.д. Он играет огромную роль в каждой сфере и значение его велико. В математике «матрица» означает систему элементов в прямоугольной таблице, в программировании – двумерный массив, в электронике – набор проводников, в фотографии – интегральная микросхема. Матрица встречается везде даже в таких таблицах как: таблица умножения, файл bmp с матрицей цветов пикселей, турнирная таблица на футбольном поле, таблица содержания в пище белков, жиров и углеводов. [2]

1.2 Понятие и виды матриц

Матрица – это набор чисел, символов или выражений, записанных в виде прямоугольной таблицы со строками и столбцами. В таблице строки распологаются горизонтально, а столбцы – вертикально. Числа, символы или выражения называются элементами матриц, которые располагаются на пересечении строк и столбцов. Размер матрицы определяют количеством строк и столбцов. Матрицу обозначают заглавной буквой латинского алфавита и записывают в круглых скобках следующим образом:

=

Данная матрица n × m типа имеет n – строк и m – столбцов, значит размер (количество элементов) матрицы равен n × m.

Матрицы 2 × 2, 3 × 3, 4 × 4 имеют вид:

= ; = ; =

Кроме строк и столбцов матрицы имеют такое понятие как диагональ.

Различают 2 диагонали матрицы:

1) Главная диагональ – это диагональ, проводимая из верхнего левого угла в нижний правый угол матрицы.

2) Побочная диагональ – это диагональ, проводимая из верхнего правого угла в нижний левый угол матрицы.

Д ля матрицы = главная диагональ , побочная – ;

Для матрицы = главная диагональ , побочная – ;

Для матрицы = главная диагональ , побочная – .

Существует несколько видов матриц:

1) Квадратная матрица – это матрица, у которой n = m, т.е. одинаковое количество строк и столбцов. Квадратные матрицы это матрицы 2 × 2, 3 × 3, 4 × 4 и т.д.

Из квадратных матриц можно получить диагональный, треугольный и единичный вид матрицы.

2) Диагональная матрица – это квадратная матрица, где все элементы кроме главной диагонали равны нулю. Такую матрицу можно считать и треугольной.

Диагональные матрицы 2 × 2, 3 × 3, 4 × 4 имеют вид:

= ; = ; =

3) Треугольная матрица – это квадратная матрица, где элементы, расположенные над (под) главной диагональю равны нулю. Примеры нижней и верхней треугольной матрицы:

а) верхняя треугольная матрица

= ; = ; =

в) нижняя треугольная матрица

= ; = ; =

4) Единичная матрица – это диагональная матрица с диагональными элементами равными 1.

= ; = ; =

5) Нулевая матрица – это матрица, состоящая из всех нулевых элементов.

= ; =

6) Вектор-строка – это матрица с одной строкой. Пример, А = .

7) Вектор-столбец – это матрица с одним столбцом. Пример, В = .

8) Транспонированная матрица – это матрица, полученная из произвольной матрицы путем замены строк на столбцы. Для матрицы A {displaystyle A} А с размерами m × n {displaystyle mtimes n} m × n транспонированная матрица A^ТA T {displaystyle A^{T}} будет с размерами n × m {displaystyle ntimes m} n × m. Например,

= ; =

9) Симметричной матрицей называется квадратная матрица, элементы которой симметричны относительной главной диагонали, т.е. A^Т = А. Например, симметричные матрицы:

= ; =

Рассмотрены основные понятия матриц, их виды необходимые для вычисления матриц и выполнения различных действий над ними. [3]

1.3 Вычисление определителей матриц

Для нахождения определителя матрицы используют различные способы вычисления.

Определитель матрицы второго порядка вычисляется как разность произведения элементов главной диагонали и элементов побочной диагонали. Допустим, дана матрица вида:

= ,

то определитель матрицы = – .

Пример 1. Вычислить определитель матрицы: =

Определитель матрицы = 4·11 – 7·5 = 9

Ответ: = 9.

Определитель матрицы третьего порядка вычисляется разными способами:

1) Правило треугольника:

Допустим, дана матрица = , то определитель матрицы находим, применяя правило треугольника:

– =

+ + – ( + + )

2) Правило Саррюса:

Допустим, дана матрица = . Для нахождения определителя матрицы, применяя, правило Саррюса нужно справа от матрицы дописать первые два столбца и из суммы произведения главных диагоналей (красные линии) вычесть сумму произведения побочных диагоналей (синие линии):

=

+ + – ( + + )

Пример 2. Вычислить определитель матрицы: =

Определитель матрицы = 7·1·8 + 5·2·6 + 3·4·4 – 3·1·6 – 5·4·8 – 7·2·4 = 164 – 234 = -70

Ответ: = -70.

Определитель матрицы третьего и высшего порядка вычисляется различными способами:

3) Разложение определителя матрицы: а) по любой строке, b) по любому столбцу

Пример 3. Вычислить определитель матрицы: =

Разложим определитель матрицы по четвертой строке:

= 3· · + 2· · + 0· · + 8· ·

= -3· + 2· + 8·

Далее разложим определители третьего порядка: первое слагаемое по первому столбцу, второе – по второму столбцу, третье – по третьему столбцу.

= -3·2· · -3·4· · -3·6· · +

2·1· · + 2·3· · + 2·5· · +

8·1· · + 8·3· · + 8·5· ·

= -6 · + 12 · -18· – 2 · + 6 · – 10 · +

8 · – 18 · + 40 · = 0

Ответ: = 0

4) Нахождение определителя матрицы приведением к треугольному виду, с помощью различных преобразований со строками и столбцами на основе свойств определителя. [4]

Пример 4. Вычислить определитель матрицы: =

Перепишем в определитель четвертого порядка, приведем его к треугольному виду, выполнив следующие действия:

1) первую строку поделим на 3, чтоб элемент = 1:

= ~

2) умножить 1 строку на (-2) и сложить со 2-ой строкой;

умножить 1 строку на (-5) и сложить с 4-ой строкой;

= ~

3) умножить 2 строку на 4 и сложить со 3-ей строкой;

умножить 2 строку на (-8) и сложить с 4-ой строкой;

= ~

3) разделить 3 строку на 30;

умножить 3 строку на 41 и сложить с 4-ой строкой;

= ~

4) используя свойство треугольной матрицы, вычислим определитель как произведение элементов диагонали:

= 1 · (-1) · (-1) · 21 = 21

Ответ: = 21

1.4 Действия над матрицами

Рассмотрим, какие действия можно выполнять над матрицами.

Для начала определим, что значит равенство матриц. Матрицы называются равными, если они имеют одинаковую размерность и соответствующие элементы данных матриц равны. Например, матрица А и В

= , =

Данные матрицы будут равны, если выполняется условие:

1) имеют одинаковую размерность 3 × 3;

2 ) = = , = , = , = , = , = , = , = , = .

Действия над матрицами:

1) Сложение (вычитание) матриц.

При сложении (вычитании) матриц необходимым условием, как и при равенстве матриц, является одинаковая размерность, т.е. при различном порядке данных матриц сложение (вычитание) матриц НЕВОЗМОЖНО. Сумма (разность) матриц есть матрица, элементы которой равны сумме (разности) соответствующих элементов данных матриц и имеет ту же размерность, что и матрицы слагаемых (уменьшаемого и вычитаемого). Если даны матрицы А и В, то сумма (разность) равны:

= , =

А + В = ;

А – В =

Сложение следующих матриц и невозможно, так как размерность не одинакова, т.е. количество строк и столбцов в матрицах различны:

= и =

Пример, Найдите матрицу (А + В) – С, если

А = , В = , С = .

(А + В) – С = –

Ответ: (А + В) – С = .

Из определения и приведенных примеров вытекают свойства сложения (вычитания) матриц:

1) А + В = В + А коммутативность сложения;

2) А + О = О + А = А;

3) А − А = О;

4) (А + В) + С = А + (В + С) ассоциативность сложения,

где матрицы А, В, С, О, имеют одинаковую размерность.

2) Умножение матрицы на ненулевое число.

Чтобы умножить матрицу на число (число на матрицу) необходимо данное число умножить на каждый элемент матрицы с сохранением размерности. Если дана матрица А и некоторое число λ, то произведение будет равно:

λ × А = λ × =

Пример, найдите произведение матрицы А = на число λ = -0,5.

λ × А = -0,5 × =

Перечислим свойства умножения матрицы на число:

1) 1 × А = А нейтральное число 1;

2) 0 × А = 0;

3) λ × (А + В) = λА + λВ дистрибутивность умножение относительно сложения;

4) (λ + μ) × А = λА + μА дистрибутивность умножение;

5) (λ × μ) × А = λ × (μ × А) ассоциативность умножения,

где А, В матрицы и λ, μ любые числа.

3)Умножение матриц.

Чтобы умножить матрицу на матрицу нужно строку первой матрицы умножить на столбец второй матрицы и сложить, т .е.

× = ,

где матрицы и должны быть согласованными, т.е. количество столбцов матрицы и количество строк матрицы обязательно должны быть равными. Значит, результатом произведения матриц является новая матрица с количеством строк равных строкам первого множителя и количеством стобцов равных столбцам второго множителя. Если даны матрицы и , то произведение будет равно:

= ×

=

Пример, найдите произведение матриц × и × , если

= и =

Произведение матриц:

× = =

Произведение матриц × не имеет смыла, так как эти матрицы не согласованы, т.е. матрица имеет 2 стобца, а матрица имеет 3 строки.

Перечислим свойства умножения матриц:

1) (А × В) × С = А × (В × С) ассоциативность умножения;

2) (А + В) × С = АС + ВС или С × (А + В) = СА + СВ дистрибутивность умножение относительно сложения;

3) А × В ≠ В × А некоммутативность умножения;

4) λ × (А × В) = (λ × А) × В;

5) × = × = умножение на единичную матрицу,

где А, В матрицы, Е единичная матрица и λ любые числа.

В третьем свойстве говорится о некоммутативности умножения, т.е.

А × В ≠ В × А, но в некоторых случаях умножение матриц может быть коммутативным, в этом случае матрицы называют перестановочными.

4)Возведение матриц в степень.

В озведение матриц в степень основано на произведении матриц. Допустим, это и есть произведение сомножителей А n раз, т.е.

= А × А × … × А

n раз

Перечислим некоторые правила для степеней матрицы с натуральной степенью:

1) = Е;

2) × = ;

3) = .

5) Нахождение обратной матрицы.

Для нахождения обратной матрицы существует разные способы. Рассмотрим одно из них:

Для вычисления обратной матрицы с помощью алгебраических дополнений необходимо знать:

1) Как найти определитель матрицы?

2) Как найти транспонированную матрицу?

3) Как найти элементы союзной матрицы и что значит союзная матрица?

4) Какую применить формулу для вычисления обратной матрицы?

5) Как проверить на верность полученной обратной матрицы?

Пункты 2 и 3 применяют и в обратном порядке, т.е. вперед находят союзную матрицу, а потом транспонируют матрицу, но результат от этого не должен меняться.

Если матрица А имеет вид квадратный, то обратную матрицу можно найти с помощью формулы:

= · ,

где – определитель матрицы, – союзная матрица.

Рассмотрим примеры с матрицами 3 × 3 и ответим на 5 вопросов при вычислении обратной матрицы:

Например, если дана матрица = , то

1) определитель матрицы = 3·5·8 + 7·2·6 + 1·4·10 – (1·5·7 + 3·6·10 + 8·2·4) = 120 + 84 + 40 – (35 + 180 + 64) = 244 – 279 = -35 ≠ 0. Так как = -35 ≠ 0, значит, можно продолжить нахождение матрицы.

Если же = 0, то обратной матрицы не существует, так как матрица вырожденная.

2) транспонированная матрица = .

3) найдем алгебраические дополнения матрицы (элементы союзной матрицы), транспонированной матрицы:

= = -20 = = 10 = = 5

= = -6 = = 17 = = -16

= = 7 = = -14 = = 7

Союзная матрица: =

4) Подставить вычисления из 1 и 3 в формулу и найдем обратную матрицу:

= · = ·

Внесем «-» в матрицу, то получим:

= ·

5) проверим на правильность полученной обратной матрицы. Для этого умножим данную с обратной матрицей и в результате должны получить единичную матрицу. Если этого не произойдет, значит, обратная матрица найдена не верно.

· · =

= ·

= · = = Е

Ответ: =

В данном разделе приведены различные вычисления определителей матриц, перечислены основные действия над матрицами для решения заданий на матрицы и проведения дальнейшего исследования. [5]

2. Решение практических задач

Рассмотрим несколько практических задач на применение матриц в математике. В задачах используются различные виды действий над матрицами, а также доказательство верности утверждения.

Задача 1. Найти (4А + В) – 2С, если даны матрицы А, В и С:

Решение

1) Вычислить матрицу 4А и 2С:

2) Сложить матрицы 4А и В, затем вычитать от результата матрицу 2С:

=

Ответ:

Задача 2. Вычислить определитель , разлагая его по элементам второй строки.

Решение

Разложить определитель по элементам второй строки:

Вычисляя, получим:

x(-27-8-8-(-3-24-24)) – у((18+24+16)-(9+48+16)) + z((-12-18-4)-(-6-36-4)) –

t((-16-27-16)-(-24-48-6)) = 8x + 15y + 12z – 19t

Ответ: 8x + 15y + 12z – 19t

Задача 3. Найти матрицу Х из уравнения:

+ 2Х =

Решение

1) Найти неизвестное слагаемое 2Х:

=

2) Найти матрицу Х:

Х =

Ответ: Х =

Задача 4. Найди АВ, если: [6]

Решение

Найдем произведение матриц, используя правило умножения [6]

Ответ:

Задача 5. Не раскрывая определителя показать, что он равен нулю

Решение

По свойству определителя: если к элементам любой строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменится.

Если прибавить 1 и 2 столбец определителя, то , , . Значит, в определителе два столбца имеют одинаковые элементы, равные 1.

Следующее свойство гласит, что определитель с двумя равными строками (столбцами) равен нулю.

Поэтому данный определитель будет равен 0.

Ответ: 0

Задача 6. Числа 1370, 1644, 2055, 3425 делятся на 137. Доказать, что определитель также делится на 137.

Решение

Необходимо доказать, что определитель делиться на 137, при этом каждая строка состоит из цифр, составляющие числа: 1370, 1644, 2055, 3425.

Разложим числа на разрядные слагаемые:

1370 = 1 · 1000 + 3 · 100 + 7 · 10 + 0;

1644 = 1 · 1000 + 6 · 100 + 4 · 10 + 4;

2055 = 2 · 1000 + 0 · 100 + 5 · 10 + 5;

3425 = 3 · 1000 + 4 · 100 + 2 · 10 + 5.

Отсюда видно, что число получается из цифр самого числа, т.е. к последней цифре прибавляется предыдущая, умноженная на 10, третья, умноженная на 100, вторая, умноженная на 1000. Применим данные действия к столбцам определителя, основываясь на свойстве определителя: если к элементам одной строки (столбца) прибавить элементы другой строки, умноженные на произвольное число, то определитель не измениться. В конечном результате, последний столбец будет располагать числа, данные в условии задачи, которые делятся на 137.

На основании свойства: общий множитель строки или столбца можно выносить за знак определителя.

В данном случае, определитель делиться на общий множитель 137.

Задача7. Найди матрицу Х, если

XA – 2B = E, где

Решение

Чтобы найти матрицу, выполним необходимые действия.

1) Найдем произведение числа 2 и матрицы В:

2) сложим матрицы 2В и Е:

3) разделим матрицу 2В + Е на матрицу А, т.е. умножим матрицу 2В + Е на обратную матрицу . Вычислим обратную матрицу :

А =

Определитель матрицы:

= 1·5·2 + 3·1·(-2) + (-1)·7·(-1) – (-1·5·3 + 2·(-2)·(-1) + 1·1·7) =

10 – 6 + 7 – (-15 + 4 + 7) = 15 ≠ 0.

Транспонированная матрица:

= .

Найдем алгебраические дополнения матрицы (элементы союзной матрицы), транспонированной матрицы:

= = 3 = = -3 = = 3

= = 5 = = 5 = = 0

= = -22 = = -13 = = 3

Союзная матрица: =

Найдем обратную матрицу:

= · = ·

(2В + Е) · =

(2В + Е) · =

Ответ:

В данном разделе рассмотрели различные способы решения практических задач с применением матриц. Далее рассмотрим применение матриц в некоторых сферах деятельности человека. [7]

3. Практические задачи на матричные исчисления в экономике

Рассмотрели применение матриц в математике. Как оказалось основным применением матриц является компактная запись, особенно инструментов линейной алгебры. Проиллюстрируем несколько задач связывающие теорию и практику. В прикладных науках матрица используется для записи данных и их преобразования. Разберём несколько экономических задач.

Задача 1. (умножение числа на матрицу)В магазине предлагаются скидки в 30% на товары С1, С2, С3, С4 в конце года. В таблице приведены запасы товаров в трех филиалах В1, В2, В3. Используя матрицу, найди стоимость акций в каждом из филиалов после скидок.

Таблица 1. Стоимость запасов в филиалах В1, В2, В3

	С1	С2	С3	С4
В1	65 000	40 000	55 000	35 000
В2	50 000	30 000	60 000	45 000
В3	70 000	55 000	75 000	50 000

Решение

Снижение на 30% означает, что товары продаются за 70% от стоимости. Используя данные таблицы 1, можно записать матрицу

Тогда после скидки стоимость акций будет выражаться выражением:

Представим в виде матрицы

Задача 2. (Дистрибутивный закон умножения матриц) В магазине продаются товары С1, С2, С3 в двух филиалах В1, В2. В таблице 2 приведены данные за неделю о количестве проданных товаров, о ценах на товары, о затратах магазина. Найдите прибыль каждого магазина за неделю, используя

а) общий анализ

в) удельный анализ

показать, что матричное умножение дистрибутивно.

Таблица 2. Стоимость товаров С1, С2, С3

	Количество товаров	Цена за товар	Расходы магазина
	В1	В2
С1	200	250	2.00	1.50
С2	350	400	4.00	3.00
С3	100	150	5.00	4.00

Решение

Количество товаров (Q), отпускные цены (P) и затраты магазина (C) могут быть представлены в матричной форме:

а) общий анализ

Общий доход в В1 составляет:

200 · 2.00 + 350 · 4.00 + 100 · 5.00 = 2300

и в В2:

250 · 2.00 + 400 · 4.00 + 150 · 5.00 = 2850

Эти расчеты можно записать в виде произведения двух матриц, т.е. общий доход равен произведению :

Аналогично находится общая стоимость

Тогда прибыль можно найти как разность двух матриц :

в) удельный анализ

Удельная прибыль составляет:

Общая прибыль определяется произведение количества товаров на удельную прибыль:

Из пунктов а) и в) имеем, что и равны, а . Значит,

Задача 3. (Дистрибутивный закон умножения матриц) Предприятие выпускает три вида продукции С1, С2, С3 и на производство данной продукции использует два вида сырья К1 и К2. В таблице 3 приведены данные о ценах каждого типа сырья, о планируемым выпуске продукции. Найдите затраты на сырье используя данные таблицы 3.

Таблица 3. Количество продукции С1, С2, С3

Виды сырья	Количество продукции	Цена каждого типа сырья
С1	С2	С3
К1	5	3	4	80
К2	7	1	2	50
Планируемый выпуск продукции	160	120	70

Решение

Количество три вида продукции каждого вида сырья (А), планируемый выпуск продукции (В) и цена каждого типа сырья (С) могут быть представлены в матричной форме:

, ,

Затраты сырья К₁ составляет:

5

и затраты сырья К₂ составляет:

7

Эти расчеты можно записать в виде произведения двух матриц, т.е. затрата на сырье равна произведению АВ:

Общая стоимость сырья будет равна:

Р = 1440

Эти расчеты можно записать в виде произведения двух матриц, т.е. общая стоимость сырья равна произведению АВ

АВ = 184 200

Задача 4. (сложение матриц и умножение числа на матрицу) В склад А1 и В1 поступили 9 одинаковых товаров в разном количестве. Данные о количестве товаров приведены в таблице 4. По договору производится ежемесячный завоз одинаковых партий товаров в каждый из складов. Найдите а) суммарный завоз товаров; в) годовой завоз товаров.

Таблица 4. Количество товаров на складах А₁ иВ₁

Вид товаров	Количество товаров в складе А1	Количество товаров в склад В1
Набор посуды (столовые приборы, чашки и тарелки)	14	23	19	12	45	50
Бытовая техника (чайник, пылесос и микроволновка)	38	41	11	17	21	36
Мебель (диваны, столы и шкафы)	8	32	17	15	18	29

Решение

Для удобства количество товаров в складах А₁ и В₁ могут быть представлены в матричной форме:

а) Расчет суммарного завоза можно записать в виде сложения двух матриц А₁ и В₁ :

А₁ + В₁ =

в) Расчет годового завоза можно записать в виде умножения числа на матрицу. Год состоит из 12 месяцев, поэтому умножаем 12 на матрицу А₁+В₁

А₁+В₁)=

Задача 5. (разность двух матриц) По заказу с завода в магазин поступили товары. Однако не все товары пользуются большим спросом. В таблице 5 приведены данные о начальном количестве товаров и о купленном количестве товаров. Найдите количество оставшихся товаров в магазине, используя данные таблицы. [8]

Таблица 5. Количество товаров

Товары	Начальное количество товаров	Купленное количество товаров
870	350	260	690	240	197
490	620	170	375	540	148
570	702	127	390	604	84

Решение

Начальное количество товаров (А) и купленное количество товаров (К) можно представить в матричной форме:

А=

Расчет количества оставшихся товаров в магазине можно найти как разность двух матриц А и К:

Заключение

В первую очередь работать над исследовательской работой под названием «Матрица и ее практическое применение» было очень интересно, так как во время работы я узнала много интересной информации. В особенности про виды матрицы и операции над ними. Перед нами стояла цель – узнать что такое матрица, их основное применение и каково значение в сферах жизни. Как оказалось, данный термин употребляется не только в математике, но и в других науках, как информатика, биология, химия, физика, экономика и психология. В первобытном обществе существовала теория бракосочетания, которая имела сходство с матрицей. С помощью этой абстрактной модели были представлены допустимые варианты бракосочетания.

В настоящее время матрицы получили широкое применение, так как матричный язык является неотъемлимой частью в сферах жизни. Матричная алгебра применима к решению большого круга важных задач, ведь она упрощает процедуру вычисления и облегчает понимание процесса. Если в математике и физике они используются в качестве компактной записи, то в биологии в решении реальных задач генетики, популяции и систематики. В экономике матрицы позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал (особенность социально-экономического комплекса, исходные данные, характеризующий уровень и структура), а также вести расчеты с ними. Все эти сведения и примеры ведут к тому, что матрицы использовались и будут использоваться в будущем. Поэтому я делаю вывод о том, что матричная алгебра широко применялась и применяется до сих пор, а также она всегда будет актуальной в разных сферах жизни. Следовательно, высказанная гипотеза полностью подтвердилась, а поставленная цель – достигнута.

Список использованной литературы

1. Ахмедханова А.И., Кожемякина В.А., Мамаев И.И. ПРИМЕНЕНИЕ МАТРИЦ В ЭКОНОМИКЕ // Международный студенческий научный вестник. – 2015. – № 3-4.; https://clck.ru/Rkcq3

2. В.Н.Задорожный, В.Ф.Зальмеж, А.Ю.Трифонов, А.В.Шаповалов. Линейная алгебра: Учебное пособие. – Томск: Изд-во ТПУ, 2009. – 310с.

3. П.С.Александров, А.И.Маркушевич, А.Я.Хинчин. Энциклопедия элементарной математики. ГТТИ, 1951. С.424

4. Интерактивный справочник https://clck.ru/RkcpJ

5. Д.К.Агишева, С.А.Зотова, В.Б.Светличная, Матрицы и их применение к решению систем линейных уравнений, /Методическое пособие. – 2001. – 61с

6. А.В.Конюх, В.В.Косьянчук, С.В.Майоровская, О.Н.Поддубная, Е.И.Шилкина. Сборник задач и упражнений по высшей математике: в 2ч. – Минск: БГЭУ, 2014. – 299с

7. Хомицкий Д.В., Горевский А.С., Тележников А.В. Сборник задач по линейной алгебре: практикум. Нижний Новгород: Издательство Нижегородского госуниверситета, 2010. – 51с. https://clck.ru/RkcrE

8. Shivdeep Kaur Assistant professor Mata Gujri College, Fatehgarh Sahib. Applications of Matrices. International Journal of Engineering Technology Science and Research IJETSR www.ijetsr.com ISSN 2394 – 3386 Volume 4, Issue 11 November 2017. https://clck.ru/Rkcrx

9. Лайтхилл Дж. и др. В.И. Новые области применения математики Под ред. Дж. Эндрюса и Р. Мак−Лауна. −М.: Мир, 2009.

10. Алгебра и начала математического анализа: учебник для общеобразоват.организаций: базов. и углубл. уровни/ Ш.А. Алимов, Ю.М.Колягин, М.В.Ткачева и др. – М.: Просвещение, 2016, – 463с.

11. Высшая математика для экономистов: Учебное пособие. – К.: Знания, Макаренко В.А., 2008 – 517с.

12. Математика: Учебник/ О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001.

13.Дидактический материал по математике: Учебное пособие/ О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001.

14. Практические занятия по математике. Н.В. Богомолов. – М.: Высшая школа, 1983.

Просмотров работы: 13470

Обратная матрица

Продолжаем изучать матрицы и сегодня на уроке мы научимся находить и вычислять обратную матрицу.

Обратная матрица

Матрица называется транспонированной к матрице , если выполняется условие:

, для всех , где и — элементы матриц и соответственно.

Проще говоря, транспонированная матрица — это перевернутая матрица, т.е. столбцы записаны строками, а строки столбцами.

Пример №1 Транспонировать матрицу А

Как я написал выше, транспонировать матрицу, значит, записать строки столбцами, а столбцы строками, т.е. первая строка становится первым столбцом, вторая строка — вторым столбцом и т.д.

И на этом, все — ничего ведь сложного? правда?

Свойства транспонированной матрицы А:

• 
• 
• 

Квадратная матрица А называется вырожденной (особенной), если ее определитель равен нулю, и невырожденной в противном случае.

Если А — невырожденная матрица, то существует и при том единственная матрица такая, что

, где

E — единичная матрица .

Матрица называется обратной к матрице А.

К большому сожалению найти обратную матрицу — это не значит поменять знаки на противоположные)) — это целый комплекс вычислений.

Мы с вами рассмотрим два основных метода решения обратной матрицы.

Метод присоединенной матрицы

Присоединенная (союзная) матрица определяется, как транспонированная к матрице, составленная из алгебраических дополнений соответствующих элементов матрицы А.

⇒ если А — невырожденная матрица, то

Пример №2 Найти обратную матрицу А

В первую очередь, мы должны доказать, что матрица — невырожденная, а значит, вычислим определитель:

det A = 0+6+16-0-30+4 = -4 ≠ 0 — матрица невырожденная.

Теперь находим присоединенную матрицу, а здесь. ВНИМАНИЕ.

Чтобы найти первый член присоединенной матрицы, т.е. нужно вычеркнуть первую строку и первый столбец и найти определитель оставшейся части:

Т.е. цифры над буквой А, обозначают не только место определителя в присоединенной матрице, но и какую строку и какой столбец нужно вычеркнуть из исходной, (1 цифра — строка, 2 цифра — столбец) и, конечно, определяют знак матрицы.

Для наглядности также распишу, как найти второй член :

Теперь, я думаю, принцип вам понятен.

Для большего удобства предлагаю вам записывать результаты на листе, также как они строят в матрице:

Собрав все полученные числа и расставив их по своим местам, получаем матрицу:

Но согласно определению, нам требуется транспонированная матрица, поэтому делаем это преобразование и получаем союзную матрицу:

Ну и последний штрих, чтобы найти обратную матрицу нужно каждый член союзной матрицы разделить на определитель исходной матрицы (который мы находили в самом начале, т.е. на -4):

Это и будет наш ответ, при желании сделать проверку нужно перемножить главную матрицу на обратную и если в результате получается единичная матрица — то решение верное!

Метод элементарных преобразований

Данный метод еще называют методом Гаусса и мы будем его еще применять при решении систем линейных уравнений.

К элементарным преобразования относятся:

1. перестановки строк (столбцов);
2. умножение строки (столбца) на некоторое число, отличное от нуля;
3. прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженные на некоторое число.

Пример №3 Найти обратную матрицу методом элементарных преобразований

Составляем расширенную матрицу :

Теперь наша задача состоит в том, чтобы первая часть матрицы (до черты) стала единичной, т.е. принимают значение , а остальные значение .

Займемся первым столбцом

Число в первой строке нужно превратить в для этого всю строку умножим на .

Чтобы во второй строке получить нужно из второй строки отнять первую строку, предварительно умноженную на .

Чтобы в третьей строке получить нужно из третьей строки вычесть вторую строку, предварительно умноженную на .

Все действия делаем от исходной расширенной матрицы, получаем:

Первый столбец теперь соответствует единичной матрице, поэтому

Займемся вторым столбцом

Теперь мы работаем уже с полученной матрицей, после преобразований первого столбца.

Чтобы в первой строке получить мы из первой строки отнимем вторую строку, предварительно умноженную на .

Чтобы во второй строке получить мы домножим вторую строку на .

Чтобы в третьей строке получить мы к третьей строке прибавим вторую строку, предварительно умноженную на

Выполнив данные действия, получаем:

Работаем дальше с третьим столбцом:

Чтобы в первой строке получить нужно из третьей строки вычесть первую строку, предварительно умножив на .

Чтобы получить во второй строке нужно к третьей строке прибавить вторую строку, предварительно умножив на .

Чтобы в третьей строке получить нужно домножить третью строку на .

В первой части матрицы мы получили единичную матрицу, а вторая часть матрицы (после черты) и будет нашей обратной матрицей:

Оба способа нахождения обратной матрицы, довольно простые, если в них вникнуть, самое главное — не допустить ошибок в вычислениях, а остальное придет со временем.

Источник

Теорема. Опр. Матрица называется присоединенной (союзной) к квадратной матрице А, если она состоит из алгебраических дополнений элементов транспонированной матрицы

Обратная матрица

Опр. Матрица 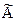называется присоединенной (союзной) к квадратной матрице А, если она состоит из алгебраических дополнений элементов транспонированной матрицы А т . Чтобы получить присоединенную матрицу 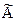, следует транспонировать матрицу А, а затем все ее элементы заменить их алгебраическими дополнениями, то есть

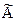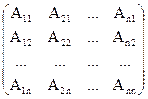= (3.1)

Опр. Квадратная матрица А называется вырожденной (особенной), если ее определитель |A|=0, и невырожденной, если ее определитель |A|¹0.

Опр. Квадратная матрица А — 1 называется обратной (инверсной) к квадратной матрице А, если выполняется условие

А — 1 ×А = А×А — 1 = Е (3.2)

NB. Обратная матрица А -1 возможна только для невырожденной матрицы А.

Для любой невырожденной квадратной матрицы А существует единственная обратная матрица А — 1 , которая находится по формуле

А — 1 = 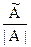(3.3)

1) Из определения А — 1 ×А = А×А — 1 следует, что А и А — 1 — это квадратные матрицы одного порядка.

Пусть матрица А – невырожденная, то есть |A|¹0. Тогда, по правилу умножения матриц, по теореме Лапласа и по свойству 9 определителей, получим

А× = × = =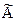

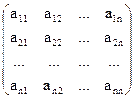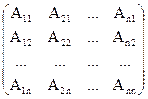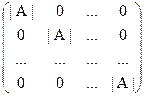= |A|× 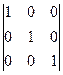= |A|×E

Следовательно, А× 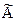= |A|×E. Аналогично доказывается, что 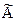×А = |A|×E.

Из А× 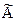= |A|×E Þ А — 1 ×А× 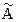= А — 1 ×|A|×E Þ Е× 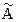=А — 1 ×|A| Þ 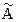=А — 1 ×|A| Þ А — 1 = .

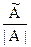2) Докажем единственность обратной матрицы. Предположим, что для матрицы А существует еще одна обратная матрица В. Тогда, согласно определению произведение А×В=Е. Обе части последнего равенства умножим слева на обратную матрицу А — 1 и получим: А — 1 ×А×В = А — 1 ×Е Þ Е×В = А — 1 ×Е Þ В = А — 1 . Fin.

Свойства обратной матрицы:

1) |A — 1 | = ;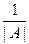

Источник