Как найти транспортиром тупой угол

Как найти транспортиром тупой угол

  1. Главная
  2. Справочники
  3. Справочник по математике 5-9 класс
  4. Геометрия
  5. Измерение углов. Транспортир. Виды углов

Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения (1 мм, 1 см, 1 м и т.д.). Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения –  с  градусом, записывают так 1°.

Градусная мера угла – это число, которое показывает, сколько раз градус и его части укладываются в данном угле.

Пример:

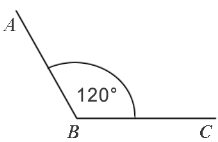
Градусная мера угла ABC равна 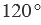. Говорят: “Угол ABC равен 120 градусам”. Пишут: .

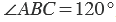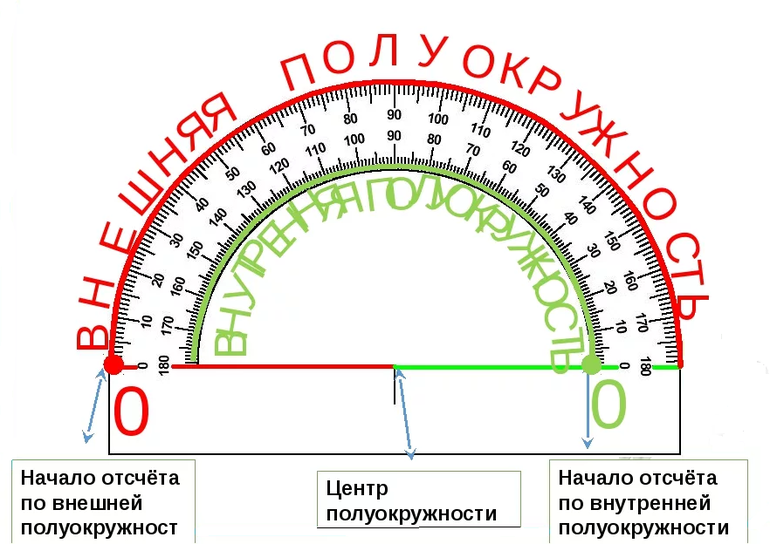
Транспортир – это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .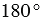

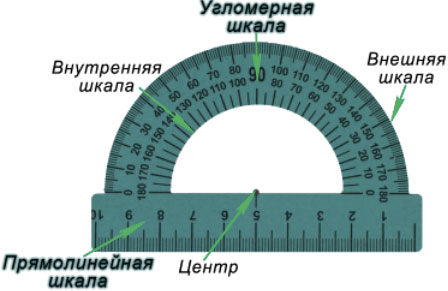
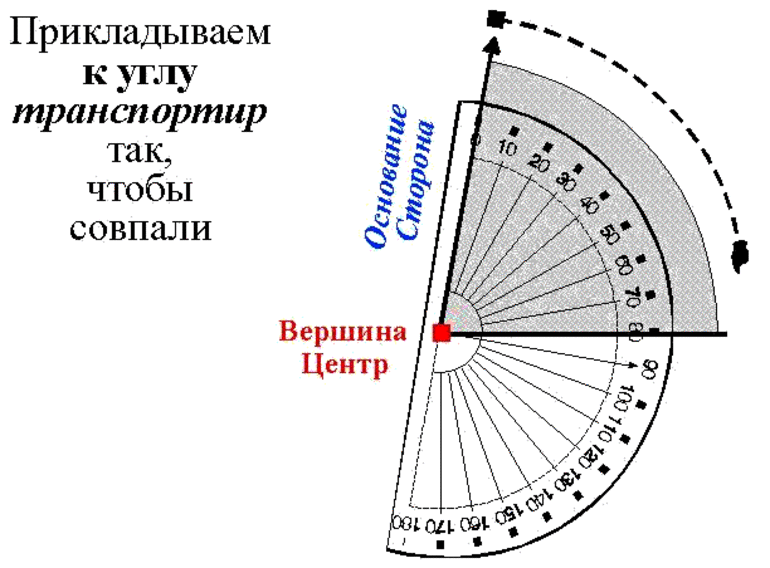
Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.

Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).

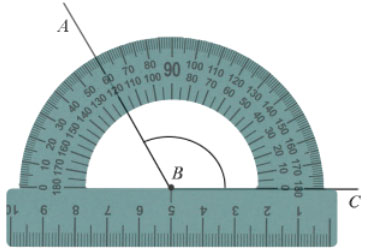
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .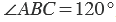

Свойства:

         АОС = АОВ + ВОС.

Виды углов:

  1. Острый угол – угол, градусная мера которого меньше 90°.

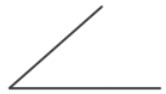
  1. Прямой угол – угол, градусная мера которого равна 90°.

  1. Тупой угол – угол, градусная мера которого больше 90°, но меньше 180°.

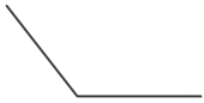
  1. Развернутый угол – угол, градусная мера которого равна 180°.

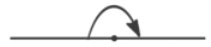
Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 900.

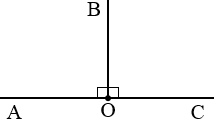
АОС – развернутый, ОВ – биссектриса, АОВ = ВОС = 900.

Советуем посмотреть:

Отрезок

Ломаная

Четырехугольники

Единицы измерения площадей. Свойства площадей

Прямоугольник, его периметр и площадь. Ось симметрии фигуры

Квадрат. Периметр и площадь квадрата.

Многоугольники. Правильные многоугольники. Равенство фигур.

Плоскость

Прямая

Луч

Шкалы и координаты

Прямоугольный параллелепипед. Пирамида.

Объем прямоугольного параллелепипеда

Куб. Площадь поверхности куба

Куб. Объем куба

Угол. Обозначение углов

Прямой и развернутый угол

Чертежный треугольник

Треугольник и его виды

Окружность, круг, шар

Цилиндр, конус

Отрезок-xx

Геометрия


Правило встречается в следующих упражнениях:

5 класс

Задание 1650,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1655,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1660,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1693,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1771,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 311,
Мерзляк, Полонский, Якир, Учебник

Номер 1029,
Мерзляк, Полонский, Якир, Учебник

Номер 1190,
Мерзляк, Полонский, Якир, Учебник

Номер 5,
Мерзляк, Полонский, Якир, Учебник

Номер 14,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 206,
Мерзляк, Полонский, Якир, Учебник

Номер 392,
Мерзляк, Полонский, Якир, Учебник

Номер 1217,
Мерзляк, Полонский, Якир, Учебник

Номер 1283,
Мерзляк, Полонский, Якир, Учебник

Задание 173,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 287,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 724,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 773,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1352,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1385,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 759,
Мерзляк, Полонский, Якир, Учебник

Источник


Загрузить PDF


Загрузить PDF

Транспортир — это простой и удобный инструмент для измерения и построения углов. В основном распространены транспортиры полукруглой формы, хотя существуют и круглые транспортиры, рассчитанные на 360 градусов. Если вы впервые столкнулись с транспортиром и не знаете, как им пользоваться, прочитайте эту статью! Это совсем несложно: несколько простых шагов, и вы как следует освоите этот полезный инструмент.

  1. Изображение с названием Use a Protractor Step 1

    1

    Оцените, к какому типу относится интересующий вас угол. Углы можно разделить на три класса: острые, тупые и прямые. Острые углы относительно узки (менее 90 градусов), тупые углы шире (более 90 градусов), а величина прямых углов составляет 90 градусов (их стороны перпендикулярны друг другу).[1]
     Оцените на глаз, к какому типу принадлежит тот угол, который вы собираетесь измерить. Предварительная оценка поможет вам определить необходимый диапазон и правильно выбрать шкалу транспортира.

    • На первый взгляд мы можем сказать, что выше изображен острый угол, то есть его величина меньше 90 градусов.

  2. 2

    Приложите центр транспортира к вершине измеряемого угла.[2]
     В середине транспортира есть небольшое отверстие. Приложите транспортир к углу так, чтобы это отверстие совпало с вершиной угла.

  3. Изображение с названием Use a Protractor Step 3

    3

    Поверните транспортир так, чтобы одна из сторон угла совпала с основанием инструмента. Не спеша поворачивайте транспортир и следите за тем, чтобы вершина угла оставалась в центре. В результате одна из сторон угла должна совместиться с основанием транспортира.[3]

    • При этом вторая сторона угла должна пересекать дугу транспортира (его округлую часть).

  4. 4

    Проследите за второй стороной угла, которая пересекает дугу транспортира. Если вторая сторона не доходит до дуги инструмента, продлите ее. Можно также приложить к этой стороне угла лист бумаги, который доходил бы до дуги транспортира. Пересекаемое число покажет вам величину угла в градусах.

    • В приведенном выше примере величина угла составляет 70 градусов. При этом мы пользуемся меньшей шкалой, так как определили ранее, что имеем дело с острым углом, то есть его величина не превышает 90 градусов. Для тупых углов следует использовать более крупную шкалу со значениями больше 90 градусов.
    • На первых порах можно путаться со шкалой. Большинство транспортиров имеют две шкалы, одну на внутренней и вторую на внешней стороне округлой части. Это сделано для того, чтобы было удобно измерять углы как левой, так и правой ориентации.

    Реклама

  1. 1

    Проведите прямую линию. Это будет опорная линия, которая послужит одной из двух сторон будущего угла. С ее помощью вы определите направление, в котором следует провести вторую сторону угла. Как правило, первую прямую линию удобно провести горизонтально.

    • При этом можно воспользоваться прямым краем транспортира.
    • Длина линии не важна.

  2. 2

    Расположите центр транспортира на одном из концов проведенной линии. Это будет вершина будущего угла. Отметьте на бумаге точку вершины.[4]

    • Не обязательно располагать вершину на краю линии. Вершина угла может размещаться в любой точке на линии, просто удобнее использовать крайнюю точку.

  3. 3

    Отыщите на соответствующей шкале транспортира необходимый вам угол. Приложите к прямой линии основание транспортира и отметьте на бумаге соответствующее число градусов. Если необходимо построить острый угол (менее 90 градусов), используйте шкалу с меньшими значениями. Для тупого угла воспользуйтесь шкалой с большими величинами.

    • Помните о том, что основание транспортира — это его прямая часть. Совместите его центр с вершиной будущего угла и отметьте на бумаге необходимую величину угла.
    • На приведенном выше видео величина угла составляет 36 градусов.

  4. 4

    Проведите вторую сторону угла. С помощью линейки, прямого края транспортира или другого инструмента проведите вторую сторону угла — соедините вершину со сделанной ранее меткой. В результате у вас получится заданный угол. С помощью транспортира можно измерить угол и убедиться, что все правильно.

    Реклама

Что вам понадобится

  • карандаш или ручка
  • бумага
  • транспортир
  • линейка (необязательно)

Об этой статье

Эту страницу просматривали 242 008 раз.

Была ли эта статья полезной?

Источник

Транспортир

Люди обычно сталкиваются с транспортирами в математике, когда учатся в школе создавать точные геометрические фигуры. Возможно, у многих из них никогда больше не будет причин снова использовать эти приборы, тем не менее транспортиры имеют долгую историю применения в различных областях.

История изобретения

Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.

Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников. Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.

Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.

Как измерить угол транспортиром

Возможно, в то же время, учёные Индии также разработали тригонометрическую систему, основанную на функции синуса, которая, в отличие от используемого в настоящее время синуса, была не пропорцией, а длиной стороны, противоположной углу в прямом треугольнике этой гипотенузы. Индийские математики использовали разные значения для этого в своих таблицах.

Томас Бландевиль рассказал о приборе специально созданном, для рисования и измерения фигур в своём «Кратком описании универсальных карт» 1589 года. Как видно из названия, он применял его, чтобы править навигационные карты для использования в высоких широтах.

Другие европейские математики также описывали подобные приборы примерно в то же время. Независимо от того, кто первым придумал этот инструмент, к началу XVII века он вошёл в стандартную практику мореплавателей и геодезистов. К XVIII веку транспортиры начали появляться в учебниках по геодезии и геометрии.

Транспортиры в современном понимании возникли во второй половине XVIII века, когда такие учёные, как Джесси Рамсден и Георг Фридрих Брандер, усовершенствовали ранее созданные устройства.

В то время предпочтительными материалами для их изготовления были:

что такое транспортир в математике

  • дерево;
  • латунь;
  • серебро;
  • медь;
  • слоновая кость.

В первой половине XX века начали применять олово и целлулоид.

Называться транспортиром (рус.) прибор стал в 1610 году. Термин произошёл от средневекового слова protractor, что означает «переносить», который, в свою очередь, произошел от латинского слова protrahere «тянуть вперёд».

Разновидности и использование

Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением. Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).

как правильно пользоваться транспортиром

Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.

Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.

Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.

Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.

Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:

  • теодолит;
  • оптический транспортир в строительной промышленности и геодезии;
  • инклинометр для определения уклонов и косвенной альтиметрии;
  • секстант для навигации.

Измерение градусов угла

Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.

Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.

как пользоваться транспортиром инструкция

Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.

Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.

Нижнюю планку (основание) транспортира нужно выставить горизонтально. Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.

Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.

Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.

Построение угла

Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.

Как пользоваться транспортиром

Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом. И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.

Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса. И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.

Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.

Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.

Источник


Download Article


Download Article

Using a protractor can be tricky, especially if you are using one with two sets of numbers. If you understand the concept of acute and obtuse angles, however, learning how to use a protractor is easy. It is first necessary to understand the features on a protractor, so that you understand how to use it. Once you have this understanding, you can quickly use a protractor to make any size angle between 0 and 180 degrees.

  1. Image titled Make Angles in Math Using a Protractor Step 1

    1

    Locate the base line. This horizontal line is at the bottom of the protractor. One vector of your angle should always line up with the base line.[1]

    • Since a straight line is 180 degrees, the base line marks a 180-degree angle.

  2. Image titled Make Angles in Math Using a Protractor Step 2

    2

    Locate the origin hole. This is a small hole at the midpoint of the base line. You use this hole to create the vertex of the angle. The vertex is the point at which the two vectors meet, creating an angle.[2]

    Advertisement

  3. Image titled Make Angles in Math Using a Protractor Step 3

    3

    Locate the degree measurements. Most protractors have two sets of numbers, an outer set and an inner set. Which set of numbers you use will depend on whether your angle opens to the right, or opens to the left. The sets of numbers can be set up differently on each protractor, so you need to figure out for yourself which set of numbers to use. To determine which set of numbers to use, you need to understand right, acute, and obtuse angles.[3]

    4. Advertisement

  1. Image titled Make Angles in Math Using a Protractor Step 4

    1

    Identify a right angle. A right angle has a measurement of 90 degrees.[4]
     A 90-degree angle will look like the corner of a square. The two vectors of the angle are perpendicular, and open exactly halfway towards a straight line (which is 180 degrees).

    • When you line up the base line of the protractor with one vector of a right angle, the other vector will line up with the 90-degree mark of the protractor. This is halfway between either side of the protractor. Both the inner and outer sets of numbers on the protractor will show 90 degrees at this point.

  2. Image titled Make Angles in Math Using a Protractor Step 5

    2

    Identify an acute angle. An acute angle has a measurement of less than 90 degrees.[5]
     This means that the two vectors will be closer together than they are in a 90-degree angle. They will open less than halfway towards a straight line. If the angle you are drawing is less than 90 degrees, make sure you use the set of numbers that gives you the smaller angle.

    • For example, a 45-degree angle is acute, because 45 is less than 90. If you line up the base line of the protractor with one vector of a 45-degree angle, the other vector will line up with the 45-degree mark and the 135-degree mark of the protractor. You will know which line to look at because you know it is an acute angle, and an acute angle should be less open than a 90-degree angle.

  3. Image titled Make Angles in Math Using a Protractor Step 6

    3

    Identify an obtuse angle. An obtuse angle has a measurement of more than 90 degrees.[6]
     The two vectors of an obtuse angle are farther apart than they are in a 90-degree angle. They will open more than halfway to a straight line. If the angle you are drawing is more than 90 degrees, make sure you use the set of numbers that gives you the larger angle.

    • For example, a 120-degree angle is obtuse, because 120 is greater than 90. If you line up the base line of the protractor with one vector of a 120-degree angle, the other vector will line up with the 120-degree mark and the 60-degree mark. If you know you are looking for an obtuse angle, you know to use the 120-degree mark, because an obtuse angle should be more open than a 90-degree angle.

  4. Image titled Make Angles in Math Using a Protractor Step 7

    4

    Ignore the orientation of the angle. Whether an angle opens to the left or to the right does not affect whether it is right, acute, or obtuse. All that matters is the measurement of the angle in degrees. The way the angle opens only changes the set of numbers you will look at on your protractor.

    • For example, if a 45-degree angle opens to the right, you might have to look at the inner set of numbers. But if you were to turn that angle around so that it opens to the left, it would still measure 45 degrees, but this time when you measure it, you would have to look at the outer set of numbers.

    5. Advertisement

  1. Image titled Make Angles in Math Using a Protractor Step 8

    1

    Determine the measurement of the angle you are drawing. Note whether the angle is acute or obtuse.

    • For example, you might need to draw a 45 degree angle. Since 45 is less than 90, this is an acute angle. That means you will use the set of numbers that gives you the smaller angle, since the angle will open less than halfway towards a straight line.

  2. Image titled Make Angles in Math Using a Protractor Step 9

    2

    Draw a straight line. You can do this using a ruler or the straightedge of your protractor. This line will form the first vector of your angle.[7]

    • The length of the line does not necessarily matter, but the longer it is, the easier it will be to line it up to the base line. The best method is to draw a line running the length of the protractor’s edge.

  3. Image titled Make Angles in Math Using a Protractor Step 10

    3

    Align the origin hole at about the midpoint of the line. Make sure that the base line of the protractor lines up with the line you drew.[8]
     Draw a midpoint for your reference.

  4. Image titled Make Angles in Math Using a Protractor Step 11

    4

    Mark the angle measurement. Make this mark along the outside of the protractor by the appropriate degree mark. To make sure you are making the mark at the correct place, ask yourself the following questions:

    • Will my angle open to the right, or to the left?
    • Is my angle less (acute) or greater (obtuse) than 90 degrees?

  5. Image titled Make Angles in Math Using a Protractor Step 12

    5

    Draw the second vector of the angle. Use a ruler or straightedge to join the origin point on the base line to the degree mark.[9]

  6. Image titled Make Angles in Math Using a Protractor Step 13

    6

    Erase any unnecessary lines. You will likely need to erase part of the base line you drew. Otherwise, you may have two angles drawn, and it may be unclear to another person which is your intended angle.

    7. Advertisement

Add New Question

  • Question

    What are angles opening to the left called?

    Community Answer

    The type of angle is not determined by which way it opens. An angle is either acute, right, or obtuse, no matter which way it opens. All that matters is the size of the angle. For example, you can draw a 45 degree angle opening to the left, or opening to the right. Either way, it is an acute angle.

  • Question

    How do I use a protractor that doesn’t have a hole?

    Donagan

    Use the outside, curved edge.

  • Question

    What about the angle that we want to make in the circle?

    Donagan

    If you’re referring to a central angle, draw a diameter. Line up the bottom of the protractor with the diameter so that the midpoint of the protractor aligns with the center of the circle. Use the protractor to draw any central angle up to 180°, using another diameter (or radius) to complete the angle.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Advertisement

  • An acute angle is an angle from 0 to 89 degrees, which is less than a right angle.

  • A right angle is an angle that is exactly 90 degrees.

  • An obtuse angle is an angle greater than a right angle, but less than a straight angle. It can be anything ranging from 91 degrees to 179 degrees.

Show More Tips

Thanks for submitting a tip for review!

Advertisement

References

About This Article

Thanks to all authors for creating a page that has been read 47,815 times.

Did this article help you?

Источник

На этом уроке мы познакомимся с прибором для
измерения углов – транспортиром. Научимся с помощью транспортира измерять и
строить углы.

Коснёмся истории, чтобы узнать, как появился транспортир.

Понятие «градуса» и появление первых инструментов для
измерения углов связывают с развитием цивилизации в древнем Вавилоне. Хотя само
слово градус имеет латинское происхождение (градус
– от лат. gradus – “шаг, ступень”). Предполагают, что создание
транспортира было связано с созданием первого календаря.

Древние вавилонские математики и астрономы полный
оборот (окружность) разделили на столько частей, сколько дней в году. Они
думали, что в году 360 дней. Поэтому круг,
обозначающий год, они разделили на 360
равных частей. Такое изображение было очень удобным. На нём можно было отмечать
каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой
части дали название – градус.
Каждый градус разделили на 60 минут,
а минуту – на 60 секунд.
Градусная мера сохранилась и до наших дней.

Итак, для измерения углов применяют транспортир.

Транспортир
состоит из линейки (прямолинейной шкалы) и полуокружности
(угломерной шкалы). Центр этой полуокружности отмечен на транспортире
или штрихом, или отверстием. Штрихи шкалы транспортира делят полуокружность на 180 долей. В некоторых моделях – на 360 долей – это круглые транспортиры.

Если из центра этой полуокружности провести лучи
через каждый штрих, то получится 180 углов.
Каждый, из которых равен  доле
развернутого угла.

Определение

Такие углы принято называть градусами. 

Градусы обозначают вот таким знаком °.

Каждое деление шкалы транспортира равно 1°. Кроме делений по 1°
на шкале транспортира есть ещё деления по 5°
и по 10°.

А
теперь давайте разберёмся, как с помощью транспортира измерить угол. Запомните алгоритм
измерения углов:

1) 
Совместить вершину угла с центром транспортира.

2) 
Расположить транспортир так, чтобы одна из сторон угла проходила через
начало отсчёта на шкале транспортира; 0 –
начало отсчёта.

3)
Найдём штрих на шкале, через который пройдёт вторая сторона угла; (заметьте,
используем ту шкалу для определения градусной меры угла, где располагается
нулевой градус).

4) 
Смотрим, через какой штрих проходит вторая сторона и какой градус
соответствует этому штриху.

На нашем слайде угол АОВ
равен 50°. Пишут так: 

Развёрнутый угол равен 180°.
Так как мы с вами выяснили, что прямой угол равен половине развёрнутого угла,
то он равен

Прямой угол
равен 90°.

Так как равные углы полностью совмещаются при наложении,
то равные углы имеют равные градусные меры. Следовательно, больший
угол имеет большую градусную меру, меньший угол имеет меньшую
градусную меру.

Транспортир применяют и не только для измерения углов, а
также и для их построения.

Запомним алгоритм построения углов.

Алгоритм будем исследовать на конкретном примере:
построить угол МКN
равный 110°.

1.    
Отметим
произвольную точку и обозначим её буквой К.

2.    
Начертим
луч с началом в точке А и на нём отметим произвольную точку М. Получили луч КМ.

3.    
Наложим
транспортир так, чтобы центр его совпал с точкой К, а луч КМ прошёл через
начало отсчёта на шкале.

4.    
На
этой же шкале транспортира найдём штрих, который соответствует 110°. Отметим на
чертеже точку N
против штриха с отметкой 110°.

5.    
Проведём
луч КN.
Построенный нами угол МКN и есть искомый.

6.    
Не
забудем записать МКN = 110°.

Такой же угол можно построить и по другую сторону от луча КМ.

Повсюду есть углы
любые:
Прямые, острые, тупые,
Есть смежные, развёрнутые есть,
Их много, всех не перечесть.

Определение

Если угол меньше 90°,
то его называют острым углом.

Если угол больше 90°,
но меньше 180°, то его называют тупым
углом.

На экране изображены угол АОС
– острый и угол МКN – тупой. Градусная мера угла АОС
равна 30°,
т.е. меньше 90°, следовательно, он острый.
Градусная мера угла МКN
равна 120°, т.е. больше 90°, но меньше 180°,
следовательно, он тупой.

Итоги

Итак, сегодня на уроке мы познакомились с прибором для
измерения углов – транспортиром. Научились с помощью него измерять и строить
углы.

Источник

Добавить комментарий