This is an answer to your second question, about the relation $R={langle 1,2rangle,langle 2,2rangle,langle 3,2rangle}$. We can check transitivity in several ways.
(1) List all of the linked pairs:
$$begin{align*}
&langle 1,2ranglelandlangle 2,2rangletag{1}\
&langle 2,2ranglelandlangle 2,2rangletag{2}\
&langle 3,2ranglelandlangle 2,2rangletag{3}
end{align*}$$
If $R$ is to be transitive, $(1)$ requires that $langle 1,2rangle$ be in $R$, $(2)$ requires that $langle 2,2rangle$ be in $R$, and $(3)$ requires that $langle 3,2rangle$ be in $R$. And since all of these required pairs are in $R$, $R$ is indeed transitive.
(2) Check all possible pairs of endpoints. For example, to see whether $langle 1,3rangle$ is needed in order for $R$ to be transitive, see whether there is a ‘stepping-stone’ from $1$ to $3$: is there an $a$ such that $langle 1,arangle$ and $langle a,3rangle$ are both in $R$? If so, transitivity will require that $langle 1,3rangle$ be in $R$ as well. As it happens, there is no such $a$, so transitivity of $R$ doesn’t require that $langle 1,3rangle$ be in $R$. Do this check for each of the nine ordered pairs in ${1,2,3}times{1,2,3}$.
(3) Use the matrix
$$M_R=begin{bmatrix}0&1&0\0&1&0\0&1&0end{bmatrix}$$
of the relation. You may not have learned this yet, but just as $M_R$ tells you what ‘one-step paths’ in ${1,2,3}$ are in $R$,
$$M_R^2=begin{bmatrix}0&1&0\0&1&0\0&1&0end{bmatrix}begin{bmatrix}0&1&0\0&1&0\0&1&0end{bmatrix}=begin{bmatrix}0&1&0\0&1&0\0&1&0end{bmatrix}$$
counts the number of $2$-step paths between elements of ${1,2,3}$. The entry in row $i$, column $j$ is the number of $2$-step paths from $i$ to $j$. (By a $2$-step path I mean something like $langle 3,2ranglelandlangle 2,2rangle$: the first pair takes you from $3$ to $2$, the second takes from $2$ to $2$, and the two together take you from $3$ to $2$.)
In order for $R$ to be transitive, $langle i,jrangle$ must be in $R$ whenever there is a $2$-step path from $i$ to $j$. For this relation that’s certainly the case: $M_R^2$ shows that the only $2$-step paths are from $1$ to $2$, from $2$ to $2$, and from $3$ to $2$, and those pairs are already in $R$.
In the original problem you have the matrix
$$M_R=begin{bmatrix}1&0&1\0&1&0\1&0&1end{bmatrix};,$$
and
$$M_R^2=begin{bmatrix}1&0&1\0&1&0\1&0&1end{bmatrix}begin{bmatrix}1&0&1\0&1&0\1&0&1end{bmatrix}=begin{bmatrix}2&0&2\0&1&0\2&0&2end{bmatrix};.$$
The $2$’s indicate that there are two $2$-step paths from $1$ to $1$, from $1$ to $3$, from $3$ to $1$, and from $3$ to $3$; there is only one $2$-step path from $2$ to $2$. From $1$ to $1$, for instance, you have both $langle 1,1ranglelandlangle 1,1rangle$ and $langle 1,3ranglelandlangle 3,1rangle$. But the important thing for transitivity is that wherever $M_R^2$ shows at least one $2$-step path, $M_R$ shows that there is already a one-step path, and $R$ is therefore transitive.
In short, find the non-zero entries in $M_R^2$. If $M_R$ already has a $1$ in each of those positions, $R$ is transitive; if not, it’s not.
Рассмотрим
специальные
свойства бинарных отношений на множестве
A.
Свойства бинарных отношений.
1. Отношение
на AA
называется рефлексивным,
если (a,a)
принадлежит
для всех a
из A.
2. Отношение
называется антирефлексивным,
если из (a,b)
следует ab.
3. Отношение
симметрично,
если для a
и b,
принадлежащих A,
из (a,b)
следует, что (b,a).
4. Отношение
называется антисимметричным,
если для a
и b
из A,
из принадлежности (a,b)
и (b,a)
отношению
следует, что a=b.
5. Отношение
транзитивно,
если для a,
b
и c
из A
из того, что (a,b)
и (b,c),
следует, что (a,c).
Пример ..
-
Отношения
«=» и «£»
являются рефлексивными отношениями
на множестве N, но отношение «<» таковым
не является.
-
Отношение
«=» является симметричным, а «<» и «£»
– нет.
-
Отношение
на N
«являются взаимно простыми» является
симметричным.
-
Отношения
«<», «£»
и «=» являются транзитивными, а отношение
= {(a,b):
a,b
ÎN
и b
= a+1}
– нет, так как 34
и 45,
но не 35.

Как по матрице представления определить свойства бинарного отношения
1. Рефлексивность:
на главной диагонали стоят все единицы,
звездочками обозначены нули или единицы.
 .
.
2.
Антирефлексивность:
на главной диагонали все нули.
3. Симметричность:
если
![]() .
.
-
Антисииметричность:
Mij=1,
i
≠j,
Mji=0
Матрицы бинарных отношений
Рассмотрим
два конечных множества A
={a1,a2,…,am}
и B={b1,b2,…,bn}
и бинарное отношение
![]() .
.
Определим
матрицу
![]() размераm×n
размераm×n
бинарного отношения Р по следующему
правилу:
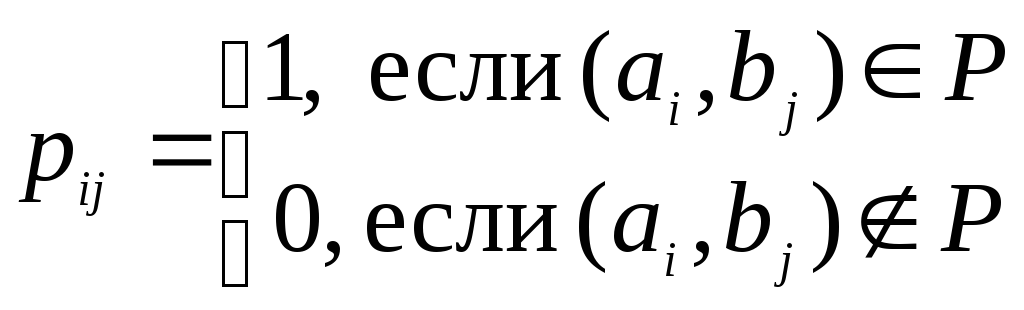
Полученная
матрица содержит полную информацию о
связях между элементами.Любая матрица,
состоящая из 0 и 1, является матрицей
некоторого бинарного отношения.
П РИМЕР
РИМЕР
1. Матрица бинарного отношения![]() ,A={1,2,3},
,A={1,2,3},
заданного на рисунке
имеет
вид 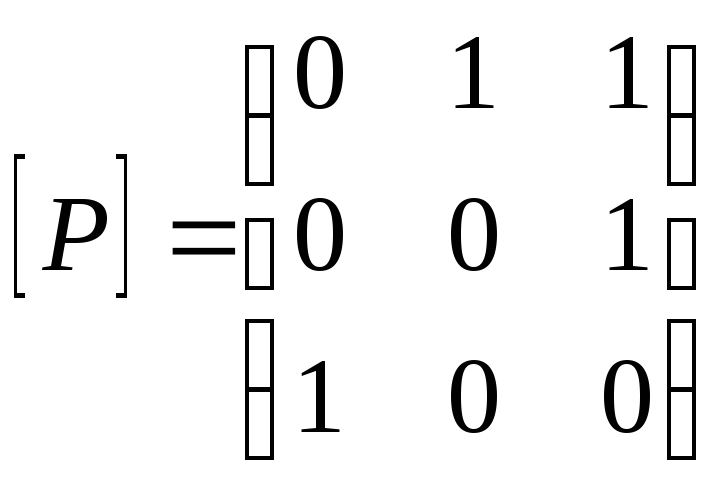
Основные
свойства матриц бинарных отношений:
-
Если
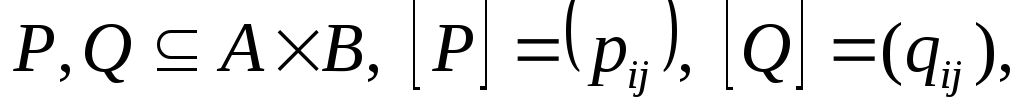 то
то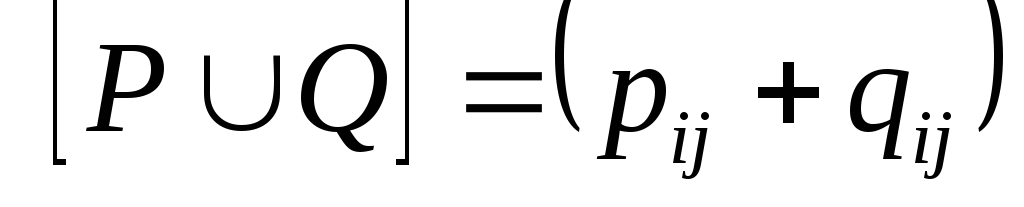 и
и
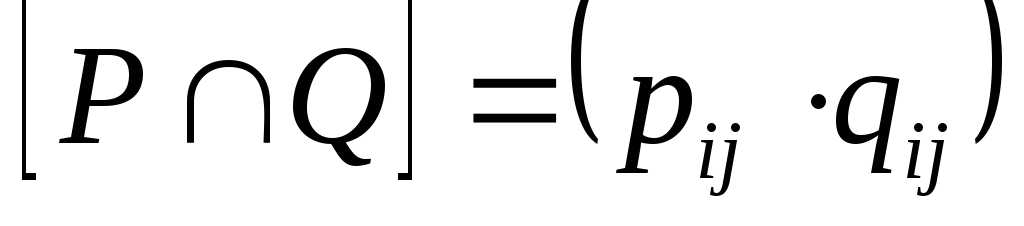 ,
,
где сложение осуществляется по правилам
0+0=0, 1+1=0+1=1+0=1, а умножение – обычным
способом.
Итак,
![]()
-
Матрица
 получается перемножением соответствующих
получается перемножением соответствующих
элементов из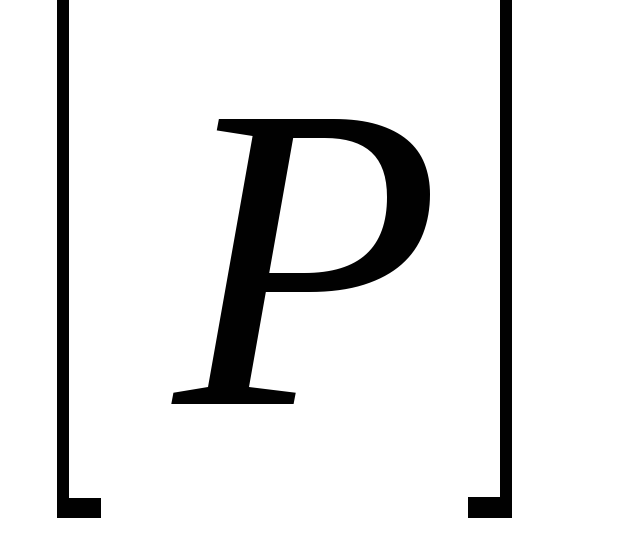 и
и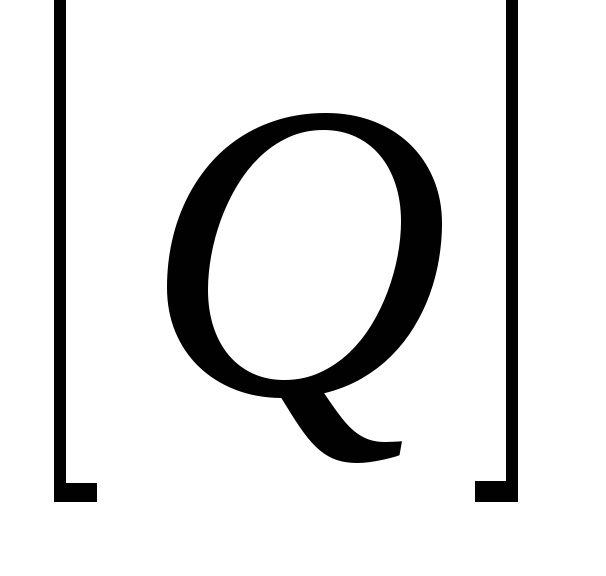 :
: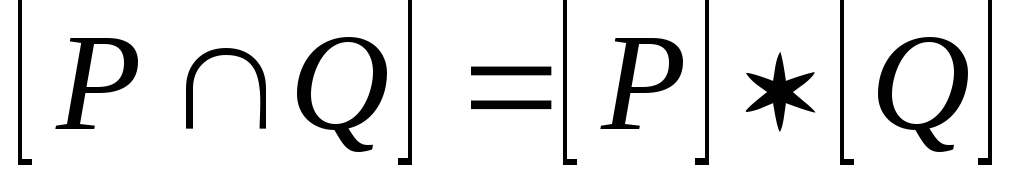 .
. -
Если
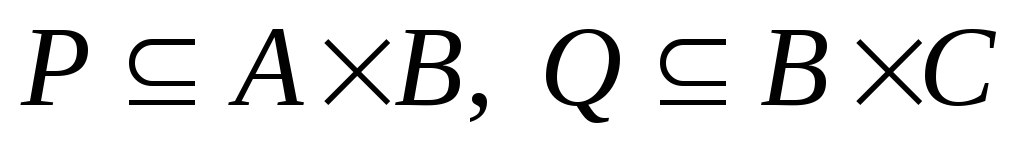 ,
,
то
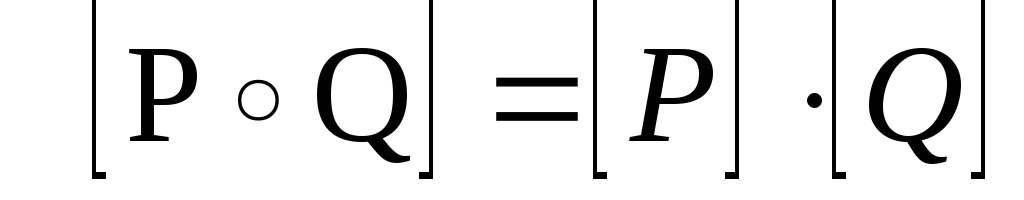 ,
,
где умножение матриц производится по
обычному правилу умножения матриц, но
произведение и сумма элементов – по
определённым в свойстве 1 правилам. -
Матрица
обратного отношения Р-1
равна транспонированной матрице
отношения Р:
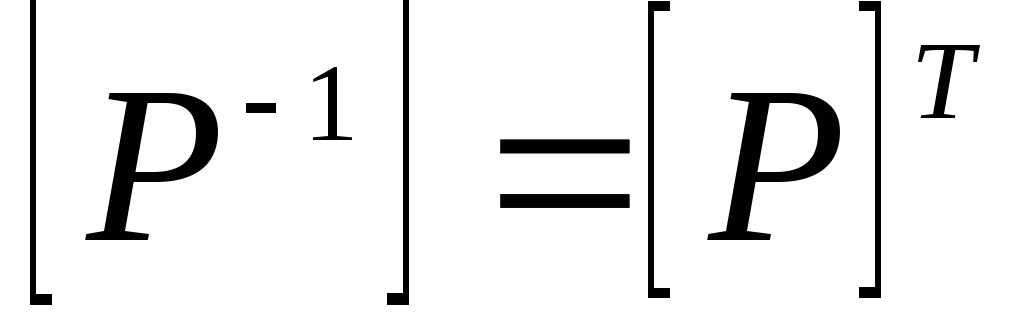 .
. -
Если
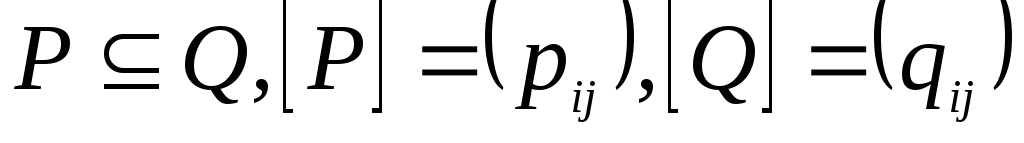 ,
,
то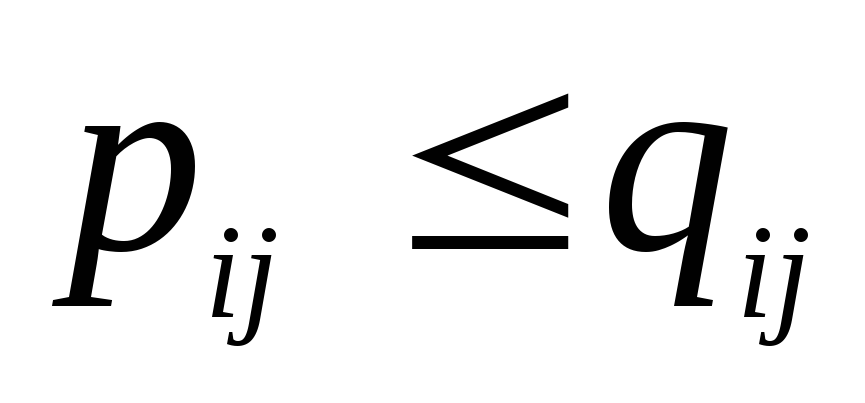 .
. -
Матрица
тождественного отношения idA
единична:
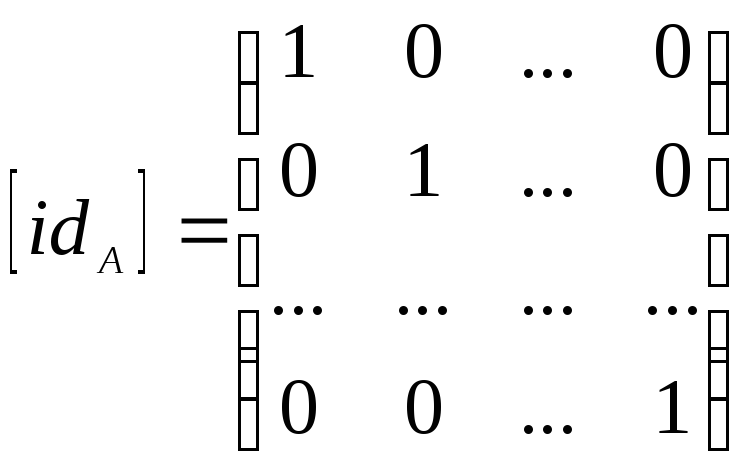
ПРИМЕР
2. Пусть
![]()
![]() – матрицы отношений P и Q. Тогда
– матрицы отношений P и Q. Тогда
![]()
![]()
ПРИМЕР
3.
Если
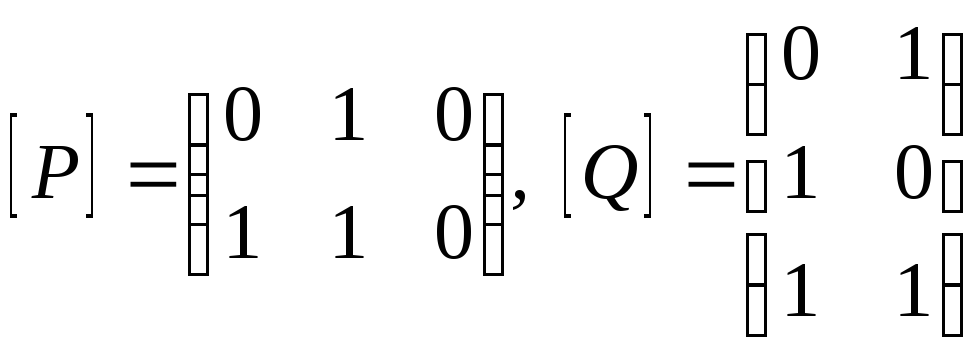 ,
,
то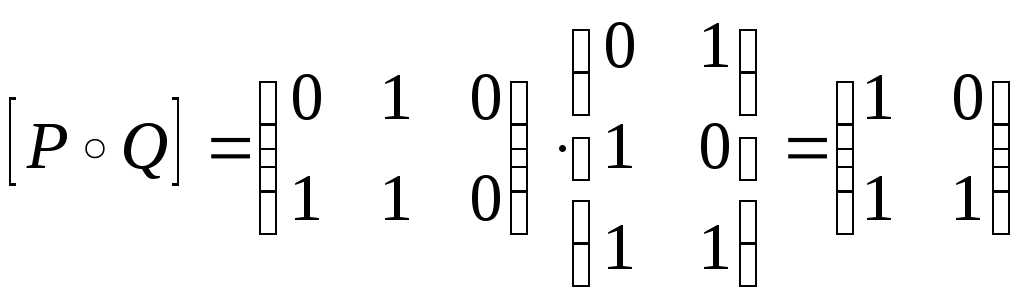
Рассмотрим
свойства отношений на языке матриц.
Пусть
Р – бинарное отношение на множестве
![]() .
.
Отношение
Р:
-
рефлексивно,
если на главной диагонали матрицы
отношения расположены только единицы; -
симметрично,
если матрица симметрична относительно
главной диагонали; -
антисимметрично,
если в матрице
 все
все
элементы вне главной диагонали являются
нулевыми; -
транзитивно,
если выполнено соотношение
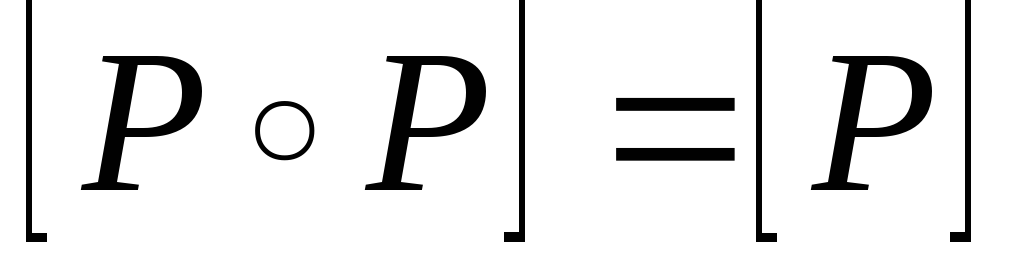 .
.
ПРИМЕР
4. Проверим, какими свойствами обладает
отношение
![]() ,
,
А={1,2,3}, изображённое на рисунке.
С оставим
оставим
матрицу отношения Р:
Так
как в матрице
![]() на главной диагонали имеются нулевые
на главной диагонали имеются нулевые
элементы, отношение Рне
рефлексивно.
Несимметричность
матрицы
![]() означает, что отношение Рне
означает, что отношение Рне
симметрично.
Для
проверки антисимметричности вычислим
матрицу
 .
.
Поскольку
в полученной матрице все элементы,
стоящие вне главной диагонали, нулевые,
отношение Р антисимметрично.
Так
как
![]() (проверьте!), то есть Р являетсятранзитивным
(проверьте!), то есть Р являетсятранзитивным
отношением.
Соседние файлы в папке Лекции_2
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Отношения и их свойства
Условия:
Даны два конечных множества: А={a,b,c}, B={1,2,3,4};
бинарные отношения P1
Í A´
B, P2
Í B2.
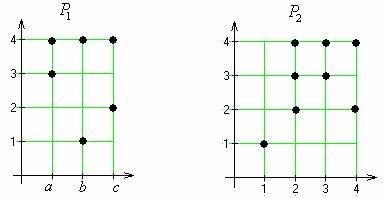
Изобразить P1, P2 графически. Найти P = (P2◦P1)–1.
Выписать области определения и области значений всех трех
отношений: P1, P2, Р. Построить матрицу [P2],
проверить с ее помощью, является ли отношение P2
рефлексивным, симметричным, антисимметричным, транзитивным. P1 = {(b,1),(b,4),(a,3),(a,4),(c,4),(c,2)};
P2 = {(1,1),(2,4),(2,3),(2,2),(3,3),(3,4),(4,2),(4,4)}.
Решение:
Произведением
![]() отношений
отношений
![]() и
и
![]() называется
называется
отношение
![]() .
.
Запишем
![]() в
в
виде пар.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Убрав одинаковые пары, получим
![]() .
.
Обратное отношение
![]() .
.
Областью определения
отношения
![]() называется
называется
множество
![]() .
.
Областью значений
называется множество:
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Матрица отношения
![]() :
:
 .
.
Бинарное отношение
![]() на
на
![]() называется
называется
рефлексивным, если
![]() .
.
На главной диагонали матрицы такого отношения
стоят единицы.
Отношение
![]() рефлексивно.
рефлексивно.
Отношение называется симметричным, если
![]() ,
,
т. е.
![]() или
или
![]() .
.
Матрица симметричного отношения симметрична.
Отношение
![]() не
не
симметрично.
Отношение называется антисимметричным,
если
![]() ,
,
т. е. в матрице
![]()
вне главной
диагонали все элементы равны нулю.
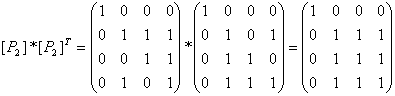
Отношение
![]() не
не
является антисимметричным.
Отношение называется транзитивным, если
![]() ,
,
т. е.
![]() .
.
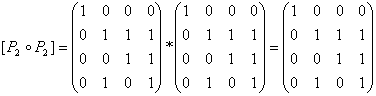
Отношение
![]() транзитивно.
транзитивно.
Пусть А – бинарное отношение в множестве Х. Определим общие свойства таких отношений, которые должны выполняться для всех пар (Xi, Xj) Î A.
· Рефлексивность.
Отношение А рефлексивно, если А É Е (Е – тождественное отношение), т. е. оно всегда выполняется между объектом и им самим: Х А Х.
· Антирефлексивность.
Отношение А антирефлексивно, если А ![]() Е =
Е = ![]() , т. е. оно выполняется только для несовпадающих объектов: из Xi А Xj следует, что Xi ¹ Xj (строгое неравенство; «быть старше»).
, т. е. оно выполняется только для несовпадающих объектов: из Xi А Xj следует, что Xi ¹ Xj (строгое неравенство; «быть старше»).
· Симметричность.
Отношение А симметрично, если А = А-1, т. е. при выполнении соотношения Xi А Xj выполняется соотношение Xj А Xi («быть братом»).
· Асимметричность.
Отношение А асимметрично, если А ![]() А-1 = Æ, т. е. из двух соотношений Xi А Xj и Xj А Xi одно неверно («быть отцом»). Если отношение А асимметрично, то оно и антирефлексивно.
А-1 = Æ, т. е. из двух соотношений Xi А Xj и Xj А Xi одно неверно («быть отцом»). Если отношение А асимметрично, то оно и антирефлексивно.
· Антисимметричность.
Отношение А антисимметрично, если А ![]() А-1 Ì Е, т. е. оба соотношения Xi А Xj и Xj А Xi выполняются одновременно только тогда, когда Xi = Xj.
А-1 Ì Е, т. е. оба соотношения Xi А Xj и Xj А Xi выполняются одновременно только тогда, когда Xi = Xj.
· Транзитивность.
Отношение А транзитивно, если из соотношений Xi А Xj и Xj А Xk следует соотношение Xi А Xk («быть делителем»).
Для Рефлексивного Отношения все элементы матрицы на главной диагонали равны 1; для Антирефлексивного Отношения – это нули.
Симметричность отношения влечет за собой и симметричность матрицы; Асимметричность Отношения – несимметричность матрицы с нулевыми элементами на главной диагонали; Антисимметричность – только несимметричность матрицы.
В матрице Транзитивного отношения для каждой пары единичных элементов, один из которых расположен в I-м столбце и J-й строке, а другой – в J-м столбце и K–Й строке, обязательно существует единичный элемент, расположенный в I-м столбце и K–Й строке. Наличие единичных элементов на главной диагонали не нарушает транзитивности.
| < Предыдущая | Следующая > |
|---|
Голосование за лучший ответ
Николай Гречишкин
Мудрец
(16350)
8 лет назад
Линейная алгебра кочует в другую категорию.
Сергей Гаврилов
Искусственный Интеллект
(184997)
8 лет назад
Транзитивность это свойство бинарного отношения. Матрица-то причем?
Liza ShУченик (98)
8 лет назад
Все верно, отношение на множестве определяется матрицей.
и как мы угадаем, какой там у тебя урок был?
Liza ShУченик (98)
8 лет назад
Как я понимаю, для проверка на транзитивное отношение, необходимо умножить матрицу саму на себя, если в результате получается точно такая же матрица, то исходная является транзитивной. Источник: http://sdb.su/diskretka/page,4,333-glava-binarnye-otnosheniya-rabochij-uchebnik-po-diskretnoj-matematike.html
Сергей Гаврилов
Искусственный Интеллект
(184997)
А, так это дискретка, с этого бы и начинали.
В этом я слаб.
