Как найти транзитивным отношения

Определение 2.6.
Бинарное отношение
называюттранзитивным
бинарным отношением,
если для любых
,ииз того, чтои,
вытекает, что.

Символически
определение 2.6 записано формулой (2.7).

(2.7)

Другими словами,
отношение
транзитивно, если оно покрывает все
опосредованные связи между элементами.
Отсюда вытекает, чтоусловием
транзитивности
отношения

является выполнение условия

(2.8)

Используя матрицы
отношений, условие (2.8) можно переписать
так:

(2.9)

Пример.

На множестве
={a,b,c}
задано отношение
:

Покажем, что
не является транзитивным отношением.

инесравнимы между собой, следовательно,
не транзитивно.

Найдем более высокие степени отношения

,
т.е. матрицы отношений,,,…,:

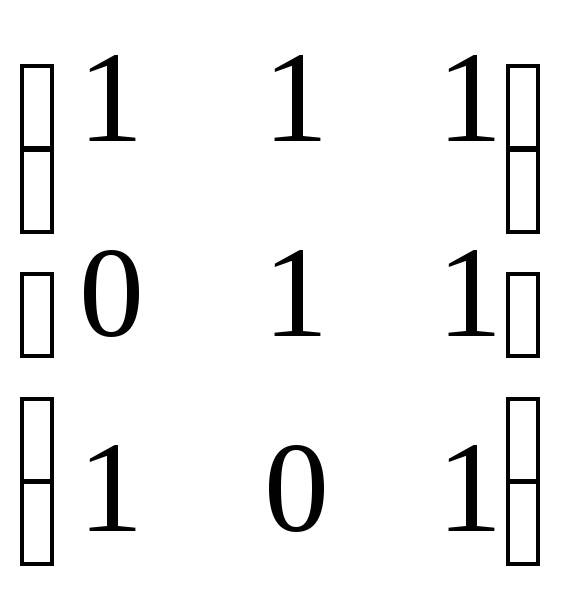
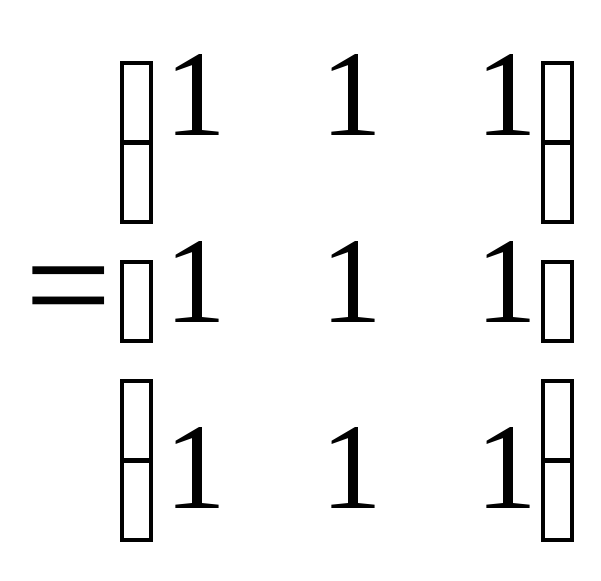Легко проверить, что
…=.

Определение 2.7.
Транзитивным
замыканием
бинарного отношения
называют объединение степеней этого
бинарного отношения:

(2.10)

Транзитивное
замыкание
отношения
в рассмотренном примере имеет вид.

Пусть на множестве
отношениезадано графом (рис.2.4). Запишем матрицуэтого отношения и найдем его транзитивное
замыкание.

Матрица отношения
.

Для нахождения
транзитивного замыкания будем умножать
матрицу
на себя, получая,,…,,
до тех пор, пока не выполнится равенство.
Дальнейшее умножение не будет приводить
к изменению матриц.

==.

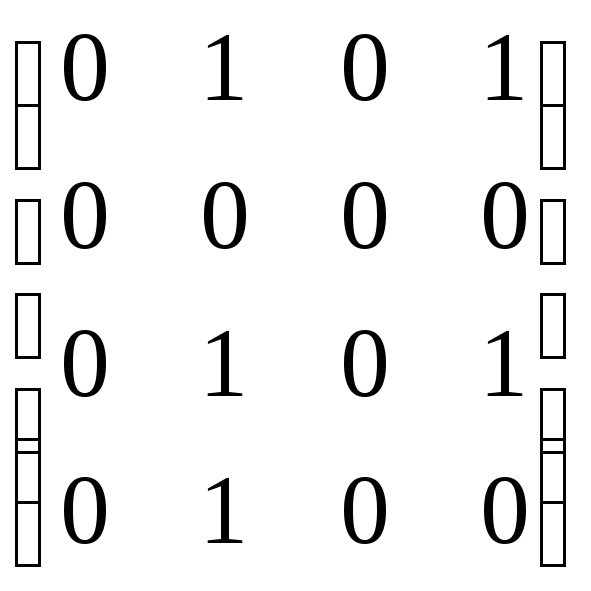Любой элемент
матрицы
не превосходит соответствующий элемент
матрицы,
т.е..
Это означает, чтовключает все опосредованные связи между
элементами, следовательно,является транзитивным бинарным
отношением. Покажем, что его транзитивное
замыкание совпадает с самим.

==.

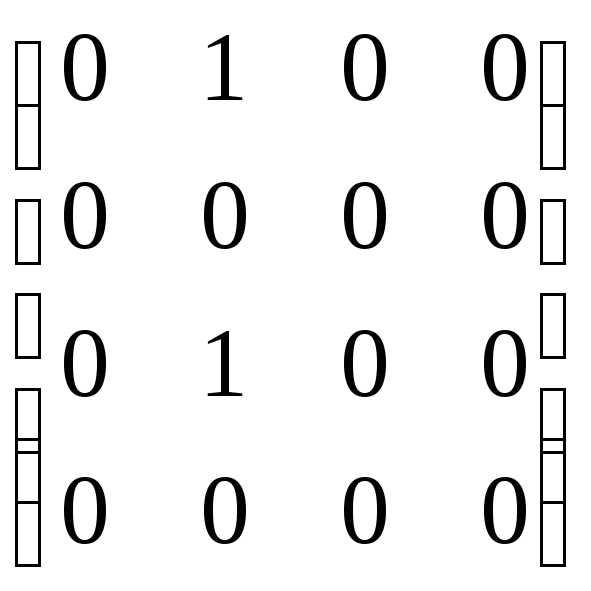
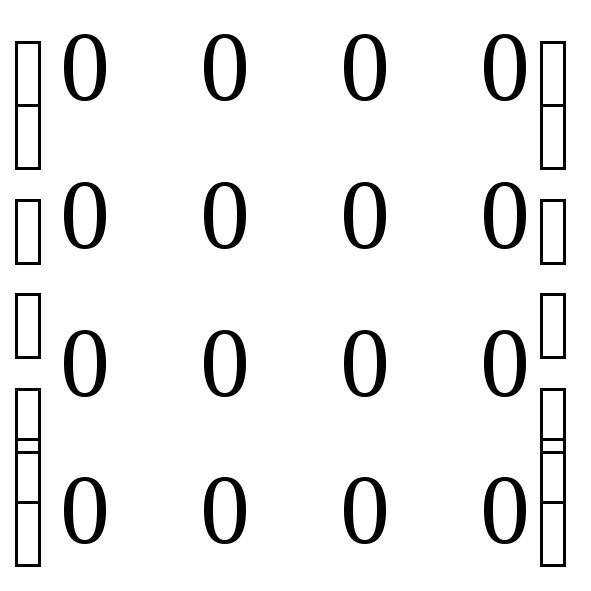
Умножение
нуль-матрицы на любую другую матрицу
есть нуль-матрица. Поэтому
для любых.

Транзитивное
замыкание отношения
найдем, используя формулу (2.10) и матрицыи:

Как и следовало
ожидать, поскольку отношение
является транзитивным отношением, оно
совпадает со своим транзитивным
замыканием.

Справедливы
следующие утверждения.

Утверждение 1.
Транзитивное бинарное отношение
совпадает со своим транзитивным
замыканием.

Утверждение 2.
Транзитивное замыкание бинарного
отношения есть наименьшее по числу
элементов транзитивное отношение,
содержащее данное бинарное отношение.

Утверждение 3.
Транзитивное замыкание

есть ближайшее
к
транзитивное отношение.

Использование
термина “ближайшее отношение”
предполагает, что между отношениями
определено расстояние. Для определения
расстояния
между множествами
используют формулу линейного расстояния
(формула 2.11), или формулу евклидова
расстояния (формула 2.12).

(2.11)

(2.12)

где
– расстояние между подмножествамииуниверсального множества,ихарактеристические функции этих
подмножеств. Суммирование выполняется
по всем элементам универсального
множества.

Для бинарного
отношения, заданного на множестве
,
универсальным множеством является
множество.
Если,
тоназываютполным
отношением.
Очевидно, что все элементы матрицы
полного отношения есть единицы:
,
где– число элементов множества.
Формулы (2.11) и (2.12) для бинарных отношений
имеют следующий вид:

(2.13)

(2.14)

где
– число элементов универсального
множества,,.

Не следует думать,
что последовательность степеней матрицы
отношения всегда имеет предел, т. е.,
начиная с некоторого шага
,
выполняется равенство.
Приведем простой пример, показывающий,
что это не так.

Пусть матрица
отношения
на множествеимеет вид.

Тогда

,,….,,

для любого
.

Тем не менее
.

Соседние файлы в папке учебник

Источник

From Wikipedia, the free encyclopedia

Transitive relation

Type	Binary relation
Field	Elementary algebra
Statement	A relation on a set is transitive if, for all elements , , in , whenever relates to and to , then also relates to .
Symbolic statement

In mathematics, a relation R on a set X is transitive if, for all elements a, b, c in X, whenever R relates a to b and b to c, then R also relates a to c. Each partial order as well as each equivalence relation needs to be transitive.

Definition[edit]

A homogeneous relation R on the set X is a transitive relation if,^[1]

for all a, b, c ∈ X, if a R b and b R c, then a R c.

Or in terms of first-order logic:

forall a,b,cin X:(aRbwedge bRc)Rightarrow aRc

where a R b is the infix notation for (a, b) ∈ R.

Examples[edit]

As a non-mathematical example, the relation “is an ancestor of” is transitive. For example, if Amy is an ancestor of Becky, and Becky is an ancestor of Carrie, then Amy, too, is an ancestor of Carrie.

On the other hand, “is the birth parent of” is not a transitive relation, because if Alice is the birth parent of Brenda, and Brenda is the birth parent of Claire, then this does not imply that Alice is the birth parent of Claire. What is more, it is antitransitive: Alice can never be the birth parent of Claire.

Non-transitive, non-antitransitive relations include sports fixtures, ‘knows’ and ‘talks to’.

“Is greater than”, “is at least as great as”, and “is equal to” (equality) are transitive relations on various sets, for instance, the set of real numbers or the set of natural numbers:

whenever x > y and y > z, then also x > z

whenever x ≥ y and y ≥ z, then also x ≥ z

whenever x = y and y = z, then also x = z.

More examples of transitive relations:

“is a subset of” (set inclusion, a relation on sets)
“divides” (divisibility, a relation on natural numbers)
“implies” (implication, symbolized by “⇒”, a relation on propositions)

Examples of non-transitive relations:

“is the successor of” (a relation on natural numbers)
“is a member of the set” (symbolized as “∈”)^[2]
“is perpendicular to” (a relation on lines in Euclidean geometry)

The empty relation on any set is transitive^[3]^[4] because there are no elements such that and , and hence the transitivity condition is vacuously true. A relation R containing only one ordered pair is also transitive: if the ordered pair is of the form (x,x) for some xin X the only such elements are , and indeed in this case , while if the ordered pair is not of the form (x,x) then there are no such elements and hence is vacuously transitive.

Properties[edit]

Closure properties[edit]

The converse (inverse) of a transitive relation is always transitive. For instance, knowing that “is a subset of” is transitive and “is a superset of” is its converse, one can conclude that the latter is transitive as well.
The intersection of two transitive relations is always transitive.^[5] For instance, knowing that “was born before” and “has the same first name as” are transitive, one can conclude that “was born before and also has the same first name as” is also transitive.
The union of two transitive relations need not be transitive. For instance, “was born before or has the same first name as” is not a transitive relation, since e.g. Herbert Hoover is related to Franklin D. Roosevelt, which is in turn related to Franklin Pierce, while Hoover is not related to Franklin Pierce.
The complement of a transitive relation need not be transitive.^[6] For instance, while “equal to” is transitive, “not equal to” is only transitive on sets with at most one element.

Other properties[edit]

A transitive relation is asymmetric if and only if it is irreflexive.^[7]

A transitive relation need not be reflexive. When it is, it is called a preorder. For example, on set X = {1,2,3}:

R = { (1,1), (2,2), (3,3), (1,3), (3,2) } is reflexive, but not transitive, as the pair (1,2) is absent,
R = { (1,1), (2,2), (3,3), (1,3) } is reflexive as well as transitive, so it is a preorder,
R = { (1,1), (2,2), (3,3) } is reflexive as well as transitive, another preorder.

Transitive extensions and transitive closure[edit]

Let R be a binary relation on set X. The transitive extension of R, denoted R₁, is the smallest binary relation on X such that R₁ contains R, and if (a, b) ∈ R and (b, c) ∈ R then (a, c) ∈ R₁.^[8] For example, suppose X is a set of towns, some of which are connected by roads. Let R be the relation on towns where (A, B) ∈ R if there is a road directly linking town A and town B. This relation need not be transitive. The transitive extension of this relation can be defined by (A, C) ∈ R₁ if you can travel between towns A and C by using at most two roads.

If a relation is transitive then its transitive extension is itself, that is, if R is a transitive relation then R₁ = R.

The transitive extension of R₁ would be denoted by R₂, and continuing in this way, in general, the transitive extension of R_i would be R_{i + 1}. The transitive closure of R, denoted by R* or R^∞ is the set union of R, R₁, R₂, … .^[9]

The transitive closure of a relation is a transitive relation.^[9]

The relation “is the birth parent of” on a set of people is not a transitive relation. However, in biology the need often arises to consider birth parenthood over an arbitrary number of generations: the relation “is a birth ancestor of” is a transitive relation and it is the transitive closure of the relation “is the birth parent of”.

For the example of towns and roads above, (A, C) ∈ R* provided you can travel between towns A and C using any number of roads.

Relation types that require transitivity[edit]

Preorder – a reflexive and transitive relation
Partial order – an antisymmetric preorder
Total preorder – a connected (formerly called total) preorder
Equivalence relation – a symmetric preorder
Strict weak ordering – a strict partial order in which incomparability is an equivalence relation
Total ordering – a connected (total), antisymmetric, and transitive relation

Counting transitive relations[edit]

No general formula that counts the number of transitive relations on a finite set (sequence A006905 in the OEIS) is known.^[10] However, there is a formula for finding the number of relations that are simultaneously reflexive, symmetric, and transitive – in other words, equivalence relations – (sequence A000110 in the OEIS), those that are symmetric and transitive, those that are symmetric, transitive, and antisymmetric, and those that are total, transitive, and antisymmetric. Pfeiffer^[11] has made some progress in this direction, expressing relations with combinations of these properties in terms of each other, but still calculating any one is difficult. See also Brinkmann and McKay (2005).^[12] Mala showed that no polynomial with integer coefficients can represent a formula for the number of transitive relations on a set,^[13] and found certain recursive relations that provide lower bounds for that number. He also showed that that number is a polynomial of degree two if the set^[clarify] contains exactly two ordered pairs.^[14]

Number of n-element binary relations of different types

Elements	Any	Transitive	Reflexive	Symmetric	Preorder	Partial order	Total preorder	Total order	Equivalence relation
0	1	1	1	1	1	1	1	1	1
1	2	2	1	2	1	1	1	1	1
2	16	13	4	8	4	3	3	2	2
3	512	171	64	64	29	19	13	6	5
4	65,536	3,994	4,096	1,024	355	219	75	24	15
n	2^n²		2^n²−n	2^n(n+1)/2			${textstyle sum _{k=0}^{n}k!S(n,k)}$	n!	${textstyle sum _{k=0}^{n}S(n,k)}$
OEIS	A002416	A006905	A053763	A006125	A000798	A001035	A000670	A000142	A000110

Note that S(n, k) refers to Stirling numbers of the second kind.

[edit]

The Rock–paper–scissors game is based on an intransitive and antitransitive relation “x beats y“.

A relation R is called intransitive if it is not transitive, that is, if xRy and yRz, but not xRz, for some x, y, z.
In contrast, a relation R is called antitransitive if xRy and yRz always implies that xRz does not hold.
For example, the relation defined by xRy if xy is an even number is intransitive,^[15] but not antitransitive.^[16] The relation defined by xRy if x is even and y is odd is both transitive and antitransitive.^[17]
The relation defined by xRy if x is the successor number of y is both intransitive^[18] and antitransitive.^[19] Unexpected examples of intransitivity arise in situations such as political questions or group preferences.^[20]

Generalized to stochastic versions (stochastic transitivity), the study of transitivity finds applications of in decision theory, psychometrics and utility models.^[21]

A quasitransitive relation is another generalization;^[6] it is required to be transitive only on its non-symmetric part. Such relations are used in social choice theory or microeconomics.^[22]

Proposition: If R is a univalent, then R;R^T is transitive.

proof: Suppose ${displaystyle xR;R^{T}yR;R^{T}z.}$

Then there are a and b such that ${displaystyle xRaR^{T}yRbR^{T}z.}$

Since R is univalent, yRb and aR^Ty imply a=b. Therefore xRaR^Tz, hence xR;R^Tz and R;R^T is transitive.

Corollary: If R is univalent, then R;R^T is an equivalence relation on the domain of R.

proof: R;R^T is symmetric and reflexive on its domain. With univalence of R, the transitive requirement for equivalence is fulfilled.

Notes[edit]

^ Smith, Eggen & St. Andre 2006, p. 145
^ However, the class of von Neumann ordinals is constructed in a way such that ∈ is transitive when restricted to that class.
^ Smith, Eggen & St. Andre 2006, p. 146
^ https://courses.engr.illinois.edu/cs173/sp2011/Lectures/relations.pdf Archived 2023-02-04 at the Wayback Machine^{[bare URL PDF]}
^ Bianchi, Mariagrazia; Mauri, Anna Gillio Berta; Herzog, Marcel; Verardi, Libero (2000-01-12). “On finite solvable groups in which normality is a transitive relation”. Journal of Group Theory. 3 (2). doi:10.1515/jgth.2000.012. ISSN 1433-5883. Archived from the original on 2023-02-04. Retrieved 2022-12-29.
^ ^a ^b Robinson, Derek J. S. (January 1964). “Groups in which normality is a transitive relation”. Mathematical Proceedings of the Cambridge Philosophical Society. 60 (1): 21–38. doi:10.1017/S0305004100037403. ISSN 0305-0041. Archived from the original on 2023-02-04. Retrieved 2022-12-29.
^ Flaška, V.; Ježek, J.; Kepka, T.; Kortelainen, J. (2007). Transitive Closures of Binary Relations I (PDF). Prague: School of Mathematics – Physics Charles University. p. 1. Archived from the original (PDF) on 2013-11-02. Lemma 1.1 (iv). Note that this source refers to asymmetric relations as “strictly antisymmetric”.
^ Liu 1985, p. 111
^ ^a ^b Liu 1985, p. 112
^ Steven R. Finch, “Transitive relations, topologies and partial orders” Archived 2016-03-04 at the Wayback Machine, 2003.
^ Götz Pfeiffer, “Counting Transitive Relations Archived 2023-02-04 at the Wayback Machine”, Journal of Integer Sequences, Vol. 7 (2004), Article 04.3.2.
^ Gunnar Brinkmann and Brendan D. McKay,”Counting unlabelled topologies and transitive relations Archived 2005-07-20 at the Wayback Machine”
^ Mala, Firdous Ahmad (2021-06-14). “On the number of transitive relations on a set”. Indian Journal of Pure and Applied Mathematics. doi:10.1007/s13226-021-00100-0. ISSN 0975-7465. Archived from the original on 2023-02-04. Retrieved 2021-12-06.
^ Mala, Firdous Ahmad (2021-10-13). “Counting Transitive Relations with Two Ordered Pairs”. Journal of Applied Mathematics and Computation. 5 (4): 247–251. doi:10.26855/jamc.2021.12.002. ISSN 2576-0645. Archived from the original on 2023-02-04. Retrieved 2021-12-06.
^ since e.g. 3R4 and 4R5, but not 3R5
^ since e.g. 2R3 and 3R4 and 2R4
^ since xRy and yRz can never happen
^ since e.g. 3R2 and 2R1, but not 3R1
^ since, more generally, xRy and yRz implies x=y+1=z+2≠z+1, i.e. not xRz, for all x, y, z
^ Drum, Kevin (November 2018). “Preferences are not transitive”. Mother Jones. Archived from the original on 2018-11-29. Retrieved 2018-11-29.
^ Oliveira, I.F.D.; Zehavi, S.; Davidov, O. (August 2018). “Stochastic transitivity: Axioms and models”. Journal of Mathematical Psychology. 85: 25–35. doi:10.1016/j.jmp.2018.06.002. ISSN 0022-2496.
^ Sen, A. (1969). “Quasi-transitivity, rational choice and collective decisions”. Rev. Econ. Stud. 36 (3): 381–393. doi:10.2307/2296434. JSTOR 2296434. Zbl 0181.47302.

References[edit]

Grimaldi, Ralph P. (1994), Discrete and Combinatorial Mathematics (3rd ed.), Addison-Wesley, ISBN 0-201-19912-2
Liu, C.L. (1985), Elements of Discrete Mathematics, McGraw-Hill, ISBN 0-07-038133-X
Gunther Schmidt, 2010. Relational Mathematics. Cambridge University Press, ISBN 978-0-521-76268-7.
Smith, Douglas; Eggen, Maurice; St.Andre, Richard (2006), A Transition to Advanced Mathematics (6th ed.), Brooks/Cole, ISBN 978-0-534-39900-9
Pfeiffer, G. (2004). Counting transitive relations. Journal of Integer Sequences, 7(2), 3.

External links[edit]

“Transitivity”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Transitivity in Action at cut-the-knot

Источник

Прочие статьи цикла

Отношения. Часть I
Отношения. Часть II
Количественные характеристики отношений

Формальная теория моделирования использует алгебраические отношения, включая их в сигнатуры моделей алгебраических структур, которыми описывает реальные физические, технические объекты и процессы их функционирования. Эта публикация является продолжением предшествующей, прочтение которой желательно, так как многие понятия и термины, используемые здесь, описываются там.

Предлагается изложение не в традиционном (стрелочном) стиле, а так, как мне самому пришлось всю эту кухню представлять и осваивать и по учебникам/пособиям, и по журнальным статьям. Особенно полезной вещью считаю созданный мной каталог, он позволяет выделить практически любое пространство и представить его элементы в удобном виде: матрицей, графом и др. Сразу видишь с чем имеешь дело и свойства (они уже выписаны) проверять часто не требуется.

Понятие отношения

Думаю, что термин отношение знаком каждому читателю, но просьба дать определение поставит большинство в тупик. Причин для этого много. Они чаще всего в преподавателях, которые, если и использовали отношения в процессе преподавания, внимания на этом термине не заостряли, запоминающихся примеров не приводили. Некоторые комментаторы статьи отнесли замечания на свой счет и насыпали минусов. Но шила в мешке не утаишь. Серьезных публикаций как не было, так и нет. Задайте себе вопрос, работали ли Вы с каким-либо пространством отношений? И честно себе ответьте. Что об этом пространстве можете миру поведать, для начала хотя-бы перечислить его элементы и указать свойства. Даже на СУБД Вы смотрите глазами их создателей, а они ведь тоже не все видят, или не все показывают, как, например, в микросхемах.

Здесь сделаю небольшой повтор. Начинать следует с абстрактного множества А ={a1,a2,a3,…, an}. О нем почитать можно здесь. Для лучшего понимания сократим множество до 3 элементов, т.е. А ={a1, a2, a3}. Теперь выполним декартово умножение А×А =А² и явно перечислим все элементы декартова квадрата
А×А={(a1, a1),(a1, а2),(a1, a3),(a2, а1),(a2, a2),(a2, a3),(a3, a1),(a3, a2),(a3, a3)}.
Получили 9 упорядоченных пар элементов из А×А, в паре первый элемент из первого сомножителя, второй — из второго. Теперь попробуем получить все подмножества из декартова квадрата А×А. Подмножества будут содержать разное количество пар: одну, две, три и так до всех 9 пар, включаем в этот список и пустое множество ∅. Сколько же получилось подмножеств? Много, а именно 2⁹ = 512 элементов.

Определение. Подмножество декартова квадрата множества называется бинарным отношением. Если декартов квадрат из двух сомножителей отношение бинарное, если из 3-х -тернарное, из 4-х — тетрарное, из n — n-арное. Арность — число мест в элементе отношения.
Определение. Множество всех подмножеств множества А называется булеаном. Булеан состоит из 2^|A| элементов, здесь |A| — мощность множества.

Отношения можно задавать в разном представлении:

перечислением элементов; R1 ={(a2,a2),(a2,a3),(a3,a1)}; R2 ={(a3,a3)}
двоичным вектором; <000011100>; <000000001>
матрицей;
графом и др. способами.

Далее переходим к рассмотрению пространств отношений, считая, что понятие, свойства отношений и операции с ними, читателю знакомы хотя бы в объеме нашей публикации в ссылке.

Пространства бинарных отношений

Предварительно уточним, что отношения могут быть строгими (это все антирефлексивные отношения) или нестрогими (все остальные). Внимание сосредоточим на отношениях безразличия и предпочтения, последние подразделяются на слабые предпочтения и строгие предпочтения (почему-то не сильные). Вообще в науке с терминологией нет порядка и скорее всего не будет. В криптографии, например, снятие шифра с криптограммы при наличии ключа -расшифрование, а без ключа — дешифрование. Казалось бы, дешифратор — дешифрует, но нет.

Пространством бинарных отношений с множеством-носителем называется произвольное подмножество множества бинарных отношений заданных на. Рассмотрим основные пространства для отношений предпочтений (рис. 2.15).

Р – пространство всех отношений слабого предпочтения, удовлетворяют условию рефлексивности и полноты.
QT – слабые предпочтения, удовлетворяющие условию квазитранзитивности.
QO – пространство линейных квазипорядков, т. е. отношения из QT, которые являются транзитивными.
ТО – пространство всех совершенных порядков, т. е. отношения из QO, которые являются антисимметричными.
SP – пространство всех отношений строгого предпочтения, удовлетворяют свойствам антирефлексивности и антисимметричности.
РО – отношения строгого частичного порядка, или транзитивные строгие предпочтения. Так как отношения строгого частичного порядка транзитивны, естественно пользоваться, для их представления сокращенными графами, то есть такими, в которых опущены дуги, реализующие транзитивность. Такие сокращенные графы называются диаграммами Хассе.
QS – пространство квазисерий, т. е. строгие частичные порядки, для которых отношение I=¬(PUP^-1) – эквивалентность.
TSO – пространство строгих линейных порядков, т. е. тех частичных порядков, для которых выполняется свойство полноты.
Необходимо отметить, всего таких отношений n!.. Например, для n = 3, число совершенных отношений равно 6 и все они приведены на рис. 2.13.
Т – пространство всех отношений толерантности (безразличия), они обладают свойствами симметричности и рефлексивности.
ТОТ – пространство транзитивно ориентируемых отношений толерантности, т. е. такие отношения, что дополнение к I представляется в виде объединения взаимно обратных транзитивных отношений, т. е.
¬I =R∩R^-1.
I – пространство всех отношений эквивалентности, т. е. симметричных, рефлексивных и транзитивных отношений.
Е – пространство отношений равенства, состоит из одного отношения представленного диагональной матрицей. Между пространствами R, P и I имеется взаимно-однозначная связь, определяемая отображением отношений предпочтения.

Рисунок 2.15 Схема пространств бинарных отношений

Выявленные связи между пространствами используются для переноса задач принятия решений (ЗПР) из одних пространств в другие, где они могут быть решены более простым путем, а затем полученное решение возвращают в исходное пространство, где была сформулирована ЗПР.
Эти отношения представлены диаграммой на рис. 2.14. Пространства бинарных отношений (типы отношений) представлены рис. 2.15.

Отношения эквивалентности

Определение. Бинарное отношение σ ⊆ А×А, обладающее тремя свойствами рефлексивности, симметричности, транзитивности, называется, бинарным отношением эквивалентности (БОЭ). Обозначается отношение эквивалентности σ(х, у), (х, у)∊σ, хσу, х≈у. Удобно использовать матричное (табличное) представление отношения. Ниже на рис 2.24 приведено как раз матричное представление. Над множеством из 4-х элементов существует 15 БОЭ, которые все изображены.

Представление и анализ структуры отношений эквивалентности (n = 4)
Эквивалентность из бинарных отношений, пожалуй, самое распространенное БО. Редкая наука обходится без этого понятия, но даже тогда, когда эквивалентности используются в изложении каких-либо вопросов, бывает трудно понять, что в виду имел автор. Даже при корректном определении и перечислении свойств, присущих этому бинарному отношению – трудности восприятия остаются.

Начнем с примера об эквивалентностях, который иллюстрирует ограниченность их количества.

Пример 1. Пусть имеется три кубика. Составим список свойств, которыми наделены кубики и практическое использование которых (свойств кубиков) делает их как бы взаимозаменяемыми. Кубикам присвоим номера, а их свойства представим таблицей 1.

По каждому из свойств возникает БОЭ и классы эквивалентности. Продолжая список свойств, мы новых отношений эквивалентности не получим. Будут только повторы уже построенных, но для других признаков. Покажем связь БОЭ с множествами.

Рассмотрим множество из трех элементов А ={1,2,3} и получим для него все возможные разбиения на все части. ①1|2|3; ②12|3; ③13|2; ④ 1|23; ⑤123. Последнее разбиения на одну часть. Номера разбиений и БО в кружках.

Определение. Разбиением множества А называют семейство Аi, i = 1(1)I, непустых попарно непересекающихся подмножеств из А, объединение которых образует все исходное множество А=UАi, Аi∩Аj =∅, ∀ i ≠ j. Под-множества Аi называют классами эквивалентности разбиения исходного множества.

Это все разбиения множества (5 штук). Анализ БО показывает, что различных отношений эквивалентности тоже только 5 штук. Случайно ли это совпадение? Мы можем каждому разбиению сопоставить матрицу из девяти ячеек (3×3 = 9), в каждой из которых либо размещается упорядоченная пара элементов из множества А, либо ячейка остается пустой, если для соответствующей пары нет объекта. Строки и столбцы матрицы размечаются элементами множества А, а пересечению строка – столбец соответствует упорядоченная пара (i, j). В ячейку матрицы вписывается не пара, а просто единица или нуль, впрочем, нуль часто не пишут совсем.

Нет, совпадение не случайное. Оказывается, каждому разбиению множества взаимно однозначно соответствует БОЭ, при этом мощность множества может быть любой |A| = n.

Это отношение едва ли не самое частое по использованию в научном обороте, но совокупность свойств, реализуемых в этом отношении, сильно ограничивает его распространенность.
Так среди всех абстрактных бинарных отношений над множеством из трех элементов (всего их 2⁹ = 512 отношений) только пять являются эквивалентностями — носителями требуемых свойств, менее одного процента.

Для |A| = 4 отношений существует 2¹⁶ = 65536, но эквивалентностей лишь 15 штук. Это весьма редкий тип отношений. С другой стороны, отношения эквивалентности широко распространены в прикладных задачах. Везде, где имеются и рассматриваются множества самых различных объектов и различные разбиения таких множеств (не чисел) на части возникают отношения эквивалентности. Их можно назвать математическими (алгебраическими) моделями таких разбиений, классифицирующими множества объектов по различным признакам.

Минимальное разбиение множества А, образованное из одноэлементных подмножеств А= U{a} и разбиение А, состоящее из самого множества {А}, называются тривиальными (несобственными) разбиениями.

Решетка Р(4): все разбиения множества А = {a1,a2,a3,a4} = {1,2,3,4}

Минимальному разбиению соответствует отношение эквивалентности П15, которое называется равенством или единичным отношением. В каждом классе эквивалентности — единственный элемент. Разбиению множества А, включающему лишь само множество А, соответствует отношение эквивалентности, содержащее все элементы декартова квадрата А×А.

Ближайший тип к отношениям эквивалентности – отношения толерантности. Множество отношений толерантности содержит в себе все отношения эквивалентности. Для носителя А из трех элементов толерантностей 8. Все они обладают свойствами рефлексивности и симметричности.

При выполнении свойства транзитивности пять из восьми толерантностей преобразует в эквивалентности (рис. 2.24 и 2.25).

Определение. Совокупность классов [a]σ эквивалентности элементов множества А называется фактор-множеством (обозначается А/σ) множества А по эквивалентности σ.

Определение. Естественным (каноническим) отображением f: A→ А/σ называется такое отображение f, при котором f(а) = [a]σ.

Отношения толерантности и их анализ

Об этих БО ранее уже упоминалось, а здесь рассмотрим их подробнее. Всем известны понятия сходство, похожесть, одинаковость, неразличимость, взаимозаменяемость объектов. Они кажутся близкими по содержанию, но при этом не одно и то же. Когда для объектов указано только сходство, то невозможно разбить их на четкие классы так, что внутри класса объекты похожи, а между объектами разных классов сходства нет. В случае сходства возникает размытая ситуация без четких границ. С другой стороны, накапливание несущественных различий у сходных объектов может привести к совершенно непохожим объектам.

В предыдущей части мы обсудили содержательный смысл отношения одинаковости (эквивалентности) объектов. Не менее важной является ситуация, когда приходится устанавливать сходство объектов.

Пусть изучается форма геометрических тел. Если одинаковость формы объектов, например, кубиков, означает их полную взаимозаменяемость в определенной ситуации обучения, то сходство – это частичная взаимозаменяемость, (когда среди кубиков встречаются очень похожие на них параллелепипеды) т. е. возможность взаимной замены с некоторыми (допустимыми в данной ситуации) потерями.

Наибольшая мера для сходства – неразличимость, а вовсе не одинаковость, как может показаться на первый взгляд. Одинаковость – свойство качественно иное. Одинаковость можно рассматривать только как частный случай неразличимости и сходства.

Все дело в том, что неразличимые объекты (так же, как и сходные, похожие) не удается разбить на классы так, чтобы в каждом классе элементы не различались, а элементы разных классов заведомо различались.

В самом деле, будем рассматривать множество точек (х, у) на плоскости. Пусть величина d имеет значение меньшее порога разрешимости глаза, т. е. d – такое расстояние, при котором две точки, находящиеся на этом расстоянии, сливаются в одну, т.е. визуально неразличимы (при выбранном удалении плоскости от наблюдателя). Рассмотрим теперь n точек, лежащих на одной прямой и отстоящих (каждая от соседних) на расстоянии d. Каждая пара
соседних точек неразличима, но, если n достаточно велико, первая и последняя точки будут отстоять друг от друга на большое расстояние и заведомо будут различимы.

Традиционный подход к изучению сходства или неразличимости состоит в том, чтобы сначала определить меру сходства, а затем исследовать взаимное расположение сходных объектов. Английский математик Зиман, изучая модели зрительного аппарата, предложил аксиоматическое определение сходства. Тем самым свойства сходства стало возможным изучать независимо от того, как конкретно оно задано в той или иной ситуации: расстоянием между объектами, совпадением каких-то признаков или субъективным мнением наблюдателя.
Введем экспликацию понятия сходства или неразличимости.

Определение. Отношение Т на множестве M называется отношением толерантности или толерантностью, если оно рефлексивно и симметрично.

Корректность такого определения видна из того, что объект заведомо неразличим сам с собой и, конечно, похож на себя (это задает рефлексивность отношения). Порядок рассмотрения двух объектов не влияет на окончательный вывод об их сходстве или несходстве (симметричность).
Из примера со зрительной неразличимостью точек плоскости видим, что транзитивность толерантности выполняется не для всех пар объектов.

Ясно также, что поскольку одинаковость есть частный случай сходства, то эквивалентность должна быть частным случаем толерантности. Сравнивая определения эквивалентности и толерантности, убеждаемся, что так оно и есть. Философский принцип: «частное богаче общего» наглядно подтверждается. Дополнительное свойство – транзитивности делает часть отношений толерантности эквивалентностями. Двое близнецов бывают настолько одинаковыми, что без риска могут сдавать экзамены друг за друга. Однако если два студента только похожи, то такая проделка, хотя и осуществима, но рискованна.

Каждый элемент множества несет определенную информацию о похожих на него элементах. Но не всю информацию, как в случае одинаковых элементов. Здесь возможны разные степени информации, которую один элемент содержит относительно другого.

Рассмотрим примеры, где толерантность задается разными способами.

Пример 2. Множество M состоит из четырехбуквенных русских слов — нарицательных существительных в именительном падеже. Будем называть такие слова сходными, если они отличаются не более чем на одну букву. Известная задача «Превращение мухи в слона» в точных терминах формулируется так. Найти последовательность слов, начинающуюся словом «муха» и кончающуюся словом «слон», любые два соседних слова в которой сходны в смысле только что данного определения. Решение этой задачи:

муха — мура — тура — тара — кара — каре — кафе — кафр — каюр — каюк — крюк — крок — срок — сток — стон — слон.

Пример 3. Пусть p — натуральное число. Обозначим через Sp совокупность всех непустых подмножеств множества М = {1, 2, …, p}. Отношение «иметь хотя бы один общий элемент» на множестве Sp – это отношение толерантности. Тогда два таких подмножества назовем толерантными, если у них есть хотя бы один общий элемент. Легко видеть, что рефлексивность и симметричность отношения выполнены.

Множество Sp называется (p –1) -мерным симплексом. Это понятие обобщает понятие отрезка, треугольника и тетраэдра на многомерный случай. Числа 1, 2, 3, …, p интерпретируются как вершины симплекса. Двухэлементные подмножества – как ребра, трехэлементные – как плоские (двумерные) грани, прочие k-элементные подмножества – как (k –1)-мерные грани. Число всех элементов (подмножеств) из Sp равно 2^р −1.

Толерантность подмножеств (граней) означает наличие у них общих вершин.

Определение. Множество M с заданным на нем отношением толерантности τ называется пространством толерантности. Таким образом, пространство толерантности есть пара (M, τ).

Пример 4. Пространство толерантности Sp допускает обобщение на бесконечный случай. Пусть H — произвольное множество. Если SH – совокупность всех непустых подмножеств множества H, то отношение толерантности Т на SH задается условием: X Т Y, если X∩Y ≠ ∅. Симметричность и рефлексивность этого отношения очевидны. Пространство SH обозначается <Н, Т> и называется «универсальным» пространством толерантности.

Пример 5. Пусть p — натуральное число. Обозначим Bp множество всех точек p-мерного пространства, координаты которых равны 0 или 1. Толерантность в Bp задается правилом: xτy, если x и y содержат хотя бы одну совпадающую компоненту (координату). Общее количество элементов в Bp равно 2^р. Для каждого элемента x = (a1, a2, …,ap) из множества Bp существует только один не толерантный ему элемент y = (1−a1, 1−a2, …, 1−ap ).
Очевидно, что Bp состоит из всех вершин p-мерного куба.

Пример 6. Рассмотрим пространство толерантности, компоненты которого принимают любые действительные значения.

В частности, это множество всех точек x = (a1, a2) декартовой плоскости. Толерантность двух точек означает совпадение у них хотя бы одной координаты. Значит, две толерантные точки находятся либо на общей вертикали, либо на общей горизонтали.

При других значениях p пространство можно интерпретировать как множество точек p-мерного пространства. В частности, каждый элемент x можно считать числовой функцией, заданной на множестве натуральных чисел {1, 2, 3, …}, которая каждому натуральному числу i: 1 ≤ i ≤ p сопоставляет действительное число ai (конечная числовая последовательность). Тогда толерантность двух функций x и y означает, что они хотя бы в одной точке равны.

Отношения частичного порядка и их анализ

Упорядоченные множества – это множества с введенным на нем отношением порядка. Определение. Множество А и бинарное отношение порядка R на нем (≤) называется частично упорядоченным, если для отношения выполнены (как и в БОЭ) три условия (одно условие другое):

рефлексивность ∀ х ∊ А (хRx); (антирефлексивность ∀ х ∊ А ¬(хRx));
антисимметричность ∀ х, y ∊ А (хRy yRx→x = y);
транзитивность ∀ х, у, z ∊ А (хRy& yRz →xRz).

При антирефлексивном отношении возникает строгий частичный порядок. Множество В(А) всех подмножеств множества А, упорядоченное по включению элементов является частично упорядоченным множеством (ЧУМ). Частично упорядоченное множество (В(А), ⊆) часто называют булеаном.

Элемент х∊А ЧУМ А покрывает элемент у∊А, если х > y и не существует z∊А такого, что х > z > y. Пара элементов х, у∊А называется сравнимой, если х ≥ у или х ≤ у.

Если в ЧУМ А всякая пара его элементов является сравнимой, то А называют линейно упорядоченным множеством или цепью.

Если же некоторое ЧУМ В состоит лишь из несравнимых друг с другом элементов, то множество В называют антицепью. Цепь в ЧУМ А называется насыщенной, если она не может быть вложена ни в какую другую цепь, отличную от себя.

Аналогично определяется насыщенная антицепь. Максимальной цепью (антицепью) называется цепь (антицепь), содержащая максимальное количество элементов.

Элемент m ЧУМ А называется минимальным, если в А нет элемента х∊А, отличного от m и такого, что х≤m. Элемент M ЧУМ А называется максимальным, если в А нет элемента х «большего», чем M, отличного от M и такого, что х ≥ M.

Элемент у∊А ЧУМ А называется наибольшим, если ∀ х∊ А х ≤ у. Элемент у∊ А ЧУМ А называется наименьшим, если ∀ х∊А х ≥ у. Для наибольшего и наименьшего элементов принято использовать обозначения 1 и 0 соответственно. Их называют универсальными границами. Всякое ЧУМ А имеет не более одного наименьшего и не более одного наибольшего элементов. В ЧУМ А допустимо несколько минимальных и несколько максимальных элементов
Изображать конечное ЧУМ А удобно диаграммой Хассе, которая представляет собой ориентированный граф, его вершины распределены по уровням диаграммы и соответствуют элементам из А, а каждая дуга направляется вниз и рисуется тогда и только тогда, когда элемент х∊А покрывает элемент у∊А.

Транзитивные дуги не изображаются. Уровни диаграммы Хассе содержат элементы одинакового ранга, т.е. связанные с минимальными элементами ЧУМ путями равной длины (по числу дуг).
Пусть В непустое подмножество ЧУМ А, тогда элемент х∊А называется точной верхней гранью (обозначается sup_AB) множества В, если х ≥ у для всех у∊В и, если из истинности соотношения z ≥ у для всех у∊В вытекает, что z ≥ х.

Точной нижней гранью (обозначается inf_AB) множества В называется элемент х∊А, если х ≤ у для всех у∊В и, если из условия z ≤ у для всех у∊ В вытекает, что z ≤ х.

Пример 7. Заданы два конечных числовых множества
А = {0,1,2,…,21} и B = {6,7,10,11}.

ЧУМ (А, ≤) представлено рис. 2.26.

Совокупность В^Δ всех верхних граней для В называется верхним конусом для множества В. Совокупность В^∇ всех нижних граней для В называется нижним конусом для В.

Всякое подмножество ЧУМ также является ЧУМ относительно наследованного порядка. Если в множестве существуют наибольший и/или наименьший элементы, то они являются максимальным (минимальным соответственно). Обратное неверно. Булеан обладает единственным наименьшим (Ø) и единственным наибольшим элементами.

В приведенном множестве наименьший элемент нуль (0) и он совпадает с единственным минимальным элементом, а наибольшего элемента не существует. Максимальными элементами являются {19, 20, 21}. Точная верхняя грань для B = {6,7,10,11} есть элемент 21 (это наименьший элемент в верхнем конусе).

Общая ситуация. Пусть задано множество, мощность которого*******. Из всех бинарных отношений, возможных на этом множестве, выделим бинарные отношения предпочтения и связанные с ними отношения строгих частичных порядков.

Частичные порядки отличаются от строгих частичных порядков только тем, что содержат в своем составе дополнительные элементы (в матричном представлении – диагональные) (аi, ai ) = 1, i = 1(1)n, а число тех и других порядков в полном множестве отношений одинаково. До настоящего времени не найдены зависимости (формула, алгоритм), которые позволяли бы подсчитывать и перечислять при любом n число частичных порядков.

Разными авторами непосредственным подсчетом определены и опубликованы следующие результаты (табл. 2.12).

Вычислительные эксперименты автора позволили получить не только число, но и вид (представление) частичных порядков при разных мощностях множителя-носителя отношений. Принтер задыхался печатая такие огромные списки, но не только красота требует жертв, наука тоже не отказывается от них.

В таблице 2.12 показаны: n = |A| – мощность множества-носителя; вторая строка – количество всех бинарных отношений на множестве А; и далее

|Ин(n)| – количество классов неизоморфных отношений;
|Г(n)| – количество отношений частичного порядка;
|Гн(n)| – количество классов неизоморфны отношений частичного порядка;
|Гл(n)| = n! – количество отношений линейного порядка.

Как видим, в таблице для небольших n, например, Г(n=4) имеется всего 219, приводятся данные, значения которых с увеличением n очень быстро растут, что существенно усложняет их количественный (и качественный) непосредственный анализ даже с помощью ЭВМ.

Таблица ниже иллюстрирует возможность порождения Г(n=4) всех частичных порядков из пересечения каждого с каждым линейных частичных порядков. Но в этой ситуации возникают избыточные (повторяющиеся), которые при малых n можно отсечь вручную (пересчитать). Получаются 300 матриц, но ЧУМ среди них лишь 219. Общие формулы так и не были получены. На мировом уровне ситуация аналогичная, хотя мне не довелось видеть публикаций о перечислениях ЧУМ западных авторов. Наши алгоритмы вполне оригинальны и пионерские.

Приведу возможную схему решения задачи перечисления элементов пространства частичных порядков (n=4).

Множество строгих частичных порядков при лексикографическом упорядочении линейных порядков (n=4) порождается при их взаимном пересечении.

Несколько важных определений математики, для встречающихся часто в текстах понятий.

Определение. Замкнутый интервал – это множество вида {x: a ≤ x ≤ b}; открытый интервал не замкнут, и полуоткрытый интервал, т. е. множество вида {x: a < x ≤ b}, где а < b, или вида {x: a ≤ x < b} не открыт и не замкнут.

Определение. Граница произвольного интервала вещественной прямой в обычной топологии вещественных чисел состоит лишь из концов этого интервала, независимо от того, открыт этот интервал, замкнут или полуоткрыт. Границей множества рациональных чисел, так же, как и границей множества всех иррациональных чисел, служит все множество вещественных чисел.

Определение. Каждое линейно упорядоченное множество, в любом непустом подмножестве которого есть наименьший элемент, называется вполне упорядоченным.

Определение. Семейство R называется цепью (иногда башней, гнездом) тогда и только тогда, когда для любых его элементов А и В либо А ⊂ В, либо В ⊂ А. Это условие равносильно утверждению, что семейство R линейно упорядочено по включению или – в принятой терминологии – что семейство R вместе с отношением включения является цепью.

П р и н ц и п м а к с и м а л ь н о с т и Х а у с д о р ф а. Для любого семейства множеств A и любого гнезда R, образованного элементами семейства A существует максимальное гнездо M в A, содержащее R.

Важная теорема о множествах и их семействах (Дж.Л.Kелли «Общая топология» стр.55).
Теорема. (а) П р и н ц и п м а к с и м а л ь н о г о э л е м е н т а. Максимальный элемент в семействе A множества существует, если для каждого гнезда, лежащего в A, в A найдется элемент, который содержит произвольный элемент этого гнезда.

(б) П р и н ц и п м и н и м а л ь н о г о э л е м е н т а. Минимальный элемент в семействе A существует, если для каждого гнезда, лежащего в A, в A найдется элемент, содержащийся в каждом элементе этого гнезда.

(в) Л е м м а Т ь ю к и. В каждом семействе множеств конечного характера есть максимальный элемент.

(г) Л е м м а К у р а т о в с к о г о. Каждая цепь в (частично) упорядоченном множестве содержится в некоторой максимальной цепи.

(д) Л е м м а Ц о р н а. Если каждая цепь некоторого частично упорядоченного множества ограничена сверху, то в этом множестве есть максимальный элемент.

(е) А к с и о м а в ы б о р а. Пусть Хα – непустое множество для каждого элемента а из множества индексов А. Тогда на А существует функция с такая, что с(а)∊ Хα для каждого а из А.

(ж) П о с т у л а т Ц е р м е л о. Для любого семейства A непересекающихся непустых множеств существует такое множество С, что АUС для каждого А из A состоит ровно из одной точки.

(з) П р и н ц и п в п о л н е у п о р я д о ч е н и я. Каждое множество можно вполне упорядочить.

Источник

Содержание

1 Определение
2 Свойства
3 Примеры транзитивных отношений
4 Примеры нетранзитивных отношений
5 Примеры антитранзитивных отношений
6 См. также
7 Источники информации

Определение

Бинарное отношение на множестве называется транзитивным, если для любых трёх элементов из выполнения отношений и следует выполнение отношения .

Определение:

Бинарное отношение , заданное на множестве называется транзитивным (англ. transitive binary relation), если для .

Если это условие соблюдается не для всех троек , то такое отношение называется нетранзитивным. Например, не для всех троек верно, что .

Определение:

Бинарное отношение , заданное на множестве называется нетранзитивным (англ. intransitive binary relation), если .

Существует более “сильное” свойство — антитранзитивность. Под этим термином понимается, что для любых троек отсутствует транзитивность. Антитранзитивное отношение, например — отношение победить в турнирах «на вылет»: если победил игрока , а победил игрока , то не играл с , следовательно, не мог его победить.

Определение:

Бинарное отношение , заданное на множестве называется антитранзитивным (англ. antitransitive binary relation), если для .

Свойства

Если отношение транзитивно, то обратное отношение также транзитивно. Пусть , но по определению обратного отношения . Так как транзитивно, то и , что и требовалось доказать.
Если отношения транзитивны, то отношение транзитивно. Пусть . Из транзитивности следует , но из определения пересечения отношений получаем , что и требовалось доказать.

Примеры транзитивных отношений

Отношения частичного порядка:
- строгое неравенство
- нестрогое неравенство
- включение подмножества:
  - строгое подмножество
  - нестрогое подмножество
- делимость:
Равенство
Эквивалентность
Импликация
Параллельность
Отношение подобия геометрических фигур
Являться предком

Примеры нетранзитивных отношений

Пищевая цепочка: это отношение не всегда является транзитивным (пример — волки едят оленей, олени едят траву, но волки не едят траву).
Быть предпочтительнее чем. Если мы хотим яблоко вместо апельсина, а вместо яблока мы бы хотели арбуз, то это не значит, что мы предпочтём арбуз апельсину.
Быть другом.
Являться коллегой по работе.
Быть подчиненным. Например, во времена феодального строя в Западной Европе была в ходу поговорка: Вассал моего вассала — не мой вассал.
Быть похожим на другого человека.

Примеры антитранзитивных отношений

Быть сыном (отцом, бабушкой).
Игра “Камень, ножницы, бумага”. Камень побеждает ножницы, ножницы выигрывают у бумаги, но камень проигрывает бумаге и т. д.

См. также

Определение отношения
Транзитивное замыкание
Алгоритм Флойда-Уоршалла (построение транзитивного замыкания отношения)
Транзитивный остов
Отношение порядка
Отношение эквивалентности

Источники информации

Wikipedia — Transitive relation
Wikipedia — Intransivity
Wikipedia — Отношение эквивалентности
Парадокс Кондорсе
Отношения на графах
Развитие понимания транзитивности и нетранзитивности
Бинарные отношения. Отношения эквивалентности (очень хорошая статья про отношения, в ней суть раскрыта более подробно)

Источник

Специальные свойства бинарных отношений

Рефлексивные и иррефлексивные бинарные отношения

В этой лекции дана определенная классификация бинарных отношений на множестве. В основе этой классификации лежат специальные свойства отношений.

Бинарное отношение rho на множестве называют рефлексивным, если диагональ operatorname{id}A множества содержится в rhocolon,operatorname{id}A subseteq rho , т.е. xrho x для любого элемента множества .

Если же operatorname{id}Acaprho=varnothing , то бинарное отношение rho на множестве называют иррефлексивным.

Указанные свойства бинарных отношений на множестве называют рефлексивностью и иррефлексивностью.

Бинарные отношения равенства и подобия на множестве геометрических фигур рефлексивны: каждый треугольник равен самому себе и подобен самому себе. На самом деле рефлексивны все отношения равенства: равенство чисел, равенство векторов, равенство множеств и т.п. Также рефлексивными являются, например, бинарное отношение нестрогого неравенства на множестве действительных чисел, поскольку для любого числа всегда xleqslant x , и отношение subseteq включения множеств, так как для любого множества всегда Xsubseteq X .

Напротив, бинарное отношение на множестве действительных чисел, задаваемое строгим неравенством x<y , иррефлексивно, равно как и отношение subset строгого включения множеств.

Не следует путать иррефлексивное отношение с нерефлексивным, т.е. не являющимся рефлексивным, отношением. Иррефлексивное отношение нерефлексивно, но не всякое нерефлексивное отношение иррефлексивно. Иррефлексивному отношению на не принадлежит ни один элемент диагонали operatorname{id}A , а нерефлексивное отношение может содержать некоторые (но не все!) элементы диагонали. На рис. 1.7 приведены примеры графиков иррефлексивного и нерефлексивного отношений (пунктиром указаны диагонали множеств).

Примеры графиков иррефлексивного и нерефлексивного отношений (пунктиром указаны диагонали множеств)

Симметричные и антисимметричные бинарные отношения

Бинарное отношение rho на множестве называют:

1) симметричным, если для любых x,yin A из xrho y следует yrho x ;
2) антисимметричным, если для любых x,yin A из одновременной справедливости xrho y и yrho x следует, что x=y .

График симметричного бинарного отношения на множестве A относительно диагонали

Соответствующие свойства бинарных отношений на множестве называют симметричностью и антисимметричностью.

График симметричного бинарного отношения на множестве симметричен относительно диагонали (рис. 1.8).

Теорема 1.1. Бинарное отношение rho на множестве симметрично, если и только если бинарное отношение на множестве , обратное к rho , совпадает с $rhocolon, rho^{-1}=rho$ .

Пусть $(x,y)inrho^{-1}$ , то есть (y,x)inrho . Тогда, в силу симметричности rho,, (x,y)inrho . Следовательно, $rho^{-1}subseteqrho$ . Аналогично доказывается включение $rhosubseteqrho^{-1}$ .

Теперь пусть $rho=rho^{-1}$ . Тогда (x,y)inrho и $(x,y)inrho^{-1}$ . Из определения обратного отношения вытекает, что (y,x)inrho . Следовательно, rho — симметричное бинарное отношение.

Теорема 1.2. Бинарное отношение rho на множестве антисимметрично, если и только если $rhocap rho^{-1} subseteq operatorname{id}A$ .

Действительно, если $(x,y)inrhocaprho^{-1}$ , то и $(x,y)inrho^{-1}$ (т.е. (y,x)inrho ). Но из выполнения соотношений xrho y и yrho x ввиду антисимметричности rho следует, что x=y , то есть (x,y)inoperatorname{id}A .

Обратно, пусть $rhocaprho^{-1}subseteq operatorname{id}A$ . Предположим, что (x,y)inrho и (y,x)inrho , причем xne y . Тогда $(x,y)inrho^{-1}$ и $(x,y)inrhocaprho^{-1}$ , но (x,y)notin operatorname{id}A . Получаем противоречие.

Отметим, что для антисимметричного бинарного отношения на множестве может иметь место равенство $rhocaprho^{-1}=varnothing$ .

Все бинарные отношения в геометрии типа равенства или подобия симметричны. Так, если треугольник ABC подобен треугольнику A'B'C' , то и второй из этих треугольников подобен первому. Бинарные отношения неравенства чисел и включения множеств, как строгие, так и не строгие, антисимметричны.

Бинарное отношение rho на множестве называют транзитивным, если для любых x,y,zin A из того, что x,rho,y и y,rho,z , следует x,rho,z . Соответствующее свойство бинарного отношения называют транзитивностью.

Пример 1.12. а. Пусть — некоторое множество населенных пунктов. Зададим на нем бинарное отношение достижимости: из пункта достижим пункт , если есть дорога, по которой можно доехать из в . Это отношение транзитивно, поскольку если из пункта можно доехать до пункта , а из есть дорога до , то из можно проехать в .

б. Бинарные отношения равенства и подобия в геометрии являются транзитивными: если треугольник ABC подобен треугольнику A_1B_1C_1 , а этот последний подобен треугольнику A_2B_2C_2 , то первый треугольник подобен третьему.

в. Бинарное отношение неравенства на множестве действительных чисел не транзитивно, так как из того, что xne y и yne z , вовсе не следует, что xne z . Аналогично, если друг , а друг , то — вопреки известной поговорке — это не означает, что друг .

Транзитивность бинарного отношения

Докажем следующее важное свойство транзитивного бинарного отношения.

Теорема 1.3. Бинарное отношение rho на множестве транзитивно тогда и только тогда, когда его квадрат содержится в нем, т.е. rhocircrho subseteqrho .

Пусть бинарное отношение rho на множестве транзитивно и (x,z)inrho^2=rhocircrho . В силу определения композиции бинарных отношений на множестве существует такой элемент , что x,rho,y и y,rho,z , откуда ввиду транзитивности rho получаем x,rho,z , то есть (x,z)inrho , а значит, rho^2 subseteqrho .

Обратно, пусть бинарное отношение rho на множестве таково, что rho^2 subseteqrho , а (x,y)inrho и (y,z)inrho . Тогда в силу определения композиции бинарных отношений на множестве имеем (x,z)inrho^2 . Поскольку , то . Таким образом, из того, что и , следует, что , т.е. бинарное отношение rho на множестве транзитивно.

Доказанное свойство целесообразно использовать для проверки транзитивности бинарного отношения rho на некотором множестве в тех случаях, когда построение квадрата rho является более легкой задачей по сравнению с исследованием свойства транзитивности rho на основе определения.

Плотное бинарное отношение

Бинарное отношение rho на множестве называется плотным, если для любых x,yin A , отличных друг от друга и таких, что x,rho,y , найдется , отличный и от и от , такой, что x,rho,z и z,rho,,y .

Образно говоря, для любой пары элементов, связанных плотным отношением, всегда найдется третий элемент, который “встраивается между ними” и связан с каждым из них тем же отношением. Так, отношения неравенства (строгого и нестрогого) на множествах рациональных и действительных чисел плотны, но аналогичные отношения на множествах целых и натуральных чисел плотными не являются. В самом деле, каковы бы ни были рациональные (или действительные) числа и , из того, что x<y , следует, что существует число , отличное как от , так и от , такое, что x<z<y . Например, подходит число z=(x+y)/2 . Но для целых чисел и m+1 такого “промежуточного” целого числа нет.

Если rho — плотное бинарное отношение на множестве и для некоторых x,yin A имеет место x,rho,y , то найдется zin A , такой, что xne z,~yne z и x,rho,,z,~ z,rho,,y . Отсюда в силу определения композиции отношений следует, что x,rho^2,y . Значит, из (x,y)inrho следует (x,y)inrho^2 , то есть rhosubseteq rho^2 .

Итак, если rho плотно, то оно содержится в своем квадрате. Напомним, что для транзитивного бинарного отношения rho^2subseteqrho . Следовательно, если бинарное отношение rho одновременно плотно и транзитивно, то rho=rho^2 .

Классы бинарных отношений

Среди всех бинарных отношений на произвольном множестве выделяют классы отношений в зависимости от свойств, которыми эти отношения обладают.

Бинарное отношение на некотором множестве называют:

1) эквивалентностью, если оно рефлексивно, симметрично и транзитивно;
2) толерантностью, если оно рефлексивно и симметрично;
3) порядком (или частичным порядком), если оно рефлексивно, антисимметрично и транзитивно;
4) предпорядком (или квазипорядком), если оно рефлексивно и транзитивно;
5) строгим порядком, если оно иррефлексивно, антисимметрично и транзитивно;
6) строгим предпорядком, если оно иррефлексивно и транзитивно.

Определенные выше бинарные отношения называют отношениями эквивалентности, толерантности, порядка (частичного порядка), предпорядка (квазипорядка), строгого порядка, строгого предпорядка.

Пример 1.13. а. Бинарное отношение параллельности двух прямых или двух плоскостей в евклидовой геометрии, если считать каждую прямую (плоскость) параллельной самой себе, есть отношение эквивалентности.

Бинарное отношение на множестве всех непустых подмножеств универсального множества

б. Бинарное отношение rho на множестве всех непустых подмножеств некоторого множества , для которого A,rho,B тогда и только тогда, когда Acap Bne varnothing , является толерантностью. Это отношение рефлексивно и симметрично, но не транзитивно. Действительно, из того, что и Bcap Cne varnothing , никак не следует, что Acap Cne varnothing (рис. 1.9).

в. Примером отношения порядка является естественный числовой порядок, т.е. отношение неравенства на любом числовом множестве.

Часто это отношение называют просто естественным порядком. Поскольку в дискретной математике нам приходится иметь дело со многими порядками на нечисловых множествах, мы все время будем говорить „естественный числовой порядок”, подчеркивая тем самым, что речь идет об отношении порядка на множестве действительных чисел (или об его ограничении на множества рациональных, целых или натуральных чисел).

г. На множестве натуральных чисел mathbb{N} зададим бинарное отношение amid b , означающее, что делит ( является делителем ). Это отношение рефлексивно, поскольку любое число является делителем самого себя. Покажем антисимметричнсть. Пусть делит и в то же время делит . Тогда найдется натуральное число t_1 , такое, что b=at_1 , и найдется t_2 , такое, что a=bt_2 . Отсюда b=bt_2t_1 , что на множестве натуральных чисел возможно только при t_1=t_2=1 . Следовательно, a=b . Покажем транзитивность. Если делит , а делит , то найдутся натуральные числа t_1,t_2 , такие, что b=at_1 и c=bt_2 . Отсюда имеем c=at_1t_2 , т.е. — делитель . Таким образом, “отношение делимости” на множестве mathbb{N} является отношением порядка.

Если распространить это отношение на множество целых чисел, то оно будет уже только предпорядком, поскольку теряется свойство антисимметричности. Например, 2 делится на –2 и –2 делится на 2, однако 2ne-2 .

д. Рассмотрим множество 2^A всех подмножеств множества . Покажем, что отношение включения subseteq на множестве 2^A есть порядок. Это отношение рефлексивно, так как для любого множества справедливо включение Xsubseteq S . Поскольку для любых двух множеств и из Xsubseteq Y и Ysubseteq X следует, что X=Y , рассматриваемое отношение антисимметрично. Из определения включения вытекает, что если и Ysubseteq Z , то Xsubseteq Z . Следовательно, отношение транзитивно.

е. Отношение строгого неравенства на числовом множестве, равно как и отношение строгого включения множеств, есть отношение строгого порядка.

ж. В качестве примера отношения строгого предпорядка можно привести отношение “строгой достижимости” на некотором множестве населенных пунктов: пункт считаем строго достижимым из отличного от него пункта , если есть дорога (автомобильная, железная и т.п.) из в , причем принимается, что никакой пункт не является строго достижимым из себя самого.

Связь между классами бинарных отношений

Отношения толерантности, эквивалентности, предпорядка и порядка — важнейшие в современной математике. Связь между этими четырьмя классами бинарных отношений показана на рис. 1.10. Можно сказать, что эквивалентность есть транзитивная толерантность или симметричный предпорядок. Порядок же есть антисимметричный предпорядок.

Связь между четырьмя классами бинарных отношений

Для любого бинарного отношения rhosubseteq A^2 можно построить отношение $rho^{ast}$ следующим образом: $x,rho^{ast},y$ тогда и только тогда, когда x=y или существует последовательность x_0,x_1, ldots, x_n, ngeqslant1 , такая, что x_0=x, x_n=y и для каждого i=overline{0,n-1} выполняется $x_i,rho,x_{i+1}$ . В частности, если (x,y)inrho , то есть x,rho,y , то это означает, что приведенное условие выполняется при n=1 . Следовательно, $(x,y)inrho^{ast}$ , то есть $rhosubseteqrho^{ast}$ .

Отношение $rho^{ast}$ называют рефлексивно-транзитивным замыканием бинарного отношения rho на соответствующем множестве.

Можно также обозначить $rho^0=operatorname{id}A,~ rho^1=rho,~ rho^n=rhocircrho^{n-1},~ n>1$ , и тогда $rho^{ast}=bigcuplimits_{i=0}^{infty}rho^{i}$ .

Отношение $rho^{ast}$ является рефлексивным, так как $operatorname{id}A subseteq rho^{ast}$ . Докажем его транзитивность. Пусть для каких-то x,y,z выполняется $x,rho^{ast},y$ и $y,rho^{ast},z$ . Докажем, что $x,rho^{ast},z$ . Будем считать, что элементы x,y,z попарно различны (так как при x=y или y=z доказывать нечего). Тогда существуют последовательности

x=x_0,x_1,ldots,x_n=y и y=y_0,y_1,ldots,y_m=z ,

такие, что $x_i,rho,x_{i+1}$ для каждого i=overline{0,n-1} и $y_j,rho,y_{j+1}$ для каждого j=overline{0,m-1}~ (n,mgeqslant1) .

В итоге получаем последовательность

$z_0,ldots,z_n,z_{n+1},ldots,z_{n+m}$ , где $z_0=y,~ z_n=y,~ z_{n+m}=z,~ z_i=x_i$ ,

для всякого i=overline{0,n-1} , $z_{n+j}=y_j$ для всякого j=overline{0, m-1} , такую, что $z_i,rho,z_{i+1}$ для любого i=overline{0,n+m-1} , то есть $x,rho^{ast},z$ , что и требовалось доказать.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Definition[edit]

Examples[edit]

Properties[edit]

Closure properties[edit]

Other properties[edit]

Transitive extensions and transitive closure[edit]

Relation types that require transitivity[edit]

Counting transitive relations[edit]

[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Понятие отношения

Пространства бинарных отношений

Отношения эквивалентности

Отношения толерантности и их анализ

Отношения частичного порядка и их анализ

Содержание

Определение

Свойства

Примеры транзитивных отношений

Примеры нетранзитивных отношений

Примеры антитранзитивных отношений

См. также

Источники информации

Специальные свойства бинарных отношений

Рефлексивные и иррефлексивные бинарные отношения

Симметричные и антисимметричные бинарные отношения

Транзитивность бинарного отношения

Плотное бинарное отношение

Классы бинарных отношений

Связь между классами бинарных отношений

Добавить комментарий Отменить ответ

Definition[edit]

Examples[edit]

Properties[edit]

Closure properties[edit]

Other properties[edit]

Transitive extensions and transitive closure[edit]

Relation types that require transitivity[edit]

Counting transitive relations[edit]

[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Понятие отношения

Пространства бинарных отношений

Отношения эквивалентности

Отношения толерантности и их анализ

Отношения частичного порядка и их анализ

Содержание

Определение

Свойства

Примеры транзитивных отношений

Примеры нетранзитивных отношений

Примеры антитранзитивных отношений

См. также

Источники информации

Специальные свойства бинарных отношений

Рефлексивные и иррефлексивные бинарные отношения

Симметричные и антисимметричные бинарные отношения

Транзитивность бинарного отношения

Плотное бинарное отношение

Классы бинарных отношений

Связь между классами бинарных отношений

Вам также может понравиться

Как составить лид форму

Как найти друга чтобы погулять

Как составить фундаментные блоки на фундамент

Добавить комментарий Отменить ответ