Как найти требуемую мощность электродвигателя

1. Расчёт привода

1.1 Определение требуемой мощности электродвигателя

Требуемая мощность
электродвигателя определяется по
формуле

кBт,

где

– общий КПД привода,

где ₁=0,965
– КПД закрытой цилиндрической зубчатой
передачи в масляной ванне с учетом
потерь в подшипниках,

₂=0,91
– КПД цепной втулочно-роликовой передачи
с учетом потерь в подшипниках. [1, т.3]

Находим требуемую
мощность электродвигателя

=
6,834 кBт.

1.2 Выбор
электродвигателя по ГОСТ

Выбираем
электродвигатель по ГОСТ [1,т. 4] при
условии:

Р_дв

Р_тр

Выбираем
электродвигатель с числом оборотов
970.

Тип электродвигателя
АО 2-52-6

Р_дв
= 7,5 кBт,

n_дв
= 970 об/мин
– число оборотов вала двигателя

1.3 Выбор диаметр
вала электродвигателя

Выбираем диаметр
вала электродвигателя по типоразмеру
[1, т. 6]

d­_дв
= 38 мм.

1.4 Определение
мощностей

Определяем мощность
на каждом валу привода:

кBт – мощность на ведущем
валу привода,

кBт – мощность на
промежуточном валу привода,

кBт – мощность на ведомом
валу привода.

1.5 Определение
передаточных отношений редуктора

Передаточное
число показывает во сколько раз снижается
угловая скорость и частота вращения
выходной величины по сравнению с
входной.

Определяем общее
передаточное отношение

где

об/мин – число оборотов вала
электродвигателя,

=
об/мин – число оборотов ведущего вала
привода,

Тогда общее
передаточное отношение примет вид

Разбиваем общее
передаточное отношение по ступеням
привода

где u₁
–
передаточное число закрытой зубчатой
передачи,

u₂
– передаточное
число цепной втулочно-роликовой
передачи.

Принимаем для
редуктора u₁
= 3,15 [1, т. 7
], тогда u₂
=

1.6 Определение
числа оборотов и угловых скоростей
привода

Определяем угловые
скорости и число оборотов привода, на
каждом валу привода:

n₁
= 970 об/мин,

рад/с – угловая скорость и число оборотов
ведущего вала привода,

об/мин – число
оборотов выходного вала цилиндрического
редуктора,

1/с – угловая
скорость выходного вала цилиндрического
редуктора,

об/мин
– число оборотов ведомого вала привода,

1/с – угловая
скорость вращения ведомой звездочки
цепной передачи.

1.7 Определение крутящих моментов на каждом валу привода

– крутящий момент
на ведущем валу привода,

– крутящий момент
на выходном валу цилиндрического
редуктора,

– крутящий момент
на ведомом валу привода.

2. Расчет втулочной
муфты и соединение с валом.

2.1 Выбор муфты по диаметру вала двигателя по гост

d_дв = 38 мм – диаметр
вала двигателя

Определяем
расчетный крутящий момент

,

где К_р=1,5
– коэффициент режима работы для привода
электродвигателя,

Т₁
= 74 Нм
– номинальный крутящий момент.

Муфту выбираем при условии:

Т_р ≤ [Т_р]

[T_p]
=200 Н·м – максимально допустимый
крутящий момент.

Выбираем муфту по справочнику в зависимости от крутящего момента [2, т.17.2].

Размеры втулочной
муфты:

D = 55 мм – наружный
диаметр муфты,

L
= 105 мм – длина муфты,

l
= 25 мм – расстояние до отверстия под
штифт.

2.2 Расчет втулки
на кручение:

– касательное
напряжение кручения.

где


– допускаемое
напряжение кручения;

W_ρ
– полярный момент сопротивления:

где

– коэффициент отношения диаметров.

.
Условие прочности выполняется.

Соседние файлы в папке Расчёт привода,муфты

• #
• #

Энергетический расчёт и выбор на этой основе исполнительных двигателей

Блог компании Специальный Технологический Центр

Разберём, как можно выбрать исполнительные двигатели для своего проекта, самоделки и иных целей. Будет использоваться подход к синтезу, который получил название синтеза цифровой системы по ее непрерывному аналогу. Начальным этапом процесса проектирования является выполнение энергетического расчёта и выбор на этой основе исполнительных двигателей, механических передач и силовых преобразователей (усилителей мощности), в совокупности обеспечивающих возможность реализации силового воздействия на объект управления.

1. Энергетический расчёт.

Целью энергетического расчета является рациональный выбор исполнительных элементов приводов системы, которые обладают энергетическими возможностями для обеспечения механического объекта управления по заданному закону во всех предусмотренных режимах работы. Задача энергетического расчета состоит в анализе сил (моментов сил) и скоростей, которые должны развивать приводы системы и выборе исполнительных элементов, энергетически обеспечивающих возможность получения требуемых сил и скоростей движения механических объектов управления и удовлетворяющих заданным критериям эффективности такого выбора.

Считаем, что динамическая жёсткость приводов бесконечно высока и поэтому взаимовлияние степеней подвижности манипулятора не проявляется. Тогда можно считать, что при движении одного из звеньев второе звено остаётся неподвижным.

Примем себе техническое задание:

Спроектировать привода для двухзвенного плоского манипулятора робота.  Возьмём для этого упрощенную модель двухзвенного механизма манипулятора (рис.1), имеющего “плечевое” и “локтевое” звенья, причем рабочий орган (РО) условно считается закрепленным непосредственно на конце “локтевого” звена.

На рисунке приняты обозначения:

q₁ и q₂ – обобщённые координаты манипуляционного механизма. Они представляют собой углы поворота “плечевого” и “локтевого” звеньев манипулятора, соответственно. Угол q₁ определяется как отклонение “плечевого” звена от вертикали, а угол q₂ определяется как отклонение “локтевого” звена от продольной оси “плечевого” звена. Положительные значения этих углов соответствуют вращению звеньев по часовой стрелке;

L₁ и L₂ – длины «плечевого» и «локтевого» звеньев, соответственно. L₂ – расстояние от оси поворота “локтевого” звена до центра масс рабочего органа с объектом манипулирования;

m₁ и m₂ – массы «плечевого» и «локтевого» звеньев, соответственно.

Считается, что каждая из этих масс сосредоточена в центре соответствующего звена;

m₀ – суммарная масса рабочего органа и объекта манипулирования;

m_ДВ1 и m_ДВ2 – массы исполнительных двигателей;

V и a – скорость и ускорение конечной точки манипулятора соответственно;

R – расстояние от оси вращения «плечевого» звена до конечной точки манипулятора;

M₁ и M₂ – моменты сил, развиваемые приводами и действующие на звенья манипулятора.

Таблица 1. Параметры манипуляционного механизма:

Таблица 2. Основные требования к исполнительной системе робота:

1.1 Выбор двигателя и редуктора привода второго звена.

Кинематический анализ:

Найдём максимальные значения угловой скорости и углового ускорения для второго звена манипулятора.

Максимальное угловое ускорение 2-го звена:

Максимальная угловая скорость рабочего движения 2-го звена:

Максимальное угловое ускорение рабочего движения 2-го звена:

Максимальный суммарный момент сил  M2max , который должен развивать привод второго звена, определяется по формуле.

η – КПД механической передачи.

Статический момент относительно оси вращения 2-го звена определяется по формуле:

где g =9.807 м/с2 –  ускорение свободного падения.

Mст2  имеет максимальное значение при выполнении условия sin(q1+q2)=1. Mст2 = 30.4 Н*м.

Для вычисления динамического момента, действующего на второе звено, находим эквивалентный момент инерции Jэкв2 этого звена по формуле:

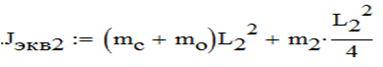
Jэкв2 = 0.62 кг*м2

Максимальное значение динамического момента (для режима переброски) получим:

       

С целью обеспечения точной работы приводов манипулятора могут быть

выбраны волновые или планетарные редукторы. Предварительно выбираем волновой редуктор HDUR-32 компании Harmonic drive gearing. По данным производителя КПД такого редуктора η2̗ = 0.85 В этом случае максимальный суммарный момент сил M2max , который должен развивать привод второго звена:

Оценка мощности двигателя второго звена:

Максимальное значение мощности механического движения второго звена:

Требуемую мощность двигателя второго звена P2 выбираем из условия.

P2≈(2…3)*P2max.  P2= 420 Вт

Выбор исполнительного двигателя производим по требуемой мощности. Выбираем двигатель TETRA 85SR2.2, обладающий следующими параметрами:

Pн2 = 650 Вт – номинальная мощность.

Мн2 = 2.2  ̗- номинальный момент Н*м.

 J дв2 =1.8Έ10˕4 кг*Ем2  – момент инерции ротора.

mдв2 = 4.2 кг – масса двигателя.

 n2ном  =  3000 об/мин – номинальная частота вращения.

Rя  = 19.76  Ом – активное сопротивление якоря.

U2ном = 250 В – номинальное напряжение якоря.

Определение требуемого передаточного отношения и марки редуктора.

Оценка значения передаточного отношения редуктора привода второго звена:

Выбираем редуктор HDUR FDD-32-260, обладающий следующими параметрами:

i_р2 = 260 – передаточное отношение.

m_p2 ̗= 1.7 кг- масса редуктора.

Для дальнейших расчётов и выбора компонентов привода первого звена принимаем массу привода второго звена равной:

Теперь проверим выполнения необходимых условий правильности выбора

двигателя и редуктора. Проверяем выбранный двигатель по моменту:

Следовательно, подсистема «двигатель-редуктор» способна создавать момент, не меньше требуемого.

1.2 Выбор двигателя и редуктора привода первого звена.

Кинематический анализ манипуляционного механизма

Расчёты проводятся в соответствии с кинематической схемой и схемой действия сил, представленной на рис. 3

В таком положении момент М1 первого звена будет иметь значения, наиболее близкие к максимально возможным значениям. Скорость вращения первого звена Ω1 определяется по формуле:

где q2 – обобщённая координата, характеризующая положение второго звена

относительно продольной оси первого звена. Таким образом, видно, что скорость вращения первого звена Ω1 зависит от обобщенной координаты q2

Угловое ускорение, с которым движется первое звено, определяется по формуле:

Следовательно, угловое ускорение тоже зависит от q2.

Силовой анализ манипуляционного механизма.

Определяется момент сил, который должен развивать привод первого звена. При этом считаем, что силы приложены в центрах масс первого и второго звеньев, рабочего органа и объекта манипулирования

Статический момент Мст1 действующий относительно оси поворота первого звена, зависит от обобщённых координат:

Динамический момент Mдин1 , зависящий от углового ускорения ε1 и

эквивалентного момента инерции Jэкв1 вычисляется по формуле:

Эквивалентный момент инерции манипуляционного механизма, перемещаемого первым приводом, можно оценить по формуле:

где ρ – расстояние от оси вращения первого звена до центра масс второго звена, причём

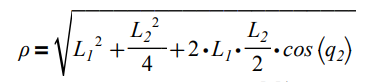
Максимальное значение суммарного момента М1 можно определить, варьируя значения переменных q1 и q2. Для упрощения решения задачи будем рассматривать конфигурацию манипулятора, представленную на рис. 3, при которой рабочий орган находится на горизонтальной прямой линии, проходящей через ось вращения первого звена. Тогда между переменными q1 и q2 будет существовать связь следующего вида:

КПД редуктора привода первого звена примем η1̗0.85

Оценка мощности механического движения первого звена.

Для определения максимального значения мощности механического движения первого звена воспользуемся графиком зависимости требуемой мощности P1 от обобщенной координаты q2.

P1max = 303 Вт. Примем q2pmax = 58 град.

1.3 Выбор двигателя привода первого звена.

Выбираем двигатель по мощности из расчета P1≈(2…3)*P1max. P1 = 2.5 * P1max = 757.5 Вт.

Выбираем двигатель ESA 3L обладающий следующими параметрами:

Pн1 = 800 Вт – номинальная мощность.

Мн1 = 1.75 Н*м – номинальный момент.

Jдв1 = 0.64 * 10^-4 кг*м^2 – момент инерции ротора.

Mдв1 = 3.05 кг – масса двигателя.

n1ном = 3000 обмин – номинальная частота вращения.

Rя1 = 5.24 Ом – сопротивление якоря.

U1ном = 250 В – номинальное напряжение якоря.

Iяном = 2.5 А – номинальный ток якоря.

Tэ = 0.00275  – электромагнитная постоянная времени.

Вычислим номинальную угловую скорость двигателя:

Выбираем редуктор аналогичный редуктору второго звена HDUR-32-260

обладающий следующими параметрами:

i = 260 – передаточное отношение.

m 1.7 кг- масса редуктора.

В этой статье мы разберем, что такое мощность трехфазного асинхронного двигателя и как ее рассчитать.

Понятие мощности электродвигателя

Мощность – пожалуй, самый важный параметр при выборе электродвигателя. Традиционно она указывается в киловаттах (кВт), у импортных моделей – в киловаттах и лошадиных силах (л.с., HP, Horse Power). Для справки: 1 л.с. приблизительно равна 0,75 кВт.

На шильдике двигателя указана номинальная полезная (отдаваемая механическая) мощность. Это та мощность, которую двигатель может отдавать механической нагрузке с заявленными параметрами без перегрева. В формулах номинальная механическая мощность обозначается через Р₂.

Электрическая (потребляемая) мощность двигателя Р₁ всегда больше отдаваемой Р₂, поскольку в любом устройстве преобразования энергии существуют потери. Основные потери в электродвигателе – механические, обусловленные трением. Как известно из курса физики, потери в любом устройстве определяются через КПД (ƞ), который всегда менее 100%. В данном случае справедлива формула:

Р₂ = Р₁ · ƞ

КПД в двигателях зависит от номинальной мощности – у маломощных моделей он может быть менее 0,75, у мощных превышает 0,95. Приведенная формула справедлива для активной потребляемой мощности. Но, поскольку электродвигатель является активно-реактивной нагрузкой, для расчета полной потребляемой мощности S (с учетом реактивной составляющей) нужно учитывать реактивные потери. Реактивная составляющая выражается через коэффициент мощности (cosϕ). С её учетом формула номинальной мощности двигателя выглядит так:

Р₂ = Р₁ · ƞ = S · ƞ · cosϕ

Мощность и нагрев двигателя

Номинальная мощность обычно указывается для температуры окружающей среды 40°С и ограничена предельной температурой нагрева. Поскольку самым слабым местом в двигателе с точки зрения перегрева является изоляция, мощность ограничивается классом изоляции обмотки статора. Например, для наиболее распространенного класса изоляции F допустимый нагрев составляет 155°С при температуре окружающей среды 40°С.

В документации на электродвигатели приводятся данные, из которых видно, что номинальная мощность двигателя падает при повышении температуры окружающей среды. С другой стороны, при должном охлаждении двигатели могут длительное время работать на мощности выше номинала.

Мы рассмотрели потребляемую и отдаваемую мощности, но следует сказать, что реальная рабочая потребляемая мощность P (мощность на валу двигателя в данный момент) всегда должна быть меньше номинальной:

Р < Р₂ < Р₁ < S

Это необходимо для предотвращения перегрева двигателя и наличия запаса по перегрузке. Кратковременные перегрузки допустимы, но они ограничены прежде всего нагревом двигателя. Защиту двигателя по перегрузке также желательно устанавливать не по номинальному току (который прямо пропорционален мощности), а исходя из реального рабочего тока.

Современные производители в основном выпускают двигатели из ряда номиналов: 1,5, 2,2, 5,5, 7,5, 11, 15, 18,5, 22 кВт и т.д.

Расчет мощности двигателя на основе измерений

На практике мощность двигателя можно рассчитать, прежде всего, исходя из рабочего тока. Ток измеряется токовыми клещами в максимальном рабочем режиме, когда рабочая мощность приближается к номинальной. При этом температура корпуса двигателя может превышать 100 °С, в зависимости от класса нагревостойкости изоляции.

Измеренный ток подставляем в формулу для расчета реальной механической мощности на валу:

Р = 1,73 · U · I · cosϕ · ƞ, где

• U – напряжение питания (380 или 220 В, в зависимости от схемы подключения – «звезда» или «треугольник»),
• I – измеренный ток,
• cosϕ и ƞ – коэффициент мощности и КПД, значения которых можно принять равными 0,8 для маломощных двигателей (менее 5,5 кВт) или 0,9 для двигателей мощностью более 15 кВт.

Если нужно найти номинальную мощность двигателя, то полученный результат округляем в бОльшую сторону до ближайшего значения из ряда номиналов.

Р₂ > Р

Если необходимо рассчитать потребляемую активную мощность, используем следующую формулу:

Р₁ = 1,73 · U · I · ƞ

Именно активную мощность измеряют счетчики электроэнергии. В промышленности для измерения реактивной (и полной мощности S) применяют дополнительное оборудование. При данном способе можно не использовать приведенную формулу, а поступить проще – если двигатель подключен в «звезду», измеренное значение тока умножаем на 2 и получаем приблизительную мощность в кВт.

Расчет мощности при помощи счетчика электроэнергии

Этот способ прост и не требует дополнительных инструментов и знаний. Достаточно подключить двигатель через счетчик (трехфазный узел учета) и узнать разницу показаний за строго определенное время. Например, при работе двигателя в течении часа разница показаний счетчика будет численно равна активной мощности двигателя (Р₁). Но чтобы получить номинальную мощность Р₂, нужно воспользоваться приведенной выше формулой.

Другие полезные материалы:
Степени защиты IP
Трехфазный двигатель в однофазной сети
Типичные неисправности электродвигателей