Как найти трехгранник френе

Как найти трехгранник френе

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 марта 2021 года; проверки требуют 2 правки.

Репер или трёхгранник Френе
или Френе — Серре
известный также, как
естественный,
сопровождающий,
сопутствующий — ортонормированный репер в трёхмерном пространстве, возникающий при изучении бирегулярных кривых, то есть таких, что первая и вторая производная линейно независимы в любой точке.

Определение[править | править код]

Пусть {displaystyle r(s)} — произвольная натурально параметризованная бирегулярная кривая в евклидовом пространстве. Под репером Френе понимают тройку векторов tau , nu , beta , сопоставленную каждой точке бирегулярной кривой {displaystyle r(s)}, где

Свойства[править | править код]

называемыми формулами Френе. Величины

{displaystyle k=||{ddot {r}}(s)||,quad t=-langle {dot {beta }},;{nu }rangle }
называют, соответственно, кривизной и кручением кривой в данной точке.

Скорость и ускорение в осях естественного трёхгранника[править | править код]

Трёхгранник Френе играет важную роль в кинематике точки при описании её движения в «сопутствующих осях». Пусть материальная точка движется по произвольной бирегулярной кривой. Тогда, очевидно, скорость точки направлена по касательному вектору {displaystyle {v}=v{tau }}. Дифференцируя по времени находим выражение для ускорения: {displaystyle {a}={dot {v}}{tau }+v^{2}k{nu }}. Компоненту при векторе {displaystyle {tau }} называют тангенциальным ускорением, она характеризует изменение модуля скорости точки. Компоненту при векторе {displaystyle {nu }} называют нормальным ускорением.
Она показывает, как меняется направление движения точки.

Вариации и обобщения[править | править код]

При описании плоских кривых часто вводят понятие так называемой ориентированной кривизны.

Пусть {displaystyle gamma (s)} — произвольная натурально параметризованная плоская регулярная кривая. Рассмотрим семейство единичных нормалей {displaystyle {nu _{o}}}, таких что двойка {displaystyle ({tau },{nu _{o}})} образуют правый базис в каждой точке {displaystyle mathbf {gamma } (s)}. Ориентированной кривизной кривой gamma в точке s называют число {displaystyle k_{o}=langle {ddot {gamma }}(s),;{nu _{o}}rangle }. В сделанных предположениях имеет место следующая система уравнений, называемая формулами Френе для ориентированной кривизны

{displaystyle {dot {tau }}=k_{o}{nu _{o}}quad {dot {nu _{o}}}=-k_{o}{tau }}.

По аналогии с трёхмерным случаем, уравнения вида {displaystyle k_{o}=f(s)} называются натуральными уравнениями плоской регулярной кривой и полностью её определяют.

См. также[править | править код]

  • Трёхгранник Дарбу — аналогичная конструкция для кривой на поверхности.

Литература[править | править код]

  • Топоногов, В. А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 978-5-89155-213-5.
Источник

В предыдущих параграфах были введены два единичных ортогональных вектора: вектор , направленный по касательной к кривой, и вектор главной нормали , который определён первой формулой Френе (1.9). Введём единичный вектор , ортогональный векторам и , как векторное произведение на

. (2.1)

Нормаль, которая определяется вектором , называется Бинормалью. Очевидно, что получена правая тройка ортогональных векторов. Этот подвижный базис (или репер), который сопровождает точку М при её движении по кривой, называется Подвижным, а также Естественным базисом или Репером Френе (Френе – французский геометр XIX века, который в 1847 году первым написал формулы для производных по длине дуги трёх базисных векторов , , ).

Плоскость, проходящая через вектора и , называется Соприкасающейся, через вектора и – Нормальной, а через вектора и – Спрямляющей. Эти три плоскости образуют так называемый Естественный трехгранник, или Трехгранник Френе (рис. 2.1).

Уравнение (1.9) определяет производную . Для того, чтобы получить производные от векторов и , обратимся к формуле (2.1). Дифференцируя по и используя формулу (1.9), имеем

.

Отсюда следует, что вектора и ортогональны. Кроме того, ортогонально (см п.3о в 1.2). Таким образом, направление вектора совпадает с направлением вектора главной нормали

. (2.2)

Это Вторая формула Френе, где коэффициент характеризует степень изменяемости вектора по длине дуги, то есть поворот соприкасающейся плоскости. Если , то кривая лежит в этой плоскости. Коэффициент называется кручением.

Теперь рассмотрим . Этот вектор ортогонален (по формуле (1.4)), поэтому в разложении по ортогональному базису , , ,

, (2.3)

Коэффициент .

Продифференцируем равенство

: .

В последнее соотношение подставим выражение из (2.3) и из (1.9). Получаем равенство , отсюда коэффициент .

Поскольку , получаем

. (2.4)

С другой стороны, по второй формуле Френе

.

Таким образом, С= , и

. (2.5)

Это Третья формула Френе.

По определению кривизна , но кручение может быть любого знака.

Для вычисления кручения используем вторую формулу Френе . Умножив скалярно на левую и правую части равенства, получим

.

С учётом равенства (см. формулу (2.4)), имеем

,

Где в круглых скобках записано смешанное произведение трёх векторов. Поскольку , а из первой формулы Френе следует, что , то

, (2.6)

Где в данном случае штрих означает дифференцирование по .

< Предыдущая   Следующая >
Источник

Рассмотрим

гладкую кривую

в пространстве

.

Пусть

– любая точка кривой. Найдем плоскость,
проходящую через

и «ближе всего подходящую» к кривой

в окрестности точки

.
Заметим, что если кривая

– плоская (то есть лежащая в некоторой
плоскости

),
то искомой плоскостью будет плоскость

.

Определение
3.1. Соприкасающейся
плоскостью к
кривой

в точке

называется предел секущей плоскости,
проходящей через точки

кривой

при
стремлении

Более
строго, плоскость

,
проходящая через точку

кривой

,
является соприкасающейся к кривой

в точке

,
если


.

Теорема
3.1.

-гладкая
кривая

имеет в каждой точке

соприкасающуюся плоскость.

Дадим
необходимые разъяснения для кривой
более высокого порядка гладкости.

Пусть
в
пространстве

задана прямоугольная система координат
Оxyz.

Пусть
r
(t)

– одна из гладких параметризаций кривой

:


и

Рассмотрим
произвольную точку

,
близкую к точке

.

Разложим
в ряд Тейлора вектор смещения

:

Пусть

– неколлинеарные векторы.

Тогда
искомая плоскость единственна и проходит
через точку

параллельно векторам

.

Замечание
3.1.
Неколлинеарность векторов

не
зависит от способа параметризации
кривой.
В частности, для любой допустимой замены
параметра

,
где

,
векторы

также будут неколлинеарны.

Пусть

– коллинеарные векторы.

Тогда
соприкасающаяся плоскость не единственна.
В качестве одной из соприкасающихся
плоскостей можно взять любую из
плоскостей, проходящих через касательную
к кривой в точке

.

Определение
3.2. Спрямляющей
плоскостью к
кривой

в точке

называется плоскость, проходящая через
точку

кривой

перпендикулярно
спрямляющей и нормальной плоскостям в
этой точке.

Определение
3.3. Главной
нормалью к
кривой

в точке

называется прямая пересечения
соприкасающейся и нормальной плоскостей,
проведенных в точке

.

Главная
нормаль перпендикулярна спрямляющей
плоскости

.

Определение
3.4. Бинормалью
к
кривой

в точке

называется прямая пересечения спрямляющей
и нормальной плоскостей, проведенных
в точке

.

Бинормаль
перпендикулярна соприкасающейся
плоскости в точке

.

Определение
3.5. Сопровождающим
трехгранником (или
репером
Френе)
кривой

в точке

называется совокупность трех прямых
– касательной, главной нормали и
бинормали, и трех плоскостей – нормальной
спрямляющей и соприкасающейся, проведенных
в точке

.

Рисунок 12.

Пусть
r
(t)

– одна из гладких параметризаций кривой

:


,
и

– любая точка кривой.

Напишем
уравнения всех прямых и всех плоскостей
сопровождающего трехгранника кривой.

Уравнения
касательной прямой и нормальной плоскости
мы уже выписывали в §2.

Если
соприкасающаяся плоскость к кривой

в точке

единственна, то она может быть задана
параметрическими уравнениями

,
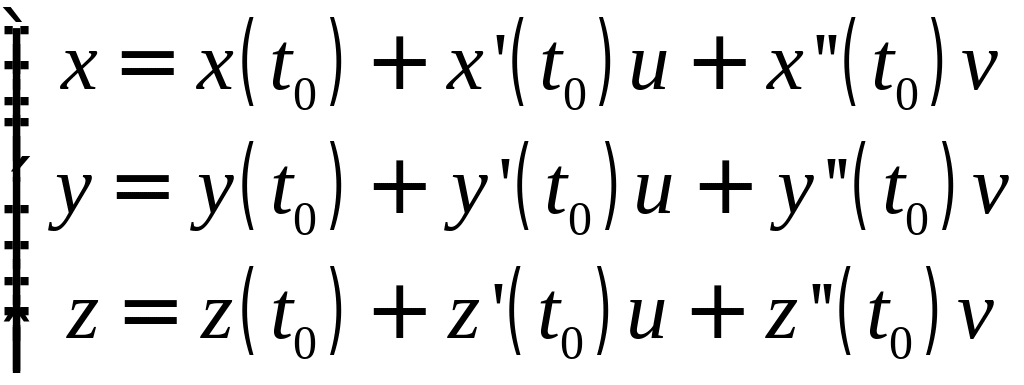
где

.

В
качестве направляющего вектора бинормали
возьмем вектор

.
Уравнение бинормали в параметрическом
виде

,
где

.

В
качестве направляющего вектора главной
нормали возьмем вектор

.
Уравнение главной нормали в параметрическом
виде

,
где

.

Уравнение спрямляющей
плоскости в параметрическом виде

,
где

.

Уравнение
соприкасающейся плоскости можно также
написать в общем виде как уравнение
плоскости, проходящей через точку

перпендикулярно вектору

:


.

Аналогично,
так как спрямляющая плоскость проходит
через точку

перпендикулярно вектору

,
то ее общее уравнение имеет вид:


.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Репер или трёхгранник Френе
или Френе — Серре
известный также, как
естественный,
сопровождающий,
сопутствующий — ортонормированный репер в трёхмерном пространстве, возникающий при изучении бирегулярных кривых, то есть таких, что первая и вторая производная линейно независимы в любой точке.

Определение

Пусть [math]displaystyle{ r(s) }[/math] — произвольная натурально параметризованная бирегулярная кривая в евклидовом пространстве. Под репером Френе понимают тройку векторов [math]displaystyle{ tau }[/math], [math]displaystyle{ nu }[/math], [math]displaystyle{ beta }[/math], сопоставленную каждой точке бирегулярной кривой [math]displaystyle{ r(s) }[/math], где

  • [math]displaystyle{ tau = dot{r}(s) }[/math] — единичный касательный вектор,
  • [math]displaystyle{ nu = frac{ddot{r}(s)}{||ddot{r}(s)||} }[/math] — единичный вектор главной нормали,
  • [math]displaystyle{ beta = [tau,nu] }[/math] — единичный вектор бинормали к кривой в данной точке.

Свойства

  • Если [math]displaystyle{ s }[/math] — естественный параметр [math]displaystyle{ s }[/math] кривой, то векторы [math]displaystyle{ {tau}, {nu}, {beta} }[/math] связаны соотношениями:
    [math]displaystyle{ begin{aligned}dot{tau} &= kcdot {nu},
    \ dot{nu} &= – kcdot {tau} + tcdot{beta},
    \ dot{beta} &= – tcdot {nu},end{aligned} }[/math]
называемыми формулами Френе. Величины

[math]displaystyle{ k = ||ddotgamma (s)||, quad t = – langle dot{beta},; {nu} rangle }[/math]
называют, соответственно, кривизной и кручением кривой в данной точке.
  • Функции [math]displaystyle{ k(s) }[/math] и [math]displaystyle{ t(s), }[/math] определяют кривую с точностью до движения пространства.
    • Более того в случае если [math]displaystyle{ k(s)gt 0 }[/math], такая кривая существует.

Скорость и ускорение в осях естественного трёхгранника

Трёхгранник Френе играет важную роль в кинематике точки при описании её движения в «сопутствующих осях». Пусть материальная точка движется по произвольной бирегулярной кривой. Тогда, очевидно, скорость точки направлена по касательному вектору [math]displaystyle{ {v} = v {tau} }[/math]. Дифференцируя по времени находим выражение для ускорения: [math]displaystyle{ {a} = dot{v} {tau} + v^2 k {nu} }[/math]. Компоненту при векторе [math]displaystyle{ {tau} }[/math] называют тангенциальным ускорением, она характеризует изменение модуля скорости точки. Компоненту при векторе [math]displaystyle{ {nu} }[/math] называют нормальным ускорением.
Она показывает, как меняется направление движения точки.

Вариации и обобщения

При описании плоских кривых часто вводят понятие так называемой ориентированной кривизны.

Пусть [math]displaystyle{ gamma(s) }[/math] — произвольная натурально параметризованная плоская регулярная кривая. Рассмотрим семейство единичных нормалей [math]displaystyle{ {nu _o} }[/math], таких что двойка [math]displaystyle{ ({tau},{nu _o}) }[/math] образуют правый базис в каждой точке [math]displaystyle{ mathbf gamma(s) }[/math]. Ориентированной кривизной кривой [math]displaystyle{ gamma }[/math] в точке [math]displaystyle{ s }[/math] называют число [math]displaystyle{ k _o = langle ddotgamma (s),; {nu _o} rangle }[/math]. В сделанных предположениях имеет место следующая система уравнений, называемая формулами Френе для ориентированной кривизны

[math]displaystyle{ dot{tau} = k _o {nu _o} quad dot{nu _o} = -k _o {tau} }[/math].

По аналогии с трёхмерным случаем, уравнения вида [math]displaystyle{ k _o = f(s) }[/math] называются натуральными уравнениями плоской регулярной кривой и полностью её определяют.

См. также

  • Трёхгранник Дарбу — аналогичная конструкция для кривой на поверхности.

Литература

  • Топоногов, В. А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 978-5-89155-213-5.
Источник

Репер Френе

Репер Френе

Репер или трёхгранник Френе или Френе — Серре известный также, как естественный, сопровождающий, сопутствующий — ортонормированный репер в трёхмерном пространстве, возникающий при изучении бирегулярных кривых.

Содержание

  • 1 Определение
  • 2 Формулы Френе
  • 3 Скорость и ускорение в осях естественного трёхгранника
  • 4 Вариации и обобщения

Определение

Пусть γ(s) — произвольная натурально параметризованная бирегулярная кривая в евклидовом пространстве. Под репером Френе понимают тройку векторов vec{tau}, vec{nu}, vec{beta}, сопоставленную каждой точке бирегулярной кривой mathbf{ gamma(s)} , где

к кривой в данной точке.

Формулы Френе

Если s — натуральный параметр вдоль кривой, то векторы vec{tau}, vec{nu}, vec{b} связаны соотношениями:

dotvec{tau} = k vec{nu}, quad dotvec{nu} = - k vec{tau} + kappa vec{beta}, quad dotvec{beta} = - kappa vec{nu},

называемыми формулами Френе. Величины k = ||ddotgamma (s)||, quad kappa = - langle dotvec{beta},; vec{nu} rangle называют, соответственно, кривизной и кручением кривой в данной точке. Уравнения вида k = f(s), quad kappa = g(s), где f(s) всюду положительна называются натуральными уравнениями бирегулярной кривой и полностью её определяют.

Скорость и ускорение в осях естественного трёхгранника

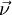Трёхгранник Френе играет важную роль в кинематике точки при описании её движения в «сопутствующих осях». Пусть материальная точка движется по произвольной бирегулярной кривой. Тогда, очевидно, скорость точки направлена по касательному вектору vec{v} = v vec{tau} . Дифференцируя по времени находим выражение для ускорения: vec{a} = dot{v} vec{tau} + v^2 k vec{nu}. Компоненту при векторе vec{tau} называют тангенциальным ускорением, она характеризует изменение модуля скорости точки. Компоненту при векторе vec{nu} называют нормальным ускорением. Она показывает, как меняется траектория движения точки.

Вариации и обобщения

При описании плоских кривых часто вводят понятие так называемой ориентированной кривизны.

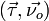Пусть γ(s) – произвольная натурально параметризованная плоская регулярная кривая. Рассмотрим семейство единичных нормалей vec{nu _o}, таких что двойка (vec{tau},vec{nu _o}) образуют правый базис в каждой точке mathbf gamma(s). Ориентированной кривизной кривой γ в точке s называют число k _o = langle ddotgamma (s),; vec{nu _o} rangle . В сделанных предположениях имеет место следующая система уравнений, называемая формулами Френе для ориентированной кривизны

dotvec{tau} = k _o vec{nu _o} quad dotvec{nu _o} = -k _o vec{tau}.

По аналогии с трёхмерным случаем, уравнения вида ko = f(s) называются натуральными уравнениями плоской регулярной кривой и полностью её определяют.

Wikimedia Foundation.
2010.

Полезное

Смотреть что такое “Репер Френе” в других словарях:

  • НАТУРАЛЬНЫЙ РЕПЕР, — трехгранник (или репер) Френе, естественный трехгранник, фигура, составленная из касательной, главной нормали, бинормали и трех плоскостей, попарно содержащих эти прямые. Если ребра Н. р. в данной точке кривой принять за оси прямоугольной… …   Математическая энциклопедия

  • Трёхгранник Френе — Репер или трёхгранник Френе или Френе  Серре известный также, как естественный, сопровождающий, сопутствующий  ортонормированный репер в трёхмерном пространстве, возникающий при изучении бирегулярных кривых. Содержание 1 Определение 2… …   Википедия

  • ПЛАСТИЧНОСТИ ТЕОРИЯ — раздел механики, в к ром изучаются законы, отражающие связи между напряжениями и упругопластич. деформациями (физ. основы П. т.), и разрабатываются методы решения задач о равновесии и движении деформируемых тв. тел (матем. П. т.). П. т. явл.… …   Физическая энциклопедия

  • Естественный трёхгранник — Репер или трёхгранник Френе или Френе Серре известный также, как естественный, сопровождающий, сопутствующий ортонормированный репер в трёхмерном пространстве, возникающий при изучении бирегулярных кривых. Содержание 1 Определение 2 Формулы Френе …   Википедия

  • ПОДВИЖНОГО РЕПЕРА МЕТОД — дифференциально геометрический метод локального исследования подмногообразий различных однородных пространств, исходным моментом к poro является отнесение самого подмногообразия и всех его геометрич. объектов к возможно более общему (подвижному)… …   Математическая энциклопедия

  • КРИВИЗНА — количеств. характеристика, описывающая отклонение кривой, поверхности, риманова пространства и др. соответственно от прямой, плоскости, евклидова пространства и др. Обычно понятие К. вводится локально, т. е. в каждой точке. В декартовых… …   Физическая энциклопедия

Источник

Добавить комментарий