Эта статья отвечает на вопрос, как найти силу трения без коэффициента. Мы все знакомы с трением и, должно быть, сталкивались с трением каждый день в нашей повседневной жизни.
Мы также знаем, что для расчета величины силы трения требуется коэффициент трения. Но что происходит, когда мы не знаем значение коэффициента трения, а нам все еще нужно найти величину силы трения? Мы изучим это в этой статье.
Что такое трение?
Мы все знаем о трение и его влияние на нашу повседневную жизнь. Мы не можем ходить или бегать без помощи трения. Несмотря на то, что это противостоящая сила, она помогает нам двигаться вперед.
Сопротивление нашему движению называется трением. Трение возникает из-за простых неровностей на поверхности предметов. Ничто в этом мире не идеально, как и любая поверхность. Должны быть хотя бы какие-то неровности, которые вызовут трение.

Изображение кредита: ЦаоХао, Трение между поверхностями, CC BY-SA 4.0
Что такое коэффициент трения?
Коэффициент трения – это отношение силы трения к нормальной силе реакции, действующей на тело.
Используется для нахождения значения усилие за счет трения. Этот коэффициент также говорит нам о величине шероховатости на поверхности. Проще говоря, коэффициент трения является мерой шероховатости поверхности и позволяет нам легко найти величину силы трения.
Как найти значение трения без коэффициента?
Без коэффициента силы трения мы не можем найти силу трения. Коэффициент трения можно найти двумя способами.
Один очень простой, мы можем просто проверить стандартные значения из учебника. Стандартные значения различных материалов перечислены в книге стандартных значений. Другой способ узнать коэффициент трения — экспериментировать. Для наклонной плоскости тангенс угла наклона дает значение коэффициента трения.
Применение трения
Трение не всегда плохо. Он используется во многих приложениях, которые мы увидим в списке, приведенном ниже:
- Прогулки– При ходьбе лучше всего используется трение. Без трения человеческое тело оставалось бы на одном месте, пытаясь двигаться вперед. Это связано с тем, что во время ходьбы реакция вперед дает мощный толчок нашему телу, что помогает нам двигаться вперед.
- Бег – Бег – это преемник ходьбы. Если мы бежим по беговой дорожке, мы не двигаемся вперед. Это связано с тем, что беговая дорожка будет двигаться назад с той же скоростью. В случае гладкой дороги тело не получит достаточной силы реакции для движения вперед, поэтому тело будет продолжать бежать в одном и том же месте, как на беговой дорожке.
- Вождение – Вождение – еще одно важное применение трения. Колеса автомобиля испытывают огромное трение, которое отвечает за движение автомобиля вперед. Без трения автомобиль остался бы на том же месте.
- тормоза – Тормоза также являются примером, где трение играет жизненно важную роль. Без тормозов было бы почти невозможно остановить машину, не повредив ее. Тормоза спасли много жизней, и вся заслуга в наличии трения. Трение является ключевым моментом во всем процессе остановки автомобиля. Именно из-за трения автомобиль останавливается.
- Остановка мяча – Если мы бросим мяч и рассчитываем, что он переместится только на определенное расстояние, мы бросим его с некоторой силой. Но где гарантия, что мяч не будет двигаться вечно? Это трение между поверхностью земли и мячом, из-за которого мяч обязательно остановится. У нас всегда есть приблизительное представление о величине трения, которое будет производить поверхность, благодаря нашему опыту. Таким образом, мяч останавливается в нужном месте.
- Вращение мяча для крикета– Спиннер вращает мяч, выпуская его из руки. Мяч поворачивается после касания земли. Это происходит из-за трения между полем и мячом. Сила обратной реакции толкает мяч в направлении вращения, тем самым создавая эффект поворота.
- Живопись – Во время рисования краска прилипает к поверхности бумаги. Это происходит из-за трения. Молекулы красок прилипают к неровностям на поверхности бумаги. Таким образом, краска не осыпается с бумаги даже после высыхания. Если полировать на гладкой поверхности, краска иногда может отвалиться, потому что она не создает адгезионного эффекта с поверхностью.
- Рисование – Как и в живописи, в рисовании также используется трение. По этой причине очень трудно писать на гладкой поверхности. В основном шероховатые поверхности являются наиболее подходящими для письма, но чрезмерная шероховатость создаст трудности при письме, поэтому для письма требуется оптимальная шероховатость.
- ВЕЛО МАСКИ – Велоспорт использует трение для движения вперед по той же причине, что и при ходьбе, беге и вождении автомобиля. Шины велосипеда подвергаются толчку вперед, заданному нормальной реакцией. Это возможно с помощью трения. Без трения цикл не двигался бы вперед. Важно заметить, что по скользкой дороге трудно двигаться. Потому что на скользких дорогах очень меньше трения.
- Очистка рук — Пока мы чистим руки, мы начинаем растирать руки, благодаря чему молекулы мыла комфортно сидят внутри неровностей и убирают грязь с рук. Вот почему наши руки скользкие, когда мы наносим мыло. Это в основном связано с тем, что молекулы мыла располагаются внутри неровностей и, следовательно, сводят к минимуму вероятность трения.
- Gears– Зацепление зубчатых колес представляет собой приложение трения. Поскольку зубья, входящие в зацепление, являются просто неровностями, о которых мы говорим, обсуждая трение, эти шестерни прилипают друг к другу, в результате чего происходит передача движения.
Автор:
Louise Ward
Дата создания:
9 Февраль 2021
Дата обновления:
12 Май 2023

Содержание
- Нахождение силы трения экспериментально
- подсказки
- Нахождение силы трения без эксперимента
Большинство людей понимают трение интуитивно. Когда вы пытаетесь протолкнуть объект вдоль поверхности, контакт между объектом и поверхностью противостоит вашему толчку до определенной силы толчка. При математическом расчете силы трения обычно используется «коэффициент трения», который описывает, как два конкретных материала «слипаются», чтобы противостоять движению, и нечто, называемое «нормальной силой», которая относится к массе объекта. Но если вы не знаете коэффициент трения, как вы распределяете силу? Вы можете добиться этого либо путем поиска стандартного результата в Интернете, либо проведением небольшого эксперимента.
Нахождение силы трения экспериментально
Используйте рассматриваемый объект и небольшой участок поверхности, который вы можете свободно перемещать, чтобы установить наклонную рампу. Если вы не можете использовать всю поверхность или весь объект, просто используйте кусок чего-то, сделанного из того же материала. Например, если у вас плиточный пол в качестве поверхности, вы можете использовать одну плитку для создания рампы. Если у вас есть деревянный шкаф в качестве объекта, используйте другой, меньший объект, сделанный из дерева (в идеале с аналогичной отделкой на дереве). Чем ближе вы окажетесь к реальной ситуации, тем точнее будет ваш расчет.
Убедитесь, что вы можете отрегулировать наклон рампы, составив серию книг или что-то подобное, чтобы вы могли внести небольшие изменения в ее максимальную высоту.
Чем больше наклонная поверхность, тем больше сила гравитации будет тянуть ее вниз по наклонной плоскости. Сила трения работает против этого, но в какой-то момент сила гравитации преодолевает ее. Это говорит вам о максимальной силе трения для этих материалов, и физики описывают это через коэффициент статического трения (μстатический). Эксперимент позволяет найти значение для этого.
Поместите объект на поверхность под небольшим углом, который не заставит его скользить по трапу. Постепенно увеличивайте наклон ската, добавляя книги или другие тонкие объекты в свой стек, и найдите самый крутой наклон, на котором вы можете удерживать его, не двигая объект. Вы будете изо всех сил пытаться получить полностью точный ответ, но ваша лучшая оценка будет достаточно близка к истинному значению для расчета. Измерьте высоту рампы и длину основания рампы, когда она находится под этим наклоном. По сути, вы рассматриваете рампу как формирование прямоугольного треугольника с полом и измерение длины и высоты треугольника.
Математика для ситуации получается аккуратно, и получается, что тангенс угла наклона говорит вам о значении коэффициента. Так:
μстатический = загар (θ)
Или, поскольку tan = противоположный / соседний = длина основания / рост, вы рассчитываете:
μстатический = загар (длина основания / высота ската)
Выполните этот расчет, чтобы найти значение коэффициента для вашей конкретной ситуации.
подсказки
F = μстатический N
Где “N”Означает нормальную силу. Для плоской поверхности это значение равно весу объекта, поэтому вы можете использовать:
F = μстатический мг
Вот, м это масса объекта и грамм ускорение силы тяжести (9,8 м / с2).
Например, древесина на каменной поверхности имеет коэффициент трения μстатический = 0,3, поэтому, используя это значение для деревянного шкафа весом 10 кг на каменной поверхности:
F = μстатический мг
= 0,3 × 10 кг × 9,8 м / с2
= 29,4 ньютона
Нахождение силы трения без эксперимента
Посмотрите в Интернете, чтобы найти коэффициент трения между вашими двумя веществами. Например, автомобильная шина на асфальте имеет коэффициент μстатический = 0,72, лед на дереве μстатический = 0,05 и дерево на кирпиче μстатический = 0,6 Найдите значение для вашей ситуации (включая использование коэффициента скольжения, если вы не рассчитываете трение от неподвижного) и запишите его.
Следующее уравнение говорит о силе силы трения (с коэффициентом статического трения):
F = μстатический N
Если ваша поверхность ровная и параллельна земле, вы можете использовать:
F = μстатический мг
Если это не так, нормальная сила слабее. В этом случае найдите угол наклона θи рассчитать:
F = cos (θ) μстатический мг
Например, используя кусок льда весом 1 кг на дереве, наклоненный до 30 °, и помня, что грамм = 9,8 м / с2, это дает:
F = cos (θ) μстатический мг
= cos (30 °) × 0,05 × 1 кг × 9,8 м / с2
= 0,424 ньютона
Ответы Mail.ru
Наука, Техника, Языки
Гуманитарные науки
Естественные науки
Лингвистика
Техника
Вопросы – лидеры.
От скольки до скольки частот можно сделать передатчик на транзисторах?
1 ставка
Про скорость света
1 ставка
Зачем после квадратурного демодулятора необходимо наличие фильтра нижних частот (ФНЧ)
1 ставка
Короткое замыкание в плате Гранит-3.
1 ставка
Работа в ArtCAM со станком чпу
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Как найти силу трения без коэффициента трения?
slipstrim
Профи
(739),
закрыт
1 год назад
Спасибо за ответ!
Лучший ответ
Аркаша
Высший разум
(538966)
2 года назад
Привязать к безмену и тащить !
Остальные ответы
Полосатый жираф Алик
Искусственный Интеллект
(310536)
2 года назад
Измеряй. Например, динамометром.
Иван Непомнящий
Искусственный Интеллект
(177178)
2 года назад
В корыто посади кого нибудь тяни через безмен. Через момент вращения можно
Сергей Логинов
Оракул
(87323)
2 года назад
Только имей в виду, что их две — есть еще сила трения покоя. Она больше. Поэтому и двери скрипят, и на лыжах катаются…
david.gorelikУченик (210)
2 года назад
их 3
Похожие вопросы

{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения – зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу

mu = dfrac{F_{тр}}{mg}
Fтр – сила трения
m – масса тела
g – ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона

mu = tg(alpha)
α – угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.
Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как Fтр. Единица измерения — Н (Ньютон).
Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.
Виды сухого трения:
- трение скольжения;
- трение качения;
- трение покоя.
Трение скольжения
Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: Fтр↑↓v.
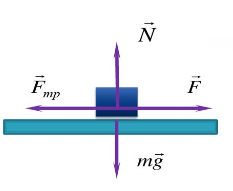
Сила трения скольжения определяется формулой:
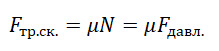
μ — коэффициент трения, N — сила реакции опоры, Fдавл. — сила нормального давления
Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.
Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.
Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.
Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.
Полезные факты
- Если тело движется по гладкой поверхности, сила трения между ними отсутствует.
- Сила трения скольжения не зависит от площади соприкосновения тел.
- Сила трения качения обычно в несколько раз меньше силы трения скольжения. Поэтому тяжелые грузы перемещают не волоком, а с помощью тележек на колесах.
Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?
Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:
Трение покоя
Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).
Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:
0 < Fтр.пок. < Fтр. ск.
Способы определения вида силы трения, возникающей между телами, и ее модуля:
- Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F < Fтр. ск., Fтр.пок. = F.
- Когда к телу прикладывается сила, модуль которой равен силе трения скольжения или превышает ее, возникает сила трения скольжения. Тело при этом начинает двигаться. Сила трения определяется формулой силы трения скольжения. Если F ≥ Fтр. ск., Fтр. = Fтр.ск.
Графически это можно изобразить так:
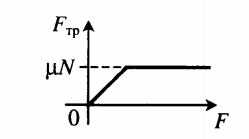
Пример №2. На горизонтальном полу стоит ящик массой 20 кг. Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?
Чтобы определить вид трения, возникающего между ящиком и полом, нужно найти силу трения скольжения и сравнить с ней приложенную к ящику силу.
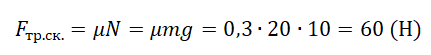
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
Fтр.пок. = F = 36 (Н).
Описание движения тел с учетом сил трения
Тело может двигаться по горизонтальной, наклонной или вертикальной плоскости. Оно может покоиться, двигаться равномерно или с ускорением, а сила тяги, под действием которой движется тело, может быть направлена, как в сторону движения тела, так и под углом к плоскости. Поэтому применение законов Ньютона к каждому из случаев имеет свои особенности.
Движение тела по горизонтальной плоскости
Равноускоренное движение по горизонтали, сила тяги параллельная плоскости |
|
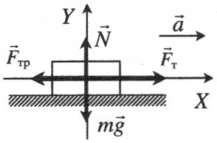 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fт – Fтр = ma Проекция на ось ОУ: N – mg = 0 |
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости |
|
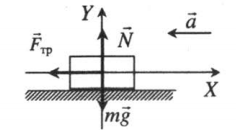 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: – Fтр = –ma Проекция на ось ОУ: N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх) |
|
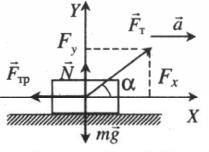 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: Fтsinα + N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз) |
|
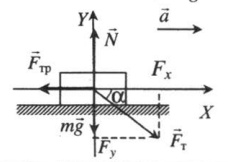 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: N – Fтsinα – mg = 0 |
Внимание! В случаях, когда сила тяги Fт направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.
Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения?
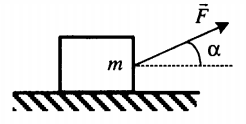
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:
Fтр = μN
Проекция сил на ось ОУ выглядит так:
N – Fтsinα – mg = 0
Отсюда силы реакции опоры равна:
N = Fтsinα + mg
Подставим ее в формулу для вычисления силы трения и получим:
Fтр = μN = μ (Fтsinα + mg) = 0,4(10∙0,5 + 1∙10) = 6 (Н)
Движение тела по вертикальной плоскости
Тело прижали к вертикальной плоскости и удерживают |
|
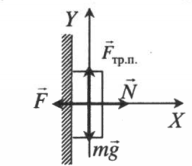 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – F = 0 Проекция на ось ОУ: Fт.п. – mg = 0 |
Тело поднимается под действием силы тяги, направленной под углом к вертикали |
|
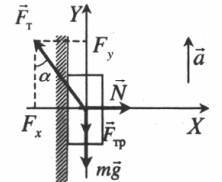 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – Fтsinα = 0 Проекция на ось ОУ: Fтcosα – Fтр – mg = 0 |
Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя.
Проекция на ось ОХ:
N – F = 0
Отсюда следует, что сила должна быть равна силе реакции опоры.
Проекция на ось ОУ:
Fт.п. – mg = 0
Перепишем, выразив силу трения через силу реакции опоры:
μN – mg = 0
Отсюда выразим силу реакции опоры:
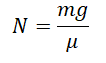
Следовательно:
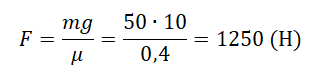
Движение тела по наклонной плоскости
Движение вниз без трения |
|
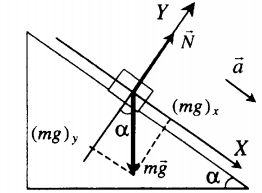 |
Второй закон Ньютона в векторной форме: |
|
mg + N = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело покоится на наклонной плоскости |
|
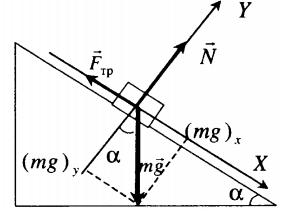 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα – Fтр.п. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело удерживают на наклонной плоскости |
|
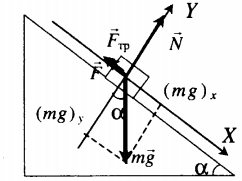 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
F + Fтр. – mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равноускоренное движение вверх с учетом силы трения |
|
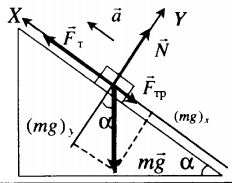 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fт + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равномерное движение вверх с учетом силы трения |
|
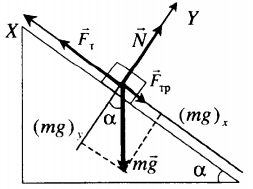 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам.
Переведем массу в килограммы: 200 г = 0,2 кг.
Проекция сил, действующих на тело, на ось ОХ:
mg sinα – Fтр.п. = 0
Отсюда сила трения равна:
Fтр.п. = mg sin α
Подставляем известные данные и вычисляем:
Fтр.п. = 0,2∙10∙sin30o = 2∙0,5 = 1 (Н)
Полезная информация
Задание EF18204
При исследовании зависимости силы трения скольжения Fтр от силы нормального давления Fд были получены следующие данные:
|
Fтр, Н |
1,0 |
2,0 |
3,0 |
4,0 |
|
Fд, Н |
2,0 |
4,0 |
6,0 |
8,0 |
Из результатов исследования можно сделать вывод, что коэффициент трения скольжения равен:
а) 0,2
б) 2
в) 0,5
г) 5
Алгоритм решения
1.Записать формулу, связывающую силу трения с силой нормального давления.
2.Выразить из нее коэффициент трения.
3.Взять значения силы трения и силы нормального давления из любого опыта (из любого столбца таблицы).
4.Вычислить коэффициент трения на основании табличных данных.
Решение
Силу трения и силу нормального давления связывает формула:
Fтр = μN
Отсюда коэффициент трения равен:
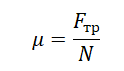
Сделаем расчет коэффициента трения на основании данных первого опыта (1 столбца):
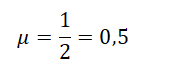
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17513
Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.
Алгоритм решения
1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.
2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.
3.Записать второй закон Ньютона в виде проекций на оси.
4.Через систему уравнений вывести искомую величину.
Решение
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
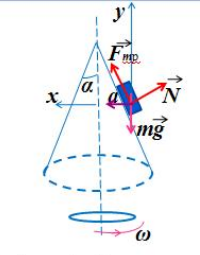
Второй закон Ньютона в векторном виде выглядит следующим образом:
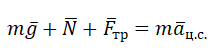
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
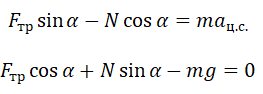
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
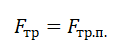
Максимальное значение силы трения равно:
![]()
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
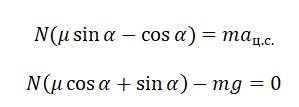
Запишем систему уравнение в следующем виде:
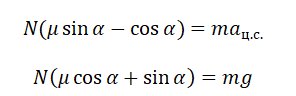
Поделим первое уравнение на второе и получим:
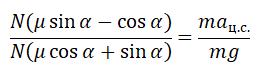
Сделаем сокращения и получим:
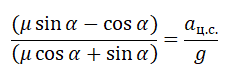
Отсюда центростремительное ускорение равно:
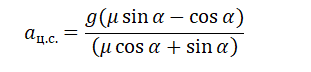
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
![]()
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
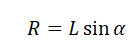
Отсюда центростремительное ускорение равно:
![]()
Выразим искомую величину L:
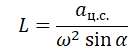
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
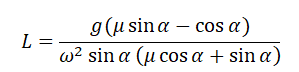
Поделим числитель на синус угла α, чтобы упростить выражение, и получим:
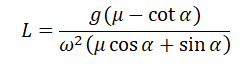
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18051
Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью υ, совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен μ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж. Указать все силы, действующие на грузовик во время торможения. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Записать формулу для нахождения силы трения скольжения.
6.Записать формулу для расчета перемещения при движении с постоянным ускорением.
7.Использовать второй закон Ньютона для определения тормозного пути.
Решение
Из условий задачи нам известны следующие величины:
• Начальная скорость грузовика (до начала торможения) v0 = v.
• Коэффициент трения между колесами и дорогой μ.
Выполним чертеж. Выберем такую систему координат, в которой направление движения грузовика во время торможения совпадает с направлением оси ОХ:
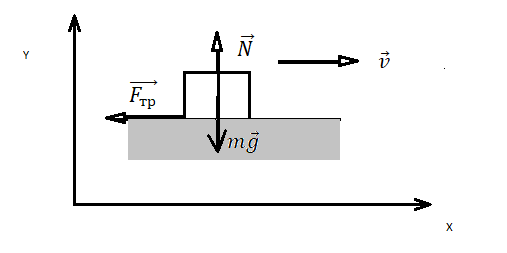
Запишем второй закон Ньютона в векторной форме:
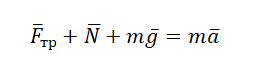
Запишем второй закон Ньютона в проекциях на оси:
Fтр = ma
N – mg = 0
Известно, что сила трения скольжения определяется формулой:
Fтр = μN = μmg
Значит, в первую ячейку таблицы мы должны поставить «1».
Перемещение при равнозамедленном движении определяется формулой (учтем, что конечная скорость равна 0, так как грузовик остановился):
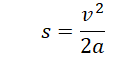
Выразим ускорение через проекцию сил на ось ОХ:
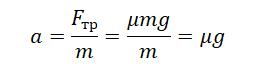
Подставим найденное ускорение в формулу тормозного пути и получим:
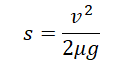
Следовательно, во вторую ячейку таблицы мы должны поставить «4».
Полный ответ: «14».
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.3k
