Векторная алгебра и аналитическая геометрия примеры решения задач
Линейные операции над векторами Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.
Векторы. Основные понятия Вектором называется направленный отрезок. Обозначается вектор  ,
,  ,
,  ,
,  , AB , a ( А – начало вектора, В – его конец).
, AB , a ( А – начало вектора, В – его конец).
Вычитание векторов. Разностью  векторов
векторов  и
и  называется такой вектор
называется такой вектор  , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор  :
:  Û
Û  .
.
Умножение вектора на число. Произведением вектора  на действительное число
на действительное число  называется вектор
называется вектор  (обозначают
(обозначают  ), определяемый следующими условиями: 1)
), определяемый следующими условиями: 1)  , 2)
, 2)  при
при  и
и  при
при  .
.
Проекция вектора на ось Углом между двумя ненулевыми векторами  и
и  называется наименьший угол
называется наименьший угол  (
(  ), на который надо повернуть один из векторов до его совпадения со вторым. Предварительно нужно привести векторы к общему началу О
), на который надо повернуть один из векторов до его совпадения со вторым. Предварительно нужно привести векторы к общему началу О
Пример При каком условии  ?
?
Координаты вектора Рассмотрим декартову прямоугольную систему координат Oxyz . Обозначим  ,
,  ,
,  – единичные векторы, направленные соответственно вдоль осей Ox , Oy , Oz (орты осей). Эти векторы называются декартовым прямоугольным базисом в пространстве.
– единичные векторы, направленные соответственно вдоль осей Ox , Oy , Oz (орты осей). Эти векторы называются декартовым прямоугольным базисом в пространстве.
Направляющие косинусы вектора Направление вектора в пространстве определяется углами  , которые вектор образует с осями координат. Косинусы этих углов называются направляющими косинусами вектора :
, которые вектор образует с осями координат. Косинусы этих углов называются направляющими косинусами вектора :  ,
,  ,
,  .
.
Пример. Даны вершины треугольника  ,
,  ,
,  . Найти точку пересечения медиан этого треугольника и орт вектора
. Найти точку пересечения медиан этого треугольника и орт вектора 
Пример. Показать, что точки  ,
,  ,
,  лежат на одной прямой, причем A – между B и C .
лежат на одной прямой, причем A – между B и C .
Скалярное произведение векторов Скалярным произведением двух векторов (обозначается  или
или  ) называется число, равное произведению длин этих векторов на косинус угла между ними:
) называется число, равное произведению длин этих векторов на косинус угла между ними:  , где
, где  .
.
Пример. Найти угол между диагоналями параллелограмма, построенного на векторах  и
и  .
.
Смешанное произведение векторов Смешанным , или векторно-скалярным произведением трех векторов (обозначается  ) называется произведение вида
) называется произведение вида  .
.
Теорема. Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Прямая на плоскости Пусть  – заданная точка на прямой
– заданная точка на прямой  ,
,  – вектор, перпендикулярный прямой
– вектор, перпендикулярный прямой  , его называют нормальным вектором прямой, и пусть
, его называют нормальным вектором прямой, и пусть  – произвольная точка прямой
– произвольная точка прямой  . Пусть
. Пусть  – заданная точка на прямой
– заданная точка на прямой  ,
,  – вектор, параллельный прямой, его называют направляющим вектором прямой, и пусть
– вектор, параллельный прямой, его называют направляющим вектором прямой, и пусть  – произвольная точка прямой
– произвольная точка прямой  Пусть
Пусть  – заданная точка на прямой
– заданная точка на прямой  ,
,  – угол наклона прямой к оси
– угол наклона прямой к оси  ,
, 
Угол между двумя прямыми. Пусть прямые  и
и  заданы соответственно уравнениями
заданы соответственно уравнениями  ,
,  , где
, где  ,
, 
Расстояние от точки до прямой. Пусть прямая  на плоскости задана уравнением
на плоскости задана уравнением  и точка
и точка  имеет координаты
имеет координаты 
Пример. Прямая  задана уравнением
задана уравнением  . Составить уравнения а) прямой
. Составить уравнения а) прямой  , проходящей через точку
, проходящей через точку  параллельно прямой
параллельно прямой  ; б) прямой
; б) прямой  , проходящей через начало координат перпендикулярно прямой
, проходящей через начало координат перпендикулярно прямой  .
.
Пример. В треугольнике с вершинами  ,
,  ,
,  составить уравнения медианы
составить уравнения медианы  , высоты
, высоты  , найти длину высоты
, найти длину высоты 
Кривые второго порядка Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат х, у
Уравнение содержит только четные степени х, у, следовательно, кривая симметрична относительно осей координат.
Гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Полагая в каноническом уравнении у = 0, найдем точки пересечения гиперболы с осью ОХ: х = ±а. При х = 0 уравнение не имеет решений, то есть с осью ОУ гипербола не пересекается. Точки А 1 (-а; 0) и А 2 (а; 0) называются вершинами гиперболы. Фокальная ось (ось, на которой лежат фокусы) называется действительной осью гиперболы, а перпендикулярная ей ось – мнимой осью.
Из симметрии гиперболы относительно осей координат следует, что этим же свойством обладает прямая  Прямые
Прямые  и
и  называются асимптотами гиперболы .
называются асимптотами гиперболы .
Параболой называется множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Уравнение содержит у лишь в четной степени, следовательно, кривая симметрична относительно оси ОХ. При х = 0 у = 0, то есть парабола проходит через начало координат.
Общее уравнение кривой второго порядка имеет вид 
Полярная система координат на плоскости определяется заданием некоторой точки О, называемой полюсом, луча Ор, исходящего из этой точки и называемого полярной осью, и единицы масштаба 
Пример. Построить в полярной системе координат точки 
Пример. Дано полярное уравнение линии  Построить эту линию по точкам. Найти ее декартово уравнение, расположив систему Охy
Построить эту линию по точкам. Найти ее декартово уравнение, расположив систему Охy
Пример. Найти полярное уравнение окружности 
Неполные уравнения плоскостей Если в уравнении плоскости  какие-либо из коэффициентов равны нулю, то получится неполное уравнение плоскости.
какие-либо из коэффициентов равны нулю, то получится неполное уравнение плоскости.
Прямая в пространстве Прямую в пространстве можно задать уравнениями, аналогичными уравнениям прямой на плоскости
Пример. Записать канонические уравнения прямой, заданной общими уравнениями 
Уравнение такого вида может определять: 1) эллипс (в частности, окружность), 2) гиперболу, 3) параболу, 4) пару прямых (параллельных, пересекающихся либо совпадающих), 5) точку или не определять никакой линии.
Вершины четырехугольника находятся в точках A(1, 2), B(7,– 6), C(11,–3), D(8, 1). Показать, что ABCD – трапеция. Найти длины оснований трапеции, ее площадь и cos Ð DAB.
Решение. Находим координаты векторов (6,–8), (4, 3), (–3 , 4), (7,–1). Проверяем векторы, определяемые противоположными сторонами четырехугольника на коллинеарность:
= – неверно, значит неколлинеарен .

Таким образом, в четырехугольнике две противоположные стороны коллинеарны, а две – нет. Значит это – трапеция, и основаниями являются AB и CD. Находим длины сторон:
и аналогично ½ ½ = 5; ½ ½ = 5; ½ ½ = 5 .
следовательно Ð BAD = 45o. Не во всех вариантах может получиться табличный угол, поэтому далее действуем так: зная cos a , находим
Tогда h = ½ ½ · sin a = 5. Зная высоту и длины оснований находим площадь: S = (AB + CD)· h = .
Ответ: ½ ½ = 10, ½ ½ = 5, cos a = , SABCD = .
6. Дано ½ ½ = 10, ½ ½ = 3, a = Ð (, ) = 30o. Найти площадь треугольника, построенного на векторах = – 3 и = 2 + 5, отложенных из одной точки. Найти длину медианы, исходящей из этой же точки.
Решение. Площадь параллелограмма построенного на векторах и , численно равна модулю их векторного произведения. Площадь треугольника, построенного на этих векторах равна половине площади параллелограмма: SΔ= ½ ´ ½ . Пользуясь свойствами и определением векторного произведения находим
½ ´ ½ = ½ ( – 3 ) ´ (2 + 5 ) ½ = ½ ´ + 5 ´ – 3 ´ – 15 ´ ½ =
= ½ + 5 ´ + 3 ´ +15 ½ = 8 ½ ´ ½ = 8 ½ ½ · ½ ½ ·sin a =
 SΔ= ½ ´ ½ = 60 .
SΔ= ½ ´ ½ = 60 .
Если AD – медиана D ABC, то = ( +). В нашем случае, если
– вектор, задающий медиану, то = ( + ) = +.
Нам требуется найти длину этого вектора. Самое первое следствие из определения скалярного произведения: скалярный квадрат вектора 2 = · равен квадрату его длины ½ ½ 2. Имеем
Ответ: SΔ= 60, длина медианы равна .
Подчеркнем, что ни в коем случае нельзя использовать обозначение 2 вместо ´ ; 2 означает · . Особо обращаем внимание, что при решении использовалось свойство ´ = – ´ .
7. Докажите, что векторы (10, 11, 2) и (10,–10, 5) отложенные из одной точки, можно взять в качестве ребер куба, и найдите третье ребро куба, исходящее из этой же точки.
 Решение. Для того, чтобы векторы и могли служить ребрами куба, они должны быть друг другу перпендикулярны и иметь одинаковую длину. Проверяем:
Решение. Для того, чтобы векторы и могли служить ребрами куба, они должны быть друг другу перпендикулярны и иметь одинаковую длину. Проверяем:
Вектор , задающий третье ребро куба, должен быть перпендикулярен и и должен иметь одинаковую с ними длину.
Согласно определению векторного произведения вектор ´ будет перпендикулярен и . Выясним, какую он будет иметь длину:
½ ´ ½ = ½ ½ · ½ ½ × sin Ð ( , ) = 15·15· sin 90o = 225.
Искомый вектор должен иметь длину 15. Следовательно, = ´ . Находим
 ´ = = 75i – 30j – 210k , (5, –2,–14).
´ = = 75i – 30j – 210k , (5, –2,–14).
Очевидно, что вектор = – тоже удовлетворяе т условиям задачи.
8. Даны координаты вершин треугольной пирамиды SABC: A(4, 0, 1), B(5,–1, 1), C(4, 7,–5), S(7, 5, 2). Найти объем пирамиды, площадь основания ABC и высоту (с помощью векторного и смешанного произведений). Найти угол Ð BAC. Укажите, какой вектор перпендикулярен основанию. Изобразите данную пирамиду в декартовой системе координат.
Решение. Находим координаты трех векторов, лежащих на ребрах пирамиды и исходящих из одной вершины:
Находим координаты трех векторов, лежащих на ребрах пирамиды и исходящих из одной вершины:
Модуль смешанного произведения этих векторов равен объему параллелепипеда, построенного на этих векторах. Объем же пирамиды составляет 1/6 от объема параллелепипеда: V= ½ ½ .
Смешанное произведение можно вычислить так:
ощади основания нам понадобится векторное произведение ´ , то намного проще воспользоваться определением смешанного произведения: =( ´ )· . При этом, вероятность арифметической ошибки будет намного меньше. Рекомендуем для проверки правильности вычислений использовать оба способа. ´ = = i –
i –  j +
j +  k = 6i + 6j + 7k.
k = 6i + 6j + 7k.
C другой стороны, V = SΔABC ·h . Отсюда h = = = 5 .
Согласно определению векторного произведения вектор ´ перпендикулярен и . Поэтому вектор = ´ будет перпендикулярен основанию пирамиды; (6, 6, 7). Угол Ð BAC ищется так же, как и в задаче 5.
Построим изображение данной пирамиды в декартовой системе координат Оxyz.

Ответ: V = , SΔABC = , h = 5, (6, 6, 7).
9. Вычислить площадь треугольника ABC, если вершина A находится в полюсе, а две другие имеют заданные полярные координаты: B(6, ), C(4, ). Найти длину BC. Изобразить данный треугольник.
 AB = 6, AC = 4.
AB = 6, AC = 4.
SΔABC = AB × AC × sin Ð BAC = × 6 × 4 × sin = 12 × = 6.
BC2 = AB2 + AC2 – 2 × AB × AC × cos Ð BAC = 36 + 16 – 2 × 6 × 4 × (– ) = 76.
10. Новая декартова СК получена из старой переносом начала в точку O ¢ (2,–1) и поворотом на угол a = arccos .
а) Выпишите формулы, выражающие новые координаты через старые. Найдите новые координаты точки A, если известны её старые координаты: A(6, 2).
б) Выпишите формулы, выражающие старые координаты через новые. Найдите старые координаты точки B, если известны её новые координаты: B(5, 5).
Решение. а) Новые координаты выражаются через старые по формулам
 x ¢ = (x – a) × cos a + (y – b) × sin a ,
x ¢ = (x – a) × cos a + (y – b) × sin a ,
y ¢ = –(x – a) × sin a + (y – b) × cos a ,
где (a, b) – координаты точки O ¢ , a – угол поворота координатных осей. Зная cos a находим sin a и подставляем в формулы:
 x ¢ = (x – 2) + (y + 1),
x ¢ = (x – 2) + (y + 1),
Для точки A(6, 2)Oxy находим x ¢ = 5, y ¢ = 0. Значит A(5, 0)O ¢ x ¢ y ¢ .
б) Старые координаты выражаются через новые по формулам
 x = x ¢ × cos a – y ¢ × sin a + a,
x = x ¢ × cos a – y ¢ × sin a + a,
y = x ¢ × sin a + y ¢ × cos a + b.
 x = x ¢ – y ¢ + 2,
x = x ¢ – y ¢ + 2,
Подставляя сюда координаты точки B(5, 5)O ¢ x ¢ y ¢ находим B(3, 6)Oxy .
Ответ: A(5, 0)O ¢ x ¢ y ¢ , B(3, 6)Oxy .
Источник
Если векторы можно взять в качестве ребер куба, то они должны быть перпендикулярны (скалярное произведение = 0 ) и иметь одинаковую длину
(a*b) = 2*(-2) + 1*2 + 2*1 = 0 – векторы перпендикулярны
|a|=|b|, то есть векторы имеют одинаковую длину равную 3
Третье ребро куба должно иметь длину 3 и быть перпендикулярным как вектору a, так и вектору b. Получаем систему уравнений
2x + y + 2z = 0
-2x + 2y + z = 0
x^2 + y^2 + z^2 = 9
Из суммы уравнений (1) + (2) получаем
y = -z
Из разности (1) – 2 (2) получаем
2x = y
Подставив эти тождества в третье получаем
x^2 + 4x^2 + 4x^2 = 9
9x^2 = 9
x = +-1
То есть третий вектор может быть (1, 2, -2) или (-1, -2, 2)
Задача 1. В прямоугольном параллелепипеде известно, что
Найдите длину диагонали

Решение: + показать
Задача 2. Найдите угол прямоугольного параллелепипеда, для которого
. Ответ дайте в градусах.

Решение: + показать
Задача 3. В прямоугольном параллелепипеде известны длины рёбер
Найдите синус угла между прямыми
и

Решение: + показать
Задача 4. Площадь поверхности куба равна Найдите его диагональ.

Решение: + показать
Задача 5. Объем куба равен Найдите площадь его поверхности.

Решение: + показать
Задача 6. Диагональ куба равна . Найдите его объем.

Решение: + показать
Задача 6. Объем куба равна . Найдите его диагональ.

Решение: + показать
Задача 7. Во сколько раз увеличится объем куба, если его ребра увеличить в десять раз?

Решение: + показать
Задача 8. Если каждое ребро куба увеличить на , то его площадь поверхности увеличится на
Найдите ребро куба.
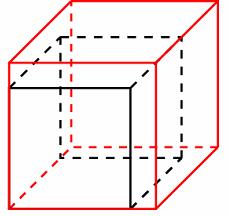
Решение: + показать
Задача 9. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в раза?

Решение: + показать
Задача 10. Объем одного куба в раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Решение: + показать
Задача 11. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и
Площадь поверхности этого параллелепипеда равна
Найдите третье ребро, выходящее из той же вершины.

Решение: + показать
Задача 12. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны
и
Найдите ребро равновеликого ему куба.

Решение: + показать
Задача 13. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и
Диагональ параллелепипеда равна
Найдите объем параллелепипеда.
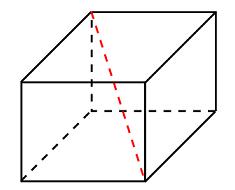
Решение: + показать
Задача 14. Площадь грани прямоугольного параллелепипеда равна Ребро, перпендикулярное этой грани, равно
Найдите объем параллелепипеда.

Решение: + показать
Задача 15. В прямоугольном параллелепипеде известны длины рёбер:
Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки
и

Решение: + показать
Задача 16. Диагональ прямоугольного параллелепипеда равна и образует углы
,
и
с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
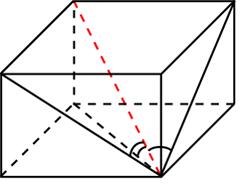
Решение: + показать
Задача 17. В прямоугольном параллелепипеде ребро
, ребро
, ребро
. Точка
— середина ребра
Найдите площадь сечения, проходящего через точки
.
Решение: + показать
Задача 18. Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна и образует с плоскостью этой грани угол
°. Найдите объем параллелепипеда.

Решение: + показать
Задача 19. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда
у которого

Решение: + показать
Задача 20. Найдите объем параллелепипеда , если объем треугольной пирамиды
равен

Решение: + показать
Задача 21. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда
у которого

Решение: + показать
Задача 22. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда
у которого

Решение: + показать
Задача 23. Объем параллелепипеда равен
Найдите объем треугольной пирамиды
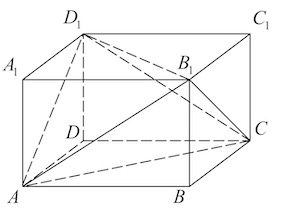
Решение: + показать
Задача 24. В кубе точка
— середина ребра
, точка
— середина ребра
, точка
— середина ребра
Найдите угол
. Ответ дайте в градусах.

Решение: + показать

Вы можете пройти тест
Длина ребра куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Длина ребра куба
Чтобы найти длину ребра куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Длина ребра куба через объём
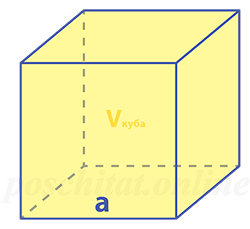
Чему равна длина ребра куба, если:
объём Vкуба =
a =
0
Округление ответа:
Длина ребра куба через диагональ
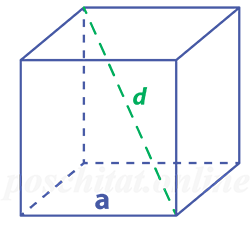
Чему равна длина ребра куба, если:
диагональ d =
a =
0
Округление ответа:
Длина ребра куба через площадь поверхности куба
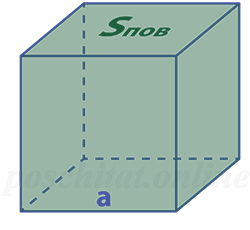
Чему равна длина ребра куба, если:
Sпов =
a =
0
Округление ответа:
Теория
Как найти ребро куба зная его объём
Чему равна длина ребра куба a, если объём куба Vкуба:
Формула
a = 3√Vкуба
Пример
Для примера, посчитаем чему равна длина ребра куба a, если его объём Vкуба = 8 см³:
a = 3√8 = 2 см
Как найти ребро куба зная его диагональ
Чему равна длина ребра куба a, если его диагональ d:
Формула
a = d ⁄√3
Пример
Для примера, посчитаем чему равна длина ребра куба a, если длина его диагонали d = 9 см:
a = 9 ⁄ √3 ≈ 9/1.732 ≈ 5.196 см
Как найти ребро куба через площадь поверхности
Чему равна длина ребра куба a, если площадь его поверхности Sпов:
Формула
a = √Sпов⁄ 6
Пример
Для примера, посчитаем чему равна длина ребра куба a, если площадь его поверхности Sпов = 150 см²:
a = √150 / 6 = √25 = 5 см
См. также

Как найти ребро куба
Нередко встречаются задачи, в которых необходимо найти ребро куба, зачастую это следует проделать на основе информации о его объеме, площади грани или её диагонали. Существует несколько вариантов определения ребра куба.
1
В том случае, если известна площадь куба, то можно легко определить ребро. Грань куба представляет собой квадрат со стороной, равной ребру куба. Соответственно, её площадь равняется квадрату ребра куба. Следует воспользоваться формулой: а=√S, где а – это длина ребра куба, а S – это площадь грани куба.
2
Найти ребро куба по его объему – еще более простая задача. Нужно учитывать, что объем куба равен кубу (в третьей степени) длины ребра куба. Получается, что длина ребра равняется кубическому корню из его объема. То есть, мы получаем следующую формулу: а=√V, где а – это длина ребра куба, а V – объем куба.

3
По диагоналям также можно найти ребро куба. Соответственно, нам необходимы: а – длина ребра куба, b – длина диагонали грани куба, c – длина диагонали куба. По теореме Пифагора получаем: a^2+a^2=b^2, и отсюда можно легко вывести следующую формулу: a=√(b^2/2), по которой извлекается ребро куба.

4
Еще раз по теореме Пифагора (a^2+a^2=b^2) можно получить следующую зависимость: a^2+a^2+a^2=c^2, из которой выводим: 3*a^2=c^2, следовательно, ребро куба можно получить следующим образом: a=√(c^2/3).

https://www.youtube.com/watch?v=Z8neEwmKe4s
