Формулы тройного и четырехкратного аргументов. Формулы понижения для куба и четвёртой степени
- Формулы тройного аргумента
- Формулы понижения для куба
- Формулы четырехкратного аргумента
- Формулы понижения для четвёртой степени
- Примеры
п.1. Формулы тройного аргумента
Выведем формулы тройного аргумента, исходя из формул суммы (см.§13 и §14 данного справочника) и двойного аргумента (см. §15 данного справочника).
begin{gather*} sin3alpha=sin(2alpha+alpha)=sin2alpha cosalpha+cos2alpha sinalpha=\ =2sinalpha cos^2alpha+(cos^2alpha-sin^2alpha)sinalpha=3sinalpha cos^2alpha-sin^3alpha=\ =3sinalpha(1-sin^2alpha)-sin^3alpha=3sinalpha-4sin^3alpha\ \ cos3alpha=cos(2alpha+alpha)=cos2alpha cosalpha-sin2alpha sinalpha=\ =(cos^2alpha-sin^2alpha)cosalpha-2sin^2alpha cosalpha=cos^3alpha-3sin^2alpha cosalpha=\ =cos^3alpha-3(1-cos^2alpha)cosalpha=4cos^3alpha-3cosalpha\ \ tg3alpha=frac{sin3alpha}{cos3alpha}=frac{3sinalpha cos^2alpha-sin^3alpha}{cos^3alpha-3sin^2alpha cosalpha}=frac{{3sinalpha cos^2alpha-sin^3alpha}{cos^3alpha}}{frac{cos^3alpha-3sin^2alpha cosalpha}{cos^3alpha}}=\ =frac{3tgalpha-tg^3alpha}{1-3tg^2alpha}=frac{tgalpha(3-tg^2alpha)}{1-3tg^2alpha}\ \ ctg3alpha=frac{cos3alpha}{sin3alpha}=frac{cos^3alpha-3sin^2alpha cosalpha}{3sinalpha cos^2alpha-sin^3alpha}=frac{frac{cos^3alpha-3sin^2alpha cosalpha}{sin^3alpha}}{frac{3sinalpha cos^2alpha-sin^3alpha}{sin^3alpha}}=\ =frac{ctg^3alpha-3ctgalpha}{3ctg^2alpha-1}=frac{ctgalpha(ctg^2alpha-3)}{3ctg^2alpha-1} end{gather*}
begin{gather*} sin3alpha=3sinalpha-4sin^3alpha\ \ cos3alpha=4cos^3alpha-3cosalpha\ \ tg3alpha=frac{tgalpha(3-tg^2alpha)}{1-3tg^2alpha}\ \ ctg3alpha=frac{ctgalpha(ctg^2alpha-3)}{3ctg^2alpha-1} end{gather*}
п.2. Формулы понижения для куба
Из формулы для синуса тройного аргумента получаем: begin{gather*} 4sin^3alpha=3sinalpha-sin3alpha\ sin^3alpha=frac{3sinalpha-sin3alpha}{4} end{gather*} Из формулы для косинуса тройного аргумента получаем: begin{gather*} 4cos^3alpha=3cosalpha+cos3alpha\ cos^3alpha=frac{3cosalpha+cos3alpha}{4} end{gather*}
begin{gather*} sin^3alpha=frac{3sinalpha-sin3alpha}{4}\ \ cos^3alpha=frac{3cosalpha+cos3alpha}{4} end{gather*}
п.3. Формулы четырехкратного аргумента
begin{gather*} sin4alpha=2sin2alpha cos2alpha=4sinalpha cosalpha(cos^2alpha-sin^2alpha)\ \ cos4alpha=2cos^2 2alpha-1=2(2cos^2alpha-1)^2-1=2(4cos^4alpha-4cos^2alpha+1)-1=\ =8cos^4alpha-8cos^2alpha+1\ \ tg4alpha=frac{sin4alpha}{cos4alpha}=frac{4sinalpha cosalpha(cos^2alpha-sin^2alpha)}{8cos^4alpha-8cos^2alpha+1}=frac{frac{4sinalpha cosalpha(cos^2alpha-sin^2alpha)}{cos^4alpha}}{frac{8cos^4alpha-8cos^2alpha+1}{cos^4alpha}}=\ =frac{4tgalpha(1-tg^2alpha)}{8-frac{8}{cos^2alpha}+frac{1}{cos^4alpha}}=frac{4tgalpha(1-tg^2alpha)}{8-8(1+tg^2alpha)+(1+tg^2alpha)^2}=\ =frac{4tgalpha(1-tg^2alpha)}{-8tg^2alpha+1+2tg^2alpha+tg^4alpha}=frac{4tgalpha(1-tg^2alpha)}{tg^4alpha-6tg^2alpha+1} end{gather*} Умножим дробь вверху и внизу на котангенс в квадрате, чтобы получить более удобное для практики соотношение: begin{gather*} 4tgalpha=frac{4tgalpha(1-tg^2alpha)}{tg^4alpha-6tg^2alpha+1}cdotfrac{ctg^2alpha}{ctg^2alpha}=frac{4(ctgalpha-tgalpha)}{tg^2alpha+ctg^2alpha-6} end{gather*}
begin{gather*} sin4alpha=4sinalpha cosalpha(cos^2alpha-sin^2alpha)\ \ cos4alpha=8cos^4alpha-8cos^2alpha+1\ \ tg4alpha=frac{4(ctgalpha-tgalpha)}{tg^2alpha+ctg^2alpha-6}\ \ ctg4alpha=frac{tg^2alpha+ctg^2alpha-6}{4(ctgalpha-tgalpha)} end{gather*}
п.4. Формулы понижения для четвертой степени
Первый способ вывода
Из формулы для косинуса четырехкратного аргумента: begin{gather*} 8cos^4alpha=8cos^2alpha-1+cos4alpha=8cdotfrac{1+cos2alpha}{2}-1+cos4alpha=3+4cos2alpha+cos4alpha\ cos^4alpha=frac{3+4cos2alpha+cos4alpha}{8} end{gather*} Из той же формулы: begin{gather*} 8cos^4alpha=8(1-sin^2alpha)^2=3+4cos2alpha+cos4alpha\ 8(1-2sin^2alpha+sin^4alpha)=3+4cos2alpha+cos4alpha\ 8sin^4alpha=3+4cos2alpha+cos4alpha-8+8(1-cos2alpha)=3-4cos2alpha+cos4alpha\ sin^2alpha=frac{3-4cos2alpha+cos4alpha}{8} end{gather*}
Второй способ вывода
Из формул половинного аргумента: begin{gather*} sin^4alpha=(sin^2alpha)^2=left(frac{1-cos2alpha}{2}right)^2=frac{1-2cos2alpha+cos^2 2alpha}{4}=\ =frac{1-2cos2alpha+frac{1+cos4alpha}{2}}{4}=frac{2-4cos2alpha+1+cos4alpha}{8}=frac{3-4cos2alpha+cos4alpha}{8}\ cos^4alpha=(cos^2alpha)^2=left(frac{1+cos2alpha}{2}right)^2=frac{1+2cos2alpha+cos^2 2alpha}{4}=\ frac{1+2cos2alpha+frac{1+cos4alpha}{2}}{4}=frac{2+4cos2alpha+1+cos4alpha}{8}=frac{3+4cos2alpha+cos4alpha}{8} end{gather*}
begin{gather*} sin^4alpha=frac{3-4cos2alpha+cos4alpha}{8}\ \ cos^4alpha=frac{3+4cos2alpha+cos4alpha}{8} end{gather*}
Формулы понижения степени полезны при решении тригонометрических уравнений, а также при интегрировании.
п.5. Примеры
Пример 1. Найдите:
a) (sin3alpha) и (tg3alpha), если (sinalpha=frac35, 0ltalphaltfracpi2)
Угол α в 1-й четверти, косинус положительный: (cosalpha=sqrt{1-sin^2alpha}=frac45)
Тангенс тоже положительный: (tgalpha=frac{sinalpha}{cosalpha}=frac35 : frac45=frac34)
Синус тройного угла: begin{gather*} sin3alpha=3sinalpha-4sin^3alpha=3cdotfrac35-4left(frac35right)^3=frac{9cdot 25-4cdot 27}{125}=frac{117}{125} end{gather*} Тангенс тройного угла: begin{gather*} tg3alpha=frac{3tgalpha-tg^3alpha}{1-3tg^2alpha}=frac{3cdotfrac34-left(frac34right)^3}{1-3cdotleft(frac34right)^2}=frac{frac{9cdot 16-27}{64}}{1-frac{27}{16}}=-frac{117cdot 11}{4}=-frac{1287}{4} end{gather*} Ответ: (frac{117}{125}; -frac{1287}{4})
б) (cos4alpha) и (ctg4alpha), если (cosalpha=-frac13, fracpi2ltpi)
Угол (alpha) во 2-й четверти, синус положительный: (sinalpha=sqrt{1-cos^2alpha}=sqrt{1-frac19}=frac{2sqrt{2}}{3})
Тангенс: (tgalpha=frac{sinalpha}{cosalpha}=frac{2sqrt{2}}{3} : left(-frac13right)=-2sqrt{2})
Косинус четырехкратного угла: begin{gather*} cos4alpha=8cos^4alpha-8cos^2alpha+1=8cdotleft(-frac13right)^4-8cdotleft(-frac13right)^2+1=frac{8}{81}-frac89+1=\ =frac{8-72+81}{81}=frac{17}{81} end{gather*} Котангенс четырехкратного угла: begin{gather*} ctg4alpha=frac{tg^2alpha+ctg^2alpha-6}{4(ctgalpha-tgalpha)}=frac{(-2sqrt{2})^2+left(frac{1}{-2sqrt{2}}right)^2-6}{4left(frac{1}{-2sqrt{2}}+2sqrt{2}right)}=frac{8+frac18-6}{frac{-4(8-1)}{2sqrt{2}}}=\ =-frac{17}{8} : frac{14}{sqrt{2}}=-frac{17sqrt{2}}{112} end{gather*} Ответ: (frac{17}{81}; -frac{17sqrt{2}}{112})
в) (cos2alpha), если (2cos3alpha=cosalpha)
Решим уравнение: begin{gather*} 2cos3alpha=cosalphaRightarrow 2(4cos^3alpha-3cosalpha)=cosalpha\ cosalpha(8cos^2alpha-7)=0\ left[ begin{array}{l l} cosalpha=0\ 8cos^2alpha-7=0 end{array} right. end{gather*} В первом случае, если (cosalpha=0, sinalpha=pm1). Косинус двойного угла: $$ cos2alpha=cos^2alpha-sin^2alpha=0-1=-1 $$ Во втором случае: begin{gather*} 8cos^2alpha-7=0\ 8cdotfrac{1+cos2alpha}{2}-7=0\ 4+4cos2alpha-7=0\ cos2alpha=frac34 end{gather*} Получаем два варианта (cos2alpha=-1) и (cos2alpha=frac34)
Ответ: (left{-1; frac34right})
Пример 2.Упростите выражение:
a) begin{gather*} frac{3-4cos2alpha+cos4alpha}{3+4cos2alpha+cos4alpha}=frac{frac{3-4cos2alpha+cos4alpha}{8}}{frac{3+4cos2alpha+cos4alpha}{8}}=frac{sin^4alpha}{cos^4alpha}=tg^2alpha end{gather*}
б) begin{gather*} 4(sin^3alpha-cos^3alpha)-3(sinalpha-cosalpha)+sin3alpha+cos3alpha=\ 4left(frac{3sinalpha-sin3alpha}{4}-frac{3cosalpha+cos3alpha}{4}right)-3(sinalpha-cosalpha)+sin3alpha+cos3alpha=\ =3sinalpha-sin3alpha-3cosalpha-cos3alpha-3sinalpha+3cosalpha+sin3alpha+cos3alpha=0 end{gather*}
Пример 3*.Найдите (sin18^{circ}) и (sin54^{circ})
Найдем произведение (sin18^{circ}sin54^{circ}) begin{gather*} sin18^{circ}sin54^{circ}=sin18^{circ}sin(90^{circ}-36^{circ})=sin18^{circ}cos36^{circ}=frac{sin18^{circ}cos18^{circ}cos36^{circ}}{cos18^{circ}}=\ =frac{sin36^{circ}cos36^{circ}}{2cos18^{circ}}=frac{sin72^{circ}}{4cos18^{circ}}=frac{sin(90^{circ}-18^{circ})}{4cos18^{circ}}=frac{cos18^{circ}}{4cos18^{circ}}=frac14 end{gather*} С другой стороны (54^{circ}=3cdot 18^{circ}) – тройной угол begin{gather*} sin3alpha=3sinalpha cos^2alpha-sin^3alpha=3sinalpha(1-sin^2alpha)-sin^3alpha=\ =3sinalpha-4sin^3alpha end{gather*} Обозначим (t=sin18^{circ}). Получаем уравнение: begin{gather*} t(3t-4t^3)=frac14Rightarrow 4t^4-3t^2+frac14=0\ D=(-3)^2-4cdot 4cdotfrac14=5\ t^2=frac{3pmsqrt{5}}{8} end{gather*} По условию (0lt tlt 1). Подходят два корня: (t_1=sqrt{frac{3-sqrt{5}}{8}}, t_2=sqrt{frac{3+sqrt{5}}{8}}) begin{gather*} sqrt{frac{3-sqrt{5}}{8}}=sqrt{frac{6-2sqrt{5}}{16}}=frac{sqrt{(sqrt{5}-1)^2}}{4}=frac{sqrt{5}-1}{4}\ sqrt{frac{3+sqrt{5}}{8}}=sqrt{frac{6+2sqrt{5}}{16}}=frac{sqrt{(sqrt{5}+1)^2}}{4}=frac{sqrt{5}+1}{4} end{gather*} Для первого корня (sin18^{circ}=frac{sqrt{5}-1}{4}) begin{gather*} sin54^{circ}=3cdotfrac{sqrt{5}-1}{4}-4left(frac{sqrt{5}-1}{4}right)^3=frac{sqrt{5}-1}{4}left(3-4left(frac{sqrt{5}-1}{4}right)^2right)=\ =frac{sqrt{5}-1}{4}left(3-frac{6-2sqrt{5}}{4}right)=frac{sqrt{5}-1}{4}cdotfrac{6+2sqrt{5}}{4}=frac{6sqrt{5}-6+10-2sqrt{5}}{16}=frac{sqrt{5}+1}{4}\ sin54^{circ}=frac{sqrt{5}+1}{4}gt sin18^{circ}=frac{sqrt{5}-1}{4} end{gather*} Для второго корня (sin18^{circ}=frac{sqrt{5}+1}{4}) begin{gather*} sin54^{circ}=3cdotfrac{sqrt{5}+1}{4}-4left(frac{sqrt{5}+1}{4}right)^3=frac{sqrt{5}+1}{4}left(3-4left(frac{sqrt{5}+1}{4}right)^2right)=\ =frac{sqrt{5}+1}{4}left(3-frac{6+2sqrt{5}}{4}right)=frac{sqrt{5}+1}{4}cdotfrac{6-2sqrt{5}}{4}=frac{6sqrt{5}+6-10-2sqrt{5}}{16}=frac{sqrt{5}-1}{4}\ sin54^{circ}=frac{sqrt{5}-1}{4}lt sin18^{circ}=frac{sqrt{5}+1}{4} end{gather*} Но синус возрастает в 1-й четверти, и (sin54^{circ}gt sin18^{circ}). Поэтому второй корень не подходит.
Значит: begin{gather*} sin18^{circ}=frac{sqrt{5}-1}{4}, sin54^{circ}=frac{sqrt{5}+1}{4} end{gather*}
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Длина радиус-вектора, который изображает заданное комплексное число $z=a+bi$, называется модулем данного комплексного числа.
Модуль заданного комплексного числа вычисляется по следующей формуле:
[r=|z|=|a+bi|=sqrt{a^{2} +b^{2} } .]
Пример 1
Вычислить модуль заданных комплексных чисел $z_{1} =13,, , z_{2} =4i,, , , z_{3} =4+3i$.
Решение:
Модуль комплексного числа $z=a+bi$ вычислим по формуле: $r=sqrt{a^{2} +b^{2} } $.
Для исходного комплексного числа $z_{1} =13$ получим $r_{1} =|z_{1} |=|13+0i|=sqrt{13^{2} +0^{2} } =sqrt{169} =13$
Для исходного комплексного числа $, z_{2} =4i$ получим $r_{2} =|z_{2} |=|0+4i|=sqrt{0^{2} +4^{2} } =sqrt{16} =4$
Для исходного комплексного числа $, z_{3} =4+3i$ получим $r_{3} =|z_{3} |=|4+3i|=sqrt{4^{2} +3^{2} } =sqrt{16+9} =sqrt{25} =5$

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 2
Угол $varphi $, образованный положительным направлением вещественной оси и радиус-вектором $overrightarrow{OM} $, который соответствует заданному комплексному числу $z=a+bi$, называется аргументом данного числа и обозначается $arg z$.
Примечание 1
Модуль и аргумент заданного комплексного числа в явном виде используются при представлении комплексного числа в тригонометрической или показательной форме:
- $z=rcdot (cos varphi +isin varphi )$ – тригонометрическая форма;
- $z=rcdot e^{ivarphi } $ – показательная форма.
Пример 2
Записать комплексное число в тригонометрической и показательной формах, заданное следующими данными: 1) $r=3;varphi =pi $; 2) $r=13;varphi =frac{3pi }{4} $.
«Модуль и аргумент комплексного числа» 👇
Решение:
1) Подставим данные $r=3;varphi =pi $ в соответствующие формулы и получим:
$z=3cdot (cos pi +isin pi )$ – тригонометрическая форма
$z=3cdot e^{ipi } $ – показательная форма.
2) Подставим данные $r=13;varphi =frac{3pi }{4} $ в соответствующие формулы и получим:
$z=13cdot (cos frac{3pi }{4} +isin frac{3pi }{4} )$ – тригонометрическая форма
$z=13cdot e^{ifrac{3pi }{4} } $ – показательная форма.
Пример 3
Определить модуль и аргумент заданных комплексных чисел:
1) $z=sqrt{2} cdot (cos 2pi +isin 2pi )$; 2) $z=frac{5}{3} cdot (cos frac{2pi }{3} +isin frac{2pi }{3} )$; 3) $z=sqrt{13} cdot e^{ifrac{3pi }{4} } $; 4) $z=13cdot e^{ipi } $.
Решение:
Модуль и аргумент найдем, используя формулы записи заданного комплексного числа в тригонометрической и показательной формах соответственно
[z=rcdot (cos varphi +isin varphi );] [z=rcdot e^{ivarphi } .]
1) Для исходного комплексного числа $z=sqrt{2} cdot (cos 2pi +isin 2pi )$ получим $r=sqrt{2} ;varphi =2pi $.
2) Для исходного комплексного числа $z=frac{5}{3} cdot (cos frac{2pi }{3} +isin frac{2pi }{3} )$ получим $r=frac{5}{3} ;varphi =frac{2pi }{3} $.
3) Для исходного комплексного числа $z=sqrt{13} cdot e^{ifrac{3pi }{4} } $ получим $r=sqrt{13} ;varphi =frac{3pi }{4} $.
4) Для исходного комплексного числа $z=13cdot e^{ipi } $ получим $r=13;varphi =pi $.
Аргумент $varphi $ заданного комплексного числа $z=a+bi$ можно вычислить, используя следующие формулы:
[varphi =tgfrac{b}{a} ;cos varphi =frac{a}{sqrt{a^{2} +b^{2} } } ;sin varphi =frac{b}{sqrt{a^{2} +b^{2} } } .]
На практике для вычисления значения аргумента заданного комплексного числа $z=a+bi$ обычно пользуются формулой:
$varphi =arg z=left{begin{array}{c} {arctgfrac{b}{a} ,age 0} \ {arctgfrac{b}{a} +pi ,a
или решают систему уравнений
$left{begin{array}{c} {cos varphi =frac{a}{sqrt{a^{2} +b^{2} } } } \ {sin varphi =frac{b}{sqrt{a^{2} +b^{2} } } } end{array}right. $. (**)
Пример 4
Вычислить аргумент заданных комплексных чисел: 1) $z=3$; 2) $z=4i$; 3) $z=1+i$; 4) $z=-5$; 5) $z=-2i$.
Решение:
1) $z=3$
Так как $z=3$, то $a=3,b=0$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{0}{3} =arctg0=0.]
2) $z=4i$
Так как $z=4i$, то $a=0,b=4$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{4}{0} =arctg(infty )=frac{pi }{2} .]
3) $z=1+i$.
Так как $z=1+i$, то $a=1,b=1$. Вычислим аргумент исходного комплексного числа, решая систему (**):
[left{begin{array}{c} {cos varphi =frac{1}{sqrt{1^{2} +1^{2} } } =frac{1}{sqrt{2} } =frac{sqrt{2} }{2} } \ {sin varphi =frac{1}{sqrt{1^{2} +1^{2} } } =frac{1}{sqrt{2} } =frac{sqrt{2} }{2} } end{array}right. .]
Из курса тригонометрии известно, что $cos varphi =sin varphi =frac{sqrt{2} }{2} $ для угла, соответствующего первой координатной четверти и равного $varphi =frac{pi }{4} $.
4) $z=-5$
Так как $z=-5$, то $a=-5,b=0$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{0}{-5} +pi =arctg0+pi =0+pi =pi .]
5) $z=-2i$
Так как $z=-2i$, то $a=0,b=-2$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{-2}{0} =arctg(-infty )=frac{3pi }{2} .]
Примечание 3
Аргумент чисто мнимых чисел равен соответственно:
- $frac{pi }{2} $ с положительной мнимой частью;
- $frac{3pi }{2} $ с отрицательной мнимой частью.
Решение:
Число $z_{1} $ изображено точкой $(3;0)$, следовательно, длина радиус-вектора равна 3, т.е. $r=3$, а аргумент $varphi =0$ по примечанию 2.
Число $z_{2} $ изображено точкой $(-2;0)$, следовательно, длина соответствующего радиус-вектора равна 2, т.е. $r=2$, а аргумент $varphi =pi $ по примечанию 2.
Число $z_{3} $ изображено точкой $(0;1)$, следовательно, длина соответствующего радиус-вектора равна 1, т.е. $r=1$, а аргумент $varphi =frac{pi }{2} $ по примечанию 3.
Число $z_{4} $ изображено точкой $(0;-1)$, следовательно, длина соответствующего радиус-вектора равна 1, т.е. $r=1$, а аргумент $varphi =frac{3pi }{2} $ по примечанию 3.
Число $z_{5} $ изображено точкой $(2;2)$, следовательно, длина соответствующего радиус-вектора равна $sqrt{2^{2} +2^{2} } =sqrt{4+4} =sqrt{8} =2sqrt{2} $, т.е. $r=2sqrt{2} $, а аргумент $varphi =frac{pi }{4} $ по свойству прямоугольного треугольника.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Модуль и аргумент комплексного числа
Пусть задано комплексное число $ z = a+bi $.
| Формула |
| Модуль комплексного числа равен корню квадратному из суммы квадратов мнимой и действительной части и находится по формуле: $$ |z| = sqrt{a^2 + b^2} $$ |
Если комплексное число состоит только из действительной части $ z = a $, то его модуль равен $ |z| = |a| $.
Стоит заметить, что модуль комплексных чисел всегда неотрицательный $ |z| ge 0 $ и равен нулю $ |z| = 0 $, только в случае $ z = 0 $.
| Формула |
Аргумент комплексного числа обозначается $ varphi = arg z $ и зависит от полуплоскости, в которой лежат числа $a,b$:
|
Введите комплексное число
Пример 1 Пример 2 Правила ввода
| Пример 1 |
| Найти модуль и аргумент комплексного числа $ z = 3 – 4i $. |
| Решение |
|
Комплексное число состоит из действительной и мнимой части: $$ a = Re z = 3 $$ $$ b = Im z = -4 $$ Применяя формулу вычисления модуля получаем: $$ |z| = sqrt{a^2 + b^2} = sqrt{3^2 + (-4)^2} = sqrt{9+16} = 5 $$ Теперь вычисляем аргумент. Так как $a = 3 > 0$, то получаем аргумент: $$varphi = arctg frac{b}{a} = arctg frac{-4}{3} = -arctg frac{4}{3}.$$ |
| Ответ |
| $$ |z| = 5, varphi = -arctg frac{4}{3} $$ |
| Пример 2 |
| Найти модуль и аргумент комплексного числа $ z = 3i $ |
| Решение |
|
В данном случае отсутствует действительная часть, а вернее она равна нулю: $$ a = Re z = 0 $$ Мнимая часть комплексного числа равна: $$ b = Im z = 3 $$ Вычисляем модуль по уже известной формуле: $$ |z| = sqrt{a^2 + b^2} = sqrt{0^2 + 3^2} = sqrt{9} = 3 $$ А вот аргумент здесь попадает под правило при $a = 0, b>0$ и значит равен $$varphi = frac{pi}{2}.$$ |
| Ответ |
| $$ |z| = 3, varphi = frac{pi}{2} $$ |
| Пример 3 |
| Найти модуль и аргумент комплексного числа $$ z = 1+sqrt{3}i $$ |
| Решение |
|
Выписываем действительную и мнимую часть: $$ a = 1 $$ $$ b = sqrt{3} $$ Так как $ a > 0 $, то аргумент равен $$ varphi = arctg frac{sqrt{3}}{1} = arctg sqrt{3} = frac{pi}{3} $$ Находим модуль извлекая квадратный корень из суммы квадратов действительной и мнимой части: $$|z| = sqrt{1^2 + (sqrt{3})^2} = sqrt{1+3}=2.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ varphi = frac{pi}{3}, |z| = 2 $$ |
| Пример 4 |
| Найти аргумент комплексного числа $$ z = -1 + sqrt{3}i $$ |
| Решение |
|
Действительная часть $$ a = Re z = -1 $$ Мнимая часть $$ b = Im z = sqrt{3} $$ Так как $ a < 0 $ и $ b > 0 $, то пользуемся второй формулой: $$ varphi = arg z = pi + arctg frac{sqrt{3}}{-1} = pi + arctg (-sqrt{3}) = $$ $$ = pi – arctg(sqrt{3}) = pi – frac{pi}{3} = frac{2pi}{3}. $$ |
| Ответ |
| $$ varphi = frac{2pi}{3} $$ |
Сочинение состоит из 3 частей:
1. Вступление – тезис.
2. Основная часть – доказательства (аргументы) + примеры из текста.
3. Заключение – вывод.
1. Тезис
Это мысль, которую нужно доказать. В тезисе вы должны коротко сформулировать своё понимание смысла указанного фрагмента.
Поскольку объём всего сочинения небольшой, вступление может состоять из 2-3 предложений.
Подробнее о том, как сформулировать тезис в сочинении
При написании вступления можно использовать следующие речевые клише:
• Смысл последних строк текста говорит нам о том, что…
• Текст заканчивается словами: “…”. На мой взгляд, речь идет о том, что (как и др.) …
• Я считаю, что мысль автора данного текста, выраженная в выделенном фрагменте, заключается в том, что …
• Автор данного текста привлекает читателя к размышлению над вопросом…
• По моему мнению, в указанном фрагменте выражена главная мысль текста, которая заключается в следующем: …
• В этом отрывке автор говорит о том, что…
• Смысл данного отрывка я понимаю так: …
• В выделенной фразе автор выражает мысль о том, что…
Не лишним будет употребление вводных слов: я думаю, я считаю, на мой взгляд, по моему мнению, мне кажется, я убеждён и т.д. Помните, что вводные слова всегда выделяются запятыми.
2. Основная часть.
Оформлять примеры в сочинении можно 3-мя способами:
1) цитировать предложение (если оно не очень длинное), при этом знаки препинания расставляются так же, как и в предложении с прямой речью, или же предложение заключается в скобки. В некоторых случаях цитировать можно не всё предложение, а часть его, ставя на месте пропущенных слов многоточие.
2) указывать номера предложений без цитирования (это делается в том случае, если предложение очень длинное).
3) для того чтобы включение примеров не нарушало требование связности, можно использовать следующие речевые клише:
• Чтобы подтвердить сказанное, обратимся к … предложению текста.
• Подтвердить данный аргумент можно примером из …. предложения текста.
• Справедливость этого вывода можно доказать на примере … предложения.
• В подтверждение собственных выводов приведу пример из … предложения прочитанного мною текста.
• Предложение № … подтверждает мысль о том, что … .
3. Вывод.
В начале заключения можно использовать следующие вводные слова: итак, следовательно, значит, таким образом, мы пришли к выводу, подводя итог вышесказанному, делая выводы из вышеизложенных доказательств и т.д. Помните, что вводные слова всегда выделяются запятой!
Структура сочинения-рассуждения 15.2.
ОГЭ по русскому языку:
1. Тезис.
2. Аргумент – пример 1 + комментарий.
3. Аргумент – пример 2 + комментарий.
4. Заключение (по тезису).
Как сформулировать тезис для сочинения 15.2?
Отталкиваемся от задания: Объясните, как Вы понимаете смысл финала текста: «Письма, пользуясь её слепотой, вынули не из шкатулки – их вынули из её души, и теперь ослепла и оглохла не только она, но и её душа…». Сочинение данного типа очень хорошо начать с вводных слов: на мой взгляд, по моему мнению, мне кажется, я считаю и т.п.
Пример тезиса: На мой взгляд, для Анны Федотовны фронтовые письма были больше, чем просто письмами, они были единственной памятью о сыне, не вернувшемся с войны, поэтому её душа опустела с их утратой.
АРГУМЕНТ – довод, приводимый в качестве доказательства тезиса. Аргументов в сочинении 15.2.должно быть два, они должны быть из прочитанного текста.
КОММЕНТАРИЙ – пояснение довода, аргумента. Является обязательным структурным элементом доказательной части любого сочинения-рассуждения
Пример аргументов и комментариев к ним:
Аргумент 1: В предложении № 17 автор называет письма “бесценными”.
Комментарий: Данный эпитет употребляется вместе со словом “листочками”, имеющим уменьшительно-ласкательный суффикс. Такое контрастное сочетание двух слов позволяет нам понять важность этих самых “листочков” для пожилой женщины.
Аргумент 2: В предложении 53 душа старушки сравнивается со шкатулкой.
Комментарий: В шкатулках люди обычно хранят самое ценное: драгоценности, деньги. Но для героини важней были ценности не материальные, а духовные. Она хранила в шкатулке письма, словно в своей душе (“Письма, пользуясь её слепотой, вынули не из шкатулки – их вынули из её души”). С помощью данной метафоры автор показывает всю значимость, которую имели письма для старушки.
ЗАКЛЮЧЕНИЕ – вывод по тезису, умозаключение. Должно соотноситься с утверждением, высказанным в начале. Легче всего начать заключение с вводных слов и конструкций: Подводя итог всему вышесказанному, …, Проанализировав два аргумента, можно прийти к выводу, что …, Таким образом, можно сделать вывод, что… и т.д.
Пример заключения: Подводя итог всему вышесказанному, можно сделать вывод, что фронтовые письма были для Анны Федотовны настоящим сокровищем, они представляли для нее большую духовную ценность, поэтому, лишившись их, пожилая женщина словно лишилась части своей души.
Как найти аргументы в тексте?
Самым трудным этапом работы при написании сочинения 15.2. ОГЭ по русскому языку будет подбор аргументов. Поскольку собственных аргументов здесь выдумывать не нужно, все, что Вам требуется, – проанализировать текст, при необходимости внимательно его перечитав, и найти ключевые слова, предложения, мысли, высказанные автором текста с целью сделать свои слова более убедительными.
Аргументы – это авторские доказательства. А затем использовать шаблонную конструкцию для оформления своего аргумента: Во-первых, в предложении № … говорится о … (употребляется …, используется такое средство как …). Это свидетельствует о том, что …, (это позволяет судить о том, что …, это говорит о том, что …).
Вычислить аргумент и модуль комплексного числа.
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки,
соответствующей данному комплексному числу и обозначается Arg(z) = φ
Из определения следуют следующие формулы:
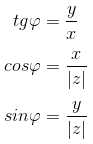
Для числа z = 0 аргумент не определен.
Главным значением аргумента называется такое значение φ, что 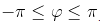 .
.
Обозначается: arg(z).
Свойства аргумента:
Модулем комплексного числа z = x + iy называется вещественное число |z| равное:
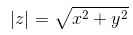
Для любых комплексных чисел z, z1, z2 имеют место следующие свойства модуля:
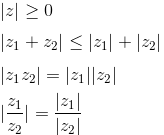
|
|
для пары комплексных чисел z1 и z2 модуль их разности |z1 − z2| равен расстоянию между соответствующими точками комплексной плоскости. |
