Понятие минора и алгебраического дополнения было рассмотрено нами в теме «Как вычислить определитель матрицы третьего порядка». В данной статье разберем тему более подробно, а также научимся вычислять миноры и алгебраические дополнения матриц высших порядков.
Сначала рекомендуется повторить вычисление определителей второго, третьего и высших порядков.
Минор
Минором MijM_{ij} к элементу aija_{ij} определителя nn-го порядка называется определитель (n−1)(n-1)-го порядка, который получается из исходного определителя вычеркиванием ii-той строки и jj-того столбца.
Таким образом, минор — это определитель, который остается после вычеркивания определенной строки и определенного столбца. Например, M12M_{12} получается вычеркиванием 1-й строки и 2-го столбца, M34M_{34} — вычеркиванием 3-й строки и 4-го столбца.
Алгоритм нахождения миноров
- вычеркиваем i-ю строку;
- вычеркиваем j-й столбец;
- записываем определитель, который получили в результате действий 1 и 2.
Пример 1
Найти минор M34M_{34} к элементу a34a_{34} определителя ∣21−23−121213−1543−31∣begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}.
Те строки и столбцы, которые будем вычеркивать, выделим зеленым цветом.
M34=∣21−23−121213−1543−31∣=∣21−2−12143−3∣=2⋅2⋅(−3)+1⋅1⋅4+(−2)⋅3⋅(−1)−(−2)⋅2⋅4−1⋅(−3)⋅(−1)−2⋅1⋅3=−12+4+6+16−3−6=5M_{34}=begin{vmatrix}2&1&-2&color{green}3\-1&2&1&color{green}2\color{green}1&color{green}3&color{green}-1&color{green}5\4&3&-3&color{green}1end{vmatrix}=begin{vmatrix}2&1&-2\-1&2&1\4&3&-3end{vmatrix}=2cdot2cdot(-3)+1cdot1cdot4+(-2)cdot3cdot(-1)-(-2)cdot2cdot4-1cdot(-3)cdot(-1)-2cdot1cdot3=-12+4+6+16-3-6=5.
Пример 2
Найти миноры матрицы K=(03−122100−2−102−5711)K= begin{pmatrix}0&3&-1&2\2&1&0&0\-2&-1&0&2\-5&7&1&1end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, выделим зеленым цветом.
M11=(03−122100−2−102−5711)=∣100−102711∣=1⋅(−1)1+1∣0211∣=1⋅(−1)2∣0211∣=∣0211∣=1⋅(−1)2+1⋅2=1⋅(−1)3⋅2=−2M_{11}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\color{green}2&1&0&0\color{green}-2&-1&0&2\color{green}-5&7&1&1end{pmatrix}=begin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=1cdot(-1)^{1+1}begin{vmatrix}0&2\1&1end{vmatrix}=1cdot(-1)^{2}begin{vmatrix}0&2\1&1end{vmatrix}=begin{vmatrix}0&2\1&1end{vmatrix}=1cdot(-1)^{2+1}cdot2=1cdot(-1)^{3}cdot2=-2,
M12=(03−122100−2−102−5711)=∣200−202−511∣=2⋅(−1)1+1∣0211∣=2⋅(−1)2∣0211∣=2∣0211∣=2⋅(−1)2+1⋅2=2⋅(−1)3⋅2=−4M_{12}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\2&color{green}1&0&0\-2&color{green}-1&0&2\-5&color{green}7&1&1end{pmatrix}=begin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=2cdot(-1)^{1+1}begin{vmatrix}0&2\1&1end{vmatrix}=2cdot(-1)^{2}begin{vmatrix}0&2\1&1end{vmatrix}=2begin{vmatrix}0&2\1&1end{vmatrix}=2cdot(-1)^{2+1}cdot2=2cdot(-1)^{3}cdot2=-4,
M13=(03−122100−2−102−5711)=∣210−2−12−571∣=2⋅(−1)⋅1+0⋅7⋅(−2)+1⋅2⋅(−5)−0⋅(−1)⋅(−5)−2⋅2⋅7−1⋅1⋅(−2)=−2−10−28+2=−38M_{13}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\2&1&color{green}0&0\-2&-1&color{green}0&2\-5&7&color{green}1&1end{pmatrix}=begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=2cdot(-1)cdot1+0cdot7cdot(-2)+1cdot2cdot(-5)-0cdot(-1)cdot(-5)-2cdot2cdot7-1cdot1cdot(-2)=-2-10-28+2=-38,
M14=(03−122100−2−102−5711)=∣210−2−10−571∣=1⋅(−1)3+3∣21−2−1∣=0M_{14}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\2&1&0&color{green}0\-2&-1&0&color{green}2\-5&7&1&color{green}1end{pmatrix}=begin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=1cdot(-1)^{3+3}begin{vmatrix}2&1\-2&-1end{vmatrix}=0,
M21=(03−122100−2−102−5711)=∣3−12−102711∣=3⋅0⋅1+2⋅1⋅(−1)+(−1)⋅2⋅7−2⋅0⋅7−(−1)⋅1⋅(−1)−3⋅2⋅1=−2−14−1−6=−23M_{21}= begin{pmatrix}color{green}0&3&-1&2\color{green}2&color{green}1&color{green}0&color{green}0\color{green}-2&-1&0&2\color{green}-5&7&1&1end{pmatrix}=begin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=3cdot0cdot1+2cdot1cdot(-1)+(-1)cdot2cdot7-2cdot0cdot7-(-1)cdot1cdot(-1)-3cdot2cdot1=-2-14-1-6=-23,
M22=(03−122100−2−102−5711)=∣0−12−202−511∣=0⋅0⋅1+(−1)⋅2⋅(−5)+2⋅1⋅(−2)−2⋅0⋅(−5)−(−1)⋅1⋅(−2)−0⋅2⋅1=10−4−2=4M_{22}= begin{pmatrix}0&color{green}3&-1&2\color{green}2&color{green}1&color{green}0&color{green}0\-2&color{green}-1&0&2\-5&color{green}7&1&1end{pmatrix}=begin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=0cdot0cdot1+(-1)cdot2cdot(-5)+2cdot1cdot(-2)-2cdot0cdot(-5)-(-1)cdot1cdot(-2)-0cdot2cdot1=10-4-2=4,
M23=(03−122100−2−102−5711)=∣032−2−12−571∣=0⋅(−1)⋅1+3⋅2⋅(−5)+2⋅7⋅(−2)−2⋅(−1)⋅(−5)−3⋅1⋅(−2)−0⋅2⋅7=−30−28−10+6=−62M_{23}= begin{pmatrix}0&3&color{green}-1&2\color{green}2&color{green}1&color{green}0&color{green}0\-2&-1&color{green}0&2\-5&7&color{green}1&1end{pmatrix}=begin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=0cdot(-1)cdot1+3cdot2cdot(-5)+2cdot7cdot(-2)-2cdot(-1)cdot(-5)-3cdot1cdot(-2)-0cdot2cdot7=-30-28-10+6=-62,
M24=(03−122100−2−102−5711)=∣03−1−2−10−571∣=0⋅(−1)⋅1+3⋅0⋅(−5)+(−1)⋅7⋅(−2)−(−1)⋅(−1)⋅(−5)−3⋅1⋅(−2)−0⋅0⋅7=14+5+6=25M_{24}= begin{pmatrix}0&3&-1&color{green}2\color{green}2&color{green}1&color{green}0&color{green}0\-2&-1&0&color{green}2\-5&7&1&color{green}1end{pmatrix}=begin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=0cdot(-1)cdot1+3cdot0cdot(-5)+(-1)cdot7cdot(-2)-(-1)cdot(-1)cdot(-5)-3cdot1cdot(-2)-0cdot0cdot7=14+5+6=25,
M31=(03−122100−2−102−5711)=∣3−12100711∣=1⋅(−1)2+1∣−1211∣=1⋅(−1)3∣−1211∣=−∣−1211∣=−(−1−2)=3M_{31}= begin{pmatrix}color{green}0&3&-1&2\color{green}2&1&0&0\color{green}-2&color{green}-1&color{green}0&color{green}2\color{green}-5&7&1&1end{pmatrix}=begin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=1cdot(-1)^{2+1}begin{vmatrix}-1&2\1&1end{vmatrix}=1cdot(-1)^{3}begin{vmatrix}-1&2\1&1end{vmatrix}=-begin{vmatrix}-1&2\1&1end{vmatrix}=-(-1-2)=3,
M32=(03−122100−2−102−5711)=∣0−12200−511∣=2⋅(−1)2+1∣−1211∣=2⋅(−1)3∣−1211∣=−2∣−1211∣=−2(−1−2)=6M_{32}= begin{pmatrix}0&color{green}3&-1&2\2&color{green}1&0&0\color{green}-2&color{green}-1&color{green}0&color{green}2\-5&color{green}7&1&1end{pmatrix}=begin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=2cdot(-1)^{2+1}begin{vmatrix}-1&2\1&1end{vmatrix}=2cdot(-1)^{3}begin{vmatrix}-1&2\1&1end{vmatrix}=-2begin{vmatrix}-1&2\1&1end{vmatrix}=-2(-1-2)=6,
M33=(03−122100−2−102−5711)=∣032210−571∣=0⋅1⋅1+3⋅0⋅(−5)+2⋅7⋅2−2⋅1⋅(−5)−0⋅0⋅7−3⋅1⋅2=28+10−6=32M_{33}= begin{pmatrix}0&3&color{green}-1&2\2&1&color{green}0&0\color{green}-2&color{green}-1&color{green}0&color{green}2\-5&7&color{green}1&1end{pmatrix}=begin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=0cdot1cdot1+3cdot0cdot(-5)+2cdot7cdot2-2cdot1cdot(-5)-0cdot0cdot7-3cdot1cdot2=28+10-6=32,
M34=(03−122100−2−102−5711)=∣03−1210−571∣=0⋅1⋅1+3⋅0⋅(−5)+(−1)⋅7⋅2−(−1)⋅1⋅(−5)−3⋅1⋅2−0⋅0⋅7=−14−5−6=−25M_{34}= begin{pmatrix}0&3&-1&color{green}2\2&1&0&color{green}0\color{green}-2&color{green}-1&color{green}0&color{green}2\-5&7&1&color{green}1end{pmatrix}=begin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=0cdot1cdot1+3cdot0cdot(-5)+(-1)cdot7cdot2-(-1)cdot1cdot(-5)-3cdot1cdot2-0cdot0cdot7=-14-5-6=-25,
M41=(03−122100−2−102−5711)=∣3−12100−102∣=1⋅(−1)2+1∣−1202∣=1⋅(−1)3∣−1202∣=−∣−1202∣=−(−1)⋅(−1)1+1⋅2=1⋅(−1)2⋅2=2M_{41}= begin{pmatrix}color{green}0&3&-1&2\color{green}2&1&0&0\color{green}-2&-1&0&2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=1cdot(-1)^{2+1}begin{vmatrix}-1&2\0&2end{vmatrix}=1cdot(-1)^{3}begin{vmatrix}-1&2\0&2end{vmatrix}=-begin{vmatrix}-1&2\0&2end{vmatrix}=-(-1)cdot(-1)^{1+1}cdot2=1cdot(-1)^{2}cdot2=2,
M42=(03−122100−2−102−5711)=∣0−12200−202∣=2⋅(−1)2+1∣−1202∣=2⋅(−1)3∣−1202∣=−2∣−1202∣=−2⋅(−1)⋅(−1)1+1⋅2=2⋅(−1)2⋅2=4M_{42}= begin{pmatrix}0&color{green}3&-1&2\2&color{green}1&0&0\-2&color{green}-1&0&2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=2cdot(-1)^{2+1}begin{vmatrix}-1&2\0&2end{vmatrix}=2cdot(-1)^{3}begin{vmatrix}-1&2\0&2end{vmatrix}=-2begin{vmatrix}-1&2\0&2end{vmatrix}=-2cdot(-1)cdot(-1)^{1+1}cdot2=2cdot(-1)^{2}cdot2=4,
M43=(03−122100−2−102−5711)=∣032210−2−12∣=0⋅1⋅2+3⋅0⋅(−2)+2⋅(−1)⋅2−2⋅1⋅(−2)−3⋅2⋅2−0⋅0⋅(−1)=−4+4−12=−12M_{43}= begin{pmatrix}0&3&color{green}-1&2\2&1&color{green}0&0\-2&-1&color{green}0&2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=0cdot1cdot2+3cdot0cdot(-2)+2cdot(-1)cdot2-2cdot1cdot(-2)-3cdot2cdot2-0cdot0cdot(-1)=-4+4-12=-12,
M44=(03−122100−2−102−5711)=∣03−1210−2−10∣=0M_{44}= begin{pmatrix}0&3&-1&color{green}2\2&1&0&color{green}0\-2&-1&0&color{green}2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0.
Алгебраическое дополнение
Алгебраическим дополнением AijA_{ij} к элементу aija_{ij} определителя n-го порядка называется число Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}, где i,ji, j — соответствующие строка и столбец, а MijM_{ij} — минор к элементу aija_{ij}.
Алгоритм нахождения алгебраических дополнений
- найти сумму номеров строки (i)(i) и столбца (j)(j);
- найти минор MijM_{ij} по алгоритму нахождения миноров, который представлен выше;
- подставить значения, полученные на шагах 1 и 2, в формулу Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}.
Пример 1
Найти алгебраическое дополнение A34A_{34} к элементу a34a_{34} определителя
∣21−23−121213−1543−31∣begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}.
A34=(−1)3+4⋅M34=(−1)7⋅∣21−23−121213−1543−31∣=−∣21−2−12143−3∣=−(2⋅2⋅(−3)+1⋅1⋅4+(−2)⋅3⋅(−1)−(−2)⋅2⋅4−1⋅(−3)⋅(−1)−2⋅1⋅3)=−(−12+4+6+16−3−6)=−5A_{34}=(-1)^{3+4}cdot M_{34}=(-1)^{7}cdot
begin{vmatrix}2&1&-2&color{green}3\-1&2&1&color{green}2\color{green}1&color{green}3&color{green}-1&color{green}5\4&3&-3&color{green}1end{vmatrix}=-begin{vmatrix}2&1&-2\-1&2&1\4&3&-3end{vmatrix}=-(2cdot2cdot(-3)+1cdot1cdot4+(-2)cdot3cdot(-1)-(-2)cdot2cdot4-1cdot(-3)cdot(-1)-2cdot1cdot3)=-(-12+4+6+16-3-6)=-5.
Пример 2
Найти алгебраические дополнения матрицы K=(03−122100−2−102−5711)K= begin{pmatrix}0&3&-1&2\2&1&0&0\-2&-1&0&2\-5&7&1&1end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, выделим зеленым цветом.
A11=(−1)1+1⋅M11=(−1)1+1⋅∣100−102711∣=(−1)2∣100−102711∣=∣100−102711∣=−2A_{11}=(-1)^{1+1}cdot M_{11}=(-1)^{1+1}cdotbegin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=(-1)^{2}begin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=begin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=-2,
A12=(−1)1+2⋅M12=(−1)1+2⋅∣200−202−511∣=(−1)3⋅∣200−202−511∣=−∣200−202−511∣=−(−4)=4A_{12}=(-1)^{1+2}cdot M_{12}=(-1)^{1+2}cdotbegin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=(-1)^{3}cdotbegin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=-begin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=-(-4)=4,
A13=(−1)1+3⋅M13=(−1)1+3⋅∣210−2−12−571∣=(−1)4⋅∣210−2−12−571∣=∣210−2−12−571∣=−38A_{13}=(-1)^{1+3}cdot M_{13}=(-1)^{1+3}cdot begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=(-1)^{4}cdot begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=-38,
A14=(−1)1+4⋅M14=(−1)1+4⋅∣210−2−10−571∣=(−1)5⋅∣210−2−10−571∣=−∣210−2−10−571∣=0A_{14}=(-1)^{1+4}cdot M_{14}=(-1)^{1+4}cdotbegin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=(-1)^{5}cdot begin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=-begin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=0,
A21=(−1)2+1⋅M21=(−1)2+1⋅∣3−12−102711∣=(−1)3⋅∣3−12−102711∣=−∣3−12−102711∣=−(−23)=23A_{21}=(-1)^{2+1}cdot M_{21}=(-1)^{2+1}cdotbegin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=(-1)^{3}cdotbegin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=-begin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=-(-23)=23,
A22=(−1)2+2⋅M22=(−1)2+2⋅∣0−12−202−511∣=(−1)4⋅∣0−12−202−511∣=∣0−12−202−511∣=4A_{22}=(-1)^{2+2}cdot M_{22}=(-1)^{2+2}cdotbegin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=(-1)^{4}cdotbegin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=begin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=4,
A23=(−1)2+3⋅M23=(−1)2+3⋅∣032−2−12−571∣=(−1)5⋅∣032−2−12−571∣=−∣032−2−12−571∣=−(−62)=62A_{23}=(-1)^{2+3}cdot M_{23}=(-1)^{2+3}cdotbegin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=(-1)^{5}cdotbegin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=-begin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=-(-62)=62,
A24=(−1)2+4⋅M24=(−1)2+4⋅∣03−1−2−10−571∣=(−1)6⋅∣03−1−2−10−571∣=∣03−1−2−10−571∣=25A_{24}=(-1)^{2+4}cdot M_{24}=(-1)^{2+4}cdotbegin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=(-1)^{6}cdotbegin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=begin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=25,
A31=(−1)3+1⋅M31=(−1)3+1⋅∣3−12100711∣=(−1)4⋅∣3−12100711∣=∣3−12100711∣=3A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{3+1}cdotbegin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=(-1)^{4}cdotbegin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=begin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=3,
A32=(−1)3+2⋅M32=(−1)3+2⋅∣0−12200−511∣=(−1)5⋅∣0−12200−511∣=−∣0−12200−511∣=−6A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{3+2}cdotbegin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=(-1)^{5}cdotbegin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=-begin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=-6,
A33=(−1)3+3⋅M33=(−1)3+3⋅∣032210−571∣=(−1)6⋅∣032210−571∣=∣032210−571∣=32A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{3+3}cdotbegin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=(-1)^{6}cdotbegin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=begin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=32,
A34=(−1)3+4⋅M34=(−1)3+4⋅∣03−1210−571∣=(−1)7⋅∣03−1210−571∣=−∣03−1210−571∣=−(−25)=25A_{34}=(-1)^{3+4}cdot M_{34}=(-1)^{3+4}cdotbegin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=(-1)^{7}cdotbegin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=-begin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=-(-25)=25,
A41=(−1)4+1⋅M41=(−1)4+1⋅∣3−12100−102∣=(−1)5⋅∣3−12100−102∣=−∣3−12100−102∣=−2A_{41}=(-1)^{4+1}cdot M_{41}=(-1)^{4+1}cdotbegin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=(-1)^{5}cdotbegin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=-begin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=-2,
A42=(−1)4+2⋅M42=(−1)4+2⋅∣0−12200−202∣=(−1)6⋅∣0−12200−202∣=∣0−12200−202∣=4A_{42}=(-1)^{4+2}cdot M_{42}=(-1)^{4+2}cdotbegin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=(-1)^{6}cdotbegin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=begin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=4,
A43=(−1)4+3⋅M43=(−1)4+3⋅∣032210−2−12∣=(−1)7⋅∣032210−2−12∣=−∣032210−2−12∣=−(−12)=12A_{43}=(-1)^{4+3}cdot M_{43}=(-1)^{4+3}cdotbegin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=(-1)^{7}cdotbegin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=-begin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=-(-12)=12,
A44=(−1)4+4⋅M44=(−1)4+4⋅∣03−1210−2−10∣=(−1)8⋅∣03−1210−2−10∣=∣03−1210−2−10∣=0A_{44}=(-1)^{4+4}cdot M_{44}=(-1)^{4+4}cdotbegin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=(-1)^{8}cdotbegin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0.
Задачи на заказ недорого по любому предмету от наших экспертов!
Тест по теме «Минор матрицы и алгебраическое дополнение матрицы»
Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву, химии, теормеху, сопромату и другим предметам можно здесь всего за 10 минут.
Минор матрицы
| Определение |
| Минор матрицы – это определитель $ n-1 $ порядка, составленный путём вычеркивания $ i $-ой строки и $ j $-го столбца из матрицы $ A $ порядка $ n $. Обозначается минор $ M_{ij} $ |
Формула минора матрицы выводится для каждого элемента этой матрицы отдельно. Пусть задана квадратная матрица $ A $ порядка $ n = 3 $:
$$ A = begin{pmatrix} a_{11}&a_{12}&a_{13} \ a_{21}&a_{22}&a_{23} \ a_{31}&a_{32}&a_{33} end{pmatrix} $$
По определению каждый минор $ M_{ij} $ равен определителю, получаемому при вычеркивании $ i $-ой строки и $ j $-ого столбца из матрицы $ A $.
$$ M_{11} = begin{vmatrix} a_{22}&a_{23} \ a_{32}&a_{33} end{vmatrix}; M_{12} = begin{vmatrix} a_{21}&a_{23} \ a_{31}&a_{33} end{vmatrix}; M_{13} = begin{vmatrix} a_{21}&a_{22} \ a_{31}&a_{32} end{vmatrix}; $$
$$ M_{21} = begin{vmatrix} a_{12}&a_{13} \ a_{32}&a_{33} end{vmatrix}; M_{22} = begin{vmatrix} a_{11}&a_{13} \ a_{31}&a_{33} end{vmatrix}; M_{33} = begin{vmatrix} a_{11}&a_{12} \ a_{21}&a_{22} end{vmatrix}; $$
$$ M_{31} = begin{vmatrix} a_{12}&a_{13} \ a_{22}&a_{23} end{vmatrix}; M_{32} = begin{vmatrix} a_{11}&a_{13} \ a_{21}&a_{23} end{vmatrix}; M_{33} = begin{vmatrix} a_{11}&a_{12} \ a_{21}&a_{22} end{vmatrix}; $$
Аналогично миноры находятся для любого порядка. В частности для матрицы второго порядка в определитель будет входить одно число.
Как найти?
Чтобы найти миноры матрицы $ M_{ij} $ нужно составить определители, полученные путем вычеркивания из матрицы $ A $ соответствующие строку и столбец.
Пример для матрицы второго порядка:
$$ M_{12} = begin{pmatrix} {a_{11}} & {a_{12}} \ a_{21}&{a_{22}} end{pmatrix} = a_{21} $$
Пример для матрицы третьего порядка:
$$ M_{12} = begin{pmatrix} {a_{11}}&{a_{12}}&{a_{13}} \ a_{21}&{a_{22}}&a_{23} \ a_{31}&{a_{32}}&a_{33} end{pmatrix} = begin{vmatrix} a_{21}&a_{23} \ a_{31}&a_{33} end{vmatrix} = a_{21}a_{33}-a_{23}a_{31} $$
Если полученный определитель:
- Первого порядка, то записываем оставшееся число
- Второго или третьего порядка, то вычисляем его по правилу треугольников
- Четвертого и выше порядка, то выполняем разложение по строке (столбцу), либо методом Гаусса
Примеры решений
| Пример 1 |
|
Определить миноры матрицы: $$ A = begin{pmatrix} 2&1 \ 0&5 end{pmatrix} $$ |
| Решение |
|
Вычеркиваем строку и столбец, которые соответствуют индексу при $M$: $$ M_{11} = begin{pmatrix} {2}&{1} \ {0}&5 end{pmatrix} = 5 $$ $$ M_{12} = begin{pmatrix} {2}&{1} \ 0&{5} end{pmatrix} = 0 $$ $$ M_{21} = begin{pmatrix} {2}&1 \ {0}&{5} end{pmatrix} = 1 $$ $$ M_{22} = begin{pmatrix} 2&{1} \ {0}&{5} end{pmatrix} = 2 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ M_{11} = 5; M_{12} = 0; M_{21} = 1; M_{22} = 2 $$ |
| Пример 2 |
|
Найти миноры элементов на главной диагонали матрицы: $$ A = begin{pmatrix} 2&3&1 \ 1&-2&-3 \ 0&1&2 end{pmatrix} $$ |
| Решение |
|
Рассчитываем миноры: $$ M_{11} = begin{pmatrix} {2}&{3}&{1} \ {1}&-2&-3 \ {0}&1&2 end{pmatrix} = begin{vmatrix} -2&-3 \ 1&2 end{vmatrix} = -4+3 = -1 $$ $$ M_{22} = begin{pmatrix} 2&{3}&1 \ {1}&{-2}&{-3} \ 0&{1}&2 end{pmatrix} = begin{vmatrix} 2&1 \ 0&2 end{vmatrix} = 4-0 = 4 $$ $$ M_{33} = begin{pmatrix} 2&3&{1} \ 1&-2&{-3} \ {0}&{1}&{2} end{pmatrix} = begin{vmatrix} 2&3 \ 1&-2 end{vmatrix} = -4-3 = -7 $$ |
| Ответ |
| $$ M_{11} = -1; M_{22} = 4; M_{33} = -7 $$ |
Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений.
В данной теме рассмотрим понятия алгебраического дополнения и минора. Изложение материала опирается на термины, пояснённые в теме “Матрицы. Виды матриц. Основные термины”. Также нам понадобятся некоторые формулы для вычисления определителей. Так как в данной теме немало терминов, относящихся к минорам и алгебраическим дополнениям, то я добавлю краткое содержание, чтобы ориентироваться в материале было проще.
Содержание темы:
- Минор $M_{ij}$ элемента $a_{ij}$.
- Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$.
- Минор k-го порядка матрицы $A_{mtimes n}$. Главный минор, базисный минор, окаймляющий минор.
- Минор k-го порядка матрицы $A_{ntimes n}$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.
Минор $M_{ij}$ элемента $a_{ij}$
Пусть задана квадратная матрица $A_{ntimes n}$ (т.е. квадратная матрица n-го порядка).
Минором $M_{ij}$ элемента $a_{ij}$ матрицы $A_{ntimes n}$ именуют определитель матрицы, полученной из матрицы $A$ вычёркиванием i-й строки и j-го столбца (т.е. строки и столбца, на пересечении которых находится элемент $a_{ij}$).
Для примера рассмотрим квадратную матрицу четвёртого порядка:
$A=left( begin{array} {cccc}
1 & 0 & -3 & 9\
2 & -7 & 11 & 5 \
-9 & 4 & 25 & 84\
3 & 12 & -5 & 58 end{array} right)$. Найдём минор элемента $a_{32}$, т.е. найдём $M_{32}$. Сперва запишем минор $M_{32}$, а потом вычислим его значение. Для того, чтобы составить $M_{32}$, вычеркнем из матрицы $A$ третью строку и второй столбец (именно на пересечении третьей строки и второго столбца расположен элемент $a_{32}$). Мы получим новую матрицу, определитель которой и есть искомый минор $M_{32}$:
Этот минор несложно вычислить, используя формулу №2 из темы вычисления определителей второго и третьего порядков:
$$
M_{32}=left| begin{array} {ccc}
1 & -3 & 9\
2 & 11 & 5 \
3 & -5 & 58 end{array} right|=
1cdot 11cdot 58+(-3)cdot 5cdot 3+2cdot (-5)cdot 9-9cdot 11cdot 3-(-3)cdot 2cdot 58-5cdot (-5)cdot 1=579.
$$
Итак, минор элемента $a_{32}$ равен 579, т.е. $M_{32}=579$.
Часто вместо словосочетания “минор элемента матрицы” в литературе встречается “минор элемента определителя”. Суть остается неизменной: чтобы получить минор элемента $a_{ij}$ нужно вычеркнуть из исходного определителя i-ю строку и j-й столбец. Оставшиеся элементы записывают в новый определитель, который и является минором элемента $a_{ij}$. Например, найдём минор элемента $a_{12}$ определителя
$left| begin{array} {ccc}
-1 & 3 & 2\
9 & 0 & -5 \
4 & -3 & 7 end{array} right|$. Чтобы записать требуемый минор $M_{12}$ нам понадобится вычеркнуть из заданного определителя первую строку и второй столбец:
Чтобы найти значение данного минора используем формулу №1 из темы вычисления определителей второго и третьего порядков:
$$
M_{12}=left| begin{array} {cc}
9 & -5\
4 & 7 end{array} right|=9cdot 7-(-5)cdot 4=83.
$$
Итак, минор элемента $a_{12}$ равен 83, т.е. $M_{12}=83$.
Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$
Пусть задана квадратная матрица $A_{ntimes n}$ (т.е. квадратная матрица n-го порядка).
Алгебраическое дополнением $A_{ij}$ элемента $a_{ij}$ матрицы $A_{ntimes n}$ находится по следующей формуле:
$$
A_{ij}=(-1)^{i+j}cdot M_{ij},
$$
где $M_{ij}$ – минор элемента $a_{ij}$.
Найдем алгебраическое дополнение элемента $a_{32}$ матрицы $A=left( begin{array} {cccc}
1 & 0 & -3 & 9\
2 & -7 & 11 & 5 \
-9 & 4 & 25 & 84\
3 & 12 & -5 & 58 end{array} right)$, т.е. найдём $A_{32}$. Ранее мы уже находили минор $M_{32}=579$, поэтому используем полученный результат:
Обычно при нахождении алгебраических дополнений не вычисляют отдельно минор, а уж потом само дополнение. Запись минора опускают. Например, найдем $A_{12}$, если $A=left( begin{array} {ccc}
-5 & 10 & 2\
6 & 9 & -4 \
4 & -3 & 1 end{array} right)$. Согласно формуле $A_{12}=(-1)^{1+2}cdot M_{12}=-M_{12}$. Однако чтобы получить $M_{12}$ достаточно вычеркнуть первую строку и второй столбец матрицы $A$, так зачем же вводить лишнее обозначение для минора? Сразу запишем выражение для алгебраического дополнения $A_{12}$:
Минор k-го порядка матрицы $A_{mtimes n}$
Если в предыдущих двух пунктах мы говорили лишь о квадратных матрицах, то здесь поведём речь также и о прямоугольных матрицах, у которых количество строк вовсе не обязательно равняется количеству столбцов. Итак, пусть задана матрица $A_{mtimes n}$, т.е. матрица, содержащая m строк и n столбцов.
Минором k-го порядка матрицы $A_{mtimes n}$ называется определитель, элементы которого расположены на пересечении k строк и k столбцов матрицы $A$ (при этом предполагается, что $k≤ m$ и $k≤ n$).
Например, рассмотрим такую матрицу:
$$A=left( begin{array} {cccc}
-1 & 0 & -3 & 9\
2 & 7 & 14 & 6 \
15 & -27 & 18 & 31\
0 & 1 & 19 & 8\
0 & -12 & 20 & 14\
5 & 3 & -21 & 9\
23 & -10 & -5 & 58 end{array} right)
$$
Запишем для неё какой-либо минор третьего порядка. Чтобы записать минор третьего порядка нам потребуется выбрать какие-либо три строки и три столбца данной матрицы. Например, возьмём строки №2, №4, №6 и столбцы №1, №2, №4. На пересечении этих строк и столбцов будут располагаться элементы требуемого минора. На рисунке элементы минора показаны синим цветом:
$$
left( begin{array} {cccc}
-1 & 0 & -3 & 9 \
boldblue{2} & boldblue{7} & 14 & boldblue{6} \
15 & -27 & 18 & 31\
boldblue{0} & boldblue{1} & 19 & boldblue{8}\
0 & -12 & 20 & 14\
boldblue{5} & boldblue{3} & -21 & boldblue{9}\
23 & -10 & -5 & 58 end{array} right);;
M=left|begin{array} {ccc}
2 & 7 & 6 \
0 & 1 & 8 \
5 & 3 & 9 end{array} right|.
$$
Миноры первого порядка находятся на пересечении одной строки и одного столбца, т.е. миноры первого порядка равны элементам заданной матрицы.
Минор k-го порядка матрицы $A_{mtimes n}=(a_{ij})$ называется главным, если на главной диагонали данного минора находятся только главные диагональные элементы матрицы $A$.
Напомню, что главными диагональными элементами именуют те элементы матрицы, у которых индексы равны: $a_{11}$, $a_{22}$, $a_{33}$ и так далее. Например, для рассмотренной выше матрицы $A$ такими элементами будут $a_{11}=-1$, $a_{22}=7$, $a_{33}=18$, $a_{44}=8$. На рисунке они выделены зелёным цветом:
$$left( begin{array} {cccc}
boldgreen{-1} & 0 & -3 & 9\
2 & boldgreen{7} & 14 & 6 \
15 & -27 & boldgreen{18} & 31\
0 & 1 & 19 & boldgreen{8}\
0 & -12 & 20 & 14\
5 & 3 & -21 & 9\
23 & -10 & -5 & 58 end{array} right)
$$
Например, если в матрице $A$ мы вычеркнем строки и столбцы с номерами 1 и 3, то на их пересечении будут расположены элементы минора второго порядка, на главной диагонали которого будут находиться только диагональные элементы матрицы $A$ (элементы $a_{11}=-1$ и $a_{33}=18$ матрицы $A$). Следовательно, мы получим главный минор второго порядка:
$$
M=left|begin{array} {cc}
boldgreen{-1} & -3 \
15 & boldgreen{18} end{array} right|
$$
Естественно, что мы могли взять иные строки и столбцы, – например, с номерами 2 и 4, получив при этом иной главный минор второго порядка.
Пусть некий минор $M$ k-го порядка матрицы $A_{mtimes n}$ не равен нулю, т.е. $Mneq 0$. При этом все миноры, порядок которых выше k, равны нулю. Тогда минор $M$ называют базисным, а строки и столбцы, на которых расположены элементы базисного минора, именуют базисными строками и базисными столбцами.
Для примера рассмотрим такую матрицу:
$$A=left( begin{array} {ccc}
-1 & 0 & 3 & 0 & 0 \
2 & 0 & 4 & 1 & 0\
1 & 0 & -2 & -1 & 0\
0 & 0 & 0 & 0 & 0 end{array} right)
$$
Запишем минор этой матрицы, элементы которого расположены на пересечении строк №1, №2, №3 и столбцов с №1, №3, №4. Мы получим минор третьего порядка (его элементы выделены в матрице $A$ фиолетовым цветом):
$$
left( begin{array} {ccc}
boldpurple{-1} & 0 & boldpurple{3} & boldpurple{0} & 0 \
boldpurple{2} & 0 & boldpurple{4} & boldpurple{1} & 0\
boldpurple{1} & 0 & boldpurple{-2} & boldpurple{-1} & 0\
0 & 0 & 0 & 0 & 0 end{array} right);;
M=left|begin{array} {ccc}
-1 & 3 & 0 \
2 & 4 & 1 \
1 & -2 & -1 end{array} right|.
$$
Найдём значение этого минора, используя формулу №2 из темы вычисления определителей второго и третьего порядков:
$$
M=left| begin{array} {ccc}
-1 & 3 & 0\
2 & 4 & 1 \
1 & -2 & -1 end{array} right|=4+3+6-2=11.
$$
Итак, $M=11neq 0$. Теперь попробуем составить любой минор, порядок которого выше трёх. Чтобы составить минор четвёртого порядка, нам придётся использовать четвёртую строку, однако все элементы этой строки равны нулю. Следовательно, в любом миноре четвёртого порядка будет нулевая строка, а это означает, что все миноры четвёртого порядка равны нулю. Миноры пятого и более высоких порядков составить мы не можем, так как матрица $A$ имеет всего 4 строки.
Мы нашли минор третьего порядка, не равный нулю. При этом все миноры высших порядков равны нулю, следовательно, рассмотренный нами минор – базисный. Строки матрицы $A$, на которых расположены элементы этого минора (первая, вторая и третья), – базисные строки, а первый, третий и четвёртый столбцы матрицы $A$ – базисные столбцы.
Данный пример, конечно, тривиальный, так как его цель – наглядно показать суть базисного минора. Вообще, базисных миноров может быть несколько, и обычно процесс поиска такого минора куда сложнее и объёмнее.
Введём ещё одно понятие – окаймляющий минор.
Пусть некий минор k-го порядка $M$ матрицы $A_{mtimes n}$ расположен на пересечении k строк и k столбцов. Добавим к набору этих строк и столбцов ещё одну строку и столбец. Полученный минор (k+1)-го порядка именуют окаймляющим минором для минора $M$.
Для примера обратимся к такой матрице:
$$A=left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & -17 & -3 & 19 & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & 12 & 20 & 21 & 54\
-7 & 10 & 14 & -36 & 79 end{array} right)
$$
Запишем минор второго порядка, элементы которого расположены на пересечении строк №2 и №5, а также столбцов №2 и №4. Эти элементы выделены в матрице красным цветом:
$$
left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & boldred{-17} & -3 & boldred{19} & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & boldred{12} & 20 & boldred{21} & 54\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M=left|begin{array} {ccc}
-17 & 19 \
12 & 21 end{array} right|.
$$
Добавим к набору строк, на которых лежат элементы минора $M$, ещё строку №1, а к набору столбцов – столбец №5. Получим новый минор $M’$ (уже третьего порядка), элементы которого расположены на пересечении строк №1, №2, №5 и столбцов №2, №4, №5. Элементы минора $M$ на рисунке выделены красным цветом, а элементы, которые мы добавляем к минору $M$ – синим:
$$
left( begin{array} {ccccc}
-1 & boldblue{2} & 0 & boldblue{-2} & boldblue{-14}\
3 & boldred{-17} & -3 & boldred{19} & boldblue{29}\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & boldred{12} & 20 & boldred{21} & boldblue{54}\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M’=left|begin{array} {ccc}
2 & -2 & -14 \
-17 & 19 & 29 \
12 & 21 & 54 end{array} right|.
$$
Минор $M’$ является окаймляющим минором для минора $M$. Аналогично, добавляя к набору строк, на которых лежат элементы минора $M$, строку №4, а к набору столбцов – столбец №3, получим минор $M”$ (минор третьего порядка):
$$
left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & boldred{-17} & boldblue{-3} & boldred{19} & 29\
5 & -6 & 8 & -9 & 41\
-5 & boldblue{11} & boldblue{19} & boldblue{-20} & -98\
6 & boldred{12} & boldblue{20} & boldred{21} & 54\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M”=left|begin{array} {ccc}
-17 & -3 & 19 \
11 & 19 & -20 \
12 & 20 & 21 end{array} right|.
$$
Минор $M”$ также является окаймляющим минором для минора $M$.
Минор k-го порядка матрицы $A_{ntimes n}$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.
Вновь вернёмся к квадратным матрицам. Введём понятие дополнительного минора.
Пусть задан некий минор $M$ k-го порядка матрицы $A_{ntimes n}$. Определитель (n-k)-го порядка, элементы которого получены из матрицы $A$ после вычеркивания строк и столбцов, содержащих минор $M$, называется минором, дополнительным к минору $M$.
Для примера рассмотрим квадратную матрицу пятого порядка:
$$
A=left( begin{array}{ccccc}
-1 & 2 & 0 & -2 & -14\
3 & -17 & -3 & 19 & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 16 & -20 & -98\
-7 & 10 & 14 & -36 & 79 end{array} right)
$$
Выберем в ней строки №1 и №3, а также столбцы №2 и №5. На пересечении оных строк и столбцов будут элементы минора $M$ второго порядка. Эти элементы выделены в матрице $A$ зелёным цветом:
$$
left(begin{array}{ccccc}
-1 & boldgreen{2} & 0 & -2 & boldgreen{-14}\
3 & -17 & -3 & 19 & 29\
5 & boldgreen{-6} & 8 & -9 & boldgreen{41}\
-5 & 11 & 16 & -20 & -98\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M=left|begin{array}{cc}
2 & -14 \
-6 & 41 end{array} right|.
$$
Теперь уберём из матрицы $A$ строки №1 и №3 и столбцы №2 и №5, на пересечении которых находятся элементы минора $M$ (элементы убираемых строк и столбцов показаны красным цветом на рисунке ниже). Оставшиеся элементы образуют минор $M’$:
$$
left( begin{array}{ccccc}
boldred{-1} & boldred{2} & boldred{0} & boldred{-2} & boldred{-14}\
3 & boldred{-17} & -3 & 19 & boldred{29}\
boldred{5} & boldred{-6} & boldred{8} & boldred{-9} & boldred{41}\
-5 & boldred{11} & 16 & -20 & boldred{-98}\
-7 & boldred{10} & 14 & -36 & boldred{79} end{array} right);;
M’=left|begin{array} {ccc}
3 & -3 & 19 \
-5 & 16 & -20 \
-7 & 14 & -36 end{array}right|.
$$
Минор $M’$, порядок которого равен $5-2=3$, является минором, дополнительным к минору $M$.
Алгебраическим дополнением к минору $M$ квадратной матрицы $A_{ntimes n}$ называется выражение $(-1)^{alpha}cdot M’$, где $alpha$ – сумма номеров строк и столбцов матрицы $A$, на которых расположены элементы минора $M$, а $M’$ – минор, дополнительный к минору $M$.
Словосочетание “алгебраическое дополнение к минору $M$” часто заменяют словосочетанием “алгебраическое дополнение минора $M$”.
Для примера рассмотрим матрицу $A$, для которой мы находили минор второго порядка
$
M=left| begin{array} {ccc}
2 & -14 \
-6 & 41 end{array} right|
$ и дополнительный к нему минор третьего порядка:
$M’=left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|$. Обозначим алгебраическое дополнение минора $M$ как $M^*$. Тогда согласно определению:
$$
M^*=(-1)^alphacdot M’.
$$
Параметр $alpha$ равен сумме номеров строк и столбцов, на которых находится минор $M$. Этот минор расположен на пересечении строк №1, №3 и столбцов №2, №5. Следовательно, $alpha=1+3+2+5=11$. Итак:
$$
M^*=(-1)^{11}cdot M’=-left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|.
$$
В принципе, используя формулу №2 из темы вычисления определителей второго и третьего порядков, можно довести вычисления до конца, получив значение $M^*$:
$$
M^*=-left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|=-30.
$$
Этот онлайн калькулятор позволит вам очень просто найти произведение двух матриц.
Для того чтобы найти произведение матриц онлайн (умножить матрицы онлайн).
Заполните матрицу:
– порядок матрицы
| r | = | – строка | |
| c | = | – столбец |
Количество знаков после разделителя дроби в числах:
|
Mi,j |
= | = |
Скачать калькулятор
Рейтинг: 2.6 (Голосов 269)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Операции с матрицами | Действия с векторами | Решение СЛУ | Ранг матрицы | Решение матриц |
| Определитель матрицы | Геометрия | Математический анализ | Аналитическая геометрия | Арифметика |
Миноры и алгебраические дополнения элементов определителя
Определитель матрицы А порядка n также записывается в виде A или
det(A) и вычисляется через определители порядка n-1. Для того, чтобы ввести понятие определителя n-гопорядка и задать способ его вычисления, введем сначала понятие минора элемента матрицы.
Минором элемента aij матрицы А n-го порядка называется определитель матрицы (n-1) порядка, которая получается из матрицы А после вычеркивания в А ее i-йстроки и j-гостолбца. Минор элемента aij обозначается Мij. При этом определитель матрицы первого порядка считается равным единственному элементу этой матрицы.
Это определение проще всего освоить для определителей 2 и 3 порядка. Пример 3.5. Выписать миноры элементов матриц:
|
3 |
7 |
−13 |
5 |
1 |
3 |
5 |
||||
|
1) |
2) |
3) |
7 |
9 |
11 |
|||||
|
4 |
11 |
17 |
1 |
13 |
15 |
17 |
||||
В первом определителе, после вычеркивания первой строки и первого столбца сразу получаем: М11=11, так как оставшееся после вычеркивания единственное число можно рассматривать как определитель первого порядка. Аналогично получаем М12 =4, М21 =7, М22 =3. Для второго определителя М11=1, М12=17, М21 =5, М22= -13. Для последнего определителя придется вычислять определители второго порядка, которые будут оставаться после вычеркивания строки и столбца определителя. Так,
|
М11= |
9 11 |
= |
9 |
11 |
= 6 |
9 |
2 |
= −12 |
|||||||||||||||||||||||||||
|
15 |
17 |
6 |
6 |
1 |
0 |
||||||||||||||||||||||||||||||
|
M12 = |
7 11 |
= |
7 |
11 |
= 6 |
7 |
4 |
= −24 |
М13= |
7 9 |
= |
7 |
2 |
= 2 |
7 |
1 |
= −12 |
||||||||||||||||||
|
13 |
17 |
6 |
6 |
1 |
0 |
13 |
15 |
13 |
2 |
6 |
0 |
Аналогично вычисляются миноры всех остальных элементов:
|
М21= |
3 5 |
= 3 |
1 |
5 |
= 3 |
1 |
5 |
= −24 |
М22= |
1 5 |
= |
1 5 |
= −48 |
|||||||||||||||||||||
|
15 |
17 |
5 |
17 |
2 |
2 |
13 |
17 |
12 |
12 |
|||||||||||||||||||||||||
|
М23= |
1 |
3 |
= −24, М31= |
3 |
5 |
−12 М32 = |
1 |
5 |
= −24, М33= |
1 |
3 |
= −24 |
||||||||||||||||||||||
|
13 |
15 |
9 |
11 |
7 |
11 |
13 |
15 |
|||||||||||||||||||||||||||
Приведенный пример показывает, что отыскание миноров элементов определителей третьего порядка сводится к правильному вычеркиванию столбца и строки, а затем – к вычислению определителей второго порядка.
Задача 3.4. Вычислить миноры всех элементов определителей:
|
−2 |
7 |
6 |
3 |
4 |
|||
|
1) |
2) |
5 |
7 |
−3 |
|||
|
5 |
13 |
17 |
−8 |
9 |
|||
Для отыскания определителя произвольного порядка нужно еще понятие алгебраического дополнения элемента определителя.
34
Алгебраическим дополнением элемента аij определителя называется ми-
нор этого элемента, если сумма мест элемента (i+j) четная, и минор этого элемента с противоположным знаком, если сумма мест элемента (i+j) – не-
четная. Алгебраическое дополнение элемента аij обозначается Аij. Таким образом, Аij = (-1)i+j Мij.
Пример 3.6. Найти алгебраические дополнения всех элементов определителей из предыдущего примера.
Поскольку миноры элементов были выписаны, получаем: для элементов
первого определителя: А11=М11=11, А12= -М12= -4, А21= — М21= -7, А22=М22=3; для элементов второго определителя: А11=М11=1, А12= -М12= -17, А21= — М21= -5,
А22=М22= -13; для элементов третьего определителя: А11=М11= -12, А12=
-М12=24, А13= М13= -12, А21= -М21=24, А22=М22= -48, А23= -М23=24, А31= М31= -12, А32= М32=24, А33= М33= -12.
Задача 3.5. Найдите алгебраические дополнения всех элементов определителей:
|
1) |
4 |
7 |
−9 |
−3 |
2 |
5 |
|||||
|
−3 |
2 |
5 |
2) |
4 |
7 |
−9 |
|||||
|
8 |
−11 |
6 |
8 |
−11 |
6 |
Рекомендация.
Задача 3.6. Для определителей задачи 3.5. сосчитайте суммы
S1 = a11 A11 + a12 A12 + a13 A13 S2 = a21 A21 + a22 A22 + a23 A23
и сравните их с суммами
|
S3 |
= a31 A31 |
+ a32 A32 |
+ a33 A33 |
Z 3 |
= a13 A13 |
+ a23 A23 |
+ a33 A33 |
|
Z 2 |
= a12 A12 |
+ a22 A22 |
+ a32 A32 |
Z1 |
= a11 A11 |
+ a21 A21 |
+ a31 A31 |
Предостережение. Для каждого определителя все шесть сумм, которые надо вычислить в этой задаче, должны получиться одинаковыми.
Задача 3.7. Для определителей задачи 3.5 сосчитайте суммы:
S12 = a21 A11 + a22 A12 + a23 A13 , S13 = a31 A11 + a32 A12 + a33 A13 .
Указание. Эти суммы отличаются от суммы S1 в задаче 3.6 только тем, что в каждом слагаемом алгебраическое дополнение элемента первой строки умножается на соответствующий элемент второй строки в S12 и третьей строки в S13. Сосчитайте аналогичные суммы с алгебраическими элементами других строк и столбцов определителей. Убедитесь, что все они равны нулю.
Задача 3.8. Сосчитайте суммы аналогичные S1, S2, Z1, Z2, S12, S21, Z12, Z21 для первого определителя в задаче 3.4. или для любого другого определителя второго порядка. Сравните результаты и обдумайте их.
Результаты задач 3.5.-3.8. заставляют внимательно отнестись к суммам произведений алгебраических дополнений элементов на соответствующие элементы строк (столбцов). Ведь не случайно они совпадают! Наверняка это свойство может пригодиться.
35
Определителем матрицы А n-го порядка называется сумма произведе-
ний всех элементов любой строки (или любого столбца) этой матрицы на их алгебраические дополнения. Формально это значит, что
A = ai1 Ai1 + ai2 Ai 2 +… + ain Ain = a1 j A1 j + a2 j A2 j +… + anj Anj
где i и j могут принимать любые значения 1,2,…,n.
Объяснение. Можно доказать, что независимо от выбора номера строки или столбца сумма произведений всех элементов любой строки на их алгебраические дополнения всегда равна одному и то же числу. Доказательство этого утверждения в общем случае опущено. Для определителей второго и третьего порядка оно проверялось в задачах 3.4., 3.6. и 3.8.
Приведенные записи A по элементам i-й строки называются соответ-
ственно разложениями определителя по i-й строке и по j-му столбцу. Пример 3.7. Найти определитель третьего порядка:
|
A |
3 |
7 |
2 |
||
|
= |
2 |
5 |
− 4 |
||
|
6 |
1 |
0 |
Выберем i=1.
A = 3A11 + 7 A12 + 2A13
После вычисления алгебраических дополнений
|
A11 = |
5 |
− 4 |
= 4, A12 |
= − |
2 |
− 4 |
= −24, A13 = |
2 |
5 |
= 2 − 30 = −28 |
||||||
|
1 |
0 |
6 |
0 |
6 |
1 |
получаем теперь
A = 3×4 +7 ×(−24) + 2×(−28) =12 −168 −56 = −212
Немного проще тот же результат получится, если воспользоваться i =3.
|
A = |
7 |
2 |
= −28 −10 = −38, |
A = − |
3 |
2 |
= −(−12 − 4) =16. |
|
31 |
5 |
− 4 |
32 |
2 |
− 4 |
||
Поэтому
A = 6×(−38) +16 = −228 +16 = −212.
Таким образом, результат вычисления не зависит от выбора i и j.
В задача 3.6. вычисления сумм S1, S2, S3 означало отыскание определителя третьего порядка разложением по столбцам определителя, а вычисления сумм Z1, Z2, Z3 – отыскание того же определителя разложением по строкам. Проверьте, что при решении этой задачи все результаты действительно получились одинаковыми.
Задача 3.9. Убедитесь, что для определителей второго порядка приведенное определение дает прежний результат a22 a11 − a12 a21 при разложении по
любой строке или столбцу определителя.
Указание. Выпишите сначала все алгебраические дополнения элементов для произвольного определителя второго порядка, а затем подставляйте их в разложения по строкам и по столбцам.
36
Пример 3.8. Вычислить определители:
|
7 |
9 |
3 |
3 |
0 |
7 |
11 |
||
|
− 2 |
5 |
9 |
− 4 |
|||||
|
1) |
2 |
5 |
−6 |
2) |
||||
|
9 |
− 4 |
11 |
1 |
0 |
3 |
8 |
||
|
4 |
−1 |
6 |
0 |
|||||
Вычислим первый определитель разложением по первой строке.
|
A |
= |
5 |
−6 |
= 55−24 = 31, A |
= − |
2 |
−6 |
= −(22 +54) = −76, A |
= |
2 |
5 |
= −8 −45 = −53 |
|
11 |
−4 |
11 |
12 |
9 |
11 |
13 |
9 |
−4 |
Теперь разложение по первой строке дает: A =7×31-9×76-3×53=217-684-
159 = -626
Тот же самый результат должен получиться при разложении по любому столбцу. Так, разложением по второму столбцу находим: A = 9А21+5А22-4А23,
где
|
A |
= − |
2 |
− 6 |
= −(22 + 54) = −76, A |
22 |
= |
7 |
3 |
= 50, A |
32 |
= − |
7 |
3 |
= −(−42 − 6) = 48 |
|
12 |
9 |
11 |
9 |
11 |
2 |
− 6 |
Поэтому после подстановки получаем: A = -9×76+5×50-4×48= -684+250-
192 = -626
Совпадение результатов вычислений, полученных с помощью двух разных разложений, можно считать доказательством отсутствия ошибок.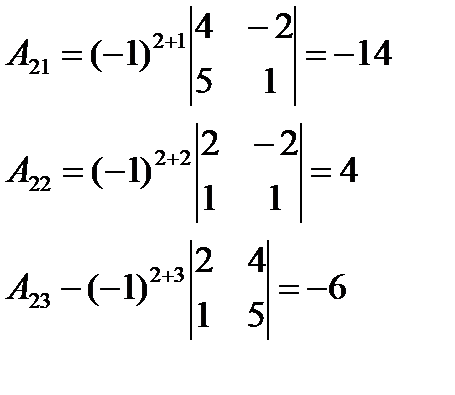
Для вычисления второго определителя воспользуемся разложением по второму столбцу, так как в нем два элемента равны нулю. Получаем
A = 5A22 − A42 и
|
3 |
7 |
11 |
3 |
7 |
11 |
||
|
A22 = |
1 |
3 |
8 |
, A42 = |
−2 9 |
−4 |
|
|
4 |
6 |
0 |
1 |
3 |
8 |
Вычисление первого из этих алгебраических дополнений как определителя третьего порядка разложением по последнему столбцу дает:
|
A22 |
=11 |
1 |
3 |
−8 |
3 |
7 |
=11(6 −12) −8(18 −28) = −66 +80 =14 |
|
4 |
6 |
4 |
6 |
Для проверки вычислим его и разложением по последней строке:
|
A 22 = 4 |
7 |
11 |
− 6 |
3 |
11 |
= 4(56 − 33) − 6(24 −11) = 4 × 23 − 6 ×13 = 92 − 78 = 14 |
|
3 |
8 |
1 |
8 |
Оставшийся определитель также сосчитаем разложением по последней строке:
|
A42 = |
7 |
11 |
−3 |
3 |
11 |
+ 8 |
3 |
7 |
= (−28 − 99) −3(−12 |
+ 22) |
+ 8(27 +14) |
= |
|
9 |
− 4 |
− 2 |
− 4 |
− 2 |
9 |
|||||||
|
= |
−127 − |
30 + 328 =171 |
Теперь подстановка дает: A = 5 ×14 −171 = −101.
37
Сайт-визитка
МЕНЮ
Форум
|
РЕШЕБНИК РЯБУШКО
Назад |
Миноры и кофакторы — определение, формула, применение, примеры, часто задаваемые вопросы
Миноры и кофакторы могут быть вычислены для каждого из элементов матрицы.
Кофактор элемента = (-1) i + j × минор элемента
Здесь i и j — позиционные значения строки и столбца элемента. Давайте узнаем больше о минорах и кофакторах, а также об их применении, с помощью примеров и часто задаваемых вопросов.
| 1. | Что такое миноры и кофакторы? |
| 2. | Сравнение миноров и кофакторов |
| 3. | Применение миноров и кофакторов |
| 4. | Примеры миноров и кофакторов |
| 5. | Практические вопросы |
| 6. | Часто задаваемые вопросы о минорах и кофакторах |
Что такое миноры и кофакторы?
Миноры и кофакторы определены для каждого элемента матрицы.
A = (begin{bmatrix}a&b&c\d&e&f\g&h&i end{bmatrix})
Минор a = (begin{bmatrix}e&f\h&i end{bmatrix})
Минор первого элемента первой строки вышеуказанной матрицы A был получен после игнорирования первой строки и первого столбца вышеуказанной матрицы и формирования новой матрицы. Далее, кофактор элемента а получается путем умножения минора на (-1) в степени строки значения позиции и столбца элемента а.
Кофактор a = (-1) i + j × Минор a
Кофактор a = (-1) 1 + 1 × (begin{bmatrix}e&f\h&i end{bmatrix })
Минор и кофактор матрицы — это простые числовые значения, которые получаются после взятия определителя остальных элементов данной матрицы.
Сравнение миноров и кофакторов
Кофактор получается из минора элемента матрицы. Кофактор равен произведению минора элемента матрицы и -1 степени суммы позиционного значения строки и столбца, содержащего элемент. Числовое значение минора или кофактора элемента матрицы равно, но отличается только знаком, который зависит от (-1) я + я .
Кофактор элемента = (-1) i + j × Минор элемента
Здесь i и j — позиционные значения и относятся к строке и столбцу, которым принадлежит элемент. Минор и кофактор элемента матрицы могут иметь одинаковый или разный знак. Минор используется только для нахождения определителя матрицы, а кофактор используется для нахождения сопряженной и обратной матрицы.
Применение миноров и кофакторов
Миноры и кофакторы полезны для нахождения сопряженной и обратной матрицы. Сопряженная матрица равна перестановке сомножителей элементов данной матрицы. Обратная матрица равна сопряженной матрице, деленной на определитель матрицы.
Давайте узнаем о применении миноров и кофакторов для нахождения определителя, сопряженной и обратной матрицы.
Определитель матрицы
Определитель матрицы представляет собой суммарное значение и рассчитывается с использованием элементов матрицы. Определитель матрицы равен сумме произведений элементов определенной строки или столбца с их соответствующими сомножителями. Определитель матрицы определен только для квадратных матриц. Определитель матрицы A обозначается как |A|.
(A = left[begin{массив}{ccc}
а_{11} и а_{12} и а_{13} \
а_{21} и а_{22} и а_{23} \ 9{1 + 3} left|begin{matrix}a_{21}&a_{22}\a_{31}&a_{32}end{matrix}right|)
Примыкание к матрице
сопряженную матрицу 3 x 3 можно получить, выполнив два простых шага. Сначала нам нужно найти матрицу сомножителей данной матрицы, а затем выполняется транспонирование этой матрицы сомножителей для получения сопряженной матрицы.
Adj A = транспонирование матрицы кофакторов = транспонирование (begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_ {31}&A_{32}&A_{33}end{pmatrix}) =(begin{pmatrix} A_{11}&A_{21}&A_{31}\A_{12}&A_{22}&A_{ 32}\A_{13}&A_{23}&A_{33}end{pmatrix})
Обратная матрица
Обратная матрица может быть вычислена путем деления сопряженной матрицы на определитель матрица. Для матрицы A ее обратная A -1 9{1 + 3} left|begin{matrix}a_{21}&a_{22}\a_{31}&a_{32}end{matrix}right|)
Adj A = Транспонировать Co- Матрица факторов = транспонирование (begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{32}&A_{ 33}end{pmatrix}) =(begin{pmatrix} A_{11}&A_{21}&A_{31}\A_{12}&A_{22}&A_{32}\A_{13}&A_ {23}&A_{33}end{pmatrix})
A -1 = (dfrac{1}{|A|}).
☛ Связанные темы
- Минор матрицы
- Матрица кофакторов
- Сопряженная матрица
- Определитель матрицы
- Обратная матрица
Часто задаваемые вопросы о минорах и кофакторах
Что такое миноры и кофакторы?
Миноры и кофакторы являются репрезентативными значениями каждого из элементов матрицы. Минор получается путем взятия определителя элементов, оставшихся после исключения строки и столбца определенного элемента. Кофактор получается из минора и равен произведению минора элемента с -1 на показатель степени суммы значений позиций строки и столбца.
Как найти миноры и кофакторы?
Для каждого элемента можно вычислить минор и кофакторы. Минор элемента равен определителю матрицы, оставшейся после исключения строки и столбца, содержащего элемент.
Кофактор элемента = (-1) i + j × минор элемента
Какая формула для миноров и кофакторов?
Формула для минора и кофактора элемента: Кофактор элемента = (-1) i + j × Минор элемента. Здесь i и j — позиционное значение строки и столбца элемента.
Миноры и кофакторы — одно и то же?
Миноры и кофакторы разные, и кофактор можно получить из минора элемента. Кофактор элемента равен произведению минора элемента и -1 степени строки и столбца элемента.
Каков порядок миноров и кофакторов?
Миноры и кофакторы не имеют порядка. Миноры и кофакторы представляют собой простые числовые значения, которые вычисляются из определителя.
В чем разница между минорами и кофакторами?
Миноры и кофакторы отличаются знаком значения. Кофактор можно вычислить по минору матрицы. Кофактор равен произведению минора элемента и -1 сумме строки и столбца элемента.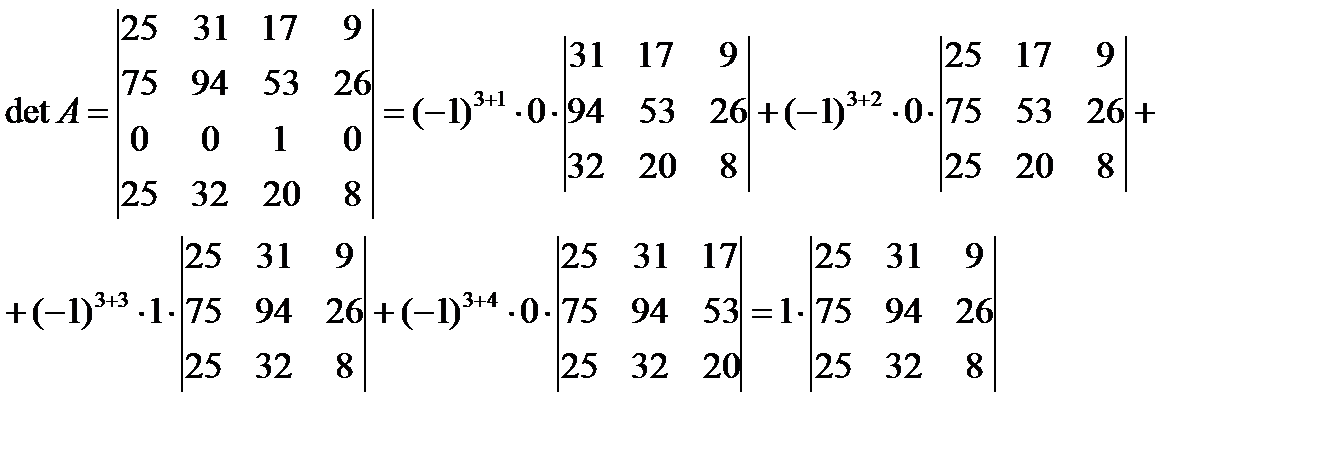
Для чего используются миноры и кофакторы?
Миноры и кофакторы полезны для определителя матрицы, примыкания к матрице и обратной матрицы.
Как найти миноры матрицы nxn?
Найти минор матрицы (n times n) легко, и шаги почти такие же, как поиск определителя. Это первый шаг, чтобы найти матрицу кофакторов. Мы начнем в этой статье с общей формы нахождения минора, как найти минор матрицы (2times 2), (3times 3) и (4times 4) , где каждый раздел заканчивается примером.
Каковы миноры матрицы
Пусть (A) будет (n times n) матрицей. В частности:
(A = begin{bmatrix}begin{array}{cccc} a_{1,1} & a_{1,2} & cdots & a_{1,n} \ a_{2, 1} & a_{2,2} & cdots & a_{2,n} \ vdots & vdots & ddots & vdots \ a_{n,1} & a_{n,2} & cdots & a_{n,n} end{array}end{bmatrix})
Минор (M_{i,j}) матрицы (A) является определителем (n-1 times n-1) подматрица (A), где удаляются (i)-я строка и (j)-й столбец.
(M_{i,j} = begin{vmatrix} a_{1,1} & a_{1,2} & cdots & a_{1,j-1} & a_{1,j+1} & cdots & a_{1,n} \ a_{2,1} & a_{2,2} & cdots & a_{2,j-1} & a_{2,j+1} & cdots & a_{2,n} \ vdots & vdots & ddots & vdots & vdots & cdots & vdots \ a_{i-1,1} & a_{i-1,2} & cdots & a_{i-1,j-1} & a_{i-1,j+1} & cdots & a_{i-1,n} \ a_{i+1,1} & a_{i+1 ,2} & cdots & a_{i+1,j-1} & a_{i+1,j+1} & cdots & a_{i+1,n} \ vdots & vdots & cdots & vdots & vdots & ddots & vdots \ a_{n,1} & a_{n,2} & cdots & a_{n,j-1} & a_{n,j+1} & cdots & a_{n,n} end{vmatrix} )
Нахождение всех миноров матрицы (A) и объединение их вместе в новую матрицу называется матрицей миноров , которую мы будем обозначать как (M):
( M = begin {bmatrix}begin{array}{cccc} M_{1,1} & M_{1,2} & cdots & M_{1,n} \ M_{2,1} & M_{2,2} & cdots & M_{2,n} \ vdots & vdots & ddots & vdots \ M_{n,1} & M_{n,2} & cdots & M_{n,n} end{ array}end{bmatrix} )
В итоге это почти то же самое, что вычисление определителя.
Как найти миноры матрицы 2×2?
Мы начнем с поиска миноров матрицы (2times 2). Итак, пусть (A) будет матрицей (2times 2). В частности:
(A = begin{bmatrix}begin{array}{cc} a_{1,1} & a_{1,2} \ a_{2,1} & a_{2,2} end{array}end{bmatrix})
Для каждого минора (M_{1,1}), (M_{1,2}), (M_{2,1}) и (M_{2,2}), нам нужно найти его определитель подматрицы (1times 1) матрицы (A). Но матрица (1times 1) — это один элемент. Следовательно, мы можем переписать миноры как:
begin{equation*} M_{1,1} = a_{2,2}, quad M_{1,2} = a_{2,1}, quad M_{2,1} = a_{1 ,2}, quad text{and} quad M_{2,2} = a_{1,1} end{equation*} и это приводит к следующей матрице миноров (M)
( M = begin{bmatrix}begin{array}{cc} M_{1,1} & M_{1,2} \ M_{2,1} & M_{2,2} end{массив}end {bmatrix} = begin{bmatrix}begin{array}{cc} a_{2,2} & a_{2,1} \ a_{1,2} & a_{1,1} end{array} end{bmatrix} )
Пример.
(A = begin{bmatrix}begin{array}{cc} 5 & -2 \ 7 & 3 end{array}end{bmatrix} Rightarrow M = begin{bmatrix} begin{массив}{cc} 3 и 7 \ -2 и 5 end{массив}end{bmatrix} )
Как найти миноры матрицы 3×3?
Теперь нам нужно произвести дополнительные вычисления, так как у нас есть 9 определителей. А именно, пусть (A) будет матрицей
(A = begin{bmatrix}begin{array}{ccc} a_{1,1} & a_{1,2} & a_{1,3} \ a_{2,1} & a_{2,2} & a_{2,3} \ a_{3,1} & a_{3,2} & a_{3,3} end{массив} end{bmatrix})
Тогда матрица миноров (A) равна
[ M = begin{bmatrix}begin{array}{ccc} M_{1,1} & M_{1, 2} & M_{1,3} \ M_{2,1} & M_{2,2} & M_{2,3} \ M_{3,1} & M_{3,2} & M_{3 ,3} end{массив} end{bmatrix} ] [ quad = begin{bmatrix}begin{array}{ccc} begin{vmatrix} a_{2,2} & a_{2,3 }\ a_{3,2} & a_{3,3}\ end{vmatrix} & begin{vmatrix} a_{2,1} & a_{2,3}\ a_{3,1} & a_{3,3}\ end{vmatrix} & begin{vmatrix} a_{2,1} & a_{2,2}\ a_{3,1} & a_{3,2}\ end{vmatrix} \\ begin{vmatrix} a_{1,2} & a_{1,3}\ a_{3,2}& a_{3,3}\ end{vmatrix} & begin{vmatrix} a_{1,1} & a_{1,3}\ a_{3,1}& a_{3,3}\ end{vmatrix} & begin{vmatrix} a_{1, 1} & a_{1,2}\ a_{3,1}& a_{3,2}\ end{vmatrix} \\ begin{vmatrix} a_{1,2} & a_{1 ,3}\ a_{2,2}& a_{2,3}\ end{vmatrix} & begin{vmatrix} a _{1,1} & a_{1,3}\ a_{2,1}& a_{2,3}\ end{vmatrix} & begin{vmatrix} a_{1,1} & a_{ 1,2}\ a_{2,1} & a_{2,2}\ end{vmatrix} end{массив} end{bmatrix} ]
Пример.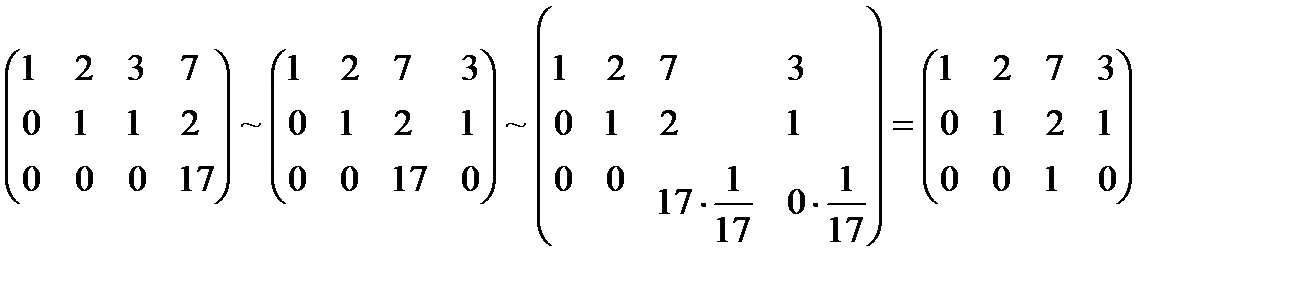
[ A = begin{bmatrix}begin{array}{ccc} 3 & -1 & 6 \ 2 & 5 & 7 \ 1 & -3 & 1 end{массив} end{bmatrix } \Rightarrow M = begin{bmatrix}begin{array}{ccc} 26 & -5 & -11 \ 17 & -3 & -8 \ -37 & 9 & 17 end{array} end{bmatrix} ]
Как найти миноры матрицы 4×4?
В предыдущих разделах мы видели, что найти минор — это довольно простое и прямолинейное вычисление. Чтобы решить матрицу (4times 4), нам нужно вычислить 16 определителей подматриц (3times 3). Это очень много вычислений! Обычно это делают компьютеры, но здесь мы дадим несколько вычислений, как найти миноры матрицы (4 times 4).
[ A = begin{bmatrix}begin{array}{cccc} 3 & -1 & 6 & 2 \ 2 & 5 & 7 & 4 \ 1 & -3 & 1 & 9 \ 4 & 1 & 3 & 7 end{array}end{bmatrix} ] Приведем пример для вычисления миноров (M_{1,1}) и (M_{4,2}). [ M_{1,1} = begin{vmatrix} 5 & 7 & 4\ -3 & 1 & 9\ 1 & 3 & 7 end{vmatrix} = 5 cdot begin{vmatrix} 1 & 9\ 3 и 7 end{vmatrix} + 3 cdot begin{vmatrix} 7 и 4\ 3 и 7 end{vmatrix} + 1 cdot begin{vmatrix} 7 и 4\ 1 и 9end{vmatrix} ] [= 5 cdot (-20) + 3 cdot 37 + 1 cdot 59 = 70] [ M_{4,2} = begin{vmatrix} 3 & 6 & 2 \ 2 & 7 & 4 \ 1 & 1 & 9 \ end{vmatrix} = 3 cdot begin{vmatrix} 7 & 4 \ 1 & 9 \ end{vmatrix} – 2 cdot begin{vmatrix} 6 & 2 \ 1 & 9 \ end{vmatrix} + 1 cdot begin{vmatrix} 6 & 2 \ 7 & 4 \ end{vmatrix} ] [= 3 cdot 59 – 2 cdot 52 + 1 cdot 14 = 83 ]
Заключение
Нахождение миноров матрицы может быть сделано легко и быстро для матриц (2 times 2) и (3 times 3 ), но большее значение увеличит сложность вычислений.




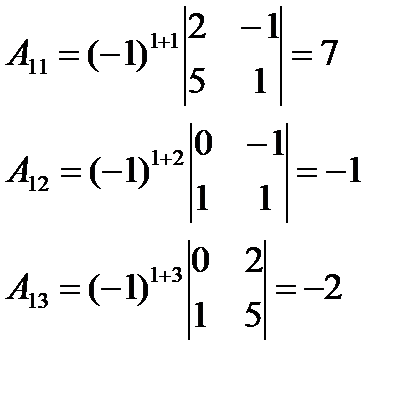
 Вычислим четыре минора которые понадобятся нам при вычислении определителя
7. Вычислим определитель пользуясь полученными данными
8. Вычислим определитель, разложив его по элементам j-го столбца
9. Вычислим четыре минора которые понадобятся нам при вычислении определителя
10. Вычислим определитель пользуясь полученными данными
11. Вычислим определитель, получив нули i-й строке
Умножим четвертый столбец на 8 и вычтем его из столбца 1
Умножим четвертый столбец на -3 и вычтем его из столбца 2
Умножим четвертый столбец на -2 и вычтем его из столбца 3
Мы получили матрицу с нулевой строкой. Ее определитель можно
найти через минор нашей матрицы
Общий определитель равен определителю минора, умноженному на коэффициент
Вычислим четыре минора которые понадобятся нам при вычислении определителя
7. Вычислим определитель пользуясь полученными данными
8. Вычислим определитель, разложив его по элементам j-го столбца
9. Вычислим четыре минора которые понадобятся нам при вычислении определителя
10. Вычислим определитель пользуясь полученными данными
11. Вычислим определитель, получив нули i-й строке
Умножим четвертый столбец на 8 и вычтем его из столбца 1
Умножим четвертый столбец на -3 и вычтем его из столбца 2
Умножим четвертый столбец на -2 и вычтем его из столбца 3
Мы получили матрицу с нулевой строкой. Ее определитель можно
найти через минор нашей матрицы
Общий определитель равен определителю минора, умноженному на коэффициент

