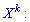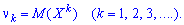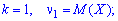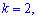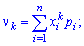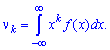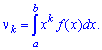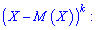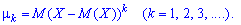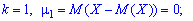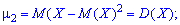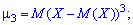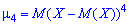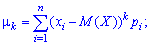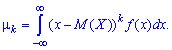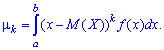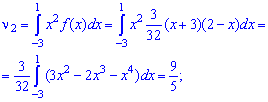Начальные и центральные моменты случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Начальные моменты
Начальным моментом порядка
случайной величины
называют математическое ожидание величины
:
В
частности:
Пользуясь
этими моментами, формулу для вычисления дисперсии
можно записать так:
Центральные моменты
Кроме
моментов случайной величины
целесообразно рассматривать моменты отклонения
.
Центральным моментом порядка
случайной величины
называют математическое ожидание величины
:
В
частности,
Взаимосвязь центральных и начальных моментов
Легко
выводятся соотношения, связывающие начальные и центральные моменты:
Моменты
более высоких порядков применяются редко.
Формулы для вычисления моментов дискретных и непрерывных случайных величин
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Нетрудно
заметить, что при
первый
начальный момент случайной величины
есть ее
математическое ожидание, то есть
, при
второй
центральный момент – дисперсия, то есть
.
Асимметрия и эксцесс случайной величины
Третий центральный момент
служит для
характеристики асимметрии (скошенности) распределения. Он имеет размерность
куба случайной величины. Чтобы получить безразмерную величину, ее делят на
, где
– среднее
квадратическое отклонение случайной величины
. Полученная величина
называется
коэффициентом асимметрии случайной величины:
Если распределение симметрично относительно
математического ожидания, то коэффициент асимметрии
.
Четвертый центральный момент
служит для
характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом (или коэффициентом
эксцесса) случайной величины называется число
Число 3 вычитается из отношения
потому, что для
наиболее часто встречающегося нормального распределения отношение
. Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные – отрицательным
эксцессом.
Смежные темы решебника:
- Асимметрия и эксцесс распределения
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Дискретная
случайная величина X задана законом распределения:
|
|
1 | 3 | 4 | 5 |
|
|
0,2 | 0,3 | 0,1 | 0,4 |
Найти начальные моменты первого, второго и третьего
порядков.
Решение
Найдем
начальный момент 1-го порядка:
Начальный
момент 2-го порядка:
Начальный
момент 3-го порядка:
Ответ:
.
Пример 2
Дискретная
случайная величина X задана законом распределения:
|
|
0 | 3 | 5 | 6 |
|
|
0,3 | 0,2 | 0,3 | 0,2 |
Найти центральные моменты первого, второго,
третьего и четвертого порядков.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Центральный
момент первого порядка равен нулю:
Для
вычисления центральных моментов удобно воспользоваться формулами, выражающими
центральные моменты через начальные, поэтому предварительно найдем начальные
моменты:
Начальный
момент 2-го порядка:
Начальный
момент 3-го порядка:
Начальный
момент 4-го порядка:
Найдем центральные моменты:
Ответ:
.
Пример 3
Непрерывная случайная
величина X задана плотностью распределения:
Найти
математическое ожидание, дисперсию, асимметрию и эксцесс.
Решение
Математическое
ожидание (начальный момент первого порядка):
Начальный
момент второго порядка:
Дисперсия
(центральный момент второго порядка):
Среднее
квадратическое отклонение:
Начальный
момент третьего порядка:
Начальный
момент четвертого порядка:
Вычисляем
центральные моменты третьего и четвертого порядков:
Коэффициент
асимметрии:
Эксцесс:
Ответ:
.
- Краткая теория
- Примеры решения задач
3.4. Моменты
случайной величины.
Выше мы познакомились
с исчерпывающими характеристиками СВ:
функцией распределения и рядом
распределения – для дискретной СВ,
функцией распределения и плотностью
вероятности – для непрерывной СВ. Эти
попарно эквивалентные по информационному
содержанию характеристики представляют
собой функции
и полностью описывают СВ с вероятностной
точки зрения. Однако, во многих практических
ситуациях или невозможно, или нет
необходимости характеризовать случайную
величину исчерпывающим образом. Зачастую
бывает достаточно указать один или
несколько числовых
параметров, до некоторой степени
описывающих основные черты распределения,
а иногда нахождение исчерпывающих
характеристик является хотя и желательным,
но слишком трудным математически, и
оперируя числовыми параметрами, мы
ограничиваемся хотя и приближенным, но
более простым описанием. Указанные
числовые параметры называются числовыми
характеристиками случайной
величины и играют большую роль в
применениях теории вероятности к
различным областям науки и техники,
облегчая решение задач и позволяя
представить результаты решения в простой
и наглядной форме.
Наиболее часто
применяемые числовые характеристики
можно условно разбить на два вида:
моменты и
характеристики положения.
Существует несколько видов моментов,
из них наиболее часто применяются два
вида: начальные
и центральные.
Другие виды моментов, например, абсолютные
моменты, факториальные моменты,
мы не рассматриваем. Чтобы избегнуть
применения обобщения интеграла – так
называемого интеграла Стильтьеса, дадим
определения моментов по отдельности
для непрерывных и дискретных СВ.
Определения. 1.
Начальным
моментом k-го
порядка дискретной СВ называется
величина
|
|
(3.4.1) |
где {xi}
, i=1,
2, …, N
– значения
СВ, {pi}
, i=1,
2, …, N
– вероятности
этих значений, N
– число
значений (при бесконечном числе значений
следует вместо N
писать
).
2. Начальным
моментом k-го
порядка непрерывной СВ называется
величина
|
|
(3.4.2) |
где f(x)
– плотность вероятности данной СВ.
3. Центральным
моментом k-го
порядка дискретной СВ
называется величина
|
|
(3.4.3) |
где m=
– начальный
момент первого порядка (об этой важной
величине см. ниже), остальные обозначения
в правой части – те же, что и в (3.4.1).
4. Центральным
моментом k-го
порядка непрерывной СВ
называется величина
|
|
(3.4.4) |
В случаях, когда
одновременно в рассмотрении находятся
несколько СВ, удобно, во избежание
недоразумений, указывать принадлежность
момента; мы будем это делать, указывая
обозначение соответствующей СВ в
скобках, например,
,
и т. д. Не следует путать это обозначение
с записью функции, а букву в скобках – с
аргументом функции. Суммы и интегралы
в правых частях равенств (3.4.1 – 3.4.4) могут
сходиться или расходиться в зависимости
от значения k
и конкретного распределения. В первом
случае говорят, что момент не
существует или расходится,
во втором – что момент
существует или сходится. Если
у дискретной СВ конечное число конечных
значений (N
конечно),
то все ее моменты конечного порядка k
существуют. При бесконечном N,
начиная с некоторого k
и для бо¢льших
порядков, моменты дискретной СВ
(одновременно начальные и центральные)
могут не существовать. Моменты непрерывной
СВ, как видно из определений, выражаются
несобственными интегралами, которые
могут расходится, начиная с некоторого
k
и для бо¢льших
порядков (одновременно начальные и
центральные). Моменты нулевого порядка
всегда сходятся.
Рассмотрим более
подробно сначала начальные, а затем
центральные моменты. С математической
точки зрения начальный момент k-го
порядка есть «взвешенное среднее» k-ых
степеней значений СВ; в случае дискретной
СВ весами являются вероятности значений,
в случае непрерывной СВ весовой функцией
является плотность вероятности. Такого
рода операции широко применяются в
механике для описания распределения
масс (статические моменты, моменты
инерции и т. д.); возникающие в связи с
этим аналогии рассмотрены ниже.
Для лучшего
понимания начальных моментов рассмотрим
их отдельно при заданных k.
В теории вероятностей наиболее важны
моменты низших порядков, т. е. при малых
k,
поэтому рассмотрение следует вести в
порядке возрастания
значений k.
Начальный момент нулевого порядка равен
=1
, для дискретной СВ;
=1
, для непрерывной СВ,
т.е. для любой СВ
он равен одному и тому же значению –
единице, и поэтому не несет никакой
информации о статистических свойствах
СВ.
Начальный момент
первого порядка (или первый начальный
момент) равен
,
для дискретной СВ;
,
для непрерывной СВ.
Этот момент –
важнейшая числовая характеристика
любой СВ, чему есть несколько взаимосвязанных
причин. Во-первых, согласно теореме
Чебышёва (см. п. 7.4), при неограниченном
числе испытаний над СВ среднее
арифметическое наблюденных значений
стремится (в некотором смысле) к
,
таким образом, для любой СВ
– это характерное число, вокруг которого
группируются ее значения на опыте.
Во-вторых, для непрерывной СВ
численно равен х-овой
координате центра тяжести криволинейной
трапеции, образуемой кривой f(x)
(аналогичное свойство имеет место и для
дискретной СВ), поэтому этот момент
можно было бы назвать «центром тяжести
распределения». В-третьих, этот момент
имеет замечательные математические
свойства, которые выяснятся в процессе
прохождения курса, в частности, поэтому
его величина входит в выражения для
центральных моментов (см. (3.4.3) и (3.4.4)).
Важность этого
момента для теоретических и практических
задач теории вероятностей и его
замечательные математические свойства
привели к тому, что кроме обозначения
и названия «первый начальный момент»
в литературе используются и другие
обозначения и названия, в большей или
меньшей мере удобные и отражающие
упомянутые свойства. Наиболее часто
встречаются названия: математическое
ожидание,
среднее
значение, и
обозначения: m,
M[X],
.
Мы будем чаще всего использовать термин
«математическое ожидание» и обозначение
m;
при наличии нескольких СВ будем
использовать нижний индекс, указывающий
принадлежность математического ожидания,
например, mx
, my
и т. д.
Начальный момент
второго порядка (или второй начальный
момент) равен
,
для дискретной СВ;
,
для непрерывной СВ;
иногда он называется
средним
квадратом случайной величины
и обозначается M[].
Начальный момент
третьего порядка (или третий начальный
момент) равен
,
для дискретной СВ;
,
для непрерывной СВ
иногда он называется
средним кубом
случайной величины
и обозначается M[X3].
Нет смысла продолжать
дальше перечисление начальных моментов.
Остановимся на важной интерпретации
моментов порядка k>1.
Пусть, наряду со СВ X
имеется
также СВ Y,
причем Y=Xk
(k=2,
3, …). Это
равенство означает, что случайные
величины X
и Y
связаны
детерминировано в том смысле, что когда
СВ X
принимает
значение x,
СВ Y
принимает значение y=xk
(в
дальнейшем такая связь СВ будет
рассмотрена более подробно). Тогда,
согласно (3.4.1) и (3.4.2)
=my
, k=2,
3, …,
т. е. k-ый
начальный момент СВ равен математическому
ожиданию k-ой
степени этой случайной величины.
Например, третий начальный момент длины
ребра случайного кубика равен
математическому ожиданию объема кубика.
Возможность понимания моментов как
неких математических ожиданий – еще
одна грань важности понятия математического
ожидания.
Перейдем к
рассмотрению центральных моментов.
Поскольку, как выяснится несколько
ниже, центральные моменты однозначно
выражаются через начальные и наоборот,
встает вопрос, зачем вообще нужны
центральные моменты и почему недостаточно
начальных моментов. Рассмотрим СВ X
(непрерывную или дискретную) и другую
СВ Y,
связанную с первой как Y=X+a
, где a0
– неслучайное вещественное число. Каждому
значению x
случайной
величины X
соответствует значение y=x+a
случайной
величины Y,
следовательно распределение СВ Y
будет иметь ту же форму
(выраженную
многоугольником распределения в
дискретном случае или плотностью
вероятности – в непрерывном случае), что
и распределение СВ X,
но сдвинуто по оси абсцисс на величину
a
. Следовательно, начальные моменты СВ
Y
будут
отличаться от соответствующих моментов
СВ X.
Например,
как нетрудно видеть, my=mx+a
(моменты
более высокого порядка связаны более
сложными соотношениями). Итак, мы
установили, что начальные
моменты не инвариантны относительно
сдвига распределения в целом.
Тот же результат получится, если сдвигать
не распределение, а начало оси абсцисс
по горизонтали на величину –a,
т.е. справедлив и эквивалентный вывод:
начальные
моменты не инвариантны относительно
сдвига начала оси абсцисс по горизонтали.
От этого недостатка
свободны центральные моменты,
предназначенные для описания тех свойств
распределений, которые не зависят от
их сдвига в целом. Действительно, как
видно из (3.4.3) и (3.4.4), при сдвиге распределения
в целом на величину a,
или, что то же самое, сдвиге начала оси
абсцисс на величину –a,
все значения x,
при тех же вероятностях (в дискретном
случае) или той же плотности вероятности
(в непрерывном случае), изменятся на
величину a,
но настолько же изменится величина m,
так что значения скобок в правых частях
равенств не изменятся. Таким образом,
центральные
моменты инвариантны относительно сдвига
распределения в целом, или, что то же
самое, относительно сдвига начала оси
абсцисс по горизонтали.
Название
«центральные» эти моменты получили в
те времена, когда первый начальный
момент назывался «центром». Полезно
заметить, что центральный момент СВ X
можно
понимать как соответствующий начальный
момент СВ X0,
равной
|
X0=X-mx |
(3.4.5) |
СВ X0
называется
центрированной
(по отношению к СВ X),
а приводящая к ней операция, т. е. вычитание
из случайной величины ее математического
ожидания, называется центрированием.
Как мы увидим в дальнейшем, это понятие
и эта операция будут полезны на протяжении
всего курса. Заметим, что центральный
момент порядка k>1
можно
рассматривать как математическое
ожидание (среднее) k-ой
степени центрированной СВ:
.
Рассмотрим по
отдельности центральные моменты низших
порядков. Центральный момент нулевого
порядка равен
,
для дискретных СВ;
,
для непрерывных СВ;
т. е. для любой СВ
и не несет никакой информации о
статистических свойствах этой СВ.
Центральный момент
первого порядка (или первый центральный
момент) равен
,
для дискретной
СВ;
,
для непрерывной
СВ; т. е. для любой СВ
и не несет никакой информации о
статистических свойствах этой СВ.
Центральный момент
второго порядка (или второй центральный
момент) равен
,
для дискретной СВ;
,
для непрерывной СВ.
Как выяснится
ниже, этот момент – один из важнейших в
теории вероятностей, т. к. используется
как характеристика меры разброса (или
рассеяния) значений СВ, поэтому часто
называется дисперсией
и обозначается Dх
.
Заметим, что
можно понимать как средний квадрат
центрированной СВ.
Центральный момент
третьего порядка (третий центральный
момент) равен
, для дискретной
СВ;
, для непрерывной
СВ;
и может пониматься
как математическое ожидание куба
центрированной СВ.
Центральный момент
четвертого порядка (четвертый центральный
момент) равен
, для дискретной
СВ;
, для непрерывной
СВ;
и может пониматься
как математическое ожидание четвертой
степени центрированной СВ.
Нет смысла продолжать
дальше перечисление центральных
моментов. Установим связь между начальными
и центральными моментами. Для непрерывной
СВ
;
разлагая степень
скобки в подынтегральном выражении в
бином Ньютона:
,
(–
число сочетаний из k
по s),
меняя порядок интегрирования и
суммирования:
,
и учитывая, что
интеграл в правой части равен
, находим
|
|
(3.4.6) |
Полученное равенство
показывает, что центральный момент k-го
порядка выражается через начальные
моменты порядков до k-го
включительно. Аналогичным путем то же
самое равенство выводится и для дискретных
СВ. Из (3.4.6) находим:
,
,
|
|
(3.4.7) |
,
,
……………………………………………
Первые два равенства
нам уже были известны, равенство (3.4.7)
исключительно важно и будет в дальнейшем
часто использоваться (его необходимо
помнить наизусть).
Мы выразили
центральные моменты через начальные,
теперь, наоборот, выразим начальные
моменты через центральные. Для непрерывной
СВ, обозначив x-mx=x0
,
находим:
т. е.
|
|
(3.4.8) |
Полученное равенство
показывает, что начальный момент k-го
порядка выражается через центральные
моменты порядков до k-го
включительно. Аналогичным путем то же
самое равенство выводится и для дискретных
СВ. Из (3.4.8) находим:
,
,
,
,
,
………………………………………..
Первые два равенства
нам уже были известны, третье повторяет
равенство (3.4.7).
Соседние файлы в папке Конспект лекций Глазова
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кроме
характеристик положения – средних, типичных значений случайной величины, –
употребляется еще ряд характеристик, каждая из которых описывает то или иное
свойство распределения. В качестве таких характеристик чаще всего применяются
так называемые моменты.
Понятие
момента широко применяется в механике для описания распределения масс
(статические моменты, моменты инерции и т.д.). Совершенно теми же приемами
пользуются в теории вероятностей для описания основных свойств распределения
случайной величины. Чаще всего применяются на практике моменты двух видов:
начальные и центральные.
Начальным
моментом s-го порядка прерывной случайной
величины называется
сумма вида:

Очевидно, это определение
совпадает с определением начального момента порядка s
в механике, если на оси абсцисс в точках сосредоточены массы
.
Для
непрерывной случайной величины Х начальным моментом s-го
порядка называется интеграл

Нетрудно
убедиться, что введенная в предыдущем n° основная
характеристика положения – математическое ожидание – представляет собой не что
иное, как первый начальный момент случайной величины .
Пользуясь
знаком математического ожидания, можно объединить две формулы (5.7.1) и (5.7.2)
в одну. Действительно, формулы (5.7.1) и (5.7.2) по структуре полностью
аналогичны формулам (5.6.1) и (5.6.2), с той разницей, что в них вместо и
стоят, соответственно,
и
. Поэтому можно написать общее
определение начального момента -го порядка, справедливое как для
прерывных, так и для непрерывных величин:
, (5.7.3)
т.е. начальным моментом -го порядка случайной
величины называется
математическое ожидание -й степени этой случайной величины.
Перед тем, как
дать определение центрального момента, введем новое понятие «центрированной
случайной величины».
Пусть имеется
случайная величина с
математическим ожиданием . Центрированной случайной величиной,
соответствующей величине , называется отклонение случайной величины
от её
математического ожидания:
. (5.7.4)
Условимся в
дальнейшем везде обозначать центрированную случайную величину, соответствующую
данной случайной величине, той же буквой со значком наверху.
Нетрудно
убедиться, что математическое ожидание центрированной случайной величины равно
нулю. Действительно, для прерывной величины

аналогично и для непрерывной
величины.
Центрирование
случайной величины, очевидно, равносильно переносу начала координат в среднюю,
«центральную» точку, абсцисса которой равна математическому ожиданию.
Моменты
центрированной случайной величины носят название центральных моментов.
Они аналогичны моментам относительно центра тяжести в механике.
Таким образом,
центральным моментом порядка s случайной
величины называется
математическое ожидание -й степени соответствующей центрированной
случайной величины:
, (5.7.6)
а для непрерывной – интегралом

В дальнейшем в
тех случаях, когда не возникает сомнений, к какой случайной величине относится
данный момент, мы будем для краткости вместо и
писать просто
и
.
Очевидно, для
любой случайной величины центральный момент первого порядка равен нулю:
, (5.7.9)
так как математическое ожидание
центрированной случайной величины всегда равно нулю.
Выведем
соотношения, связывающие центральные и начальные моменты различных порядков.
Вывод мы проведем только для прерывных величин; легко убедится, что точно те же
соотношения справедливы и для непрерывных величин, если заменить конечные суммы
интегралами, а вероятности – элементами вероятности.
Рассмотрим
второй центральный момент:
Аналогично для
третьего центрального момента получим:
Выражения для и т.д. могут быть
получены аналогичным путем.
Таким образом,
для центральных моментов любой случайной величины справедливы формулы:

Вообще говоря,
моменты могут рассматриваться не только относительно начала координат
(начальные моменты) или математического ожидания (центральные моменты), но и
относительно произвольной точки :
. (5.7.11)
Однако центральные моменты имеют
перед всеми другими преимущество: первый центральный момент, как мы видели,
всегда равен нулю, а следующий за ним, второй центральный момент при этой
системе отсчета имеет минимальное значение. Докажем это. Для прерывной
случайной величины при
формула
(5.7.11) имеет вид:

Преобразуем это выражение:
Очевидно, эта
величина достигает своего минимума, когда , т.е. когда момент берется относительно
точки .
Из всех
моментов в качестве характеристик случайной величины чаще всего применяются
первый начальный момент (математическое ожидание) и второй центральный момент
.
Второй
центральный момент называется дисперсией случайной величины. Ввиду
крайней важности этой характеристики среди других моментов введем для нее
специальное обозначение :
.
Согласно
определению центрального момента
, (5.7.13)
т.е. дисперсией случайной
величины Х называется математическое ожидание квадрата соответствующей
центрированной величины.
Заменяя в
выражении (5.7.13) величину её выражением, имеем также:
. (5.7.14)
Для
непосредственного вычисления дисперсии служат формулы:


– соответственно для прерывных и
непрерывных величин.
Дисперсия
случайной величины есть характеристика рассеивания, разбросанности
значений случайной величины около её математического ожидания. Само слово
«дисперсия» означает «рассеивание».
Если
обратиться к механической интерпретации распределения, то дисперсия
представляет собой не что иное, как момент инерции заданного
распределения масс относительно центра тяжести (математического ожидания).
Дисперсия
случайной величины имеет размерность квадрата случайной величины; для наглядной
характеристики рассеивания удобнее пользоваться величиной, размерность которой
совпадает с размерностью случайной величины. Для этого из дисперсии извлекают
квадратный корень. Полученная величина называется средним квадратическим
отклонением (иначе – «стандартом») случайной величины . Среднее квадратическое
отклонение будем обозначать :
, (5.7.17)
Для упрощения
записей мы часто будем пользоваться сокращенными обозначениями среднего
квадратического отклонения и дисперсии: и
. В случае, когда не возникает сомнения, к
какой случайной величине относятся эти характеристики, мы будем иногда опускать
значок х у и
и писать
просто и
. Слова «среднее
квадратическое отклонение» иногда будем сокращенно заменять буквами с.к.о.
На практике
часто применяется формула, выражающая дисперсию случайной величины через её
второй начальный момент (вторая из формул (5.7.10)). В новых обозначениях она
будет иметь вид:
. (5.7.18)
Математическое
ожидание и
дисперсия (или
среднее квардратическое отклонение ) – наиболее часто применяемые
характеристики случайной величины. Они характеризуют наиболее важные черты
распределения: его положение и степень разбросанности. Для более подробного
описания распределения применяются моменты высших порядков.
Третий
центральный момент служит для характеристики асимметрии (или
«скошенности») распределения. Если распределение симметрично относительно
математического ожидания (или, в механической интерпретации, масса распределена
симметрично относительно центра тяжести), то все моменты нечетного порядка
(если они существуют) равны нулю. Действительно, в сумме
при симметричном относительно законе распределения и
нечетном каждому
положительному слагаемому соответствует равное ему по абсолютной величине
отрицательное слагаемое, так что вся сумма равна нулю. То же, очевидно,
справедливо и для интеграла

который равен нулю, как интеграл
в симметричных пределах от нечетной функции.
Естественно поэтому
в качестве характеристики асимметрии распределения выбрать какой-либо из
нечетных моментов. Простейший из них есть третий центральный момент. Он имеет
размерность куба случайной величины: чтобы получить безразмерную
характеристику, третий момент делят на куб среднего квадратического
отклонения. Полученная величина носит название «коэффициент асимметрии» или
просто «асимметрии»; мы обозначим её :
. (5.7.19)
На рис. 5.7.1
показано два асимметричных распределения; одно из них (кривая I) имеет положительную асимметрию (); другое (кривая II) – отрицательную (
).
Рис.
5.7.1
Четвертый
центральный момент служит для характеристики так называемой «крутости», т.е.
островершинности или плосковершинности распределения. Эти свойства
распределения описываются с помощью так называемого эксцесса. Эксцессом
случайной величины называется
величина
. (5.7.20)
Число 3
вычитается из отношения потому, что для весьма важного и широко
распространенного в природе нормального закона распределения (с которым мы
подробно познакомимся в дальнейшем) . Таки образом, для нормального
распределения эксцесс равен нулю; кривые, более островершинные по сравнении с
нормальной, обладают положительным эксцессом; кривые более плосковершинные –
отрицательным эксцессом.
На рис. 5.7.2
представлены: нормальное распределение (кривая I),
распределение с положительным эксцессом (кривая II)
и распределение с отрицательным эксцессом (кривая III).
Рис.
5.7.2
Кроме
рассмотренных выше начальных и центральных моментов, на практике иногда
применяются так называемые абсолютные моменты (начальные и центральные),
определяемые формулами
;

Очевидно,
абсолютные моменты четных порядков совпадают с обычными моментами.
Из абсолютных
моментов наиболее часто применяется первый абсолютный центральный момент
, (5.7.21)
называемый средним
арифметическим отклонением. Наряду с дисперсией и средним квадратическим
отклонением среднее арифметическое отклонение иногда применяется как
характеристика рассеивания.
Математическое
ожидание, мода, медиана, начальные и центральные моменты и, в частности,
дисперсия, среднее квадратическое отклонение, асимметрия и эксцесс представляют
собой наиболее употребительные числовые характеристики случайных величин. Во
многих задачах практики полная характеристика случайной величины – закон
распределения – или не нужна, или не может быть получена. В этих случаях
ограничиваются приблизительным описанием случайной величины с помощь. Числовых
характеристик, каждая из которых выражает какое-либо характерное свойство
распределения.
Очень часто
числовыми характеристиками пользуются для приближенной замены одного
распределения другим, причем обычно стремятся произвести эту замену так, чтобы
сохранились неизменными несколько важнейших моментов.
Пример 1. Производится один опыт, в
результате которого может появиться или не появиться событие , вероятность которого
равна .
Рассматривается случайная величина – число появлений события
(характеристическая
случайная величина события ). Определить её характеристики:
математическое ожидание, дисперсию, среднее квадратическое отклонение.
Решение. Ряд распределения величины имеет
вид:
где – вероятность непоявления события
.
По формуле
(5.6.1) находим математическое ожидание величины :
.
Дисперсию
величины определяем
по формуле (5.7.15):
,
откуда
.
(Предлагаем читателю получить тот
же результат, выразив дисперсию через второй начальный момент).
Пример 2. Производится три независимых
выстрела по мишени; вероятность попадания при каждом выстреле равна 0,4.
случайная величина –
число попаданий. Определить характеристики величины – математическое ожидание,
дисперсию, с.к.о., асимметрию.
Решение. Ряд распределения величины имеет вид:
Вычисляем
числовые характеристики величины :
Заметим, что
те же характеристики могли бы быть вычислены значительно проще с помощью теорем
о числовых характеристиках функций (см. главу 10).
Пример 3.
Производится ряд независимых опытов до первого появления события (см. пример 3 n° 5.1). Вероятность события
в каждом опыте равна
. Найти математическое ожидание,
дисперсию и с.к.о. числа опытов, которое будет произведено.
Решение. Ряд
распределения величины имеет вид:
Математическое
ожидание величины выражается
суммой ряда
.
Нетрудно
видеть, что ряд, стоящий в скобках, представляет собой результат
дифференцирования геометрической прогрессии:
Следовательно,
откуда
.
Для
определения дисперсии величины Х вычислим сначала её второй начальный
момент:

Для вычисления ряда, стоящего в
скобках, умножим на q ряд:
Получим:
Дифференцируя этот ряд по , имеем:
Умножая на , получим:
По формуле (5.7.18) выразим дисперсию:
откуда
Пример 4. Непрерывная случайная величина подчинена закону
распределения с плотностью:
(рис. 5.7.3).
Найти коэффициент . Определить м.о.,
дисперсию, с.к.о., асимметрию, эксцесс величины .
Рис. 5.7.3.
Решение. Для определения воспользуемся
свойством плотности распределения:
отсюда .
Так как функция нечетная, то м.о.
величины равно
нулю:

Дисперсия и с.к.о. равны,
соответственно:
.
Так как
распределение симметрично, то .
Для вычисления
эксцесса находим :
откуда
.
Пример 5. Случайная величина подчинена закону
распределения, плотность которого задана графически на рис. 5.7.4.
Написать
выражение плотности распределения. Найти м.о., дисперсию, с.к.о. и асимметрию
распределения.
Рис.
5.7.4.
Решение. Выражение плотности распределения
имеет вид:
Пользуясь
свойством плотности распределения, находим .
Математическое
ожидание величины :
Дисперсию
найдем через второй начальный момент:
отсюда
Третий
начальный момент равен
Пользуясь
третьей из формул (5.7.10), выражающей через начальные моменты, имеем:
откуда
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 февраля 2020 года; проверки требуют 19 правок.
Моме́нт случа́йной величины́ — числовая характеристика распределения данной случайной величины.
Происхождение понятия[править | править код]
Момент в математике — прямая аналогия с понятием момента в физике и механике. В математике моменты функции — это количественные измерения, связанные с формой графика функции. Например, если функция представляет собой распределение вероятностей, то первый момент — это ожидаемое значение, второй центральный момент (англ.) — это дисперсия, третий стандартизированный момент (англ.) — это асимметрия, а четвертый стандартизированный момент — это эксцесс. Если функция описывает плотность массы, то нулевой момент — это полная масса, первый момент (нормализованный по полной массе) — это центр масс, а второй момент — это момент инерции.
Определения[править | править код]
Если дана случайная величина 
-
- если математическое ожидание
в правой части этого равенства определено;
-
и
- если математическое ожидание в правой части этого равенства определено.[1]
Абсолютные моменты могут быть определены не только для целых, но и для любых положительных действительных чисел 
Замечания[править | править код]
Геометрический смысл некоторых моментов[править | править код]
-
- называется коэффициентом асимметрии.
показывает, насколько тяжелые у распределения хвосты. Величина
-
- называется коэффициентом эксцесса распределения
Вычисление моментов[править | править код]
- Моменты могут быть вычислены напрямую через определение путём интегрирования соответствующих степеней случайной величины. В частности, для абсолютно непрерывного распределения с плотностью
имеем:
если 
- а для дискретного распределения с функцией вероятности
если 
- Также моменты случайной величины могут быть вычислены через её характеристическую функцию
:
- Если распределение таково, что для него в некоторой окрестности нуля определена производящая функция моментов
то моменты могут быть вычислены по следующей формуле:
Обобщения[править | править код]
Можно также рассматривать нецелые значения 

Можно рассматривать моменты многомерной случайной величины. Тогда первый момент будет вектором той же размерности, второй — тензором второго ранга (см. матрица ковариации) над пространством той же размерности (хотя можно рассматривать и след этой матрицы, дающий скалярное обобщение дисперсии). И т. д.
См. также[править | править код]
- Момент изображения
Примечания[править | править код]
- ↑ Г. Крамер. Математические методы статистики. — 2-е изд. — М.: Мир, 1975. — С. 196-197, 284. — 648 с.
Обобщенными числовыми характеристиками для случайных величин в теории вероятностей а также математической статистике являются начальные и центральные моменты. Задачи на отыскание моментов являются неотъемлемой частью теории вероятностей и математической статистики. Начальным моментом k-го порядка случайной величины Х называют математическое ожидание от величины в k-ой степени
Когда
Когда 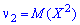
Для дискретной случайной величины 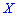
для непрерывной интегрированием
Если непрерывная величина задана интервалом 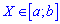
Центральным моментом k-го порядка называют математическое ожидание от величины
Когда
для 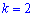
при 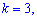
при 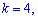
и так далее.
Для дискретной случайной величины центральные моменты вычисляют по формуле
для непрерывной по следующей
Если случайная величина определена интервалом 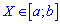
Рассмотрим пример отыскания приведенных величин.
———————————–
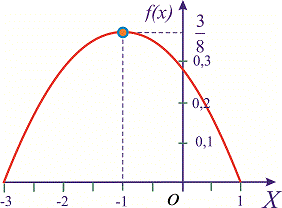
Пример 1. Задана функция плотности вероятностей
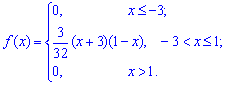
Вычислить начальные и центральные моменты второго и третьего порядка 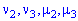
Решение. Для вычисления начальных моментов выполним интегрирование по вышеприведенным формулам
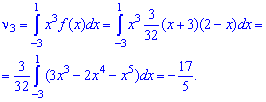
Промежуточные операции при интегрировании пропущены, они занимают много места, а Вам главное иметь инструкцию для вычислений, так как примеры у Вас будут другие.
Для вычисления центральных моментов инерции необходимо знать математическое ожидание случайной величины, поэтому определяем его первее
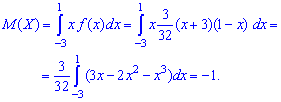
Найдено математическое ожидание подставляем в формулу центральных моментов. В случае 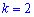
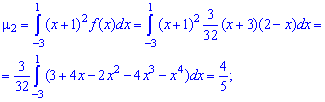
и при 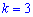
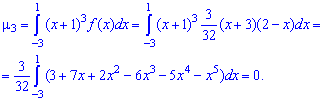
На этом решения примера завершено, функция плотности вероятностей приведена на графике
———————————–
Примеры нахождения начальных и центральных моментов будут рассмотрены в следующей статье. Задачи совсем не сложные, а вычисления величин сводится к возведения в степень, интегрирование, умножение и суммирование.
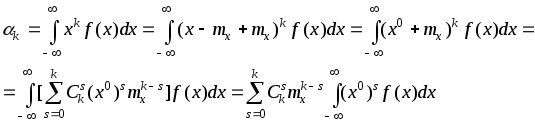

















![{displaystyle nu _{k}=mathbb {M} left[X^{k}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e859ee783c97df459238a867977268a1be057c96)
![{displaystyle mathbb {M} [*]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41e0651f3c7b6c97f6d6bce4be940e0b88dde0fd)
![{displaystyle mu _{k}=mathbb {M} left[(X-mathbb {M} X)^{k}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b84dc1582c641c508b1faf8c8671c4165dbc2559)
![{displaystyle nu _{k}=mathbb {M} left[|X|^{k}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e40cbd61883fb31df775d91d7602a4b8468631)
![{displaystyle mu _{k}=mathbb {M} left[|X-mathbb {M} X|^{k}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc700a97bd94d34a22ba2a2961c50de7f9525e38)
![{displaystyle mu _{k}=mathbb {M} left[X(X-1)...(X-k+1)right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f7dae2d81aadb91a59d1903f5e4e1e9c6b78524)