Как найти третью координату точку треугольника

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

И, наконец, находим угол C:

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Найти третью точку правильного треугольника?

Логика у вас правильная – взять середину отрезка AB и отложить от него перпендикуляр длинной sqrt(3)/2*d.

Но не надо искать углы, вектор перпендикуляр находится тривиально – это (Можно доказать перпендикулярность через скалярное произведение, например). Более того, длина этого вектора будет уже d (это ведь повернутый на 90 градусов вектор по стороне треугольника). Значит его остается тупо домножить на sqrt(3)/2.

Таким образом формула x3 = (x1+x2)/2 +sqrt(3)/2*(y2-y1).

Зная координаты точки 1(x1,y1) и координаты точки 2(x2,y2) найти третью точку(x3,y3) правильного треугольника со стороной d.

Безграмотная формулировка. Не точки, а вершины. d вообще лишнее.

Если A(x1,y1), B(x2,y2), то третья вершина C(x3,y3) находится поворотом вершины B вокруг A на 60 градусов по часовой и против часовой стрелки.

Как найти координаты точки?

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

• Координатные оси — это прямые, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

1. Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
   точка С (0, 2).
2. Если точка лежит на оси Ox, то ее ордината равна 0. Например,
   точка F (3, 0).
3. Начало координат — точка O. Ее координаты равны нулю: O (0,0).
4. Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
5. Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
6. Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
7. Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

1. Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
2. Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
3. Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.

Способ второй. Как определить положение точки D (-4, 2):

1. Сместить прямую по оси Ox влево на 4 единицы, так как у нас
   перед 4 стоит знак минус.
2. Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

[spoiler title=”источники:”]

http://qna.habr.com/q/872623

http://skysmart.ru/articles/mathematic/kak-najti-koordinaty-tochki

[/spoiler]

Автор	Сообщение
	Заголовок сообщения: Координаты третьей вершины треугольника Добавлено: 26 мар 2013, 05:26
Начинающий Зарегистрирован: 26 мар 2013, 05:23 Сообщений: 2 Cпасибо сказано: 3 Спасибо получено: 0 раз в 0 сообщении Очков репутации: 1	Здравствуйте, уважаемые форумчане. Помогите пожалуйста с формулой Как найти координаты третьей вершины треугольника по длинам трёх сторон и двум координатам вершин? Известны координаты точек А(x1,y1), С(x2,y2). длины сторон а, в, с необходимо вычислить координаты точки В(x3,y3) Использовать для вычислений Косинус и Синус угла АСВ и смещение прямой АС относительно системы координат нельзя из-за получающейся огромной погрешности при вычислениях. Я про формулу такого вида: x3 = x2 + a*cosС, y3 = y2 + a*sinС Последний раз редактировалось Andy 11 дек 2019, 10:12, всего редактировалось 1 раз. Название темы изменено модератором.
Вернуться к началу

Avgust	Заголовок сообщения: Re: Найти координаты третьей вершины треугольника по длинам трёх Добавлено: 26 мар 2013, 08:29
	Точка А – центр окружности радиусом с Точка С – центр окружности радиусом a Пересечение двух окружностей дадут точку B, то есть ее координаты. Всего-то нужно решить систему относительно [math]x,[/math] и [math]y[/math] [math](y-y_1)^2+(x-x_1)^2=c^2[/math] [math](y-y_2)^2+(x-x_2)^2=a^2[/math] Получим два решения при допустимых соотношениях параметров (при которых треугольник может существовать) Последний раз редактировалось Avgust 26 мар 2013, 09:10, всего редактировалось 1 раз.
Вернуться к началу
	За это сообщение пользователю Avgust “Спасибо” сказали: panda

panda	Заголовок сообщения: Re: Найти координаты третьей вершины треугольника по длинам трёх Добавлено: 26 мар 2013, 08:47
	Спасибо за ответ. А не могли бы вы оформить его в виде формулы?
Вернуться к началу

Avgust	Заголовок сообщения: Re: Найти координаты третьей вершины треугольника по длинам трёх Добавлено: 26 мар 2013, 09:34
	Формулы я получил. Но они такие громоздкие, что писать полчаса надо. Вот численно элементарно делается. Например, зададим параметры пифагорова треугольника: [math]x_1=0,;, y_1=0, ; , x_2=4,;, y_2=3 ,;, a=3, ;, c=4[/math] Тогда по команде Maple solve({(y-y1)^2+(x-x1)^2 = c^2, (y-y2)^2+(x-x2)^2 = a^2}, [x, y]); получим два решения: 1) [math]x=4 , ; , y=0[/math] 2) [math]x=frac{28}{25}, ; , y=frac{96}{25}[/math] Графическое представление этой задачи:
Вернуться к началу
	За это сообщение пользователю Avgust “Спасибо” сказали: panda

Avgust	Заголовок сообщения: Re: Найти координаты третьей вершины треугольника по длинам трёх Добавлено: 26 мар 2013, 10:00
	Я добавил рисунок… Вот формулы только для одного из решений: x:=(1/2)*((y1-y2)*sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2))*(x1-x2)^2)+(x1^3-x1^2*x2+(y2^2-2*y1*y2-c^2+y1^2+a^2-x2^2)*x1-x2*(a^2-c^2-x2^2-y2^2+2*y1*y2-y1^2))*(x1-x2))/((x1-x2)*(x1^2-2*x2*x1+x2^2+(y1-y2)^2)); y := (-sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2))*(x1-x2)^2)+y1^3-y1^2*y2+(a^2+x1^2-c^2+x2^2-2*x2*x1-y2^2)*y1+y2^3+(x2^2-2*x2*x1+c^2-a^2+x1^2)*y2)/(2*y1^2-4*y1*y2+2*y2^2+2*(x1-x2)^2); Второе решение: x := (1/2)*((-y1+y2)*sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(x1-x2)^2*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2)))+(x1-x2)*(x1^3-x1^2*x2+(y1^2-2*y1*y2+y2^2+a^2-c^2-x2^2)*x1-x2*(-c^2-x2^2+a^2-y1^2+2*y1*y2-y2^2)))/((x1^2-2*x2*x1+x2^2+(y1-y2)^2)*(x1-x2)); y := (sqrt(-(x1-x2)^2*(-x1^2+2*x2*x1-x2^2+(c+a+y1-y2)*(c+a-y1+y2))*(-x1^2+2*x2*x1-x2^2+(-c+a+y1-y2)*(-c+a-y1+y2)))+y1^3-y1^2*y2+(a^2+x1^2-c^2+x2^2-2*x2*x1-y2^2)*y1+y2^3+(x2^2-2*x2*x1+c^2-a^2+x1^2)*y2)/(2*y1^2-4*y1*y2+2*y2^2+2*(x1-x2)^2); Формулы проверил – работают отлично. Вот если бы их суметь упростить!
Вернуться к началу
	За это сообщение пользователю Avgust “Спасибо” сказали: amjava, panda, Realdreamer

Realdreamer	Заголовок сообщения: Re: Найти координаты третьей вершины треугольника по длинам трёх Добавлено: 10 дек 2019, 17:11
	Уважаемые математики Чтобы не плодить темы, разрешить поднять текущую. Пишу программу, но к сожалению не очень силен в математических науках. Нужно как раз вершины треугольника Но исходные данные немного другие. Есть длина стороны равностороннего треугольника и угол между ними. Строится всё из начала координат в сторону x (вверх) Вообще в итоге мне нужно написать симуляцию работы вентилятора. Крутится то я его заставлю. Нарисовать не могу (( вот такой должен получится. Стороны 70 Угол лопасти 30 град Угол между лопастями 120 Три лопасти. У меня получается есть только координаты центра. Чтобы нарисовать треугольники мне нужны остальные координаты вершин Пытался сам найти, но видимо не так запрос формирую.
Вернуться к началу

Realdreamer	Заголовок сообщения: Re: Найти координаты третьей вершины треугольника по длинам трёх Добавлено: 11 дек 2019, 16:20
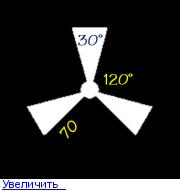
	vvvv Большое спасибо за потраченное время. К сожалению ваше решение только добавило мне вопросов (( Координат всего должно быть 9 для каждой оси, но в таблице их 10 Так же вижу на графике что есть координата с х = -70 но в таблице для Х такого значения нет. В итоге я пошёл по другому пути Нарисовал первую лопасть вверх от начала координат и посчитал основание равнобедренного треугольника зная его стороны и угол между ними a = 70 b = a * sin(30) / 2 и разделил её пополам. Получил координату по Y в обе стороны Лопасть это два прямоугольных треугольника в которых по теореме пифагора нашёл вторую сторону которая и является второй коорлинатой y1 = sqrt(a ** 2 – b ** 2) А потом по формуле окружности просто сдвинул на 120 градусов влево и вправо xn1 = sin(120 – 15) * a yn1 = cos(120 – 15) * a xn2 = sin(120 + 15) * a yn2 = cos(120 + 15) * a xn1 = sin(-120 – 15) * a yn1 = cos(-120 – 15) * a xn2 = sin(-120 + 15) * a yn2 = cos(-120 + 15) * a От меня вам всё равно спасибо что откликнулись!
Вернуться к началу