Как найти третью сторону треугольника зная площадь

Ну или не совсем простая, но способов решений будет много. Ну и рисунок-подсказка должен натолкнуть на «продолжение»… Ну или запутать.

Задача в продолжение темы «метрическое соотношение сторон в треугольнике», поэтому стоит этот раз решить как раз схожим (с предыдущими задачами) способом. Но как сказано выше — способов тут не мало я перечислю несколько в подсказках, а Вы попробуйте найти свой.

Условие

Две стороны треугольника равны 2√2 и 3, площадь треугольника равна 3. Найдите третью сторону.

Подсказки

Начнём с оптимального (по теме прошлых задач) варианта решения — теорема косинусов. Да да. Но вот известного угла только между сторонами нет. Что делать? Вспоминать про площадь! Через площадь и две стороны можно узнать синус угла, а там и косинус через основное тригонометрическое тождество (если синус совсем неприглядный или узнать угол по табличному значению). Тут главное не ошибиться и не проморгать угол (острый или тупой).

Второй вариант, прям напрашивается из условия — теорема Геррона.

Третий способ, к которому многие (зачем-то?) прибегают — дополнительное построение высоты. Ну и «беспорядочное» использование теоремы Пифагора. Тут так тоже можно.

Последние два способа — не исключение. Надо внимательно следить за углами. Треугольник-то может быть как тупоугольным, так и…

#школьное образование #огэ по математике #егэ по математике #задачи по математике

Если известна площадь треугольника, то можно выяснить длину одной из его сторон. Эта задача может быть решена с помощью нескольких формул, при условии, что достаточно данных о других сторонах и свойствах треугольника.

Для начала необходимо разобраться с терминами. Треугольник — это фигура, состоящая из трех сторон и трех углов. Площадь треугольника определяется как половина произведения его основания и высоты. Основание — это произвольная сторона треугольника, на которую опущена высота.

Если треугольник является прямоугольным, то существуют методы расчета сторон, используя теорему Пифагора. Если же треугольник не является прямоугольным, то есть не существует правильной формулы для вычисления длины его сторон. Однако, можно использовать некоторые соотношения между сторонами и углами треугольника, чтобы решить эту задачу.

Как найти сторону треугольника по площади: простые способы расчета

Формула для прямоугольного треугольника

Если известны площадь прямоугольного треугольника и значение одной из его катетов, то можно легко вычислить длину второго катета. Формула для этого такая:

b = 2S / a

где b – длина второго катета, S – площадь треугольника, a – длина известного катета.

Например, если площадь треугольника равна 60 квадратных сантиметров, а длина одного из его катетов составляет 6 сантиметров, то:

Дано:	S = 60 см2	a = 6 см
Найти:	b?
Решение:	b = 2S / a = 2 * 60 / 6 = 20 см

Таким образом, второй катет прямоугольного треугольника равен 20 сантиметров.

Формула для равностороннего треугольника

Равносторонний треугольник — это треугольник, у которого все стороны и все углы равны между собой. Периметр такого треугольника можно легко вычислить, умножив длину одной стороны на три:

Периметр треугольника = 3 x длина стороны

Чтобы найти длину одной стороны, нужно поделить периметр на три:

Длина стороны = Периметр треугольника / 3

Также существует формула для нахождения площади равностороннего треугольника:

Площадь треугольника = (длина стороны)² x √3 / 4

Эта формула основывается на том, что высота равностороннего треугольника проходит через центр окружности, описанной около него. Длина высоты, в свою очередь, равна √3 / 2 умножить на длину стороны.

Формула для любого треугольника с известной высотой

Один из простых способов найти любую сторону треугольника – использовать формулу, основанную на площади и высоте.

Известно, что площадь треугольника равна половине произведения одной из сторон на высоту, опущенную к этой стороне. Таким образом, если известна площадь и высота, то можно легко найти длину любой стороны.

Формула выглядит так:

где S – площадь треугольника, h – высота, опущенная к стороне a.

Используя данную формулу, вы можете рассчитать длину любой стороны треугольника при известных площади и высоте. Это позволяет не только более точно определить геометрические параметры фигуры, но и решить многие задачи, связанные с расчетом треугольников в жизни и профессиональной деятельности.

Формула Герона для любого треугольника

Формула Герона — это универсальный метод нахождения площади треугольника по знанию длин всех его сторон. Она получила свое название в честь Герона Александрийского, жившего в I веке, который сформулировал и доказал эту формулу.

Согласно этой формуле, площадь треугольника можно вычислить по формуле:

S = √(p(p-a)(p-b)(p-c)),

где S — площадь треугольника, a, b и c — длины сторон треугольника, а p — полупериметр, который вычисляется как

p = (a + b + c)/2 .

Формула Герона универсальна, так как она применима для любых типов треугольников, включая остроугольные, тупоугольные и равнобедренные треугольники.

Примеры расчетов по формулам

Представим себе треугольник с площадью 12 квадратных единиц и высотой 4 единицы. С помощью классической формулы S=1/2*a*h мы можем найти длину основания треугольника: a=2*S/h=2*12/4=6. Таким образом, сторона треугольника равна 6 единиц.

Если даны две стороны треугольника и угол между ними, мы можем найти площадь треугольника по формуле S=1/2*a*b*sin(α), где α — угол между сторонами. Пусть у нас есть треугольник со сторонами длиной 3 и 4 единицы и углом между ними в 60 градусов. Тогда S=1/2*3*4*sin(60°)=6√3/2=3√3 квадратных единиц.

Если известны все три стороны треугольника, мы можем найти его площадь, используя формулу Герона S=√p(p-a)(p-b)(p-c), где p=(a+b+c)/2 — полупериметр треугольника. Рассмотрим треугольник со сторонами 5, 6 и 7 единиц. Полупериметр равен p=(5+6+7)/2=9, и тогда S=√9*(9-5)*(9-6)*(9-7)=√9*4*3*2=6√6 квадратных единиц.

Таким образом, используя различные формулы, мы можем рассчитать длину сторон треугольника, зная его площадь.

Как найти сторону треугольника, зная его площадь и угол между сторонами

Расчет сторон треугольника может быть сложной задачей, особенно если известна только площадь и угол между сторонами. Однако, существует несколько простых способов решения этой задачи.

Первый способ — использование формулы для расчета площади треугольника: S = (a * b * sin(C)) / 2, где a и b — длины двух сторон треугольника, а С — угол между ними. Зная площадь треугольника и значение угла С, можно выразить длину неизвестной стороны через длину известных сторон и угол С.

Второй способ — использование теоремы косинусов. Если известны длины двух сторон треугольника и угол между ними, можно найти длину третьей стороны с помощью формулы c^2 = a^2 + b^2 — 2ab cos(C), где c — длина третьей стороны.

Третий способ — использование теоремы синусов. Если известны длины двух сторон треугольника и угол между ними, можно найти длину третьей стороны с помощью формулы a / sin(A) = b / sin(B) = c / sin(C), где A, B и C — углы при соответствующих сторонах.

Для удобства расчета можно использовать таблицу, где в первом столбце указаны известные величины, во втором — соответствующие им формулы для расчета неизвестной величины, а в третьем — результат расчета.

Известные величины	Формула для расчета неизвестной величины	Результат
S, a, C	b = 2S / (a * sin(C))
S, b, C	a = 2S / (b * sin(C))
a, b, C	c = sqrt(a^2 + b^2 — 2ab cos(C))
a, b, C	c = a / sin(A) = b / sin(B)

Выводы

Исходя из вышеприведенных методов расчета сторон треугольника по его площади, можно сделать несколько выводов. Во-первых, чем данная площадь больше, тем длиннее будут стороны треугольника. Во-вторых, при наличии стороны, длину которой известна, расчет других сторон может производиться более точно.

Например: если известны площадь и боковая сторона, то можно использовать формулу синусов для расчета угла между этой стороной и неизвестной. После этого, применяя формулу для нахождения высоты, можно рассчитать длину недостающей стороны.

Важно отметить, что для получения точных результатов необходимо правильно измерять площадь треугольника. Измерять нужно по высоте, опущенной на наибольшую сторону — это поможет избежать ошибок в расчетах.

Также необходимо помнить о том, что методы расчета, приведенные в данной статье, относятся к треугольникам со сторонами и углами, которые исследованы и не являются применимыми для особенных треугольников, например, равнобедренных.

• В целом, знание формул для расчета сторон треугольника по площади может оказаться полезным в ряде практических задач, связанных с геометрией, архитектурой и строительством.
• Наконец, следует отметить, что существуют и другие методы расчета сторон треугольника, которые могут оказаться более точными и удобными в различных ситуациях.

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

1. Найти все стороны треугольника.
2. Найти все углы треугольника.
3. Найти площадь (S) и периметр (P) треугольника.
4. Найти радиус (r) вписанной окружности.
5. Найти радиус (R) описанной окружности.
6. Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
 

Сторона треугольника (или длина сторон) может быть найдена различными методами. 
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет

где a и b – катеты, с – гипотенуза.

2) Найти гипотенузу по двум катетам

где a и b – катеты, с – гипотенуза.

3) Найти катет по гипотенузе и противолежащему углу

где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.

4) Найти гипотенузу через катет и противолежащий угол

где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.

Для равнобедренного треугольника:

1) Найти основание через боковые стороны и угол между ними

где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.

2) Найти основание через боковые стороны и угол при основании

где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.

3) Найти боковые стороны по углу между ними

где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.

4) Найти боковые стороны по углу при основании

где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.

​​​​​Для равностороннего треугольника:

1) Найти сторону через площадь

где a – искомая сторона, S – площадь треугольника.

2) Найти сторону через высоту

где a – искомая сторона,h – высота треугольника.

3) Найти сторону через радиус вписанной окружности

где a – искомая сторона,r – радиус вписанной окружности.

4) Найти сторону через радиус описанной окружности

где a – искомая сторона,R – радиус описанной окружности.

​​​​​Для произвольного треугольника:

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

где a – искомая сторона, b – известная сторона, α° и β° известные углы.

Скачать все формулы в формате Word

Треугольником называется фигура, которая состоит их трех точек (вершины), которые не лежат на одной
прямой и трех попарно соединяющих эти точки отрезков (стороны). Треугольники бывают остроугольными,
тупоугольными, прямоугольными, равнобедренными, равносторонними, разносторонними. С данной фигурой
связано много формул, теорем, правил. Ниже приведены формулы и примеры по нахождению стороны
треугольника.

Сторона равностороннего треугольника через радиус описанной окружности

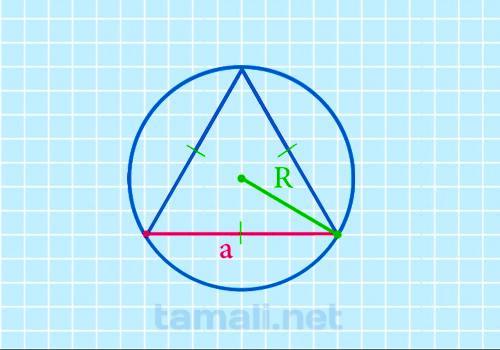
Для того чтобы найти сторону равностороннего треугольника через радиус описанной окружности
необходимо ее радиус умножить на корень квадратный из трех. Таким образом, формула будет выглядеть
следующим образом:

a = R * √3

где а — сторона треугольника, R — радиус описанной окружности.

Пример. Пусть дан равносторонний треугольник с радиусом описанной окружности 10см. Подставим в
формулу и получится: a = 10*√3 = 10 * 1,732 ≈ 17,3 см.

Сторона равностороннего треугольника через радиус вписанной окружности

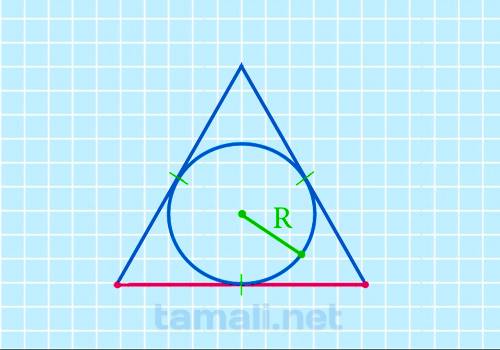
Для нахождения стороны правильного треугольника через радиус вписанной окружности следует
использовать формулу радиуса r= a (√3 / 6). Отсюда можно вывести формулу следующим образом: a = r (6
/ √3) = r *(6√3 / √3√3) = r * (6√3 / 3). Формула будет следующая (удвоенный радиус умножить на
квадратный корень из трех):

a = 2r * √3

где а — сторона треугольника, R — радиус вписанной окружности.

Пример. Пусть дан равносторонний треугольник с радиусом вписанной окружности 23см. Подставим в
формулу и получится: a = 2 * 23 * √3 = 2 * 23 * 1,732 ≈ 79,7см.

Сторона равностороннего треугольника через высоту

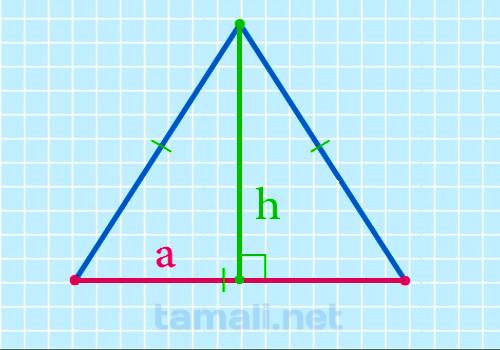
Для того чтобы найти сторону равностороннего треугольника через высоту следует применить теорему
Пифагора. Сторона равностороннего треугольника a² будет равна сумме квадратов высоты и половины
основания, которое также является стороной a: a² = h² + (a/2)² ⇒ a² = h² + a²/4 ⇒ a² — a²/4
=h² ⇒ (4a² — a²) / 4 = h² ⇒ 3a²/4 = h² ⇒ a² = 4*h²/3 ⇒a = √(4h²/3). Отсюда можно вывести
формулу для нахождения стороны через высоту:

a = 2h / √3

где а — сторона, h —  высота равностороннего треугольника.

Пример. Пусть дан равносторонний треугольник с высотой 45см. Подставим в формулу и получится: a = 2 *
45 / √3 = 2 * 45 / 1,732 ≈ 51,963 см.

Сторона равностороннего треугольника через площадь

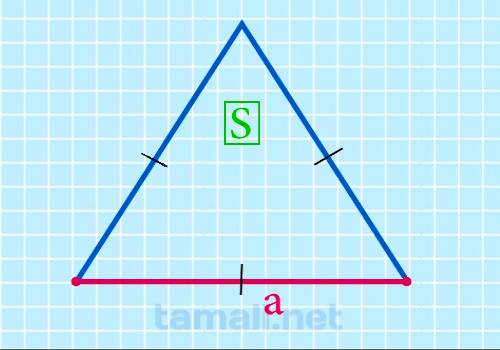
Для того чтобы найти сторону равностороннего треугольника через площадь нужно применить следующую
формулу

a = √(4S / √3)

где а — сторона, S —  площадь равностороннего треугольника.

Пример. Пусть дан равносторонний треугольник с площадью 64м². Подставим в формулу и получится: a =
√(4*64 / √3)= √(4 * 64 / 1,732) ≈ 12,157 см.

Основание равнобедренного треугольника через боковые стороны и угол между ними

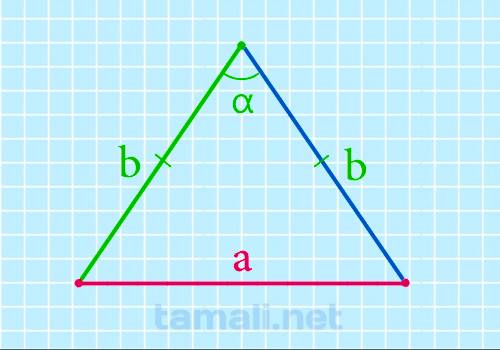
Равнобедренным называется треугольник, у которого есть две равные стороны, называемые ребрами, а
третья сторона основанием. Для того чтобы найти основание нужно знать или один из углов, или высоту
треугольника, приводящаяся к основанию. Его можно вычислить по данной формуле:

a = 2b * sin (α/2)

где a — длина основания треугольника, b — длина стороны треугольника; α — это угол,
который противоположен основанию.

Пример. Если сторона a = 10 см, а ∠β = 12°, то: a = 2⋅10⋅sin 12/2 = 2⋅10⋅0,1045 =2,09 см.

Основание равнобедренного треугольника через боковые стороны и угол при основании

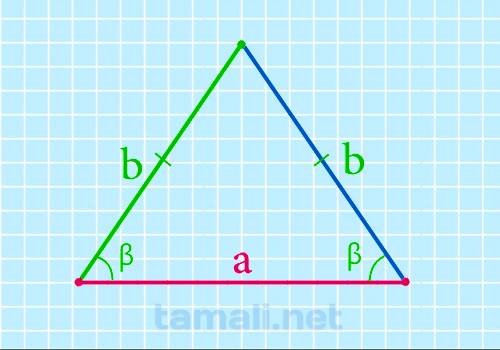
Угол при основании равнобедренного треугольника равен разности 90º и половины угла при его вершине и
чем больше угол при вершине равнобедренного треугольника, тем он меньше. Может быть только острым,
то есть прямым или тупым он быть не может. Если известен угол при основании и боковые стороны, то
можно найти основание равнобедренного треугольника по следующей формуле:

a = 2b + cos β

где b — боковая сторона, β — угол при основании.

Пример. Если сторона a = 10 см, а ∠β = 40°, то: a = 2⋅10⋅cos 40 = 2⋅10⋅0,766 =15.32 см.

Боковая сторона равнобедренного треугольника через основание и угол между боковыми сторонами

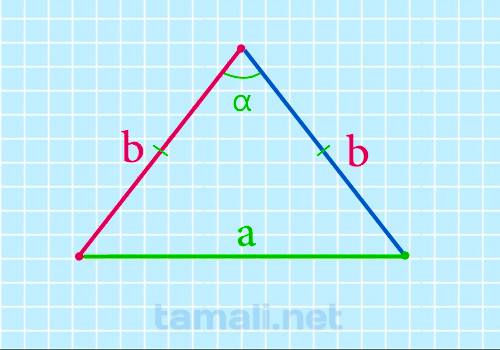
В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны,
из чего можно сделать вывод что если углы при основании треугольника одинаковы по значению, значит
он является равнобедренным.  Это значит, что α = β.

Формула, выражающая боковую сторону равнобедренного треугольника через основание и угол боковыми
сторонами:

b = a / (2 * sin(α/2))

где d — основание равнобедренного треугольника, α — угол между боковыми сторонами.

Пример. Если сторона a = 17 см, а ∠α = 50°, то: a = 17 / 2 * sin (50/2) = 17 / 2 * sin 25 = 20.11
см.

Боковая сторона равнобедренного треугольника через основание и угол при основании

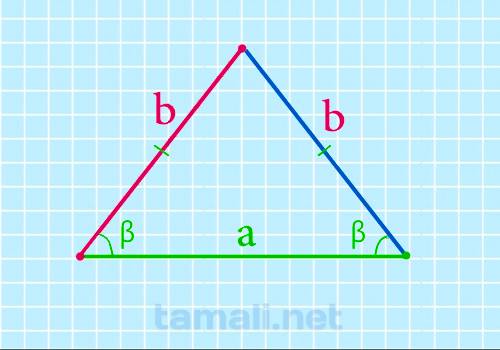
Если известно основание и угол при нем, то формула боковой стороны равнобедренного треугольника будет
выглядеть следующим образом:

b = a / 2 * cos β

где a — это основание, β — угол при основании равнобедренного треугольника.

Здесь длина боковых сторон будет равно b: AB=BC=b, длина основания a: AC=a. Для доказательства
формулы боковой стороны применяется теорема косинусов, вернее, ее следствие.

Пример. Пусть основание (a) равно 35мм, а угол β — 60º, тогда подставив в формулу получим b =
35 / 2 * 0,5=35 мм.

Катет прямоугольного треугольника через гипотенузу и острый угол

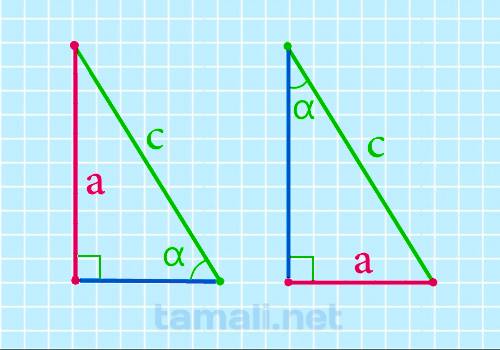
Катет прямоугольного треугольника через гипотенузу и острый угол выражается данным образом: катет,
противолежащий углу α, равен произведению гипотенузы на sin α, то есть формула будет выглядеть
следующим образом:

a = c * sin α

где c — гипотенуза, α — острый угол прямоугольного треугольника.

Пример. Пусть гипотенуза с равна 77см, а острый угол 80º, тогда подставив в формулу значения получим
следующее:  a = 77 * 0,98 = 75,8см.

Катет прямоугольного треугольника через гипотенузу и другой известный катет

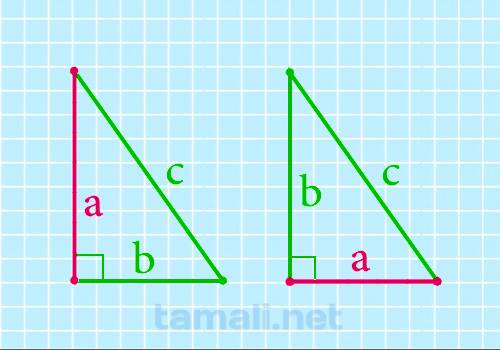
Если известен один катет и гипотенузу, то можно найти другой катет. Для этого необходимо
воспользоваться формулой:

a = √(c² — b²)

где c — гипотенуза, b — катет который известен прямоугольного треугольника.

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а
катет b = 4 см: a = √(5² — 4)² = √(25 — 16) = √9 = 3 см

Гипотенуза прямоугольного треугольника через катет и острый угол

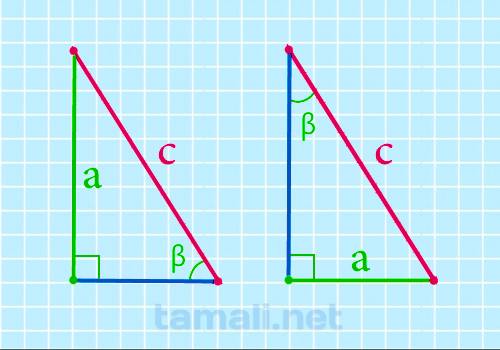
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему
угол можно узнать по формуле:

c = a / sin(β)

где a — катет, β — острый угол прямоугольного треугольника.

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 4 см, а
противолежащий к нему ∠β =60°: c = 4 / sin(60) = 4 / 0,87 = 8,04 см.

Гипотенуза прямоугольного треугольника через катеты

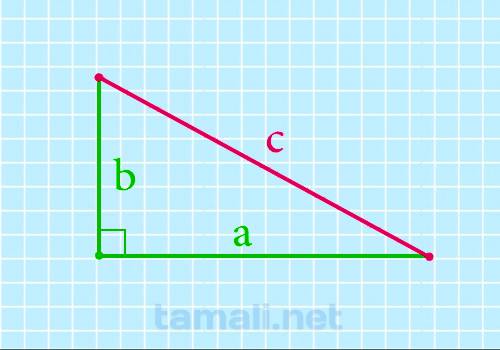
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b) можно рассчитать по
формуле используя теорему Пифагора. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов
катетов: c² = a² + b² следовательно:

c = √(a² + b²)

где c — гипотенуза, a и b — катеты.

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет
b = 4 см: c = √3² + 4² = √9 + 16 = √25 = 5 см

Сторона треугольника через две известные стороны и угол между ними

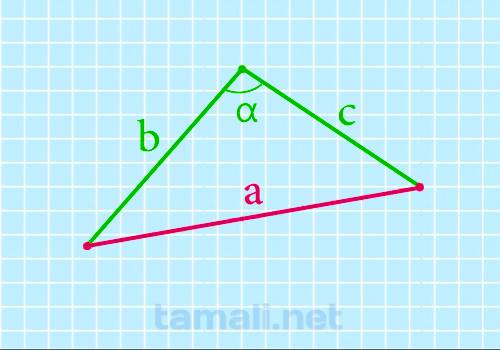
По стороне и двум углам или по двум сторонам и углу можно тоже вычислить длину стороны
треугольника:

a = b² + c² — 2bc * cos α

где a, b, c — стороны произвольного треугольника, α — угол между сторонами который
известен.

Обязательно обратите внимание что при подстановке в формулу, для тупого угла (α>90), cosα
принимает отрицательное значение.

Пример. Пусть сторона с равна 10 см, сторона b — 7, угол α — 60 градусов. Таким образом
получим подставив в формулу:
a = 7² + 10² — 2 * 7 * 10 * cos 60 = 8,89 см.

Сторона треугольника через известную сторону и два угла

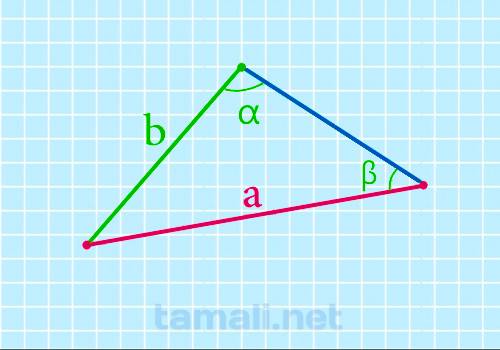
Для нахождения стороны треугольника через известную сторону и два угла необходимо воспользоваться
теоремой синусов и формула будут следующая:

a = (b * sin α) / sin β

где b — сторона треугольника; β, α — углы треугольника.

Пример. Пусть сторона треугольника b равна 10, угол β  = 30º, угол α = 35º. Тогда получим подставив в
формулу следующие значения: Сторона (a) = (10 * sin 35) / sin 30   = 8.71723 мм.