Как найти треугольник по трем точкам

Как найти треугольник по трем точкам

построение треугольника по двум сторонам и углу между ними.

Даны два отрезка (a) и (b), они равны сторонам искомого треугольника, и угол

∠

 (1), равный углу треугольника между сторонами. Необходимо построить треугольник с элементами, равными данным отрезкам и углу.

Trijst_konstr1.png

1. Провести прямую.

2. На прямой от выбранной точки (A) отложить отрезок, равный данному отрезку (a).

3. Построить угол, равный данному

∠

 (1) (вершина угла (A), одна сторона угла лежит на прямой).

4. На другой стороне угла отложить отрезок, равный данному отрезку (b).

5. Соединить концы отрезков.

Согласно признаку равенства треугольников по двум сторонам и углу между ними построенный треугольник равен со всеми треугольниками, которые имеют данные элементы.

Источник

Построение треугольника по трем элементам в геометрии

Содержание:

  • Как построить треугольник по трем элементам в геометрии
  • Какие элементы могут быть для этого использованы

    • Построение треугольника по трем сторонам
    • Построение треугольника по двум сторонам и углу между ними
    • По известной стороне и двум прилежащим к ней углам
  • Как построить треугольник по трем элементам с помощью циркуля
  • Решение задач на построение треугольника по трем элементам

Как построить треугольник по трем элементам в геометрии

Определение

Треугольник — геометрическая фигура, которая состоит из трех точек, не принадлежащих одной прямой, и трех отрезков, последовательно соединяющих данные точки.

В определении треугольника точки представляют собой вершины, а отрезки — являются его сторонами.

При определении расстояния от точки до прямой необходимо учитывать нескольких ключевых принципов:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

  1. В том случае, когда из точки С к прямой а проведена перпендикулярная линия СА, все другие отрезки, которые проведены из этой точки к прямой, называют наклонными.
  2. Перпендикуляр, который проведен из точки к прямой, меньше, чем любая наклонная, проведенная из той же точки к данной прямой, так как в прямоугольном треугольнике гипотенуза больше катета.
  3. Длина перпендикуляра, который проведен из точки к прямой, является расстоянием от этой точки до прямой.

Треугольник

 

Определить расстояние, на которое удалены друг от друга параллельные прямые, можно, исходя из того, что каждая из точек этих прямых равноудалена от другой параллельной прямой. Таким образом, расстояние между двумя параллельными прямыми соответствует длине перпендикуляра, который опущен из какой-либо точки, расположенной на одной прямой, на другую прямую.

Две прямые и перпендикуляры

 

При построении треугольника по трем элементам необходимо использовать следующие навыки:

  • построение окружности при известном центре и радиусе;
  • определение отрезка на заданном луче, равного данному;
  • построение угла, равного данному;
  • определение биссектрисы угла;
  • построение перпендикулярной прямой;
  • определение середины отрезка.

Какие элементы могут быть для этого использованы

Смысл задачи на построение какой-либо геометрической фигуры заключается в том, что требуется с помощью линейки и циркуля построить тот или иной объект, согласно заданным исходным условиям. Общие принципы решения подобных заданий:

  1. Анализ условий. Эта стадия предусматривает установление взаимосвязей между начальными условиями и объектом, который требуется построить. По итогам составляют алгоритм построения.
  2. Построение. Исходя из разработанного плана, необходимо построить геометрическую фигуру.
  3. Доказательство. В процессе нужно доказать соответствие изображенной фигуры условиям задачи.
  4. Изучение. Данный этап предполагает анализ исходных данных и определение условий, при которых задание имеет единственное решение, обладает несколькими решениями, не имеет ни одного ответа.

Построение треугольника по трем сторонам

Изобразить данную геометрическую фигуру с тремя углами можно по трем ее сторонам. Предположим, что существуют отрезки a, b, c, которые соответствуют сторонам искомого треугольника. По условиям задания требуется построить треугольник со сторонами, соответствующими рассматриваемым отрезкам.

В первую очередь следует доказать неравенство треугольника, то есть определить, что длина любого из отрезков меньше, чем сумма длин двух других отрезков. В случае удовлетворения этого условия допустимо, что рассматриваемые отрезки являются сторонами треугольника.

Построение треугольника по трем сторонам

 

Алгоритм действий:

  • построение прямой;
  • отложение отрезка на прямой от заданной точки А, равного данному отрезку а, и определение другого конца отрезка В;
  • построение окружности с центром в точке А и радиусом, который соответствует отрезку b;
  • изображение окружности с центром В и радиусом, который соответствует отрезку С;
  • точка, в которой пересекаются окружности, представляет собой третью вершину треугольника.

Исходя из признака равенства треугольников по трем сторонам, изображенный треугольник совпадает со всеми треугольниками, обладающими данными сторонами.

Построение треугольника по двум сторонам и углу между ними

Предположим, что существуют два отрезка a и b, которые соответствуют сторонам треугольника. Также имеется угол 1, который равен углу треугольника, расположенного между его сторонами. Необходимо изобразить треугольник с элементами, аналогичными тем, что даны в условии.

Построение треугольника по двум сторонам и углу между ними

 

Порядок действий при построении треугольника по двум сторонам и углу между ними следующий:

  • проведение прямой;
  • отложение отрезка на прямой от заданной точки А, который соответствует отрезку а из условия задания;
  • построение угла, равного углу 1, таким образом, что вершина угла А и одна из сторон угла расположены на прямой;
  • на другой стороне угла определить отрезок, который соответствует заданному отрезку b;
  • соединить концы изображенных отрезков.

Исходя из признака равенства треугольников по двум сторонам и углу между ними, геометрическая фигура, построенная в соответствии с алгоритмом, равна всем треугольникам, которые обладают такими же элементами.

По известной стороне и двум прилежащим к ней углам

Построение треугольника по стороне и двум углам, которые к ней прилегают, начинается с изучения условий задания. Согласно задаче, имеется отрезок а и пара углов 1 и 2, которые равны углам треугольника, прилежащим к данной стороне. Требуется изобразить треугольник с элементами, аналогичными заданному отрезку и углам.

По известной стороне и двум прилежащим к ней углам

 

Действия необходимо выполнять в следующем порядке:

  • провести прямую;
  • на данной прямой изобразить отрезок, который соответствует отрезку а и начинается в точке А, а также отметить другой его конец в точке В;
  • определить угол, соответствующий углу 1, таким образом, что вершина угла А и одна из его сторон расположены на прямой;
  • построить угол, равный углу 2, так, чтобы вершина угла В и одна сторона угла лежали на прямой;
  • точка, в которой пересекаются другие стороны углов, представляет собой третью вершину искомого треугольника.

По признаку равенства треугольников по стороне и паре углов, которые прилегают к ней, изображенный треугольник равен всем треугольникам, имеющим данные элементы.

Как построить треугольник по трем элементам с помощью циркуля

Изобразить треугольник, зная три его элемента, можно с помощью циркуля. К примеру, имеется три стороны в виде отрезков МК, ОЕ, FG, по которым необходимо построить треугольник АВС. При этом должно соблюдаться условие:

АВ = МК, ВС = FG, АС = ОЕ

Как построить треугольник по трем элементам с помощью циркуля

 

Используя линейку, следует провести прямую а. На данной прямой с помощью циркуля нужно отложить отрезок АВ, который соответствует отрезку МК. В процессе на прямой а можно отметить некую точку А. После измерения циркулем отрезка МК требуется изобразить окружность, центр которой совпадает с точкой А, а радиус равен МК. Строить окружность полностью нет необходимости, достаточно изобразить дугу, как показано на рисунке. Точку, в которой окружность пересекает прямую а можно обозначить, как В.

Как построить треугольник по трем элементам с помощью циркуля

 

С помощью циркуля нужно измерить отрезок ОЕ и построить окружность, центр которой совпадает с точкой А, а радиус соответствует отрезку ОЕ. Дуга выделена на изображении синим цветом.

Как построить треугольник по трем элементам с помощью циркуля

 

На следующем этапе, используя циркуль, можно измерить отрезок FG, чтобы построить окружность. Центр данной окружности совпадает с точкой В, а ее радиус соответствует отрезку FG. На рисунке дуга выделена зеленым цветом.

Как построить треугольник по трем элементам с помощью циркуля

 

Точка, в которой пересекаются окружности с центрами А и В, радиусами ОЕ и FG, следует обозначить, как С. С помощью линейки удобно соединить точки А, В и С. В результате получилось построить геометрическую фигуру в виде треугольника АВС, в котором:

АВ = МК, ВС = FG, АС = ОЕ

Так как условия задания соблюдены, изображенный треугольник является искомым.

Как построить треугольник по трем элементам с помощью циркуля

 

Примечание

Важно отметить, что подобное задание не во всех случаях имеет решение. Причина заключается в необходимости выполнения неравенства треугольника для каждого треугольника, то есть в каком-либо треугольнике сумма любых двух сторон больше третьей стороны. В том случае, когда один отрезок из заданных условием больше или равен сумме двух других, построить треугольник со сторонами, соответствующими данным отрезкам, не представляется возможным.

Изобразить треугольник с помощью циркуля можно, когда известны две стороны и угол между ними. К примеру, существуют отрезки МК и ОЕ, а также угол hk. Необходимо построить треугольник АВС при условии, что:

АВ = МК, АС = ОЕ,  ВАС = hk

Изобразить треугольник с помощью циркуля

 

Используя линейку, нужно провести прямую а и отложить на ней циркулем отрезок АВ, который соответствует отрезку МК. В данном случае необходимо в любой части прямой а поставить точку А. Далее с помощью циркуля можно измерить отрезок МК и построить окружность с центром в точке А и радиусом, равным МК. Точку, в которой окружность пересекает прямую, можно обозначить, как В. На рисунке дуга данной окружности выделена красным цветом.

Изобразить треугольник с помощью циркуля

 

На втором этапе требуется изобразить угол BAF, который соответствует углу hk. В процессе, используя циркуль, нужно построить окружность с радиусом МК и центром, который совпадает с вершиной угла hk. Допустимо изобразить лишь дугу этой окружности, которая на рисунке отмечена красным цветом. Точки, в которых окружность пересекает стороны угла hk, следует обозначить, как N и P.

Изобразить треугольник с помощью циркуля

 

Циркулем можно измерить длину отрезка NP и построить окружность с радиусом NP и центром в точке В. На изображении полученная дуга выделена синим цветом. Точкой F следует обозначить точку, в которой построенная окружность пересекает окружность с радиусом МК и центром в точке А.

Изобразить треугольник с помощью циркуля

 

Далее нужно построить луч AF, используя обычную линейку.

Изобразить треугольник с помощью циркуля

 

Затем с помощью циркуля удобно измерить отрезок ОЕ и построить с соответствующим радиусом окружность, центр которой совпадает с точкой А. На рисунке дуга этой окружности изображена зеленым цветом. Точка С является точкой, в которой пересекается окружность с лучом AF.

Изобразить треугольник с помощью циркуля

 

В конце следует соединить точки В и С с помощью линейки. В результате удалось построить треугольник АВС, в котором:

АВ = МК, АС = ОЕ, ВАС = hk

Таким образом, условия задания выполнены, и треугольник является искомым.

Изобразить треугольник с помощью циркуля

 

Примечание

Следует заметить, что при любых МК и ОЕ и неразвернутом угле hk построение искомого треугольника возможно. Прямую а и точку А допустимо выбирать произвольно. Таким образом, имеется бесконечное множество треугольников, которые соответствуют условию задания. Все эти треугольники будут взаимно равны, исходя из первого признака равенства треугольников (по двум сторонам и углу между ними). В связи с этим, можно заключить, что данная задача имеет единственное решение.

При построении треугольника по стороне и двум углам, которые к ней прилегают, можно воспользоваться линейкой и циркулем.

К примеру, по условию задачи имеется отрезок МК, а также пара углов 1 и 2. Требуется изобразить такой треугольник АВС, в котором:

АВ = МК, ВАС = 1, АВС = 2

Построении треугольника по стороне и двум углам

 

Решение задачи следует начинать с построения прямой а при помощи обычной линейки. Используя циркуль, можно отметить на этой прямой отрезок АВ, который совпадает по длине с отрезком МК. На прямой а нужно поставить точку А. После измерения циркулем отрезка МК требуется изобразить окружность, центр которой совпадает с точкой А, а радиус равен МК. Окружность не обязательно строить полностью, достаточно дуги, представленной на рисунке красным цветом. Точка В будет обозначать точку пересечения окружности и прямой а.

Построении треугольника по стороне и двум углам

 

Второй шаг заключается в построении угла BAF, который идентичен углу 1. При этом, используя циркуль, следует изобразить окружность с радиусом МК и центром, совпадающим с вершиной угла 1. На изображении дуга показана красным цветом. Точки, в которых пересекаются окружность и стороны угла 1, можно обозначить за N и P.

Построении треугольника по стороне и двум углам

 

Циркулем удобно измерить длину отрезка NP. Далее остается построить окружность с радиусом, соответствующим данному отрезку, и центром в точке В. На изображении такая окружность выделена синим цветом. Точкой F можно обозначить точку, в которой пересекается окружность радиуса NP с окружностью радиуса МК с центром в точке А.

Построении треугольника по стороне и двум углам

 

Затем необходимо построить луч АF, используя линейку.

Построении треугольника по стороне и двум углам

 

На следующем шаге можно изобразить угол АВD, который соответствует углу 2. В процессе следует, применяя циркуль, начертить окружность с радиусом МК и центром, который соответствует вершине угла 2. На рисунке дуга данной окружности обозначена красным цветом. Точки О и Е соответствуют местам пересечений построенной окружности со сторонами угла 2.

Построении треугольника по стороне и двум углам

 

Затем нужно циркулем построить окружность с радиусом МК и центром в точке В, которая отмечена красным цветом на изображении. Далее необходимо определить, какова длина отрезка ОЕ, и построить окружность с соответствующим радиусом и центром в точке А. На рисунке дуга этой окружности выделена синим цветом. Точка D является точкой, в которой пересекаются построенные окружности.

Построении треугольника по стороне и двум углам

 

С помощью линейки нужно отметить луч BD.

Построении треугольника по стороне и двум углам

 

Точку, в которой пересекаются лучи AF и BD, можно обозначить С. В результате построен треугольник АВС, который соответствует следующим условиям:

АВ = МК, ВАС = 1, АВС = 2

Можно сделать вывод, что изображенный треугольник является искомым.

Построении треугольника по стороне и двум углам

 

Примечание

Рассмотренный пример не во всех случаях будет иметь решение. К примеру, согласно теореме о сумме углов треугольника: сумма углов любого треугольника составляет 180 градусов. Следовательно, два угла по условию в сумме должны быть меньше, чем 180 градусов. В противном случае, нельзя построить треугольник, углы которого равнялись бы данным углам.

Решение задач на построение треугольника по трем элементам

Задача 1

Существует некая сторона треугольника ВС, к которой прилегают углы alpha и beta. Необходимо построить треугольник по трем известным элементам.

Решение

Пусть углы треугольника АВС соответствуют следующему условию:

К = alpha

М = beta

Можно составить план действий, согласно стандартному алгоритму:

  1. Построить прямую а и отмерить на ней отрезок ВС.
  2. Начертить угол К с вершиной В на стороне ВС.
  3. Изобразить угол М с вершиной С на стороне ВС.
  4. На пересечении лучей изображенных углов получить точку А, соединить ее с точками С и В для получения отрезков АС и АВ.

Построим треугольник:

Задач на построение треугольника по трем элементам

 

В процессе доказательства следует рассмотреть изображение треугольника. Можно прийти к выводу, что условия задачи выполнены. Заданные углы могут быть построены и в противоположную сторону, соответственно можно изобразить второй треугольник. Однако, так как он аналогичен первому, можно заключить, что задача имеет единственное решение. В том случае, когда углы alpha и beta равны или больше, чем 180 градусов, задача не имеет решения.

Задача 2

Даны три стороны треугольника АВ, АС и ВС. Необходимо построить треугольник.

Решение

В процессе анализа условий задания можно составить план решения:

  1. Начертить прямую а и отметить на ней отрезок АВ.
  2. Используя циркуль, изобразить пару окружностей. Одна из них имеет радиус АС и центр в точке А, а вторая — радиус ВС и центр в точке В.
  3. Точку, где пересекаются данные окружности, можно обозначить С. Далее следует соединить точку С с точками А и В. В результате получаются отрезки АС и ВС.
  4. Затем остается построить треугольник.

Задач на построение треугольника по трем элементам

 

Полученная геометрическая фигура соответствует условиям задачи. Изображенные окружности обладают двумя точками пересечения, что позволяет построить еще один треугольник. Он будет аналогичен первому, поэтому у задачи есть одно единственное решение. С учетом того, что сумма двух сторон треугольника всегда больше третьей его стороны, можно заключить следующее: при невыполнении данного условия для заданных сторон задача не будет иметь решение.

Задача 3

У треугольника имеется две стороны АВ и АС, а также угол alpha между ними. Требуется изобразить треугольник.

Решение

Порядок действий следующий:

  • начертить прямую а, отметить отрезок АВ;
  • отмерить угол МАВ, соответствующий углу alpha;
  • отложить отрезок АС на прямой АМ;
  • начертить третью сторону треугольника СВ, соединив точки В и С.

В результате получится треугольник:

Задач на построение треугольника по трем элементам

 

Согласно изображенной геометрической фигуре, можно сделать вывод о выполнении условий задания. Прямая а является бесконечной. По этой причине можно начертить множество подобных треугольников. Исходя из того, что все они будут одинаковы, сделаем вывод о единственном решении задачи. В том случае, когда угол alpha будет равен или больше 180 градусов, у задания не будет ответа, так как сумма всех углов треугольника должна составлять 180 градусов.

Источник

Геометрия

7 класс

Урок № 27

Построение треугольника по трём элементам

Перечень вопросов, рассматриваемых в теме:

  • Задачи на построение циркулем и линейкой.
  • Алгоритмы решения простейших задач на построение.
  • Способы решения задач на построение треугольника по трём заданным элементам.
  • Этапы решения задач на построение: анализ, построение, доказательство, исследование.

Тезаурус:

Задачей на построение называется предложение, указывающее, по каким данным, какую геометрическую фигуру требуется построить, чтобы эта фигура удовлетворяла определённым условиям.

Построение треугольника по трём элементам:

  • по 2 сторонам и углу между ними;
  • по стороне и двум прилежащим к нему углам;
  • по трём сторонам.

Задачи на построение:

  • позволяют моделировать те или иные практические ситуации
  • устанавливают связь между геометрией и черчением, геометрией и рисованием.

Основная литература:

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Дополнительная литература:

  1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
  2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
  3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
  4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
  5. Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения

Построение треугольника по трём элементам.

Чтобы построить треугольник, нужно уметь строить:

1. Отрезок, равный данному.

2. Угол, равный данному.

Любая задача на построение включает в себя четыре основных этапа.

Анализ: предположить, что задача решена, сделать чертеж от руки искомой фигуры, составить план решения задачи.

Построение: описать способ построения.

Доказательство: доказать, что построенная фигура или множество точек – искомые.

Исследование: выяснить, всегда ли построение возможно.

Задача 1.

Построить треугольник по трём заданным сторонам.

Условие:

Дано:

Построить: ∆A1B1C1 = ∆ABC

Схема построения:

Задача 2.

Построить треугольник по двум сторонам и углу между ними.

Условие:

Дано:

Построить: ∆A1B1C1 такой, что A1B1 = AB, A1C1 = AC, ∠B1A1C1 = ∠BAC.

Схема построения:

Задача 3.

Построить треугольник по стороне и двум прилежащим к ней углам.

Условие:

Дано:

Построить: ∆A1B1C1 такой, что A1B1 = AB, ∠A1 = ∠A, ∠B1 = ∠B.

Схема построения:

Разбор решения заданий тренировочного модуля.

Задача 1. Найдите расстояние от вершины В до прямой АС.

Дано. В треугольнике АВС: АВ = ВС = 10 см, ∠АВС = 120°.

Решение.

∆АВС – равнобедренный. ВН – расстояние от точки В до прямой АС, т. е. ВН ⊥ АС. В равнобедренном треугольнике высота является биссектрисой. ∠АВН = 120°: 2 =60°, значит, ∠А = 30°. Против угла 30° лежит катет ВН равный половине гипотенузы АВ. Значит, ВН = 10 : 2 = 5 см.

Ответ: 5 см расстояние от вершины В до прямой АС.

Задача 2. Построить прямоугольный треугольник по гипотенузе и острому углу.

Дано: отрезок р, угол α.

Решение.

  1. Построим ∠В = α.
  2. Проведем окружность с центром В и радиусом р.
  3. С – точка пересечения окружности и угла.
  4. Построим перпендикуляр к другой стороне угла.
  5. ∆АВС – искомый.

Задача 3. Построить треугольник по стороне, прилежащему к ней углу и биссектрисе треугольника, проведенной из вершины этого угла.

Дано: отрезки р и q, угол α.

Решение.

Требуется построить треугольник АВС, у которого одна из сторон, например АС = р, ∠А =α , а биссектриса АD = q.

Построение:

1) Построим ∠А = α.

2) Отложим отрезок АС = р.

3) Построим биссектрису АD угла А.

4) Отложим отрезок АD = q.

5) В – точка пересечения АВ и СD.

∆АВС – искомый.

Ответ: ∆АВС – искомый.

Источник

Конспект урока: Построение треугольников по трем элементам

Геометрические построения


Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трём элементам

План урока

  • Расстояние от точки до прямой;
  • Расстояние между параллельными прямыми;
  • Построение треугольника по трём элементам.

Цели урока

  • Знать, что называют расстоянием от точки до прямой;
  • Знать, что называют расстоянием между параллельными прямыми;
  • Уметь находить расстояние от точки до прямой, между параллельными прямыми при решении задач;
  • Уметь выполнять построение треугольника по трём элементам.

Разминка

  • Как найти расстояние между двумя точками?
  • Отметьте точку в любом месте тетрадного листа. С помощью линейки измерьте расстояние до границы тетрадного листа. Объясните, длину какого отрезка вы измерили?
  • Что называется перпендикуляром, проведённым из данной точки к данной прямой?

Расстояние от точки до прямой


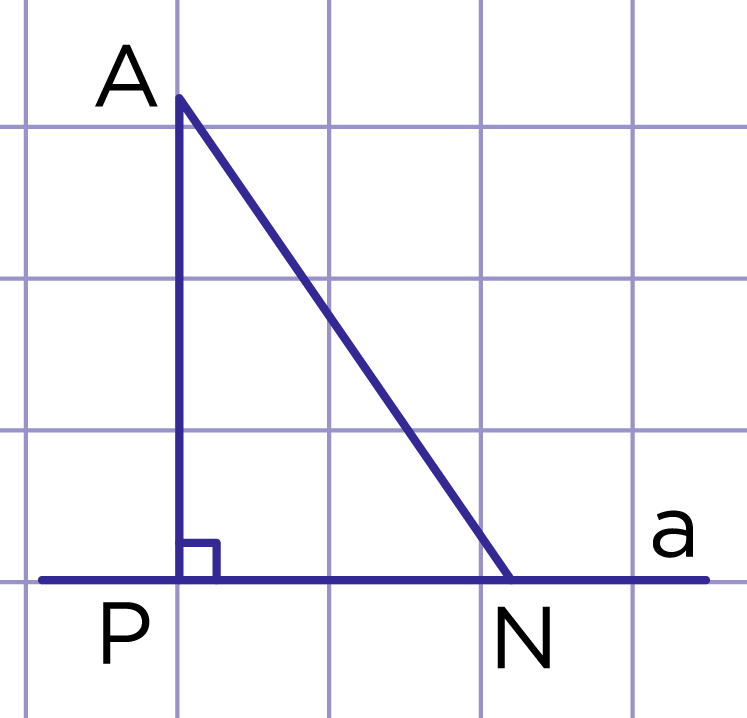
Рис. 1. АР – перпендикуляр, АN – наклонная, РN – проекция наклонной

Пусть дана прямая a и точка A, не принадлежащая этой прямой. Опустим перпендикуляр из точки A к прямой a, точка P – основание перпендикуляра (рис. 1).

На прямой a отметим любую точку N, не совпадающую с точкой P. Проведём отрезок AN – это наклонная. Отрезок PN называется проекцией наклонной AN на прямую a.

Перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.

Длина перпендикуляра, проведённого из точки к прямой, называется
расстоянием от этой точки до прямой
.

Расстояние между параллельными прямыми

Теорема (свойство параллельных прямых)

Все точки каждой из двух параллельных прямых равноудалены от другой прямой

Доказательство


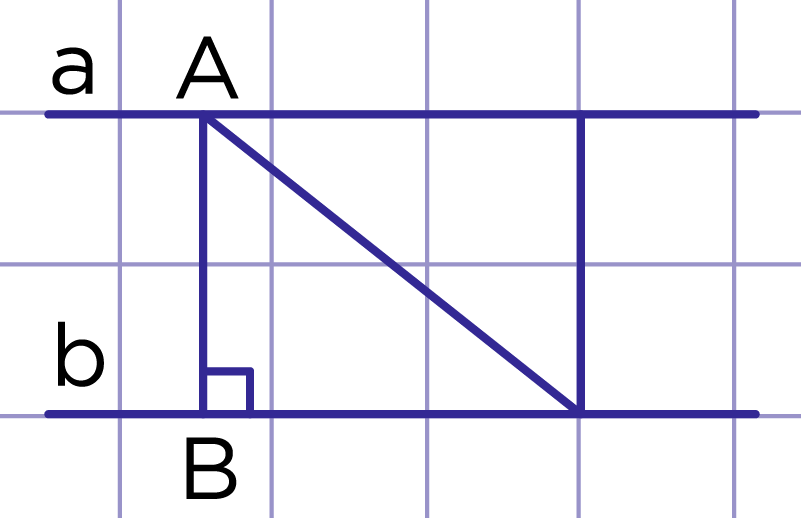
Рис. 2. Теорема (свойство параллельных прямых)

Рассмотрим прямые a и b, известно, что a∥b. Пусть A∈a. Проведём AB так, что AB⊥b (рис. 2). Надо доказать, что расстояние от любой точки X (X∈a) до прямой b равно AB. 

Проведём XP, XP⊥b (рис. 3). Если XP⊥b, a∥b, значит, XP⊥a.


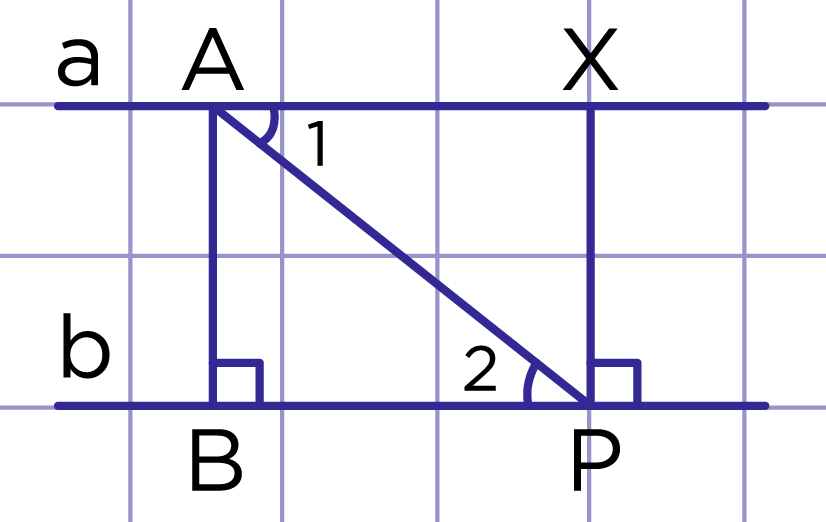
Рис. 3. Точка Х – любая

Рассмотрим треугольники ABP и AXP. AP – общая, ∠1=∠2 как накрест лежащие при пересечении параллельных прямых a и b секущей AP. Тогда ∆ABP=∆AXP по гипотенузе и острому углу. AB=XP как соответствующие элементы в равных треугольниках.

Получили, что любая точка X, лежащая на прямой a, находится на расстоянии AB от прямой b.

Очевидно, что все точки прямой a находятся на таком же расстоянии от прямой b.

Теорема доказана.

Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется
расстоянием между этими (параллельными) прямыми
.

Расстояние между параллельными прямыми равно наименьшему из расстояний от точек одной прямой до точек другой прямой.

Замечание (утверждение, обратное теореме):


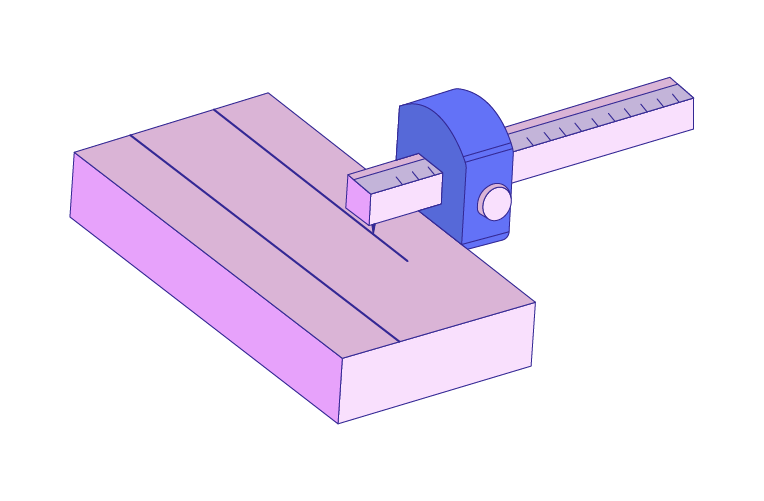
Рис. 4. Рейсмус

Все точки плоскости, расположенные по одну сторону от данной прямой а и равноудалённые от неё, лежат на прямой, параллельной данной.

Из доказанной теоремы и ей обратной следует, что множество всех точек плоскости, находящихся на данном расстоянии от данной прямой и лежащих по одну сторону от нее, есть прямая параллельная данной.


Рейсмус
 – инструмент, принцип работы которого основан на применении этого свойства. Если передвигать рейсмус вдоль края бруска, то металлическая игла прочертит отрезок прямой, параллельной краю бруска.

Пример 1


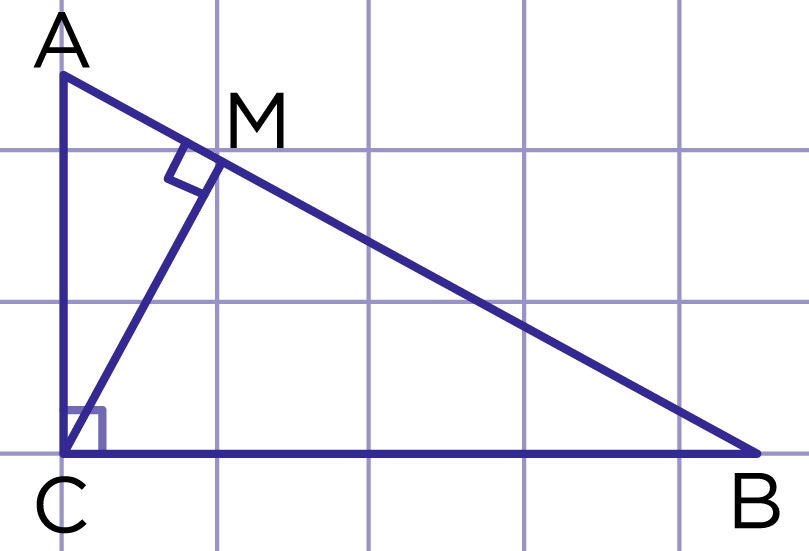
Рис. 5. Пример 1

В прямоугольном треугольнике ABC катет AC равен 3 см, катет BC равен 7 см (рис. 5). Найдите расстояние: 

  1. от точки A до прямой BC;
  2. от точки B до прямой AC;
  3. может ли расстояние от точки C до гипотенузы быть равным 5 см?

Решение

  1. Расстояние от точки A до прямой BC – это длина отрезка AC, AC⊥BC, AC=3 см.
  2. Расстояние от точки B до прямой AC – это длина отрезка BC, BC⊥AC, BC=7 см.
  3. Расстояние от точки C до прямой AB – это длина отрезка CM, CM⊥AB. Рассмотрим треугольник ACM, он прямоугольный, AC – гипотенуза, CM – катет. Гипотенуза всегда больше катета. AC=3 см, тогда CM не может быть равным 5 см.

Ответ: 

  1. 3 см;
  2. 7 см;
  3. нет.

Упражнение 1


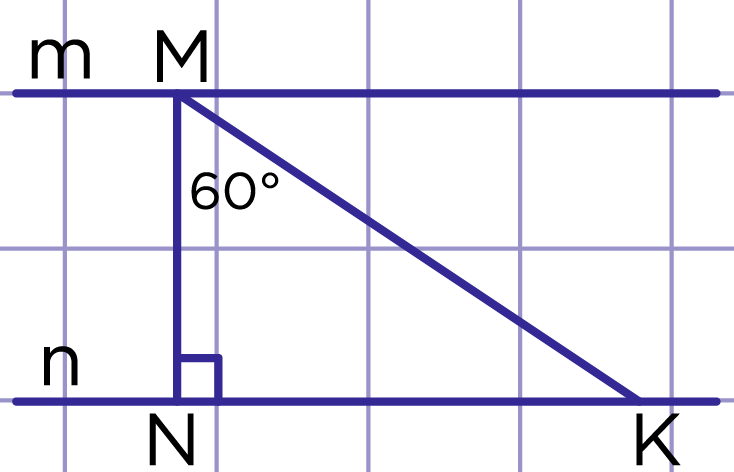
Рис. 6. Упражнение 1

1. Расстояние от точки A до прямой p равно 4 см, расстояние от точки B до прямой p равно 5 см (точки A и B лежат по разные стороны от прямой p). Может ли расстояние между точками A и B быть равным 8 см?

2. На рисунке 6 изображены параллельные прямые m и n, MK=10 см, ∠KMN=60°. Найдите расстояние между прямыми m и n.

Построение треугольника по трём элементам

Все построения выполняются с помощью двух инструментов: циркуля и линейки без масштабной шкалы, т. е. без делений.

Для решения задач на построение треугольника необходимо вспомнить пять простейших задач на построение:

  1. построение отрезка, равного данному;
  2. построение угла, равного данному;
  3. построение биссектрисы угла;
  4. построение перпендикулярных прямых;
  5. построение середины отрезка.


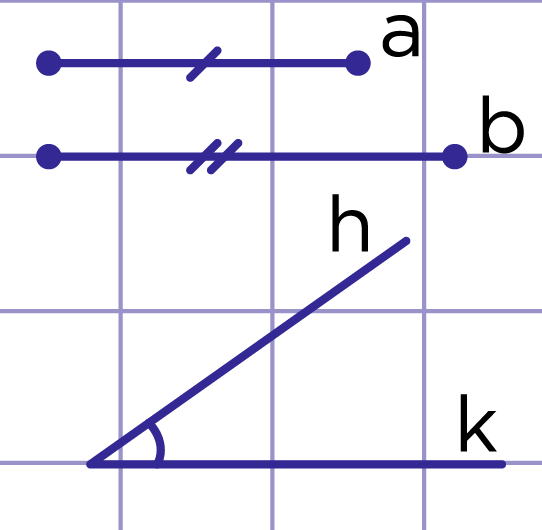
Рис. 7. Задача 1

Задача 1

Построить треугольник по двум сторонам и углу между ними.

Решение

По условию даны два отрезка и угол (рис. 7). Надо построить треугольник ABC такой, что AC=b, BC=a, ∠C=∠hk.


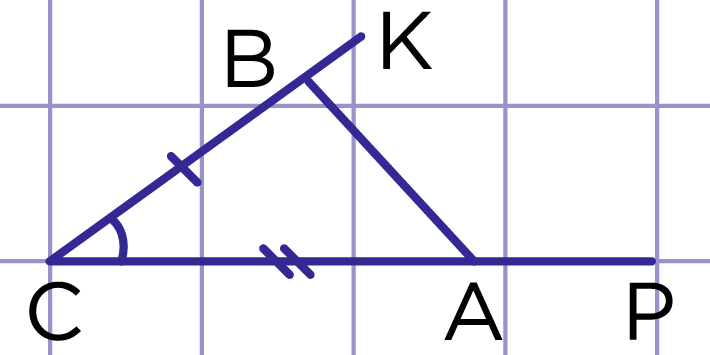
Рис. 8. Задача 1

  1. Построим ∠PCK=∠hk.
  2. На луче CK отложим отрезок CB, равный a.
  3. На луче CP отложим отрезок CA, равный b.
  4. Проведём отрезок AB.

∆ABC – искомый (рис. 8).                                                                                                         


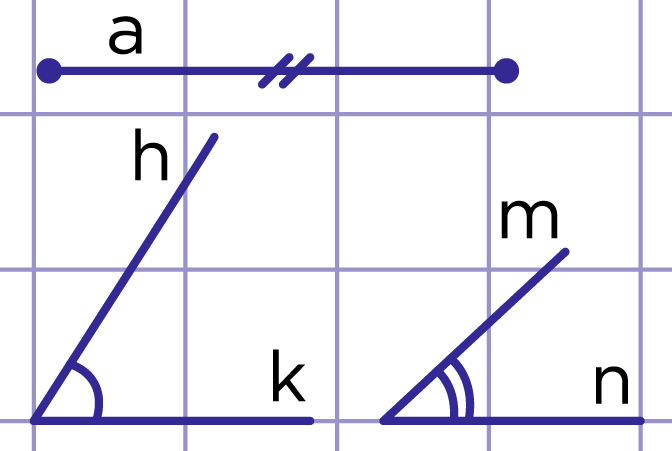
Рис. 9. Задача 2

Задача 2

Построить треугольник по стороне и двум прилежащим к ней углам.

Решение


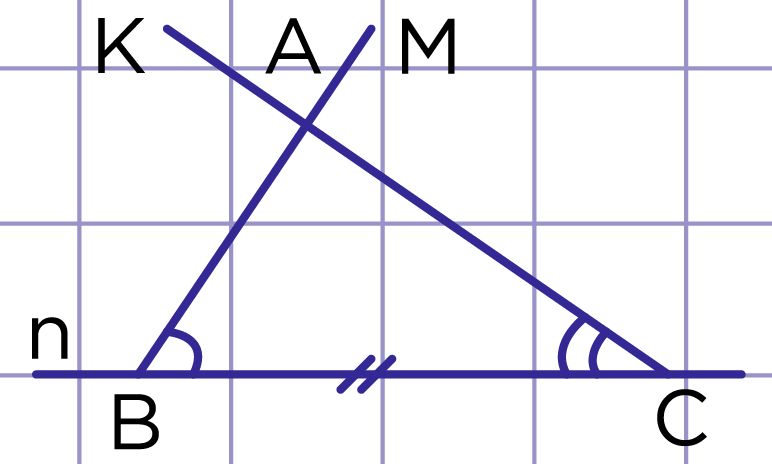
Рис. 10. Задача 2

По условию даны отрезок и два угла (рис. 9). Надо построить треугольник ABC такой, что BC=a, ∠B=∠hk, ∠C=∠mn.

  1. Проведём прямую n, на ней отложим отрезок BC, равный a.
  2. Построим ∠MBC, равный ∠hk.
  3. Построим ∠BCK, равный ∠mn.
  4. Точка A – точка пересечения лучей BM и CK.

∆ABC – искомый (рис. 10).


Рис. 11. Задача 3

Задача 3

Построить треугольник по трем его сторонам.                                                                    

Решение

По условию даны три отрезка (рис. 11). Надо построить треугольник ABC такой, что AB=c, BC=a, AC=b.


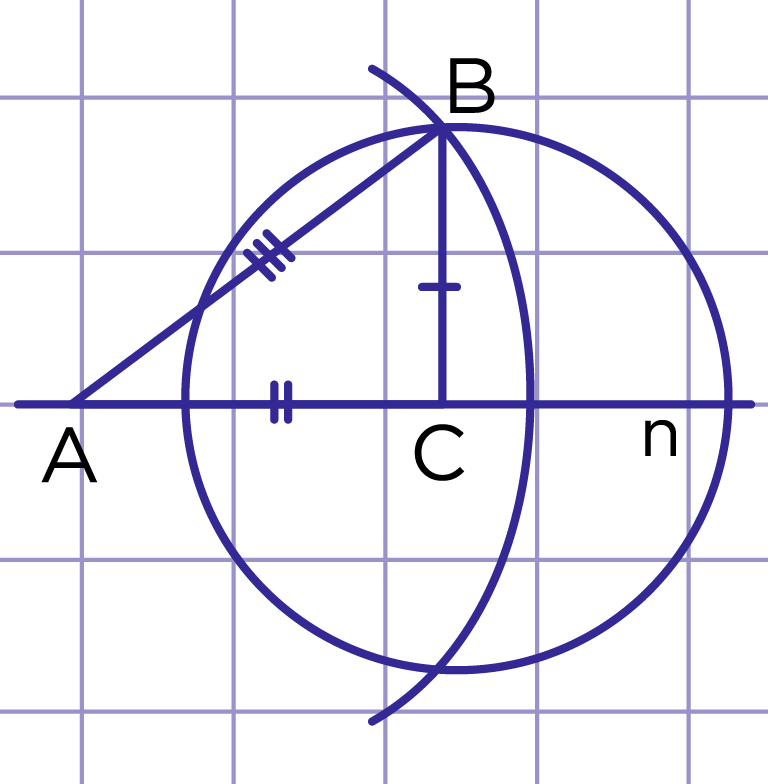
Рис. 12. Задача 3

  1. Проведём прямую n, на ней отложим отрезок AC=b.
  2. Построим окружность с центром в точке A и радиусом c.
  3. Построим окружность с центром в точке C и радиусом a.
  4. Точка B – одна из точек пересечения окружностей.

∆ABC – искомый (рис. 12).

Задача 3 не всегда имеет решение, т. к. должно выполняться неравенство треугольника.

Упражнение 2

  1. Постройте прямоугольный треугольник по катету и гипотенузе.
  2. Постройте равнобедренный треугольник по боковой стороне и углу при основании.

Контрольные вопросы

1. Что называется расстоянием от точки до прямой?

2. Что называется расстоянием между двумя параллельными прямыми? 

3. Запомните алгоритмы решения трёх основных задач на построение треугольника. 

Ответы

Упражнение 1


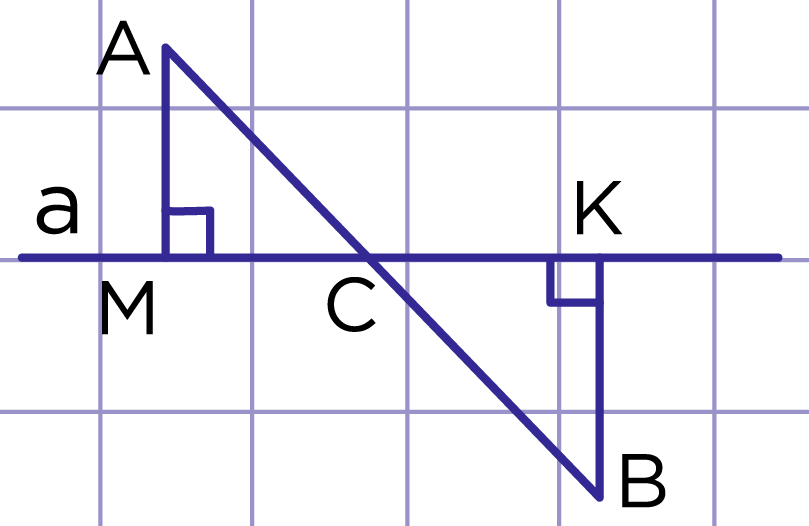
Рис. 13. Упражнение 1. Ответ

1. Нет (рис. 13)

AB=AC+BC, 

AC – гипотенуза в треугольнике ACM, 

AC больше катета, значит, AC>4 см; 

BC – гипотенуза в треугольнике BCK, BC больше катета, значит, BC>5 см. Получили, что AC>8 см.

2. 5 см.

Упражнение 2

1. Построение:


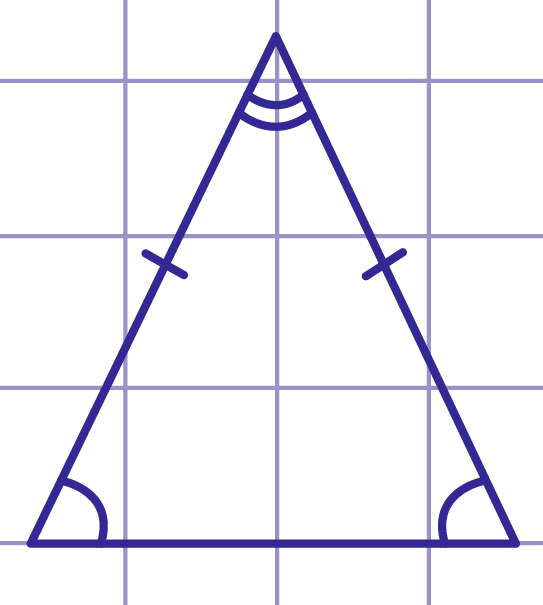
Рис. 14. Упражнение 2. Ответ

  1. построить прямой угол (построение перпендикулярных прямых);
  2. на одной стороне прямого угла от вершины отложить отрезок, равный катету;
  3. построить окружность, центром которой будет другой конец катета, радиус равен гипотенузе;
  4. точка пересечения окружности и второй стороны прямого угла будет третьей вершиной искомого треугольника.


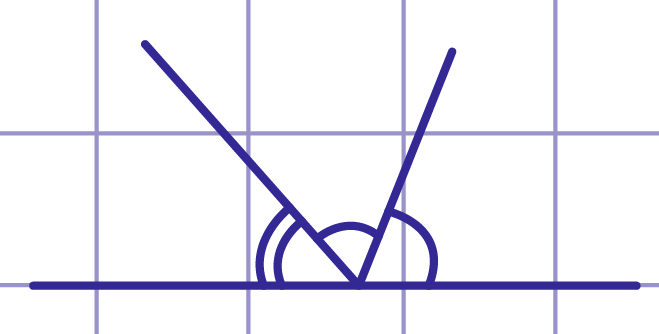
Рис. 15. Упражнение 2. Ответ

2. Решение задачи начнём с анализа. Допустим, что такой треугольник построен (рис. 14). 

Построение сводится к построению треугольника по стороне и двум прилежащим к ней углам или к построению треугольника по двум сторонам и углу между ними, но сначала надо построить угол, лежащий против основания, применяя теорему о сумме углов треугольника (рис. 15).

Предыдущий урок

Измерение углов

Общие геометрические сведения

Следующий урок

Задачи на построение

Геометрические построения

Источник

Как найти площадь треугольника по координатам его вершин?

1способ:

Найти длины трёх сторон треугольника и вычислить площадь по формуле Герона. Способ удобен, если длины сторон являются целыми числами. В противном случае предстоят громоздкие вычисления.

2 способ:

вывести формулу для нахождения площади и использовать её для вычисления.

Утверждение

Площадь треугольника ABC с вершинами в точках A(x1;y1), B(x2;y2), C(x3;y3) можно вычислить с помощью формулы

    [S_{Delta ABC} = frac{1}{2}left| {(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )} right|.]

Доказательство:

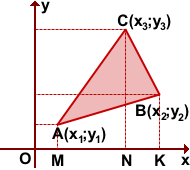ploshchad-treugolnika-po-koordinatamРассмотрим треугольник ABC,

A(x1;y1), B(x2;y2), C(x3;y3)

Опустим перпендикуляры из вершин треугольника на координатные оси.

    [S_{Delta ABC} = S_{MACN} + S_{NCBK} - S_{MABK} ]

    [S_{MACN} = frac{{MA + CN}}{2} cdot MN = frac{{y_1 + y_3 }}{2} cdot (x_3 - x_1 ),]

    [S_{NCBK} = frac{{NC + BK}}{2} cdot NK = frac{{y_3 + y_2 }}{2} cdot (x_2 - x_3 ),]

    [S_{MABK} = frac{{MA + BK}}{2} cdot MK = frac{{y_1 + y_2 }}{2} cdot (x_2 - x_1 ).]

    [S_{Delta ABC} = ]

    [= frac{{y_1 + y_3 }}{2} cdot (x_3 - x_1 ) + frac{{y_3 + y_2 }}{2} cdot (x_2 - x_3 ) - frac{{y_1 + y_2 }}{2} cdot (x_2 - x_1 ) = ]

    [= frac{1}{2}[(y_1 + y_3 )(x_3 - x_1 ) + (y_3 + y_2 )(x_2 - x_3 ) - (y_1 + y_2 )(x_2 - x_1 )] = ]

    [= frac{1}{2}[x_3 y_1 - x_1 y_1 underline { + x_3 y_3 } - x_1 y_3 + x_2 y_3 underline { - x_3 y_3 } + x_2 y_2 - x_3 y_2 - ]

    [- x_2 y_1 + x_1 y_1 - x_2 y_2 + x_1 y_2 ] =]

    [= frac{1}{2}[(x_2 y_3 - x_2 y_1 ) + ( - x_1 y_3 + x_1 y_1 ) + (x_1 y_2 - x_1 y_1 ) + ]

    [+ ( - x_3 y_2 + x_3 y_1 )] = ]

    [= frac{1}{2}[x_2 (y_3 - y_1 ) - x_1 (y_3 - y_1 ) + x_1 (y_2 - y_1 ) - x_3 (y_2 - y_1 )] = ]

    [= frac{1}{2}[(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )].]

С учетом вариантов взаимного расположения точек A, B и C формула для вычисления площади треугольника по координатам его вершин приобретает вид:

    [ S_{Delta ABC} = frac{1}{2}left| {(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )} right|. ]

Что и требовалось доказать.

3 способ:

Найти длины двух сторон и косинус угла между ними и вычислить площадь треугольника через стороны и синус угла между ними.

4 способ:

Найти длину и уравнение одной стороны треугольника и длину высоты, проведённой к этой стороне. Вычислить площадь через сторону и высоту.

Рассмотрим эти способы на конкретном примере.

Найти площадь треугольника, вершины которого имеют координаты A(-1;-3), B(3;4), C(5;-5).

1 способ:

Находим длины сторон треугольника ABC.

    [AB = sqrt {(x_B - x_A )^2 + (y_B - y_A )^2 } ]

    [ AB = sqrt {(3 - ( - 1))^2 + (4 - ( - 3))^2 } = sqrt {16 + 49} = sqrt {65} ;]

    [AC = sqrt {(x_C - x_A )^2 + (y_C - y_A )^2 } ]

    [AC = sqrt {(5 - ( - 1))^2 + ( - 5 - ( - 3))^2 } = sqrt {36 + 4} = sqrt {40} ;]

    [BC = sqrt {(x_C - x_B )^2 + (y_C - y_B )^2 } ]

    [BC = sqrt {(5 - 3)^2 + ( - 5 - 4)^2 } = sqrt {4 + 81} = sqrt {85} .]

Поскольку длины сторон выражены иррациональными числами, вычислять площадь треугольника по формуле Герона — не самый лучший способ.

2 способ:

Подставляем в формулу x1=-1, y1=-3, x2=3, y2=4, x3=5, y3=-5:

    [S_{Delta ABC} = frac{1}{2}left| {(3 - ( - 1))( - 5 - ( - 3)) - (5 - ( - 1))(4 - ( - 3))} right| = ]

    [= frac{1}{2}left| {4 cdot ( - 2) - 6 cdot 7} right| = frac{1}{2} cdot 50 = 25.]

3 способ:

Угол A образован векторами AC и AB. Отсюда

    [ cos angle A = frac{{overrightarrow {AB} cdot overrightarrow {AC} }}{{left| {overrightarrow {AB} } right| cdot left| {overrightarrow {AC} } right|}} ]

Находим координаты векторов:

    [overrightarrow {AB} (x_B - x_A ;y_B - y_A )]

    [overrightarrow {AB} (3 - ( - 1);4 - ( - 3))]

    [overrightarrow {AB} (4;7);]

    [overrightarrow {AC} (x_C - x_A ;y_C - y_A )]

    [overrightarrow {AC} (5 - ( - 1); - 5 - ( - 3))]

    [overrightarrow {AC} (6; - 2).]

Скалярное произведение

    [overrightarrow {AB} cdot overrightarrow {AC} = 4 cdot 6 + 7 cdot ( - 2) = 10.]

Длины AB и AC уже знаем:

    [left| {overrightarrow {AB} } right| = sqrt {65} ,left| {overrightarrow {AC} } right| = sqrt {40} .]

    [cos angle A = frac{{10}}{{sqrt {65} cdot sqrt {40} }} = frac{{10}}{{sqrt {5 cdot 13} cdot sqrt {5 cdot 4 cdot 2} }} = ]

    [= frac{{10}}{{5 cdot 2sqrt {26} }} = frac{1}{{sqrt {26} }}.]

Синус и косинус одного угла связаны соотношением:

    [sin ^2 angle A + cos ^2 angle A = 1]

Синус угла от 0° до 180° является положительным числом, поэтому

    [sin angle A = sqrt {1 - cos ^2 angle A} ]

    [sin angle A = sqrt {1 - frac{1}{{26}}} = sqrt {frac{{25}}{{26}}} = frac{5}{{sqrt {26} }}.]

Отсюда

    [S_{Delta ABC} = frac{1}{2} cdot AB cdot AC cdot sin angle A,]

    [S_{Delta ABC} = frac{1}{2} cdot sqrt {65} cdot sqrt {40} cdot frac{5}{{sqrt {26} }} = 25.]

4 способ:

Найдём уравнение прямой AB. Подставляем координаты A и B в уравнение y=kx+b:

    [left{ begin{array}{l} - 3 = k cdot ( - 1) + b \ 4 = k cdot 3 + b \ end{array} right.]

Отсюда k=7/4, b=-5/4

    [y = frac{7}{4}x - frac{5}{4},4y = 7x - 5,]

    [7x - 4y - 5 = 0.]

Найдём расстояние от точки C до прямой AB:

    [d = frac{{left| {7 cdot 5 - 4 cdot ( - 5) - 5} right|}}{{sqrt {7^2 + 4^4 } }} = frac{{50}}{{sqrt {65} }}.]

Это расстояние равно высоте треугольника, проведённой из вершины C к стороне AB. Отсюда

    [S_{Delta ABC} = frac{1}{2} cdot AB cdot d = frac{1}{2} cdot sqrt {65} cdot frac{{50}}{{sqrt {65} }} = 25.]

Источник

Добавить комментарий