Найдите отношение площадей треугольников PQR и ABC, если PQ = 16 см, QR = 20 см, PR = 28 см, АВ= 12 см, ВС = 15 см, АС = 21 см.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,283
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,084
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем  .
.



 |
(1) |
 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
 .
.
Пример 1. Известны стороны треугольника ABC:  Найти
Найти  (Рис.1).
(Рис.1).
Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:
 .
.
 .
.
Далее, из формулы
 .
.
 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
 .
.
Пример 2. Известны две стороны треугольника ABC:  и
и  (Рис.2). Найти сторону c и углы A и B.
(Рис.2). Найти сторону c и углы A и B.
Решение. Иcпользуя теорму косинусов найдем сторону c:
 ,
,
Из формулы (3) найдем cosA:
 .
.
Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:
 .
.
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC:  и углы
и углы  (Рис.3). Найти стороны b и c и угол С.
(Рис.3). Найти стороны b и c и угол С.
Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:


Найдем сторону с. Из теоремы синусов имеем:
№ 36. Треугольники АВС и PQR равны. Известно, что АВ = 5 см, ВС = 6 см, АС = 7 см. Найдите стороны треугольника PQR. Объясните ответ.
По условию треугольники АВС и PQR равны, значит, равны и их соответствующие стороны, тогда, AC = PR, АВ = PQ, BC =
Получим: PQ = 5 см, PR = 7 см, QR = 6 см. Ответ: PQ = 5 см, PR = 7 см, QR = 6 см.
 Решебник по геометрии за 7 класс (А.В. Погорелов, 2001 год),
Решебник по геометрии за 7 класс (А.В. Погорелов, 2001 год),
задача №36
к главе «§ 1. Основные свойства простейших геометрических фигур».
[spoiler title=”источники:”]
http://matworld.ru/geometry/reshenie-treugolnikov.php
http://5terka.com/node/2896
[/spoiler]
Всего ответов: 1
Так как ∠PQM = ∠RQM, то QM – биссектриса ∠PQR.
Так как PM = MR, то QM – медиана к стороне PR.
Очевидно, раз QM является биссектрисой и медианой, то QM⊥PR.
Треугольники ΔPQM и ΔRQM равны по стороне QM и двум прилегающим к ней углам. Следовательно PQ = QR и ΔPQR – равнобедренный.
На основании полученных данных сказать что-то о величинах углов PQR, PRQ и QPR нельзя, так как треугольник PRQ может быть как половиной квадрата с углом Q = 90°, так и половиной ромба (см. рис.)
Диагонали ромба пересекаются под прямым углом, делятся точкой пересечения пополам и являются биссектрисами для своих углов.
Regent1828_zn
БОГ

|
Варианты ответов: (А) 50° (Б) 60° (В) 65° (Г) 70° (Д) 80°
Чтобы решить эту задачу, надо понимать, что на рисунке изображён равнобедренный треугольник, у которого боковые стороны равны, а значит равны и острые углы у соединения основания и его сторон. Если это не так, и углы у его основания разные, то боковые стороны треугольника не могут быть равны. Исходя из этих утверждений, можно принять следующие выражения: 1) для углов: L(QPR)=L(QSR)=20 градусов; для вычисления основания: PR=RS, PS=2*PR. Этот треугольник разбит на 2 части биссектрисой угла PQS. Найдём этот угол: L(PQS)=180-L(QPR)-L(QSR)=180-20-20=140 градусов. Если малый треугольник равнобедренный, то L(PQR)=L(PRQ)=(180-20)/2=80 градусов. Тогда угол QRS равен L(QRS)=140-80=60 градусов (вариант Б). автор вопроса выбрал этот ответ лучшим
Ведрусс58 3 года назад Треугольник PQS равнобедренный (PQ=QS), следовательно углы при вершинах P и S равны, т.е. угол QPS= углу QSP=20 гр. Тогда угол PQS=180-(20+20)=140 гр (сумма углов треугольника=180 гр). Треугольник PQR по условиям задачи тоже равнобедренный (PQ=PR), значит угол PQR= QRP=(180-20)/2=80 гр. Тогда угол RQS=140-80=60 гр. Ответ: (Б) 60 гр. Знаете ответ? |
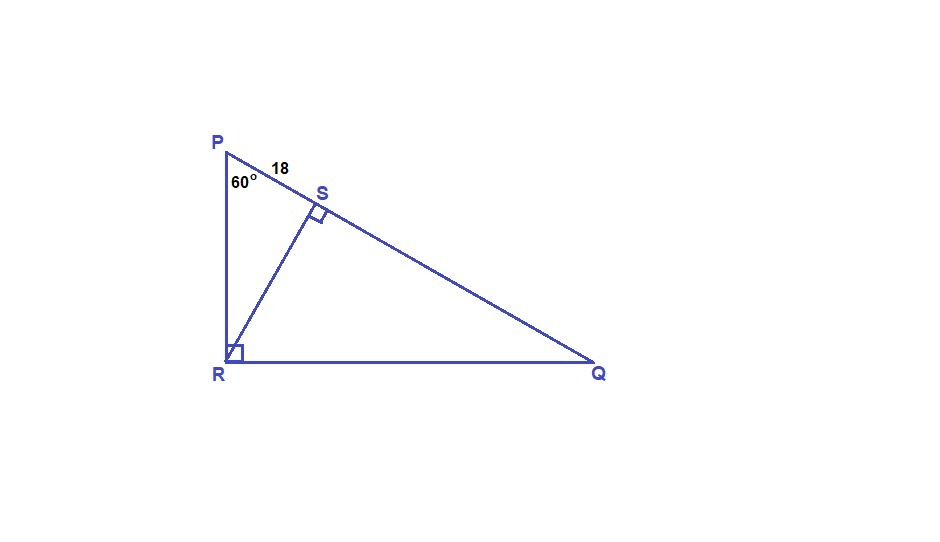
В условии опечатка: ∠PRQ = 90°.
Сумма острых углов прямоугольного треугольника равна 90°.
ΔPRS: ∠PSR = 90°, ∠SPR = 60°, ⇒
∠PRS = 90° – 60° = 30°
PR = 2PS = 2 · 18 = 36 м по свойству катета, лежащего против угла в 30°.
ΔPRQ: ∠PRQ = 90°, ∠RPQ = 60°, ⇒
∠PQR = 90° – 60° = 30°
PQ = 2PR = 2 · 36 = 72 м по свойству катета, лежащего против угла в 30°.
QS = PQ – SP = 72 – 18 = 54 м
Приложения:
- Учебники
- 5 класс
- Математика 👍
- Мерзляк
- №147

авторы: Мерзляк, Полонский, Якир.
издательство: “Вентана-Граф”
Посмотреть глоссарий
Раздел:
- ГЛАВА 2. Сложение натуральных чисел. Свойства сложения
- §14. Треугольник и его виды
ГДЗ рабочая тетрадь №1 по математике 5 класс Мерзляк. §14. Треугольник и его виды. Номер №147
- Предыдущее
- Следующее
Определите вид треугольника.
1)
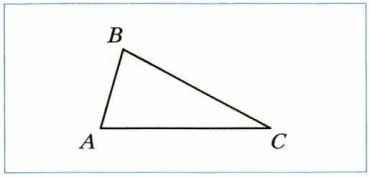
Треугольник ABC − разносторонний остроугольный
2)
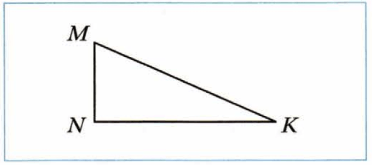
Треугольник NMK − _
3)
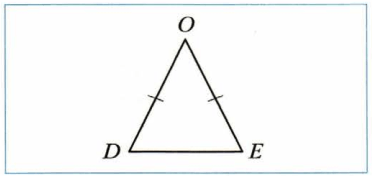
Треугольник _ − _
4)
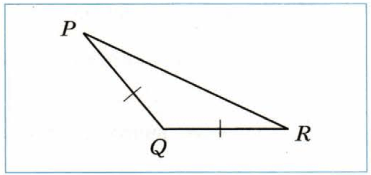
Треугольник _ − _
5)

Треугольник _ − _
6)

Треугольник _ − _

reshalka.com
ГДЗ рабочая тетрадь №1 по математике 5 класс Мерзляк. §14. Треугольник и его виды. Номер №147
Решение
![]() Получай решения и ответы с помощью нашего бота
Получай решения и ответы с помощью нашего бота
![]() Посмотреть калькулятор Вычисления в столбик
Посмотреть калькулятор Вычисления в столбик
1)

Треугольник ABC − разносторонний остроугольный
2)

Треугольник NMK − прямоугольный разносторонний.
3)

Треугольник DOE − равнобедренный остроугольный.
4)

Треугольник PQR − равнобедренный тупоугольный.
5)

Треугольник SFT − равнобедренный прямоугольный.
6)

Треугольник ACE − равносторонний.
- Предыдущее
- Следующее
Нашли ошибку?
Посмотреть глоссарий
![]()
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом

