Сегодня на уроке мы
подытожим наши знания по разделу «Соотношения между сторонами и углами
треугольника».
Прежде чем
приступить к решению задач, давайте вспомним основной теоритический материал
этой темы.
Формула для
вычисления площади треугольника:
Теорема
косинусов:
Теорема синусов:
Стороны треугольника пропорциональны синусам противолежащих углов.
Расширенная
теорема синусов:
Решить
треугольник – это значит найти все его элементы (три стороны и три угла) по
каким-нибудь известным трем элементам, определяющим треугольник.
К задачам такого
плана относятся следующие задачи: решение треугольника по трем сторонам;
решение треугольника по трем углам; решение треугольника по двум сторонам и
углу между ними; решение треугольника по двум сторонам и углу, не лежащего
между ними; решение треугольника по стороне и прилежащим к ней углам; решение
треугольников по стороне и произвольным двум углам.
Рассмотрим каждый
вид таких задач отдельно.
Начнем с решения
треугольника по трем углам.
Запишем теорему
синусов и косинусов и подумаем, с помощью какой из них можно решить
треугольник.
Обе эти теоремы
содержат длины сторон, поэтому зная только углы треугольника нельзя найти длины
сторон треугольника.
Попробуем теперь решить
треугольник по трем сторонам.
Зная длины всех
сторон треугольника, по теореме косинусов можно найти косинусы всех углов
треугольника. А, зная косинус угла, сам угол найти несложно. Для этого можно
воспользоваться либо калькулятором либо таблицами Брадиса.
Значит в этом
случае решить треугольник можно с помощью теоремы косинусов.
Рассмотрим пример.
Задача. Найти
углы треугольника, если стороны треугольника равны 25, 20, 17.
Решение.
Ответ: ;
;
.
Следующим мы
рассмотрим решение треугольника по стороне и прилежащим к ней углам.
Сразу замечаем, что
третий угол найти нетрудно, он равен разности 180° и известных углов .
Запишем теорему
синусов.
Из каждого
равенства, мы можем найти сторону треугольника. Таким образом, зная длину одной
стороны и величину двух прилежащих к ней углов, можно найти все остальные
элементы треугольника, используя теорему синусов.
Задача. Решить
треугольник, если одна из сторон треугольника равна , а углы
прилежащие к этой стороне равны и
°
соответственно.
Решение.
Ответ:
.
Задача. Решить
треугольник если две стороны его равны см и
см
соответственно, а угол между ними равен .
Решение.
Ответ:
.
Теперь давайте
посмотрим, а можно ли решить треугольник, если мы знаем две стороны и угол,
который не лежит между ними. Да, можно. Для этого по теореме синусов надо
найти второй угол треугольника, а затем и третий угол и по теореме косинусов
найти третью сторону треугольника.
То есть и в этом
случае треугольник можно решить с помощью теоремы синусов или теоремы
косинусов.
Задача. Решить
треугольник, если две его стороны равны и
, а один из
углов, не лежащий между этими сторонами, равен .
Решение.
Ответ:
.
Итак, давайте
обобщим.
Если в треугольнике
известны величины трех углов, то решить его нельзя.
Если в треугольнике
известны три стороны, то решить такой треугольник можно по теореме косинусов.
Если в треугольнике
известна сторона и два любых угла, то решить такой треугольник можно с помощью
теоремы синусов.
Если в треугольнике
известны две стороны и угол между ними, то решить такой треугольник можно с
помощью теоремы косинусов или теоремы синусов.
Если же нам
известны две стороны и любой угол, который не лежит между ними, то треугольник
можно решить по теореме синусов и косинусов.
Урок “Решение треугольников”
Краткое описание документа:
Видеоурок «Решение треугольников» демонстрирует, как в решении геометрических задач применяются полученные теоретические знания. В дальнейшем при изучении математики не раз будут возникать основные и промежуточные задачи, требующие умения применять знания из этого раздела. В видеоуроке рассматривается три вида задач по решению треугольников, а также продемонстрирован пример решения практической задачи с использованием знаний данной раздела математики. Задача видеоурока –формировать умение решать задачи по данной теме, закреплять имеющиеся знания. Ученикам может быть продемонстрирован данный материал перед тем, как начать решать задачи. Он может заменить объяснение учителя, а также может послужить наглядным пособием, сопровождающим объяснение учителя.
В видеоуроке используются анимационные эффекты, выделение цветом, голосовое сопровождение. Такое сочетание инструментов создает комплексное влияние на удержание внимания, на процессы запоминания.
Видеоурок начинается с названия темы. Далее разъясняется смысл понятия «решение треугольника». Отмечается, что данное понятие связано с нахождением всех его шести элементов – сторон и углов по заданным некоторым элементам. Предлагается рассмотреть решение типовых задач на решение треугольника. Для этого на экране строится треугольник АВС, стороны которого обозначены АВ=с, ВС=а, СА=b. На примере этого треугольника демонстрируется решение типовых задач.
Задача первого типа – на решение треугольника по двум его сторонам и углу, образованному ими. На рисунке отмечаются и выделяются цветом заданные элементы a, b, угол C. Необходимо найти недостающие углы А и В, а также оставшуюся неизвестной сторону с. Решение данной задачи требует применения теоремы косинусов, освоенной на предыдущих уроках. Значение длины стороны с определяется по формуле с=√(а 2 +b 2 -2аbcosC). Также используя теорему косинусов определяется косинус угла А по формуле cosA=(b 2 +c 2 -a 2 )/2bc. Величину оставшегося угла можно найти, используя теорему о сумме углов треугольника ∠В=180°-∠А-∠С.
Вторая задача состоит в поиске неизвестного угла и двух сторон по известным двум углам и стороне, к которой они прилежат. На экране демонстрируется треугольник АВС, в котором выделены известная сторона а, а также углы ∠С и ∠В. Неизвестный угол легко находится по теореме суммы углов в треугольнике ∠А=180⁰-∠В-∠С. Для нахождение длин сторон можно использовать известную школьникам теорему синусов. Применяя ее, получаем b=а·sinВ/ sinА и с= а·sinС/ sinА
В задаче третьего вида требуется найти углы треугольника, в котором известны три его стороны. На экране построен треугольник АВС. В нем отмечены стороны а, b, c. Для вычисления величины предлагается применить теорему косинусов. Из нее следует, что cosA=(b 2 +c 2 -a 2 )/2bc, cosВ=( a 2 +c 2 – b 2 )/2аc. Для нахождения угла С можно применить теорему о сумме углов треугольника ∠С=180⁰-∠А-∠В.
В качестве примера для закрепления материала рассматривается решение задачи, в которой футболист бьет мячом по воротам, от одного основания которых до места удара 23 м, а от второго основания – 24 м. Линия ворот вместе линиями, проведенными от игрока до снований ворот, составляет треугольник с игроком в вершине А и основаниями ворот в вершинах В и С. Известно, что ширина ворот 7 м. Необходимо найти величину угла α, который составляет угол попадания мяча в ворота. Уточняется, что сторонами данного треугольника будут с=АВ=23 м, b=АС=24 м, а=ВС=7 м. Очевидно, для решения данного треугольника следует применить теорему косинусов cosA=(b 2 +c 2 -a 2 )/2bc=(24 2 +23 2 -7 2 )/2·24·23. По таблице косинусов находится значение угла α≈16⁰57‘.
Видеоурок «Решение треугольников» поможет поднять эффективность традиционного урока в школе. Также данный материал может помочь ученику самостоятельно освоить материал, углубить его понимание. Наглядное пособие пригодится и в ходе дистанционного обучения.
Решение треугольников
Корзина


Треугольник ΔABC,
a = BC, b = AC, c = AB — стороны треугольника,













Как пользоваться онлайн-калькулятором. В форме укажите три значения: одну сторону и 2 дополнительных параметра (например, угол и сторону, два угла или две стороны). Заполните поле “Текст с картинки”. Нажмите “Решить”.
Теоретический урок для решения задач по теме “Решение треугольников”. Бесплатное обучение.
Содержание данной онлайн страницы электронного справочника по предмету математики для школьников:
- – задачи 76 – 77 представлены с примерами решений и ответами;
- – онлайн задания, как найти решение треугольника через синус и косинус угла, рассматриваются в тестах 78 – 81;
- – решения, как найти угол, сторону треугольника, объясняются на данном уроке в контрольных работах 82 – 85.
Задача 76.


стороны треугольника a=10, b=7
Угол 

Решить треугольник: Угол по сторонам треугольника 




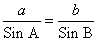
Sin B = 
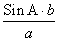

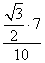

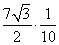

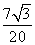
Используя Sin B ≈ 0,6062, находим из тригонометрической таблицы (“Четырехзначные математические таблицы” Владимира Модестовича Брадиса)


Тогда 

Используя теорему синусов

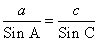

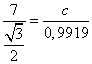



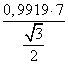
Ответ: 



Задача 77.
Треугольник ΔABC, стороны треугольника




Найти: Угол по сторонам треугольника 



Т.к. a=b=6,3, то треугольник ΔABC – равнобедренный.
Тогда 



Используя теорему синусов

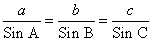

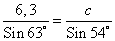



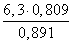

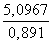
Ответ: 



Решение треугольников через синус и косинус угла
Задача 78.






Найти: угол треугольника 



Используя теорему синусов

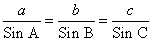

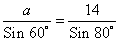



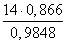

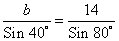



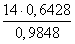
Ответ: 

Задача 79.


Найти: углы треугольника 






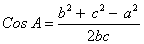
Cos B = 
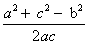

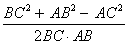

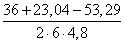

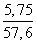
Используя тригонометрические таблицы (“Четырехзначные математические таблицы” В. М. Брадиса), находим значение угла B


Используя формулу теоремы косинусов, находим косинус угла C
Cos C = 
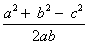

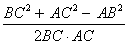
= 
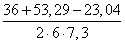
Используя тригонометрические таблицы (“Четырехзначные математические таблицы” В. М. Брадиса), находим значение угла C


Тогда угол A равен 

Ответ: 





Задача 80.




Найти: угол 



Т.к. два угла в треугольнике равны 



Значит, две стороны равны AC=AB=b=c=4,5
Используя теорему синусов

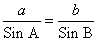
находим сторону BC=a





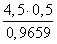
Ответ: 

Задача 81.
Треугольник ΔABC, длины трех его сторон
Найти: является ли треугольник тупоугольным, прямоугольным, остроугольным
1) Т.к. b=c=4, то треугольник ΔABC – равнобедренный, и, значит, остроугольный.



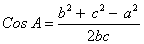
Cos A = 
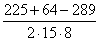

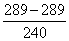
Тогда угол A равен 

3) Используя формулу теоремы косинусов

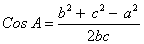
Cos B = 
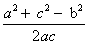

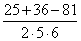

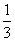

Треугольник ΔABC, два угла и сторона




Найти: длину всех сторон треугольника ΔABC = ?
Зная размер двух углов в треугольнике ΔABC, находим третий угол 

Найдем угол 





Используя теорему синусов

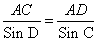

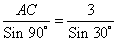

AC = (3 • 1) • 2 = 6 (м)
Используя теорему синусов

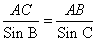

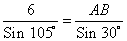

AB = 
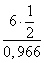
Используя теорему синусов

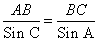

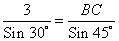



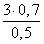
Ответ: AB ≈ 3 м, AC = 6 м, BC ≈ 4 м.


Три стороны a = 14, b = 18,
все углы треугольника ΔABC = ?
Т.к. против большего угла лежит большая сторона, то используя формулу теоремы косинусов
Cos C = 
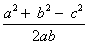
Cos C = 
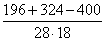

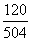
Используя тригонометрические таблицы (“Четырехзначные математические таблицы” В. М. Брадиса), находим приближенное значение угла C


Используя формулу теоремы косинусов
Cos B = 
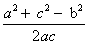
Cos B = 
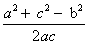

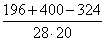

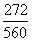
Используя тригонометрические таблицы (“Четырехзначные математические таблицы” В. М. Брадиса), находим приближенное значение угла B


Следовательно, 

Ответ: 






Задача 84.
Треугольник ΔEKP, сторона и два угла




Найти: сторону треугольника PK = ?
Используя теорему синусов

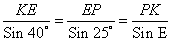


Sin 115° = Sin (180° – 65°) = Sin 65°
Тогда 
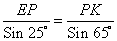



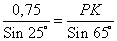




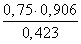
Задача 85.
Треугольник ΔABC, две стороны и угол


Найти: решить треугольник – определить значение стороны и двух углов
(a, 



Используя формулу теоремы косинусов

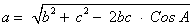
a = 
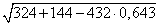

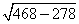
Используя формулу теоремы косинусов
Cos C = 
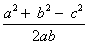
Cos C = 
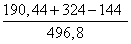

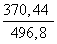
Используя тригонометрические таблицы (“Четырехзначные математические таблицы” В. М. Брадиса), находим приближенное значение угла C


Следовательно, 

Ответ: a ≈ 13,8 ; 



[spoiler title=”источники:”]
http://www.petrovskov.ru/uchebniki/geometriya-9/reshenie-treugolnikov.html
[/spoiler]
Виды треугольников
Урок. Как найти периметр треугольника. Математика 2 класс. #учусьсам
Математика 2 класс (Урок№15 – Периметр многоугольника.)
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Определение треугольника
Треугольник – многоугольник с тремя сторонами и тремя углами.
Угол ∠ A – угол, образованный сторонами A B и A C и противолежащий стороне B C .
Угол ∠ B – угол, образованный сторонами B A и B C и противолежащий стороне A C .
Угол ∠ C – угол, образованный сторонами C B и C A и противолежащий стороне A B .
Виды треугольников
Треугольник остроугольный, если все три угла в треугольнике острые.
Треугольник прямоугольный, если у него один из углов прямой ( = 90 ° ) .
Треугольник тупоугольный, если у него один из углов тупой.
Примеры:


Основные свойства треугольника:
- Против большей стороны лежит больший угол.
- Против равных сторон лежат равные углы.
- Сумма углов в треугольнике равна 180 ° .
- Если продолжить одну из сторон треугольника, например, A C , и взять на продолжении стороны точку D , образуется внешний угол ∠ B C D к исходному углу ∠ A C B .
Внешний угол равен сумме двух внутренних углов, не смежных с ним. ∠ B C D = 180 ° − ∠ A C B ∠ B C D = ∠ A + ∠ B
- Неравенство треугольника: любая из сторон треугольника меньше суммы двух других сторон и больше их разности.
Отрезки в треугольнике
Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.
Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.
Свойства биссектрис треугольника:
- Биссектриса угла – геометрическое место точек, равноудаленных от сторон угла.
- Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам:
a b = m n
- Биссектрисы пересекаются в одной точке. Точка пересечения биссектрис – центр вписанной в треугольник окружности.
Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.
Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Свойства медиан треугольника:
- Медиана разбивает треугольник на два равновеликих треугольника (два треугольника, имеющих одинаковую площадь).
- Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
- Три медианы, проведенные в одном треугольнике, разбивают его на шесть равновеликих треугольников.
S 1 = S 2 = S 3 = S 4 = S 5 = S 6
Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.
Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.
Пример:

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.
m = a 2
Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.
Площадь треугольника
Площадь произвольного треугольника можно найти следующими способами:
- Полупроизведение стороны на высоту, проведенную к этой стороне.
S = 1 2 a ⋅ h a
- Полупроизведение двух сторон на синус угла между ними.
S = 1 2 a ⋅ b ⋅ sin α
- По формуле Герона.
S = p ( p − a ) ( p − b ) ( p − c ) p = a + b + c 2
Равнобедренный треугольник
Равнобедренным называется треугольник, у которого две стороны равны.
Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.


Свойства равноберенного треугольника:
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике медиана, высота и биссектриса, проведенные к основанию, совпадают.
Равносторонний треугольник
Равносторонним называется треугольник, у которого все стороны и все углы равны.
Площадь равностороннего треугольника находится по формуле S = a 2 3 4
Высота равностороннего треугольника находится по формуле h = a 3 2
Прямоугольный треугольник
Треугольник называется прямоугольным, если у него один из углов равен 90 ° .
Свойства прямоугольного треугольника:
- Сумма двух острых углов треугольника равна 90 ° .
- Катет, лежащий напротив угла в 30 ° , равен половине гипотенузы.
- Если катет равен половине гипотенузы, он лежит напротив угла в 30 ° .
a = c 2 c = 2 ⋅ a
- Медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
m = c 2
- Пропорциональные отрезки в прямоугольном треугольнике
a = m ⋅ c b = n ⋅ c h = m ⋅ n
Теорема Пифагора
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
c 2 = a 2 + b 2
У прямоугольного треугольника катеты перпендикулярны друг другу, следовательно, площадь можно найти по формуле:
S = 1 2 a ⋅ b
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с треугольниками
Скачать домашнее задание к уроку 3.
|
Планиметрия |
||||||
|
||||||
|
||||||
|
||||||
|
|
|
Вся информация предоставленная на данном сайте взята из открытых источников и носит информационный характер,для ознакомления и тестирования данного материала. Администрация данного ресурса не несет ответственности за содержание материалов,всю предоставленную информацию взятую с данного сайта Вы используете на свой страх и риск. Если Вы являетесь правообладателем материала выставленного на сайте,форуме без Вашего ведома,обратитесь к администратору и материал будет немедленно удален.

























