Как найти три первых значения

Когда нужно найти какие-либо данные в таблице Excel, вы можете использовать несколько функций. Например, функция ВПР или ИНДЕКС вместе с ПОИСКПОЗ.

Эти функции ищут в таблице заданный фрагмент и останавливаются на первом совпадении. Но что если вам нужно найти не только первое совпадение, а все?

Итак, начнём!

В этой статье я продемонстрирую вам, как можно сделать это.

Поиск фрагмента по всей таблице, второе, третье и N-ое совпадение

С помощью добавления нового столбца

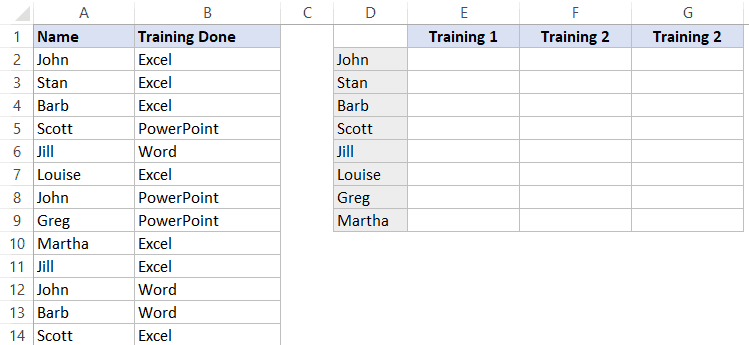
Допустим, у вас есть следующая табличка:

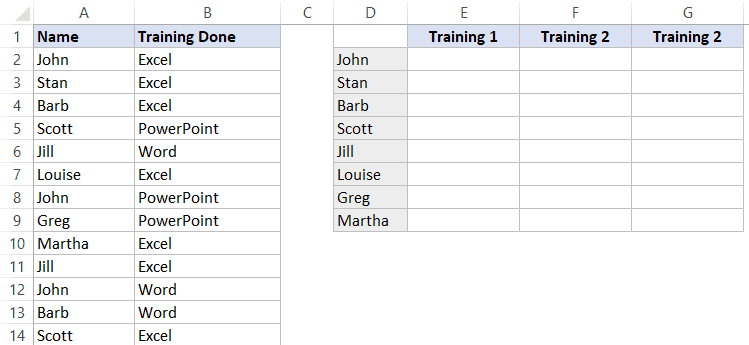
Например, вам необходимо перечислить все «Training» которые прошел человек, в ячейках после его имени.

Итак, мы можем вызвать функцию ВПР или ИНДЕКС (вместе с ПОИСКПОЗ), но тут есть небольшая проблема — когда функция найдет первое совпадение (например для Джона) она остановится и вернет вам результат.

К примеру, Джон прошел все тренинги, но если мы будем использовать вышеуказанные функции, результатом будет только «Excel». Функция нашла первое совпадение имени Джон, остановилась и передала нам результат. Но как же сделать так, чтобы она не останавливалась на первом совпадении?

Можно добавить столбец и провести нехитрые манипуляции с ним.

Пошаговая инструкция:

• Вставим столбец «Помощник» сразу после имени;

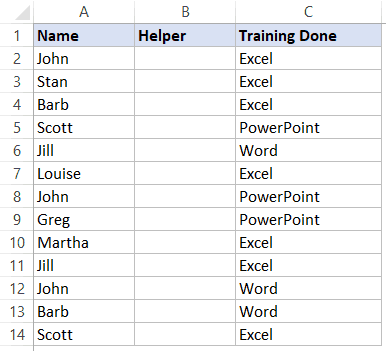
• В первую свободную ячейку пропишем:

=A2&СЧЁТЕСЛИ($A$2:$A2;A2)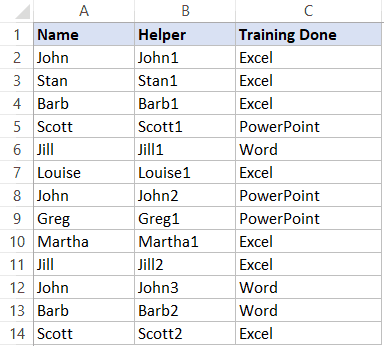

• А теперь, в другой столбик пропишем следующую функцию:

=ЕСНД(ВПР($E2&ЧИСЛСТОЛБ($F$1:F1);$B$2:$C$14;2;0);"")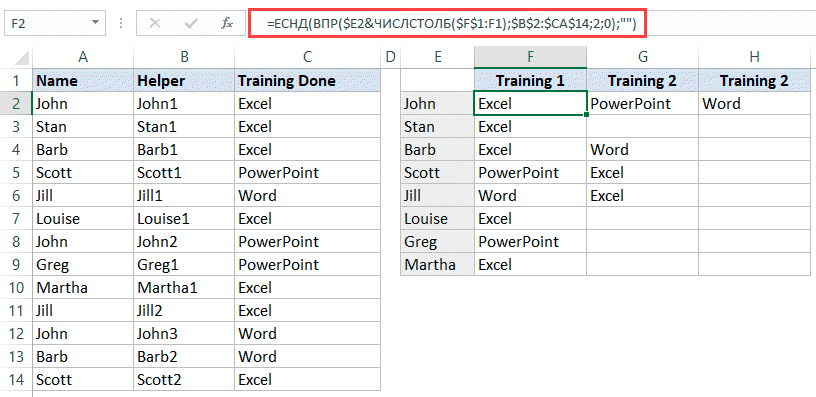

Эта функция, в следующих столбиках, укажет какие тренинги прошел человек, если какой-то тренинг он не прошел — будет просто пустое место.

Что делает эта функция?

Мы используем небольшую хитрость. Функция СЧЁТЕСЛИ делает каждое новое имя человека уникальным. Как она это делает? — очень просто, она добавляет цифру к имени, например, Джон1, Джон2 и так далее.

Получается, что теперь функция ВПР не остановится при первом совпадении, потому что их не будет. Теперь все имена и даже одинаковые — уникальны (из-за цифр в конце имени).

$E2&ЧИСЛСТОЛБ ($F$1:F1) это сам фрагмент, по которому происходит поиск. Функция ЧИСЛСТОЛБ добавляет цифру, ориентируясь на номер строки, к концу имени, а дальше уже происходит поиск по этому фрагменту.

С помощью массива

Если вам, по каким-то причинам, не нравится, или вы не можете использовать способ с добавлением столбика, есть еще один вариант.

Допустим, у нас та же табличка:

Такая функция тоже вернет правильный результат:

=ЕСЛИОШИБКА(ИНДЕКС($B$2:$B$14;НАИМЕНЬШИЙ(ЕСЛИ($A$2:$A$14=$D2;СТРОКА($A$2:$A$14)-1;"");ЧИСЛСТОЛБ($E$1:E1)));"")

Чтобы вставить её, вам нужно выделить ячейки, в которые нужно вставить данные (в нашем случае, от E2 до G9).

И еще, важный момент, когда пропишете саму функцию, нажмите CTRL+SHIFT+ENTER, вместо ENTER. Так нужно сделать, потому что мы работаем с массивом данных.

Что делает эта функция?

Итак, давайте разберемся:

$A$2:$A$14=$D2

Этот фрагмент нашей функции сравнивает значения с ячейкой D2.

Результат либо ИСТИНА либо ЛОЖЬ.

Пример результата выполнения:

{ИСТИНА;ЛОЖЬ;ЛОЖЬ;ЛОЖЬ;ЛОЖЬ;ЛОЖЬ;ИСТИНА;ЛОЖЬ;ЛОЖЬ;ЛОЖЬ;ИСТИНА;ЛОЖЬ;ЛОЖЬ}

Продолжим и рассмотрим следующий фрагмент:

ЕСЛИ($A$2:$A$14=$D2;СТРОКА($A$2:$A$14)-1;””)

Этот фрагмент нашей функции получает на входе массив данных (ИСТИНА или ЛОЖЬ) и заменяет истину на номер строки из таблички, а ЛОЖЬ на пустое место.

Вот пример выполнения этого фрагмента:

{1;””;””;””;””;””;7;””;””;””;11;””;””}

Далее:

НАИМЕНЬШИЙ(ЕСЛИ($A$2:$A$14=$D2;СТРОКА($A$2:$A$14)-1;””);ЧИСЛСТОЛБ($E$1:E1))

А теперь функция НАИМЕНЬШИЙ запишет все наименьшие порядковые числа, первое, второе, третье и так далее. А функция ЧИСЛСТОЛБ присваивает им номера, в соответствии с номером строки.

ИНДЕКС($B$2:$B$14;НАИМЕНЬШИЙ(ЕСЛИ($A$2:$A$14=$D2;СТРОКА($A$2:$A$14)-1;””);ЧИСЛСТОЛБ($E$1:E1)))

В итоге функция ИНДЕКС, по порядковым номерам, полученным от функции ЧИСЛСТОЛБ, вернет их значения. То есть в первом совпадении возвращается «Excel» и так далее.

Но если возникнет ошибка, а она обязательно возникнет, потому что, в нашем случае, не все люди прошли по 3 тренинга, функция ЕСЛИОШИБКА заменит все ошибки на пустые места.

Итак, в этом разделе статьи мы использовали функцию массива. Это удобно, потому что её можно копировать без каких-либо проблем. Мое мнение — это лучший способ, может быть он и сложнее, но его можно без проблем масштабировать.

нные варианты найти все совпадения, просто я считаю что это самые практичные. Если у вас есть свои «удобные» способы, пожалуйста, поделитесь ими в комментариях.

Three Consecutive Numbers are the numbers that follow each other from the smallest number to the largest number. There are two types of consecutive numbers. They are even consecutive numbers and odd consecutive numbers. Know more on Consecutive Numbers Definition, Facts, Formulas, Procedure on How to find the Three Consecutive Numbers when Sum or Product is known. Have a look at the examples related to three consecutive numbers.

Also, Read: Prime and Composite Numbers

Consecutive Numbers are the sequence or chain of numbers where each number is one more than the previous number. Consecutive Numbers are represented as n, n + 1, n + 2, n + 3, n + 4, …….

Consecutive Numbers Formula

The formula to find the three consecutive numbers is n, n + 1, n + 2.
The formula for consecutive even numbers are 2n, 2n + 2, 2n + 4, 2n + 6,…
The formula for consecutive odd number are 2n + 1, 2n + 3, 2n + 5, 2n + 7,…

How to find Three Consecutive Numbers?

Follow the simple steps provided to know about the procedure for finding the three consecutive numbers. They are as follows

• We know the three consecutive numbers are in general as n, n + 1, n + 2…
• You can find the value of integer ‘n’ you will be given either three consecutive numbers sum or product.
• Frame an equation on what the question is asked for.
• Solve for the variable ‘n’ as per the equation and then substitute the value of n in the consecutive numbers.

Three Consecutive Numbers Examples with Solutions

Example 1.
What are the first three consecutive natural numbers?
Solution:
Natural Numbers are the numbers that start with 1.
N = 1, 2, 3, 4, 5, 6….
The formula for three consecutive numbers is n, n + 1, n + 2
1, 1 + 1, 1 + 2 = 1, 2, 3
Thus the first three consecutive natural numbers are 1, 2, 3.

Example 2.
Find the three consecutive numbers of 54.
Solution:
Let n be 54.
The formula to find the three consecutive numbers is n, n + 1, n + 2.
n = 54
n + 1 = 55
n + 2 = 56
n + 3 = 57
Thus the three consecutive numbers after 54 are 55, 56, 57.

Example 3.
What is the sum of three consecutive odd numbers?
Solution:
The formula for consecutive even numbers are 2n, 2n + 2, 2n + 4, 2n + 6,…
2n + 2n + 2 + 2n + 4
For n = 1
2n = 2(1) = 2
2n + 2 = 2(1) + 2 = 2 + 2 = 4
2n + 4 = 2(1) + 4 = 2 + 4 = 6
Thus the three consecutive even numbers are 2, 4, 6

Example 4.
The sum of three consecutive even numbers is 84. How do you find the numbers?
Solution:
Given,
The sum of three consecutive even numbers is 84.
The formula for consecutive even numbers are 2n, 2n + 2, 2n + 4.
2n + 2n + 2 + 2n + 4 = 84
6n + 6 = 84
6n = 84 – 6
6n = 78
n = 78/6
n = 13

Example 5.
The sum of three consecutive odd numbers is 27, how do you find the numbers?
Solution:
Given,
The sum of three consecutive odd numbers is 30
The formula for consecutive odd number are 2n + 1, 2n + 3, 2n + 5
2n + 1 + 2n + 3 + 2n + 5 = 27
6n + 9 = 27
6n = 18
n = 18/6
n = 3
2n + 1 = 2(3) + 1 = 6 + 1 = 7
2n + 3 = 2(3) + 3 = 6 + 3 = 9
2n + 5 = 2(3) + 5 = 6 + 5 = 11
Thus the three consecutive odd numbers are 7, 9, 11.

FAQs on Three Consecutive Numbers

1. What are Consecutive Numbers?
The Numbers that follow each other from smallest to largest are known as Consecutive Numbers.

2. The Sum of Three Consecutive Integers is 48. How do you find the Numbers?
Three Consecutive Integers Sum is 48 i.e. n+n+1+n+2 = 48
3n+3=48
3n=48-3
3n=45
n=45/3 =15
Substituting the n value in the formula for three consecutive numbers we have n =15, n+1 = 15+1, n+2 =15+2
Thus, three consecutive integers are 15, 16, 17.

3. What is the algebraic expression for the sum of three consecutive integers?

The Sum of Three Consecutive Integers is 3 times the middle value i.e. 3n

4. What is the product of three consecutive integers?

The Product of Three Consecutive Integers is always divisible by 6.

В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.

Как найти значение числового выражения?

Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.

Простейшие случаи

Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами. 

Если в выражении есть только числа и арифметические знаки “+”, “·”, “-“, “÷”, то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.

Выражения со скобками

Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.

Значение выражений, содержащих скобки в скобках, находится по такому же принципу.

В нахождении значений выражений со скобками главное – соблюдать последовательность действий.

Выражения с корнями

Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.

Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.

Выражения со степенями

Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.

Также часто целесообразно бывает провести упрощение выражения  с использованием свойств степени.

Выражения с дробями

Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения. 

Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.

Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.

Выражения с логарифмами

Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.

Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:

log5-6÷352+2+7=log327+7=3+7=10.

Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.

Выражения с тригонометрическими функциями

Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.

Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.

Общий случай числового выражения

В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.

Разберем пример.

В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.

Вычисление значений выражений рациональными способами

Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.

Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.

Еще один прием, позволяющий ускорить процесс – использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями – сокращение одинаковых выражений в числителе и знаменателе. 

Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.

Нахождение значений выражений с переменными

Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных. 

Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.

Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.

Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений. 

Еще один пример. Значение выражения xx равно единице для всех положительных иксов.