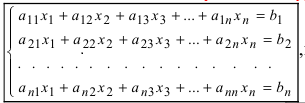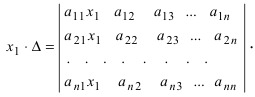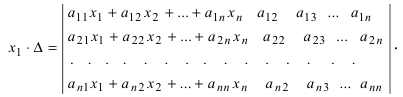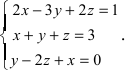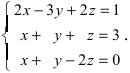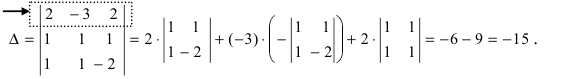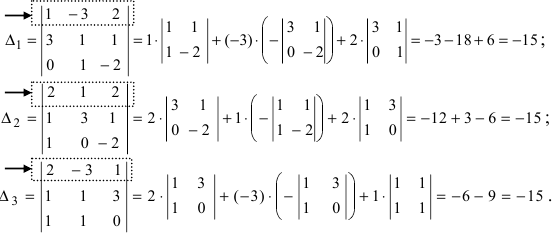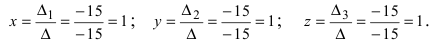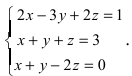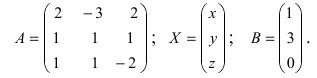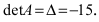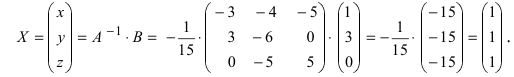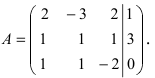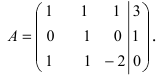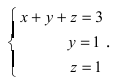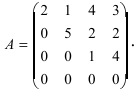Как найти три решения системы

Литература: (1,
с. 18-34; 2, с. 82-100; 3, с. 286-275)

1. Основные
   понятия

Системой линейных
уравнений называется совокупность
рассматриваемых совместно нескольких
линейных уравнений.

В системе может
быть любое число уравнений с любым
числом неизвестных.

Решением системы
уравнений называется совокупность
значений неизвестных, удовлетворяющая
всем уравнениям системы, то есть
обращающая их в тождества.

Система, имеющая
решение, называется совместной, в
противном случае – несовместной.

Для решения системы
применяют различные методы.

1. Решение систем
   линейных уравнений снеизвестными

Пусть
(число уравнений равно числу неизвестных).

Метод Крамера

Рассмотрим решение
системы трёх линейных уравнений с тремя
неизвестными:

(7)

Для нахождения
неизвестных
применим формулу Крамера:

(8)

где
– определитель системы, элементы которого
есть коэффициенты при неизвестных:

.

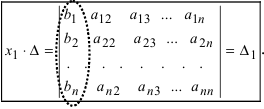
получается путём
замены первого столбца определителя
столбцом свободных членов:

.

Аналогично:

;.

Пример 1. Решить
систему по формуле Крамера:

.

Решение: Воспользуемся
формулами (8):

;

;

;

;

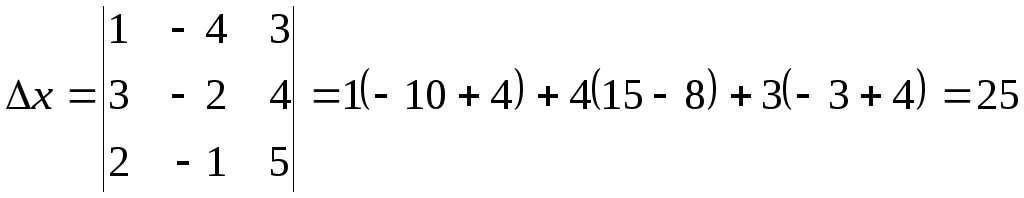
Тогда

Ответ:
.

Для любой системы
линейных уравнений снеизвестными можно утверждать:

1. Если определить
   системы
   ,
   то система имеет единственное решение,
   которое может быть найдено по формулам
   Крамера.

2. Если
   ,
   то правило Крамера неприменимо. В этом
   случае система может иметь бесчисленное
   множество решений, еслиили не иметь их, если хотя бы один из
   определителейне равен нулю.

Матричный способ
решения

Рассмотрим решение
системы (7) трёх линейных уравнений с
тремя неизвестными матричным способом.

Используя правила
умножения матриц, данную систему
уравнений можно записать в виде:
,
где

.

Пусть матрица
невырожденная, т.е..
Умножая обе части матричного уравнения
слева на матрицу,
обратную матрице,
получим:.

Учитывая, что
,
имеем

(9)

Пример 2. Решить
систему матричным способом:

.

Решение: Введём
матрицы:

–
из коэффициентов при неизвестных;

–
столбец свободных членов.

Тогда систему
можно записать матричным уравнением:
.

Воспользуемся
формулой (9). Найдём обратную матрицу
по формуле (6):

;

Тогда

.

Следовательно,

Получили:

.

Ответ:
.

Метод последовательного
исключения неизвестных (метод Гаусса)

Основная идея
применяемого метода заключается в
последовательном исключении неизвестных.
Поясним смысл этого метода на системе
трёх уравнений с тремя неизвестными:

.

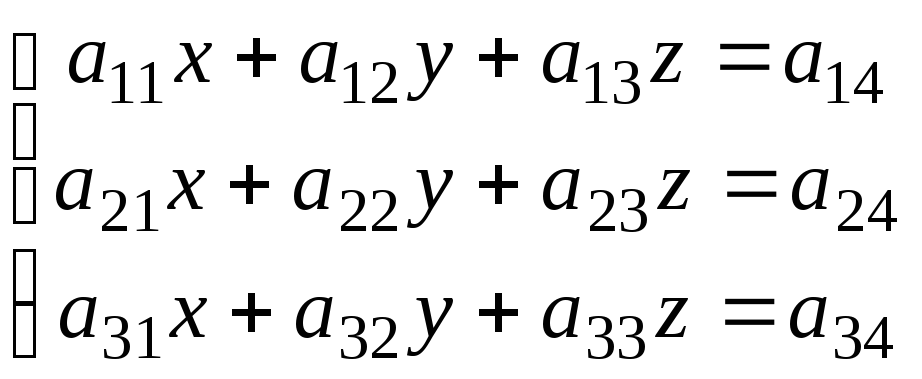
Допустим, что
(если,
то изменим порядок уравнений, выбрав
первым уравнением то, в котором коэффициент
прине равен нулю).

Первый шаг: а) делим
уравнение
на;
б) умножаем полученное уравнение наи вычитаем из;
в) затем полученное умножаем наи вычитаем из.
В результате первого шага будем иметь
систему:

причём

,

Второй шаг: поступаем
с уравнением
иточно так же, как с уравнениями.

В итоге исходная
система преобразуется к так называемому
ступенчатому виду:

Из преобразованной
системы все неизвестные определяются
последовательно без труда.

Замечание.
Практически удобнее приводить к
ступенчатому виду не саму систему
уравнений, а матрицу из коэффициентов,
при неизвестных, и свободных членов.

Пример 3. Решить
методом Гаусса систему:

.

Переход от одной
матрицы к другой будем записывать при
помощи знака эквивалентности ~.

~~~~

~.

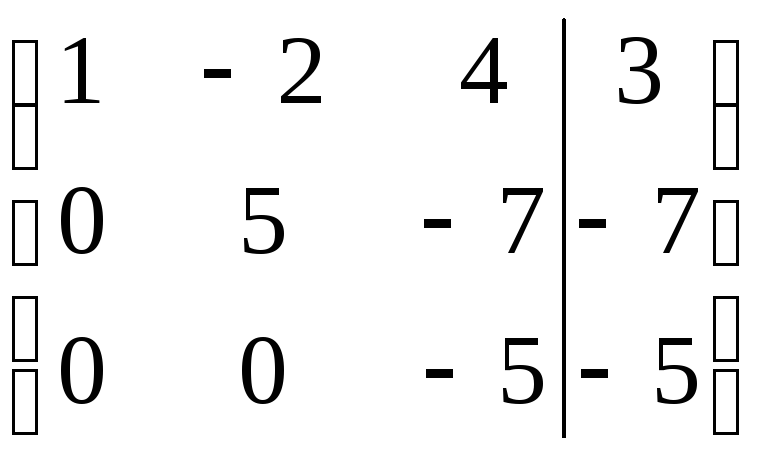
По полученной
матрице выписываем преобразованную
систему:

.

Тогда

Ответ:
.

Замечание: Если
система имеет единственное решение, то
ступенчатая система приводится к
треугольной, то есть к такой, в которой
последнее уравнение будет содержать
одно неизвестное. В случае неопределённой
системы, то есть такой, в которой число
неизвестных больше числа линейно
независимых уравнений, треугольной
системы не будет, так как последнее
уравнение будет содержать более одного
неизвестного (система имеет бесчисленное
множество решений). Когда же система
несовместна, то, после приведения её к
ступенчатому виду, она будет содержать
хотя бы одно
значение вида,
то есть уравнение, в котором все
неизвестные имеют нулевые коэффициенты,
а правая часть отлична от нуля (система
решений не имеет). Метод Гаусса применим
к произвольной системе линейных уравнений
(при любыхи).

1. Теорема
   существования решения системы линейных
   уравнений

При решении системы
линейных уравнений методом гаусса ответ
на вопрос, совместна или несовместна
данная система может быть дан лишь в
конце вычислений. Однако часто бывает
важно решить вопрос о совместности или
несовместности системы уравнений, не
находя самих решений. Ответ на этот
вопрос даёт следующая теорема
Кронекера-Капелли.

Пусть дана система
линейных уравнений снеизвестными:

(10)

Для того, чтобы
система (10) была совместной, необходимо
и достаточно чтобы ранг матрицы системы

.

был равен рангу
её расширенной матрицы

.

Причём, если
,
то система (10) имеет единственное решение;
если же,
то система имеет бесчисленное множество
решений.

1. Линейная,
   однородная система
   уравнений снеизвестными

Рассмотрим
однородную систему (все свободные члены
равны нулю) линейных уравнений:

.

Эта система всегда
совместна, так как она имеет нулевое
решение
.

В следующей теореме
даны условия, при которых система имеет
также решения, отличные от нулевого.

Терема. Для того,
чтобы однородная система линейчатых
уравнений имела нулевое решение,
необходимо и достаточно, чтобы её
определитель
был равен нулю:

.

Таким образом,
если
,
то решение– единственное. Если,
то существует бесконечноё множество
других ненулевых решений. Укажем один
из способов отыскания решений для
однородной системы трёх линейных
уравнений с тремя неизвестными в случае.

Можно доказать,
что если
,
а первое и второе уравнения непропорциональны
(линейно независимы), то третье уравнение
есть следствие первых двух. Решение
однородной системы трёх уравнений с
тремя неизвестными сводится к решению
двух уравнений с тремя неизвестными.
Появляется так называемое свободное
неизвестное, которому можно придавать
произвольные значения.

Пример 4. Найти
все решения системы:

.

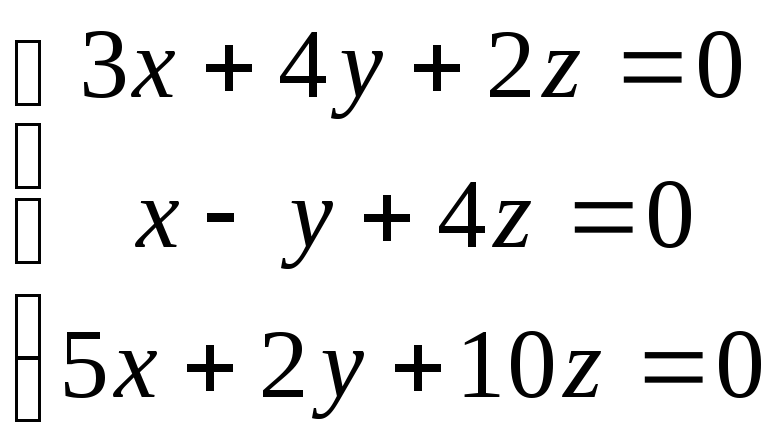
Решение. Определитель
этой системы

.

Поэтому система
имеет нулевые решения. Можно заметить,
что первые два уравнения, например,
непропорциональны, следовательно, они
линейно независимые. Третье является
следствием первых двух (получается,
если к первому уравнению прибавить
удвоенное второе). Отбросив его, получим
систему двух уравнений с тремя
неизвестными:

.

Полагая, например,
,
получим

.

Решая систему двух
линейных уравнений, выразим
ичерез:.
Следовательно, решение системы можно
записать в виде:,
где– произвольное число.

Пример 5. Найти
все решения системы:

.

Решение. Нетрудно
видеть, что в данной системе только одно
независимое уравнение (два других ему
пропорциональны). Система из трёх
уравнений с тремя неизвестными свелась
к одному уравнению с тремя неизвестными.
Появляются два свободных неизвестных.
Найдя, например, из первого уравнения
при произвольныхи,
получим решения данной системы. Общих
вид решения можно записать,
гдеи– произвольные числа.

1. Вопросы для
   самопроверки

Сформулируйте
правило Крамера для решения системы
линейных уравнений снеизвестными.

В чём сущность
матричного способа решения систем?

В чём заключается
метод Гаусса решения системы линейных
уравнений?

Сформулируйте
теорему Кронекера-Капелли.

Сформулируйте
необходимое и достаточноё условие
существования ненулевых решений
однородной системы линейных уравнений.

1. Примеры для
   самостоятельного решения

Найдите все решения
систем:

1.
; 2.;

3.
; 4.;

5.
; 6.;

7.
; 8.;

9.
; 10.;

11.
; 12.;

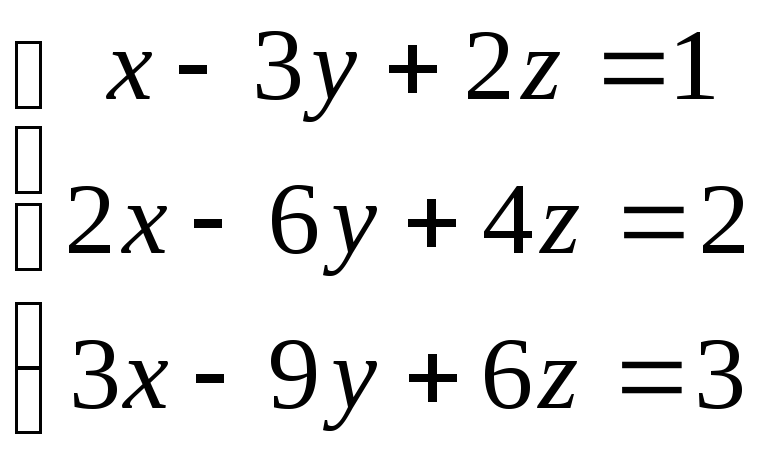
13.
;
14.
;

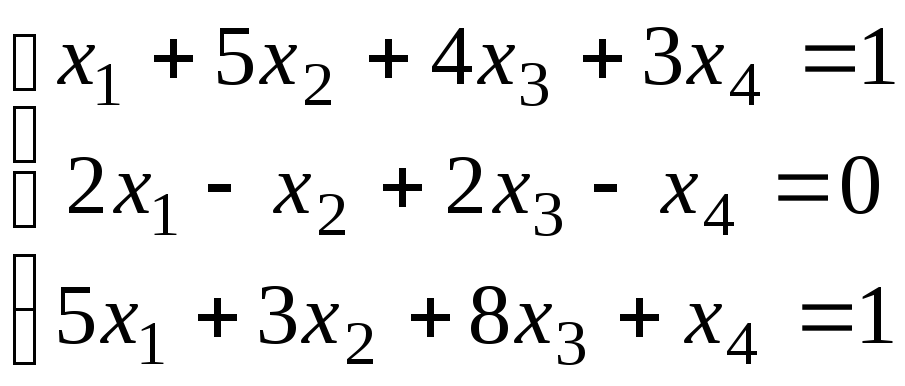
15.
.

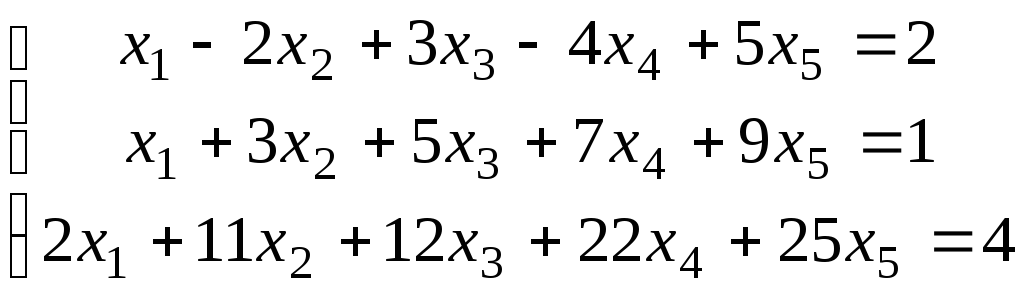
Определите, при
каких значениях
исистема уравнений

а) имеет единственное
решение;

б) не имеет решения;

в) имеет бесконечно
много решений.

16.
; 17.;

Найти все решения
следующих однородных систем:

18.
; 19.;

20.
; 21.;

22.
; 23.;

1. Ответы к
   примерам

1.
; 2.; 3.
Ǿ; 4. Ǿ;

5.
– произвольное число.

6.
,
где– произвольное число.

7.
; 8.; 9.
Ǿ; 10. Ǿ;

11.
,
где– произвольное число.

12.
,
гдеи– произвольные числа.

13.
; 14.гдеи– произвольные числа.

15. Ǿ; 16. а)
;
б);
в).

17. а)
;
б);
в);

18.
; 19.; 20.,
где– произвольное число.

21.
,
где– произвольное число.

22.
,
где– произвольное число.

23.
,
гдеи– произвольные числа.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Пример:

а) (begin{cases}x-2y=5\3x+2y=7end{cases})	г) (begin{cases}3(5-x)-4y=0\y-2x+4=0 end{cases})
б)(begin{cases}3b=13-2a\5a=5-2b end{cases})	д)(begin{cases}frac{p}{3} + frac{m-6}{2} = 1-9m \11p+3(m-p-1)=-2(m+1) end{cases})
в)(begin{cases}3x-8=2y\x+y=6end{cases})	е)(begin{cases}0,02y=1,25-3,21x \1,5x-frac{3}{4}=4-0,1yend{cases})

Пример:
Пара значений (x=3);(y=-1) является решением первой системы, потому что при подстановке этих тройки и минус единицы в вместо (x) и (y), оба уравнения превратятся в верные равенства (begin{cases}3-2cdot (-1)=5 \3 cdot 3+2 cdot (-1)=7 end{cases})

А вот (x=1); (y=-2) – не является решением первой системы, потому что после подстановки второе уравнение «не сходится» (begin{cases}1-2cdot(-2)=5 \3cdot1+2cdot(-2)≠7 end{cases})

Отметим, что такие пары часто записывают короче: вместо “(x=3); (y=-1)” пишут так: ((3;-1)).

Как решить систему линейных уравнений?

Есть три основных способа решения систем линейных уравнений:

1. Способ подстановки.

1. Возьмите любое из уравнений системы и выразите из него любую переменную.

   (begin{cases}x-2y=5\3x+2y=7 end{cases})(Leftrightarrow) (begin{cases}x=5+2y\3x+2y=7end{cases})(Leftrightarrow)

2. Полученное выражение подставьте вместо этой переменной в другое линейное уравнение системы.

   (Leftrightarrow) (begin{cases}x=5+2y\3(5+2y)+2y=7end{cases})(Leftrightarrow)

3. Равносильными преобразованиями уравнений найдите  по очереди каждое неизвестное.

   (Leftrightarrow) (begin{cases}x=5+2y\15+6y+2y=7end{cases})(Leftrightarrow)(begin{cases}x=5+2y\8y=-8end{cases})(Leftrightarrow)(begin{cases}x=5+2y\y=-1end{cases})(Leftrightarrow)(begin{cases}x=5-2\y=-1end{cases})(Leftrightarrow)(begin{cases}x=3\y=-1end{cases})

4. Ответ запишите парой чисел ((x_0;y_0))

   Ответ: ((3;-1))

Замечание к шагу 1: нет никакой разницы какую переменную и из какого уравнения выражать. Обычно более удобно выражать ту переменную, перед которой нет коэффициента или, говоря точнее, коэффициент которой равен единице (в примере выше это был икс в первом уравнении).

Почему так? Потому что во всех остальных случаях у нас при выражении переменной получилась бы дробное выражение. Попробуем, например, выразить икс из второго уравнения системы:

(begin{cases}x-2y=5\3x+2y=7 end{cases})(Leftrightarrow) (begin{cases}x=5+2y\3x=7-2yend{cases})(Leftrightarrow)(begin{cases}x=5+2y\x=frac{7-2y}{3}end{cases})

И сейчас нам нужно будет эту  дробь
подставлять в первое уравнение и решать то, что получиться. До верного ответа мы бы всё равно дошли, но идти было бы неудобнее

2. Способ алгебраического сложения.

1. Равносильно преобразовывая каждое уравнение в отдельности, запишите систему в виде:(begin{cases}a_1 x+b_1 y=c_1\a_2 x+b_2 y=c_2end{cases}).

   (begin{cases}3y=13-2x\5x=5-2yend{cases})(Leftrightarrow)(begin{cases}2x+3y=13\5x+2y=5end{cases})(Leftrightarrow)

2. Теперь нужно сделать так, чтоб коэффициенты  при одном из неизвестных стали одинаковы (например, ((3) и (3)) или противоположны по значению (например, (5) и (-5)). В нашем примере уравняем коэффициенты при игреках. Для этого первое уравнение домножим на (2), а второе – на (3).

   (begin{cases}2x+3y=13 |cdot 2\ 5x+2y=5 |cdot 3end{cases})(Leftrightarrow)(begin{cases}4x+6y=26\15x+6y=15end{cases})(Leftrightarrow)

3. Сложите (или вычтите) почленно обе части уравнения так, чтобы получилось уравнение с одним неизвестным.

   

4. Найдите неизвестное из полученного уравнения.

   (-11x=11)     (|∶(-11))
   (x=-1)                

5. Подставьте найденное значение неизвестного в любое из исходных уравнений и найдите второе неизвестное.

   (3y=13-2x)
   (3y=13-2·(-1))
   (3y=15)
   (y=5)

6. Ответ запишите парой чисел ((x_0;y_0)).

   Ответ: ((-1;5))

Замечание к шагу 3: В каком случае уравнения складывают, а в каком вычитают? Ответ прост – делайте так, чтоб пропала переменная: если «уравненные» коэффициенты имеют один и тот же знак – вычитайте, а если разные – складывайте.

Пример. Решите систему уравнений: (begin{cases}12x-7y=2\5y=4x-6end{cases})

Решение:

(begin{cases}12x-7y=2\5y=4x-6end{cases})		Приводим систему к виду (begin{cases}a_1 x+b_1 y=c_1\a_2 x+b_2 y=c_2end{cases}) преобразовывая второе уравнение.
(begin{cases}12x-7y=2\-4x+5y=-6end{cases})		«Уравняем» коэффициенты при иксах. Для этого домножим второе уравнение на (3).
(begin{cases}12x-7y=2\-12x+15y=-18end{cases})		Знаки при иксах разные, поэтому чтоб иксы пропали, уравнения надо сложить.
(0·x+8y=-16)		Делим уравнение на (8), чтобы найти (y).
(y=-2)		Игрек нашли. Теперь найдем (x), подставив вместо игрека (-2) в любое из уравнений системы.
(12x-7·(-2)=2) (12x+14=2) (12x=-12) (x=-1)		Икс тоже найден. Пишем ответ.

Ответ: ((-1;-2))

3. Графический способ.

1. Приведите каждое уравнение к виду линейной функции
    (y=kx+b).

   (begin{cases}3x-8=2y\x+y=6end{cases})(Leftrightarrow)(begin{cases}2y=3x-8 |:2\y=6-xend{cases})(Leftrightarrow)(begin{cases}y=frac{3}{2}x-4\y=-x+6end{cases})

2. Постройте  графики  этих  функций.  Как?  Можете  прочитать  здесь.

   

3. Найдите координаты ((x;y)) точки пересечения графиков и запишите их в ответ в виде ((x_0;y_0 )).
   Ответ: ((4;2))

Матхак. Если сомневаетесь в правильности ответа (неважно каким способом вы решали), проверьте подстановкой значений (x_0) и (y_0) в каждое уравнение. Если оба уравнения превратятся в верные равенства, то ответ правильный.
Пример: решая систему (begin{cases}3x-8=2y\x+y=6end{cases}), мы получили ответ ((4;2)). Проверим его, подставив вместо икса (4), а вместо игрека (2).

(begin{cases}3cdot 4-8=2cdot 2\4+2=6end{cases})(Leftrightarrow)(begin{cases} 12-8=4\6=6end{cases})(Leftrightarrow)(begin{cases} 4=4\6=6end{cases})

Оба уравнения сошлись, решение системы найдено верно.

Пример. Решите систему уравнений: (begin{cases}3(5x+3y)-6=2x+11\4x-15=11-2(4x-y)end{cases})

Решение:

(begin{cases}3(5x+3y)-6=2x+11\4x-15=11-2(4x-y)end{cases})		Раскроем скобки в уравнениях.
(begin{cases}15x+9y-6=2x+11\4x-15=11-8x+2yend{cases})		Перенесем все выражения с буквами в одну сторону, а числа в другую.
(begin{cases}15x-2x+9y=11+6\4x+8x-2y=11+15end{cases})		Приведем подобные слагаемые.
(begin{cases}13x+9y=17\12x-2y=26end{cases})		Во втором уравнении каждое слагаемое – четное, поэтому упрощаем уравнение, деля его на (2).
(begin{cases}13x+9y=17\6x-y=13end{cases})		Эту систему линейных уравнений можно решить любым из способов, но мне кажется, что способ подстановки здесь удобнее всего. Выразим y из второго уравнения.
(begin{cases}13x+9y=17\y=6x-13end{cases})		Подставим (6x-13) вместо (y) в первое уравнение.
(begin{cases}13x+9(6x-13)=17\y=6x-13end{cases})		Первое уравнение превратилась в обычное линейное.  Решаем его. Сначала раскроем скобки.
(begin{cases}13x+54x-117=17\y=6x-13end{cases})		Перенесем (117) вправо и приведем подобные слагаемые.
(begin{cases}67x=134\y=6x-13end{cases})		Поделим обе части первого уравнения на (67).
(begin{cases}x=2\y=6x-13end{cases})		Ура, мы нашли (x)! Подставим его значение во второе уравнение и найдем (y).
(begin{cases}x=2\y=12-13end{cases})(Leftrightarrow)(begin{cases}x=2\y=-1end{cases})		Запишем ответ.

Ответ: ((2;-1))

Скачать статью

Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.

Метод Гаусса

1. Метод Гаусса
   1. Пример 1
   2. Пример 2
2. Несовместность системы (нет решений)
   1. Пример 3
3. Общее и частное решение системы (бесконечное множество решений)
   1. Пример 4

Пусть задана система линейных алгебраических уравнений: $$begin{cases} a_{11} x_1 + a_{12} x_2 + a_{13} x_3 = b_1 \ a_{21} x_1 + a_{22} x_2 + a_{23} x_3 = b_2 \ a_{31} x_1 + a_{32} x_2 + a_{33} x_3 = b_3 end{cases}. $$

1. Запишем систему уравнений в виде расширенной матрицы, состоящей из коэффициентов и столбца свободных членов. Вертикальная черта используется для удобства оформления. $$ begin{pmatrix} a_{11} & a_{12} & a_{13} & | & b_1 \ a_{21} & a_{22} & a_{23} & | & b_2 \ a_{31} & a_{32} & a_{33} & | & b_3 end{pmatrix} $$
2. С помощью элементарных преобразований матрицы (вычитание одной строки из другой, умноженной на коэффициент, удаление одинаковых и нулевых строк, деление строки на число отличное от нуля) получаем нули под главной диагональю $$ begin{pmatrix} a_{11} & a_{12} & a_{13} & | & b_1 \ 0 & a_{22} & a_{23} & | & b_2 \ 0 & 0 & a_{33} & | & b_3 end{pmatrix} $$
3. Используя элементарные преобразования, изложенные в пункте 2, приводим матрицу к виду содержащему нули везде, кроме главной диагонали $$ begin{pmatrix} a_{11} & 0 & 0 & | & b_1 \ 0 & a_{22} & 0 & | & b_2 \ 0 & 0 & a_{33} & | & b_3 end{pmatrix} $$

Несовместность системы (нет решений)

Если в результате элементарных преобразований появилась нулевая строка вида $$begin{pmatrix} 0&0&0&|&b end{pmatrix} text{ где } b neq 0,$$то система уравнений не имеет решений. На этом алгоритм Гаусса заканчивает свою работу и можно записывать ответ, что система несовместна, то есть нет решений. 

Содержание:

1. Примеры с решением
2. Правило Крамера

1°. Решение системы двух линейных уравнений с двумя неизвестными

по формулам Крамера имеет вид

где

основной и дополнительные определители системы.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

При решении системы могут встретиться три следующих случая:

а) — система совместна, имеет единственное решение;

б) — система несовместна, не имеет решения;

в) — система неопределена, т. е. имеет бесчисленное множество решений (система сводится к одному уравнению).

2°. Система двух однородных линейных уравнений с тремя неизвестными

имеет ненулевые решения, определяемые формулами

где к — произвольное число.

Если все определители (4) окажутся нулями, то система сводится к одному уравнению.

Возможно вам будут полезны данные страницы:

3°. Однородная система трех линейных уравнений с тремя неизвестными

При решении системы возможны три случая:

а) Основной определитель системы

Система имеет только нулевое решение.

б) но, по крайней мере, найдется один элемент, минор которого отличен от нуля. В этом случае уравнение, в котором данный элемент является коэффициентом при неизвестной, является следствием двух других уравнений и задача сводится к решению этих уравнений.

Таким образом, задача сводится к решению системы (3) и имеет бесчисленное множество решений.

в) и все его миноры равны нулю. В этом случае два уравнения являются следствием одного, т. е. система сводится к одному уравнению с тремя неизвестными, совместна и имеет бесчисленное множество решений.

4°. Система трех линейных неоднородных уравнений с тремя неизвестными

При решении возможны три случая:

а) , система имеет единственное решение, определяемое по формулам Крамера аналогично решению (2)

б) но найдется, по крайней мере, один элемент, минор которого не равен нулю. Если в главном определителе заменить столбец, где находится этот элемент, столбцом из свободных членов и дополнительный определитель не будет равен нулю, то система несовместна. Если же дополнительный определитель будет равен нулю, то уравнение в котором данный элемент является коэффициентом при неизвестной, будет следствием двух других уравнений и система имеет бесчисленное множество решений.

в) и все его миноры равны нулю. Если хотя бы один минор дополнительных определителей отличен от нуля, то система несовместна. Если же все миноры дополнительных определителей равны нулю, то система сводится к одному уравнению, совместна и имеет бесчисленное множство решений.

Примеры с решением

Пример 1.

Пользуясь определителями 2-го порядка решить системы:

Решение:

а) Главный определитель системы

Дополнительные определители

Отсюда по формулам Крамера

б) Система несовместна.

а) Второе уравнение системы есть следствие первого; система имеет бесчисленное множество решений.

Пример 2.

Найти решения системы

Решение:

Ненулевые решения находим по формулам (4)

где к — произвольное число.

Задаваясь различными значениями к получим бесчисленное множество решений.

Пример 3.

Решить системы:

Решение:

а) Главный определитель

Система имеет только нулевое решение

б) Минор первого элемента первой строки не равен нулю, следовательно, система сводится к двум уравнениям (третье уравнение есть сумма первых двух). Решая первые два уравнения по формулам (4), получим

Пример 4.

Решить системы:

Решение:

а) Находим главный определитель

и дополнительные

По формулам Крамера

Третье уравнение есть сумма первых двух и система сводится к решению первых двух уравнений

где — произвольно, т. е. система имеет множество решений.

и все миноры равны нулю.

Поскольку все миноры дополнительных определителей равны нулю, то система сводится к одному уравнению

где — произвольны.

и все миноры равны нулю.

Поскольку миноры дополнительных определителей отличны от нулей, то система несовместна.

Пример 5.

Определить значение коэффициента а, при котором система линейных однородных уравнений имеет ненулевое решение

Решение:

Поскольку система однородная, то она ненулевое решение имеет только в том случае, когда определитель системы равен нулю

Разрешая определитель относительно , получим , откуда . Подставим найденное значение в систему.

Поскольку определитель системы , а среди миноров второго порядка имеются отличные от нуля, к примеру,

то одно из уравнений является следствием двух других, и система равносильна системе двух уравнений с тремя неизвестными

Решение находим по формулам (4)

или — произвольное число.

Задаваясь различными значениями к, получаем бесчисленное множество решений.

Правило Крамера

Рассмотрим систему п линейных уравнений с неизвестными

Или же в матричной форме . где квадратная матрица имеет компоненты а столбцы — соответственно компоненты Определение 6.4.1. Упорядоченный набор чисел будем называть решением системы линейных уравнений, если при подстановке этих чисел в систему мы получаем тождество. Имеет место

Теорема 6.4.1. (Правило Крамера)

Если то существует единственное решение системы линейных уравнений 6.4.1.г определяемое формулами

-Й столбец

— определитель матрицы, получаемой из матрицы системы уравнений , заменой ее -го столбца на столбец свободных членов . Доказательство:

1°. Получим вначале утверждение теоремы в предположении, что система (6.4.1.) имеет решение то есть когда выполняются равенства

Умножив обе части этих равенств на алгебраическое дополнение и просуммировав по j , получим

Изменим порядок суммирования (то есть выполним перегруппировку слагаемых) в левой части этого равенства:

Но выражение в круглых скобках равно (по теореме 6.3.2.), поэтому, учитывая, что

Или, окончательно, 2°. Докажем теперь, что в условиях теоремы совокупность чисел

есть решение данной системы линейных уравнений. Пре — А

образуем левые части исходной системы линейных уравнений (6.4.1.)

Для получения последнего равенства мы снова изменили порядок суммирования и воспользовались теоремой 6.3.2.

Теорема доказана.

Содержание:

Методы решения систем линейных алгебраических уравнений (СЛАУ)

Метод Крамера

Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение

Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы

Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 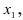для этого умножим все элементы первого столбца на эту неизвестную:

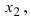
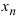
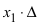
Второй столбец умножим на третий столбец – на -ый столбец – на и все эти произведения прибавим к первому столбцу, при этом произведение не изменится:

Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.

Определение: Определитель 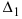называется первым вспомогательным определителем СЛАУ.

Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:

31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.

Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 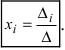Проанализируем полученные формулы:

Пример:

Решить СЛАУ методом Крамера

Решение:

Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом

Найдем главный определитель СЛАУ (раскрываем по первой строке)

Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя

Воспользуемся формулами Крамера

Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.

Выполним проверку 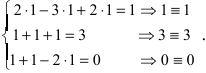Отсюда видно, что СЛАУ решена верно.

• Заказать решение задач по высшей математике

Матричный способ решения СЛАУ

Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных матpицы-столбцы неизвестных и свободных коэффициентов

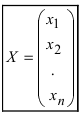
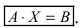
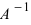
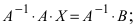
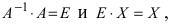
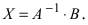
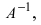
Тогда СЛАУ можно записать в матричном виде Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу к матрице А, получим в силу того, что произведение найдем Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к А матрицу после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.

Пример:

Решить СЛАУ матричным способом

Решение:

Введем в рассмотрение следующие матрицы

Найдем матрицу 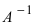(см. Лекцию № 2): найдем детерминант матрицы А.

Пример:

Решение:

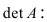
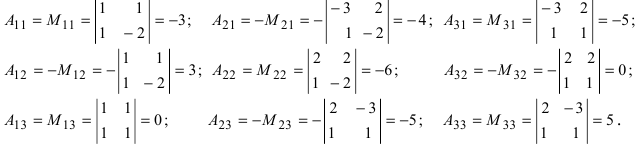
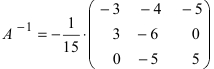
Найдем алгебраические дополнения всех элементов Запишем обратную матрицу (в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В:

Отсюда находим, что х = 1; y = l; z = l.

Метод Гаусса

Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:

Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.

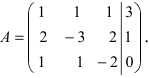
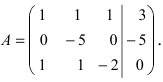
Обменяем в расширенной матрице первую и вторую строки местами, получим Приведем матрицу к треугольному виду, выполнив следующие преобразования: умножим элементы первой строки на (-2) и прибавим к соответствующим элементам второй строки Разделим все элементы второй строки на (-5), получим эквивалентную матрицу

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки Разделим все элементы третьей строки на (-3), получим Таким образом, эквивалентная СЛАУ имеет вид (напомним, что первый столбец это коэффициенты при неизвестной х, второй – при неизвестной у, третий – при неизвестной z, а за вертикальной чертой находится столбец свободных коэффициентов):

Из первого уравнения находим, что х = 1.

Вывод: Из вышеизложенного материала следует, что вне зависимости от

способа решения СЛАУ всегда должен получаться один и тот же ответ.

Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.

Ранг матрицы. Теорема Кронекера-Капелли

Определение: Рангом матрицы 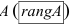называется наивысший порядок отличного от нуля минора этой матрицы.

Если 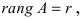то среди всевозможных миноров этой матрицы есть хотя бы один минор порядка r, который отличен от нулю, а все миноры порядков больших, чем r, равны нулю.

При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.

Пример:

Найти ранг матрицы

Решение:

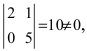
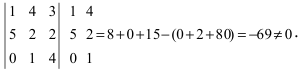
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, среди миноров третьего порядка также есть миноры, которые не равны нулю, например, Очевидно, что определитель четвертого порядка равен нулю, так как он будет содержать строку, состоящую из одних нулей (см. свойство для определителей). Следовательно, ранг матрицы А равен 3.

Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.

Следствия из теоремы Кронекера – Капелли

Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).

Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).

В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.