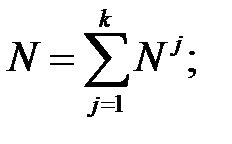Правило трех сигм
Содержание:
- В чем заключается правило трех сигм (3-sigma rule) в статистике
- Нормальное распределение случайной величины
- Примеры решения задач
В чем заключается правило трех сигм (3-sigma rule) в статистике
Определение
Математическое ожидание — это среднее значение случайной величины. Обозначается как (mu).
Определение
Стандартное или среднеквадратичное отклонение — это наиболее частый показатель рассеивания значений величины относительно математического ожидания. Обозначается символом (sigma), который произносится как «сигма».
Определение
Правило трех сигм заключается в том, что при нормальном распределении практически все значения величины с вероятностью 0,9973 лежат не далее трех сигм в любую сторону от математического ожидания, то есть находятся в диапазоне (left[mu-3sigma;;mu+3sigmaright]).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Приблизительно 99,7% всех значений лежат в пределе трех сигм от математического ожидания, около 95% — в пределах двух сигм, а примерно 68% значений лежат в пределах всего одной сигмы.
Те значения, которые выходят за рамки 3 сигм, принято считать грубыми ошибками. Большое количество таких ошибок может свидетельствовать о том, что распределение на самом деле не является нормальным. В этом заключается практическая польза правила 3 сигм.
Нормальное распределение случайной величины
Определение
Нормальное распределение (распределение Гаусса) — это такое распределение вероятностей, функция плотности которого совпадает с функцией Гаусса.
(fleft(xright)=frac1{sigmasqrt{2pi}}expleft(-frac{left(x-muright)^2}{2sigma^2}right))
где (mu) — значение математического ожидания, (sigma) – величина среднеквадратического отклонения, (sigma^2) — дисперсия распределения.
Определение
Функция плотности — это функция, которая характеризует сравнительную вероятность реализации определенных значений случайной переменной или переменных.
Иными словами, функция плотности показывает, с какой вероятностью случайное значение будет равно заданному. Чем «выше» значение по оси ординат, тем больше вероятность, что случайное значение будет равно данному по оси абсцисс. Таким образом, на графике нормального распределения наиболее вероятно то значение, которое совпадает с точкой максимума. А те значения, которые находятся в «основании» графика, то есть находятся низко по оси Y, менее вероятны.
Нормальное распределение величины центрировано и нормировано.
График нормального распределения тесно связан с центральной предельной теоремой (ЦПТ). Согласно ЦПТ, сумма достаточно большого количества слабо зависимых случайных величин имеет распределение, близкое к нормальному.
Пример
Нормальное распределение не является абстрактным понятием. Ему соответствуют некоторые характеристики живых организмов в популяции, отклонение от мишени при стрельбе, измерения и их погрешности. Во всех этих случаях наиболее распространена группа близких значений, но есть отклонения как в большую, так и в меньшую сторону.
Примеры решения задач
Рассмотрим несколько простых задач на применение правила 3 сигм.
Задача 1
Имеется выборка жителей богатого дома. Средняя зарплата жильцов составляет 150 000 рублей, среднеквадратичное отклонение равно 20 000 рублей. Определите, жители с какой зарплатой вряд ли могут жить в этом доме: А) 205 000 рублей; Б) 95 000; В) 230 000; Г) 87 000.
Решение
Чтобы решить данную задачу, необходимо определить, каковы верхние и нижние границы возможных зарплат в доме. Для этого воспользуемся правилом 3 сигм.
(s_{нижн.}=mu-3sigma=150;000-3cdot20;000=150;000-60;000=90;000)
(s_{верх.}=mu+3sigma=150;000+3cdot20;000=150;000+60;000=210;000)
Значения А, Б входят в диапазон (left[90;000;;210;000right]). Значения В, Г не входят в него и, следовательно, являются искомыми грубыми ошибками.
Ответ: В, Г.
Задача 2
Завод выпускает партии по 100 цилиндрических деталей. Диаметр каждой детали — случайная величина, распределенная по нормальному закону. Математическое ожидание равно 65 мм, а среднее отклонение составляет 0,9 мм. Для упаковки партии используют коробки шириной 6600 мм. Детали кладут в один ряд. Если детали не поместятся в одну коробку, придется брать еще одну. Найдите вероятность, что понадобится только одна коробка.
Решение
Т. к. диаметр каждой детали распределен нормально, то и их общий диаметр также будет распределен нормально.
Чтобы все детали поместились в одну коробку, необходимо, чтобы отклонение диаметра всех деталей отклонялось от ожидаемого не более чем на 100 мм. Это следует из того, что математическое ожидание общего диаметра всех деталей равно (65cdot100=6500). А ширина коробки составляет 6600 мм.
Для расчета воспользуемся формулами дисперсии и правилом 3 сигм, чтобы вычислить вероятность, что понадобится только одна коробка.
(Pleft|X-M(X)right|<100;Rightarrow2Phileft[frac{100}{100sigma}right]=2Phileft[1,111right]=2cdot0,3665=0,733)
Ответ: 0,733
Нормальным называют распределение вероятностей непрерывной случайной величины
, плотность которого имеет вид:
где
–
математическое ожидание,
–
среднее квадратическое отклонение
.
Вероятность того, что
примет
значение, принадлежащее интервалу
:
где
– функция Лапласа:
Вероятность того, что абсолютная
величина отклонения меньше положительного числа
:
В частности, при
справедливо
равенство:
Асимметрия, эксцесс,
мода и медиана нормального распределения соответственно равны:
, где
Правило трех сигм
Преобразуем формулу:
Положив
. В итоге получим
если
, и, следовательно,
, то
то есть вероятность того, что
отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонение, равна 0,9973.
Другими словами, вероятность того,
что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна
0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие
события исходя из принципа невозможности маловероятных
событий можно считать практически невозможными. В этом и состоит
сущность правила трех сигм: если случайная величина распределена нормально, то
абсолютная величина ее отклонения от математического ожидания не превосходит
утроенного среднего квадратического отклонения.
На практике правило трех сигм
применяют так: если распределение изучаемой случайной величины неизвестно, но
условие, указанное в приведенном правиле, выполняется, то есть основание
предполагать, что изучаемая величина распределена нормально; в противном случае
она не распределена нормально.
Смежные темы решебника:
- Таблица значений функции Лапласа
- Непрерывная случайная величина
- Показательный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Пример 2
Ошибка
высотометра распределена нормально с математическим ожиданием 20 мм и средним
квадратичным отклонением 10 мм.
а) Найти
вероятность того, что отклонение ошибки от среднего ее значения не превзойдет 5
мм по абсолютной величине.
б) Какова
вероятность, что из 4 измерений два попадут в указанный интервал, а 2 – не
превысят 15 мм?
в)
Сформулируйте правило трех сигм для данной случайной величины и изобразите
схематично функции плотности вероятностей и распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
а) Вероятность того, что случайная величина, распределенная по
нормальному закону, отклонится от среднего не более чем на величину
:
В нашем
случае получаем:
б) Найдем
вероятность того, что отклонение ошибки от среднего значения не превзойдет 15
мм:
Пусть событие
– ошибки 2
измерений не превзойдут 5 мм и ошибки 2 измерений не превзойдут 0,8664 мм
– ошибка не
превзошла 5 мм;
– ошибка не
превзошла 15 мм
в)
Для заданной нормальной величины получаем следующее правило трех сигм:
Ошибка высотометра будет лежать в интервале:
Функция плотности вероятностей:
График плотности распределения нормально распределенной случайной величины
Функция распределения:
График функции
распределения нормально распределенной случайной величины
Задача 1
Среднее
количество осадков за июнь 19 см. Среднеквадратическое отклонение количества
осадков 5 см. Предполагая, что количество осадков нормально-распределенная
случайная величина найти вероятность того, что будет не менее 13 см осадков.
Какой уровень превзойдет количество осадков с вероятностью 0,95?
Задача 2
Найти
закон распределения среднего арифметического девяти измерений нормальной
случайной величины с параметрами m=1.0 σ=3.0. Чему равна вероятность того, что
модуль разности между средним арифметическим и математическим ожиданием
превысит 0,5?
Указание:
воспользоваться таблицами нормального распределения (функции Лапласа).
Задача 3
Отклонение
напряжения в сети переменного тока описывается нормальным законом
распределения. Дисперсия составляет 20 В. Какова вероятность при изменении
выйти за пределы требуемых 10% (22 В).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Автомат
штампует детали. Контролируется длина детали Х, которая распределена нормально
с математическим ожиданием (проектная длинна), равная 50 мм. Фактическая длина
изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что
длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.
Задача 5
Случайная
величина X распределена нормально с математическим ожиданием a=10и средним
квадратическим отклонением σ=5. Найти
интервал, симметричный относительно математического ожидания, в котором с
вероятностью 0,9973 попадает величина Х в результате испытания.
Задача 6
Заданы
математическое ожидание ax=19 и среднее квадратическое отклонение σ=4
нормально распределенной случайной величины X. Найти: 1) вероятность
того, что X примет значение, принадлежащее интервалу (α=15;
β=19); 2) вероятность того, что абсолютная величина отклонения значения
величины от математического ожидания окажется меньше δ=18.
Задача 7
Диаметр
выпускаемой детали – случайная величина, распределенная по нормальному закону с
математическим ожиданием и дисперсией, равными соответственно 10 см и 0,16 см2.
Найти вероятность того, что две взятые наудачу детали имеют отклонение от
математического ожидания по абсолютной величине не более 0,16 см.
Задача 8
Ошибка
прогноза температуры воздуха есть случайная величина с m=0,σ=2℃. Найти вероятность
того, что в течение недели ошибка прогноза трижды превысит по абсолютной
величине 4℃.
Задача 9
Непрерывная
случайная величина X распределена по нормальному
закону: X∈N(a,σ).
а) Написать
плотность распределения вероятностей и функцию распределения.
б) Найти
вероятность того, что в результате испытания случайная величина примет значение
из интервала (α,β).
в) Определить
приближенно минимальное и максимальное значения случайной величины X.
г) Найти
интервал, симметричный относительно математического ожидания a, в котором с
вероятностью 0,98 будут заключены значения X.
a=5; σ=1.3;
α=4; β=6
Задача 10
Производится измерение вала без
систематических ошибок. Случайные ошибки измерения X
подчинены нормальному закону с σx=10. Найти вероятность того, что измерение будет
произведено с ошибкой, превышающей по абсолютной величине 15 мм.
Задача 11
Высота
стебля озимой пшеницы – случайная величина, распределенная по нормальному закону
с параметрами a = 75 см, σ = 1 см. Найти вероятность того, что высота стебля:
а) окажется от 72 до 80 см; б) отклонится от среднего не более чем на 0,5 см.
Задача 12
Деталь,
изготовленная автоматом, считается годной, если отклонение контролируемого
размера от номинала не превышает 10 мм. Точность изготовления деталей
характеризуется средним квадратическим отклонением, при данной технологии
равным 5 мм.
а)
Считая, что отклонение размера детали от номинала есть нормально распределенная
случайная величина, найти долю годных деталей, изготовляемых автоматом.
б) Какой
должна быть точность изготовления, чтобы процент годных деталей повысился до
98?
в)
Написать выражение для функции плотности вероятности и распределения случайной
величины.
Задача 13
Диаметр
детали, изготовленной цехом, является случайной величиной, распределенной по
нормальному закону. Дисперсия ее равна 0,0001 см, а математическое ожидание –
2,5 см. Найдите границы, симметричные относительно математического ожидания, в
которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали. Какова
вероятность того, что в серии из 1000 испытаний размер диаметра двух деталей
выйдет за найденные границы?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Предприятие
производит детали, размер которых распределен по нормальному закону с
математическим ожиданием 20 см и стандартным отклонением 2 см. Деталь будет
забракована, если ее размер отклонится от среднего (математического ожидания)
более, чем на 2 стандартных отклонения. Наугад выбрали две детали. Какова вероятность
того, что хотя бы одна из них будет забракована?
Задача 15
Диаметры
деталей распределены по нормальному закону. Среднее значение диаметра равно d=14 мм
, среднее квадратическое
отклонение σ=2 мм
. Найти вероятность того,
что диаметр наудачу взятой детали будет больше α=15 мм и не меньше β=19 мм; вероятность того, что диаметр детали
отклонится от стандартной длины не более, чем на Δ=1,5 мм.
Задача 16
В
электропечи установлена термопара, показывающая температуру с некоторой
ошибкой, распределенной по нормальному закону с нулевым математическим
ожиданием и средним квадратическим отклонением σ=10℃. В момент когда термопара
покажет температуру не ниже 600℃, печь автоматически отключается. Найти
вероятность того, что печь отключается при температуре не превышающей 540℃ (то
есть ошибка будет не меньше 30℃).
Задача 17
Длина
детали представляет собой нормальную случайную величину с математическим
ожиданием 40 мм и среднеквадратическим отклонением 3 мм. Найти:
а)
Вероятность того, что длина взятой наугад детали будет больше 34 мм и меньше 43
мм;
б)
Вероятность того, что длина взятой наугад детали отклонится от ее
математического ожидания не более, чем на 1,5 мм.
Задача 18
Случайное
отклонение размера детали от номинала распределены нормально. Математическое
ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно
0,25 мм, стандартами считаются детали, размер которых заключен между 199,5 мм и
200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась
и характеризуется средним квадратическим отклонением 0,4 мм. На сколько
повысился процент бракованных деталей?
Задача 19
Случайная
величина X~N(1,22). Найти P{2
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 20
Заряд пороха для охотничьего ружья
должен составлять 2,3 г. Заряд отвешивается на весах, имеющих ошибку
взвешивания, распределенную по нормальному закону со средним квадратическим
отклонением, равным 0,2 г. Определить вероятность повреждения ружья, если максимально
допустимый вес заряда составляет 2,8 г.
Задача 21
Заряд
охотничьего пороха отвешивается на весах, имеющих среднеквадратическую ошибку
взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить
вероятность повреждения ружья, если максимально допустимый вес порохового
заряда 2,5 г.
Задача 21
Найти
вероятность попадания снарядов в интервал (α1=10.7; α2=11.2).
Если случайная величина X распределена по
нормальному закону с параметрами m=11;
σ=0.2.
Задача 22
Плотность
вероятности распределения случайной величины имеет вид
Найти
вероятность того, что из 3 независимых случайных величин, распределенных по
данному закону, 3 окажутся на интервале (-∞;5).
Задача 23
Непрерывная
случайная величина имеет нормальное распределение. Её математическое ожидание
равно 12, среднее квадратичное отклонение равно 2. Найти вероятность того, что
в результате испытания случайная величина примет значение в интервале (8,14)
Задача 24
Вероятность
попадания нормально распределенной случайной величины с математическим
ожиданием m=4 в интервал (3;5) равна 0,6. Найти дисперсию данной случайной
величины.
Задача 25
В
нормально распределенной совокупности 17% значений случайной величины X
меньше 13% и 47% значений случайной величины X
больше 19%. Найти параметры этой совокупности.
Задача 26
Студенты
мужского пола образовательного учреждения были обследованы на предмет
физических характеристик и обнаружили, что средний рост составляет 182 см, со
стандартным отклонением 6 см. Предполагая нормальное распределение для роста,
найдите вероятность того, что конкретный студент-мужчина имеет рост более 185
см.
Найдем
вероятность того, что нормально
распределенная случайная величина
примет значение из интервала (а
– 3σ,
а + 3σ):
Следовательно,
вероятность того, что значение случайной
величины окажется вне
этого интервала, равна 0,0027, то есть
составляет 0,27% и может считаться
пренебрежимо малой. Таким образом, на
практике можно считать, что все
возможные значения нормально распределенной
случайной величины лежат в интервале
(а
– 3σ,
а + 3σ).
Полученный
результат позволяет сформулировать
правило
«трех сигм»:
если
случайная величина распределена
нормально, то модуль ее отклонения от
х = а не превосходит 3σ.
16.7. Показательное распределение.
Определение.
Показательным
(экспоненциальным) называют
распределение вероятностей непрерывной
случайной величины Х,
которое описывается плотностью
В
отличие от нормального распределения,
показательный закон определяется только
одним параметром λ.
В этом его преимущество, так как обычно
параметры распределения заранее не
известны и их приходится оценивать
приближенно. Понятно, что оценить один
параметр проще, чем несколько.
Найдем
функцию распределения показательного
закона:
Следовательно,
Теперь
можно найти вероятность попадания
показательно распределенной случайной
величины в интервал (а,
b):
.
Значения
функции е-х
можно найти из таблиц.
16.8. Функция надежности.
Пусть
элемент
(то
есть некоторое устройство) начинает
работать в момент времени t0
= 0
и должен проработать в течение периода
времени t.
Обозначим за Т
непрерывную случайную величину – время
безотказной работы элемента, тогда
функция F(t)
= p(T
> t)
определяет вероятность отказа за время
t.
Следовательно, вероятность безотказной
работы за это же время равна
R(t)
= p(T
> t)
= 1 – F(t).
Эта
функция называется функцией
надежности.
16.9. Показательный закон надежности.
Часто
длительность безотказной работы элемента
имеет показательное распределение, то
есть
F(t)
= 1 – e–λt
.
Следовательно,
функция надежности в этом случае имеет
вид:
R(t)
= 1 – F(t)
= 1 – (1 – e-λt)
= e-λt
.
Определение.
Показательным
законом надежности
называют функцию надежности, определяемую
равенством
R(t)
= e–λt
,
где
λ
–
интенсивность отказов.
Пример.
Пусть время безотказной работы элемента
распределено по показательному закону
с плотностью распределения f(t)
= 0,1 e–0,1t
при
t
≥ 0. Найти вероятность того, что элемент
проработает безотказно в течение 10
часов.
Решение.
Так как λ
= 0,1, R(10)
= e-0,1·10
= e-1
= 0,368.
16.10. Математическое ожидание.
Определение.
Математическим
ожиданием дискретной
случайной величины называется сумма
произведений ее возможных значений на
соответствующие им вероятности:
М(Х)
= х1р1
+ х2р2
+ … + хпрп
.
Если
число возможных значений случайной
величины бесконечно, то
,
если полученный ряд сходится абсолютно.
Замечание
1. Математическое
ожидание называют иногда взвешенным
средним,
так как оно приближенно равно среднему
арифметическому наблюдаемых значений
случайной величины при большом числе
опытов.
Замечание
2. Из
определения математического ожидания
следует, что его значение не меньше
наименьшего возможного значения
случайной величины и не больше
наибольше-го.
Замечание
3. Математическое
ожидание дискретной случайной величины
есть неслучай-ная
(постоянная)
величина. В дальнейшем увидим, что это
же справедливо и для непре-рывных
случайных величин.
Пример.
Найдем математическое ожидание случайной
величины Х
– числа стандартных деталей среди трех,
отобранных из партии в 10 деталей, среди
которых 2 бракованных. Составим ряд
распределения для Х.
Из условия задачи следует, что Х
может принимать значения 1, 2, 3.

Пример
2. Определим математическое ожидание
случайной величины Х
– числа бросков монеты до первого
появления герба. Эта величина может
принимать бесконечное число значений
(множество возможных значений есть
множество натуральных чисел). Ряд ее
распределения имеет вид:
|
Х |
1 |
2 |
… |
п |
… |
|
р |
0,5 |
(0,5)2 |
… |
(0,5)п |
… |
Тогда
..+
+(при вычислении дважды использовалась
формула суммы бесконечно убывающей
геометрической прогрессии:,
откуда).
Свойства
математического ожидания.
-
Математическое
ожидание постоянной равно самой
постоянной:
М(С)
= С.
Доказательство.
Если рассматривать С
как дискретную случайную величину,
принимающую только одно значение С
с вероятностью р
= 1, то М(С)
= С·1
= С.
-
Постоянный
множитель можно выносит за знак
математического ожидания:
М(СХ)
= С
М(Х).
Доказательство.
Если случайная величина Х
задана рядом распределения
|
xi |
x1 |
x2 |
… |
xn |
|
pi |
p1 |
p2 |
… |
pn |
то
ряд распределения для СХ
имеет вид:
|
Сxi |
Сx1 |
Сx2 |
… |
Сxn |
|
pi |
p1 |
p2 |
… |
pn |
Тогда
М(СХ)
= Сх1р1
+ Сх2р2
+ … + Схпрп
= С(
х1р1
+ х2р2
+ … + хпрп)
= СМ(Х).
Определение.
Две случайные величины называются
независимыми,
если закон распределения одной из них
не зависит от того, какие значения
приняла другая. В противном случае
случайные величины зависимы.
Определение.
Назовем произведением
независимых случайных величин Х
и Y
случайную величину XY,
возможные значения которой равны
произведениям всех возможных значений
Х
на все возможные значения Y,
а соответствующие им вероят-ности равны
произведениям вероятностей сомножителей.
-
Математическое
ожидание произведения двух независимых
случайных величин равно произведению
их математических ожиданий:
M(XY)
= M(X)M(Y).
Доказательство.
Для упрощения вычислений ограничимся
случаем, когда Х
и Y
принимают только по два возможных
значения:
|
xi |
x1 |
x2 |
|
pi |
p1 |
p2 |
|
уi |
у1 |
у2 |
|
gi |
g1 |
g2 |
Тогда
ряд распределения для XY
выглядит так:
|
ХY |
x1y1 |
x2y1 |
x1y2 |
x2y2 |
|
p |
p1g1 |
p2 |
p1g2 |
p2g2 |
Следовательно,
M(XY)
= x1y1·p1g1
+ x2y1·p2g1
+ x1y2·p1g2
+ x2y2·p2g2
= y1g1(x1p1
+ x2p2)
+ + y2g2(x1p1
+ x2p2)
= (y1g1
+ y2g2)
(x1p1
+ x2p2)
= M(X)·M(Y).
Замечание
1. Аналогично
можно доказать это свойство для большего
количества возможных значений
сомножителей.
Замечание
2.
Свойство 3 справедливо для произведения
любого числа независимых случайных
величин, что доказывается методом
математической индукции.
Определение.
Определим
сумму
случайных величин Х
и Y
как случайную величину Х
+ Y,
возможные значения которой равны суммам
каждого возможного значения Х
с каждым возможным значением Y;
вероятности таких сумм равны произведениям
вероятностей слагаемых (для зависимых
случайных величин – произведениям
вероятности одного слагаемого на
условную вероятность второго).
4)
Математическое ожидание суммы двух
случайных величин ( зависимых или
незави-симых ) равно сумме математических
ожиданий слагаемых:
M
(X
+ Y)
= M
(X)
+ M
(Y).
Доказательство.
Вновь
рассмотрим случайные величины, заданные
рядами распределения, приведен-ными
при доказательстве свойства 3. Тогда
возможными значениями X
+ Y
являются х1
+ у1,
х1
+ у2,
х2
+ у1,
х2
+ у2.
Обозначим их вероятности соответственно
как р11,
р12,
р21
и р22.
Найдем М(
Х
+Y
) = (x1
+ y1)p11
+ (x1
+ y2)p12
+ (x2
+ y1)p21
+ (x2
+ y2)p22
=
=
x1(p11
+ p12)
+ x2(p21
+ p22)
+ y1(p11
+ p21)
+ y2(p12
+ p22).
Докажем,
что р11
+ р22
= р1.
Действительно, событие, состоящее в
том, что X
+ Y
примет
значения х1
+ у1
или
х1
+ у2
и вероятность которого равна р11
+ р22,
совпадает с событием, заключающемся в
том, что Х
= х1
(его вероятность – р1).
Аналогично дока-зывается, что p21
+ p22
= р2,
p11
+ p21
= g1,
p12
+ p22
= g2.
Значит,
M(X
+ Y)
= x1p1
+ x2p2
+ y1g1
+ y2g2
= M
(X)
+ M
(Y).
Замечание.
Из свойства 4 следует, что сумма любого
числа случайных величин равна сумме
математических ожиданий слагаемых.
Пример.
Найти математическое ожидание суммы
числа очков, выпавших при броске пяти
игральных костей.
Найдем
математическое ожидание числа очков,
выпавших при броске одной кости:
М(Х1)
= (1 + 2 + 3 + 4 + 5 + 6)Тому же числу равно математическое
ожидание числа очков, выпавших на любой
кости. Следовательно, по свойству 4М(Х)=
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
16.11.201535.49 Кб15контрольная-реферат по конфликтологии
- #
- #
- #
- #
- #
- #
- #
Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
- среднеквадратическое отклонение,
- среднее квадратическое отклонение,
- среднеквадратичное отклонение,
- квадратичное отклонение,
- стандартный разброс.
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
- в финансах в качестве меры волатильности,
- в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.
Пример:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
| Пред.А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
- А -> (19 + 21 + 19+ 21) / 4 = 20
- Б -> (15 + 26 + 15+ 24) / 4 = 20
Однако, глядя на цифры, можно заметить:
- в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
- в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
- стандартное отклонение компании A = 1,
- стандартное отклонение компании Б ≈ 5.
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения

σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение “xср” вместо “μ”.
Разница между формулами S и σ (“n” и “n–1”)
Состоит в том, что мы анализируем — всю выборку или только её часть:
- только её часть – используется формула S (с “n–1”),
- полностью все данные – используется формула σ (с “n”).
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
x1 – μ = 15 – 20 = -5
x2 – μ = 26 – 20 = 6
x3 – μ = 15 – 20 = -5
x4 – μ = 24 – 20 = 4
3. Каждую полученную разницу возвести в квадрат:
(x1 – μ)² = (-5)² = 25
(x2 – μ)² = 6² = 36
(x3 – μ)² = (-5)² = 25
(x4 – μ)² = 4² = 16
4. Сделать сумму полученных значений:
Σ (xi – μ)² = 25 + 36+ 25+ 16 = 102
5. Поделить на размер выборки (т.е. на n):
(Σ (xi – μ)²)/n = 102 / 4 = 25,5
6. Найти квадратный корень:
√((Σ (xi – μ)²)/n) = √ 25,5 ≈ 5,0498
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
(X1 – Xср)² = (2,5)² = 6,25
(X2 – Xср)² = (–4,5)² = 20,25
(X3 – Xср)² = (–1,5)² = 2,25
(X4 – Xср)² = (–2,5)² = 6,25
(X5 – Xср)² = 5,5² = 30,25
(X6 – Xср)² = 0,5² = 0,25
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это “среднее квадратов отклонений от среднего”. Чтобы её вычислить нужно:
- Вычесть среднее значение из каждого числа
- Возвести каждый результат в квадрат (так получатся квадраты разностей)
- Найти среднее значение квадратов разностей.
Ещё расчёт дисперсии можно сделать по этой формуле:

S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
- одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
- двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
- трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с “n – 1” в знаменателе (случай выборки из генеральной совокупности):
1. Занесите все данные в документ Excel.
2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле “=СТАНДОТКЛОНА(“
4. Выделите поля, где находятся данные, потом закройте скобки.
5. Нажмите Ввод (Enter).
В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.
Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
- при <10% выборка слабо вариабельна,
- при 10% – 20 % — средне вариабельна,
- при >20 % — выборка сильно вариабельна.
Узнайте также про:
- Корреляции,
- Метод Крамера,
- Метод наименьших квадратов,
- Теорию вероятностей
- Интегралы.
Содержание
- Как в офисе.
- Правило трёх сигм
- Среднеквадратическое отклонение. Правило 3-сигма
Как в офисе.
Функция стандартное отклонение это уже из разряда высшей математики относящейся к статистики. В Excel существует несколько вариантов использования Функции стандартного отклонения это:
- Функция СТАНДОТКЛОНП.
- Функция СТАНДОТКЛОН.
- Функция СТАНДОТКЛОНПА
Данные функции в статистике продаж нам понадобятся для выявления стабильности продаж (анализ XYZ). Эти данные можно использовать как для ценообразования, так и для формирования (корректирования) ассортиментной матрицы и для других полезных анализов продаж, о которых я обязательно расскажу в следующих статьях.
Предисловие
Давайте посмотрим на формулы сначала математическим языком, а после (ниже по тексту) подробно разберем формулу в Excel и как получившийся результат применяется в анализе статистических данных продаж.
Итак, Стандартное отклонение — это оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии )))) Не пугайтесь не понятных слов, потерпите и Вы все поймете!
Чтобы рассчитать Стандартное отклонение, нам нужно выяснить Среднеквадратическое отклонение по формуле
Описание формулы: Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины
Теперь стандартное отклонение — оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии:
— i -й элемент выборки;
— среднее арифметическое выборки:
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной.
Правило трёх сигм () — практически все значения нормально распределённой случайной величины лежат в интервале . Более строго — приблизительно с 0,9973 вероятностью значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина истинная, а не полученная в результате обработки выборки). Мы же будем использовать округленный интервал 0,1
Если же истинная величина неизвестна, то следует пользоваться не , а s . Таким образом, правило трёх сигм преобразуется в правило трёх s . Именно это правило поможет нам определить стабильность продаж, но об этом чуть позже.
Теперь Функция стандартного отклонения в Excel
Надеюсь я не слишком Вас загрузил математикой? Возможно кому то данная информация потребуется для реферата или еще каких-нибудь целей. Теперь разжуем как эти формулы работают в Excel.
Для определения стабильности продаж нам не потребуется вникать во все варианты функций стандартного отклонения. Мы будем пользоваться всего одной:
Функция СТАНДОТКЛОНП
СТАНДОТКЛОНП(число1;число2;. )
Число1, число2. — от 1 до 30 числовых аргументов, соответствующих генеральной совокупности.
Теперь разберем на примере:
Давайте создадим книгу и импровизированную таблицу. Данный пример в Excel Вы скачаете в конце статьи.
Продолжение следует.
Подпишитесь на рассылку, что бы не пропустить самое интересное
И снова здравствуйте. Ну что!? Выдалась свободная минутка. Давайте продолжим?
И так стабильность продаж при помощи Функции СТАНДОТКЛОНП
Для наглядности возьмем несколько импровизированных товаров:
В аналитике, будь то прогноз, исследование или еще что то, что связано с статистикой всегда необходимо брать три периода. Это может быть неделя, месяц, квартал или год. Можно и даже лучше всего брать как можно больше периодов, но не менее трех.
Я специально показал утрированные продажи, где не вооруженным глазом видно, что продается стабильно, а что нет. Так проще будет понять как работают формулы.
И так у нас есть продажи, теперь нам нужно рассчитать средние значения продаж по периодам.
Формула среднего значения СРЗНАЧ(данные периода) в моем случае формула выглядит вот так =СРЗНАЧ(C6:E6)
Протягиваем формулу по всем товарам. Это можно сделать взявшись за правый угол выделенной ячейки и протянуть до конца списка. Или поставить курсор на столбец с товаром и нажать следующие комбинации клавиш:
Ctrl + Вниз курсор переместиться в коней списка.
Ctrl + Вправо, курсор переместиться в правую часть таблицы. Еще раз вправо и мы попадем на столбец с формулой.
Ctrl + Shift и нажимаем вверх. Так мы выделим область протягивания формулы.
И комбинация клавиш Ctrl + D протянет функцию там где нам надо.
Запомните эти комбинации, они реально увеличивают Вашу скорость работы в Excel, особенно когда Вы работаете с большими массивами.
Следующий этап, сама функция стандартного откланения, как я уже говорил мы будем пользоваться всего одной СТАНДОТКЛОНП
Прописываем функцию и в значениях функции ставим значения продаж каждого периода. Если у Вас продажи в таблице друг за другом можно использовать диапазон, как у меня в формуле =СТАНДОТКЛОНП(C6:E6) или через точку с запятой перечисляем нужные ячейки =СТАНДОТКЛОНП(C6;D6;E6)
Ну вот, пол дела сделано. Далее находим вариацию для этого Стандартное отклонение делим на среднее значение.
Вот все расчеты и готовы. Но как понять, что продается стабильно, а что нет? Просто проставим условность XYZ где,
Х — это стабильно
Y — с не большими отклонениями
Z — не стабильно
Для этого используем интервалы погрешности. если колебания происходят в пределах 10% будем считать что продажи стабильны.
Если в пределах от 10 до 25 процентов — это будет Y.
И если значения вариации превышает 25% — это не стабильность.
Что бы правильно задать буквы каждому товару, воспользуемся формулой ЕСЛИ подробнее про функцию ЕСЛИ читайте тут. В моей таблице данная функция будет выглядеть так:
Источник
Правило трёх сигм
«Правило трёх сигм» на самом деле очень приблизительное. Оно даёт хорошее приближение только для определённого объёма выборки. Конечно, есть теория, которая предлагает красивую многоэтажную формулу для распределения показателя размаха вариации. Мы поступим попроще и пойдём путём практического знакомства.
Нас интересует, как размах значений зависит от объёма выборки. Чем больше выборка, тем больше шанс, что может появиться очень редкое значение, которое сильно отклонится от среднего. Гораздо дальше, чем на три сигмы.
Попробуем оценить зависимость размаха от объёма выборки. Используем нормальное распределение с нашими параметрами среднего и сигмы. Сгенерируем выборку размером в миллион значений. Первое, что мы обнаруживаем, — ограничение встроенного генератора случайных чисел надстройки Excel: Integer is not valid. Миллион чисел сгенерировать в надстройке не удаётся.
Попробуем сгенерировать хотя бы десять тысяч чисел. На этот раз попытка удалась. Вычислим размах и выразим его в сигмах.
Размах в сигмах
Построим график: объём выборки — размах в сигмах.
Размах и объём выборки
Рассмотрим начало графика поподробнее. Для этого используем логарифмический масштаб. Вместо объёма выборки используем его логарифм. Вставим новый столбец и вычислим lg (n). Здесь нам пригодится функция LOG10.
На графике видно несколько ступенек. Скорее всего, это вызвано недостаточным качеством псевдослучайных чисел. Тем не менее, общая картина просматривается.
При выборке 10 размах равен трём сигмам. При выборке 100 размах 6 сигм. При выборке 10 000 размах равен 13 сигм.
Пользуясь случаем, проверим качество другого генератора случайных чисел Excel. Создадим новый лист и повторим наш эксперимент. Используем метод преобразования — возьмём равномерное распределение и пропустим его через обратное нормальное распределение.
RAND ()
СЛЧИС ()
позволяет сгенерировать случайное число с равномерным распределением в интервале от 0 до 1. Аргументов у функции нет.
Чтобы из равномерного распределения получить нормальное, вызываем функцию NORM.INV. Формат вызова:
=NORM.INV (probability, mean, standard_dev)
=НОРМ. ОБР (вероятность; среднее; стандартное_откл)
Функция работает по принципу x (p). Это обратное преобразование для функции распределения p (x).
probability — вероятность. В нашем случае это равномерно распределённая величина.
mean — среднее. В нашем примере это 250.
standard_dev — с.к. о. В нашем варианте это 20.
Таким образом, вызываем функция со следующими параметрами
=NORM.INV (B2,250,20)
Используем логарифмический масштаб, как в предыдущем варианте.
Размах в сигмах
Особенность функции генератора случайных чисел в том, что он генерирует новые числа (пересчитывает значение функции) при каждом сохранении файла. Попробуем сохранить файл несколько раз. Сделаем копию графиков и вставим их как рисунки на новый лист.
Графики немного отличаются друг от друга. Но при этом общая картина зависимости сохраняется. Чем больше выборка, тем больше размах.
Подведём итоги эксперимента. Правило трёх сигм хорошо работает для выборки объёмом в несколько сотен единиц. Для инженерной работы этого достаточно. А вот если взять хорошую, большую выборку, то размах может вырасти.
Источник
Среднеквадратическое отклонение. Правило 3-сигма
Среднеквадратическое отклонение вычисляется как квадратный корень из выборочной или исправленной дисперсии:
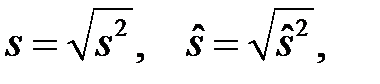
где s 2 и 
В программе Excel среднеквадратическое отклонение (называется стандартное отклонение) вычисляется с помощью функций СТАНДОТКЛОН() и СТАНДОТКЛОНП(). При этом СТАНДОТКЛОНП() соответствует выборочной дисперсии, т.е. значению s, а СТАНДОТКЛОН() отвечает значению 
Пример 3.3. Найти выборочную и исправленную дисперсии для выборки из 10 значений, записанных в диапазоне В2:В11 (рис.3.2).
Решение. В ячейку В12 введите формулу =ДИСП(B2:B11), а в ячейку В13 — формулу =ДИСПР(B2:B11).
Для контроля введем в ячейку С12 формулу
а в ячейку С13 — формулу
Мы увидим, что функция ДИСП() вычисляет исправленную дисперсию, а ДИСПР() — выборочную.
Введите в ячейку В14 формулу
а в ячейку В15 — формулу
Для контроля введите в ячейку С14 формулу =КОРЕНЬ(B12), а в ячейку С15 — формулу =КОРЕНЬ(B13).
Мы видим, что функция СТАНДОТКЛОНП() соответствует квадратному корню из выборочной дисперсии, а СТАНДОТКЛОН() отвечает значению квадратного корня из исправленной дисперсии.
Правило «3-сигма» применяется для приближенной проверки гипотезы о том, что выборка соответствует генеральной совокупности с нормальным законом распределения и выводится из следующего факта. Для нормальной случайной величины с математическим ожиданием a и среднеквадратическим отклонением σ вероятность попадания в интервал (a – 3σ, a + 3σ) равна 0,997. Это следует из формулы (1.7):
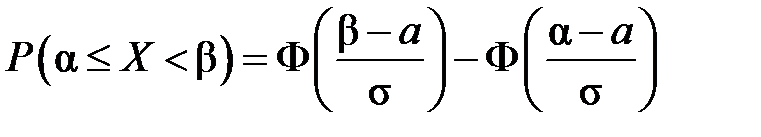
В нашем случае α = a – 3σ, β = a + 3σ. По формуле (1.7) имеем

Значение функции Лапласа можно найти по таблице или с помощью формулы в Excel. Введите в любой ячейке формулу =НОРМСТРАСП(3)-0,5. Получим значение 0,498650102, умножив это значение на 2, получим приближенно 0,997.
Правило «3-сигма».Если «почти все» элементы выборки попадают в интервал 


1.4. Общая, межгрупповая и внутригрупповая дисперсии.
Правило сложения дисперсий
Пусть выборочные данные представлены в виде k групп (верхние индексы обозначают принадлежность группе, а не возведение в степень!):



Общий объем выборки равен
Тогда можно вычислитьобщую, межгрупповую и внутригрупповую дисперсии в следующем порядке.
Групповые средние 



Внутригрупповой дисперсией называется взвешенная средняя групповых дисперсий:

Внутригрупповая дисперсия отражает случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки.
Общая средняя и общая дисперсия вычисляются по формулам:


Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию.
Межгрупповая дисперсия вычисляется по формуле:

Межгрупповая дисперсия характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки.
Существует закон, связывающий три вида дисперсий:

Данное соотношение называютправилом сложения дисперсий.Согласно этому правилу общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.
Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида.
Для демонстрации равенства (3.15) рассмотрим следующий пример.
Пример 3.4. Определить групповые средние, групповые дисперсии, среднюю из групповых дисперсий (внутригрупповую дисперсию), межгрупповую дисперсию, общую дисперсию по данным табл. 3.1, в которой приведены данные о производительности труда трех бригад рабочих-токарей за десять дней работы (за каждый день приведено среднее число изготовленных за час деталей на одного рабочего и число работавших в этот день рабочих в бригаде).
Дать толкование полученным результатам.
| Дни | 1-я бригада | Число работавших | 2-я бригада | Число работавших | 3-я бригада | Число работавших |
Решение. Введите данные в программе Excel в ячейках A1:D11, как показано на рис.3.3.
Объедините следующие группы ячеек: А12:В12, А13:В13, А14:В14, А15:D15, А16:D16, А17:D17, А18:D18, А19:D19 и впишите в них тексты, как показано на рис. 3.3.
В ячейках С12, Е12, G12 просуммируйте соответствующие столбцы с помощью значка «Автосумма» или введите в эти ячейки формулы:
=СУММ(C2:C11), =СУММ(E2:E11), =СУММ(G2:G11).
В ячейку С13 введите формулу
Выделите ячейку С13 и маркером заполнения протяните вправо до ячейки G13, а затем удалите в ячейках D13, F13 содержимое с помощью клавиши «Delete». В ячейках E13, G13 должны получиться формулы:
В ячейки С14, Е14, G14 для вычисления групповых дисперсий введите, соответственно, формулы:
Для вычисления общей средней в ячейку Е15 введите формулу:
Для вычисления внутригрупповой дисперсии в ячейку Е16 введите формулу:
Для вычисления межгрупповой дисперсии в ячейку Е17 введите формулу:
Для вычисления суммы межгрупповой и внутригрупповой дисперсий в ячейку Е18 введите формулу =E16+E17.
Для вычисления общей дисперсии в ячейку Е19 введите формулу:
Результаты вычислений приведены на рис. 3.3. как видим, равенство (3.15) выполняется.
Дадим теперь толкование полученным результатам.
Средняя производительность на одного рабочего за десять дней составляет
в первой бригаде 13,89 деталей в час,
во второй бригаде — 14,52 детали в час,
в третьей бригаде — 16,64 деталей в час.
Средняя производительность на одного рабочего (по всему цеху) за десять дней составляет 15,39 деталей в час.
Межгрупповая дисперсия, равная 1,44, характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки, т.е., в данном случае, принадлежность определенной бригаде.
Внутригрупповая дисперсия равна 1,29 и отражает случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов, другими словами, остаточную дисперсию.
Источник