Тригонометрические функции острого угла
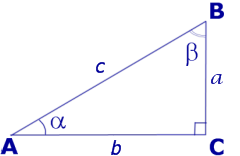
Катеты BC и AC прямоугольного треугольника ABC (рис. 1) называют противолежащим катетом угла α и прилежащим катетом угла α соответственно.
Рис.1
Катеты AC и BC прямоугольного треугольника ABC (рис. 2) называют противолежащим катетом угла β и прилежащим катетом угла β соответственно.
Рис.2
Синусом угла называют дробь:
Косинусом угла называют дробь:
Тангенсом угла называют дробь:
Котангенсом угла называют дробь:
Синус, косинус, тангенс и котангенс, и их комбинации называют тригонометрическими функциями. В данном разделе справочника тригонометрические функции вводятся для острых углов. В следующем разделе даётся определение тригонометрических функций для произвольных углов.
Для синуса, косинуса, тангенса и котангенса угла α используют обозначения
sin α , cos α , tg α , ctg α
Рис.3
В соответствии с рисунком 3 справедливы формулы:
Следовательно,
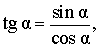
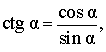
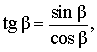
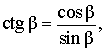
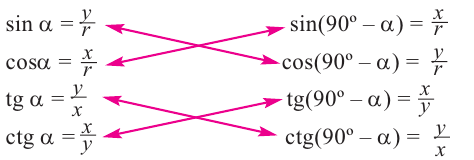
Кроме того, справедливы формулы:
sin α = cos β, cos α = sin β, tg α = ctg β, ctg α = tg β,
которые можно переписать в виде:
sin α = cos (90° – α), cos α = sin (90° – α),
tg α = ctg (90° – α), ctg α = tg (90° – α).
ПРИМЕР. Найти тригонометрические функции углов 30°, 45°, 60°.
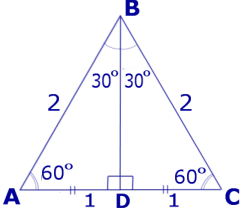
РЕШЕНИЕ. Рассмотрим равносторонний треугольник ABC, сторона которого равна 2 (рис. 4), и проведем высоту BD.
Рис.4
Тогда
Поэтому
Кроме того
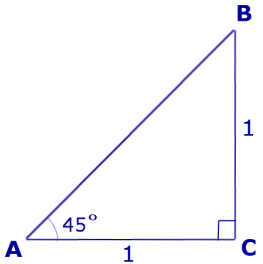
Теперь рассмотрим прямоугольный равнобедренный треугольник ABC, катеты которого равны 1 (рис. 5).
Тогда
Поэтому
Определение тригонометрических функций произвольного угла приводится в разделе справочника “Тригонометрические функции произвольного угла”.
Содержание:
Тригонометрические функции произвольного угла
Угол поворота
До недавнего времени говоря об угле мы имели в виду угол, полученный между двумя неподвижными сторонами. Угол также можно рассматривать как измерение поворота. Например, радиус колеса, расположенного по горизонтали при вращении вокруг неподвижной оси, через определённое время относительно начального положения образует некоторый угол. К тому же значение угла зависит от направления поворота. Любой угол можно рассматривать как фигуру, полученную вращением луча вокруг начальной точки.
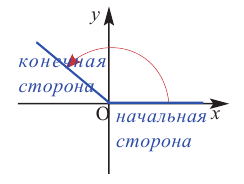
Начальное положение луча соответствует одной стороне угла, конечное положение – другой стороне. При вращении луча на координатной плоскости относительно начала координат в направлении по часовой стрелке или против часовой стрелки, можно получить различные углы.
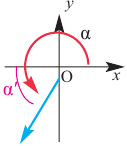
Начальная сторона угла поворота совпадает с положительным направлением оси абсцисс. Сторону, полученную при вращении относительно начала координат (вершины угла), назовём конечной стороной. Принято считать, что если поворот происходит в направлении против часовой стрелки, то угол имеет положительное значение, при повороте в направлении по часовой стрелке, угол имеет отрицательное значение,
положительный угол отрицательный угол
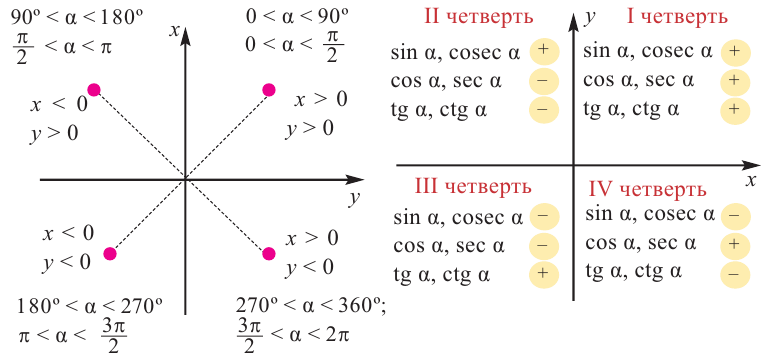
Координатные оси разбивают координатную плоскость на 4 четверти. Значение угла, в зависимости от того, в какой четверти расположена его конечная сторона, меняется в определенном интервале.
Конечная сторона угла может совершить один или несколько оборотов относительно начала координат. Один полный оборот соответствует углу 360°. Существует бесконечное число углов поворота, у которых начальная и конечная стороны совпадают. Например, конечные стороны углов 30°и 390° совпадают. В общем, для углов поворота 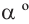
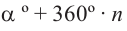
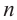
Радианная и градусная мера угла
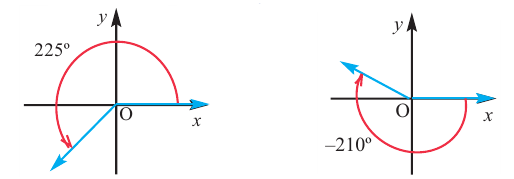
Пример 1. Нарисуйте угол заданной величины. Определите какой четверти принадлежит конечная сторона угла.
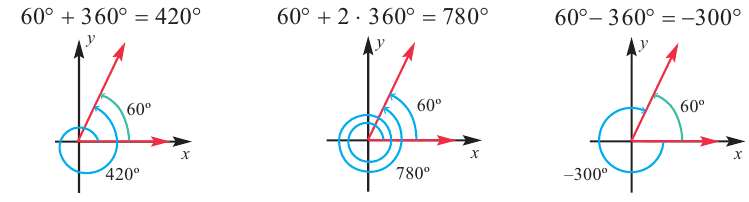
Пример 2. На координатной плоскости покажите и запишите градусные меры двух положительных и одного отрицательного угла поворота, конечные стороны которых совпадают с конечной стороной угла 60°.
Радианное измерение углов
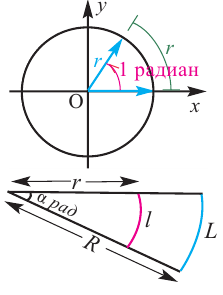
Угол в один радиан-это центральный угол, у которого длина дуги равна радиусу. Радианная мера угла есть отношение длины соответствующей дуги к радиусу окружности: 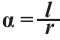
Пример 1. Сколько радиан составляет центральный угол, длина дуги которого равна 12 см, если радиус окружности равен 4 см?
Решение: 1 радиан соответствует длине дуги 4 см. Дуге длиной 12 см будет соответствовать угол 12 : 4 = 3 радиан. Длина окружности 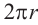
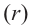
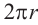
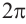
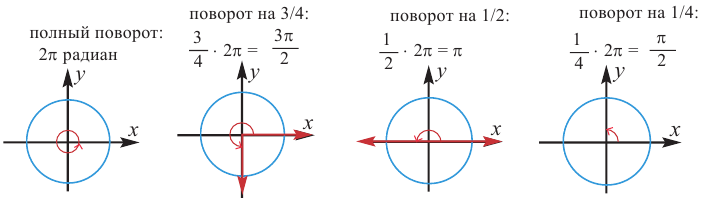
Радианная мера одного целого оборота равна 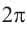
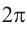
Преобразование градусов в радианы:
Таким образом, 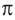
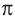
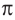
Используя соответствующие радианные и градусные меры углов, расположенных в первой четверти, можно найти увеличенные в разы значения других углов. Например, если 30° =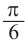
Пример 2. Выразите углы, заданные в градусах радианами, а углы, заданные радианами в градусах, а) 60° ; б)
Решение.
а)60° =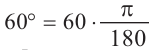
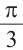

б)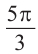
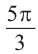
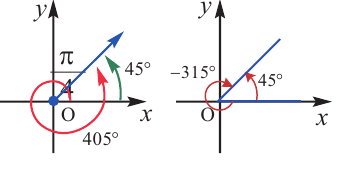
Пример 3. Выразите углы, конечная сторона которых совпадает с углом 45°, в градусах и радианах.
Решение: Конечная сторона угла 45°совпадает с углами 405° и 315°, а также существует бесконечно много углов, конечные стороны которых совпадают с конечной стороной угла 45°: 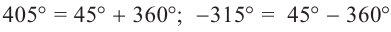
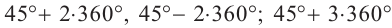
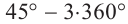
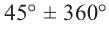
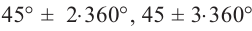
В радианах это можно записать как
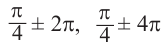
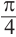
Пример, а)
Все углы поворота, конечные стороны которых совпадают с углом
можно найти но формуле 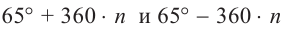
Как видно, в заданном интервале, расположен всего один угол 425°. Пример. д)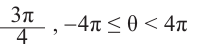
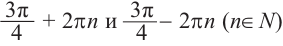
Интервалу 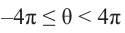
Длина дуги
Запишем формулу нахождения длины дуги, соответствующей центральному углу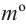
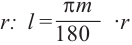
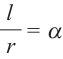
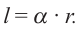
Площадь сектора
Центральному углу 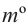
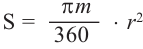
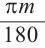
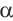
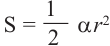
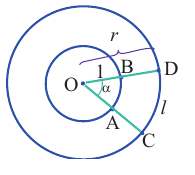
Решение. Секундная стрелка за 60 минут совершают один полный оборот. Это соответствует 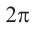
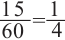
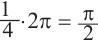
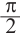
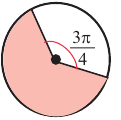
Пример 2. Найдите площадь и периметр закрашенного сектора на рисунке, если радиус круга равен 8 см. Закрашенной части круга соответствует центральный угол:
Площадь сектора равна:
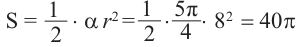
Периметр сектора равен сумме длин двух радиусов и длины дуги: 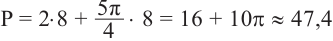
Линейная скорость и угловая скорость
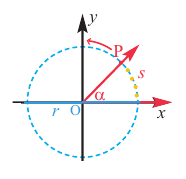
Скорость при движении по окружности, например, скорость движения произвольной точки Р колеса, которое вращается вокруг точки О, может быть вычислена двумя способами.
В первом случае, её можно найти используя расстояние и время. Эта скорость называется линейной скоростью. Во втором случае – используя угол поворота (центральный угол). Эта скорость называется угловой скоростью.
Если тело движется но окружности, то линейная скорость равна отношению пройденного пути (длины дуги окружности) к промежутку времени.
Если тело движется по окружности, то угловая скорость равна отношению угла поворота к промежутку времени.
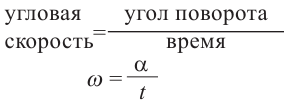
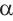
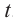
линейная скорость = 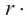
Пример 3. Карусель совершает за минуту 8 полных оборотов.
а)Чему равна угловая скорость карусели за минуту(в радианах)?
б)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 3 м от центра окружности?
в)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 2 м от центра окружности?
Решение:
а) Один целый оборот при вращении соответствует центральному углу 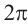
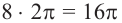
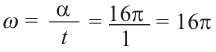
б)Если лошадь находится на расстоянии 3 м от центра, то она движется по окружности радиуса 3 м.
Линейная скорость: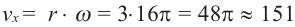
в)Если лошадь находится на расстоянии 2 м от центра, то она движется по окружности радиуса 2 м.
Линейная скорость: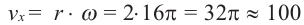
Тригонометрические функции
Тригонометрические отношении для угла зависят только от значения угла.
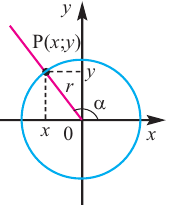
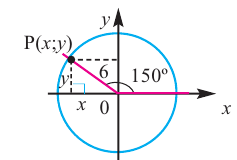
Пусть конечная сторона угла а при повороте пересекается с окружностью радиусом г, центр которой находится в начале координат, в точке Р(х; у).

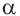

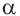

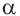
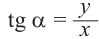
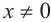

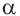
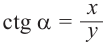
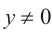

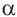
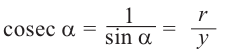
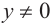

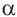
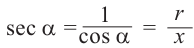
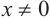
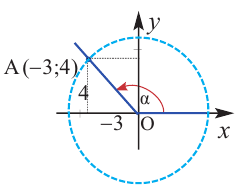
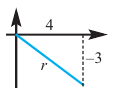
Пример 1. Точка А (- 3; 4) расположена на конечной стороне угла поворота 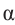
а) Изобразите решение примера.
б) Определите значения тригонометрических отношений для угла поворота 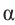
Решение:
а)
б)
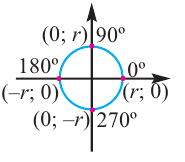
Координаты точки на окружности
Если заданная точка Р окружности находится на конечной стороне угла поворота 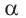
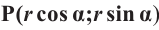
Пример 2. По данным рисунка найдите координаты точки Р.
Точка Р находится во II четверти и косинус отрицательный.
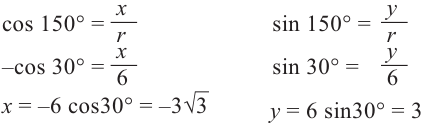
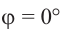
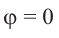
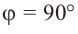
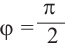
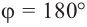
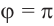
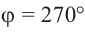
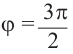
В этом случае координаты х или у равны или нулю, или абсолютному значению длины радиуса.
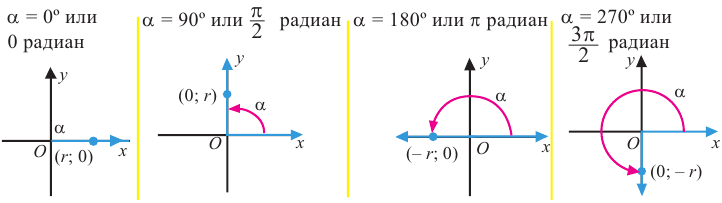
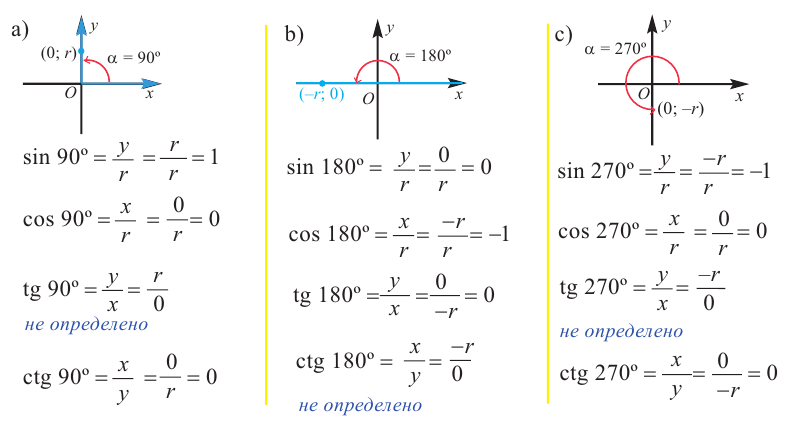
Пример 3. Найдём значения тригонометрических отношений для:
а) а = 90° ; б) а = 180°; в) а = 270° .
При всех допустимых значениях, каждому значению 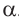
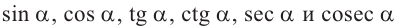
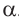
Так как 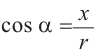
Так как 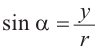
Тригонометрические функции произвольного угла. Нахождение значений тригонометрических функций произвольного угла при помощи острого угла
Чтобы вычислить тригонометрические отношения для углов больше 90°, удобно использовать тригонометрические отношения острого угла.
Для любого угла поворота 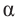
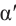
Используя соответствующие острые углы можно определить тригонометрические отношения для любого произвольного угла. Эти значения можно вычислить точно для углов 30°, 45°, 60°, а для остальных острых углов – при помощи калькулятора.
Пример 1. Для следующих углов, определите острые углы:
а)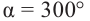
Решение:
а) конечная сторона угла 300° расположена в IV четверти. Соответствующий острый угол равен: 360°- 300° = 60°
б) конечная сторона угла расположена в III четверти. Соответствующий
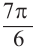
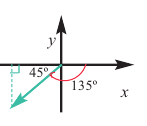
Пример 2. Найдём значение основных тригонометрических функций для угла 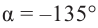
1.Найдём наименьший положительный угол, конечная сторона которого совпадает с заданным углом и дополняет его до 360°: -135° + 360° = 225°
2.Для угла 225° найдём соответствующий острый угол 225° – 180° = 45°.
3.Определим какой четверти принадлежит угол -135° – угол III четверти.
4.Найдём значение тригонометрических функций для угла 45° и учтём знак этих функций в III четверти. Получим:
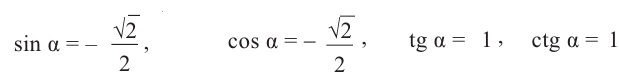
•определяем соответствующий острый угол;
•находим значение тригонометрических функций для этого угла;
•определяем знак значения тригонометрических функций в зависимости от четверти.
Так как конечные стороны углов 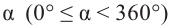
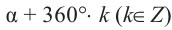
Заметим, что если угол меняется на пол оборота, то значения тангенса и котангенса не изменяются.
На самом деле, если углу поворота 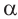
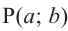
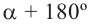

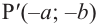
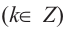
Пример 3. Найдём допустимые значения 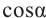
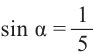
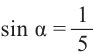
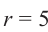
Абсцисса этой точки
Тогда 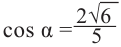
Единичная окружность и тригонометрические функции
Значения тригонометрических функций зависят только от значения угла 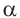
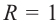
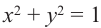
Если точка 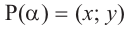
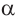
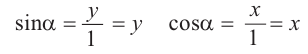
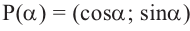
Также по заданным координатам можно найти следующие тригонометрические функции: 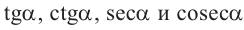
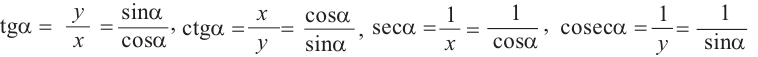
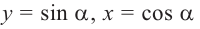
Для этого надо выполнить следующие шаги:
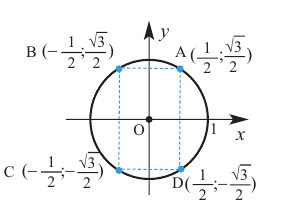
1) На единичной окружности отметим точки, соотвегствующие углу поворота 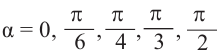
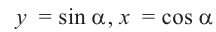
2)Для некоторой точки, принадлежащей единичной окружности, например 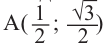
Точка В симметрична точке А относительно оси у, точка С – относительно начала координат, а точка D – относительно оси х. Абсолютные значения координат этих точек равны и отличаются только знаком.
3)Таким образом, можно определить координаты новых точек, зная координаты точки, принадлежащей I четверти. Т.е. получаем единичную окружность, на которой отмечены углы поворота и координаты точек.
- Заказать решение задач по высшей математике
Единичная окружность и тригонометрические функции произвольного угла
Так как координаты точек на единичной окружности удовлетворяют условиям 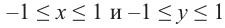
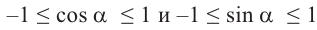
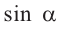
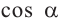
Пример 1. Для угла поворота 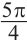
Решение: Конечная сторона угла поворота 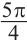
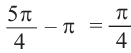
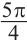
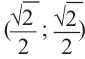
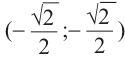
Тогда ,
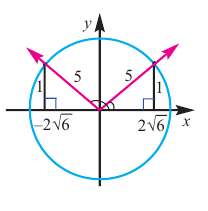
Пример 2. Точка А, с абсциссой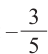
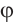
а)Найдём ординату точки А.
б)Изобразим рисунок, соответствующий условию и для угла 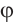
Решение:
а)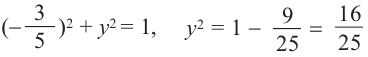
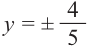
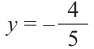
б)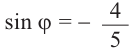
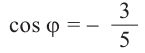
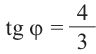
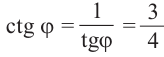
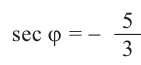
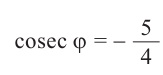
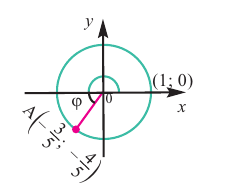
Пример 3. Найдём наибольшее и наименьшее значение выражения 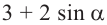
Решение:
Таким образом, для выражения 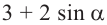
Формулы приведения
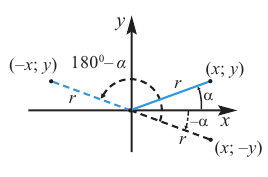
Если объект находится в I четверти, то симметричный ему относительно оси у объект находится во II четверти. Симметричный последнему относительно оси х, объект находится в III четверти, и он совпадает с объектом, симметричным начальному объекту из I относительно начала координат. Обратите внимание, что отображение относительно оси у и отображение, относительно оси х, совпадают с поворотом на 180°.
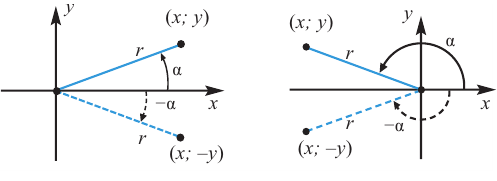
При отображении относительно оси х, точка расположенная на конечной стороне угла изменяет координаты, как показано на рисунке.
То есть, при этом знак меняет только координата у. Таким образом, так как косинус зависит от х он не меняется, зато меняется знак синуса. Отсюда, для углов 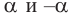
То есть, синус, тангенс и котангенс нечётные функции, косинус-чётная.
Пример 1:
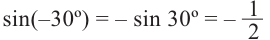
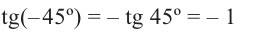
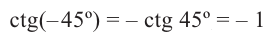

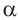
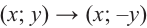
Отсюда получаем:
Запишем для углов 


При попарном сравнении равенств можно увидеть следующую связь-между значениями тригонометрических функций углов 

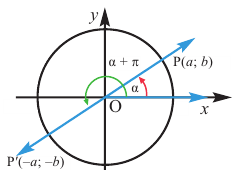
Повернём конечную сторону угла поворота 
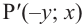
Запишем эти формулы в следующем виде:
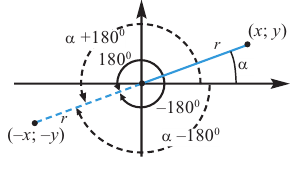
Как видно но рисунку отображения относительно оси у и оси х эквивалентны повороту на 180°. Изменение координат, можно записать следующим образом:
Как видно по рисунку, при повороте угла а на 180° конечная сторона расположена в противоположных четвертях, но на одной прямой.
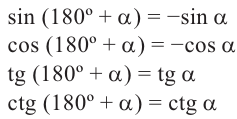
Пример 2.
Для получения аналогичных формул тригонометрических функций угла поворота 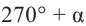
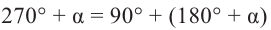
Например:
Теперь запишем соответствующие формулы для угла поворота 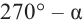
При помощи полученных формул можно найти значения тригонометрических функций произвольного угла, зная значения для соответствующего острого угла. Эти формулы называются формулами приведения. Для формул приведений можно легко увидеть следующую закономерность
1)Если аргумент имеет вид 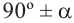
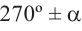
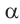
2)Если аргумент имеет вид 180° ± 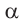
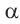
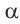
В каждом из обоих случаев, знак полученной в результате преобразования функции имеет одинаковое значение со знаком острого угла 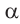
Тригонометрические тождества
Для острого угла 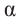
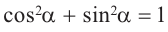
1)Запишите теорему Пифагора:
2)Каждую из сторон равенства разделите на с2:
3)Примените свойство степени:
4) Примите во внимание, что:
Связь между тригонометрическими функциями одного и того же угла
Тождество 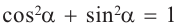
По координатам точки на единичной окружности и по определениям тригонометрических функций имеем:
Для всех значений 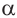
Для всех значений 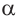
Из данных равенств имеем,что если для угла 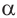
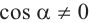
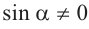
Разделив обе чаете равенства 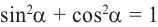
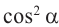
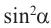
Полученные выше равенства являются тождествами. Их называют основными тригонометрическими тождествами. На основании основных тригонометрических можно написать:
При помощи основных тригонометрических тождеств можно упрощать тригонометрические выражения и вычислять модуль значения всех остальных функций, зная значение одной из них.
Пример 1. Используя основные тригонометрические тождества, докажите,что:
Доказательство:
Пример 2. Зная, что 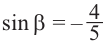
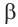
остальные тригонометрические функции.
Из формул 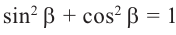
Так как угол 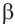
Тогда:
Формулы сложения
Практическая работа .
1)Покажем по шагам, равенство выражения
a)Для значений 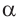
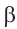
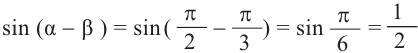
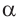
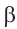
2)Как можно вычислить значение тригонометрических функций для угла 15°, используя разность значений углов 45° и 30°(15° = 45° – 30°)?
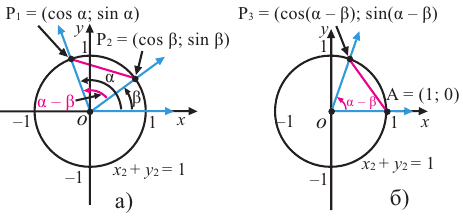
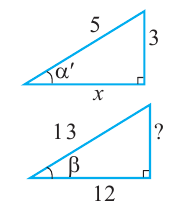
Тригонометрические функции суммы и разности двух углов.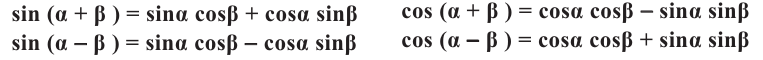

На рисунке
а)для угла 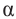
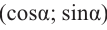
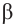
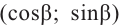
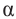
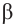
Тогда, для угла 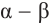
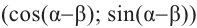
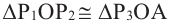
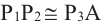

учитывая, что
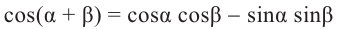

no формулам приведения группируя
no формуле косинуса разности с учётом формул приведения.

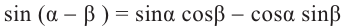
Пример 1. Найдём значение выражения 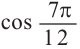
Решение.
Пример 2.
Найдём значение выражения 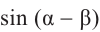
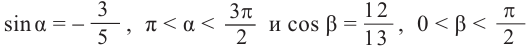
Решение.
Известно что 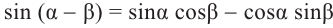
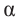
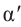
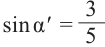
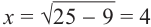
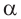
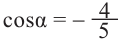
Аналогично, если зная, что 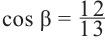
что 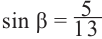
Можно записать формулы сложения для тангенса и котангенса:
no определению no формулам сложения
Аналогичным образом можно показать, что :
Следствия из формул сложения
Практическая работа.
Преобразуйте сумму 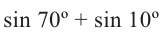
1)
решив систему уравнений найдите такие углы, чтобы их сумма была равна 70°, а разность
2)Запишите следующее 70° = 40° + 30°, 10° = 40° – 30° и упростите
Преобразование суммы(разности) в произведение
Формулы преобразования произведения
Справедливость данных тождеств можно показать при помощи формул сложения:
почленно складываем почленно складываем
Следующее тождество можно доказать аналогичным образом.
Тригонометрические функции двойного аргумента
Формулы сложения позволяют выразить 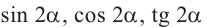
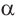
Таким образом, получаем тождества, которые называются формулами двойного аргумента:
Формулы половинного аргумента
Имеем, что
Отсюда: 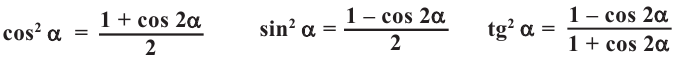
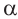
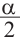
Для половинных аргументов справедливы тождества. 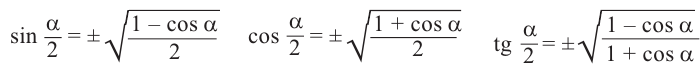
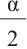
Пример 1. Упростим выражение 
Решение.
Пример 2. He используя калькулятор, вычислим значения 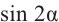
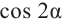

Решение.
Пример 3. Найдём значений 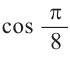
Решение:
Используем формулу половинного аргумента
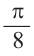
Упрощение тригонометрических выражений
Пример 1. Раскроем скобки и упростим выражение.
Пример 2. Разложим на множители и упростим выражение.
Пример 3. Упростим рациональное выражение, содержащее тригонометрические функции.
Пример 4. Освободим знаменатель от радикала
Здесь 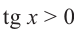
- Теоремы синусов и косинусов
- Система показательных уравнений
- Непрерывные функции и их свойства
- Правило Лопиталя
- Решение уравнений высших степеней
- Системы неравенств
- Квадратные неравенства
- Точка, прямая и плоскость в пространстве
План урока:
Основные тригонометрические функции
Взаимосвязь между тригонометрическими функциями
Тригонометрические функции стандартных углов
Поиск тангенса на квадратной решетке
Основные тригонометрические функции
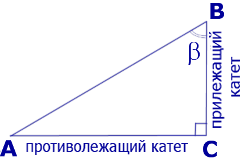
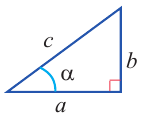
Пусть есть некоторый прямоугольный треугольник АBС, у которого∠С = 90°. Обозначим какой-нибудь его острый угол, например, ∠А, греческой буквой α. В треугольнике есть два катета. Тот из них, который, непосредственно является одной из сторон угла α, называют прилежащим катетом. Другой катет именуют противолежащим. Ещё одна сторона треугольника – это гипотенуза, для которой не надо уточнять, прилежащая она или противолежащая относительно острого угла:
Отношения этих трех сторон друг к другу имеют особое наименование.
Для обозначения этих трех величин (их именуют тригонометрическими функциями) используют сокращения sin, cos и tg. При этом после этого сокращения может писаться как обозначение угла греческой буквой, так и обычное обозначение с помощью больших латинских букв:
Задание. Найдите значения тригонометрических функций для∠А в ∆АBС, длины сторон которого указаны на рисунке:
Решение. Просто пользуемся определениями каждой функции:
Задание. Найдите величину тригонометрических функций угла∠В в ∆АBС, показанном на рисунке:
Решение. На первый взгляд кажется, что задание повторяет предыдущее, но это не так. В данном случае нам надо вычислять функции не для∠А, а для ∠В. Для него противолежащим катетом уже будет АС, а прилежащим – ВС. Тогда можно записать, что
Задание. В прямоугольном ∆АBС гипотенуза АB имеет длину 10, а sin∠A = 0,2. Найдите величину ВС.
Решение. Запишем синус как отношение двух сторон:
Задание. В прямоугольном ∆АBС АС = 8, cos∠A = 0,4. Какова длина гипотенузы АB?
Решение. Выразим известный нам косинус как отношение двух отрезков:
Принципиально важно то, что если в двух прямоугольных треугольниках острые углы одинаковы, то и значение их синусов, косинусов и тангенсов также будут одинаковы. Действительно, пусть у ∆АBС и ∆А1В1С1 одинаковы∠А и ∠А1, а ∠С и ∠С1 – прямые:
Тогда у них совпадает по два угла, а это означает, что ∆АBС и ∆А1В1С1 подобны. Из этого подобия вытекает пропорция:
Отсюда можно сделать вывод:
Другими словами, значение тригонометрической функции угла зависит только от величины угла (его градусной меры) и НЕ зависит от того, в каком прямоугольном треугольнике этот угол построен. Действительно, с помощью калькулятора или компьютера можно всегда посчитать синус для какого-то угла, если известна его величина в градусах.
Задание. Найдите тангенс угла, изображенного на рисунке:
Решение. Нам надо самостоятельно достроить угол до прямоугольного треугольника. Удобней всего просто построить вертикальную линию, длину которой будет удобно измерить с помощью клеточек. Например, можно сделать такое построение:
Тогда тангенс можно получить, поделив вертикальный отрезок (он здесь оказывается противолежащим катетом) на горизонтальный:
Заметим, что мы могли построить и треугольник с другими размерами, однако во всех случаях величина тангенса будет одной и той же:
Ответ: 0,5
Задание. Постройте такой угол, что его тангенс будет равен 1,5.
Решение. Если тангенс равен 1,5, то это означает, что противолежащий катет в 1,5 раза длиннее прилежащего катета треугольника. В 1,5 раза отличаются, например, числа 2 и 3. Значит, если мы построим треугольник с катетами 2 и 3, то мы получим необходимый нам угол:
Взаимосвязь между тригонометрическими функциями
Оказывается, что одну тригонометрическую функцию угла, например, синус, можно найти и все остальные функции, используя буквально две формулы. Для их вывода снова построим прямоугольный ∆АBС и обозначим его∠А как α:
Запишем для α все 3 тригонометрические функции:
Для вывода второй важной формулы возведем синус и косинус в квадрат, а потом сложим их:
В итоге у нас получилось так называемое основное тригонометрическое тождество:
Задание. Известно, что синус некоторого угла в прямоугольном треугольнике составляет 0,6. Найдите его косинус и тангенс.
Решение. Обозначим этот угол как α. По условию sin α = 0,6. С помощью основного тригонометрического тождества находим косинус:
имеет не одно, а два решения: 0,8 и (– 0,8). Однако понятно, что так как все длины в геометрии – это положительные числа, то и их отношение также должно быть положительным. Поэтому в прямоугольном треугольнике тригонометрические функции могут быть только положительными, и корень (– 0,8) можно отбросить.
Далее находим тангенс:
Задание. Известен косинус острого угла, который равен 7/25. Вычислите синус и тангенс угла.
Решение. Сначала определяем синус угла:
Задание. Известен тангенс острого угла, он составляет 15/8. Найдите синус и косинус угла.
Решение. Данная задача сложнее двух предыдущих, так как две известные нам тригонометрические формулы не позволяют сразу по тангенсу вычислить две другие функции. Сначала используем формулу, в которой тангенс вообще присутствует:
Мы смогли выразить синус через косинус. Теперь можно использовать и вторую формулу:
Теперь можно вычислить и синус:
Заметим важное обстоятельство – так как гипотенуза всегда длиннее катетов, то и синус с косинусом в прямоугольном треугольнике всегда меньше единицы. На тангенс же подобных ограничений нет.
Задание. В прямоугольном ∆АBС гипотенуза АB равна 20, а cos∠A = 0,8. Вычислите длину ВС.
Решение. Если бы нам был дан синус, мы могли бы сразу найти ВС, но нам известен косинус. Здесь можно предложить два алгоритма решения задачи. Первый метод заключается в том, что мы сначала находим синус, пользуясь тригонометрическими формулами:
Второй метод решения задачи заключается в том, что сначала с помощью косинуса найти неизвестный катет АС:
Тригонометрические функции стандартных углов
Итак, мы выяснили, что тригонометрические функции зависят от градусной меры угла. Попытаемся вычислить их для некоторых стандартных значений.
Начнем с угла в 30°. Построим прямоугольный ∆АBС с∠А = 30°:
Ещё из 7-ого класса нам известно, что в таком треугольнике гипотенуза вдвое длиннее, чем катет, лежащий напротив угла в 30°:
Далее можно найти и тангенс 30°:
Вернемся к рассматриваемому нами ∆АBС, в котором∠А = 30°. Ясно, что другой его острый угол, ∠В, будет составлять 90 – 30 = 60°:
Снова используем тот факт, что гипотенуза АB будет длиннее катета ВС в 2 раза:
Ещё один стандартный угол, для которого легко можно рассчитать значение его тригонометрических функций – это 45°. Рассмотрим прямоугольный ∆АBС, в котором один из острых углов составляет 45°. Тогда и другой острый угол должен также составлять 45°, ведь их сумма в прямоугольном треугольнике равна 90°:
Но если в треугольнике 2 угла одинаковы, то он – равнобедренный, то есть катеты АС и ВС равны:
Итак, в результате нам удалось получить 9 стандартных значений, которые можно представить в виде единой таблицы тригонометрических функций:
Задание. Составьте формулу для вычисления площади прямоугольного треугольника, если известен один из его катетов (он равен a) и острый угол, прилегающий к этому катету (он обозначается как α). Далее найдите c помощью формулы площадь треугольника, если а = 5 и α = 45°.
Решение. Как известно, площадь прямоугольного треугольника рассчитывается по формуле:
Задание. В прямоугольном ∆АBС к гипотенузе ВС проведена высота АН. Отрезок НВ имеет длину 16. Известно, что sinα = 0,6. Какова длина СН?
Решение. Сначала, зная sinα, найдем сosα и tgα:
Теперь заметим, что на рисунке угол α – это не только ∠АBС. Действительно, в ∆АBС
Нам известен отрезок АН и tg∠САН, поэтому можно найти СН:
Поиск тангенса на квадратной решетке
Рассмотрим задание, которое часто встречается на экзаменах и вызывает большие затруднения. На рисунке показан угол, требуется высчитать его тангенс:
Ясно, что для нахождения тангенса надо построить какой-нибудь прямоугольный треугольник, однако проблема заключается в том, что обе стороны угла не являются ни горизонтальными, ни вертикальными линиями, а потому провести к ним перпендикуляр у многих не получается. Рассмотрим, как это делается.
Посмотрим на нижнюю линию. Она представляет собой поднимающуюся прямую, причем на каждые 2 клеточки, которые эта прямая проходит вправо, приходится подъем на 1 клеточку вверх.
Оказывается, что для построения перпендикуляра к ней необходимо от какой-нибудь ее точки вести наклонную прямую, у которой, наоборот, на каждые две клеточки подъема будет приходиться 1 клетка движения вбок, причем не вправо, а влево:
Теперь, чтобы найти тангенс, надо просто поделить длину красного отрезка (он здесь оказывается противолежащим катетом) на длину зеленого отрезка. Несложно заметить, что эти отрезки одинаковы, так как являются гипотенузами в двух равных прямоугольных ∆АBС и ∆CDF:
Естественно, что отношение одинаковых отрезков равно единице, поэтому и тангенс также равен единице. Заметим, что прямой угол можно было получить, проведя перпендикуляр к нижней линии в другой точке:
Более того, перпендикуляр можно провести и к верхней стороне угла. Она представляет собой линию, которая поднимается вправо, и на каждые три клетки движения вверх приходится одна клетка смещения вправо:
Соответственно, чтобы построить к ней перпендикуляр, надо от одной из ее точек начать двигаться вправо и вниз, причем на 3 клетки движения вбок будет приходиться только 1 клетка движения вниз:
Во всех этих случаях зеленые и красные отрезки одинаковы, а потому тангенс равен единице.
Объясним, почему для построения перпендикуляра надо использовать именно такой метод. Пусть на квадратной решетке начерчена прямая АС, к которой надо провести перпендикуляр. Построив горизонтальную (показана зеленым цветом) линию АB и вертикальную (показана красным) линию ВС, мы достоим ее до прямоугольного ∆АBС. Далее отложим от точки С уже вертикально отрезок CD, равный АB, а далее от D – горизонтальный отрезок, равный ВС:
Обозначим∠А как α, тогда ∠АСВ будет составлять 90° – α. Заметим, что ∆АBС и ∆СDF – равные, так как они прямоугольные и у них одинаковы катеты:
Теперь обратим внимание на три угла, вершины которых лежат в точке С. Это ∠АСВ, ∠FCD и ∠АСF. Они вместе образуют развернутый угол ВСD, то есть их сумма составляет 180°. Но ∠АСВ и ∠FCD мы уже выразили через величину α. Тогда можно вычислить и третий угол ∠АСF:
Получили, что отрезки АС и СF действительно перпендикулярны.
Задание. Найдите тангенс угла, показанного на рисунке:
Решение. Если попытаться провести прямую, перпендикулярную нижней стороне угла, то в результате этот перпендикуляр просто не пересечется со второй стороной:
Поэтому перпендикуляр следует проводить к верхней стороне:
Теперь осталось найти отношение длин красного (здесь это противолежащий катет) зеленого отрезка. Конечно, и длины можно найти по теореме Пифагора, однако есть и более простой метод. Возьмем в качестве единичного отрезок, который получается, если на квадратной решетке сделать два шага вбок и один вверх. Этот отрезок будет укладываться на красном катете ровно 3 раза, а на зеленом – ровно 2 раза, то есть прилежащий катет равен трем единичным отрезкам, а противолежащий – двум. Тогда их отношение составляет 3/2 = 1,5
Ответ: 1,5
В прямоугольном треугольнике тригонометрические функции используются для вычисления сторон и острых углов треугольника.
sinα=противолежащий катетгипотенуза sinα=ac;cosα=прилежащий катетгипотенуза cosα=bc;tgα=противолежащий катетприлежащий катетtgα=ab.
Как выбрать правильную функцию?
Если используются только катеты, применяется tg.
Если используется гипотенуза (дана или надо вычислить), то применяются sin или cos.
Если используется противолежащий катет (дан или надо вычислить), то применяется sin.
Если используется прилежащий катет, то применяется cos.
Если в треугольнике даны оба острых угла, лучше на рисунке отметить только один угол, чтобы однозначно понять, где прилежащий и где противолежащий катеты.
Гипотенуза всегда в знаменателе.
Значения тригонометрических функций (которые нужно знать наизусть)
| (30)° | (45)° |
(60) ° |
|
| (sin)α() | 12 | 22 | 32 |
| (cos)α | 32 | 22 | 12 |
| (tg)α() | 33 | (1 ) | 3 |
Величины остальных углов можно найти в таблице или вычислить с помощью калькулятора.
Пример:
дано: (AB =) (6) (см),
∠A=60°
.
Вычислить: (AC).
Искомый отрезок — гипотенуза, дан угол и прилежащий катет, поэтому будем использовать (cos).
cosA=ABAC;AC=ABcosA=6:12=12 см.
Использование свойства прямоугольного треугольника:
Катет прямоугольного треугольника, лежащий против угла в (30)
°
, равен половине гипотенузы.
Катет, лежащий против угла в (60)
°
, равен произведению меньшего катета на
3
.
Данное соотношение удобно использовать для нахождения высоты равностороннего треугольника.
Угол равностороннего треугольника равен (60)
°
, и биссектриса делит этот угол пополам.
В правильном шестиугольнике большая диагональ, меньшая диагональ и сторона шестиугольника образуют прямоугольный треугольник, один из углов которого равен (30)
°
.
Источники:
Рис. 1-5. Треугольник, шестиугольник, © ЯКласс.
Запросы «sin» и «синус» перенаправляются сюда; у терминов sin и синус есть также другие значения.
Запрос «sec» перенаправляется сюда; см. также другие значения.
Рис. 1.
Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса
Тригонометри́ческие фу́нкции — элементарные функции[1], которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла дуги в круге). Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.
Раздел математики, изучающий свойства тригонометрических функций, называется тригонометрией.
К тригонометрическим функциям традиционно причисляют:
- прямые тригонометрические функции:
- синус (
);
- косинус (
);
- производные тригонометрические функции:
- тангенс
;
- котангенс
;
- секанс
;
- косеканс
;
- обратные тригонометрические функции:
- арксинус, арккосинус и т. д.
В типографике литературы на разных языках сокращённое обозначение тригонометрических функций различно, например, в англоязычной литературе тангенс, котангенс и косеканс обозначаются 


Кроме этих шести широко известных тригонометрических функций, иногда в литературе используются некоторые редко используемые тригонометрические функции (версинус и т. д.).
Синус и косинус вещественного аргумента представляют собой периодические, непрерывные и бесконечно дифференцируемые вещественнозначные функции. Остальные четыре функции на вещественной оси также вещественнозначны, периодичны и бесконечно дифференцируемы, за исключением счётного числа разрывов второго рода: у тангенса и секанса в точках 

Графики тригонометрических функций показаны на рис. 1.
Способы определения[править | править код]
Определение для любых углов[править | править код]
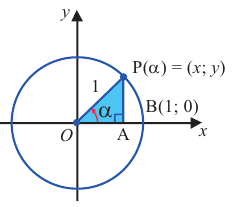
Рис. 2.
Определение тригонометрических функций
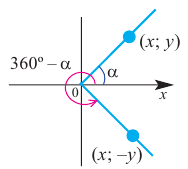
Обычно тригонометрические функции определяются геометрически[3]. В декартовой системе координат на плоскости построим окружность единичного радиуса (






Синусом угла 






Косинусом угла 






Тангенсом угла 


Котангенсом угла 


Таким образом, определения тригонометрических функций выглядят следующим образом:
Нетрудно видеть, что такое определение также основывается на отношениях прямоугольного треугольника, с тем отличием, что учитывается знак (

В тригонометрии удобным оказывается вести счёт углов не в градусной мере, а в радианной. Так, угол в 






Наконец, определим тригонометрические функции вещественного числа 

Определение для острых углов[править | править код]
Рис. 4.
Тригонометрические функции острого угла
Определение тангенса. Марка СССР 1961 года
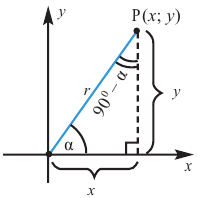
В геометрии тригонометрические функции острого угла определяются отношениями сторон прямоугольного треугольника[5]. Пусть 



Данное определение имеет некоторое методическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач о тупоугольных треугольниках. (См.: теорема синусов, теорема косинусов).
Определение как решений дифференциальных уравнений[править | править код]
Синус и косинус можно определить как единственные функции, вторые производные которых равны самим функциям, взятым со знаком минус:
То есть задать их как чётное (косинус) и нечётное (синус) решения дифференциального уравнения
с дополнительными условиями:


Определение как решений функциональных уравнений[править | править код]
Функции косинус и синус можно определить[7]
как решения (


при дополнительных условиях:




Определение через ряды[править | править код]
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу, и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:
Пользуясь этими формулами, а также равенствами 



где
— числа Бернулли,
— числа Эйлера.
Значения тригонометрических функций для некоторых углов[править | править код]
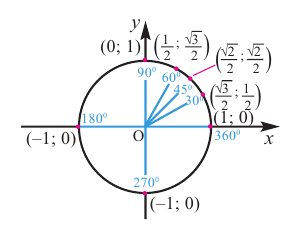
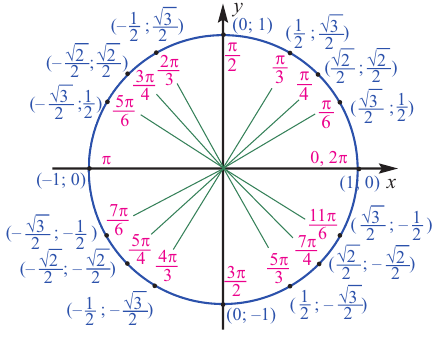
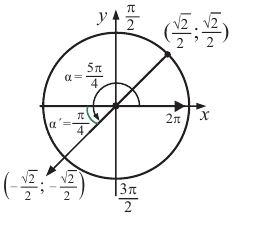
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («
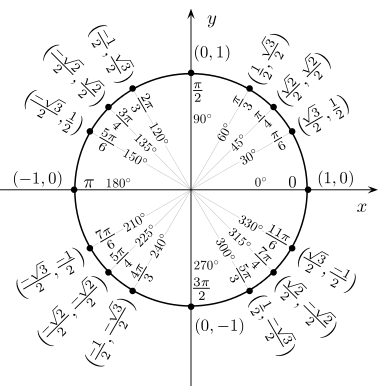
Значения косинуса и синуса на окружности
| Радианы | 
|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Значения тригонометрических функций нестандартных углов[править | править код]
| Радианы | 
|

|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
| Радианы | 
|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Значения тригонометрических функций для некоторых других углов
Свойства тригонометрических функций[править | править код]
Простейшие тождества[править | править код]
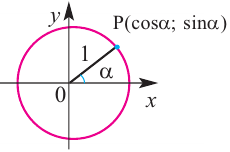
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности (
Это соотношение называется основным тригонометрическим тождеством.
Разделив это уравнение на квадрат косинуса и синуса соответственно, получим:
Из определения тангенса и котангенса следует, что
Любую тригонометрическую функцию можно выразить через любую другую тригонометрическую функцию с тем же аргументом (с точностью до знака из-за неоднозначности раскрытия квадратного корня). Нижеприведённые формулы верны для 
| sin | cos | tg | ctg | sec | cosec | |
|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Непрерывность[править | править код]
Чётность[править | править код]
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность[править | править код]
Функции 




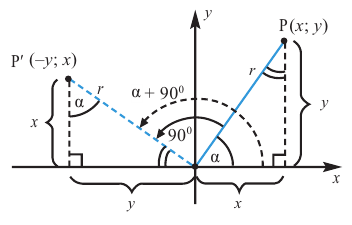
Формулы приведения[править | править код]
Формулами приведения называются формулы следующего вида:
Здесь 



или что то же самое:
Некоторые формулы приведения:

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Интересующие формулы приведения так же могут легко быть получены рассмотрением функций на единичной окружности.
Формулы сложения и вычитания[править | править код]
Значения тригонометрических функций суммы и разности двух углов:
Аналогичные формулы для суммы трёх углов:
Формулы для кратных углов[править | править код]
Формулы двойного угла:
Формулы тройного угла:
Прочие формулы для кратных углов:
следует из формулы дополнения и формулы Гаусса для гамма-функции.
Из формулы Муавра можно получить следующие общие выражения для кратных углов:
где ![[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)


Формулы половинного угла:
Произведения[править | править код]
Формулы для произведений функций двух углов:
Аналогичные формулы для произведений синусов и косинусов трёх углов:
Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.
Степени[править | править код]
Иллюстрация равенства
Суммы[править | править код]
Существует представление:
где угол 
Универсальная тригонометрическая подстановка[править | править код]
Все тригонометрические функции можно выразить через тангенс половинного угла:






Исследование функций в математическом анализе[править | править код]
Разложение в бесконечные произведения[править | править код]
Тригонометрические функции могут быть представлены в виде бесконечного произведения многочленов:
Эти соотношения выполняются при любом значении 
Непрерывные дроби[править | править код]
Разложение тангенса в непрерывную дробь:
Производные и первообразные[править | править код]
Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:






Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом[8]:






Тригонометрические функции комплексного аргумента[править | править код]
Определение[править | править код]
Формула Эйлера:
Формула Эйлера позволяет определить тригонометрические функции от комплексных аргументов через экспоненту по аналогии с гиперболическими функциями, или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:
где
Соответственно, для вещественного x:
Комплексные синус и косинус тесно связаны с гиперболическими функциями:
Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:
- комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
- все нули комплексных синуса и косинуса лежат на вещественной оси.
Комплексные графики[править | править код]
На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.
|
|
|
|
|
|
|

|

|

|

|

|

|
История названий[править | править код]
Линия синуса (линия 
Современные краткие обозначения 

Термины «тангенс» (лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функции введён Клюгелем в 1770 году.
Позднее были введены и термины для обратных тригонометрических функций — арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс — с помощью добавления приставки «арк» (от лат. arcus — дуга), — Ж. Лагранжем и др.
См. также[править | править код]
- Гиперболические функции
- Интегральный синус
- Интегральный косинус
- Интегральный секанс
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Решение треугольников
- Синус-верзус
- Сферическая тригонометрия
- Тригонометрические тождества
- Тригонометрические функции от матрицы
- Тригонометрический ряд Фурье
- Функция Гудермана
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Эллиптические функции
Литература[править | править код]
- Бермант А. Ф., Люстерник Л. А. Тригонометрия. — М.: Наука, 1967.
- Тригонометрические функции — статья из Большой советской энциклопедии. — М.: Советская энциклопедия, 1977. — Т. 26. — С. 204—206.
- Бронштейн И. Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6 www.alleng.ru/d/math/math42.htm
- Двайт Г. Б. Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М.: Наука, 1973. — С. 70—102.
- Кожеуров П. А. Тригонометрия. — М.: Физматгиз, 1963.
- Маркушевич А. И. Замечательные синусы. — М.: Наука, 1974.
- Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1984. — И. М. Виноградов. Тригонометрические функции // Математическая энциклопедия. — М.: Советская энциклопедия. — 1977—1985.
- Тригонометрические функции // Энциклопедический словарь юного математика / Ред. коллегия, Гнеденко Б. В. (гл. ред.), Савин А. П. и др. — М.: Педагогика, 1985 (1989). — С. 299—301—305. — 352 с., ил. — ISBN 5-7155-0218-7 (С. 342, 343 — таблицы тригонометрических функций 0°-90°, в том числе в радианах)
- Тригонометрические функции // Справочник по математике (для ср. уч. заведений) / Цыпкин А. Г., под ред. Степанова С. А. — 3-е изд. — М.: Наука, Гл. редакция физ.-мат. литературы, 1983. — С. 240—258. — 480 с.
Ссылки[править | править код]
- GonioLab — прояснённая единичная окружность, тригонометрические и гиперболические функции (Java Web Start)
- Weisstein, Eric W. Trigonometric Functions (англ.) на сайте Wolfram MathWorld.
- Онлайн калькулятор: вычисление значений тригонометрических функций (в том числе нахождение углов треугольника по сторонам)
- Интерактивная карта значений тригонометрических функций
- Тригонометрические таблицы (0° — 360°)
- «Синус и косинус — это проценты» — перевод статьи How To Learn Trigonometry Intuitively | BetterExplained (англ.)
Примечания[править | править код]
- ↑ Справочник: Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с. Архивная копия от 19 января 2015 на Wayback Machine относит их к специальным функциям.
- ↑ Знак математический. // Большая советская энциклопедия. 1-е изд. Т. 27. — М., 1933.
- ↑ Справочник по элементарной математике, 1978, с. 282—284.
- ↑ Шахмейстер А. Х. Определение основных тригонометрических функций // Тригонометрия : [рус.] : книга / А. Х. Шахмейстер; под ред. Б. Г. Зива. — 3-е изд., стереотипное. — М. : Издательство МЦНМО ; СПб. : «Петроглиф» : «Виктория плюс», 2013. — С. 11, 14, 18, 20. — 752 с. : илл. — (Математика. Элективные курсы). — 1500 экз. — ББК 22.141я71.6. — УДК 373.167.1:512(G). — ISBN 978-5-4439-0050-6. — ISBN 978-5-98712-042-2. — ISBN 978-5-91673-097-5.
- ↑ Справочник по элементарной математике, 1978, с. 271—272.
- ↑ Латинско-русский словарь. Дата обращения: 9 апреля 2023.
- ↑ Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. 1. — М.: Наука, 1998. — ISBN 5-02-015231-5.
- ↑ В формулах, содержащих логарифм в правой части равенств, константы интегрирования
, вообще говоря, различны для различных интервалов непрерывности.



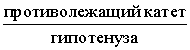
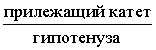
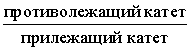
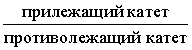


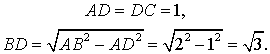

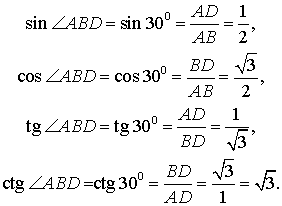

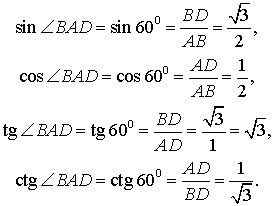


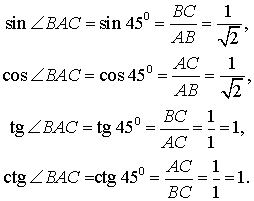

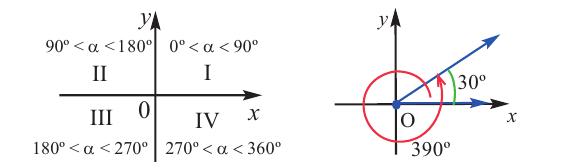

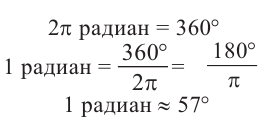
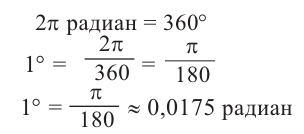
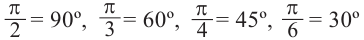
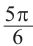
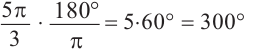
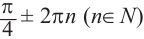
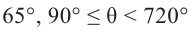


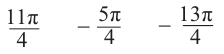
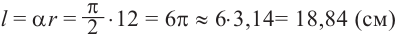
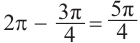
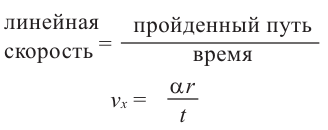
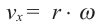

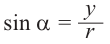
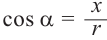
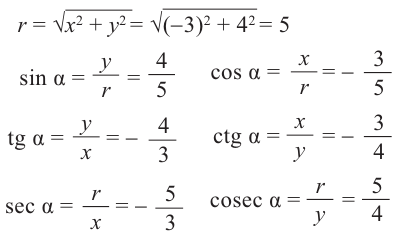
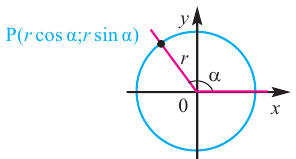
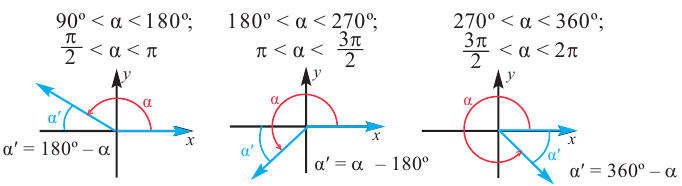
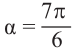

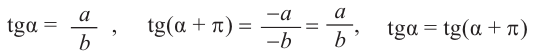
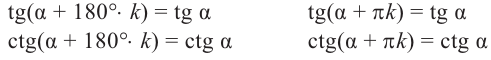
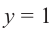
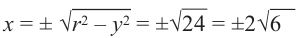
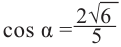
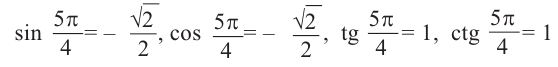
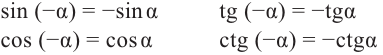

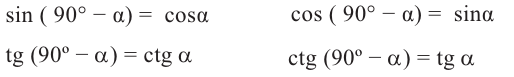
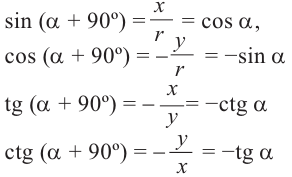
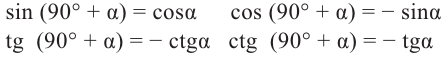
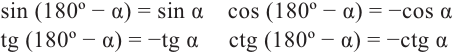
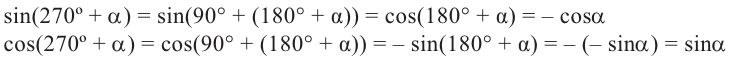
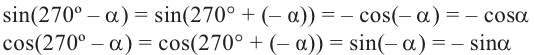
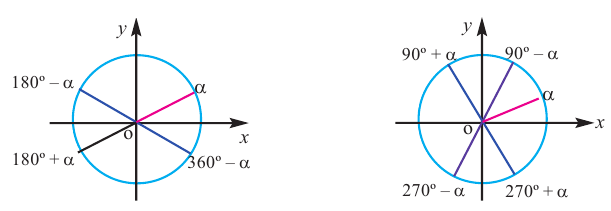
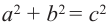
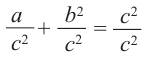
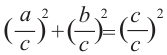
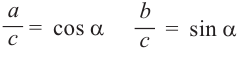
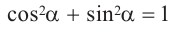
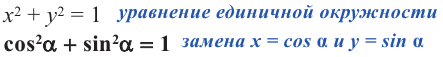
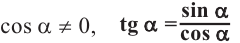
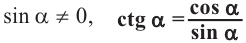
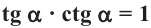

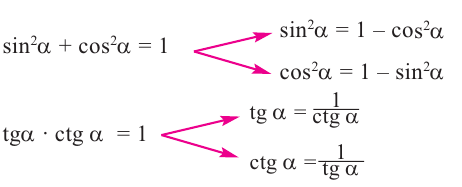
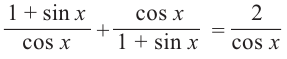
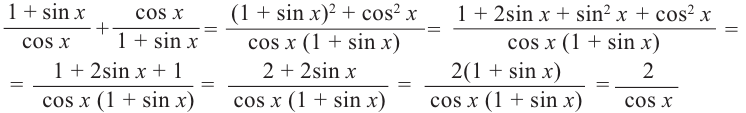
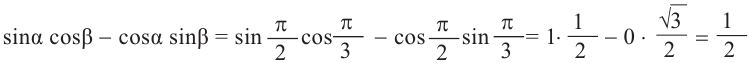
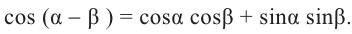

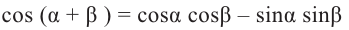
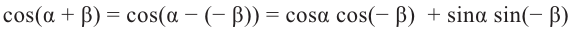

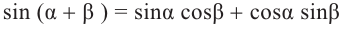
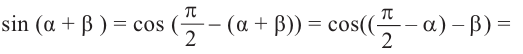
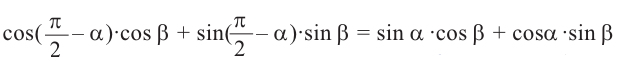
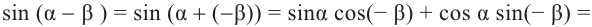
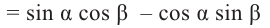
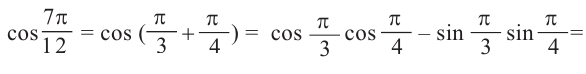
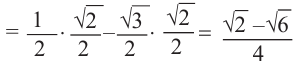
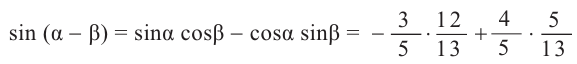
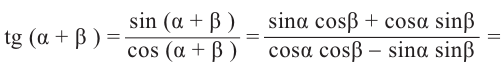
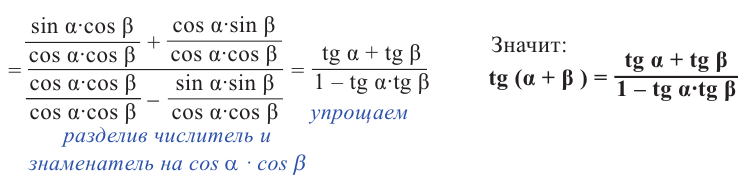
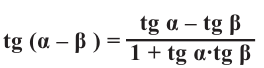
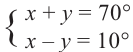

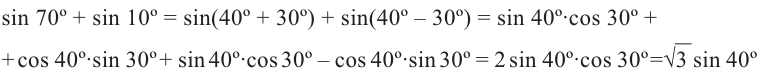
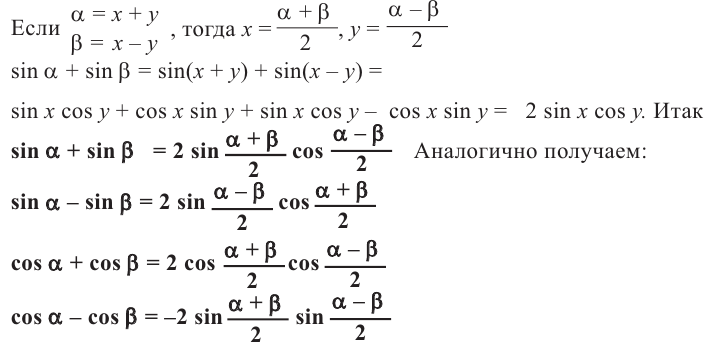
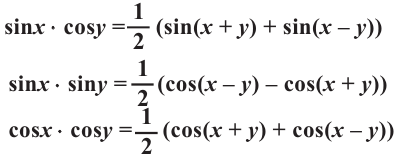
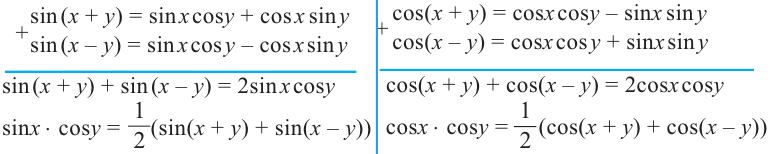
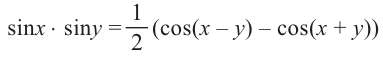
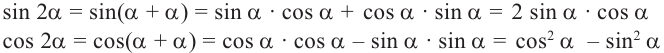
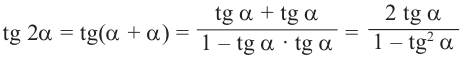
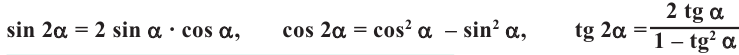
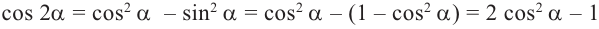
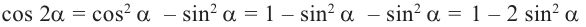
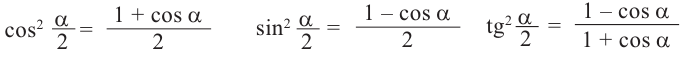
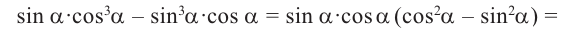
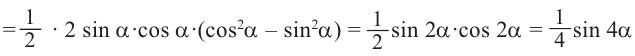
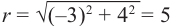

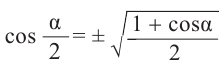
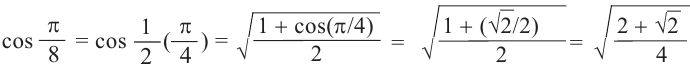
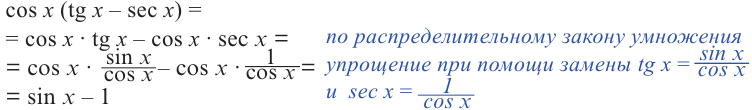


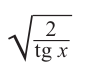
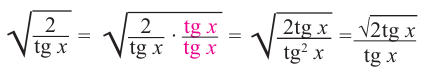


























































































































![sin(nalpha)=sum_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}cos^{n-2k-1}alpha,sin^{2k+1}alpha,](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb020e5dfc3b2d5dfe1d1a0c571487ce387a8153)
![cos(nalpha)=sum_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}cos^{n-2k}alpha,sin^{2k}alpha,](https://wikimedia.org/api/rest_v1/media/math/render/svg/84f285d7cb530e87d8a9e33cff84fd4a4c9a8205)
![mathrm{tg}(nalpha)=frac{sin(nalpha)}{cos(nalpha)}=dfrac{displaystyle{sumlimits_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}mathrm{tg}^{2k+1}alpha}}{displaystyle{sumlimits_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}mathrm{tg}^{2k}alpha}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/8800a20a70495802fc2de287bb98d155e14720b1)
![mathrm{ctg}(nalpha)=frac{cos(nalpha)}{sin(nalpha)}=dfrac{displaystyle{sumlimits_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}mathrm{ctg}^{n-2k}alpha}}{displaystyle{sumlimits_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}mathrm{ctg}^{n-2k-1}alpha}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/90744f04ee2a1e34b1f0763e310c1c1d071f240d)