Как найти трудоемкость алгоритма

Методы оценки ресурсной эффективности алгоритмов

Основными алгоритмическими конструкциями в процедурном программировании являются следование, ветвление и цикл. Для получения функций трудоемкости для лучшего, среднего и худшего случаев при фиксированной размерности входа необходимо учесть различия в оценке основных алгоритмических конструкций.

• Трудоемкость конструкции “Следование” есть сумма трудоемкостей блоков, следующих друг за другом: f=f₁+f₂+…+f_n.
• Трудоемкость конструкции “Ветвление” определяется через вероятность перехода к каждой из инструкций, определяемой условием. При этом проверка условия также имеет определенную трудоемкость. Для вычисления трудоемкости худшего случая может быть выбран тот блок ветвления, который имеет большую трудоемкость, для лучшего случая – блок с меньшей трудоемкостью. f_if=f₁+f_thenxp_then+f_elsex(1-p_then)
• Трудоемкость конструкции “Цикл” зависит от вида цикла. Для цикла с параметрами будет справедливой формула: f_for=1+3n+nf, где n – количество повторений тела цикла, f – трудоемкость тела цикла.

  Реализация цикла с предусловием и с постусловием не меняет методики оценки его трудоемкости. На каждом проходе выполняется оценка трудоемкости условия, изменения параметров (при наличии) и тела цикла. Общие рекомендации для оценки циклов с условиями затруднительны. Так как в значительной степени зависят от исходных данных.

• В случае использования вложенных циклов их трудоемкости перемножаются.

Таким образом, для оценки трудоемкости алгоритма может быть сформулирован общий метод получения функции трудоемкости.

1. Декомпозиция алгоритма предполагает выделение в алгоритме базовых конструкций и оценку их трудоемкости. При этом рассматривается следование основных алгоритмических конструкций.
2. Построчный анализ трудоемкости по базовым операциям языка подразумевает либо совокупный анализ (учет всех операций), либо пооперационный анализ (учет трудоемкости каждой операции).
3. Обратная композиция функции трудоемкости на основе методики анализа базовых алгоритмических конструкций для лучшего, среднего и худшего случаев.

Особенностью оценки ресурсной эффективности рекурсивных алгоритмов является необходимость учета дополнительных затрат памяти и механизма организации рекурсии. Поэтому трудоемкость рекурсивных реализаций алгоритмов связана с количеством операций, выполняемых при одном рекурсивном вызове, а также с количеством таких вызовов. Учитываются также затраты на возвращения значений и передачу управления в точку вызова. Для анализа трудоемкости механизма рекурсивного вызова-возврата будем учитывать следующие параметры: p – количество передаваемых фактических параметров, r – количество сохраняемых в стеке регистров, k – количество возвращаемых по адресной ссылке значений, l – количество локальных ячеек функции. Тогда функция трудоемкости на один вызов-возврат примет вид:

где дополнительная единица учитывает операции с адресом возврата.

Оценка требуемой памяти стека может быть получена следующим образом: так как рекурсивные вызовы обрабатываются последовательно, то в конкретный момент времени в стеке хранится не фрагмент дерева рекурсии, а цепочка рекурсивных вызовов – унарный фрагмент дерева. Поэтому объем стека определяется максимально возможным числом одновременно полученных рекурсивных вызовов.

Анализ совокупной трудоемкости рекурсивного алгоритма можно выполнять разными способами в зависимости от формирования итоговой суммы базовых операций: по цепочкам рекурсивных вызовов и возвратов, по вершинам рекурсивного дерева.

Пример 1. Оценка временной сложности функции пузырьковой сортировки.

//Описание функции сортировки методом "пузырька"
void BubbleSort (int k,int x[max]) {
  int i,j,buf;
  for (i=k-1;i>0;i--)
    for (j=0;j<i;j++)
    if (x[j]>x[j+1]) {
      buf=x[j];
      x[j]=x[j+1];
      x[j+1]=buf;
     }    
}

Оценим временную сложность функции пузырьковой сортировки в худшем случае, т.е. когда исходные данные отсортированы в обратном порядке. В этом случае внутренний цикл для каждого i выполнится i-1 раз и произойдет 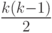обменов. Соответственно сложность алгоритма в худшем случае составит O(k²) обменов.

Оценим временную сложность алгоритма пузырьковой сортировки в среднем случае, т.е. когда исходные данные имеют произвольный порядок. В этом случае условие во внутреннем цикле может выполниться 1,2,…,i-1 раз. Складывая, получим и, соответственно, условие во внутреннем цикле для каждого i выполнится в среднем раз и произойдет обменов. Соответственно сложность алгоритма в среднем случае составит O(k²).

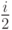
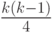
Пример 2. Оценка временной сложности функции вычисления биномиального коэффициента .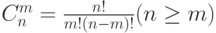

//Описание функции вычисления биномиального коэффициента
int Binom (int n,int m) {
  if (m==0) return 1; //база рекурсии
  return Binom(n-1,m-1)*n/m; //декомпозиция
}

Оценим временную сложность функции в худшем случае, т.е. когда m=n. Будет выполнено ( n+1 ) обращений к функции, которая выполнит в n случаях три операции, а в одном возвратит значение. Функция при каждом обращении передает два параметра, не использует локальных переменных, а при возвращении ( n+1 ) раз передает управление в точку вызова. Соответственно сложность алгоритма в худшем случае составит O(n) или O(m).

Оценим временную сложность функции в среднем случае, т.е. когда m<n. При этом выполняются рассуждения, аналогичные худшему случаю, только количество рекурсивных вызовов составит ( m+1 ). Соответственно сложность алгоритма в среднем случае составит O(m).

Лучший случай достигается при m=0, когда выполняется единственный вызов функции, передача двух параметров и возвращение в точку вызова, то есть оценка лучшего случая O(1).

Базовые алгоритмы обработки данных

Базовые алгоритмы обработки данных являются результатом исследований и разработок, проводившихся на протяжении десятков лет. Но они, как и прежде, продолжают играть важную роль во все расширяющемся применении вычислительных процессов.

К базовым алгоритмам процедурного программирования можно отнести:

• Алгоритмы работы со структурами данных. Они определяют базовые принципы и методологию, используемые для реализации, анализа и сравнения алгоритмов. Позволяют получить представление о методах представления данных. К таким структурам относятся связные списки и строки, деревья, абстрактные типы данных, такие как стеки и очереди.
• Алгоритмы сортировки, предназначенные для упорядочения массивов и файлов, имеют особую важность. С алгоритмами сортировки связаны, в частности, очереди по приоритету, задачи выбора и слияния.
• Алгоритмы поиска, предназначенные для поиска конкретных элементов в больших коллекциях элементов. К ним относятся основные и расширенные методы поиска с использованием деревьев и преобразований цифровых ключей, в том числе деревья цифрового поиска, сбалансированные деревья, хеширование, а также методы, которые подходят для работы с очень крупными файлами.
• Алгоритмы на графах полезны при решении ряда сложных и важных задач. Общая стратегия поиска на графах разрабатывается и применяется к фундаментальным задачам связности, в том числе к задаче отыскания кратчайшего пути, построения минимального остовного дерева, к задаче о потоках в сетях и задаче о паросочетаниях. Унифицированный подход к этим алгоритмам показывает, что в их основе лежит одна и та же функция, и что эта функция базируется на основном абстрактном типе данных очереди по приоритету.
• Алгоритмы обработки строк включают ряд методов обработки последовательностей символов. Поиск в строке приводит к сопоставлению с эталоном, что, в свою очередь, ведет к синтаксическому анализу. К этому же классу задач можно отнести и технологии сжатия файлов.
• Геометрические алгоритмы – это методы решения задач с использованием точек и линий (и других простых геометрических объектов), которые вошли в употребление достаточно недавно. К ним относятся алгоритмы построения выпуклых оболочек, заданных набором точек, определения пересечений геометрических объектов, решения задач отыскания ближайших точек и алгоритма многомерного поиска. Многие из этих методов дополняют простые методы сортировки и поиска.

Ключевые термины

Алгоритм обработки данных – это описание метода решения задачи в компьютерных науках, который в дальнейшем возможно реализовать в выбранной среде программирования.

Анализ алгоритмов – это направление компьютерных наук, занимающееся изучением оценки эффективности алгоритмов.

Трудоемкость алгоритма – это количество элементарных операций, которые учитываются при анализе алгоритма.

Худший случай трудоемкости – это наибольшее количество операций, задаваемых алгоритмом А на всех входах D определенной размерности n.

Лучший случай трудоемкости – это наименьшее количество операций в алгоритме А на всех входах D определенной размерности n.

Средний случай трудоемкости – это среднее количество операций в алгоритме А на всех входах D определенной размерности n.

Функция трудоемкости алгоритма – это зависимость трудоемкости алгоритма А от значения параметров на входе D.

Временная сложность алгоритма – это асимптотическая оценка функции трудоемкости алгоритма для худшего случая.

Объем памяти – это максимальное количество ячеек памяти, задействованных в ходе выполнения алгоритма А для входа D.

Емкостная сложность алгоритма – это асимптотическая оценка функции объема памяти алгоритма для худшего случая.

Ресурсная сложность алгоритма в худшем, среднем и лучшем случаях – это упорядоченная пара классов функций временной и емкостной сложности, заданных асимптотическими обозначениями и соответствующих рассматриваемому случаю.

Алгоритмы работы со структурами данных – это алгоритмы, которые определяют базовые принципы и методологию, используемые для получения представление о методах обработки данных.

Алгоритмы сортировки – это алгоритмы, предназначенные для упорядочения массивов и файлов.

Алгоритмы поиска – это алгоритмы, предназначенные для поиска конкретных элементов в больших коллекциях данных.

Алгоритмы на графах – это алгоритмы, предназначенные для реализации стратегий обходов и поиска на графах.

Алгоритмы обработки строк – это алгоритмы, которые включают ряд методов обработки последовательностей символов.

Геометрические алгоритмы – это алгоритмы решения задач с использованием геометрических объектов.

Краткие итоги

1. Определение ресурсной эффективности алгоритмов – необходимая составляющая этапа анализа разработанного программного обеспечения.
2. Наиболее значимыми характеристиками ресурсной эффективности алгоритмов являются оценки их временной и емкостной сложности.
3. Временная сложность алгоритма определяется асимптотической оценкой функции трудоемкости алгоритма для худшего случая.
4. В зависимости от вида функции временной сложности алгоритма выделяют пять основных классов сложности алгоритмов.
5. Емкостная сложность алгоритма определяется как асимптотическая оценка функции объема памяти алгоритма для худшего случая.
6. Ресурсная сложность алгоритма в худшем, среднем и лучшем случаях определяется как упорядоченная пара классов функций временной и емкостной сложности, заданных асимптотическими обозначениями и соответствующих рассматриваемому случаю.
7. Для получения функций трудоемкости для лучшего, среднего и худшего случаев при фиксированной размерности входа необходимо учесть особенности в оценке основных алгоритмических конструкций.
8. Особенностью оценки ресурсной эффективности рекурсивных алгоритмов является необходимость учета дополнительных затрат памяти и механизма организации рекурсии.
9. В зависимости от структур обработки данных в процедурном программировании выделяются классы базовых алгоритмов.

Анализ трудоёмкости алгоритмов

Целью
анализа трудоёмкости алгоритмов является
нахождение оптимального
алгоритма для
решения задачи.

В
качестве критерия
оптимальности
алгоритма выбирается трудоемкость
алгоритма, понимаемая как количество
элементарных операций,
которые надо выполнить для решения
задачи с помощью данного алгоритма.

Функцией
трудоемкости
называется отношение, связывающие
входные данные алгоритма с количеством
элементарных операций.

Одним
из упрощенных видов анализа,
является асимптотический
анализ алгоритмов.

Целью
асимптотического анализа является
сравнение
затрат времени и других ресурсов при
использовании
различных
алгоритмов, предназначенных для решения
одной и той же задачи, при больших объемах
входных данных.

Используемая
в асимптотическом анализе оценка функции
трудоёмкости, называемая сложностью
алгоритма,
позволяет определить, как быстро растет
трудоёмкость алгоритма с увеличением
объема данных.

Для
описания скорости роста функций
используется асимптотическая оценка
O.

Она
представляет собой верхнюю
асимптотическую оценку трудоемкости
алгоритма и позволяет определить, как
быстро растет трудоемкость алгоритма
с увеличением объема данных.

Определение.
 T(n)
= O(f(n)),
если
существуют константы
c
> 0, n₀
>
0
такие,
что выполняется неравенство: 0
<= T(n)
<= cf(n)
для
любого
n
>= n₀

Здесь
n –
величина объёма данных.

Иначе
говоря, запись  T(n)
= O(f(n))

означает, что T(n)
принадлежит классу функций, которые
растут не
быстрее,
чем функция f(n)
с точностью до постоянного множителя.

Когда
используют обозначение O(),
имеют в виду не точное время исполнения,
а только его предел
сверху,
причем с точностью до постоянного
множителя.

Напр.,
если говорят, что алгоритму требуется
время порядка O(n²),
то имеют в виду, что время выполнения задачи
растет не быстрее, чем квадрат количества
элементов.

Пример.
Функция T(n)
= 3n³+2n²
имеет
степень роста O(n³),
т.е.
время выполнения задачи растет не
быстрее, чем куб количества исходных
данных. Если c
= 5, n₀
=
0,
то 3n³+2n²
<=5n³

При
оценке трудоемкости используют правило
сумм:
в общем случае трудоемкость выполнения
программных фрагментов имеет порядок
фрагмента с наибольшим временем
выполнения.

Пример.
Пусть есть три фрагмента с временами
выполнения O(n³),
O(n²),
O(nlogn).
Тогда
время выполнения первых двух фрагментов
– это максимум из первых двух оценок –
O(n³).
Затем сравнивается результат и третья
оценка.

Для
всех трех –
O(n³).

При
оценке трудоемкости используется также
правило
произведений:
если T1(n)
и
T2(n)
имеют
степени роста O(f(n))
и
O(g(n))

соответственно, то произведение
T1(n)T2(n)
имеет
степень роста O(f(n))O(g(n)).

Например,
O(n²
/ 2)
эквивалентно O(n²).

Скорость
роста некоторых функций: 

 
n     
 

log n    

n*log n    
 
n² 

 
1           
0       
0          
1 

  16          
4       
64            
256 

256         
8      
2048        
65536 

4096       
12     
49152        16777216 

65536      
16     
1048565     4294967296 

1048476   
20     
20969520    1099301922576 

16775616  
24       402614784 
281421292179456 

Из
таблицы видно, что для задач с небольшим
значением n
метод решения задачи не влияет на
скорость, но по мере роста n
время, нужное для получения решения,
становится большим (10⁷
секунд равно 3,8 месяца, 10⁸
секунд – 3,1 года).

Оценка Ώ
задает
нижнюю асимптотическую оценку роста
функции
T(n)
и определяет класс функций, которые
растут не
медленнее,
чем f(n)
с точностью до постоянного множителя. 

Определение.
 T(n)
= Ώ(f(n)),
если
существуют константы
c
> 0, n₀
>
0
такие,
что выполняется неравенство: T(n)
>= cf(n)
>= 0
для
любого
n
>= n₀.

Например,
запись T(n)
= Ώ(nlog(n))

обозначает класс функций, которые растут
не
медленнее,
чем f(n)
= nlog(n).

(В
этот класс попадают все полиномы со
степенью, большей единицы, равно как и
все степенные функции с основанием
большим единицы).

Для
задания одновременно верхней
и нижней оценки роста
функции T(n)
используется оценка Ө  (“тэта
большое”).

Определение.
 T(n)
= Ө(f(n)),
если
при f
> 0
и n
> 0
существуют константы c₁,
c₂,
n₀
такие,
что выполняется неравенство: c₁f(n)
<= T(n)
<= c₂f(n)
для
любого
n
>= n₀.

Функция
f(n)
является асимптотически точной оценкой
функции T(n),
т.к. по определению функция T(n)
не отличается от функции f(n)
с точностью до постоянного множителя.

Например,
для метода пирамидальной сортировки
оценка трудоёмкости составляет T(n)
= Ө(nlog(n)),
то
есть f(n)
= nlogn.

Равенство 
T(n)
= Ө(f(n))
выполняется
тогда и только тогда, когда
 T(n)
= O(f(n))
и
T(n)
= Ώ (f(n)).

Важно
понимать, что Ө(f(n))
представляет
собой не функцию, а множество
функций,
описывающих рост T(n)
с
точностью до постоянного множителя.

Асимптотические
оценки можно представить в порядке
увеличения скорости их роста:

O(1)
< O(log₂
n) < O(n) < O(nlog₂
n) < O(n²)
< O(n³)
< O(2ⁿ)

Соседние файлы в папке Лекции

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Основным показателем сложности (трудоемкости) алгоритма является время, необходимое для решения задачи, и объем требуемой памяти. Существуют понятия сложности в худшем и среднем случае. Обычно оценивают сложность в худшем случае.

Временная сложность в худшем случае — функция от размера входа, равная максимальному количеству операций, выполненных в ходе работы алгоритма при решении задачи данного размера.

Емкостная сложность в худшем случае — функция от размера входа, равная максимальному количеству памяти, к которому было обращение при решении задач данного размера.

При анализе сложности для класса задач определяется некоторое число, характеризующее объем данных, которое требуется для представления входных данных задачи. Это величина называется  размер входа. Можно сделать вывод, что сложность алгоритма — функция размера входа. Размер входа может зависеть как от числа входных данных, так и от величины входных данных (пример 23.1).

Одним из упрощенных видов анализа, используемых на практике, является асимптотический анализ алгоритмов. Целью асимптотического анализа является сравнение затрат времени и других ресурсов различных алгоритмов, предназначенных для решения одной и той же задачи, при больших объемах входных данных.

Используемая в асимптотическом анализе оценка функции трудоемкости, называемая сложностью алгоритма, позволяет определить, как быстро растет трудоемкость алгоритма с увеличением объема данных.

В асимптотическом анализе алгоритмов используются обозначения, принятые в математическом асимптотическом анализе.

Чтобы определить сверху трудоемкость алгоритма, используется обозначение O, читается «о большое» (пример 23.2).

Иногда при анализе алгоритма приходится учитывать не только максимальное, но и минимальное количество операций, необходимое для решения задачи. В этом случае используется обозначение  , читается «омега».

Существует ряд важных практических причин для анализа алгоритмов. Одной из них является необходимость получения оценок или границ для объема памяти, или времени работы, которое потребуется алгоритму для успешной обработки конкретных данных. Машинное время и память — относительно дефицитные (и дорогие) ресурсы, на которые часто одновременно претендуют многие пользователи. Всегда следует избегать прогонов программы, отвергаемых системой из-за нехватки запрошенного времени. Теоретический анализ способен выявить узкие места в программах. 

Иногда невозможно составить четкое мнение об относительной эффективности двух алгоритмов. Один может в среднем лучше работать, к примеру, на случайных входных данных, в то время как другой лучше работает на каких-то специальных входных данных.

Будем пользоваться следующим критерием для оценки качества алгоритма: чем медленнее растет функция f(n) на каком-то участке области , тем алгоритм будет более эффективным (пример 23.3).

Этот критерий основан на времени работы в худшем случае, но аналогичный критерий может быть также определен для среднего времени работы.

При разработке алгоритма необходимо стремиться к тому, чтобы рост функции  f(n)  для алгоритма был как можно медленнее на той области, на которой требуется получить решение. Однако здесь могут возникать определенные трудности.

1. Очень часто отдельно взятый шаг алгоритма может быть выражен в форме, которую трудно перевести непосредственно в конструкции языка программирования.
2. Конкретная реализация (выбор различных языков программирования и/или различных структур данных) может существенно влиять на требования к памяти и на скорость алгоритма.

Алгоритм — это точное предписание, однозначно определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату [1].

При разработке алгоритмов очень важно иметь возможность оценить ресурсы, необходимые для проведения вычислений, результатом оценки является функция сложности (трудоемкости). Оцениваемым ресурсом чаще всего является процессорное время (вычислительная сложность) и память (сложность алгоритма по памяти). Оценка позволяет предсказать время выполнения и сравнивать эффективность алгоритмов.

Содержание:

1. Модель RAM (Random Access Machine)
2. Подсчет операций. Классы входных данных
3. Асимптотические обозначения
4. Примеры анализа алгоритмов
5. Математический аппарат анализа алгоритмов
   1. Формулы суммирования
   2. Суммирование и интегрирование
   3. Сравнение сложности алгоритмов. Пределы
   4. Логарифмы и сложность алгоритмов
6. Результаты анализа. Замечания. Литература

Модель RAM (Random Access Machine)

Каждое вычислительное устройство имеет свои особенности, которые могут влиять на длительность вычисления. Обычно при разработке алгоритма не берутся во внимание такие детали, как размер кэша процессора или тип многозадачности, реализуемый операционной системой. Анализ алгоритмов проводят на модели абстрактного вычислителя, называемого машиной с произвольным доступом к памяти (RAM).

Модель состоит из памяти и процессора, которые работают следующим образом:

• память состоит из ячеек, каждая из которых имеет адрес и может хранить один элемент данных;
• каждое обращение к памяти занимает одну единицу времени, независимо от номера адресуемой ячейки;
• количество памяти достаточно для выполнения любого алгоритма;
• процессор выполняет любую элементарную операцию (основные логические и арифметические операции, чтение из памяти, запись в память, вызов подпрограммы и т.п.) за один временной шаг;
• циклы и функции не считаются элементарными операциями.

Несмотря на то, что такая модель далека от реального компьютера, она замечательно подходит для анализа алгоритмов. После того, как алгоритм будет реализован для конкретной ЭВМ, вы можете заняться профилированием и низкоуровневой оптимизацией, но это будет уже оптимизация кода, а не алгоритма.

Подсчет операций. Классы входных данных

Одним из способов оценки трудоемкости ((T_n)) является подсчет количества выполняемых операций. Рассмотрим в качестве примера алгоритм поиска минимального элемента массива.

начало; поиск минимального элемента массива array из N элементов
min := array[1]
для i от 2 до N выполнять:
  если array[i] < min
    min := array[i]
конец; вернуть min

При выполнении этого алгоритма будет выполнена:

1. N — 1 операция присваивания счетчику цикла i нового значения;
2. N — 1 операция сравнения счетчика со значением N;
3. N — 1 операция сравнения элемента массива со значением min;
4. от 1 до N операций присваивания значения переменной min.

Точное количество операций будет зависеть от обрабатываемых данных, поэтому имеет смысл говорить о наилучшем, наихудшем и среднем случаях. При этом худшему случаю всегда уделяется особое внимание, в том числе потому, что «плохие» данные могут быть намеренно поданы на вход злоумышленником.

Понятие среднего случая используется для оценки поведения алгоритма с расчетом на то, что наборы данных равновероятны. Однако, такая оценка достаточно сложна:

1. исходные данные разбиваются на группы так, что трудоемкость алгоритма ((t_i)) для любого набора данных одной группы одинакова;
2. исходя из доли наборов данных группы в общем числе наборов, рассчитывается вероятность для каждой группы ((p_i));
3. оценка среднего случая вычисляется по формуле: (sumlimits_{i=1}^m p_icdot t_i).

Асимптотические обозначения

Подсчет количества операций позволяет сравнить эффективность алгоритмов. Однако, аналогичный результат можно получить более простым путем. Анализ проводят с расчетом на достаточно большой объем обрабатываемых данных (( n to infty )), поэтому ключевое значение имеет скорость роста функции сложности, а не точное количество операций.

При анализе скорости роста игнорируются постоянные члены и множители в выражении, т.е. функции (f_x = 10 cdot x^2 + 20 ) и ( g_x = x^2) эквивалентны с точки зрения скорости роста. Незначащие члены лишь добавляют «волнистости», которая затрудняет анализ.

В оценке алгоритмов используются специальные асимптотические обозначения, задающие следующие классы функций:

• (mathcal{O}(g)) — функции, растущие медленнее чем g;
• (Omega(g)) — функции, растущие быстрее чем g;
• (Theta(g)) — функции, растущие с той же скоростью, что и g.

Запись (f_n = mathcal{O}(g_n)) означает принадлежность функции f классу (mathcal{O}(g)), т.е. функция f ограничена сверху функцией g для достаточно больших значений аргумента. (exists n_0 > 0, c > 0 : forall n > n_0, f_n leq c cdot g_n).

Ограниченность функции g снизу функцией f записывается следующим образом: (g_n =Omega(f_n)). Нотации (Omega) и (mathcal{O}) взаимозаменяемы: (f_n = mathcal{O}(g_n) Leftrightarrow g_n =Omega(f_n)).

Если функции f и g имеют одинаковую скорость роста ((f_n = Theta(g_n))), то существуют положительные константы (c_1) и (c_2) такие, что (exists n_0 > 0 : forall n > n_0, f_n leq c_1 cdot g_n, f_n geq c_2 cdot g_n). При этом (f_n = Theta(g_n) Leftrightarrow g_n = Theta(f_n)).

Примеры анализа алгоритмов

Алгоритм поиска минимального элемента массива, приведенный выше, выполнит N итераций цикла. Трудоемкость каждой итерации не зависит от количества элементов массива, поэтому имеет сложность (T^{iter} = mathcal{O}(1)). В связи с этим, верхняя оценка всего алгоритма (T^{min}_n = mathcal{O}(n) cdot mathcal{O}(1) = mathcal{O}(n cdot 1) = mathcal{O}(n)). Аналогично вычисляется нижняя оценка сложности, а в силу того, что она совпадает с верхней — можно утверждать (T^{min}_n = Theta(n) ).

Алгоритм пузырьковой сортировки (bubble sort) использует два вложенных цикла. Во внутреннем последовательно сравниваются пары элементов и если оказывается, что элементы стоят в неправильном порядке — выполняется перестановка. Внешний цикл выполняется до тех пор, пока в массиве найдется хоть одна пара элементов, нарушающих требуемый порядок [2].

начало; пузырьковая сортировка массива array из N элементов
nPairs := N; количество пар элементов
hasSwapped := false; пока что ни одна пара не нарушила порядок
для всех i от 1 до nPairs-1 выполнять:
  если array[i] > array[i+1] то:
    swap(array[i], array[i+1]); обменять элементы местами
    hasSwapped := true; найдена перестановка
  nPairs := nPairs - 1; наибольший элемент гарантированно помещен в конец
 если hasSwapped = true - то перейти на п.3
 конец; массив array отсортирован

Трудоемкость функции swap не зависит от количества элементов в массиве, поэтому оценивается как (T^{swap} = Theta(1) ). В результате выполнения внутреннего цикла, наибольший элемент смещается в конец массива неупорядоченной части, поэтому через N таких вызовов массив в любом случае окажется отсортирован. Если же массив отсортирован, то внутренний цикл будет выполнен лишь один раз.

Таким образом:

• (T^{bubble}_n = mathcal{O}(sumlimits_{i=1}^n sumlimits_{j=1}^{n-i} 1) = mathcal{O}(sumlimits_{i=1}^n n) = mathcal{O}(n ^2));
• (T^{bubble}_n = Omega(1 cdot sumlimits_{j=1}^{n-i} 1) = Omega(n)).

В алгоритме сортировки выбором массив мысленно разделяется на упорядоченную и необработанную части. На каждом шаге из неупорядоченной части массива выбирается минимальный элемент и добавляется в отсортированную часть [2].

начало; selection_sort - сортировка массива array из N элементов методом выбора
для всех i от 1 до N выполнять:
  imin := indMin(array, N, i)
  swap(array[i], array[imin])
конец; массив array отсортирован

Для поиска наименьшего элемента неупорядоченной части массива используется функция indMin, принимающая массив, размер массива и номер позиции, начиная с которой нужно производить поиск. Анализ сложности этой функции можно выполнить аналогично тому, как это сделано для функции min — количество операций линейно зависит от количества обрабатываемых элементов: ( T^{indMin}_{n, i} = Theta(n — i)).

У сортировки выбором нет ветвлений, которые могут внести различия в оценку наилучшего и наихудшего случаев, ее трудоемкость: (T^{select}_n = Theta(sumlimits_{i=1}^{n} (T^{indMin}_{n, i} + T^{swap})) =Theta(sumlimits_{i=1}^{n} (n-i)) = Theta(frac{n-1}{2} cdot n) = Theta(n^2) ).

Математический аппарат анализа алгоритмов

Выше были рассмотрены асимптотические обозначения, используемые при анализе скорости роста. Они позволяют существенно упростить задачу отбросив значительную часть выражения. Однако, в математическом анализе имеется целый ворох таких приемов.

Формулы суммирования

В примерах, рассмотренных выше, мы уже сталкивались с нетривиальными формулами суммирования. Чтобы дать оценку суммы можно использовать ряд известных тождеств:

• вынос постоянного множителя за знак суммы: (sumlimits_{i=1}^{n} (c cdot f_i) = c cdot sumlimits_{i=1}^{n} cdot f_i);
• упрощение суммы составного выражения: (sumlimits_{i=1}^{n} (f_i + g_i) = sumlimits_{i=1}^{n} (f_i) + sumlimits_{i=1}^{n} (g_i));
• сумма чисел арифметической прогрессии: (sumlimits_{i=1}^{n} (i^p) = Theta(n^{p+1}));
• сумма чисел геометрической прогрессии: (sumlimits_{i=0}^{n} (a^i) = frac {a cdot (a^{n+1} — 1)}{a — 1}). При ( n to infty ) возможны 2 варианта:
  • если a < 1, то сумма стремится к константе: (Theta(1));
  • если a > 1, то сумма стремится к бесконечности: (Theta(a^{n+1}));
  • если a = 0, формула неприменима, сумма стремится к N: (Theta(n));
• логарифмическая сложность алгоритма: (sumlimits_{i=1}^{n} frac{1}{i} = Theta(log n));
• сумма логарифмов: (sumlimits_{i=1}^{n} log i = Theta(n cdot log n)).

Первые из этих тождеств достаточно просты, их можно вывести используя метод математической индукции. Если под знаком суммы стоит более сложная формула, как в двух последних тождествах — суммирование можно заменить интегрированием (взять интеграл функции гораздо проще, ведь для этого существует широкий спектр приемов).

Суммирование и интегрирование

Известно, что интеграл можно понимать как площадь фигуры, размещенной под графиком функции. Существует ряд методов аппроксимации (приближенного вычисления) интеграла, к ним относится, в частности, метод прямоугольников. Площадь под графиком делится на множество прямоугольников и приближенно вычисляется как сумма их площадей. Следовательно, возможен переход от интеграла к сумме и наоборот.

На рисунках приведен пример аппроксимации функции (f_x = log x) левыми и правыми прямоугольниками. Очевидно, они дадут верхнюю и нижнюю оценку площади под графиком:

• (intlimits_a^n f_x dx leq sumlimits_{i=a }^{n} f_i leq intlimits_{a+1}^{n+1} f_x dx) для возрастающих функций;
• (intlimits_a^n f_x dx geq sumlimits_{i=a }^{n} f_i geq intlimits_{a+1}^{n+1} f_x dx) для убывающих функций.

В частности, такой метод позволяет оценить алгоритмы, имеющие логарифмическую сложность (две последние формулы суммирования).

Сравнение сложности алгоритмов. Пределы

Сложность алгоритмов определяется для больших объемов обрабатываемых данных, т.е. при (ntoinfty). В связи с этим, при сравнении трудоемкости двух алгоритмов можно рассмотреть предел отношения функций их сложности: (limlimits_{n to infty} frac {f_n}{g_n}). В зависимости от значения предела возможно сделать вывод относительно скоростей роста функций:

• предел равен константе и не равен нулю, значит функции растут с одной скоростью:(f_n = Theta(g_n));
• предел равен нулю, следовательно (g_n) растет быстрее чем (f_n): (f_n = mathcal{O}(g_n));
• предел равен бесконечности, (g_n) растет медленнее чем (f_n): (f_n = Omega(g_n)).

Если функции достаточно сложны, то такой прием значительно упрощает задачу, т.к. вместо предела отношения функций можно анализировать предел отношения их производных (согласно правилу Лопиталя): (limlimits_{n to infty} frac {f_n}{g_n} = limlimits_{n to infty} frac {f’_n}{g’_n}). Правило Лопиталя можно использовать если функции обладают следующими свойствами:

• (limlimits_{n to infty} frac {f_n}{g_n} = frac{0}{0} или frac {infty}{infty} );
• ( f_n ) и (g_n) дифференцируемы;
• ( g’_n ne 0 ) при (n to infty);
• (exists limlimits_{n to infty} frac {f’_n}{g’_n}).

Допустим, требуется сравнить эффективность двух алгоритмов с оценками сложности (mathcal{O}(a^n)) и (mathcal{O}(n^b)), где a и b — константы. Известно, что ((c^x)’ =c^x cdot ln(c)), но ((x^c)’ = c cdot x^{c-1} ). Применим правило Лопиталя к пределу отношения наших функций b раз, получим: (limlimits_{n to infty} frac {mathcal{O}(a^n)}{mathcal{O}(n^b)} = limlimits_{n to infty} frac {mathcal{O}(a^n * ln^b (a))}{mathcal{O}(b!)} = infty). Значит функция (a^n) имеет более высокую скорость роста. Без использования пределов и правила Лопиталя такой вывод может казаться не очевидным.

Логарифмы и сложность алгоритмов. Пример

По определению (log_a{x} = b Leftrightarrow x = a^b). Необходимо знать, что (x to infty Rightarrow log_a{x} to infty), однако, логарифм — это очень медленно растущая функция. Существует ряд формул, позволяющих упрощать выражения с логарифмами:

• (log_a{x cdot y} = log_a{x} + log_a{ y});
• (log_a{x^b} = b cdot log_a{ x});
• (log_a{x} =frac{log_b{x}}{log_b{a}}).

При анализе алгоритмов обычно встречаются логарифмы по основанию 2, однако основание не играет большой роли, поэтому зачастую не указывается. Последняя формула позволяет заменить основание логарифма, домножив его на константу, но константы отбрасываются при асимптотическом анализе.

Логарифмической сложностью обладают алгоритмы, для которых не требуется обрабатывать все исходные данные, они используют принцип «разделяй и властвуй». На каждом шаге часть данных (обычно половина) отбрасывается. Примером может быть функция поиска элемента в отсортированном массиве (двоичного поиска):

начало; поиск элемента E в отсортированном по возрастанию массиве array из N элементов
left := 1, right := N; левая и правая граница, в которых находится искомый элемент
выполнять пока left =< right:
  mid := (right + left) div 2; вычисление индекса элемента посередине рассматриваемой части массива
  если array[mid] = E
    конец; вернуть true (элемент найден)
  если array[mid] < E; искомый элемент больше середины, значит все элементы левее mid можно отбросить
    left := mid + 1;
  иначе
    right := mid
конец; вернуть false (элемент не найден)

Очевидно, что на каждом шаге алгоритма количество рассматриваемых элементов сокращается в 2 раза. Количество элементов, среди которых может находиться искомый, на k-том шаге определяется формулой (frac{n}{2^k}). В худшем случае поиск будет продолжаться пока в массиве не останется один элемент, т.е. чтобы определить количество итераций для верхней оценки, достаточно решить уравнение (1 = frac{n}{2^k} Rightarrow 2^i = n Rightarrow i = log_2 n). Следовательно, алгоритм имеет логарифмическую сложность: (T^{binSearch}_n = mathcal{O}(log n)).

Результаты анализа. Замечания. Литература

Оценка сложности — замечательный способ не только сравнения алгоритмов, но и прогнозирования времени их работы. Никакие тесты производительности не дадут такой информации, т.к. зависят от особенностей конкретного компьютера и обрабатывают конкретные данные (не обязательно худший случай).

Анализ алгоритмов позволяет определить минимально возможную трудоемкость, например:

• алгоритм поиска элемента в неупорядоченном массиве не может иметь верхнюю оценку сложности лучше, чем (mathcal{O}(n)). Это связано с тем, что невозможно определить отсутствие элемента в массиве (худший случай) не просмотрев все его элементы;
• возможно формально доказать, что не возможен алгоритм сортировки произвольного массива, работающий лучше чем (mathcal{O}(n cdot log n)) [5].

Нередко на собеседованиях просят разработать алгоритм с лучшей оценкой, чем возможно. Сами задачи при этом сводятся к какому-либо стандартному алгоритму. Человек, не знакомый с асимптотическим анализом начнет писать код, но требуется лишь обосновать невозможность существования такого алгоритма.

1. Васильев В. С. Алгоритм. Свойства алгоритма [Электронный ресурс] – режим доступа: https://pro-prof.com/archives/578. Дата обращения: 06.01.2014.
2. Васильев В. С. Блок-схемы алгоритмов сортировки пузырьком, выбором и вставками [Электронный ресурс] – режим доступа: https://pro-prof.com/archives/1462. Дата обращения: 06.01.2014.
3. Дж. Макконелл Анализ алгоритмов. Активный обучающий подход. — 3-е дополненное издание. М: Техносфера, 2009. -416с.
4. Миллер, Р. Последовательные и параллельные алгоритмы: Общий подход / Р. Миллер, Л. Боксер ; пер. с англ. — М. : БИНОМ. Лаборатория знаний, 2006. — 406 с.
5. Скиена С. Алгоритмы. Руководство по разработке. 2-е изд.: Пер. с англ. — СПб.: БХВ-Петербург. 2011. — 720 с.: ил.