Определение вида треугольника по длинам его сторон
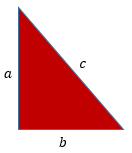
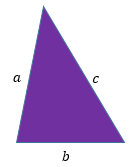
Пусть а, b и c – стороны треугольника, тогда
1) если а = b, то треугольник равнобедренный.
2) если а = b = c, то треугольник равносторонний.
3) если а ≠ b ≠ с, то треугольник разносторонний.
Пусть с – бóльшая сторона, тогда
4) если с2 > a2 + b2, то треугольник тупоугольный.
5) если с2 = a2 + b2, то треугольник прямоугольный.
6) если с2 < a2 + b2, то треугольник остроугольный.
Успешной сдачи экзаменов!
С уважением, Васильева Анна.
Гуру
(3013),
закрыт
11 лет назад
LFK
Мыслитель
(6194)
11 лет назад
Если самая большая сторона равна сумме квадратов двух других его сторон – треугольник прямоугольный. Если самая большая сторона меньше суммы квадратов двух других его сторон- треугольник остроугольный. Если самая большая сторона больше суммы квадратов двух других его сторон – треугольник тупоугольный.
Кристина
Гуру
(2806)
11 лет назад
например а – большая сторона, в и с – две другие
находишь а^2 и b^2+c^2
если они равны – прямоугольный
если левая часть меньше правой – остроугольный
если левая часть больше правой – тупоугольный
Содержание
- – Как определить остроугольный треугольник зная его стороны?
- – Как доказать что треугольник прямоугольный по сторонам?
- – Как определить треугольник по 3 сторонам?
- – Как узнать существует ли треугольник со сторонами?
- – Как определить тип треугольника по длине сторон?
- – Как определить Остроугольный?
- – Чему равны стороны треугольника?
- – В чем заключается неравенство треугольника?
Как определить остроугольный треугольник зная его стороны?
Если квадрат максимальной стороны меньше суммы квадратов других сторон треугольника, значит, он является остроугольным.
Как доказать что треугольник прямоугольный по сторонам?
Так вот, прямоугольный треугольник обладает такими свойствами:
- Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы
- Медиана прямоугольного треугольника равна половины гипотенузы
- сумма двух острых углов прямоугольного треугольника равна 90 градусов
Как определить треугольник по 3 сторонам?
У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто “лягут” на третью и треугольника не получится. Пользователь вводит длины трех сторон.
Как узнать существует ли треугольник со сторонами?
Треугольник существует только тогда, когда сумма двух его сторон больше третьей. Требуется сравнить каждую сторону с суммой двух других. Если хотя бы в одном случае сторона окажется больше либо равна сумме двух других, то треугольника с такими сторонами не существует.
Как определить тип треугольника по длине сторон?
Если выполняется теорема Пифагора: с²=a²+b² , где с – наибольшая сторона, а и b две других, – треугольник прямоугольный. Если квадрат наибольшей стороны меньше суммы квадратов двух других сторон: с² < a²+b² треугольник остроугольный.
Как определить Остроугольный?
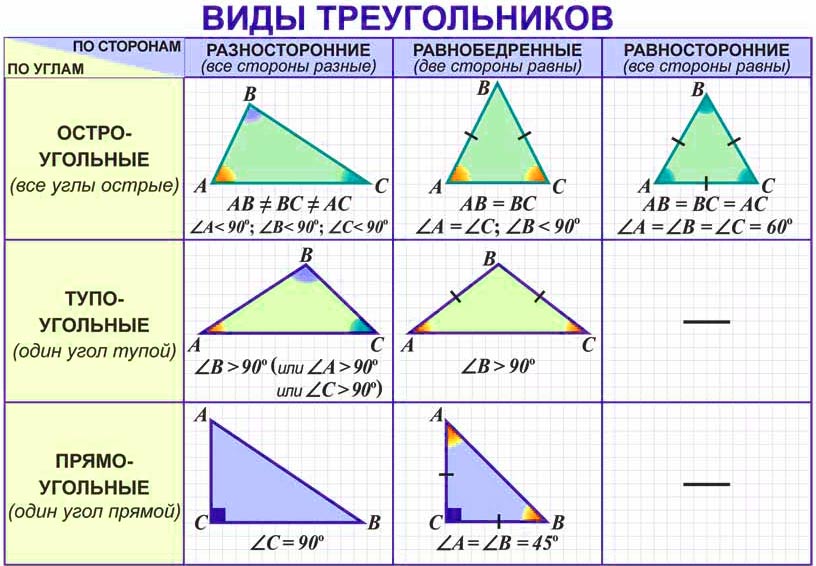
В зависимости от углов треугольник может быть:
- Прямоугольным, если один из углов равен 90 градусов;
- Тупоугольный, если один из углов тупой, т. е. больше 90 градусов;
- Остроугольным, если все углы треугольника острые.
Чему равны стороны треугольника?
По числу равных сторон
Равнобедренный треугольник – две стороны равны. Равносторонним треугольник или правильный треугольник – все три стороны равны.
В чем заключается неравенство треугольника?
Нера́венство треуго́льника в геометрии, функциональном анализе и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда меньше суммы длин двух его других сторон.
Интересные материалы:
Что насыпать под тротуарную плитку?
Что нужно для укладки клинкерной плитки?
Что нужно класть под тротуарную плитку чтоб не росла трава?
Что нужно стелить под тротуарную плитку?
Что подложить под плитку чтобы не росла трава?
Что подсыпают под тротуарную плитку?
Что положить под тротуарную плитку?
Что прочнее керамогранит или керамическая плитка?
Что прочнее плитка или керамогранит?
Что стелить под тротуарную плитку?
Как определить остроугольный или тупоугольный треугольник?
Как определить остроугольный треугольник зная его стороны?
Если квадрат максимальной стороны меньше суммы квадратов других сторон треугольника, значит, он является остроугольным.
Как доказать что треугольник прямоугольный по сторонам?
- Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы
- Медиана прямоугольного треугольника равна половины гипотенузы
- сумма двух острых углов прямоугольного треугольника равна 90 градусов
Как определить треугольник по 3 сторонам?
У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто «лягут» на третью и треугольника не получится. Пользователь вводит длины трех сторон.
Как узнать существует ли треугольник со сторонами?
Треугольник существует только тогда, когда сумма двух его сторон больше третьей. Требуется сравнить каждую сторону с суммой двух других. Если хотя бы в одном случае сторона окажется больше либо равна сумме двух других, то треугольника с такими сторонами не существует.
Как определить тип треугольника по длине сторон?
Если выполняется теорема Пифагора: с²=a²+b² , где с — наибольшая сторона, а и b две других, – треугольник прямоугольный. Если квадрат наибольшей стороны меньше суммы квадратов двух других сторон: с² Как определить Остроугольный?
- Прямоугольным, если один из углов равен 90 градусов;
- Тупоугольный, если один из углов тупой, т. е. больше 90 градусов;
- Остроугольным, если все углы треугольника острые.
Чему равны стороны треугольника?
По числу равных сторон
Равнобедренный треугольник — две стороны равны. Равносторонним треугольник или правильный треугольник — все три стороны равны.
В чем заключается неравенство треугольника?
Нера́венство треуго́льника в геометрии, функциональном анализе и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда меньше суммы длин двух его других сторон.
Тупоугольный треугольник, элементы, свойства, признаки и формулы
Тупоугольный треугольник, элементы, свойства, признаки и формулы.
Тупоугольный треугольник – это треугольник, у которого один угол тупой.
Тупоугольный треугольник (понятие и определение):
Тупоугольный треугольник – это треугольник, у которого один угол тупой, т.е. один из его углов лежит в пределах между 90° и 180°.
Тупоугольный треугольник – это треугольник, у которого один угол тупой, а два других – острые. В свою очередь, тупой угол – это угол, градусная мера которого составляет 90° до 180°, а острый угол – это угол, градусная мера которого составляет менее 90 градусов
Рис. 1. Тупоугольный треугольник
∠ BАC– тупой угол треугольника,
По определению, тупоугольным треугольником не может быть правильный (равносторонний) треугольник , т.к. у него каждый угол составляет 60°.
Рис. 2. Равносторонний треугольник
АВ = ВС = АС – стороны треугольника,
По определению, тупоугольным треугольником не может быть прямоугольный треугольник , т.к. у него один угол составляет 90° и сумма двух других углов также составляет 90°.
Рис. 3. Прямоугольный треугольник
Тупоугольный треугольник также может быть одновременно равнобедренным треугольником . Но не всякий равнобедренный треугольник тупой.
Рис. 4. Равнобедренный треугольник
АВ = AС – боковые стороны, BС – основание,
Хотя в тупоугольном треугольнике тупой угол больше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.
Элементы тупоугольного треугольника:
Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.
Рис. 5. Тупоугольный треугольник и внешний угол
Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.
Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника
MA – медиана тупоугольного треугольника
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника
MС – высота тупоугольного треугольника
Высота тупоугольного треугольника может лежать за пределами треугольника.
Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.
Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника
MA – биссектриса тупого угла тупоугольного треугольника
Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Свойства тупоугольного треугольника:
Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:
1. Против большей стороны лежит больший угол, и наоборот.
Рис. 9. Тупоугольный треугольник
2. Против равных сторон лежат равные углы, и наоборот.
Рис. 10. Тупоугольный треугольник с равными боковыми сторонами
3. Сумма углов тупоугольного треугольника равна 180°.
4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности:
Тупоугольный треугольник
Тупоугольный треугольник мало чем отличается от обычных произвольных остроугольных треугольников, но тупой угол делает треугольник непривычным для восприятия. Это зачастую приводит в недоумение, поэтому стоит рассмотреть различные варианты решения задач на нахождение параметров тупоугольного треугольника.
Определения
Тупоугольным треугольником будет называться любой треугольник, содержащий тупой угол. Тупоугольный треугольник может быть равнобедренным, но при этом не может быть равносторонним или прямоугольным. Собственно на этом свойства этой фигуры заканчиваются. В остальном, это обычный треугольник и подход к решению таких фигур ничем не отличается.
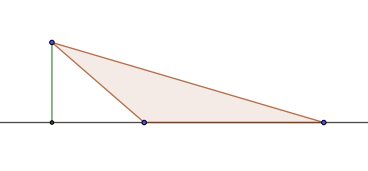
Только в тупоугольном треугольнике высота может лежать за пределами треугольника.
Рассмотрим несколько интересных задач на нахождение данных в тупоугольном треугольнике.
Пример решения задачи
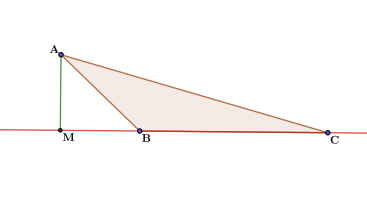
Для решения любой задачи можно найти несколько способов. В данной ситуации можно пойти через площадь треугольников, достроить тупоугольный треугольник до прямоугольного или воспользоваться теоремой косинусов. Каждый из способов дает представление о том, как можно решать задачи с тупоугольным треугольником. Воспользуемся каждым из них.
Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.
- Через площадь треугольников. Площадь можно найти как половину произведения основания на высоту, проведенную к этому основанию. А можно – как половину произведения двух сторон на синус угла между ними. Нам известен косинус угла, а через косинус всегда можно найти синус.
Теперь запишем две формулы площади, выразим через них высоту и найдем ее значение.
- Второй способ – это достроить тупоугольный треугольник до прямоугольного. Если присмотреться, то можно заметить на чертеже два прямоугольных треугольника – это треугольники АМС и АМВ. В треугольнике АМВ можно найти косинус угла АВМ с помощью формул-приведений. Затем, через значение косинуса найти значение синуса того же угла. А синус – это отношение противолежащего катета к гипотенузе. Противолежащей катет – это искомая нами высота, а гипотенуза – это сторона АВ прямоугольного треугольника.
Тогда синус, как и в первом способе, выразим через основное тригонометрическое тождество.
- Третий метод – это теорема синусов и косинусов. Для того, чтобы воспользоваться этим способом, через теорему косинусов найдем значение АС, потом через теорему синусов найдем синус угла АСВ и определим АМ из синуса угла АСВ большого прямоугольного треугольника АМС.
$$sqrt=sqrt=5$$ – по теореме косинусов.
Значение синуса угла АВС определим по основному тригонометрическому тождеству.
Выразим искомый синус угла АСВ.
Выразим из треугольника АМС и найденного значения синуса сторону АМ.
Ответы всех трех способов совпали, а, значит, задача решена верно.
Что мы узнали?
Мы поговорили об определении тупоугольного треугольника. Узнали и посмотрели на практике, какие методы решения тупоугольных треугольников существуют, а также выяснили ,какие формулы и теоремы необходимо знать для успешного решения тупоугольного треугольника.
Онлайн калькулятор поможет узнать по сторонам, является ли треугольник прямоугольным, равнобедренным, равносторонним или разносторонним.
Как определить, что треугольник прямоугольный: по Теорема Пифагора — сумма квадратов длин катетов равна квадрату длины гипотенузы
c2 = a2 + b2
Как определить, что треугольник равнобедренный: один из признаков равнобедренного треугольника – две стороны равны.
Как определить, что треугольник равносторонний: все стороны равны.
Принято выделять три типа треугольников:
тупоугольные – один из углов более 90 градусов,
прямоугольные – один из угол равен 90 градусов,
остроугольные – все углы менее 90 градусов.
Это классификация по типу углов.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»