Определение усеченного среднего
Усеченное среднее — это метод нахождения более реалистичного среднего значения путем избавления от некоторых ошибочных наблюдений. В соответствии с этим методом процент самых высоких и самых низких значений вырезается из обоих крайних значений перед вычислением среднего значения. Это исключение перед вычислением приводит к более надежному среднему значению.
- Усеченное среднее — это статистическая мера, которая избавляет от процента наблюдений из заданного списка перед выполнением вычислений среднего. Искоренение значений происходит с нижнего и верхнего конца данного набора наблюдений.
- Его также называют усеченным средним, он обеспечивает более надежное среднее статистическое значение за счет уменьшения стандартных ошибок. Другими словами, это мера дисперсии среднего значения выборки, относящаяся к среднему значению генеральной совокупности, а не стандартное отклонение. Читать далее, вызванное выбросами или экстремальными вариациями.
- Усеченное среднее применяется для определения уровня инфляции, результатов Олимпийских игр и экономических данных, которые требуют незначительных колебаний.
- Наименьшая обрезка составляет 0%, то же самое, что и среднее арифметическое.
Оглавление
- Определение усеченного среднего
- Объяснение усеченного среднего
- #1 – 5% усеченного среднего
- # 2 — 10% усеченного среднего
- #3 – 20% усеченного среднего
- Формула усеченного среднего
- Пример усеченного среднего с пошаговым расчетом
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи
- Объяснение усеченного среднего
Объяснение усеченного среднего

Усеченное среднее — это усеченный сегмент среднего арифметического. Среднее арифметическое Среднее арифметическое обозначает среднее значение всех наблюдений ряда данных. Это совокупность всех значений в наборе данных, деленная на общее количество наблюдений. Подробнее используется в статистике. Поэтому его также называют усеченным средним. Процент сокращается с обоих концов ряда наблюдений, исключая самые высокие и самые низкие значения. В этом ряду наблюдения располагаются в порядке возрастания. Существует три обычно применяемых процента обрезки, т. е. 5%, 10% и 20%.
Усеченное среднее широко применяется для уменьшения колебаний выборки. На Олимпийских играх с помощью этого метода избегают доминирования крайних точек данных. При расчете темпов инфляции усеченное среднее помогает исключить резкие изменения цен. Резервный банк Австралиикак и многие центральные банки, использует усеченные средние значения для определения темпов инфляции.
Обоснование усеченного среднего заключается в том, что иногда происходят существенные изменения цен на определенные товары, которые существенно влияют на обычное среднее всех изменений цен. Иногда комплексное среднее значение совершенно не отражает изменения цен на другие товары и услуги. Обрезка приходит на помощь в таких случаях, чтобы получить более реалистичное значение. Ниже приведены характеристики определенных процентов усеченного среднего.
#1 – 5% усеченного среднего
Общее 5% усеченное среднее обычно эффективно в случае обширных данных. 2,5% наблюдений исключены из нижнего и верхнего концов. Следовательно, 95% наблюдений в серии остаются нетронутыми. Усеченное на 5 % значение self будет отражать применение отдельной обрезки на 5 % для самых низких и самых высоких значений. Следуя этой логике, важно понимать, что при подстройке 0% не будут исключаться какие-либо значения, и будет выполняться среднее значение с учетом каждого наблюдения. Таким образом, получится среднее арифметическое.
# 2 — 10% усеченного среднего
В общей сложности 10% усеченного среднего используется очень часто. На Олимпийских играх этот метод часто используется для устранения традиционных смещений средних значений, вызванных экстремальными значениями. Таким образом, 5% наименьшего и наибольшего значений удаляются перед вычислением среднего значения с каждого конца. Следовательно, 90% наблюдений в серии остаются нетронутыми.
#3 – 20% усеченного среднего
Усечение на 20% аналогично другим процентам обрезки. Здесь 10% значений удаляются с обоих концов. Следовательно, остаток используется для расчета 20% усеченного среднего. Кроме того, сокращение на 5, 10 или 20 процентов от предлагаемого конца списка потребует выполнения расчета только для данной части. Следовательно, усечение на 10% для самого высокого значения потребует только удаления наблюдений из более высокого конца.
Формула усеченного среднего
Следующие шаги включаются в формулу усеченного среднего:
- Пройдите процент обрезки. Это может быть 10%, 20%, 30% и т.
- Умножьте процент на количество наблюдений, чтобы получить количество значений, вычтенных из каждого конца.
- Удалите самые высокие и самые низкие числа с обоих концов.
- Сократите общее количество наблюдений, вычитая количество наблюдений, которые были вырезаны.
- Применить стандартное среднее или формулу среднего. Формула среднего. Среднее значение — это значение, которое используется для представления набора значений данных, как среднее значение, рассчитанное из всех данных, и эта формула рассчитывается путем сложения всех значений заданного набора, обозначаемого суммированием X и разделив его на количество значений, заданных в наборе, обозначенном N. подробнее к остальным наблюдениям, который выглядит следующим образом: Сумма наблюдений/количество наблюдений
- После применения формулы среднего можно было бы получить усеченное среднее.
Пример усеченного среднего с пошаговым расчетом
В следующей числовой задаче показано ручное применение концепции усеченного среднего и пошаговые вычисления.
Проблема:
Толкатель ядра записывает следующие результаты: 16,8 м, 16,9 м, 17,1 м, 17,2 м, 17,8 м, 17,9 м, 18,2 м, 18,3 м, 18,3 м, 18,5 м. Найдите 10% усеченное среднее.
Решение:
Ниже приведен процесс вычисления усеченного среднего:
Шаг 1 – Подсчитайте количество наблюдений, т.е.
Количество наблюдений = 10
Шаг 2 – Расположите ряды наблюдений в порядке возрастания, т. е. от наименьшего значения к наибольшему.
Баллы расположены в порядке возрастания:
16,8 м, 16,9 м, 17,1 м, 17,2 м, 17,8 м, 17,9 м, 18,2 м, 18,3 м, 18,3 м, 18,5 м
Шаг 3 – Вычислите процент сокращения на каждом конце серии наблюдений.
Процент = 10%
Количество наблюдений, которые нужно обрезать с обоих концов = 10% * 10 = 1
Таким образом, нам нужно удалить два числа из набора наблюдений.
Шаг № 4 – Удалим наибольшее и наименьшее число с обоих концов. Это дает нам
16,9 м, 17,1 м, 17,2 м, 17,8 м, 17,9 м, 18,2 м, 18,3 м, 18,3 м,
Шаг № 5 – Применим стандартную формулу среднего или среднего для расчета среднего из оставшихся восьми значений.
16,9, 17,1, 17,2, 17,8, 17,9, 18,2, 18,3, 18,3/8
Усеченное среднее = 17,71
Для реальных приложений определение процента сокращения имеет решающее значение. Опыт, знания и практика помогают пользователям выбрать подходящий процент, который нужно вырезать из среднего арифметического. Этот процент варьируется в зависимости от ситуации, проблемы и ниши, где он применяется.
Часто задаваемые вопросы (FAQ)
Что такое 10% обрезки означает?
10% усеченное среднее значение является центральной мерой тенденции в статистике. Таким образом, мы будем обрезать 10% наблюдений с обоих концов. Предположим, что всего имеется 10 наблюдений. Обрезка на 10% будет равна 10% x 10 = 1. Мы удалим самое высокое и самое низкое значение с обоих концов. После этого мы вычисляем среднее значение оставшихся 8 значений. На Олимпийских играх этот метод часто используется для устранения традиционных смещений средних значений, вызванных экстремальными значениями.
В чем смысл усеченного среднего?
Усеченное среднее — это метод нахождения более надежного среднего, чтобы оно было ближе к фактическому результату, путем обрезки процента наблюдений по обоим крайним значениям. Это сокращение самых высоких и самых низких значений приводит к более надежному среднему значению за счет избавления от выбросов.
Как найти усеченное среднее?
Усеченное среднее может быть найдено путем вычисления среднего арифметического после сокращения процента наблюдений от обоих крайних значений. Затем к оставшимся наблюдениям мы применяем формулу стандартного среднего.
Рекомендуемые статьи
Это было руководство по усеченному среднему и его статистическому определению. Здесь мы обсуждаем пример с пошаговым расчетом вместе с формулой. Вы можете узнать больше о финансировании из следующих статей –
- Среднее геометрическое
- Формула гармонического среднего
- Формула средней численности населения
- Формула взвешенного среднего
Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами. Ведь в данной задаче могут быть поставлены определенные условия.
Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.
Как найти среднее арифметическое чисел?
Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.
Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:

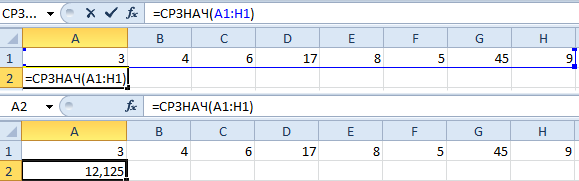
- Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» – кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула. Выделяем диапазон: A1:H1 и нажимаем ВВОД.
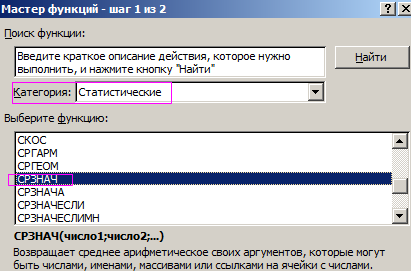
- В основе второго метода тот же принцип нахождения среднего арифметического. Но функцию СРЗНАЧ мы вызовем по-другому. С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3).
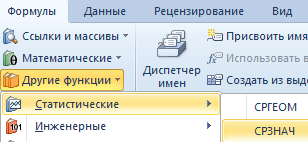
- Третий способ вызова функции СРЗНАЧ из панели: «Формула»-«Формула»-«Другие функции»-«Статические»-«СРЗНАЧ».
Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).
Теперь посмотрим, что еще умеет функция СРЗНАЧ.
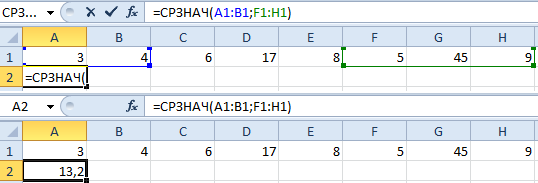
Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:H1). Результат:
Среднее значение по условию
Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().
Найти среднее арифметическое чисел, которые больше или равны 10.
Функция: =СРЗНАЧЕСЛИ(A1:A8;”>=10″)
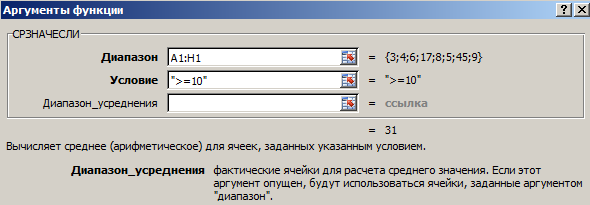
Результат использования функции СРЗНАЧЕСЛИ по условию “>=10”:

Третий аргумент – «Диапазон усреднения» – опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.
Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.
Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».
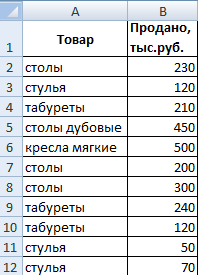
Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово “столы”). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.
В результате вычисления функции получаем следующее значение:
Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно.
Как посчитать средневзвешенную цену в Excel?
Как посчитать средний процент в Excel? Для этой цели подойдут функции СУММПРОИЗВ и СУММ. Таблица для примера:
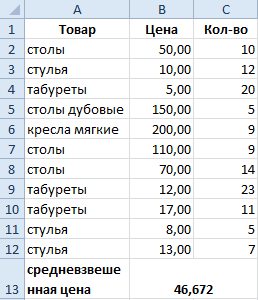
Как мы узнали средневзвешенную цену?
Формула: =СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).
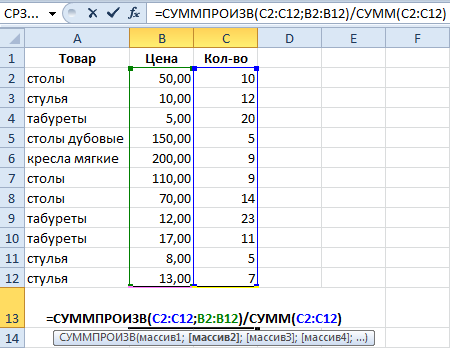
С помощью формулы СУММПРОИЗВ мы узнаем общую выручку после реализации всего количества товара. А функция СУММ – сумирует количесвто товара. Поделив общую выручку от реализации товара на общее количество единиц товара, мы нашли средневзвешенную цену. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.
Среднее квадратическое отклонение: формула в Excel
Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.
Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.
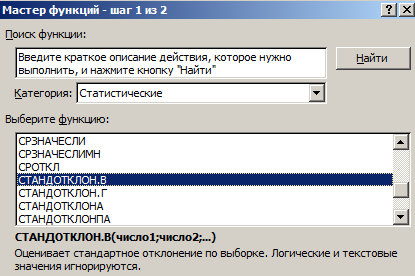
Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:
среднеквадратическое отклонение / среднее арифметическое значение
Формула в Excel выглядит следующим образом:
СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).
Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.
Как рассчитать средний процент если известны несколько процентных показателей и среди них нужно вычислить средний
Алексей Владимирович
Ученик
(160),
закрыт
3 года назад
32% 49.2% 34.2% 49.2% 41% 53% 72%
Adron
Мудрец
(17688)
3 года назад
Найти их среднее арифметическое (сложить и поделить на их количество). Но это только (!) все проценты от одинакового числа (если все проценты считались от какого-то одного показателя).
Если же показатели разные:
(0.32*x1)+(0.492*x2)+(0.342*x3)+…+(0.72*x7)=Z
И полученную сумму (Z) надо поделить на сумму показателей (x1+x2+x3+…+x7).
Как найти Срзнач?
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Чему равно среднее значение функции?
f(x)dx. Понимая интеграл как площадь под графиком, нетрудно дать геометрическую интерпрета- цию: среднее значение функции на отрезке есть площадь под графиком функции, делённая на длину отрезка.
Как в Экселе сделать формулу среднее значение?
Расчет среднего значения чисел в подрядной строке или столбце
- Щелкните ячейку снизу или справа от чисел, для которых необходимо найти среднее.
- На вкладке «Главная» в группе «Редактирование» щелкните стрелку рядом с кнопкой » «, выберите «Среднее» и нажмите клавишу ВВОД.
Как находится среднее значение выборки?
Это сумма данных чисел, деленное на количество. Если написать в виде формулы, это выглядит так. Здесь ˉx – среднее арифметическое значение. Если у Вас имеется 5 чисел {10,12,5,20,8}, то их сумма будет 10+12+3+20+8=55 .
Как рассчитать размах в Excel?
Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность. Вставка – Функция – Статистические – МАКС.
Что значит Countif?
Подсчитывает число ячеек в диапазоне, удовлетворяющих критерию. Группа ячеек для подсчёта. Значение, определяющее, какие ячейки в диапазоне будут подсчитываться (например: 15, «Здравствуй, Мир!», >25).
Как в гугл таблице посчитать среднее значение?
Примечание.
- Откройте файл в Google Таблицах на компьютере.
- Выделите нужные ячейки.
- В правом нижнем углу страницы найдите значок «Анализ данных» . Рядом с ним будет «Сумма: <значение>».
- Нажмите Сумма, чтобы увидеть все доступные вычисления: среднее арифметическое; минимум; максимум; количество; количество чисел.
Как посчитать среднее значение в Python?
Для вычисления среднего значения списка в Python можно использовать любой из следующих методов:
- Функция mean();
- Встроенный метод sum();
- Методы lambda() и reduce();
- Метод operator. add().
13 апр. 2021 г.
Как в Excel посчитать среднее значение с условием?
Для расчета среднего значения по условию в Excel используется функция СРЗНАЧЕСЛИ. Кроме суммирования и подсчета количества значений, вычисление среднего значения по условию – это одна из самый часто выполняемых операций с диапазонами ячеек в Excel.
Как рассчитать среднее значение между двумя числами?
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4. Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Как посчитать отклонение от среднего арифметического?
Таким образом, для подсчета среднеквадратического отклонения достаточно параллельно считать две суммы: сумму чисел и сумму квадратов чисел, затем обе поделить на n, второе из двух возвести в квадрат и вычесть из первого. От разности достаточно взять корень квадратный, чтобы получить само D.
Если среднее значение переменной больше медианы, ее распределение имеет положительную асимметрию. Если медиана больше среднего значения, распределение переменной имеет отрицательную асимметрию.
Как определить размах?
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел. Например: найдем размах чисел 2; 5; 8; 12; 33. Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т.
Как в Excel построить вариационный ряд?
Для построения гистограммы выполните следующие действия:
- Главное меню: Вставка – Диаграмма.
- Тип: точечная.
- Диапазон данных: выделите ячейки содержащие значения абсолютных частот.
- Ряд: Значения по X: укажите диапазон ячеек содержащий значения середины промежутков.
- Готово. назад
Как работать с Счетесли?
Формула: =СЧЁТЕСЛИ(A1:B11;»>=100″)-СЧЁТЕСЛИ(A1:B11;»>200″). Ищет значения по двум критериям сразу в двух столбцах. Если диапазоны несмежные, то применяется функция СЧЕТЕСЛИМН. Когда в качестве критерия указывается ссылка на диапазон ячеек с условиями, функция возвращает массив.
Как будет Vlookup на русском?
Функция ПРОСМОТРХ (XLOOKUP) — Справочник
Как в гугл таблицах сделать Автосумму?
Вы также можете добавить функцию СУММ из строки меню таблиц Google. Для этого выберите ячейку, в которую вы хотите ввести формулу, и перейдите к строке меню вверху. Нажмите «Вставить» в строке меню, выберите «∑ Функция» в раскрывающемся списке и выберите функцию «СУММ». Функция вставлена в электронную таблицу.
Усеченное среднее — это среднее значение набора данных, рассчитанное после удаления определенного процента наименьших и наибольших значений из набора данных.
Чтобы вычислить усеченное среднее X%, вы можете использовать следующие шаги:
Шаг 1 : Упорядочить каждое значение в наборе данных от наименьшего к наибольшему.
Шаг 2 : Удалите значения в нижних X% и верхних X% набора данных.
Шаг 3 : Рассчитайте среднее значение оставшихся значений.
В следующих примерах показано, как вычислить усеченное среднее на практике.
Пример 1. Вычисление 10% усеченного среднего
Предположим, у нас есть следующий набор данных:
Набор данных: 4, 8, 12, 15, 9, 6, 14, 18, 12, 9
Вот как рассчитать 10% усеченное среднее значение для набора данных:
Шаг 1 : Упорядочить каждое значение в наборе данных от наименьшего к наибольшему.
Упорядоченный набор данных: 4, 6, 8, 9, 9, 12, 12, 14, 15, 18
Шаг 2. Удалите значения из нижних 10 % и верхних 10 % набора данных.
Всего в наборе данных 10 значений. Таким образом, 10% * 10 = 1. Это означает, что нам нужно удалить одно наименьшее значение и одно наибольшее значение из набора данных:
Обрезанный набор данных: 6, 8, 9, 9, 12, 12, 14, 15
Шаг 3 : Рассчитайте среднее значение оставшихся значений.
10% усеченное среднее = (6+8+9+9+12+12+14+15) / 8 = 10,625
10% усеченное среднее равно 10,625 .
Пример 2. Вычисление 20% усеченного среднего
Предположим, у нас есть следующий набор данных:
Набор данных: 22, 25, 29, 11, 14, 18, 13, 13, 17, 11, 8, 8, 7, 12, 15, 6, 8, 7, 9, 12
Вот как рассчитать усеченное среднее значение 20% для набора данных:
Шаг 1 : Упорядочить каждое значение в наборе данных от наименьшего к наибольшему.
Упорядоченный набор данных: 6, 7, 7, 8, 8, 8, 9, 11, 11, 12, 12, 13, 13, 14, 15, 17, 18, 22, 25, 29
Шаг 2. Удалите значения из нижних 20 % и верхних 20 % набора данных.
Всего в наборе данных 20 значений. Таким образом, 20% * 20 = 4. Это означает, что нам нужно удалить четыре самых маленьких значения и четыре самых больших значения из набора данных:
Обрезанный набор данных: 8, 8, 9, 11, 11, 12, 12, 13, 13, 14, 15, 17
Шаг 3 : Рассчитайте среднее значение оставшихся значений.
20% усеченное среднее = (8+8+9+11+11+12+12+13+13+14+15+17) / 12 = 11,9167
Среднее значение, усеченное на 20%, составляет 11,9167 .
Бонусный ресурс: Калькулятор усеченного среднего
Если у вас очень большой набор данных и вы не хотите вычислять усеченное среднее вручную, не стесняйтесь использовать этот калькулятор усеченного среднего.
Например, вот как использовать этот калькулятор, чтобы найти усеченное на 20% среднее значение из предыдущего набора данных:

Обратите внимание, что усеченное на 20 % среднее соответствует значению, рассчитанному нами вручную.
