Как найти ударную нагрузку - Сайт, где вы сможете решить свои вопросы

Ударом
обычно называют такое явление, при
котором скорости ударяемого тела и
ударяющего тела за короткий промежуток
времени изменяются до конечной величины.
Точная теория удара связана с изучением
местных деформаций в окрестности
контакта (контактная задача теории
упругости), а также
с явлением волнового
распространения деформации в упругом
теле и оказывается довольно сложной
задачей.

В данном пособии
рассматривается инженерная теория
удара. Расчетные формулы получают,
применив закон сохранения энергии. Эта
теория является приближенной, она
строится на следующих допущениях:

1) напряжения при
ударе не превосходят предела
пропорциональности, свойства материала
не изменяются, поэтому закон Гука при
ударе остается в силе;

2) соударяющиеся
тела после удара не отделяются друг от
друг;

3) масса ударяемого
тела считается пренебрежимо малой по
сравнению с массой ударяющего тела;

4) вся энергия
удара переходит в потенциальную энергию
деформации ударяемого тела, потеря
части энергии пренебрежимо мала.

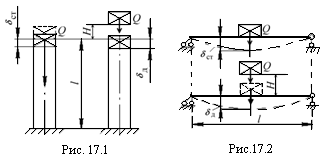
17.1. Вертикальный удар

Обозначив
кинетическую энергию падающего груза
Q
через Т,
и учитывая, что она равна изменению
потенциальной энергии груза, можно
записать:

(17.1)

где Н
– высота падения груза до соприкосновения
с ударяемым телом;
– динамическое перемещение точки
соударения при ударном приложении
нагрузкис высотыН.

Динамическая
деформация может быть выражена через
статическую формулой

(17.2)

где
– статическое перемещение той же точки
ударяемого тела при статическом
приложении силы.

Потенциальная
энергия деформации стержня, накопленная
при ударе, может быть выражена формулой

(17.3)

где
с
называется жесткостью
стержня.

На основании
закона сохранения энергии при принятых
допущениях справедливо равенство

или
(17.4)

Решая уравнение
(16.4) относительно деформаций
получим наибольший корень:

(17.5)

Таким образом, в
соответствии с зависимостью (17.2) находим
коэффициент динамический:

(17.6)

Учитывая, что
,
(– скорость падающего груза
в начале
удара), получим:

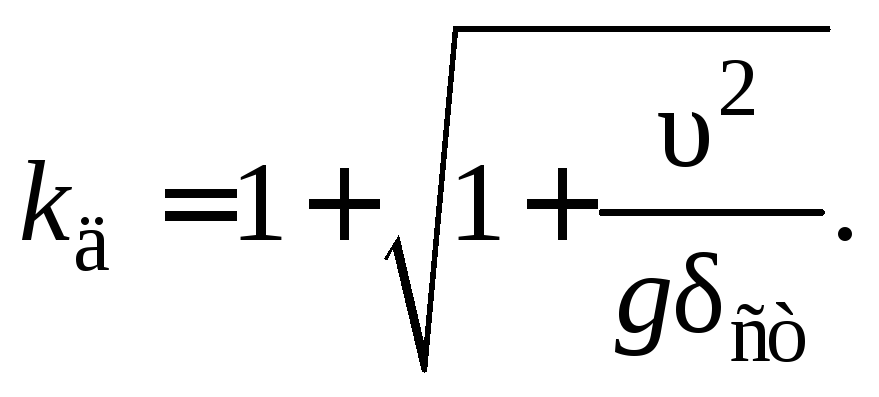(17.7)

Так как
где– кинетическая энергия падающего груза
к моменту соударения;потенциальная энергия деформации
стержня при статическом приложении
нагрузкикоэффициент динамичности можно также
выразить формулой

(17.8)

Если Н
= 0 (внезапный
удар), то

Поскольку
обычно
то в выражении (16.8) можно пренебречь
единицей под корнем, получая следующие
формулы:

(17.9)

или

(17.10)

Учитывая линейную
связь между напряжением и деформацией,
а также принимая одинаковыми модули
упругости при статическом и ударном
действии нагрузки, по аналогии с формулой
(16.2) можно записать связь между статическим
и динамическим напряжениями:

(17.11)

где
– напряжение, возникающее в стержне
при действии силой, равной весу падающего
груза.

Динамическая
нагрузка при ударе равна

(17.12)

16.2. Горизонтальный удар

Кинетическая
энергия движущегося груза

(17.13)

После того как
груз коснется ударяемого тела, скорость
его начнет уменьшаться. Когда вся
кинетическая энергия груза перейдет
в потенциальную энергию деформации
ударяемого тела, груз остановится, а
перемещение
точки удара будем максимальным.
Потенциальная энергия деформации

(17.14)

Приравнивая
кинетическую энергию движущегося груза
потенциальной энергии деформации
ударяемого тела и учитывая, что
,
получим

(17.15)

откуда
.

Умножив в подкоренном
выражении зависимости (16.15) числитель
и знаменатель на ускорение свободного
падения, получим

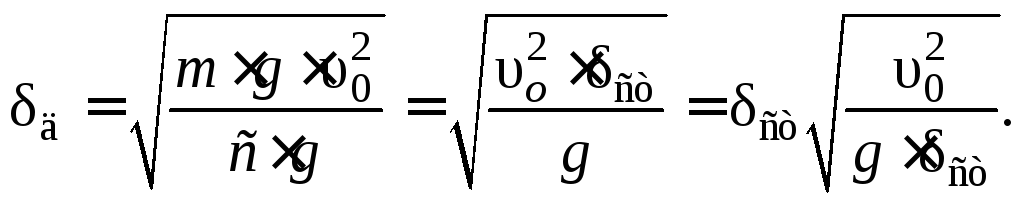(17.16)

Следовательно,
коэффициент динамический

(17.17)

Формула (17.17)
аналогична формуле (17.7).

Динамическое
напряжение и динамическая нагрузка
определяются по тем же формулам, что и
при вертикальном ударе,

Учет массы
ударяемого тела

С учетом массы
ударяемого тела коэффициент динамический
может быть записан в следующем виде:

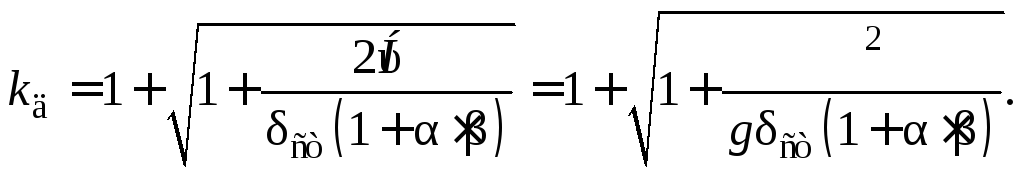(17.18)

где Q_с
– вес ударяемого тела; Q
– вес ударяющего элемента;

– коэффициент приведения массы
ударяемого тела.

Этот коэффициент
имеет для каждого конкретного случая
свое значение, данные по ним приводятся
в справочных таблицах по сопротивлению
материалов. Так,

при продольном
ударе о стержень постоянного поперечного
сечения
;
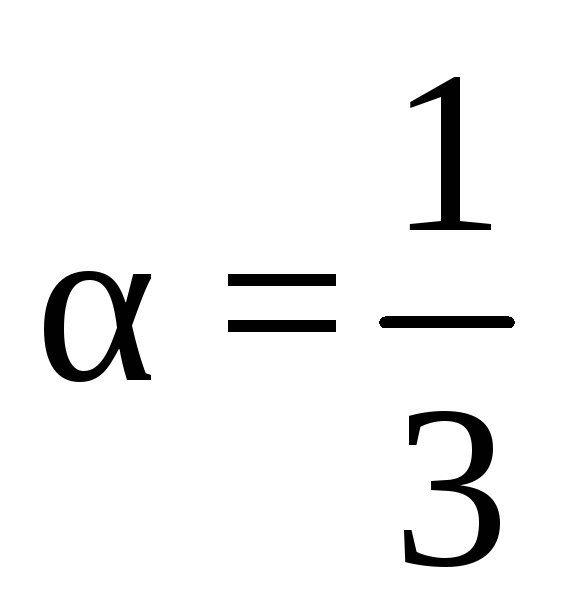при грузе, падающем
на середину двухопорной статически
определенной балки,
;
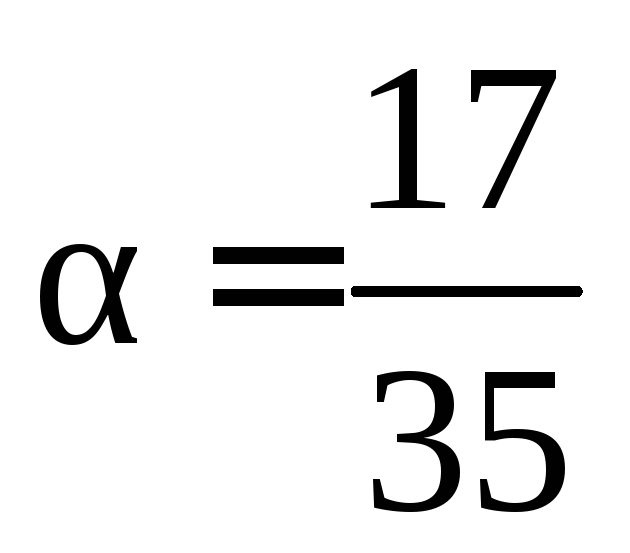на конце консольной
балки
.

Учет
массы ударяемого тела приводит к
повышению точности расчета, а
соответственно – и к снижению расхода
материала, т.к. коэффициент динамический
при учете этого фактора снижается.

Рекомендации
по снижению динамических
напряжений
при ударе

Снижение напряжений
при ударе может быть достигнуто
следующими путями:

1) увеличением
объема материала, подвергаемого удару
упругого стержня постоянного сечения;

2) в стержне с
выточкой эффект может быть получен за
счет уменьшения площади утолщенной
части и увеличения тем самым деформативности
стержня; этой же цели можно добиться,
взяв материал с более низким модулем
упругости;

3) увеличением
длины стержня;

4) применением
буферных пружин, различных податливых
прокладок на шарнирно подвижных опорах.

Ударная вязкость

Ударной вязкостью
материала
а_кназывается
величина работы разрушения образца,
отнесенная к площади его поперечного
сечения в месте надреза.

Для оценки
способности материала сопротивляться
ударным нагрузкам применяют особый
вид испытаний ударным изгибом –
определение ударной вязкости надрезанных
образцов. Эти испытания проводят на
маятниковых копрах.

Испытания
позволяют оценить особое качество
металла – его склонность к хрупкости
при динамических нагрузках в условиях
сложного напряженного состояния в
области надреза и решить вопрос о
применимости того или иного материала
для данных условий работы. Именно в
таких условиях работают многие детали
машин, имеющие отверстия, канавки для
шпонок и т.д.

На ударную вязкость
сталей, например, сильное влияние
оказывают температура, структура,
химические добавки и другие факторы.
При снижении температуры ударная
вязкость уменьшается. При этом существует
интервал температуры, называемый
критическим, когда ударная вязкость
снижается особенно быстро. Ударная
вязкость для сталей одной и той же
плавки с мелкозернистой структурой
значительно выше, чем
с крупнозернистой.

Ударная хрупкость
может появляться и при повышенных
температурах. Например, ударная вязкость
углеродистых сталей значительно
снижается в интервале температур
200–550 °С.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Shock load is the term used to describe the sudden force exerted when an object suddenly accelerates or decelerates, such as when a falling object hits the ground, a fastball strikes a catcher’s glove or a diver begins to leap off a diving board. This force is exerted on both the moving object and the object being acted on. Determining shock load can be very important in a variety of safety-related situations, for example, determining the effectiveness of a safety harness or the wire lanyard attached to it. Most harness lanyards are made to withstand a certain amount of force, and you can calculate the shock load for a falling object attached to a somewhat elastic wire rope.

Determining Shock Load

Write down the equation to determine shock load in pounds: shock load = load x [1 + (1 + (2 x FD x A x E)/(load x L))^1/2].

Plug in the values in the following example: load = 200 pounds, falling distance = 12 inches, area factor = 0.472, diameter of rope = 0.25 inches, metallic area = 0.0295 inches^2, modulus of elasticity = 15,000,000 pounds per square inch, and length of cord = 10 feet (120 inches). Therefore, in this example, shock load = 200 x [1 + (1 + (2 x 12 x 0.0295 x 15,000,000)/(200 x 120))^1/2].

Calculate the numerator then the denominator separately, as per the order of operations. So in this example, the equation simplifies to shock load = 200 x [1 + (1 + (10,620,000)/(24,000))^1/2].

Divide the numerator by the denominator, as per the order of operations. So now you have shock load = 200 x [1 + (1 + 442.5)^1/2]. Add 442.5 to 1 within the parentheses to get shock load = 200 x [1 + (443.5)^1/2].

Take the square root of 443.5 and then add 1 to perform the calculations within the brackets and get shock load = 200 x 22.059.

Multiply for the final result: shock load = 4,411.88 pounds.

Things You’ll Need

Calculating shock load for an elastic wire requires knowing several factors:
Weight of the object in pounds (load)
Falling distance in inches (FD)
Length of the cord in feet (L)
Modulus of elasticity (E) = 11,500,00 pounds per square inch (new rope) or 15,000,000 pounds per square inch (stretched rope)
Area factor of rope (area factor)—each particular kind of rope has an associated area factor
Metallic area of the rope (A) = diameter of the rope in inches x diameter of the rope in inches x area factor

Tips

Area factors for wire ropes typically range from around 0.35 to over 0.55.

Warnings

Safety harnesses should be checked regularly for damage and replaced as necessary.

Источник

Расчет ударных
нагрузок онлайн

Динамические явления характеризуются прежде всего наличием инерционных сил при движении элементов конструкций, сравнимых по значению с вешними нагрузками на систему, а так же переменных во времени таких характеристик как скорость, ускорение, нагрузки и деформации.

Анализ динамических систем всегда сложнее статических расчетов. Это связано с зависимостью внешних воздействий от реакции системы, а так же свойств самой системы от характеристик движения. Так же сложности возникают в результате того, что при построении математической модели часто невозможно заранее определить наиболее существенные свойства системы.

В машиностроении ударные нагрузки при эксплуатации часто являются определяющими, либо имеют периодический характер, либо являются следствием аварий и работы в нештатном режиме. Основной признак ударных нагрузок – кратковременность воздействия на конструкцию.

Во время удара происходит резкое изменение скоростей точек системы, а так же кратковременно возникают большие усилия. С точки зрения механики энергия удара обеспечивает возможность многократного увеличения нагрузки, действующей на конструкцию при малых перемещениях.

Условием возникновения удара является наличие относительной скорости взаимодействующих тел, в результате чего происходит обмен импульсами и энергией. При этом возникают местные деформации и напряжения, распространяющиеся волной со звуковой или сверхзвуковой скоростью.

В настоящее время задачи динамики решаются преимущественно методом конечных элементов. Воспользовавшись нашим онлайн расчетом можно рассчитать ударные нагрузки, перемещения и время соударения стержней, балок и наиболее распространенной общей вязко-упругой модели.

Расчет удара по стержню

Масса подвижного элемента m₁, кг

Площадь сечения стержня S, м²

Длина стержня L, м

Масса стержня m, кг

Модуль упругости стержня Е, Па

Высота H, м

Начальная скорость W₀, м/с

Учитывать силу тяжести

Напряжения в стержне σ, МПа

Перемещения в точке удара Х, мм

www.caetec.ru

©Copyright Кайтек 2020

Жесткость стержня:
k = E×S / L;
Перемещения точек стержня в зоне удара:
X = ((m1 + (1/3)×m)×W_0общ² / k)^1/2;
Сила удара:
P = k×X.

Расчет стержня при ударе о поверхность

Плотность материала стержня ρ, кг/м³

Модуль упругости стержня Е, Па

Начальная скорость W₀, м/с

Напряжения в стержне σ, МПа

www.caetec.ru

©Copyright Кайтек 2020

Скорость распространения звуковой волны:
с = (E / ρ)^1/2;
Деформации стержня:
ε = W₀ / c;
Напряжения в стержне:
σ = E×ε.

Расчет удара по защемленной балке

Масса подвижного элемента m₁, кг

Момент инерции балки I_x, м⁴

Длина балки L, мм

Расстояние точки удара от края балки a, мм

Масса балки m, кг

Модуль упругости балки Е, Па

Высота H, м

Начальная скорость W₀, м/с

Учитывать силу тяжести

Перемещения в точке удара Y, мм

www.caetec.ru

©Copyright Кайтек 2020

Перемещения точек балки в зоне удара:
X = ((m1 + (m×((3 + a/L – (a/L)²)/(140×(a/L)²×((1 – a/L)²)))))×W_0общ² / k)^1/2;
Сила удара:
P = k×X.

Расчет удара по шарнирно закрепленной балке

Масса подвижного элемента m₁, кг

Момент инерции балки I_x, м⁴

Длина балки L, мм

Расстояние точки удара от края балки a, мм

Масса балки m, кг

Модуль упругости балки Е, Па

Высота H, м

Начальная скорость W₀, м/с

Учитывать силу тяжести

Перемещения в точке удара Y, мм

www.caetec.ru

Перемещения точек балки в зоне удара:
X = ((m1 + ((2 + 4×(a/L) – (a/L)² – 6(a/L)³ + 3(a/L)⁴/(105(a/L)²×((1 – a/L)²)))×m)×W_0общ² / k)^1/2;
Сила удара:
P = k×X.

Расчет удара по консольной балке

Масса подвижного элемента m₁, кг

Момент инерции балки I_x, м⁴

Длина балки L, мм

Расстояние точки удара от края балки a, мм

Масса балки m, кг

Модуль упругости балки Е, Па

Высота H, м

Начальная скорость W₀, м/с

Учитывать силу тяжести

Перемещения в точке удара Y, мм

www.caetec.ru

Перемещения точек балки в зоне удара:
X = ((m1 + ((2 + 4×(a/L) – (a/L)² – 6(a/L)³ + 3(a/L)⁴/(105(a/L)²×((1 – a/L)²)))×m)×W_0общ² / k)^1/2;
Сила удара:
P = k×X.

Расчет вязкоупругой модели при ударе

Масса подвижного элемента m₁, кг

Начальная скорость подвижного элемента W₀, м/с

Жесткость конструкции К, Н/м

Коэффициент демпфирования конструкции b, Н*с/м

Приведенная масса конструкции m₂, кг

Максимальная нагрузка при ударе Р, H

Максимальное перемещения в точке удара Y, мм

www.caetec.ru

Максимальные перемещения конструкции:
X = ((m₁ + m₂)×(W_0общ²) / (b²/(m₁ + m₂)) + k)^1/2;
Нагрузки при максимальных перемещениях:
P = (W_0общ – (((X ²)×((b ²)/(m₁ + m₂) + k))/(m₁ + m₂))^1/2)×b + k×X.

©ООО”Кайтек”, 2020. Любое использование либо копирование материалов или подборки материалов сайта, может осуществляться лишь с разрешения автора (правообладателя) и только при наличии ссылки на сайт www.caetec.ru

Источник

Ударная нагрузка – это термин, используемый для описания внезапной силы, возникающей, когда объект внезапно ускоряется или замедляется, например, когда падающий объект падает на землю, фастбол ударяется в перчатку ловца или дайвер начинает прыгать с трамплина. Эта сила действует как на движущийся объект, так и на объект, на который воздействуют. Определение ударной нагрузки может быть очень важным в различных ситуациях, связанных с безопасностью, например, при определении эффективности ремня безопасности или привязанного к нему стропа. Большинство ремешков привязи выдерживают определенное усилие, и вы можете рассчитать ударную нагрузку для падающего предмета, прикрепленного к несколько упругому тросу.

Определение ударной нагрузки

Запишите уравнение для определения ударной нагрузки в фунтах: ударная нагрузка = нагрузка х.

Включите значения в следующем примере: нагрузка = 200 фунтов, расстояние падения = 12 дюймов, коэффициент площади = 0, 472, диаметр веревки = 0, 25 дюйма, металлическая площадь = 0, 0295 дюйма ^ 2, модуль упругости = 15 000 000 фунтов на квадратный дюйм, и длина шнура = 10 футов (120 дюймов). Поэтому в этом примере ударная нагрузка = 200 х.

Вычислите числитель, а затем знаменатель отдельно, согласно порядку операций. Таким образом, в этом примере уравнение упрощается до ударной нагрузки = 200 х.

Разделите числитель на знаменатель согласно порядку операций. Так что теперь у вас ударная нагрузка = 200 х. Добавьте 442, 5 к 1 в скобках, чтобы получить ударную нагрузку = 200 x.

Возьмите квадратный корень из 443, 5, а затем добавьте 1, чтобы выполнить вычисления в скобках, и получите ударную нагрузку = 200 х 22, 059.

Умножим на конечный результат: ударная нагрузка = 4 411, 88 фунтов.

подсказки

Коэффициенты площади для проволочных канатов обычно колеблются от 0, 35 до более 0, 55.

Предупреждения

Ремни безопасности следует регулярно проверять на наличие повреждений и при необходимости заменять.

Источник

На двутавровую балку (№ 20)длиной l=9м, свободно лежащую на двух жестких опорах , с высоты h=5 см падает груз Q=1200Н.

Требуется: найти наибольшее нормальное напряжение в балке и определить прогиб балки в месте падения груза.

1) Рассчитываем балку на действие статической нагрузки. Прикладываем силу Q и строим эпюру изгибающих моментов М_F. Для этого определяем реакции:

Максимальный момент будет равен:

2) В место падения груза прикладываем единичную силу и строим единичную эпюру (эпюру моментов от единичной нагрузки).

Максимальный момент будет равен:

3) Определяем максимальный прогиб балки в месте падения груза при статическом действии нагрузки по любому изученному методу определения перемещений. Например, по правилу Верещагина: