| Удельное электрическое сопротивление | |
|---|---|
 |
|
| Размерность |
СИ:L3MT-3I-2 СГС:T |
| Единицы измерения | |
| СИ | Ом·метр |
| СГС | с |
Уде́льное электри́ческое сопротивле́ние (удельное сопротивление) — физическая величина, характеризующая способность материала препятствовать прохождению электрического тока, выражается в Ом·метр. Удельное электрическое сопротивление принято обозначать греческой буквой ρ. Значение удельного сопротивления зависит от температуры в различных материалах по-разному: в проводниках, удельное электрическое сопротивление с повышением температуры возрастает, а в полупроводниках и диэлектриках — наоборот, уменьшается. Величина, учитывающая изменение электрического сопротивления от температуры называется температурный коэффициент удельного сопротивления. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле 
(при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется 
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единицы измерения[править | править код]
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м[1]. Из соотношения 
следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Зависимость от температуры[править | править код]
В проводниках удельное электрическое сопротивление увеличивается с увеличением температуры. Это объясняется тем, что с ростом температуры увеличивается интенсивность колебания атомов в узлах кристаллической решетки проводника, что препятствует движению свободных электронов[3].
В полупроводниках и диэлектриках удельное электрическое сопротивление уменьшается. Это объясняется тем, что с увеличением температуры увеличивается концентрация основных носителей заряда.
Величина, учитывающая изменение удельного электрического сопротивление от температуры называют температурным коэффициентом удельного сопротивления.
Обобщение понятия удельного сопротивления[править | править код]
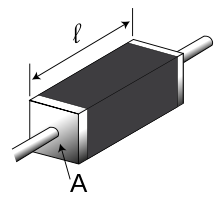
Кусок резистивного материала с электрическими контактами на обоих концах
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля 
и плотность тока 
в данной точке 
. Указанная связь выражается законом Ома в дифференциальной форме:
Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент 
. В анизотропном веществе векторы плотности тока и напряжённости электрического поля в каждой данной точке вещества не сонаправлены; связь между ними выражается соотношением
В анизотропном, но однородном веществе тензор от координат не зависит.
Тензор симметричен, то есть для любых 
и 
выполняется 
.
Как и для всякого симметричного тензора, для можно выбрать
ортогональную систему декартовых координат, в которых матрица становится диагональной, то есть приобретает вид, при котором из девяти компонент отличными от нуля являются лишь три: 
, 
и 
. В этом случае, обозначив 
как 
, вместо предыдущей формулы получаем более простую
Величины называют главными значениями тензора удельного сопротивления.
Связь с удельной проводимостью[править | править код]
В изотропных материалах связь между удельным сопротивлением и удельной проводимостью 
выражается равенством
В случае анизотропных материалов связь между компонентами тензора удельного сопротивления и тензора удельной проводимости 
имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:
Из этого равенства и приведённого ранее соотношения для 
следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
![rho _{{11}}={frac {1}{det(sigma )}}[sigma _{{22}}sigma _{{33}}-sigma _{{23}}sigma _{{32}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/08befe7409fd1685d379b9d3045f8b7d88b62e44)
![rho _{{12}}={frac {1}{det(sigma )}}[sigma _{{33}}sigma _{{12}}-sigma _{{13}}sigma _{{32}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/023c28c36a33abc59ec81a040eeeee5d6040e007)
где 
— определитель матрицы, составленной из компонент тензора . Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1, 2 и 3[4].
Удельное электрическое сопротивление некоторых веществ[править | править код]
Металлические монокристаллы[править | править код]
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[5].
| Кристалл | ρ1=ρ2, 10−8 Ом·м | ρ3, 10−8 Ом·м |
|---|---|---|
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике[править | править код]
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
|
|
Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества[править | править код]
| Вещество | ρ, Ом·мм²/м |
|---|---|
| Сжиженные углеводородные газы | 0,84⋅1010 |
Тонкие плёнки[править | править код]
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», 
Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W: 
где R — измеренное сопротивление. В общем случае, если форма образца отличается от прямоугольной, и поле в плёнке неоднородное, используют метод ван дер Пау.
См. также[править | править код]
- Электрическое сопротивление
- Сверхпроводимость
- Закон Ома
- Удельная проводимость
- Отрицательное сопротивление
- Импеданс
- Температурный коэффициент электрического сопротивления
Примечания[править | править код]
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
- ↑ Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд. — М.: Высшая школа, 1986. — 208 с.
- ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
- ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
Литература[править | править код]
- Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд., переработанное и дополненное. — М.: Высшая школа, 1986. — С. 6—7. — 208 с.
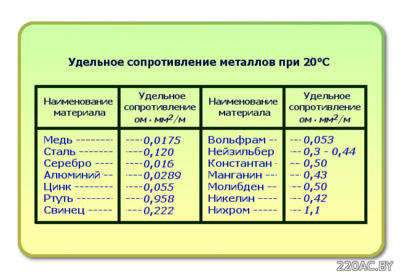
Приведенная ниже таблица удельного электрического сопротивления содержит значения удельного сопротивления для многих веществ, широко используемых в электрике и электронике. В частности, она включает в себя удельное сопротивление меди, алюминия, нихрома, стали, никеля и так далее.
Удельное электрическое сопротивление особенно важно, поскольку оно определяет электрические характеристики и, следовательно, пригодность материала для использования во многих электрических компонентах. Например, можно увидеть, что удельное сопротивление меди, удельное сопротивление алюминия, а также нихрома, никеля, серебра, золота и т.д. определяет, где эти металлы используются.
Для того чтобы сравнить способность различных материалов проводить электрический ток, используются показатели удельного сопротивления.
Что означают показатели удельного сопротивления?
Для того чтобы иметь возможность сравнивать удельное сопротивление различных материалов, от таких изделий, как медь и алюминий, до других металлов и веществ, включая висмут, латунь и даже полупроводники, необходимо использовать стандартное измерение.
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м.
Единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м2, изготовленный из этого вещества, имеет сопротивление, равное 1 Ом. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м2
[1]
Таблица удельного сопротивления для распространенных проводников
В таблице ниже приведены показатели удельного сопротивления для различных материалов, в частности металлов, используемых для электропроводности.
Показатели удельного сопротивления приведены для таких «популярных» материалов, как медь, алюминий, нихром, сталь, свинец, золото и других.
| Материал | Удельное сопротивление, ρ, при 20 °C (Ом·м) |
Источник |
|---|---|---|
| Латунь | ~0.6 — 0.9 x 10-7 | |
| Серебро | 1.59×10−8 | [3][4] |
| Медь | 1.68×10−8 | [5][6] |
| Обожжённая медь | 1.72×10−8 | [7] |
| Золото | 2.44×10−8 | [3] |
| Алюминий | 2.65×10−8 | [3] |
| Кальций | 3.36×10−8 | |
| Вольфрам | 5.60×10−8 | [3] |
| Цинк | 5.90×10−8 | |
| Кобальт | 6.24×10−8 | |
| Никель | 6.99×10−8 | |
| Рутений | 7.10×10−8 | |
| Литий | 9.28×10−8 | |
| Железо | 9.70×10−8 | [3] |
| Платина | 1.06×10−7 | [3] |
| Олово | 1.09×10−7 | |
| Тантал | 1.3×10−7 | |
| Галлий | 1.40×10−7 | |
| Ниобий | 1.40×10−7 | [8] |
| Углеродистая сталь (1010) | 1.43×10−7 | [9] |
| Свинец | 2.20×10−7 | [2][3] |
| Галинстан | 2.89×10−7 | [10] |
| Титан | 4.20×10−7 | |
| Электротехническая сталь | 4.60×10−7 | [11] |
| Манганин (сплав) | 4.82×10−7 | [2] |
| Константан (сплав) | 4.90×10−7 | [2] |
| Нержавеющая сталь | 6.90×10−7 | |
| Ртуть | 9.80×10−7 | [2] |
| Марганец | 1.44×10−6 | |
| Нихром (сплав) | 1.10×10−6 | [2][3] |
| Углерод (аморфный) | 5×10−4 — 8×10−4 | [3] |
| Углерод (графит) параллельно-базальная плоскость | 2.5×10−6 — 5.0×10−6 | |
| Углерод (графит) перпендикулярно-базальная плоскость | 3×10−3 | |
| Арсенид галлия | 10−3 to 108 | |
| Германий | 4.6×10−1 | [3][4] |
| Морская вода | 2.1×10−1 | |
| Вода в плавательном бассейне | 3.3×10−1 — 4.0×10−1 | |
| Питьевая вода | 2×101 — 2×103 | |
| Кремний | 2.3×103 | [2][3] |
| Древесина (влажная) | 103 — 104 | |
| Деионизированная вода | 1.8×105 | |
| Стекло | 1011 — 1015 | [3][4] |
| Углерод (алмаз) | 1012 | |
| Твердая резина | 1013 | [3] |
| Воздух | 109 — 1015 | |
| Древесина (сухая) | 1014 — 1016 | |
| Сера | 1015 | [3] |
| Плавленый кварц | 7.5×1017 | [3] |
| ПЭТ | 1021 | |
| Тефлон | 1023 — 1025 |
Видно, что удельное сопротивление меди и удельное сопротивление латуни оба низкие, и с учетом их стоимости, относительно серебра и золота, они становятся экономически эффективными материалами для использования для многих проводов. Удельное сопротивление меди и простота ее использования привели к тому, что она также используется крайне часто в качестве материала для проводников на печатных платах.
Изредка алюминий и особенно медь используются из-за их низкого удельного сопротивления. Большинство проводов, используемых в наши дни для межсоединений, изготовлены из меди, поскольку она обеспечивает низкий уровень удельного сопротивления при приемлемой стоимости.
Удельное сопротивление золота также важно, поскольку золото используется в некоторых критических областях, несмотря на его стоимость. Часто золотое покрытие встречается на высококачественных слаботочных разъемах, где оно обеспечивает самое низкое сопротивление контактов. Золотое покрытие очень тонкое, но даже в этом случае оно способно обеспечить требуемые характеристики разъемов.
Серебро имеет очень низкий уровень удельного сопротивления, но оно не так широко используется из-за его стоимости и из-за того, что оно тускнеет, что может привести к более высокому сопротивлению контактов.
Однако оно используется в некоторых катушках для радиопередатчиков, где низкое удельное электрическое сопротивление серебра снижает потери. При использовании в таких целях серебро обычно наносилось только на существующий медный провод. Покрытие провода серебром позволило значительно снизить затраты по сравнению с цельным серебряным проводом без существенного снижения производительности.
Другие материалы в таблице удельного электрического сопротивления могут не иметь такого очевидного применения. Тантал фигурирует в таблице, поскольку используется в конденсаторах — никель и палладий используются в торцевых соединениях многих компонентов поверхностного монтажа, таких как конденсаторы.
Кварц находит свое основное применение в качестве пьезоэлектрического резонансного элемента. Кварцевые кристаллы используются в качестве частотоопределяющих элементов во многих осцилляторах, где высокое значение Q позволяет создавать очень стабильные по частоте схемы. Аналогичным образом они используются в высокоэффективных фильтрах. Кварц имеет очень высокий уровень удельного сопротивления и не является хорошим проводником электричества, то есть его относят к категории диэлектрикам.
Список использованной литературы
- Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с.
- Giancoli, Douglas C., Physics, 4th Ed, Prentice Hall, (1995).
- Raymond A. Serway (1998). Principles of Physics (2nd ed.). Fort Worth, Texas; London: Saunders College.
- David Griffiths (1999) [1981]. «7 Electrodynamics». In Alison Reeves (ed.). Introduction to Electrodynamics (3rd ed.). Upper Saddle River, New Jersey.
- Matula, R.A. (1979). «Electrical resistivity of copper, gold, palladium, and silver». Journal of Physical and Chemical Reference Data.
- Douglas Giancoli (2009) [1984]. «25 Electric Currents and Resistance». In Jocelyn Phillips (ed.). Physics for Scientists and Engineers with Modern Physics (4th ed.). Upper Saddle River, New Jersey.
- «Copper wire tables». United States National Bureau of Standards. Retrieved 3 February 2014.
- https://www.plansee.com/en/materials/niobium.html
- AISI 1010 Steel, cold drawn. Matweb
- Karcher, Ch.; Kocourek, V. (December 2007). «Free-surface instabilities during electromagnetic shaping of liquid metals».
- «JFE steel» (PDF). Retrieved 2012-10-20.
Таблица удельных сопротивлений проводников. Таблица удельных сопротивлений металлов. Зависимость сопротивления металлов от температуры. Температурный коэффициент электрического сопротивления металлов α.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Зависимость сопротивления металлов от температуры. Температурный коэффициент сопротивления металлов.
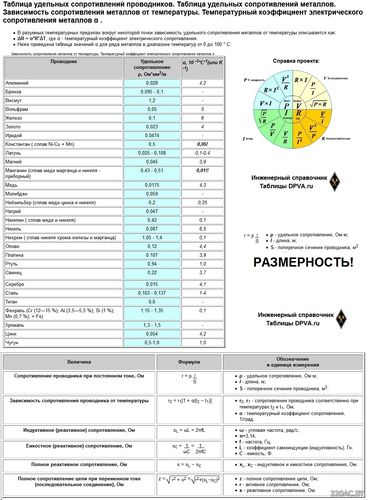
Нажмите на изображение чтобы увеличить.
Электрическое сопротивление
Электрическое сопротивление, одно из составляющих закона Ома, выражается в омах (Ом). Следует заметить, что электрическое сопротивление и удельное сопротивление — это не одно и то же. Удельное сопротивление является свойством материала, в то время как электрическое сопротивление — это свойство объекта.
Электрическое сопротивление резистора определяется сочетанием формы и удельным сопротивлением материала, из которого он сделан.
Например, проволочный резистор, изготовленный из длинной и тонкой проволоки имеет большее сопротивление, нежели резистор, сделанный из короткой и толстой проволоки того же металла.
В тоже время проволочный резистор, изготовленный из материала с высоким удельным сопротивлением, обладает большим электрическим сопротивлением, чем резистор, сделанный из материала с низким удельным сопротивлением. И все это не смотря на то, что оба резистора сделаны из проволоки одинаковой длины и диаметра.
В качестве наглядности можно провести аналогию с гидравлической системой, где вода прокачивается через трубы.
- Чем длиннее и тоньше труба, тем больше будет оказано сопротивление воде.
- Труба, заполненная песком, будет больше оказывать сопротивление воде, нежели труба без песка
Сопротивление провода
Величина сопротивления провода зависит от трех параметров: удельного сопротивления металла, длины и диаметра самого провода. Формула для расчета сопротивления провода:
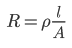
где:
R — сопротивление провода (Ом)
ρ — удельное сопротивление металла (Ом.m)
L — длина провода (м)
А — площадь поперечного сечения провода (м2)
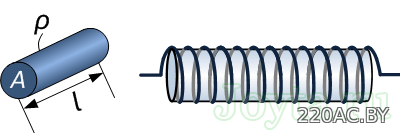
В качестве примера рассмотрим проволочный резистор из нихрома с удельным сопротивлением 1.10×10-6 Ом.м. Проволока имеет длину 1500 мм и диаметр 0,5 мм. На основе этих трех параметров рассчитаем сопротивление провода из нихрома:
R=1,1*10-6*(1,5/0,000000196) = 8,4 Ом
Нихром и константан часто используют в качестве материала для сопротивлений. Ниже в таблице вы можете посмотреть удельное сопротивление некоторых наиболее часто используемых металлов.
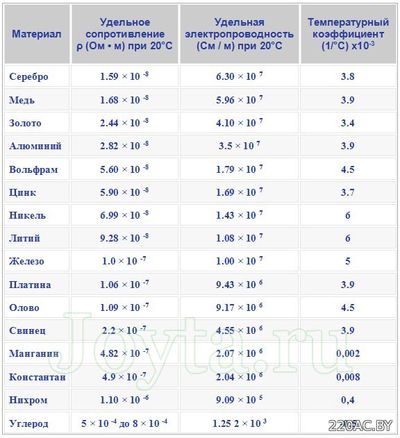
Свойства резистивных материалов
Удельное сопротивление металла зависит от температуры. Их значения приводится, как правило, для комнатной температуры (20°С). Изменение удельного сопротивления в результате изменения температуры характеризуется температурным коэффициентом.
Например, в термисторах (терморезисторах) это свойство используется для измерения температуры. С другой стороны, в точной электронике, это довольно нежелательный эффект.
Металлопленочные резисторы имеют отличные свойства температурной стабильности. Это достигается не только за счет низкого удельного сопротивления материала, но и за счет механической конструкции самого резистора.
Много различных материалов и сплавов используются в производстве резисторов. Нихром (сплав никеля и хрома), из-за его высокого удельного сопротивления и устойчивости к окислению при высоких температурах, часто используют в качестве материала для изготовления проволочных резисторов. Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко поддается пайке и имеет более низкий температурный коэффициент.
Источники: joyta.ru, dpva.ru
Для рассмотрения характеристик электрических параметров рассмотрим назначение приборов:
- сила тока в цепи определяется амперметров, который подключается последовательно с соблюдением полярности;
- напряжение на участке цепи измеряется вольтметром, который подключается параллельно к тому участку или прибору, на котором нужно узнать разность потенциалов или напряжения;
- на деревянной изолирующей подставке — устройство, имеющее провода с различными значениями сопротивления;
- значение тока можно регулировать реостатом.
Рис. (1). Цепь с возможностью выбора проводника
Определим физические параметры (величины), влияющие на значение сопротивления проводника.
Эксперимент (1). Физическая величина — длина (прямая пропорциональность).
Эксперимент (2). Физическая величина — площадь поперечного сечения (обратная пропорциональность).
Эксперимент (3). Материал проводника, физическая величина — удельное сопротивление проводника (прямая пропорциональность).
Примечание: «эксперимент» следует понимать как включение в электрическую цепь проводников с конкретными одинаковыми и различающимися физическими параметрами и сравнение значений сопротивлений данных проводников.
Впервые зависимость сопротивления проводника от вещества, из которого он изготовлен, и от длины проводника обнаружил немецкий физик Георг Ом. Он установил:
Сопротивление проводника напрямую зависит от его длины и материала, но обратным образом зависит от площади поперечного сечения проводника.
Обрати внимание!
Из этого можно сделать вывод: чем длиннее проводник, тем больше его электрическое сопротивление.
Сопротивление проводника обратно пропорционально площади его поперечного сечения, т.е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.
Чтобы лучше понять эту зависимость, представьте себе две пары сообщающихся сосудов, причём у одной пары сосудов соединяющая трубка тонкая, а у другой — толстая. Ясно, что при заполнении водой одного из сосудов (каждой пары) переход её в другой сосуд по толстой трубке произойдёт гораздо быстрее, чем по тонкой, т.е. толстая трубка окажет меньшее сопротивление течению воды. Точно так же и электрическому току легче пройти по толстому проводнику, чем по тонкому, т.е. первый оказывает ему меньшее сопротивление, чем второй.
Удельное сопротивление проводника зависит от строения вещества. Электроны при движении внутри металлов взаимодействуют с атомами (ионами), находящимися в узлах кристаллической решётки. Чем выше температура вещества, тем сильнее колеблются атомы и тем больше удельное сопротивление проводников.
Удельное электрическое сопротивление — физическая величина (rho), характеризующая свойство материала оказывать сопротивление прохождению электрического тока:
ρ=R⋅Sl
, где удельное сопротивление проводника обозначается греческой буквой (rho) (ро), (l) — длина проводника, (S) — площадь его поперечного сечения.
Определим единицу удельного сопротивления. Воспользуемся формулой
ρ=R⋅Sl
.
Как известно, единицей электрического сопротивления является (1) Ом, единицей площади поперечного сечения проводника — (1) м², а единицей длины проводника — (1) м. Подставляя в формулу, получаем:
, т.е. единицей удельного сопротивления будет
Ом⋅м
.
На практике (например, в магазине при продаже проводов) площадь поперечного сечения проводника измеряют в квадратных миллиметрах, В этом случае единицей удельного сопротивления будет:
, т.е.
Ом⋅мм2м
.
В таблице приведены значения удельного сопротивления некоторых веществ при (20) °С.
Удельное сопротивление увеличивается пропорционально температуре.
При нагревании колебания ионов металлов в узлах металлической решётки увеличиваются, поэтому свободного пространства для передвижения электронов становится меньше. Электроны чаще отбрасываются назад, поэтому значение тока уменьшается, а значение сопротивления увеличивается.
Обрати внимание!
Из всех металлов наименьшим удельным сопротивлением обладают серебро и медь. А это значит, что медь и серебро лучше остальных проводят электрический ток.
При проводке электрических цепей, например, в квартирах не используют серебро, т.к. это дорого. Зато используют медь и алюминий, так как эти вещества обладают малым удельным сопротивлением.
Порой необходимы приборы, сопротивление которых должно быть большим. В этом случаем необходимо использовать вещество или сплав с большим удельным сопротивлением. Например, нихром.
Полиэтилен, дерево, стекло и многие другие материалы отличаются очень большим удельным сопротивлением. Поэтому они не проводят электрический ток. Такие материалы называют диэлектриками или изоляторами.
Очень часто нам приходится изменять силу тока в цепи. Иногда мы ее увеличиваем, иногда уменьшаем. Водитель трамвая или троллейбуса изменяет силу тока в электродвигателе, тем самым увеличивая или уменьшая скорость транспорта.
Реостат — это резистор, значение сопротивления которого можно менять.
Реостаты используют в цепи для изменения значений силы тока и напряжения.
Реостат на рисунке состоит из провода с большим удельным сопротивлением (никелин, нихром), по которому передвигается подвижный контакт (C) по длине провода, плавно изменяя сопротивление реостата. Сопротивление такого реостата пропорционально длине провода между подвижным контактом (C) и неподвижным (A). Чем длиннее провод, тем больше сопротивление участка цепи и меньше сила тока. С помощью вольтметра и амперметра можно проследить эту зависимость.
Рис. (2). Реостат с подвижным контактом
На школьных лабораторных занятиях используют переменное сопротивление — ползунковый реостат.
Рис. (3). Ползунковый реостат
Он состоит из изолирующего керамического цилиндра, на который намотан провод с большим удельным сопротивлением. Витки проволоки должны быть изолированы друг от друга, поэтому либо проволоку обрабатывают графитом, либо оставляют на проволоке слой окалины. Сверху над проволочной обмоткой закреплен металлический стержень, по которому перемещается ползунок. Контакты ползунка плотно прижаты в виткам и при движении изолирующий слой графиты или окалины стирается, и тогда электрический ток может проходить от витков проволоки к ползунку, через него подводиться к стержню, имеющему на конце зажим (1).
Для соединения реостата в цепь используют зажим (1) и зажим (2). Ток, поступая через зажим (2), идёт по никелиновой проволоке и через ползунок подаётся на зажим (1). Перемещая ползунок от (2) к (1), можно увеличивать длину провода, в котором течёт ток, а значит, и сопротивление реостата.
В электрических схемах реостат изображается следующим образом:
Как и любой электрический прибор, реостат имеет допустимое значение силы тока, свыше которого прибор может перегореть. Маркировка реостата содержит диапазон его сопротивления и максимальное допустимое значение силы тока.
Обрати внимание!
Сопротивление реостата нужно учитывать в параметрах электрической цепи. При минимальных значениях сопротивления ток в цепи может вывести из строя амперметр.
Существуют реостаты, в которых переключатель подключается на проводники заданной длины и сопротивления: каждая спираль реостата имеет определённое сопротивление. Поэтому плавно изменять силу тока с помощью такого прибора не получится.
Рис. (4). Реостат с переключением
Сопротивление проводника:
R=ρ⋅lS
Из этой формулы можно выразить и другие величины:
Источники:
Рис. 1. Цепь с возможностью выбора проводника. © ЯКласс.
Рис. 4. “File:Rheostat hg.jpg” by Hannes Grobe (talk) is licensed under CC BY 3.0
Удельное сопротивление металлов
4.6
Средняя оценка: 4.6
Всего получено оценок: 274.
4.6
Средняя оценка: 4.6
Всего получено оценок: 274.
Величина удельного сопротивления характеризует способность вещества ограничивать электрический ток (оказывать сопротивление). Металлические проводники имеют самые низкие значения удельных сопротивлений, поэтому они используются и для передачи электроэнергии на большие расстояния, и в качестве соединительных проводов в электронных приборах, и соединительных дорожек на платах микросхем. Разберемся почему металлы обладают этим свойством и какие из них лучше всего подходят для этих целей.
Определение удельного сопротивления
Общая формула для вычисления удельного сопротивления ρ любого вещества выглядит следующим образом:
$ ρ = R * { S over L } $ (1),
где: R — сопротивление, S — площадь поперечного сечения, L — длина проводника. На основании экспериментальных данных, пользуясь законом Ома и этой формулой, определены удельные сопротивления большого числа материалов, которые приведены в справочниках и на специализированных интернет-ресурсах.
Единицы измерения удельного сопротивления
Из формулы (1) следует, что поскольку в Международной системе СИ сопротивление измеряется в омах, длина и площадь в метрах и метрах квадратных соответственно, то единицей измерения удельного сопротивления будет Ом*м:
$ [ρ] = {{[Oм]*[м^2]}over [м]} = [Oм]*[м] $ (2).
Для практических расчетов часто используется внесистемная единица Ом*мм2/м. Эта единица равна удельному сопротивлению вещества, из которого сделан проводник длиной 1 м и площадью поперечного сечения 1 мм2. Числовые значения для ρ становятся более комфортны для восприятия. Еще одна причина связана с тем, что величины сечений реальных проводов и кабелей составляют 1-10 мм2, и для вычисления их параметров внесистемная единица удобнее.
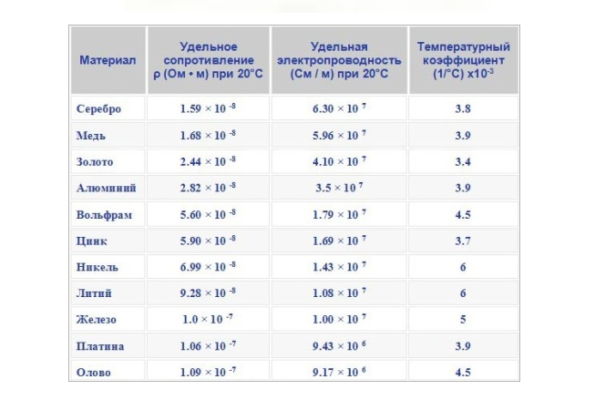
Почему у металлов самые низкие удельные сопротивления
Из приведенной таблицы видно, что самыми низкими значениями удельных сопротивлений обладают металлы: серебро, медь, золото, алюминий и др. Такое свойство металлов связано с большой концентрацией свободных электронов, “не привязанных” к конкретному атому, а блуждающих в пространстве кристаллической решетки. Напряжение, приложенное к концам проводника, создает электрическое поле, которое действует на электроны, заставляя их двигаться согласованно, в одном направлении.
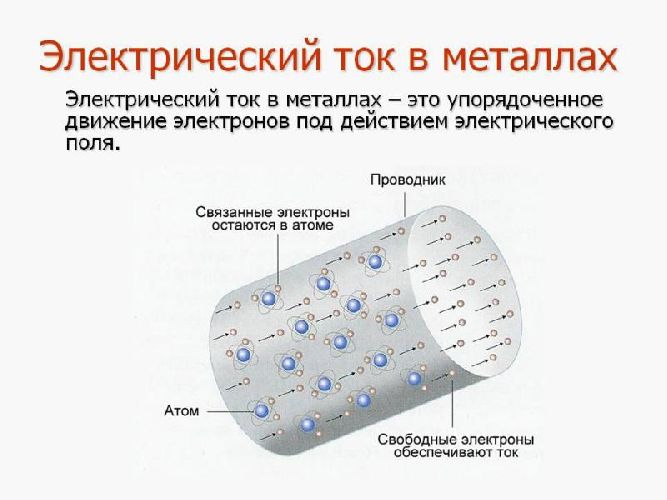
Самым низким значением ρ обладает серебро — 0,016 Ом*мм2/м. Но для повсеместного, массового, использования в сетях электроснабжения и оборудовании этот металл не используется в виду слишком большой цены. Серебро применяется для создания самых ответственных контактов в специальных электротехнических устройствах. В следующей таблице приведены величины удельных сопротивлений металлов и сплавов, часто используемых металлов в электротехнике:
Таблица
Удельные сопротивления металлов, Ом*мм2/м
(при Т = 200С)
|
Серебро |
0,016 |
Бронза (сплав) |
0,1 |
|
Медь |
0,017 |
Олово |
0,12 |
|
Золото |
0,024 |
Сталь (сплав) |
0,12 |
|
Алюминий |
0,028 |
Свинец |
0,21 |
|
Иридий |
0,047 |
Никелин (сплав) |
0,42 |
|
Молибден |
0,054 |
Манганин (сплав) |
0,45 |
|
Вольфрам |
0,055 |
Константан (сплав) |
0,48 |
|
Цинк |
0,06 |
Титан |
0,58 |
|
Латунь (сплав) |
0,071 |
Ртуть |
0,958 |
|
Никель |
0,087 |
Нихром (сплав) |
1,1 |
|
Платина |
0,1 |
Висмут |
1,2 |
Наиболее популярными в электротехнике являются медь и алюминий. Медь и медные сплавы применяются для изготовления кабельной продукции и шунтов — деталей, ограничивающих большие токи через измерительные приборы.
Влияние температуры на удельное сопротивление
В справочниках значения ρ металлов приводятся при комнатной температуре 200С. Но эксперименты показали, что зависимость ρ(Т) имеет линейный характер и описывается формулой:
$ ρ(Т) = ρ0 * (1 + α*T)$ (3),
где: ρ0 — удельное сопротивление проводника при температуре 00С, α — температурный коэффициент сопротивления, который тоже имеет тоже индивидуален для каждого вещества. Значения α, полученные опытным путем, можно узнать из справочников. Ниже приведены значения α для некоторых металлов:
- Серебро — 0,0035;
- Медь — 0,004;
- Алюминий — 0,004;
- Железо — 0,0066;
- Платина — 0,0032;
- Вольфрам — 0,0045.
Таким образом, при повышении температуры сопротивление металлов растет. Это объясняется тем, что с ростом температуры увеличивается число дефектов в кристаллической решетке из-за более интенсивных тепловых колебаний ионов, тормозящих электронный ток.
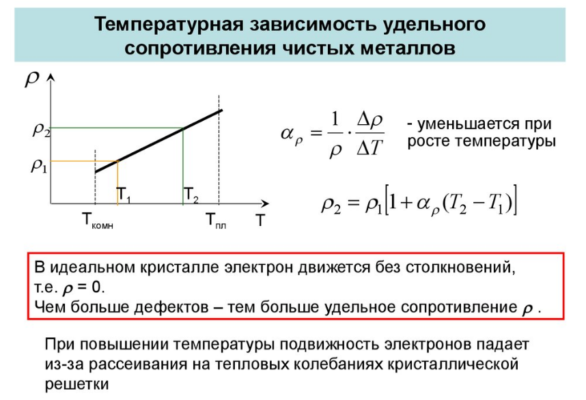
При приближении температуры металла к абсолютному нулю удельное сопротивление резко падает до нуля. Это явление называется сверхпроводимостью, а материалы, обнаруживающие такую способность, называются сверхпроводниками. Этот эффект открыл в 1911 г. голландский физик Камерлинг-Оннес. В его эксперименте удельное сопротивление ртути уменьшилось до нуля при 4,10К.
Что мы узнали?
Итак, мы узнали, что металлы обладают самыми низкими значениями удельного сопротивления среди проводников. Это свойство металлов используется для передачи электрической энергии с минимальными потерями. Алюминий, медь, сталь, серебро являются основными материалами для изготовления кабельной продукции. Удельное сопротивление металлов зависит от температуры. Таблица удельных сопротивлений металлов приведена для комнатной температуры — 200С.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 274.
А какая ваша оценка?
